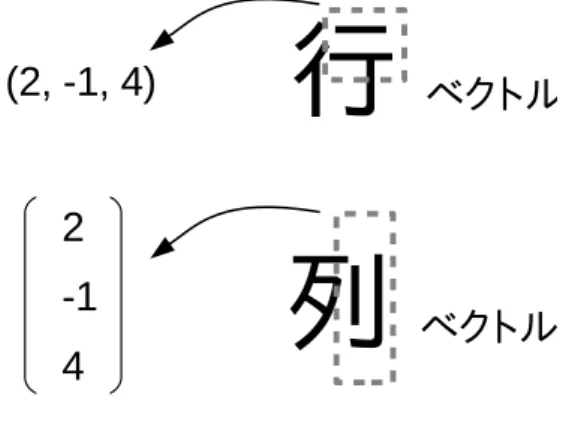
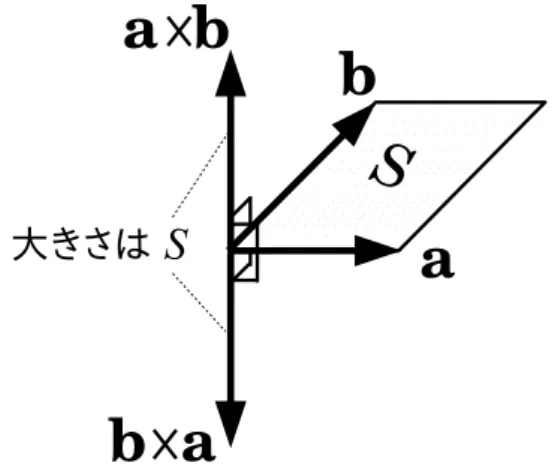
数学リメディアル教材
260
0
0
全文
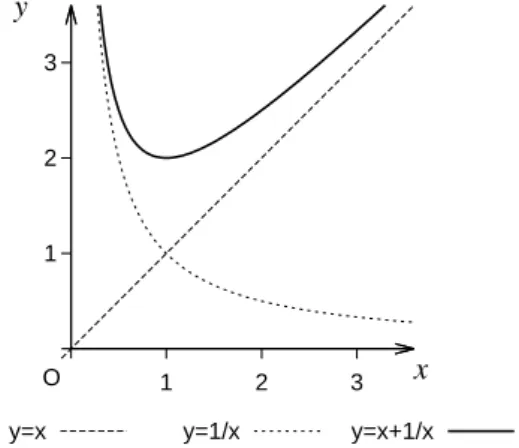
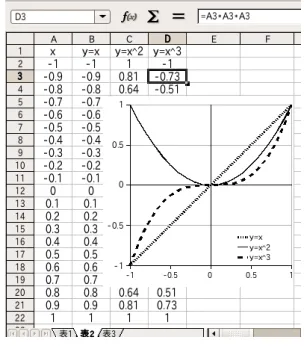
図
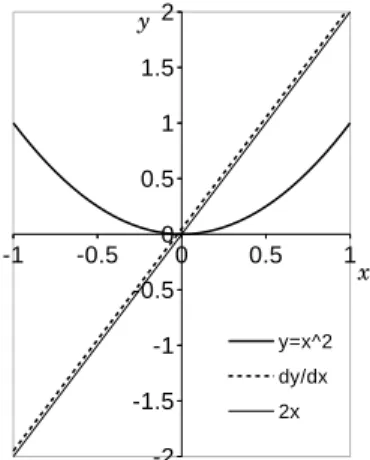
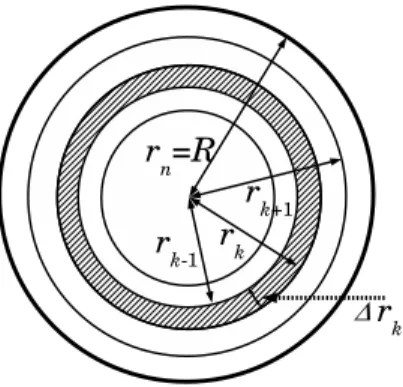
+3
関連したドキュメント
このような情念の側面を取り扱わないことには それなりの理由がある。しかし、リードもまた
ら。 自信がついたのと、新しい発見があった 空欄 あんまり… 近いから。
静岡大学 静岡キャンパス 静岡大学 浜松キャンパス 静岡県立大学 静岡県立大学短期大学部 東海大学 清水キャンパス
○齋藤部会長 ありがとうございました。..
○齋藤部会長 ありがとうございました。..
○安井会長 ありがとうございました。.
使用済自動車に搭載されているエアコンディショナーに冷媒としてフロン類が含まれている かどうかを確認する次の体制を記入してください。 (1又は2に○印をつけてください。 )
真竹は約 120 年ごとに一斉に花を咲かせ、枯れてしまう そうです。昭和 40 年代にこの開花があり、必要な量の竹