- γ 1929 γ - SI γ 137 Cs 662 kev γ NaI active target NaI γ NaI 2 NaI γ NaI(Tl) γ 2 NaI γ γ γ

学士論文

コンプトン散乱とクライン

-

仁科の公式

東京工業大学 理学部 物理学科

柴田研究室

矢澤 友貴孝

平成

28

年

2

月

15

日

概要

本研究の目的は、コンプトン散乱の微分断面積であるクライン-仁科の公式を理解する ことである。 γ 線の基本的な相互作用の一つにコンプトン散乱がある。コンプトン散乱は光子の粒 子としての性質を証明するものであり、コンプトンは 1929 年にノーベル物理学賞を受賞 した。様々な実験においてコンプトン散乱は γ 線検出に影響を与える現象として重要な 役割を果たしている。 本研究では、まずクライン-仁科の公式を量子電磁気学的に導出した。最低次の効果に ついて相互作用ハミルトニアンを始状態、終状態で挟み、電子と電磁場の部分に分けて 計算した。計算で得られた散乱振幅をトレース計算して微分断面積を求め、さらに SI 単 位系に直した。 次に実験によりコンプトン散乱の微分断面積および散乱後の γ 線エネルギーを測定し た。測定には、137_{Cs の線源からの 662 keV の γ 線を用いた。一つの NaI 検出器を active}

target として使い、この NaI 検出器の中の電子でコンプトン散乱した γ 線がもう一つの NaI 検出器で吸収される過程を 2 つの NaI 検出器の同時計測により検出した。この測定 によって得られた γ 線の計数から微分断面積を求め、理論式と比較した。エネルギーの 保存も検証した。 NaI(Tℓ) シンチレータは γ 線に対してプラスチックシンチレータより検出効率が高く、 エネルギー分解能もよい。そのため、短時間でより多くの計数を得られる。さらに、エ ネルギーの 2 次元プロットを用いて、正確な計数を決定できる。一方で、NaI 検出器内で の γ 線の減衰係数は高いためその影響を考慮に入れて測定結果を解析した。さらに、測 定される微分断面積の角度幅を小さくするために、γ 線を鉛プロックでコリメートした。 これにより最大の角度を見積もっても 10◦程度に角度幅を抑えることができた。角度分 布も調べると標準偏差としては 3–4◦程度の角度幅であることがわかった。 実験の結果、コンプトン散乱の微分断面積および γ 線のエネルギーはおよそ理論値と よい精度で一致していることが確かめられた。

目 次

第 1 章 序論 3 第 2 章 γ 線相互作用の基本的性質 5 2.1 断面積 . . . . 5 2.1.1 減衰を含まない場合の断面積 . . . . 5 2.1.2 微分断面積 . . . . 7 2.1.3 減衰を含む場合の断面積 . . . . 7 2.2 γ 線と物質の相互作用 . . . . 9 2.2.1 光電吸収 . . . . 9 2.2.2 コンプトン散乱 . . . . 9 2.2.3 電子対生成 . . . . 11 2.2.4 実際の物質中における γ 線の相互作用 . . . . 12 第 3 章 コンプトン散乱 15 3.1 コンプトン散乱における γ 線のエネルギー . . . . 15 3.2 クライン-仁科の公式の導出 . . . . 17 3.2.1 Dirac 方程式および場の量子化 . . . . 18 3.2.2 相対論的断面積 . . . . 22 3.2.3 行列要素M の計算 . . . . 28 第 4 章 実験で用いる装置 38 4.1 NaI(Tℓ) シンチレータ . . . . 38 4.1.1 シンチレーション検出器 . . . . 38 4.1.2 光電子増倍管 . . . . 39 4.1.3 NaI(Tℓ) シンチレータ検出器 . . . . 40 4.2 NIM/CAMAC モジュール . . . . 42 4.2.1 NIM モジュール . . . . 43 4.2.2 CAMAC モジュール . . . . 44 4.3 γ 線源 . . . . 45 4.3.1 原子核の崩壊 . . . . 45

4.3.2 137_{Cs . . . . 47} 4.3.3 22_{Na . . . . 48} 4.3.4 60_{Co . . . . 49} 第 5 章 実験の準備 50 5.1 同時計測の回路 . . . . 50 5.2 ADC のキャリブレーション . . . . 52 5.3 NaI(Tℓ) シンチレータの検出効率 . . . . 55 第 6 章 断面積およびエネルギーの測定 60 6.1 測定方法 . . . . 60 6.2 吸収断面積の測定 . . . . 60 6.2.1 NaI 検出器１つによる測定 . . . . 60 6.2.2 ルミノシティの計算 . . . . 65 6.2.3 吸収断面積の計算 . . . . 67 6.3 コンプトン散乱の微分断面積の測定 . . . . 69 6.3.1 γ 線のエネルギーの角度依存性 . . . . 69 6.3.2 同時計測の同時性 . . . . 78 6.3.3 微分断面積の角度依存性 . . . . 84 第 7 章 まとめ 97 付 録 A エネルギーの平均値 100 付 録 B 伝播関数 102 付 録 C ファインマンルールを使用した散乱振幅の導出法 105 付 録 D 放射線物質の崩壊図 107

第

1

章

序論

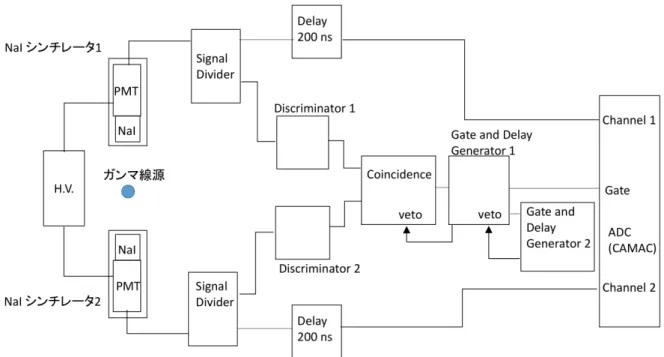
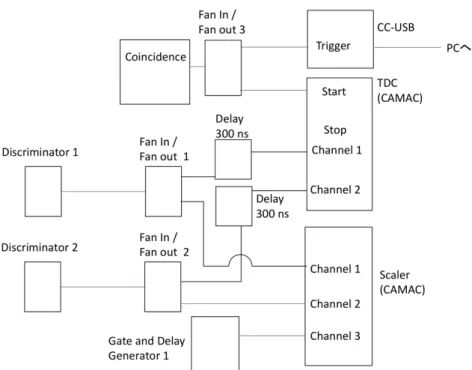
コンプトン効果は 1927 年にアーサー・コンプトンがその発見に対してノーベル賞を受 賞した現象である。コンプトン効果によって電磁波が粒子と同様の運動学に従うことが 実験的に確かめられた。さらに、1929 年にはクラインと仁科によってコンプトン散乱の 微分断面積であるクライン−仁科の公式が導かれた。クライン−仁科の公式は実験とよ く合うことが知られている。 コンプトン散乱は γ 線検出においても重要な役割を果たしており、特に一般に使用さ れる小型、中型の γ 線検出器ではエネルギースペクトルに大きな影響を及ぼす。本研究 ではコンプトン散乱の微分断面積であるクライン−仁科の公式を量子電磁力学的に導出 し、さらに NaI(Tℓ) シンチレータの同時計測法によって微分断面積を測定した。   本研究の目的は以下である。 1. γ 線と物質の基本的相互作用の理解 γ 線は物質と光電吸収、コンプトン散乱、電子対生成などによって相互作用する。 本研究では光電吸収とコンプトン散乱について実験で γ 線のシングルエネルギース ペクトルを見ることによって理解する。 2. コンプトン散乱への理解と微分断面積の導出 コンプトン散乱のファインマン・ダイアグラムを確かめ、散乱の最低次の項を計算 することによりコンプトン散乱への理解を深める。 3. 減衰を考慮した場合の断面積の導出 NaI(Tℓ) シンチレータは減衰係数が高いので、それを考慮に入れた断面積と収量の 関係式を導出する。 4. 同時計測法を利用した γ 線の断面積測定

片方の NaI 検出器を active target として用いることにより γ 線の散乱後のエネル ギーだけでなく反跳電子のエネルギーも知ることができる。このような同時計測法 の特色を活かし、実際の収量を決定する。

本論文の構成は以下のようである。第 2 章では γ 線計測における断面積および γ 線と 物質の相互作用について述べる。第 3 章ではコンプトン散乱における散乱された γ 線の エネルギーの運動学および微分断面積であるクライン−仁科の公式を導出する。第 4 章 では本研究の実験で使用する線源や検出器など装置とその性質を述べる。第 5 章では実 験の準備として本研究で使用する同時計測回路や検出器の較正について述べる。第 6 章 ではまず NaI 検出器 1 台だけを使用して吸収断面積を導出し、考察した。次に 1 台の NaI 検出器を active target としてもう 1 台の NaI 検出器と同時計測してコンプトン散乱の微 分断面積を測定した。第 7 章では本論文の内容をまとめる。

第

2

章

γ

線相互作用の基本的性質

2.1

断面積

この節では入射ビームと断面積および標的の関係を述べる。

2.1.1

減衰を含まない場合の断面積

図 2.1 のように、ビーム粒子が標的に入射し、その一部が反応する測定を考える。ここ で、I0は単位時間あたりに標的に入射する粒子数、A を標的の面積、n を標的の散乱中 心密度とする。この図を上流側 (x 軸の負の側) からみると、図 2.2 となる。 図 2.1: ビーム粒子と標的 散乱中心の個数 Ntは、 Nt= n· Ad

図 2.2: 標的の幾何学的断面積 で与えられる。図 2.2 からわかるように、各散乱中心が断面積 σtを張っていて、この断面 積内にビーム粒子が入ればビーム粒子は反応したことになる。この反応断面積の合計は、 σtNt= σtn· Ad である。ビームは標的内を微小な距離 d しか進まないので、まずはビームの減衰を考え ないものとする。その場合、標的内に入射したビーム粒子のうち反応する割合は、 σtn· Ad A = σtnd (2.1) とわかる。例えば、反応断面積の合計 σtNtが標的の面積 A と等しければ、この割合は 1 である。式 (2.1) からわかるようにビーム粒子の反応する割合は (入射するビーム粒子の 個数_{× 標的の面密度) で与えられ、ビームの幅に依存しない。したがって、単位時間あた} りに反応する粒子数 Nyは、 Ny = I0· (σtnd) (2.2) となる。 このように、断面積と反応する粒子数の関係式を導いたが、ここでいう断面積は散乱 中心がビーム粒子の必ず反応する断面積を張るという幾何学的描像に基づいていた。し かし、実際の物理において粒子の反応は相互作用による確率的事象であり、その断面積 は粒子の幾何学的広がりとは異なっている。そこで、得られた幾何学的断面積 σtの関係 式から実際に物理において考える反応断面積 σ を次のように定義する： σ≡ Ny I0nd 。 (2.3) この式 (2.3) において I0nd をルミノシティL と呼ぶ： L = I0nd 。 この値は (単位時間あたりのビーム粒子数× 標的の面密度) である。

2.1.2

微分断面積

標的内で粒子が反応するとその反応によって標的の外に出てきた粒子を測定できる。外 に出てきた粒子は図 2.3 のようにある立体角 ∆Ω の方向に放出される。ここで、立体角 図 2.3: 微分断面積 ∆Ω は、 ∆Ω = A2 l2 である。ある立体角の方向に放出される粒子の個数に関して微分断面積dσ dΩが次のように 定められる： Ny(∆Ω) = dσ dΩ∆ΩL 。

2.1.3

減衰を含む場合の断面積

今までは、ビームの減衰については考えていなかった。しかし、今回実験で用いる NaI(Tℓ) シンチレータは電子密度が大きいため γ 線の減衰の効果も考慮する必要がある。 そのために、断面積 σ と反応するビーム粒子数 Nyの減衰の効果を含んだ関係式を導出 する。 まず、図 2.4 のように、ビームが標的から距離 x まで進んだときのビームを調べる。単 位時間あたりに標的内で反応する粒子数 Nyは式 (2.2) で与えられていた。ゆえに、微小 な区間 dx を通過して減衰されるビーム−dI(x) は、 −dI(x) = σnI(x)dx となる。この微分方程式を解くと、 I(x) = I0e−σnx = I0e−µx

である。ここで、µ は減衰係数であり、次式を満たす： µ = σn 。 したがって、単位時間あたり反応する粒子数 Nyは、 図 2.4: ビーム粒子の減衰 Ny = σn ∫ d 0 dxI(x) = σnI0 ∫ d 0 e−µxdx = σn1− e −µd µ I0 (2.4) = (1− e−µd)I0 (2.5) とわかる。ここで、最後の式 (2.5) は σn = µ であることを使用している。しかし、一般に γ 線の減衰に関わる全断面積と考察している断面積とが一致しているとは限らない。そ のため、式 (2.4) の方が今後用いる一般式である。 式 (2.5) において標的の厚さ d を十分小さい厚さ dx と置き換えれば、 Ny = I0(1− e−µdx)≃ I0µdx = I0σndx となって、式 (2.2) と一致する。 ある立体角 ∆Ω に散乱される粒子数は、式 (2.4) において σ を dσ dΩ∆Ω と置き換えれば よい： Ny(∆Ω) = dσ dΩ∆Ωn 1− e−µd µ I0 。

2.2

γ

線と物質の相互作用

この節では、γ 線と物質が相互作用する主な過程である光電吸収、コンプトン散乱お よび電子対生成について述べる。

2.2.1

光電吸収

光電吸収過程では入射した光子と物質の原子が相互作用して、光子は全エネルギーを 失う。この際、光子は主に K 殻の電子と反応して、Ee−のエネルギーを電子に与えて叩 き出す (図 2.5)： Ee− = hν− Eb 。 ここで、Ebは反応した殻の電子の結合エネルギーである。一般に原子番号 Z の小さい物 質に対して Ebは数 keV、Z の大きい物質に対しても数十 keV 程度であることが知られて いる。 図 2.5: 光電吸収 光電吸収の断面積は物質の原子番号 Z5_{に比例することが知られている。K 殻電子によ} る寄与は L、M 殻などの寄与より大きく、K 殻を含むすべての殻による寄与は K 殻によ る寄与の 5/4 倍程度である。

2.2.2

コンプトン散乱

コンプトン散乱の詳細は 3 章で述べるので、ここでは運動学の概要のみを述べる。 コンプトン散乱は図 2.6 のように、光子が原子中の電子と相互作用して、エネルギーを 一部失う過程である。原子における電子の結合エネルギーに比べて大きなエネルギーの

γ 線の散乱なので、電子は自由電子で静止している、という近似が成り立つ。散乱された 光子のエネルギー hν′_は、 hν′ = hν 1 + _mhν ec2(1− cos θ) である。ただし、meは電子の質量で、hν は入射光子のエネルギー。 図 2.6: コンプトン散乱 反跳電子の運動エネルギー Ee−は、 Ee− = hν− hν 1 + _mhν ec2(1− cos θ) (2.6) である。散乱角 θ = π のとき反跳電子のエネルギーは最大となって、 Ee−(θ = π) = hν− hν 1 + 2_mhν ec2 (2.7) となる。式 (2.6) より反跳電子のエネルギーは Ee−(θ = 0) = 0 から式 (2.7) まで連続的な 値をとることがわかる。 コンプトン散乱の微分散乱断面積は後に示すようにクライン-仁科の公式によって与え られる： dσ dΩ = r2 e 2 [ 1 1 + α(1− cos θ) ]2[ 1 + cos2θ + α 2₍₁− cos θ)2 1 + α(1− cos θ) ] 。 ただし、reは古典的電子半径で、α = _mhν_ec2 である。クライン-仁科の公式は光子１個と電 子１個の微分散乱断面積である。全コンプトン断面積 σcはクライン-仁科の公式を立体角 について積分して、 σc= 2πre2 [ 1 + α α2 ( 2(1 + α) 1 + 2α − log(1 + 2α) α ) +log(1 + 2α) 2α − 1 + 3α (1 + 2α)2 ] (2.8) で与えられる。物質中でのコンプトン散乱が起こる割合はその物質の電子の個数すなわ ち物質の原子番号 Z に比例する。

2.2.3

電子対生成

電子対生成は図 2.7 のように入射した光子が原子核の電場の中で、電子-陽電子対を生 成する過程である。このとき光子は消滅する。生成された電子、陽電子の運動エネルギー Ee−、Ee+ は、 E_e−+ E_e+ = hν − 2m_ec2 を満たす。光子のエネルギーがおよそ 2mec2 = 1024 keV より大きくなければエネルギー 保存則の条件からこの過程は発生しない。 図 2.7: 電子対生成 図 2.8: 電子対生成のファインマン・ダイアグラム。 電子-陽電子対生成の反応断面積は近似的に物質の原子番号 Z の 2 乗に比例することが 知られている。図 2.8

は電子-陽電子対生成のファインマン・ダイアグラムである。電子-陽電子対生成はエネルギー・運動量保存則のため真空中では発生しない。しかし、物質 中では原子核の電場の影響を受けて対生成できる。この原子核の電場の大きさは原子番 号 Z に比例するため、図 2.8 の原子核の電場と電子または陽電子との vertex の行列要素 M への寄与は Z に比例する。したがって、反応断面積 σ は σ ∝ |M|2 _{∝ Z}2_{より Z}2_に比 例すると考えられる。

2.2.4

実際の物質中における

γ

線の相互作用

  実験を行う上で有用な γ 線と物質の相互作用の例として、ヨウ化ナトリウム (図 2.9) と 鉛 (図 2.10) の質量減衰係数および質量吸収係数を示す。質量減衰係数とは減衰係数 µ を 物質の密度 ρ で割った値である。質量吸収係数とは吸収係数 µ を物質の密度 ρ で割った 値である。このように記号 µ は両方の場合に使われるので、それを利用してまとめて書 くと、 質量減衰係数 (質量吸収係数) = µ ρ 。 物質の密度によって減衰係数ないし吸収係数 µ は変わるが、この式のように質量減衰係 数 (質量吸収係数) を新たに定義すると物質の状態によらず議論できる。 これらの図 2.9、2.10 をからわかるように、γ 線が低エネルギーのときは光電吸収、高 エネルギーのときは電子対生成、中間ではコンプトン散乱が主要な相互作用となる。実 際、ヨウ化ナトリウムの場合は、300 keV 程度までは光電吸収、300 keV–7 MeV 程度で はコンプトン散乱、7 MeV 以降は電子対生成が主要な過程である。 図 2.10 を使って鉛がどれだけ γ 線の入射を防げるかを調べられる。例えば、γ 線のエネ ルギーが 662 keV のとき質量減衰係数は 0.1 cm2_{/g 程度であるとわかる。鉛の密度 ρ} lead を 11.3 g/cm3_{、鉛の厚さを d =5 cm とする。このとき γ 線は、} e−µd= e−0.1·ρlead·d ≃= 0.0035 ≃ 0.4% にまで減衰される。

図 2.9: ヨウ化ナトリウム (NaI) の質量減衰係数および質量吸収係数 (文献 [1] 引用)。縦 軸は質量減衰係数 (質量吸収係数)(cm2_{/g)、横軸は γ 線のエネルギー (MeV) である。こ}

の図では Photo τ /ρ が光電吸収、Compton total σ/ρ がコンプトン散乱、Pair κ/ρ が電 子対生成による寄与である。全質量減衰係数は Total attenuation µ0/ρ であり、全部を足

したものであるから一番上の曲線である。全質量吸収係数は Total absorption µa/ρ であ り、ほとんど全質量減衰係数と同じである。ただし、コンプトン散乱の一部 (Compton

図 2.10: 鉛 (Pb) の質量減衰係数および質量吸収係数 (文献 [1] 引用)、軸および相互作用 は図 2.9 と同じ。

第

3

章

コンプトン散乱

この章では、1) コンプトン散乱の運動学を記述し、2) コンプトン散乱の微分断面積で あるクライン-仁科の公式を量子電磁気学に基いて導出する。

3.1

コンプトン散乱における

γ

線のエネルギー

コンプトン散乱における入射光子のエネルギー hν と散乱光子のエネルギー hν′および 反跳電子のエネルギー Ee−の関係式を導出する（図 3.1)。 図 3.1: コンプトン散乱における光子と電子の関係。入射する光子のエネルギーは hν、散 乱された光子のエネルギーは hν′、反跳電子のエネルギーは Ee−で表してある。 入射光子の方向およびそれに垂直な方向の運動量保存則およびエネルギー保存則より 以下の 3 式が成り立つ： hν c = hν′ c cos θ + γmevecos ϕ 、 (3.1) 0 = hν ′ c sin θ− γmevesin ϕ 、 (3.2) mec2+ hν = hν′+ γmec2 。 (3.3)

式 (3.1)、(3.2) より、 ( hν c − hν′ c cos θ )2 = (γmeve)2cos2ϕ ( hν c sin θ )2 = (γmeve)2sin2ϕ であるから、 ( h c )2 [(ν − ν′cos θ)2+ (ν′sin θ)2] = (γmeve)2 = γ2m2_ec2β_e2 = β 2 e 1− β2 e m2_ec2 (3.4) となる。一方、式 (3.3) より、 [mec2+ h(ν − ν′)]2 = 1 1− β2 e m2_ec4 1− β_e2 = m 2 ec4 [mec2+ h(ν − ν′)]2 β_e2 = 1− m 2 ec4 [mec2+ h(ν− ν′)]2 であるから、 β_e2 1− β2 e = 1 c2(2h(ν− ν ′_)m ec2+ (h(ν− ν′))2) (3.5) となる。これと、式 (3.4) より、 2h(ν − ν′)mec2+ (h(ν− ν′))2 = (hν)2− 2hνhν′cos θ + (hν′)2 を整理して、 mec2(E− E′) = 2hνhν′(1− cos θ) 。 ゆえに、散乱された光子のエネルギー hν′_は、 hν′ = _hν hν mec2(1− cos θ) + 1 (3.6) で与えられる。一方、反跳電子のエネルギー Ee−はエネルギー保存則より、 Ee− = hν − hν′ = hν− hν hν mec2(1− cos θ) + 1

とわかる。 入射光子のエネルギーが例えば 662 keV の場合の散乱された光子と反跳電子のエネル ギー依存性は図 3.2 となる。散乱された光子と反跳電子はそのエネルギーの和を求める と、入射光子のエネルギーを保存する。光子は角度 θ が小さいとほとんど反跳電子へエ ネルギーを渡さない。特に θ = 0◦では反跳電子へ渡すエネルギーは 0 である。一方、角 度 θ が大きいときは反跳電子へ多くエネルギーを渡すが、光子は最低でも 200 keV 程度 のエネルギーを保持する。 図 3.2: 入射光子のエネルギーが 662 keV の場合の散乱された光子と反跳電子のエネル ギーの散乱角依存性。散乱された光子と反跳電子はエネルギーの合計を求めると、入射 光子のエネルギーを保存する。光子は角度 θ が小さいとほとんど反跳電子へエネルギー を渡さない。特に θ = 0◦では反跳電子へ渡すエネルギーは 0 である。一方、角度 θ が大 きいときは反跳電子へ多くエネルギーを渡すが、光子は最低でも 200 keV 程度のエネル ギーを保持する。

3.2

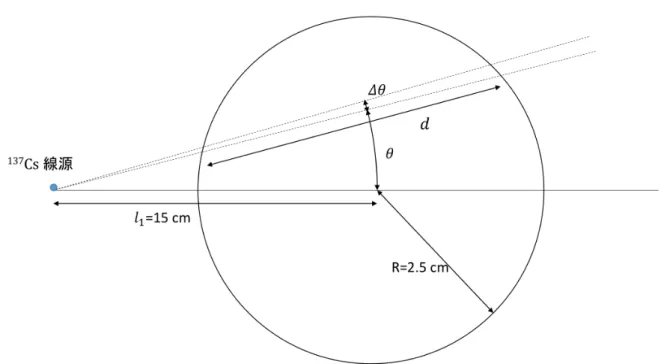
クライン

-

仁科の公式の導出

この節は文献 [2]、[3] を参照している。クライン−仁科の公式を量子電磁力学によって 導出する。3.2.1 節ではクライン−仁科の公式を導出するのに必要な γ 行列や場の量子化 の公式を示してある。3.2.2 節では断面積と散乱行列の関係性を示し、２体弾性散乱での 断面積を導出している。3.2.3 節では具体的にコンプトン散乱の行列要素M を計算して いる。

3.2.1

Dirac

方程式および場の量子化

Dirac 方程式は、 (pµγµ− m)ψ = (p/ − m)ψ = 0 (p/ = pµγµ) (3.7) である。Dirac 場 ψ について、 ¯ψ ≡ ψ†γ0_{を ψ の共役と呼ぶ。} Dirac 方程式の粒子、反粒子の平面波解をそれぞれ、ur(p), vr(p); (r = 1, 2) とすると、 その具体形は、 ur(p) = N ( χr σ·p E+mχr ) (3.8) vr(p) = N ( σ·p E+mχ3−r χ3−r ) (3.9) である。ただし、N は規格化定数で N =√E + m とする。χrはスピン固有関数であり、 次式で定義される： χ1 = ( 1 0 ) 、 χ2 = ( 0 1 ) 。 (3.10) σ はパウリ行列である。 Dirac 方程式の平面波解は次式を満たす： u†_r(p)us(p) = 2Eδrs = vr†(p)vs(p) 、 (3.11) u†_r(p)vs(p) = 0 = vr†us(p) 、 (3.12) ∑ r=1,2 ur(p)¯ur(p) = p/ + m 、 (3.13) ∑ r=1,2 vr(p)¯vr(p) = p/− m 。 (3.14) ここで、r, s はスピンに対応する。 一般にトレース内を分ける２つの行列は交換する： TrAB = TrBA 。 (3.15) ただし、A、B は行列。 γ 行列は次の反交換関係を満たす： {γµ , γν} = 2gµν 。 (3.16)

この交換関係を用いると γ 行列のトレース計算ができて、次の式が成り立つ： Tr[γµγν] = 4gµν 、 (3.17) Tr[γργσγαγβ] = 4(gρσgαβ + gρβgσα− gραgσβ) 、 (3.18) Tr[γµ1_γµ2_{. . . γ}µ2n−1 | {z } 奇数個 ] = 0 (n = 1, 2, . . . ) 。 (3.19) γ 行列は以下の性質を満たす： 㵆 = γ0γµγ0 。 (3.20) γ 行列をパウリ・ディラック表示で表すと、 γ0 = ( 1 0 0 −1 ) 、γ = ( 0 σ −σ 0 ) 。 (3.21) 電磁場の量子化 フォトンの 4 元運動量を kµ_{= (ω; k) とする。実フォトンの場合はアインシュタインの} 関係式 m2 _{= E}2_{− p}2_{と m = 0 より、} kµkµ= ω2− k2 = E2− p2 = 0 。 (3.22) フォトンの偏極ベクトル ϵ(k, λ) は実フォトンのとき横波成分のみ存在して、4 元運動量 kµ_{と次の関係式を満たす：} kµϵµ(k, λ) = 0 (λ = 1, 2) 。 (3.23) ただし、λ はフォトンの成分を示し、各横波成分では λ = 1, 2 とする。さらに、時間成分 (λ = 0) と縦波成分 (λ = 3) を定義して、直交性を ϵµ(λ)ϵµ(ρ) = gλρ (3.24) とする。 電磁場ポテンシャル Aµは次のように展開できる： Aµ = ∫ d3_k (2π)3_2ω ∑ λ [

ϵµ(k, λ)a(k, λ)e−ikx+ ϵµ∗(k, λ)a†(k, λ)eikx] 。 (3.25) ここで、ϵµ_{(k, λ) はフォトンの偏極ベクトル、a(k, λ), a}†_{(k, λ) はそれぞれ消滅・生成演算} 子である。消滅・生成演算子は以下の交換関係をみたす：

Dirac 場の量子化 Dirac 場は次のように展開できる: ψ = ∫ d3_p (2π)3_2E ∑ r [

aprur(p)e−ipx+ b†prvr(p)eipx ] 、 (3.27) ¯ ψ = ∫ d3_p (2π)3_2E ∑ r [

a†_pru¯r(p)eipx+ bprv¯r(p)e−ipx ] 。 (3.28) ここで、apr, a†prは粒子の消滅・生成演算子、bpr, b†prは反粒子の消滅・生成演算子である。 これらの生成消滅演算子には反交換関係が要求されていて、 {apr, a†qs} = (2π) 3_2Eδ3_{(p− q)δ} rs (3.29) {bpr, b†qs} = (2π)32Eδ3(p− q)δrs (3.30) を満たす。その他の反交換関係は 0 となる。 電子の伝播関数 電子の伝播関数は次式で定義される： iSF(x1− x2)≡ ⟨0|T (ψ(x1) ¯ψ(x2))|0⟩ (3.31) =    ⟨0|ψ(x1) ¯ψ(x2)|0⟩ t1 > t2 −⟨0| ¯ψ(x2)ψ(x1)|0⟩ t1 < t2 (3.32) ここで、T ( ) は時間の順序に関する演算子積である。

式 (3.11)、(3.12) および式 (3.13)、(3.14) を用いると、式 (3.32) は計算できて、 iSF(x1− x2) =⟨0| T ( ∫ d3_p (2π)3_2E ∑ r

(aprur(p)e−ipx1 + b†prvr(p)eipx1)

· ∫ d3_q (2π)3_2E ∑ s (a†_qsu(q)e¯ iqx2 _{+ b} qsv¯r(q)e−iqx2)|0⟩ =∑ r,s ⟨0| ∫ d3p (2π)3_2E ∫ d3q (2π)3_2E(apra †

qsur(p)¯us(q)eiqx2−ipx1 + b†prbqsvr(p)¯vs(q)eipx1−iqx2)|0⟩ θ(t1− t2)

−∑ r,s ⟨0| ∫ d3p (2π)3_2E ∫ d3q (2π)3_2E(a †

qsaprur(p)¯us(q)eiqx2−ipx1 + bqsbpr† vr(p)¯vs(q)eipx1−iqx2)|0⟩ θ(t2− t1)

=∑ r,s ⟨0| ∫ d3_p (2π)3_2E ∫ d3_q (2π)3_2E(apra †

qsur(p)¯us(q)eiqx2−ipx1)|0⟩ θ(t1− t2)

−∑ r,s ⟨0| ∫ d3_p (2π)3_2E ∫ d3_q (2π)3_2E(bqsb †

prvr(p)¯vs(q)eipx1−iqx2)|0⟩ θ(t2− t1) (∵ a |0⟩ = 0, b |0⟩ = 0)

= (2π)32Eδ3(p− q)δrs ∑ r,s ⟨0| ∫ d3_p (2π)3_2E ∫ d3_q (2π)3_2Eur(p)¯us(q)e iqx2−ipx1₎|0⟩ θ(t 1− t2) −∑ r,s ⟨0| ∫ d3_p (2π)3_2E ∫ d3_q (2π)3_2E(a †

qsaprur(p)¯us(q)eiqx2−ipx1)|0⟩ θ(t1− t2)

− (2π)3_2Eδ3_{(p− q)δ} rs ∑ r,s ⟨0| ∫ d3_p (2π)3_2E ∫ d3_q (2π)3_2E(vr(p)¯vs(q)e ipx1−iqx2₎|0⟩ θ(t 2− t1) +∑ r,s ⟨0| ∫ d3_p (2π)3_2E ∫ d3_q (2π)3_2E(b †

prbqsvr(p)¯vs(q)eipx1−iqx2)|0⟩ θ(t2− t1)

(∵ 式 (3.29), (3.30)) = ∫ d3_p (2π)3_2E( ∑ r

ur(p)¯ur(p)eipx2−ipx1θ(t1− t2)−

∑ r

vr(p)¯vr(p)eipx1−ipx2θ(t2− t1))

= ∫

d3_p

(2π)3_2E((p/ + m)e

ipx2−ipx1_θ(t

1− t2)− (p/ − m)eipx1−ipx2θ(t2− t1))

= i (2π)4 ∫ d4pe−ip(x1−x2) [ p / + m p2− m2_{+ iϵ} ] ここで、最後の式変形では Dirac 方程式の伝播関数に関する計算を使った。その計算は 付録 B で示している。

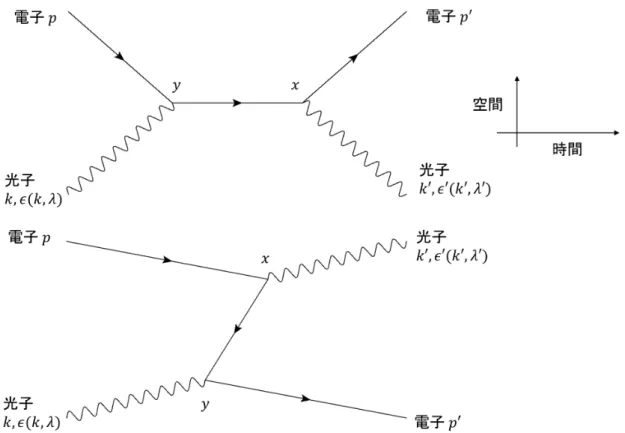
図 3.3: コンプトン散乱における２体弾性散乱。pµ_{はそれぞれの粒子の４元運動量を示す。}

3.2.2

相対論的断面積

2 体弾性散乱における断面積 断面積と行列要素_{M の関係は次式で与えられる：} dσ = |Mf i| 2 2E12E2v12 (2π)4δ4 ( p1+ p2− ∑ f pf ) ∏ f ( d3_p f (2π)3_2E f ) 。 (3.33) ただし、考えている系の体積は断面積に関して最終的には消えるので省いている。p1、p2 は始状態の粒子の四元運動量であり、pf は終状態の四元運動量である。E1、E2は始状態 の粒子のエネルギーであり、Ef は終状態のエネルギーである。v12は始状態の 2 つの粒 子の相対速度である。 図 3.3 のような２体弾性散乱の微分断面積を考える。実フォトンと電子の弾性散乱に よる断面積を考えるので、実フォトンの方は質量 m1 = m3 = 0 の条件をかけられる。ゆ えに、 E1 =| p1 |, E3 =| p3 | (3.34) である。また、始状態の電子は静止していると考えられるから、p₂ = 0。よって、 E2 = √ m2 2+ p22 = m2 (3.35) である。 まず、2E1E2v12は、 2E12E2v12 = 2E1E2 ( | p1 | E1 − | p2 | E2 ) (∵ | p | E = γmv γm = v, γはローレンツ因子) = 4E1m2 ( | p1 | E1 − | p2 | E2 ) (∵ 式 (3.35)) = 4E1m2| p 1 | E1 (∵ p₂ = 0) = 4m2 | p1 | .

よって、 1 2E12E2v12 (2π)4δ4 ( p1 + p2− ∑ f pf ) ∏ f ( d3pf (2π)3_2E f ) = 1 4m2 | p1 | (2π)4δ4 ( p1+ p2− ∑ f pf ) ∏ f ( d3_p f (2π)3_2E f ) = 1 4m2 | p1 | (2π)4δ (E1+ E2− E3− E4) δ3(p1+ p2 − p3− p4) ( d3_p 3 (2π)3_2E 3 ) ( d3_p 4 (2π)3_2E 4 ) = 1 4m2 | p1 | (2π)4δ (E1+ m2− E3− E4) δ3(p1− p3− p4) ( d3_p 3 (2π)3_2E 3 ) ( d3_p 4 (2π)3_2E 4 ) (3.36) この式を d3_p 4について積分すると、 1 4m2 | p1 | (2π)4δ (E1+ m2− E3− E4) ( d3_p 3 (2π)3_2E 3 ) ( 1 (2π)3_2E 4 ) (3.37) であり、p4 = p1− p3となる。そのため、E4は、 E4 = √ M2_{+ p}2 4 = √ M2_{+ (p} 1− p3)2. ここで、式 (3.37) を d3_p 3 =|p3|2d|p3|dΩ より d|p3| で積分するが、デルタ関数の中身が |p3| の関数であるから、次の公式を用いる： δ(f (x)) = 1 |f′_(x0)|δ(x− x0). (3.38) まず、デルタ関数の中身 E1+ m2− E3− E4について計算する： E1+ m2− E3− E4 = E1+ m2− E3− √ M2_{+ (p} 1− p3)2 = E1+ m2− |p3| − √ M2₊|p 1|2− 2|p1||p3| cos θ + |p3|2 より、 ∂(E1+ m2− E3− E4) ∂|p3| =−1 − −2|p1| cos θ + 2|p3| 2E4 =−E4+ E3− |p1cos θ E4 =−E2+ E1− |p1| cos θ E4 =−m2+|p1|(1 − cos θ) E4 . (3.39) ここで、p1− p3 = p4− p2と、

(p1− p3)2 =−2p1· p3 =−2(E1E3− |p1||p3| cos θ) = −2|p1||p3|(1 − cos θ)

(p4− p2)2 = p24+ p 2

より、 |p1|(1 − cos θ) = −m2 2+ E4m2 |p3| . (3.40) この式を式 (3.39) に代入して、 ∂(E1+ m2− E3− E4) ∂|p3| =−m2 |p3| − m2+ E4 E4|p3| =−m2 |p1| − m2+ m2 E4|p3| =−m2 |p1| E4|p3| . (3.41) 以上より、式 (3.37)、(3.38)、(3.41) を用いて、 dσ = 1 4m2 | p1 | (2π)4δ (E1+ m2− E3− E4) ( |p3|2d|p3|dΩ (2π)3_2E 3 ) ( 1 (2π)3_2E 4 ) = 1 4m2 | p1 | (2π)4_∂(E 1 1+m2−E3−E4) ∂|p3| ( |p3|2dΩ (2π)3_2E 3 ) ( 1 (2π)3_2E 4 ) = 1 16(2π)2_m 2 | p1 | E4|p3| m2|p1| ( |p3|2dΩ E3 ) ( 1 E4 ) = 1 64π2_m2 2 ( |p3| |p1| )2 dΩ (3.42) が示せた。 コンプトン散乱の散乱振幅 コンプトン散乱は光子と電子が散乱する反応である： γ + e→ γ + e 。 (3.43) この反応のファインマン・ダイアグラムは最低次で図 3.4 の２つである。片方は入射し た電子と光子が直接 vertex でつながっているのに対して、もう片方は光子が交叉して、 入射電子と散乱された光子とが vertex で結びついている。どちらのファインマン・ダイ アグラムでも２回クーロン力で散乱されているから、相互作用ハミルトニアンは、

HI(x)HI(y) = jµ(x)Aµ(x)jν(y)Aν(y) (3.44) となる。このことから散乱行列要素は次のようにかけることがわかる：

iTf i = Sf i− δf i =

(−ie)2

2! ∫

図 3.4: コンプトン散乱のファインマン・ダイアグラム。上のファインマン・ダイアグラ ムでは、電子が y 地点で光子を吸収し off-shell の電子として走った後に x 地点で光子を 放出する。下のファインマン・ダイアグラムでは、光子が y 地点で電子-陽電子対生成す る。この図では電子は on-shell、陽電子は off-shell で、x 地点で対消滅する。上のファイ ンマン・ダイアグラムの入射する光子と放出される光子が下のダイアグラムでは交叉し ている点が相違点である。

x, y の対称性より 2!が消える。さらに、フォトン部分と電子部分を分けると、 iTf i = (−i)2e2

∫

d4xd4y⟨f|T (jµ(x)Aµ(x)jν(y)Aν(y))|i⟩ (3.46)

= (−i)2e2

∫

d4xd4yT [⟨k′|Aµ(x)|0⟩⟨p′|jµ(x)jν|p⟩⟨0|Aν(y)|k⟩] (3.47) = (−i)2e2

∫

d4xd4yϵ′∗_µ(k′)⟨p′|T (jµ(x)jν(y))|p⟩ϵν(k)eik

′_x−iky . (3.48) 電磁場については、 ⟨0|Aν(y)|k⟩ = ⟨0| ∫ d3k1 (2π)3_2ω ∑ λ1 [ ϵν(k1, λ1)a(k1, λ1)e−ik1y+ ϵν∗(k1, λ1)a†(k1, λ1)eik1y ] |k, λ⟩ =⟨0| ∫ d3k1 (2π)3_2ω ∑ λ1 [ ϵν(k1, λ1)a(k1, λ1)e−ik1y ] a†(k, λ)|0⟩ (∵ ⟨0|a†= 0) =⟨0| ∫ d3k1 (2π)3_2ω ∑ λ1 [ ϵν(k1, λ1)e−ik1y ] (2π)32ωδ3(k1 − k)δλ1λ|0⟩ = ϵν(k, λ)e−iky さらに、電流密度 jµ_{= ¯ϕ(x)γ}µ_{ϕ(x) より、電子の部分は、}

⟨p′_{|T (j}µ_(x)jν_{(y)|p⟩ = ⟨p}′_{|T ( ¯ψ(x)γ}µ_{ψ(x) ¯ψ(y)γ}ν_{ψ(y))|p⟩ (3.49)} である。量子化された Dirac 場、式 (3.29)、(3.30) より ⟨p′_{| ¯ψ(x)γ}µ ψ(x) ¯ψ(y)γνψ(y)|p⟩ =⟨p′| ∫ d3_q′ 1 (2π)3_2E ∑ r1 (a†_q′ 1r1u¯r1(q ′ 1)e iq′₁x_{+ b} q′₁r1¯vr1(q ′ 1)e−iq ′ 1x)γµ ∫ d3_q′ 2 (2π)3_2E ∑ r2 (a_q′ 2r2ur2(q ′ 2)e iq₂′x_{+ b}† q′₂r2vr2(q ′ 2)e−iq ′ 2x) ∫ d3q1 (2π)3_2E ∑ s1 (a†_q1s1u¯s1(q1)e iq1y_{+ b} q1r1¯vs1(q1)e−iq 1y_)γν ∫ d3_q 2 (2π)3_2E ∑ s2 (aq2s2us2(q2)e iq2y_{+ b}† q2r2vs2(q2)e −iq2y₎|p⟩. _(3.50) この式は 16 個の項を持つが、そのうち残るのは⟨p′_|a†_aa†_{a|p⟩, ⟨p}′_|baa†_b†_{|p⟩ の項だけであ} る。その理由は、その他の項は消滅・生成演算子が_{|0⟩, ⟨0| に作用して消去されたり、散} 乱に寄与しない項であったりするからである。

残された項に関しては生成・消滅演算子の反交換関係を繰り返し用いると次のように 求められる。 ⟨p′_|a† q₁′r1aq2′r2a † q1s1aq2s2|p⟩ =⟨0|ap′ua†_q′ 1r1aq2′r2a † q1s1aq2s2a † pt|0⟩ = (2π)32Eδ3(p′ − q₁′)δur1⟨0|aq′2r2a † q1s1aq2s2a † pt|0⟩ − ⟨0|a†q′₁r1ap′uaq2′r2a † q1s1aq2s2a † pt|0⟩ = (2π)32Eδ3(p′ − q₁′)δur1⟨0|aq′2r2a † q1s1aq2s2a † pt|0⟩ = ((2π)32E)2δ3(p′− q₁′)δur1δ 3_(q 2− p)δs2t⟨0|aq2′r2a † q1s1|0⟩ = ((2π)32E)3δ3(p′− q₁′)δur1δ 3 (q2− p)δs2tδ 3 (q₂′ − q1)δr2s1 より、式 (3.50) に戻してデルタ関数を計算すると、 ∫ d3_q 1 (2π)3_2E ∑ s1 ¯ uu(p′)eip ′_x γµus1(q1)e −iq1x_u¯ s1(q1)e iq1y_γν_u t(p)e−ipy = ¯uu(p′)eip ′_x γµ ∫ d3q1 (2π)3_2E(q/ + m)e1 iq1(−x+y)_γν_u t(p)e−ipy (3.51) となる。同様に、 ⟨p′_|b q′1r1aq′2r2a † q1s1b † q2s2|p⟩ =⟨0|ap′ubq′₁r1aq′2r2a † q1s1b † q2s2a † pt|0⟩ =⟨0|bq₁′r1b † q2s2ap′uaq′2r2a † q1s1a † pt|0⟩ = (2π)32Eδ3(q₁′ − q2)δr1s2⟨0|ap′uaq2′r2a † q1s1a † pt|0⟩ = ((2π)32E)2δ3(q₁′ − q2)δr1s2δ 3_(q′ 2− q1)δr2s1⟨0|ap′ua † pt|0⟩ − (2π)3 2Eδ3(q′₁− q2)δr1s2⟨0|ap′ua † q1s1aq2′r2a † pt|0⟩ = ((2π)32E)3δ3(q₁′ − q2)δr1s2δ 3_(q′ 2− q1)δr2s1δ 3_(p′_{− p)δ} ut⟨0|0⟩ − ((2π)3 2E)3δ3(q₁′ − q2)δr1s2δ 3 (p′− q1)δus1δ 3 (q₂′ − p)δr2t⟨0|0⟩ = const.− ((2π)32E)3δ3(q₁′ − q2)δr1s2δ 3_(p′_{− q} 1)δus1δ 3_(q′ 2− p)δr2t⟨0|0⟩ → −((2π)3_2E)3_δ3_(q′ 1 − q2)δr1s2δ 3_(p′_{− q} 1)δus1δ 3_(q′ 2− p)δr2t より、 −¯uu(p′)eip ′_y γν(q2) ∫ d3q2 (2π)3_2E(−q/ + m)e2 −iq2(x−y)_γµ_u t(p)eipx (3.52) 式 (3.52) の T 積のもう一方は、x↔ y、µ ↔ ν すれば得られて、 −¯uu(p′)eip ′_x γµ(q2) ∫ d3_q 2 (2π)3_2E(−q/ + m)e2 −iq2(y−x)_γν_u t(p)eipy (3.53)

となる。式 (3.51) と式 (3.53) を合わせると、伝播関数の項となって、 ¯ uu(p′)eip ′_x γµ ∫ d3_q 1 (2π)3_2E(q/ + m)e1 iq1(−x+y)_γν_u t(p)e−ipyθ(tx− ty) − ¯uu(p′)eip ′_x γµ(q2) ∫ d3_q 2 (2π)3_2E(−q/ + m)e2 −iq2(y−x)_γν_u t(p)eipyθ(ty− tx) = ¯uu(p′)eip ′_x γµ ∫ d3_q 1 (2π)3_2E{(q/ + m)e1 iq1(−x+y)− (−q 1 / + m)eiq1(−y+x)}γν_u t(p)e−ipy = ¯uu(p′)eip ′_x γµ ∫ id4_q 1 (2π)4{ q1 / + m q2 1 − m2+ iϵ }γν_u t(p)e−ipy. したがって、片方のファインマン・ダイアグラムについては、 iTf i= (−i)2e2 ∫ d4xd4yϵ′∗_µ(k′)¯uu(p′)eip ′_x γµ ∫ id4q1 (2π)4{ q1 / + m q2 1− m2+ iϵ }γν_u

t(p)e−ipyϵν(k)eik

′_x−iky . = (2π)4δ4(k + p− k′− p′)(−i)2e2ϵ′∗_µ(k′)¯uu(p′)γµ{ i(p/ + k/ + m) (p + k)2− m2_{+ iϵ}}γ ν_u t(p)ϵν(k). である。ゆえに、散乱振幅は、 M1 = e2ϵ′∗µ(k′)¯uu(p′)γµ{ p / + k/ + m (p + k)2− m2_{+ iϵ}}γ ν_u t(p)ϵν(k). (3.54) である。もう一方のファインマン・ダイアグラムについても同様に計算すれば、 M2 = e2ϵν(k)¯uu(p′)γν{ p /− k/ + m′ (p− k′)2− m2_{+ iϵ}}γ µ_u t(p)ϵ′∗µ(k′).

3.2.3

行列要素

M

の計算

行列要素_{M を計算する。コンプトン散乱の全散乱振幅 M は、} M = M1+M2 = e2u¯s(p′) [ ϵ/′∗ (p/ + k/ + m) (p + k)2− m2ϵ/ + ϵ/ (p/− k/′+ m) (p− k′)2− m2ϵ/ ′∗ ] ur(p) (3.55) ここで、ϵ/ = ϵµγµ, k/ = kµγµである。 散乱前の電子の４元運動量を p = (m; 0)、散乱前、散乱後のフォトンの偏極ベクトルを 実粒子であるから横成分のみ考え、さらに成分を実数にとって、それぞれ ϵ = (0; ϵ), ϵ′ = (0; ϵ′) とする。

このとき、以下の式が成立する： ϵ· p = (0; ϵ) · (m; 0) = 0 (3.56) ϵ′· p = (0; ϵ′)· (m; 0) = 0 (3.57) ϵ· k = (0; ϵ) · (ω; k) = ϵ · k = 0 (3.58) ϵ′· k′ = (0; ϵ′)· (ω′; k′) = ϵ′· k′ = 0 (3.59) ϵ· (p′ + k′) = ϵ· (p + k) = ϵ · p + ϵ · k = 0 よりϵ· = −ϵ · k′ (3.60) ϵ′· (p′− k) = ϵ′· (p − k′) = ϵ′· p − ϵ′· k′ = 0 (3.61) ϵ· ϵ = ϵ′ · ϵ′ =−1 (∵ 横成分偏極ベクトル (λ = 1, 2) に式 (3.24) を適用)  . (3.62) このことから、 ϵ/p/ = ϵµγµpνγν = ϵµpν(2gµν− γνγµ) = ϵ· p − p/ϵ/ = −p/ϵ/ (3.63) ϵ′ / p/ = ϵ′_µγµpνγν = ϵ′µpν(2gµν− γνγµ) = ϵ′· p − p/ϵ/ =′ −p/ϵ/′ (3.64) ϵ/k/ = ϵµγµkνγν = ϵµkν(2gµν− γνγµ) = ϵ· k − k/ϵ/ = −k/ϵ/ (3.65) ϵ′ / k/ = ϵ′ ′_µγµk_ν′γν = ϵ′_µk′_ν(2gµν − γνγµ) = ϵ′ · k′ − k/ ϵ′/ =′ −k/ ϵ′/′ (3.66) が得られる。 p + k = p′ + k′より、 (p + k)2 = (p′+ k′)2 m2 + 2p· k + k2 = m2+ 2p′· k′+ k′2 p· k = p′ · k′ (∵ 式 (3.22)) (3.67) であり、p− k′ _{= p}′_{− k より、} (p + k′)2 = (p′− k)2 m2− 2p · k′+ k′2 = m2− 2p′· k + k2 p· k′ = p′ · k (∵ 式 (3.22)) (3.68) である。 式 (3.22) より、 (p + k)2− m2 = p2+ 2p· k + k2− m2 = 2p· k (3.69) (p− k′)2− m2 = p2 − 2p · k′+ k′2− m2 =−2p · k′ (3.70) であり、式 (3.63)、(3.64) より、

(p/ + m)ϵ/u(p) = (−ϵ/p/ + mϵ/)u(p) = −ϵ/(p/ − m)u(p) = 0 (3.71)

が成り立つから、全散乱振幅_{M は、} M = e2 ¯ ur(p′) [ ϵ/′k/ ϵ/ 2p· k + ϵ/k/′ϵ/′ 2k′· p ] us(p) (3.73) となる。式 (3.42) を用いて断面積を計算するから、スピンについて平均をとった全散乱 振幅の 2 乗を計算する： |M|2 ₌ e4 2 ∑ r,s ¯ ur(p′) [ ϵ/′k/ ϵ/ 2p· k + ϵ/k/′ϵ/′ 2k′ · p ] us(p) { ¯ ur(p′) [ ϵ/′k/ ϵ/ 2p· k + ϵ/k/′ϵ/′ 2k′· p ] us(p) }∗ (3.74) ここで、 {¯ur(p′)γµγνγρus(p)}∗ = us(p)∗γρ†γν†γµ†u¯r(p′)∗ = us(p)∗γ0γ0γρ†γ0γ0γν†γ0γ0㵆γ0ur(p′) (∵ (γ0)2 = 1 を挟んだ) = ¯us(p)(γ0γρ†γ0)(γ0γν†γ0)(γ0㵆γ0)ur(p′) = ¯us(p)γργνγµur(p′) (∵ 式 (3.20)) より、式 (3.74) は、 |M|2 ₌ e4 2 ∑ r,s ¯ ur(p′) [ ϵ/′k/ ϵ/ 2p· k + ϵ/k/′ϵ/′ 2k′ · p ] us(p)¯us(p) [ ϵ/k/ ϵ/′ 2p· k + ϵ′ / k/′ϵ/ 2k′· p ] ur(p′) = e 4 2Tr [ (p/ + m)′ { ϵ/′k/ ϵ/ 2p· k + ϵ/k/′ϵ/′ 2k′· p } (p/ + m) { ϵ/k/ ϵ/′ 2p· k + ϵ′ / k/′ϵ/ 2k′· p }] (∵ (3.13 式)) (3.75) となり、このトレースを計算すれば良い。 まず、k の２乗の項のトレースを計算する： Tr[(p/ + m)ϵ′ / k′/ ϵ/(p/ + m)ϵ/k/ϵ/ ]′ = Tr[p/ ϵ′/ k′/ ϵ/p/ϵ/k/ϵ/ ] + m′ 2Tr[ϵ/ k′/ ϵ/ϵ/k/ϵ/ ]′ (∵ m に比例する項は奇数個のγ行列のトレースであるから、式 (3.19) より 0) = Tr[p/ ϵ′/ ϵ/k′ /p/k/ ϵ/ϵ/ ] + m′ 2Tr[ϵ/ ϵ/k′ /k/ ϵ/ϵ/ ]′ (∵ 式 (3.65)) (3.76) m2に比例する第二項は、k/k/ がトレースに含まれているから 0 になる。実際、任意の行列 を A, B として、 Tr[Ak/k/B] = Tr[AkµγµkνγνB] = Tr[Akµkν(2gµν − γνγµ)B] (∵ 式 (3.15)) = 2kµkµTr[AB]− Tr[Ak/k/B] =−Tr[Ak/k/B] (∵ 式 (3.22)、kµkµ= 0)

より、 Tr[Ak/k/B] = 0 (3.77) である。式 (3.76) の第１項については、 k /p/ = 2k· p − p/k/ (3.78) より、 Tr[p/ ϵ′/ ϵ/k′ /p/k/ ϵ/ϵ/ ] = 2k′ · pTr[p/ ϵ′/ ϵ/k′ / ϵ/ϵ/ ] + Tr[p′ / ϵ′/ ϵ/p′ /k/k/ ϵ/ϵ/ ]′ = 2k· pTr[p/ ϵ′/ ϵ/k′ / ϵ/ϵ/ ]′ (∵ 式 (3.77)) = 2k· pTr[p/ ϵ′/ ϵ/(′ −ϵ/k/)ϵ/ ]′ (∵ 式 (3.65)) = 2k· pTr[p/ ϵ′/ k′/ϵ/ ]′ (∵ 式 (3.24) よりϵ/ϵ/ = 2ϵ · ϵ − ϵ/ϵ/ = −2 − ϵ/ϵ/だからϵ/ϵ/ = −1) = 2(k· p)p′_ρϵ′_σkαϵ′β4(g ρσ gαβ + gρβgσα− gραgσβ) (∵ 式 (3.18)) = 2(k· p)4{(p′· ϵ′)(k· ϵ′) + (p′· ϵ′)(ϵ′· k) − (p′· k)(ϵ′· ϵ′)} = 8(k· p){2(p′· ϵ′)(k· ϵ′) + (p′· k)} (∵ 式 (3.62)) = 8(k· p){2(k · ϵ′)2+ (p· k′)} (∵ 式 (3.60)). である。よって、まとめると、 Tr[(p/ + m)ϵ′ / k′/ ϵ/(p/ + m)ϵ/k/ϵ/ ] = 8(k′ · p){2(k · ϵ′)2+ (p′ · k)}. (3.79) 次に式 (3.75) の k′2の項について考えると、この項は第１項の k を k′に置き換えたも のに等しい。実際、 Tr[ϵ/k/ ϵ′/ (p′ / + m)ϵ/ k′/ ϵ/(p′ / + m)] = Tr[ϵ/k′ / ϵ′/ p′/ϵ/ k′/ ϵ/p′ / ] + m′ 2Tr[ϵ/k/ ϵ′/ ϵ′/ k′/ ϵ/]′ = Tr[ϵ/k/ ϵ′/ p′/ϵ/ k′/ ϵ/p′ / ]′ − m2Tr[ϵ/k/ k′/ ϵ/]′ = Tr[ϵ/k/ ϵ′/ p′/ϵ/ k′/ ϵ/p′ / ]′ = 2(ϵ′· p′)Tr[ϵ/k/ ϵ′/ k′/ ϵ/p′ / ]′ − Tr[ϵ/k/ p′/ϵ/ ϵ′/ k′/ ϵ/p′ / ]′ であり、第 1 項は、 2(ϵ′ · p′)Tr[ϵ/k/ ϵ′/ k′/ ϵ/p′ / ] = 2(ϵ′ ′· p′)Tr[ϵ/(−ϵ/ k′/ )k′ / ϵ/p′ / ] = 0 。′

第 2 項は、 Tr[ϵ/k/ p′/ϵ/ ϵ′/ k′/ ϵ/p′ / ] =′ −Tr[ϵ/k/ p′/k/ ϵ/p′ / ]′ =−2(k′ · p)Tr[ϵ/k/ ϵ/p′ / ] + Tr[ϵ/p′ /k/ k′/ ϵ/p′ / ]′ =−2(k′ · p)Tr[ϵ/k/ ϵ/p′ / ]′ =−2(k′ · p)4{(ϵ · k′)(ϵ· p′) + (ϵ· p′)(ϵ· k′)− (ϵ · ϵ)(k′· p′)} =−2(k′ · p)4{2(ϵ · p′)(ϵ· k′) + (k′· p′)} =−2(k′ · p)4{−2(ϵ · k′)2+ (k′· p′)} =−8(k′ · p){−2(ϵ · k′)2+ (k· p)} (∵ 式 (3.67)) 。 よって、 Tr[ϵ/k/ ϵ′/ (p′ / + m)ϵ/ k′/ ϵ/(p′ / + m)] = 8(k′ ′· p){−2(ϵ · k′)2+ (k· p)} (3.80) である。 最後に、k′· k に比例する項を計算する。 Tr [(p/ + m)′ {ϵ/′k/ ϵ/} (p/ + m) {ϵ/ k′/′ϵ/}] = Tr [p/ ϵ/′ ′k/ ϵ/p/ϵ/ k′/′ϵ/] + m2Tr [ϵ/′k/ ϵ/ϵ/ k′/′ϵ/] (∵ γ行列を奇数個含むトレースの項は 0) = Tr [p/ ϵ/′ ′ϵ/k/p/k/′ϵ/ ϵ/] + m′ 2Tr [ϵ/′ϵ/k/k/′ϵ/ ϵ/]′ (∵ 式 (3.65)、(3.66)) = (Tr [p/ϵ/′ϵ/k/p/k/′ϵ/ ϵ/] + m′ 2Tr [ϵ/′ϵ/k/k/′ϵ/ ϵ/]) + Tr [k′ / ϵ/′ϵ/k/p/k/′ϵ/ ϵ/]′ − Tr [k/ ϵ/′ ′ϵ/k/p/k/′ϵ/ ϵ/]′ (∵ p′ = p + k− k′) (3.81) まず、この式 (3.81) の第１項を計算する。γ 行列の交換関係より、 p /p/ = 1 2{p/, p/} = 1 2pµpν2g µν _{= p· p = m}2 _(3.82) であるから、 Tr [p/ϵ/′ϵ/k/p/k/′/ ϵ/] + mϵ′ 2Tr [ϵ/′ϵ/k/k/′ϵ/ ϵ/]′ = 2(k· p)Tr [p/ϵ/′ϵ/k/′ϵ/ ϵ/]′ − Tr [p/ϵ/′ϵ/p/k/k/′ϵ/ ϵ/] + m′ 2Tr [ϵ/′ϵ/k/k/′ϵ/ ϵ/]′ (∵ 式 (3.78)) = 2(k· p)Tr [p/ϵ/′ϵ/k/′ϵ/ ϵ/]′ − Tr [ϵ/′p/p/ϵ/k/k/′ϵ/ ϵ/] + m′ 2Tr [ϵ/′ϵ/k/k/′ϵ/ ϵ/]′ (∵ 式 (3.63)、(3.64)) = 2(k· p)Tr [p/ϵ/′ϵ/k/′ϵ/ ϵ/]′ − m2Tr [ϵ/′ϵ/k/k/′ϵ/ ϵ/] + m′ 2Tr [ϵ/′ϵ/k/k/′ϵ/ ϵ/]′ (∵ 式 (3.82)) = 2(k· p)Tr [p/ϵ/′ϵ/k/′ϵ/ ϵ/]  ′ = 2(k· p)2(ϵ′· ϵ)Tr [p/k/′ϵ/ ϵ/] + 2(k′ · p)Tr [p/ϵ/ϵ/ k′/′ϵ/ ϵ/]′ (3.83) とわかる。

この式 (3.83) の第 1 項は、 4(k· p)(ϵ′· ϵ)Tr [p/k/′ϵ/ ϵ/] = 4(k′ · p)(ϵ′· ϵ)4{(p · k′)(ϵ′· ϵ) + (p · ϵ)(k′· ϵ′)− (k′· ϵ)(p · ϵ′)} = 16(k· p)(p · k′)(ϵ′· ϵ)2 (∵ 式 (3.56)、式 (3.57)) 。 第 2 項は、 2(k· p)Tr [p/ϵ/ϵ/ k′/′/ ϵ/] = 2(kϵ′ · p)Tr [ϵ/p/ϵ/ k′/′ϵ/ ϵ/]′ = 2(k· p)Tr [ϵ/ϵ/p/ϵ/ k′/′ϵ/ ]′ (∵ 式 (3.15)) =−2(k · p)Tr [p/ϵ/ k′/′ϵ/ ]′ (∵ ϵ/)ϵ/ = −1) =−2(k · p)4((p · ϵ′)(k′· ϵ′) + (p· ϵ′)(ϵ′ · k′)− (p · k′)(ϵ′ · ϵ′)) =−8(k · p)(k′· p) (∵ 式 (3.56)、式 (3.57)) 。 である。よって、式 (3.83) は、 Tr [p/ϵ/′ϵ/k/p/k/′ϵ/ ϵ/] + m′ 2Tr [ϵ/′ϵ/k/k/′ϵ/ ϵ/] = 16(k′ · p)(p · k′)(ϵ′ · ϵ)2− 8(k · p)(k′· p) = 8(k· p)(p · k′){2(ϵ′ · ϵ)2− 1} (3.84) となる。 式 (3.81) の第２項は、 Tr [k/ ϵ/′ϵ/k/p/k/′ϵ/ ϵ/] =′ −Tr [k/ϵ/′k/ ϵ/p/k/′ϵ/ ϵ/]′ (∵ 式 (3.65)) =−2(k · ϵ′)Tr [k/ ϵ/p/k/′/ ϵ/] + Tr [ϵ/ϵ′ ′k/k/ ϵ/p/k/′ϵ/ ϵ/]′ =−2(k · ϵ′)Tr [k/ ϵ/p/k/′ϵ/ ϵ/]′ (∵ 式 (3.15) =−2(k · ϵ′)Tr [ϵ/k/ ϵ/p/k/′ϵ/ ]′ (∵ 式 (3.65)) = 2(k· ϵ′)Tr [k/ ϵ/ϵ/p/k/′ϵ/ ]′ (∵ ϵ/)ϵ/ = −1) =−2(k · ϵ′)Tr [k/p/k/′ϵ/ ]′ =−2(k · ϵ′)4((k· p)(k′ · ϵ′) + (k· ϵ′)(p· k′)− (k · k′)(p· ϵ′)) =−8(k · ϵ′)2(p· k′) (∵ 式 (3.57)、(3.59))

式 (3.81) の第３項は、 −Tr [k_{/ ϵ}′_{/ ϵ/k}′ _{/p/k/ ϵ}′_{/ ϵ/] = Tr [k}′ _{/ ϵ}′_{/ ϵ/k}′ _{/p/ϵ/ k}′_{/ ϵ/]}′ _{(∵ 式 (3.66))} = 2(k′· ϵ)Tr [k/ ϵ′/ ϵ/k′ /p/ϵ/ ]′ − Tr [k/ ϵ′/ ϵ/k′ /p/ϵ/ ϵ/k′ / ]′ = 2(k′· ϵ)Tr [k/ ϵ′/ ϵ/k′ /p/ϵ/ ]′ (∵ Tr [k/ ϵ′/ ϵ/k′ /p/ϵ/ ϵ/k′ / ] = Tr [k′ / k′/ ϵ′/ ϵ/k′ /p/ϵ/ ϵ/] = 0)′ = 2(k′· ϵ)Tr [ϵ/ k′/ ϵ′/ ϵ/k′ /p/] = 4(k′· ϵ)(k′· ϵ′)Tr [ϵ/ ϵ/k′ /p/]− 2(k′· ϵ)Tr [k/ ϵ′/ ϵ′/ ϵ/k′ /p/] =−2(k′· ϵ)Tr [k/ ϵ′/ ϵ′/ ϵ/k′ /p/] (∵ 式 (3.59)) = 2(k′· ϵ)Tr [k/ ϵ/k′ /p/] = 2(k′· ϵ)4((k′· p)(ϵ · k) + (k′· ϵ)(k · p) − (k′· k)(ϵ · p)) = 8(k′· ϵ)2(k· p) である。ゆえに、まとめると、式 (3.81) は、 Tr [(p/ + m)′ {ϵ/′k/ ϵ/} (p/ + m) {ϵ/ k′/′ϵ/}] = 8(k · p)(p · k′)(2(ϵ′· ϵ)2− 1) − 8(k · ϵ′)2(p· k′) + 8(k′· ϵ)2(k· p) (3.85) 行列要素_{M の計算は、以上をまとめると、} |M|2 ₌ e4 8(p· k)28(k· p){2(k · ϵ ′₎2 + (p′· k)} + e 4 8(p· k′)28(k ′ _{· p){−2(ϵ · k}′₎2 + (k· p)} + e 4 4(p· k)(p · k′)(8(k· p)(p · k ′_)(2(ϵ′_{· ϵ)}2_{− 1) − 8(k · ϵ}′₎2_{(p· k}′_{) + 8(k}′_{· ϵ)}2_{(k· p))} = e4 [ 2(k· ϵ′)2+ (p′· k) p· k + −2(ϵ · k′₎2_{+ (k· p)} k′ · p + 2{2(ϵ ′_{· ϵ)}2_{− 1) −} (k· ϵ′) 2 p· k + (k′ · ϵ)2 p· k′ } ] = e4 [ p· k′ p· k + k· p k′ · p+ 4(ϵ ′ _{· ϵ)}2_{− 2} ] となる。さらに、 p· k = (m; 0) · (ω; k) = mω, (3.86) p· k′ = (m; 0)· (ω′; k′) = mω′ (3.87) より、 |M|2 _{= = e}4 [ mω′ mω + mω mω′ + 4(ϵ ′_{· ϵ)}2_{− 2} ] = e4 [ ω′ ω + ω ω′ + 4(ϵ ′_{· ϵ)}2_{− 2} ]

図 3.5: 光子の波数ベクトル k, k′と偏極ベクトル ϵλの関係。偏極ベクトル ϵ1、ϵ2、波数 ベクトル k をもつ入射光子が散乱角 θ でコンプトン散乱されて、偏極ベクトル ϵ′₁、ϵ′₂、波 数ベクトル k′_{となる。その影響で ϵ} 2と ϵ′2は変わらないが、ϵ1は角度 θ だけ方向の違う ϵ′1 になる。 とわかる。断面積は式 (3.42) で与えられているから、 dσ dΩ   LAB = 1 64π2_m2 e e4 ( k′ k )2[ ω′ ω + ω ω′ + 4(ϵ ′_{· ϵ)}2_{− 2} ] (3.88) = e 4 64π2_m2 e ( ω′ ω )2[ ω′ ω + ω ω′ + 4(ϵ ′_{· ϵ)}2_{− 2} ] . (3.89) 光子の偏極方向について平均をとると、 dσ dΩ   LAB = 1 2 ∑ λ,λ′ 1 64π2_m2 e e4 ( ω′ ω )2[ ω′ ω + ω ω′ + 4(ϵλ· ϵ ′ λ′)2− 2 ] (3.90) = 1 64π2_m2 e e4 ( ω′ ω )2 2 [ ω′ ω + ω ω′ + ∑ λ,λ′ (ϵλ· ϵ′λ′) 2_{− 2} ] . (3.91) 入射する光子と散乱される光子での偏極ベクトルは図 3.5 となる。偏極ベクトル ϵ1、ϵ2、 波数ベクトル k をもつ入射光子が散乱角 θ でコンプトン散乱されて、偏極ベクトル ϵ′₁、 ϵ′₂、波数ベクトル k′となる。その影響で ϵ2と ϵ′2は変わらないが、ϵ1は角度 θ だけ方向の 違う ϵ′₁になる。そのため、 ϵ2· ϵ′2 = 1 ϵ1· ϵ′1 =|ϵ1||ϵ′1| cos θ = cos θ であるから、 dσ dΩ   LAB = 1 32π2_m2 e e4 ( ω′ ω )2[ ω′ ω + ω ω′ + (1 + cos 2_{θ)− 2} ] . (3.92) ここで、式 (3.92) を自然単位系から SI 単位系に変換し、一般に用いられる式に直す。微

分散乱断面積は距離の 2 乗の単位であるから、 1 m2 e の項について、 1 m2 e → ℏ2c2 [MeV2· cm2] m2 ec4 [MeV2] = ℏ 2 m2 ec2 (3.93) e4 → e 4_[C4_] ϵ2 0[C4/(MeV2· cm2)]ℏ2c2[MeV2· cm2] (3.94) とすれば、SI 単位系に直る。式 (3.92) の e4 32π2_m2 e において、 1 32π2 1 m2 e e4 → 1 32π2 ( ℏ2 m2 ec2 ) ( e4 ϵ2 0ℏ2c2 ) = e 4 32π2_ϵ2 0m2ec4 である。さらに、古典的電子半径 re= e 2 4πϵ0mec2 を用いれば容易に表せて、 e4 32π2_ϵ2 0m2ec4 = r 2 e 2 となる。ω′ ω は、コンプトン散乱で散乱された光子のエネルギー hν′が式 (3.6) で与えられ ているから、 ω′ ω = hν′ hν = _hν 1 mec2(1− cos θ) + 1 . = 1 α(1− cos θ) + 1 となる。ここで、 α = hν mec2 (3.95) である。ゆえに、式 (3.92) の最後の項は、 ω′ ω + ω ω′ + (1 + cos 2_{θ)− 2 =} 1

1 + α(1− cos θ) + (1 + α(1− cos θ)) + (1 + cos

2_{θ)− 2}

= (1 + cos2θ) + 1− 1 − α(1 − cos θ) + α(1 − cos θ) + α

2_{(1− cos θ)}2 1 + α(1− cos θ) = 1 + cos2θ + α 2_{(1− cos}2_θ) 1 + α(1− cos θ). したがって、式 (3.92) は SI 単位系で、 dσ dΩ   LAB = r 2 e 2 [ 1 1 + α(1− cos θ) ]2[ 1 + cos2θ + α 2_{(1− cos}2_θ) 1 + α(1− cos θ) ] . (3.96)

である。 最後に入射光子のエネルギーが 662 keV のときのコンプトン散乱の微分断面積を図 3.6 に示す。その特徴は次のようにまとめることができる。前方散乱 (θ < 90◦_{) での微分断面} 積は後方散乱 (θ < 90◦) での微分断面積に比べて最大で 8 倍程度大きいことがわかる。前 方散乱では微分断面積が大きく変化しているのに対して、後方散乱では微分断面積はほ とんど一定である。前方散乱では θ が小さいほど微分断面積は大きくなり、θ = 0◦で最 大、θ = 90◦で最小である。一方、後方散乱では θ が大きいほど僅かだが微分断面積は大 きく、θ = 180◦で最大である。 図 3.6: 入射光子のエネルギーが 662 keV のときのコンプトン散乱の微分断面積。前方散 乱 (θ < 90◦_{) での微分断面積は後方散乱 (θ < 90}◦_{) での微分断面積に比べて大きいことが} わかる。前方散乱では微分断面積が大きく変化しているのに対して、後方散乱では微分 断面積の変化量は少ない。前方散乱では θ が小さいほど微分断面積は大きくなる。一方、 後方散乱では θ が大きいほど僅かだが微分断面積は大きくなる。