高次弾性基本解の有限要素解析 : 有限要素法による弾性基本解の解析に関する研究(その3)

【論　 文】

UDC ：624

．

042：引9

．

6

　 　日本建築 学 会 構 造系論文報告果 第419号

・

1991年1月

Jour哺10f　Stru_『t

．

　Censtπ

．

　Engng

，

　A【J

，

　No

．

4】9

、

　Jan

．

、

1991

高 次

弾

性 基 本

解

の

_{有 限 要}

_素

_解析

有 限要素 法

に よる

弾性基 本解

の

解析

に

関

す

_う

研 究 （

そ の

3

）

FINITE

　

ELEMENT

　

ANALYSIS

　

OF

　

HIGH

−

ORDER

　

ELASTIC

　

FUNDAMENTAL

　 　　 　 　　 　 　 　　 　 　　 　 　 　　 　 　

SOLUTIONS

Studies

　on 　analysis 　of　elastic 　

fundamental

　solutions 　

by

　

finite

　element 　method

，　

Part

　

3

　　　　　　

L

　　

藤

谷 義 信

＊ ，

「

藤 井 大 地

＊ ＊

Yoshinobu

　

FUJITANI

　and 　

I

）

_妨

ゴ

FUJII

　

This

　_paper　

presents

　a　

procedure

　for　the　finite　element 　analysis 　o正high

−

order 　elastic 　fundamental solutions 　in　two

−

and　three

−dimensional

　

bodies．

　

Three．

dimensional

　fundamental　solutions 　can 　be　expressed 　by　the　Fourier

’

s　Series　expansion with 　respect 　to　the　

Coordinate

_¢

．

　

Its

　

Second−

order 　solution 　correspond

．

to　the　_plane　symmetric

fundamental

　solution （

Cerrttti

’

s　solution ）and 　is　formulated　in　this　paper　by　finite　element 　method

．

　

Two

−

dimensional　higher

−

order 　

fundamentat

　solutions 　under 　

following

　

load

　conditions _尹re　analy

−

sed 　

by

　

finite

　element 　method ：（1｝acoupte

，

（2）equai 　and 　opposite 　molnent 　of　couptes

，

　acting Qn　the　straight 　

bQundary

　Qf　an　infinite　_plane

．

　

It

　

is

　clarified 　that　the　usual 　two

−dimensional

　

fun．

damental

　solution 　can　

be

　solved 　by　a　simultaneous 　equation

，

　

however，

　the　above 　higher

・

order

two

−dinlensional

　

fundamental

　solutions 　are　analysed 　as　eigen

．

value 　_problem

、

　By 出e　present　finite　element 　method

_，

　the　nurnerical 　

fundamental

　so ！utions 　were 　obtained 　with

good　convergence

．

　Keyωords ：弾 性 基 本 解

，

有 限 要素法

，

　

Cerruti

_解

，

集中偶力

，

集中モ

ー

メ ン ト

1．

序 　弾 性 基 本 解は

，

境 界 要 素 法や境 界 積 分 法な ど の数値構 造解析法 に おいて重 要な役 割 を 果たす

。

また

，

弾 性基本 解や き れつ _先端近傍の固有解などの特 異 な応 力 場は

，

線 形 破壊力学の理論構 成の た めの

一

つ の重 要な手が か り と なっ てい る

。

著 者の

一

人は

，

本 研 究の第1 報 2♪ におい て

，

2

次 元弾性 体 中の Kelvin解

，

　Boussinesq _解および

Cer−

ruti 解 （図

一

1参 照 ） を2次 元 弾 性 基 本 解と呼び， こ れ を有 限 要 素 法で数 値 的に_求め る手 法に つ いて提 案 を行っ た。 また

，

第Z報 3 ） で は

，3

次 元弾 性体中の Kelvin解と Beussinesq 解を

3

次元線対称 基 本 解 と 呼び

，

これも 同 様に有限要素法で解 析す る手 法 を提 案した

。

　これ まで の研究におい て， 前 者の 2次 元 弾 性 基 本 解の 解析 問題は， 極 座 標 系 （r，θ｝で記 述 さ

拠，

離 散 化し た 変位関数ノ（θ）

，

g（θ）に関す る連 立 方 程 式 を解く問題に帰 着さ れ たの に_対し て

，

後者の 3次元弾性基 本 解の問 題は

，

球 座 標系（r

_，

θ

，

切で記述さ れ， 荷 重 点 近 傍の変 位の特 異性の 大 き さを固有 値と し

，

離 散 化 した 変 位 蝋 θ〉

，

Ue｛θ）， πψ（のを固有ベ ク トル と す る 固有 値解析問題 と な ることが 分かっ た

。

こ のよ う に

2

次元 と

3

次元 の基 本解 の解析の形 式が異なっ たの は

，3

次元基本解が荷 重 点 近 傍で応力

・

変位と もにべ _き乗型の_特異性をもつの に_対し て

，2

次元基本 解で は変位が対 数 型の特異性 をもつ た め， 両 者の 聞に定 式 化の相 違 が 生じ た た めである

。

　しか しな が ら_{， 第 2}報で_説明し た 3次 元 弾 性 基本解の 解 析 法は_， Kelvin　

ee

_や Boussinesq_解の よ うに荷 重 線に 対 して線 対 称

．

（す な わ ち軸 対 称 ）の応 力

・

変 位 解を もつ

尸一

一

一

一

一一

一

一

層

呷

腰

一

₁ ■₅ 1 Kiユvin 　 l

i

k

_i

I_「 l_l L

−＿

一

＿一

＿

＿

＿＿

＿

一

＿

＿

湯

｛e ） 無 限 領 域 　 　 　 　 Bousslnesq ・・ … ・i

↓

I_rl I　　 　 　 　　 　 　　 　 　　 　 　I I　　 　 　 　　 　 　　 　 　　 　 l I　 　 　 　幽 8　 　 　 　P 圏　 　 　 　1 幽　 　 　 　I l　　　　　　 l l　　

』

　 　 　　 　 　　 　 　　 1 し

＿

r＿

＿一

＿

＿

冒

一

一

＿

−

J （b，半 無 限 領域 図

一

1 弾 性基本解 本 稿は 文献1）に_その

一

部 を発 表して い る

。

＊ _{広 島 大 学 　 教 授}

・

_{工 博} ＃ _広 島大 学　助 手

・

工 修

Professor　of 　Hireshima　Univ

．

，

DL　Eng

．

図

一

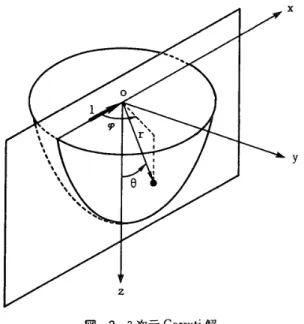
23 次元 Cerluti解 x y 場 合に対 応す るもの で あり

，Cerruti

解の よ うに荷 重 線 を含む面に_対し て対 称な問題に はその ま まで は 適用で き ない 。 この

3

次 元Cerruti解 を第2報と同様な手 法で求 め るに は_， 変 位

・

応 力の op方 向 （図

一

2参 照 ）の フ

ー

リ エ _{展 開 次 数 を高 次 化して定 式 化す る必要が ある}

。

　また_{， 第 1 報}で_説明 し た

2

次 元 問 題におけ る

Kelvin

解

，

Boussinesq解，　

Cerruti

解な ど の弾 性 基 本 解は， い ずれ も最 終 的に荷 重ベ ク トル を右辺 に もつ 連立 方 程 式 （剛 性 方 程 式 ）を解く ことによっ て得ら れ る が

，

さ_らに 集 中 偶 力や集 中モ

ー

メ ン トが 作 用す る場合も弾 性 基 本 解 の中に含め る とする と

，

こ れ らの_{弾 性i}基本解は r 方 向 に高 次の べき乗 型の特 異 性 をもつ た め

，

同 じ2次 元 問 題 であり な がら

，

連 立 方 程 式 を解く問題で は な く

，

固 有 値 問 題と なっ て くる

。

　

以上の よ うな_{考 察}か ら， 本 稿で は

，

3次 元 弾 性 基本解 につ い て は

，Cerruti

解の よ う な面 対 称 解も解け る よ う に ep方 向の フ

ー

リエ _{展 開 次 数 を 高 次}に し た と きの解 析 法 につ い て

，

ま た_， 2次 元 弾 性 基本解につ い て は_， r _方 向に高 次の ぺ _き乗型の _{特 異 性}をもつ _{場 合}の解 析 法につ い て説 明す る

。

本 稿で言 う 「高次」とい う言 葉は

，

3次 元 問 題と 2次元 問題で異 な る意 味を もつ が

，

本 稿で これら の高 次の基 本 解の解 析 法を ま と めて_示すことに よ り

，

2 次 元および 3次 元の弾 性 基 本 解の力 学 的な特性をよ り明 確にする ことが できる もの と 思 わ れ る

。

2．3

次 元 面対 称基本解の解析 2

．

1 仮 想 仕 事 方程 式の _導出 　い ま

，

図

一

2に示 す よ うな半 無 限 弾 性 体の表面上に集 中 荷 重が作 用す る

，

いわ ゆ る 3次 元

Cerruti

問題にっ い て考え る。 解 析を行う た めの座 標 系は， 同

囓

中に示す よ うに _{荷 重 点}を原 点と する球 座 標 系 〔r

，

θ

，

ep）を用い る

。

こ こに

，

g は

，

荷 重線と 2 軸 （θ

；0

）を含む平 面か ら 測る もの と す る

。

　 3次 元弾 性 論η に よ ると， 物 体 力が

一

_{定ま た は 0の} 場 合に は

，

3個の 変 位 成 分はすべ て重 調 和 関 数で あ る

。

い ま

，

調和関 数を φとする と

，

球 座 標 系で表さ れ た調 和 方程 式 は 次式で与え ら れる。

　

　

　

・φ

一

÷

毳

（

7t∂φ 　 　∂r

）

・

毒

晶（

P

芻）

　　

　

　　

・

毒

籌

一 _・

・

………一 ・

・

…・

…・

・

…

_（1_） こ こ に

，

_万

＝

sin θ で あ る

。

こ の式を満足 す る調 和 関 数 φ（r

，

θ

，

¢）の形は

，

以下の よ うに して決 定さ れ る

。

まず

，

φ を次の形の変 数 分 離 形 　 　　φ（r

，

θ

，

9）

＝

ra

・

θ（e）

・

φ（ψ）

・

・

…・

…・

…・

…・

一・

（

2

） で表し

，

こ れ を （1）式に代入 する と次 式が得られる

。

　

　

　

・

1一

體

一

・_P

噐

・

｛

… ＋

1

・

「

＄

，

｝

・

一

・ 　 　 　 　

・

…・

…・

・

…・

……・

………一…

（3）

　

　

　

窒

・〆・一 ・

・

………一 ・

…一 ………・

・

…・

_（・・ こ こに

，

ρ

＝

cos θ で あ る

。

（3） 式はル ジャ ン ドル陪 方 程 式であるの で

，

この解 θ（のは次式で表され る_。

　　　

θ（の

＝、

4P

ズ（P）

………・

・

…・

・

…・

…

〔5 ：1

一

_方

_，

_{（4 ）式の} 解 φ_（p）は次 式で_表さ れ る

。

　　 　 Φ（ψ）；

B

_，cos μψ十

B2si1

_μψ

・

……・

・

…・

・

…

（6：1 以 上よ り， 球 調 和 関 数 φ（r

，

θ

，

g）は次 式の よ うに

，

ル ジャン ドル

・

フ

ー

リエ 級 数で表 現さ れる

。

　　 　φ（r_，θ_，ψ）； _『λ

P

_員（P_）（anCOS _{ηψ 十}

b

πsin ηψ） 　 　 　 　

・

一一・

・

卜

・

・

・

・

・

・

・

・

・

・

…

　

9・

・

・

・

・

・

…

　

77・

7P

（7

．

1 　半 無 限 弾 性 体の _材質が

，

x

−

z 平 面に関し て対 称で あ ると す る と

，

x 軸 方向に集 中荷 重を受け るとき の変 位解 は x

−

z 平 面に関 して面 対 称 と なる。 し たがっ て

，3

次 元 面 対 称 基本解の_解析を行う場 合は

，

次 式の よ うな形の 変 位 解を仮 定して議 論 を 進 めて い くこ とが で き る

。

　　 　 Ur（7

，

θ，ψ）

＝

rAu 享（θ）nCOS η¢ 　　 　媚 γ

，

e

，

・o）

＝

　rλ u；（θ〉。cos ・ng 　

・

…………

（8） 　　 　u。（r

，

θ

，

ψ）

＝

γ 入 協 （θ）。sin 　nψ こ の式中の λ は

，

荷 重 点 （r

＝

0） 近 傍の_変位の_{変化 特} 性 を示すパ _{ラ メ}

ー

_タであ り

，

本 解 析においては

_，

以下に 説 明 するように_弾性 論の基礎式を満 足する 固 有な解λ を求め よ う と す る もので あ る。 （8）式に お い て， n

・

_＝0

の 場合は

，

第

2

報で すでに説 明し た線 対 称 解

，

す なわ ち 2 _軸に_対して_{対 称}な

BQussinesq

解の変 位 式 を

．

与え る

。

し た がっ て

，一

般 的 な 高 次 解 を 求め るには， n≧

1

の場 合につ い て以 後の式 展 開 を 行え ば よい

。

し か し な が ら本 稿で は

，

式が複雑に な る ため

，

以 下で は

，Cerruti

解に 対応す る η

＝1

の 場合につ い て のみ記 述す ることにす る

。

　

（

8

） 式の変 位 成分に 3次 元 弾 性 体の ひ ず み

一

変位 関係

式，お よ び応 カ

ー

ひずみ関係式を適 用 すると

，

応 力 成 分 も， r， θ，qの変数分離形に な り

，

形 式 的に次のよ うな形で 表され る

。

σ。〔γ

，

θ

，

ep）

＝

r λ

一

’ σ蓼（θ_）COS ψ σθ（7

，

θ

，

ψ）

＝

7

・

λ

一

塵 σ

X

（θ）COS ψ σ P（r

，

θ

，

の

＝

r”

一

匸 σ毒（θ）COS 　9

．

τ

．

〆r

．

8，

ψ）

＝

rλ

一

’τ萋_e（θ）cos _ψ τθワ（r

，

θ

，

ψ）

＝

rλ

ml

τ彦_o

，

（θ＞sin ¢ … （r

・

θ

・

　q｝

＝

rλ

“

’ ir：r（θ）sin・ep

・

・

…



77

・

・

…

_（

₉

_） r_， e

、

_ψ方 向の応 力の釣 合 方程式は_次式で_表さ れ る。

　

　

　

÷

蕃

（r・ ar）＋

吉

磊

（

P

レ・｝

　

　

　　

・

撮

（・_・ ）

一

÷

（ae_… ）

一

・

　

　

　

謡

… T・ej

．

・

毒

晶

励 ・） 　 　 　 　

・

……・

（10＞

　

　

　　

・

h

−

＆

（翻

一

_務

・…

　

　

　

÷

審

（・  ）＋

毒

晶

_{嗾 ・}）

　

　

　　

＋

ち磊

（

b

・｝

一

・

．

．

た だ し

，

p

＝

cos θ

，

_万

＝

sin θである

。

　

ま た

，

物 体表面上の応 力 境 界 条 件は_， 次 式で表さ_れる

。

　 　 　σ。nr＋ T，en θ＋ rPt，nrp

＝0

　　　τ

，

enr ＋σ ，n，＋ r，、，n．

＝0

　

…・

……

．

_……一

（11） 　 　 　τ9

。

nr＋ r。qn θ＋σpnp ＝

0

い ま_{・（lo 拭} の

_鉢

の

_灘

を それぞれ

R

_；

_，

・

R

_・

，

・

R

．

と

し

，

また

，

．

（ll）式の そ れ ぞれ の残差を

Tr，

　

T

_。

_，

　

Te

と す る

。

こ れ ら の残 差に よ る仮 想 仕事 方 程 式 を作る と次の ように な る

。

∫

°

°

∬

ノtf

：

（

R ，

…

．

＋

R

_，δU，＋

R

．・

V

。）…

pd

・d・d・・

　　　

・

f

。

°

°

f

二

臓 汁 ・・δu・＋・，δ・。｝・・脚

一

・

．

　 　 　 　

……・

・

…………・

…・

・

……・

…

（12） （12） 式に （

10

）

，

（11）式を代入 し

，

部 分積 分 を施し て

，

式 変 形を行っ てい くと

，

最 終 的に次の方 程 式が得ら れ る

。

ただ し， こ こ で は，

Cerruti

解を とり扱っ て い るの で

，

θの解 析 領 域は

，

0≦θ≦π／2で あ り

，

ま た

，

表面 境 界の 方 向余 弦は n。

＝

nrp

＝

O

，

　ne

＝

1であ る

。

’

　

　

∬

／

℃

［

K

・＋

1

）

P

・

r

・・＄・

−

P

〔・：＋・；）｝・ ・S2 媚

　

　

　

う ・享・

響

・ ・S…＋

1

（・＋ ・）

b

・

r

・

　

　

　

・・彦，

−

_P ・渉｝・・S・蝿

一P

・ま ∂

含

笋

・ ・S・・ 　　　十

1

_（λ十

2

）万τちr十

P

τま9

一

σ斜sin2 ¢ uさ

　

　

　

う ・：_． ∂

含

嵳

窃・・…

］

d…

一

・

・

………

（

_．

13 ） こ こで

，

sin2 ψ とcos2 ψ は

，一

π≦ψ≦π で積分す る と 0 z 図

一

3　θ領 域の有 限 要素分割 X π とな る

。

（

13

）式 をマ トリック ス で表 現 すると次のよ うにな る

。

　 　 　 　 if12 　 　 　 　

　

　　

．

∫

　 　 　

1

σ串

F

［∂

B

］

1

δu＊｝

d

θ

＝

0

・

・

…

　

t…

　

t・

一

・

・

・

・

・

・

…

　（14｝ こ こ に_，

　　　

1

σ『」

L

σ乳σ翫σさ

，

τ薮，

，

τ奮

．

，

τ

制 　 ・

　　　

1

δu_『T

＝

L

δu乳δ包者

，

δu_毒」 で あ る。 ま た

，

［

B

］は θの微 分 演 算 等を含む6×3の 大 き さのマ ト リックス で あ る

。

　ま た

，

　 　　

1

σ料

＝

［D ］［∂

B

コ

lu

零

1

・

−t・

・

一

一

・

・

・

・

・

・

・

・

・

・

・

・

・

…

　

tt…

　

一

…

　（15 ） で表され る か ら

，

（14）式は

，

　　

　

∬

／ tヨ・u・ ｝・ ［・

珈

・］［・B ］嚇

一

・

・

…

… （16） と な る。

2．2　

有限 要素法に よ る定式

化

　 第

2

報と同様に し て

，

図

一

3の ように θ方 向の領 域を 要素に分割し て

，

次式に示す よ う に

1

つ _の要素 内_の 嵯

，

uX

，

鳩の分布 を最も簡 単な線 形 分 布に仮 定す る

。

1

・’・

一

［

1

1

ξ

÷∴

劇

1

副

　　　　

一

囲

ldN

…一 ・

…・

・

……・

∵

一 …・

・

一

（

17

） 　 　 　 　θ

一

　

e

_， こ こ に

_．

_ξ皇 θ广 防で あ り

，

ld

＊ ｝は節点変位ベ _{ク ト}ル で，

　　　

｝。・

IT

−

L

蝋_，嬢_，ぬ _，協 _，祝務

；

副

…・

・

……

（18） である

。

　（17）

．

式 を （16）式に代入 す る と

_，

最終 的に

一

つ の要 素に_関す る次の よ う な特 性方程式が得ら れ る。 　 　　匚

h

（λ）］

ldn

＝0 ・

tt・

・

・

…

　

t−tt・

・

…

　

t−・

・

…

　

t−tt

・

・

・

・

…

　

−t・

（

19

） こ こに

_，

要素剛 性マ ト リッ クス ［

k，

（λ）］は次 式の形 を して い る

。

　

　

［

k

（・）］一

∬

ノ2［」

1

］

・

［

D

］［・］

d

・

…・

・

一 一 …・

・

｛・・｝ こ の式の中の核 剛 性マ トリッ ク ス ［h］

，

［h］お よび応 カ

ー

ひずみマ トリッ ク ス［D］の具 体 的な形 を示 すと次の よ う になっ て い る。 　［

k

］T_＝ ［N ］T ［∂

B

］T （λ＋1）戸（1

一

ξ｝　

− P

（1

一

ξ）　

− P

（1

一

ξ） 　 0 　 0 （λ＋1＞

P

_ξ 　 0 　

0

　 　 　 ）／

t

　 　 　（λ十

2

）

p

（

1一

ξ） 　 　 　 　0 　 　 　 　 　

−

P

／

t

　 　 　　（λ＋2）戸ξ 　 　 　 0 ［

D

］

一

_（1＋

語

一

，の 」づ／

t

　　　

−

P（

1一

ξ＞ 　0 　 　

−

（1

一

ξ）

−

_P

ξ　 　

一

P

ξ

一P

／‘

−

Pξ 　

0

　 　 　

一

ξ 　 ξ 〇

一

　

1

ξ

一

〇

1

ρ（1

一

ξ）＋

P

／

t

　（λ＋2）

P

（1

一

ξ） 　 　

0

　 　 　 ξ 　 　 ξ　 　 　

O

　

P

ξ

一

万／1　　　　（λ＋2）

P

ξ 1

一

ソ レ レ X 　 O 0

0

［il］

＝

［∂B ］［N ］ 　 レ 1

一

り レ

0

0 0 λ（1

一

ξ） 　 1

一

ξ 　 1

一

ξ 　

一1

／‘ 　 　0

−

_（1

一

_ξソ戸 　 　 　λξ 　 　 　 ξ 　 　 　 ξ 　 　 ユ／

1

　 　 　

0

’

　 　

一

ξ／万 　レ　 　 　 0 　レ　 　 　 O l

一

レ　 　 0 ・ 1

芽

レ 000 0 O

01

− 2v

0000 0 2

0

　 　 1

−

2レ 0



₂ 0 　 　

0

　

−

1／’ （P／」ヲ）〔1

一

ξ） （λ

一1

）（

1一

ξ）

一

_（1

一

_{ξ》／三戸} 　 　 0 　 0 　1／

1

（P／

P

）ξ （λ

一

D

_ξ

一

_ξ／

_P

　

O

　 　 　 　

O

　 　 　 　

o

　 　（1

一

ξ）／

P

　 　 　 　O

− 1

／

1−

（P／

7

ヲ）（

1一

ξ） 　 （λ

一

1｝（1

一

ξ） 00 ξ／

PO1

／

1−

（

P

／

P

）ξ 　 （λ

一

1）ξ

…

_（

₂₁

_） こ こ に_，

E

と v は_物体を搆 成す る材料の ヤン グ率と ボ アソ ン比であ り

，1

は要素 角の_大き さ（θ厂

e

，）で あ る。 　 （21）式 を 全要 素につ い て組み合わ せ

_，

固 有 値 λとそ れに対 応す る全 節 点 変 位ベ ク トル （固 有ベ ク トル ） を求 め る。

2．3

　モ

ー

ド倍 率の計算法 　前 節の_計算は 固有 値 問題の _{計 算}であ るの で

，

変 位 解お よび応 力 解は

，

その相 対 的な大き さ し か求ま ら ない

。

変 位 解

，

応 力 解は，

’

_{ひ と まず} ， 最 大の大き さ を1と して正 規化し た モ

ー

ドを表して お く

。

単位荷重と釣り合 う応 力 解を求め るには

，

モ

ー

ド解にあ る倍 率 （モ

ー

ド倍 率と呼 ぶ）を掛 けれ ばよい。 こ の倍 率を決 定 するに は

，

前 報で 説明し た よ うに

，

_変位モ

ー

ドか ら応力モ

ー

ドを計算し た 後

，

単 位荷重と 釣 り合 う よ うにす れ ば よい

。

　す な わ ち， この倍率

K

は次式に よ り計 算さ れ る。

　　

1

＋κ

ズ

〃

∬

／2 （・r・・・ … s φ・ T

，

e ・・s θ

’

・_・s _・

　 　　

一

τqrsin ψ）r2sin θ

d

θ

d

ψ

＝O・

…・

………

　

．

…

　 （22 ）

（

9

）式 を参 考にす る と

，Cerruti

解の 応 力は次式の 形 　 　　σT（7

・

，

θ

，

ψ）＝ r

−

z σ夛（θ）cos 　Pt 　 　　τ。e（　r，　

e

，　Q）

＝

r

−

’ τ裘e（θ）cos ψ 　

…・

……・

…

（

23

〕 　 　　τ。 r（ア

，

θ

，

¢）

＝

r

’

2 τ器Pt（θ｝sin ψ で表さ れ る か ら

，

これ を （

22

）式 に代入 す る と

，

κ を 決定する た め の次の計算 式が得られ る。 　 　 　 l 　 　 　

K ＝一

　 n π

t

Σ］（σ受S  θ十r歩eCOS θ

一

τ孝r）tsin 　

e

， 　 ‘

＝

1 　 　 　

・

…

　

一・

・

・

・

・

・

・

…

　

、

・

・

・

・

…

　

一

・

・

・

・

・

…

　

9・

・

（24｝ こ こ に

，1

は ‘番目の有 限 要 素 角の大き さ

，

Σ は

，

分 割 さ れ た各 要 素の _{中 点}に おける値の _{総 和 を表 す。}

2．

4

解析結果 　（20）式に お け る積 分は

_，

ガウス積分法に よっ て数値 積分を行っ た

。

ガ ウス ポイン ト数と要素分 割 数に よ る解 λの収 束状態 を 図

一4

に示す

。

縦軸は，λの正解値 （

− 1．0

＞ に対す る

，

本 方 法に よ る各要素分割時での λの解の相 対誤差で あ る。 本解析に よっ て得ら れ た λ の解は正 解

・

値に対し て良い収束性を示し てい る。 図

一5a

と図

一

Ei　

b

3

．

2

．

2

．

0

（

．

N

）

　 5 出 O 崑 国 1

．

0 0

．

5 D

，

0 　 工　 　 　 Z　 　 　1　 　 　4　 　 　 5　 　 　 6　 　 　 7 　 　 　 GAUSS 　POI卩T 図

一

4　3次元 Cerruti解の λ の収束 性

EOD 　

°

01 鬨 o

．

0

．

0

．

0

、

2 0

．

0

一

〇

、

2

一

〇

．

4

一

〇

．

6

一

〇

．

8

一

1

．

D MQPELO 0

．

o

．

0

．

O

．

2 D

．

o

一

〇

．

2

一

D

．

4

一

〇

．

6

＿

o

．

8

一

1

．

O 　 　 　 凸　　3　elements 　 　 　 o　 　6　element3 　 　 　 0 　　9　ele 田e囗 ℃3 　 　 　

−

　　 　　eKec じ 図

一

5a 　3次元 Cerruti解の変位モ

ー

ド 　 　 　 a 　　］　elemenL8 　 　 　 ●　　6　elements 　 　 　 o　　g　eletuen 匸s 　 　 　

−

　　　exec し 図

一

5b　3次 元Cerruti解の応力モ

ー

ド に 3_，6_，9要素分 割， ガ ウス ポイン ト数5で解 析し た変 位モ

ー

ドお よび応 力モ

ー

ドを示し た

。

本 方 法による解は

_，

Cerruti

解 （た だ し

，

モ

ー

ド表現｝の正 解に良い対 応を 示 して い る

。

ま た， モ

ー

ド倍 率

K

の厳密解に対する本 解 析結 果の誤 差の_収束 状 態を 図

一6

に示し て おい た

。

図

一6

の縦 軸 は

_，

十 分 収 束 し た と 考 え られ る

30

要素分割 時の _解を 正解と み な し

．

これに対す る そ れ ぞ れの_要素分 割 時の解との_相対 誤 差 を表 し てい る

。

6

，

0 5

．

5 5

．

0 ＆

．

5 4

．

o 　 ］

．

59

囂

3

’

° 髷 　 2

，

5 2

，

0 1

．

5 1

．

o 0

，

5 O

，

0 　 　 　 261014182226 　 　 　 　Number 　of 　elements 図

一

6　3次 元Cerruti解の モ

ー

ド倍 率の誤 差

P

　

↓

　

P

↑

　 　 　 1 一

一一

7

’

1

一

　 　 　 　

1

　 　 　 　 1 　 　 　 　 1 L

＿＿＿

」 図

一

7　2次 元集 中偶力 問 題

3

．

2

次 元 高 次 基 本 解の解 析

3．

1　 集 中偶 力 問題の有 限 要 素 解析 法 　い ま

，

図

一

7に示 す半 無 限 領 域の _{直 線 境 界}上に集 中 偶 力が作 用し た場 合の_解5）_{を求め る問 題を考え る} 。 こ こ に

2

つ の力の距離α は非 常に小さい ものと す る

。

　極 座 標系 （r

_，e

）に おい て

，

荷重点 を 中 心 と して任 意 の_半径 r で この_領域を切 断す る と

，

切 断線上の_応力 σ。 i τ。θは

，

力の釣 合いか ら次式を満足 し な く て は な ら ない。

　

　　

∫

　 　 　 　 π／2 　 　 　 （σrCOS θ

一

τresin θ）7dθ＝ 0 　 　 　 　

π

ノ2 　 　 　 　 π〆2

　

　　

f

　 　 　 （σrsin θ十 τrecos θ）rd θ

＝

O　　

……・

（25＞ 　 　 　 　 π／2 　 　 　 　 π／2

　

　　

f

　 　 　 τrer

・

rd θ＝

P

α＝ ルt（const

．

＞ 　 　 　 　 r／2 上 式の第 3式か ら

，

τ， θは r

−

2 の特 異 性を も たねば なら ない こ と が 分 か る

。

ま た

，

第

1，2

式よ り

，

σr と τ，e は 同 じ r のべ _{き乗を も た ね ば な ら な}い

。

この よ う な考 察 よ り

，

応 力 成 分は

，

ブ 2の特 異 性を もつ こ と が分か る。 し た がっ て

，

変 位は r

−

1 の特 異 性 を もつ

。

こ の よ う な 変位 成分 も応力成分 もともに r のべ _{き乗 型}の特 異 性を もつ _解は

，

文 献

6

）な どで著 者ら が提 案した有 限要 素法 を利用し た方 法で解くこと ができ る。 こ の特 異 解の数 値 計 算 法の概 略を以下に示す

。

　2次 元 弾 性 論による と， r

，

θ方 向の応 力の釣 合 式は 極 座 標 系で次 式の ような形で表 され る。 　 　 　 ∂ar 　 　 　 　1 ∂τ

．

θ σド σθ

　　　

万ア＋

i

∂r ＋

　

r

　

＝

o

　 　 　 　

…

　

t−・

・

・

…

　

一・

・

…

　（26＞ 　 　 　 　 ∂σθ 　 　 　 ∂r

，

e 　 　 　 　

2

τre 　 　 　 l

　　　

下 齎 ＋万 「＋

−

i

−

＝ e ま た

，

応 力境 界 条 件は 次 式で表さ れる。 　 　 　τ

，

e＝

O

，　σs＝

O……・

…・

…・

……・

………・

・

…・

（27） （26 ）式の各 式の残 差 をそ れ ぞ れ

Rr，

　

Re

と して

，

_{仮 想} 仕事 方程式を 作ると次の よ うにな る

。

∬

∬

（

R ・

aUr＋R、fi・、｝・d・

d

θ ・

∬

（Tr… 。＋ ae・u，）蹄

一

・

・

一 …・

・

…

（・

8

） い ま

，

荷 重 点 近 傍の r の べ き乗 型の応 力 特 異 解 を求め る ため に

，

変 位 解 を 次の よ うに変 数 分 離 形に仮 定し て み ることにする

。

　

　

　

瀦

：

_；

黝

一 ・

・

一 ………一 ・

・

… 9・ これに対 応す る応 力 も次の ような変 数 分 離 形とな る

。

　　 　σ試r

，

θ）

；

rλ

一

匚σ；（θ） 　　 　σ訊　r

，

　e）； rλ

”

σ

X

（e）　

…・

・

…・

……・

…・

・

…・

（30） 　　 　τ

。

e（r．θ〕

＝

r ”

”

’ τ

fe

（

e

） （29＞

，

（30） 式 を （28）式に代 入し

，

部 分 積 分 を行っ て 整 理す ると

，

次式が得ら れ る

。

∬

｛

（・・弊

一

・餌 ・（・＋

1

）・

fe

・露

一d

_盞

_笋

_・

_re

一

_響

_・彦

_｝

一

・

…………一

（31 ） こ の式に基づ き

，

θ座 標を要 素 分 割し

，一・

つ の要 素 内の 嚠 θ）を θ の 1 次式で仮定する と

，

最終 的に次の よ うな 要 素 方 程 式 が 得られ る

。

　 　 　

1

δu＊

1

［

k

］

ju

＊ ｝

＝

O

・

…・

…

　

…・

・

………

　

…・

…

　

……・

（32） こ こ に_， ［

h

］は要素剛 性マ ト リッ クス であ り

，

次 式の よ う な形を して い る。 ［・］

一

嗇

t

（λ2

−

₁ ）〔x十1）　　x

−

1 HODE1

．

o × 　 　

3

　 　 　 　 　

1

1

（λz

−

_1）（ κ十1） 　 　 　 x

−

1

　　

6

　　

＋

『

T

　 　 2λ

一

λx 十1 　 　 　

−

（λ＋ x） ‘偽

碧

（_型 ・

_气

L

l

（λ：

−

_1》（ κ十1

．

｝　　x

−

1 　

3

　 　 　

1

　 　 λ十x

−

_（2λ

一

_λゐ ；十1） 0

．

8 O

．

5 D

．

4 D

．

2 O

．

O

｝

O

．

2

一

D

．

4

一

〇

．

6

一

Q

，

6

一

Lo MeDE1

．

0 0

．

8 o

．

6o

．

4 o

，

2 O

．

0 3D

°

Ur Ue

凸

60e ● 　 　 　 ム　 　3　21e 旧e“ 仁8 　 　 　 0　 　6　ele ロent3 　 　 　 0 　 　9　ele

田

ents 　 　 　

−

　 　 　 　exact 図

一

8a　2次元集 中 偶 力問 題の変位モ

ー

ド 凸 ee

日

o e ム

τ

re o o　 　 　 n ， 〔

一

〇

．

2

一

〇

．

4

一

〇

．

6

re．

e

一

1

，

0 ］D

°

Or 60e ● b ● 　 　 　 　a _{3　ele 口}T 巳nt3 　 　 　 ■　 　6　elemen ヒ3 　 　 　 0 　 　9　elEmEnt8 　 　 　

−

　 　 　 exaGt 図

一

8b　2次 元 集 中 偶 力問 題の応力モ

ー

ド 日

M

（

（

．

M

一

1

．

92

曹

1

．

93

一

1

．

94 59 69

一

一

k 　

凵

O

」

_鴫

｝ 　

＝

国 U

同

国

一

L97

一

1

．

gs

一

1

．

99

一

2

．

oo l　 　 　

l

l　 　 　

I

l

　 　 　

l

l　　　　　　

8

　　　　　　 1

一

…

「

…

J

図

一

9　2次元集 中偶モ

ー

メン ト問 題 481216 Nu

口

b2r 　gf 　ele

叩

e

四

し8 　 　 　 v

■

O

．

3 　 　E

回

1

．

0 2024 図

一

10　2次元 集中偶モ

ー

メン ト問 題の解λ の収 束 性 　

一

（2λ

一

λz

−

1） 　 　 　

一

（λ

一

x）

1

（λ2

−

1）（x

−

1）　　κ十1 　 　 　3　 　 　 　 ‘ ♂偽

黔

一

1） ＋

甼

　 　 　 λ

一

x 　 　

2

λ

一

λx

− 1

1

（λ！

−

₁ ｝（x

−

1 　 　6 ）_＋

牛

1

（

M

−

1）（x

一

ユ）　κ十1 3 　 3 ‘ 3

G

は せん断 弾 性 係 数であり

，

x はボア ソ ン比に関係する 定数 で

，

x

＝

・

3

−

4v 〔平 面 ひ ずみ 状 態 ），　 x

＝

（3

一

_の／ （

1

＋の （平 面 応 力

状

態 ｝で ある

。

1

　eよ要 素 角の大き さを

．

表す。 また

，

iu

’

1

は次_φよ う な要 素 両 端の節 点

i，

ノに お ける節 点 変 位ベ ク トル である

。

　　　｝u＊ ｝「

＝

Lu

褒1

，

冠ち

，

秘翫

，

u；」」

・

・

……一 …・

・

……

（

34

） し た がっ て

，

領 域 内の全要素に 関 す る 要素剛 性マ トリッ クス _［

k

_］を作 成し

，

これ を重ね合わ せ た もの を_［κ_］とす EDD 岡 DL O，8 0

．

6 0

．

4 D

，

Z O

．

0

一

〇

．

2

一

〇

．

4

幽

o

．

6

一

〇

．

8

一

LO 　 　 　

△

　　　3　element5 　 　 　 ●　 　6　elements 　 　 　 o　　　g　elemEnts 　 　 　

−

　　 　exact 図

一

11a　2次 元 集 中 偶モ

ー

メ ン

』

卜問 題の変 位 モ

ー

ド 鬥ODε 1

．

O o

，

8 o

．

6 o

．

4 o

．

！ O

．

0

一

〇

．

2

rD．

4

一

〇

．

6

．

一

〇

．

8

一

1

．

o

3

　

1

：

1

：躍：鬻 0 　　　9　elemen ヒ8

−

　　 　etac し 図

一

11b

．

2次元集 中偶モ

ー

メ ン ト問 題の応力モ

ー

ド れ ば

，

特 異 性パ ラ メ

ー

タ λ の値は

，

次 式に示す よ うに

，

’

マ トリッ ク ス ［K ］の行 列 式が 0 とな る よ う な 固有 値 λ を計 算 する ことに よっ て求め ら れ る

。

　　　

i

［K（λ）］

1

＝

0

…

　tt・

・

tt・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

…

　

（

35

＞ ま た_， こ の 固有値に_対応する_節点変位ベ ク トル _亅

U

＊

1

_が こ の問 題の_変位モ

ー

ドで あ り

，

さ ら に

，

変位

一

ひずみ

一

応 力の関係よ り

，

応 力モ

ー

ドが求め ら れ る

。

3．2

解析 結 果 　この有限要 素 法に よっ て図

一

7の集中偶力問題の解析 を行っ た ところ， 要 素 分 割 数の増 加に伴う固 有 値λの 正解

一

1へ _の収 束_は良 好_であっ た。 変 位

，

応 力モ

ー

ドの 解 析結果 を 図

一

8a

，

　

b

に示す

。

　

参

考

ま でに_， こ の問 題の応 力 解の正 解を示 すと次の よ うにな る5｝

_。

舮 ユ

聖

。

i

。2θ 　 　 　 πデ σθ＝

0

，．θ一

聖

（

1

＋。。s2 θ｝ 　 　 πr

・

・

・

・

…



一・

・

・

・

・

・

・

・

・

…

_（36） 　ま た

，

図

一9

の _{集 中}偶モ

ー

メ ン トを受ける場 合5 ）は

，

同様の考 察か ら

，

応 力 が r

−

S の特 異 性 を も ち

，変

位が ゲ t の_特異性を もつ_。 こ の場合も本節で説

明

し た有 限 要 素 法で解 析す ること が で き る

。

固有 値λ の正 解は

一

2で あり

，

_{本 解析結}果の_{収束 性}を図

一

10に_， 変 位

，

応 力モ

ー

ドを図

一

11a

，

　

b

に示 してお く。 な お

，

こ の 問 題の応 力 の正 解は次 式で_与え ら れ る5〕 。 ・一

警

_（… S3_θ

一

_… S ・_〉 。，一

一

4

讐

_。。s・_θ 　 　 　 π 『 r

，

e− 12

竺

α c。s

・

e。

i

。・e 　 　 　 πr

・

・

・

・



・

・

…

_（37）

4．

結 　論 　本 稿で は

，3

次 元弾 性基本解の_{変位 式}を

一

般 的なフ

ー

リエ _{級 数 展 開}で表現す る と き， n

＝0

の場 合は

3

次元 Kelvin解や3次 元

Boussinesq

解な どの_{線 （軸 ）対称}解 に_，n≧1の場 合は

，

高 次の面 対 称 基 本 解に な り

，

さらに

，

こ の う ちn

＝

1の場 合は 3次 元

Cerruti

解にな ること を 示し た。 本 槁で は

，

この 3次元

Cerruti

解を有限要素法 で求め る た めの_定式化を行っ た。 解析を行っ た結果

，

前 報 （第

2

報 ）と 同様に良 好な数 値 解が得られた

。

　また_， 半 無 限2次 元 弾 性 体 表 面に集 中 偶 力また は集 中 偶モ

ー

メン トを受ける場 合の応 力

，

変 位の解を求め る問 題は_， こ の応 力

，

変 位が ともに r の べ き乗 型の特 異 性 を 有 するため

，

固 有 値 問題 と な る。 この問題に対して は

，

すで に著 者が提 案し て いる有 限 要 素 法によ る クラ ック先 端 近傍の特 異 解 析 法を適 用して解 析し た ところ良 好な数 値 解 を得ること がで き た。 　これ までの研 究 を通し て

，

以 下の よ う なこと が明らか に な っ た。   2次 元お よ び3次元弾性体におい て， 集 中 荷 重 近 傍の解 （弾 性基本解 ）を有 限要 素法により解 析 す る場 合，

一

_{般に は固 有 値 解析 問 題と な る} 。   し か し なが ら， 2次 元 問 題の弾 性 基 本 解の う ち， 通常の集 中荷 重 を 受ける問 題 （

Kelvin

解

，

　 Bottssinesq_解 ，　

Ce

【ruti 解） のみ例外で

，

こ の種の問 題は

_，

変 位 が対 数 型特異性 を も つ た め

，

固有 値 解 析 問 題と ならず

，

荷 重ベ ク トル を右辺 と する_連立 方程式を解く_問題と な るe   有限要素法で

Kelvin

解

，

　

Boussinesq

解，　

Ce

τruti 解 を解 析す る と き

，

2次元 問題では

_，

こ の 3つ の解の対 称 性 を議 論す るこ と な く解く こ と が で き る が_， 3次元問 題で は_{， ］}；elvin 解 と

Boussinesq

解は軸 対 称 問 題と し て

，

　

Cerrul

：

i

解は面 対 称 問 題と し て

，

そ れ ぞれ区別し て解 析し な く て はな ら ない。  弾 性 基 本 解の応力もク ラッ ク先 端 近 傍の 応 力 も

，

ど ち らも r＾

−

1 の形のべ _{き乗 型の特 異 性をも}つ が

，

弾 性 基本解の場合は

，

λはOま た は負の整数である の に対し て

，

ク ラック先端 近傍の応力解は

，

λ は

0

＜λ＜1の値を と る。   弾 性 基本解を有限 要素法に よっ て解 析 し た とこ ろ

，

2 次元問 題の 場合も3次元問 題の 場合も

，

解は非常 に良 好な収 束性を もっ て いる

。

　

な お

，

本 稿に示し たよ うな計算法で求め ら れ る数値弾 性 基本解 を，境 界 要 素 法に組み込んで使用す る た めに は

，

この種の数 値 解をデ

ー

タ フ ァ イル に記憶 させ

，

補間な ど の手 法 を用い て

，

任 意 点の任 意 座 標 軸 方 向の単 位 力に対 する任 意 点の応 力

，

変位の_値を取り_出せ る よ うに してお か な け ればな ら な い。 この よ うな デ

ー

タの入 出 力の 取 り 扱い につ い て は

，

これ までの研 究でふ れ ていないが， 今 後検討する必要が あ ろ う

。

謝 　辞 　 本研究を ま と め るに あ た り，広 島 大 学 吉田長 行 助 教 授

，

学生 坂田邦 宏 君 （現 鈴 与 建 設 ）の協 力 を得た。 こ こ に感 謝の意を表し ま す

。

参 考 文 献 1） 藤 谷 義 信；特異 応 力解 （ク ラッ ク先 端近傍の解

・

弾 性 基 　 　本解等〕の解 析に閧する 二

・

三 の考 察

，

日本 建 築 学 会 中 　 　国

・

九 州 支 部 研 究報 告

，

第8号 1

_，

構 造 系

，

Pp

．

445

−

448

_，

　 　1990

．

3 2） 藤谷義信 ：3次 元 弾 性 基 本 解 （線 対 称 解 ）の有 限 要 素 解 　 　析

一

有 限 要 素 法によ る弾 性 基 本 解の解析 に 関 す る研究 〔そ 　 　の 2）

，

日本建 築 学会 構 造 系 論 文 報 告 集

，

第407号

，

　 　pp

．

71

−

77

，

　1990

、

1 3｝ 藤谷義 信：2次 元 弾 性 基 本 解の 有 限 要 素 解 析

一

有 限 要 素 　 法による 弾 性 基 本 解の解 析に関す る研 究 （その 1｝EI本 　 建築 学会 搆 造系論文報 告 集

，

第393号

，

pp

．

54

−

6

．

t

_，

198811 4＞ 田 治 見宏ほ か ；地 震工学

，

彰 国社

，

1970

5＞　Timoshenko

，

　S

．

　and　GooClier

，

　

J．

N

，

：Theory　of　ELasti

．

　 　6ity

_，

2nd　Ed

．

，

McGraw

−

Hill

，

1951

6｝ 藤 谷 義 信 1有 限 要 素 法に よるZ次 元ク ラック

．

先 端の応 力

　 　特異 解の解 析

，

構造工学論文集

，

Vol

、

31　B

，

　_pp

．

103

−

114

，

　 　1985

．

3

7〕 宮本 　博 ：3次 元 弾 性 論

，

裳 華 房

，

1967