プール沸騰冷却超電導体の熱安定性

九州大学学術情報リポジトリ

Kyushu University Institutional Repository

プール沸騰冷却超電導体の熱安定性

久保田, 裕巳

https://doi.org/10.11501/3147914

出版情報：Kyushu University, 1998, 博士（工学）, 論文博士 バージョン：

権利関係：

2. 2 動的熱安定性

前の章では， まず静的平衡の古典的理論であるStcklyの)k11�1)， 最小rrr 1 復領域(MRZ)， Maddockらの等面積理論2)および最小伝情領域 (_Mfな)_:.1)の 各基準の相互関係を比較検討した. 次に， それら領域内で、それぞれ数値計

算を行なって得られた数値解を 比較吟味し， 静的平衡理論の体系化を行な った.

し か し， 多様な動作条件 に晒される現実の超電導マグネットを， このよ うな静的基準をもとに設計しでも安全性は保証できな い .

そこで， 最小伝播領域(MPZ)およひ、最小回復領域(MRZ)の動作電流領 域において， そ れぞれ非定常熱伝導方程式を現実の熱擾乱を想定した初期 加熱条件とともに数値的に解いて， 動的条件下の超電導体の応答を温度や エネルギーの観点より吟味し， 静的平衡理論との関係を明らか にする. そ の際， 現実の熱擾乱を想定した初期加熱条件には， 時間的， 空間的に なる

べく広範囲の条件を設定する. さらに加熱量を様々に変化させ， 導体の超 電導状態が壊れて常電導状態となり遂にはクエンチ(quenching)に至るか，

あるいは 超電導状態に回復する(recovery) かを調べて， その境界の条件 (しきし\値)を探る. また， そのしきし\値をもとに， 動的 なMPZおよびMRZ に対する安全性判定図を作成する.

2.2. 1 某礎方程ェ

前節と同様な十分に長い 導体を考える(図 2. 20). 記号も前章と同様に，

この導体の熱伝導率をK， 冷媒に接触して いる導体の周長をP， 導体の断 面積をA， 導体の単位表面積， 単位時間当たりの発熱をG， 導体の単位 面積， 単位時間当たりの冷却をQとし， さらに， 時間をS， 導体の比熱を C， 導体の密度をρ， 単位体積・単位時間吋たりの加熱をHとすると， 導 体断面内の温度分布を与慮、しないで一次元的に論ずることにすれば， 導体

51

ド」ovoコ刀C00

』Oω」コ日mw」ω巳Fとの日 current

sharing superconducting normal region region region

que

�

^ching

cold end

。

^X

center of symmetry hot end

orig in of co-ord in ate x

Fig.2.20 Schematics of hot region along conductor

52

の対称中心から距雌Xにおける温度T(X，S)は， 次の一次元非定常熱伝導 方程式により表される.

ダ - 一 グ ( | K

^�_

-

^òT

ì | +ー

^P

(C - Q )+ H

õs òXl ÒX) A (2. 74)

この非定常熱伝導方程式を，前章の11正次元数の式(2.6)から式(2. 14)およ び次の無次元数を使用して無次元化する.

c=-C C B

T二

一一一

S Sch

SJ =ρÞACB(To-TB)

… PQm以

q PQm似AH

(2. ₇₅₎ (2. ₇₆₎ (2. ₇₇₎

(2. ₇₈₎

ここに， Sは時間， Cは導体の比熱， ρは導体の密度， Hは単位体積・

単位時間当たりの加熱量， cは無次元比熱， ηは無次元加熱量およびZは無 次元化した時間である. また， Schは， 長さLの導体に蓄えられる熱エネノレ ギALCB(九- TB)ρを， バーンアウト熱流束での伝熱量PLQAfAXにより除去 するのに要する時間である. このSchを特性時間(characteristic time)と

呼ぶ13)

無次元化の結果は， 以下のようになる.

δ1 θ(ー δ(，

c- =一

I k � I+ (g- q + ヴ)

グτ み\ é 玩 j

^{(2. 79)}

この基礎方程式を， 動的最小伝播領域(Dynami c MPZ)および、動的最小田

復領域(Dynamic MRZ)にそれぞれ対応する初期条件， 境界条件および加熱 条件とともに数値的に解いて，それらの結果を以下の項でそれぞれ述べる.

なお， 数値計算の計算条件は， 冷媒温度と超電導体の臨界温度に関して は， 前章の2. _{1. 3} (b)と同じとする. つまり， 冷媒としては， 大気圧におけ

53

る飽和液体ヘリウムを考える. したがって， T二4.2Kにおいてf二Oであ る. 超電導導体としてはNbTiを想定し， その臨界温度を7.2Kとする. し たがって， この混度で無次元温度は式(2.6)により， /=/o二l となる. た だし特性発熱eに 関しては， e二lとする.

なお， 図2.21に， この計算に使用した無次元発熱g(t)， 無次元冷却q(t)，

超電導体の母材で、ある銅の無次元熱伝導率k 6)および無次元比熱C 6)を示す.

ただし， 無次元比熱c以外の特性は， 図2.3と同じである.

2. 2. 2 動的最小回復領域(Dynami_c MRZ)

(1)初期条件， 境界条件および発熱条件

初期条件および境界条件を以下に示す.

初期条件: ^{T(X，O)二九} 境界条件:

乙

_ôXT

₍

_、X.S

�

₁ ^{= 0}

IX=O

(2.80)

(2.81)

(2. 82)

ここで， 式(2.6)から式(2.14)および式(2. 75)から式(2.78)を用いて無次元化を 行うと， 以下のようになる.

初期条件:

市

^，0

)

^{= 0 (2. 83)}

境界条件:

え

^t

⁽

^υ

^{) /}

^{= 0 (2. 84)}

三

^t

⁽

^xτ

⁾¹

^{二O (2. 85)}

Xー今日コ

51

ιJ . l+=

101.�

cl..

CJ)

QVmwωこ

てコω N

ro

ε 0 100 ^c

よ〈 102

8

>、

吋圃d

〉

61:5

コ てコC

0 0 の戸』」ω工戸刀ωN=の戸』」OC

っι AEE 'Ft tt 4kμ1

101

100

1 2 3

nu nu nu

dEE AEE ペEE

boc=000刀ωN一一ωε」0C COZEωcω。ちω忠一CE」OC

0)

100

normalized temperature

10-1 101

Fig.2.21 Normalized generation，gの， normalized cooling， qの，

nonn�!iz�d the�al conductivity， k(りand nonnalized specific heat， c(t) ， used in calculatíon

55

b加日熱条件は，非加熱長さX又I川P

採用した. これを熊次元化して次式に示す.

XIP11<X かつ 0<τ三τI ヴ=ヴ/111

o<xs;x /111 または τ>τ1 :ヴ=0 (2. 86)

x. ^/111

- ー」ニι

x Xch (2. 87)

τ =ー」斗ι川/ S _Sch (2. 88)

である.

図2.22に，この場合の典型的な温度分布を，図2. 23に，無次元非加熱長さ Xini'無次元加熱時間τ/111および無次元加熱量ヴ/111であらわした初期加熱条件を示 す.

(2) 離散化

式(2. 79)を離散化する7)なお，離散化を行うにあたり，検査体積の設定はh' 2. 6のように行なった.

τ d x d

、‘，j d一枕 'K 〆，，‘、、 グ一み e r--d w

Jmnijr

一一

x d

r

d

d一次 C

JYilJr ept・E1'w

τ d

YA

e /EE1 q g nl M al--w

T すi1d

(2. 89)

r w

ここで

‘ ' 。

を時間的にζ古い'値とすると 左辺は，

j 下デd ^T dx = cp企x(tp -t:)

w

^{0 T}

(2.90)

56

斗-

0

superconducti ng reglon

que円ching

current normal sharing I region reglon

reqovery

cold region hot end

。

center of symmetry cold end

origin of co-ordinate

^x

X

Fig.2.22 Schematics of cold region along conductor

57

η

Fig. 2. 23 Normalized heat input introduced as disturbanc句(x， τ) for dynamic MRZ

58

右辺第1項は，

TJ ^r j _一 グ

^d

_一 x (欣k一)凶d依x '

^{d枕xd / d抗τ}

二 r 1 � 了 ^{r1 ?} l ^ド _ ^{[ " ke( ��e} _{(伊δ Xけ)e} ^{仏ド ο ん十いe 汁 / →1サ 一} ' ^んυp p ρ) 九川(t仏什(tp ^/ / " ��p (μδX吟)w ^{らケい p 〆} - ， ^一イ ' ^{1 /ヘH} w/ 1 附τ I

^{(ω2.9引刊lο )}

時間積分の際， Fully implicit scheme を採用すると，

つJUA叶υ qL

T A斗 「llIll1114 、、，，ノ 一 こり ps 一

μ、てοW一/t1、

'K 一 pa

一

e 一 一 X れτο 'K一 「hill--lL 一

一

T

x d d

、‘.，ノ

'K ，d一改

/'t\ 一Yんま37頁一戸ηJγ'r，つムgfE16Wヤコフ

山 j rm

f r f(q-g-η沖約二(q w - g _{-1J)(Xe -xw)�r}

^(2幻)

となる.

したがって， まとめると以下の様になる.

_Ike(te -Ip) kw(tp -tw) 1

C P 7

_{は 'f}

- (fpーら)- ' ^{Y Y '} | ^{L (5 x)e} - ^{(δx)w I} 卜 (q- g ーヴ)(人一 九)

(2. :94) 以上を整理すると

aplp = aEtE

+α w ₁ w _+b

^{(2. 95)}

α戸二一一三-

k '-' (&)e α ， 二 ーァ k ヱ v

" (5x)w

(2. 96)

(2. 97)

o ^{� x}

α ^{p p �τ}

^=c

一一一一-

^{(2. 98)}

α

^p

= - α+α ..，.

^E

I ^{.. .... �v I} +α ^{..，. V} P

^{(2. 99)}

ド

レ

^{i(i -i.�c)}

-

^q

+ヴ}+α:/: = _{(g -q +ヴ)釘+α;f;}

格-fこ点の番号は，

x

^{= 0 より m =} 1.2.3・・・と決める.

(2. 100)

59

佑子点m= 1 (断熱)での温度の計算は次のようになる.

αp/p =αE/E ^{+ b (2.101)}

α� - 一一一三-k L (&)e

(2. 102)

今ム一//一TX一一A斗広一p c

α op _{(2. 103)}

α_{p -}=α\AE +αo I � P (2. 104)

b二(g-q+η)位/2 +α;f; (2. 105)

m=2の点の温度は， 先に求めた格子点m二lにおける温度および、m二3におけ る温度より求めることができる• m =3以降m= 25000までこのような計算を各 時間ステップで温度が収束するまで繰り返し行なった. ただし収束条件に関し ては， この計算では，前回の計算値との温度差が10-4以下になると温度が収束し たとみなした. なお， 格子の数のmをどのくらい大きく取ると境界条件の工

(2. 85)が満たされるかどうかを計算結果の温度分布より確認してm= 25000と した.

(3) 計算結果および考察

(a) 温度応答

内I 2. 24 (a)および図2. ²⁴ (b)に， それぞれ超電導体が， (a)超電導状態に復帰

する場合(recovery)および(b)常電導状態に移行する場合(quenching)の温度応 答の1例を示す. 計算条件は， e = 1， i = 0.5， xmi = 0.5， '，m = 0.5は共通であるが，

九はそれぞれ(a)ヴlIIi = 4.84254， (b)弘=4.84255であり， 導体上の中心より片 側半分の温度分布を経過時間とともに示している. 図中， 無次元時間をパラメ

タとして記しているが， 時間の経過とともに温度が変化する様子がわかる.

60

判

1.5

ト θ二1

む」コパ苛」ωaεω一v力むN一一句εLoZ

X;n;二0.5 l二0.5

τ=0.1

30 Normalized distance from hot end ^x

Fig.2.24(a) Excursion of normalized temperature，

t(x，

_7:)

in a dynamic MPZ (recovery)

1.5

、恥叫

む」コパ芯」むaEUH℃ω丘一句ELoZ

xf力;=0.5 I =0.5

Fhυ Fhlv η/』A斗FヘunonU』斗一一一一em-m r 刀'

τ二0.1

e二1

30 Normalized distance 合om hot end ^x

Fig.224(b)Excursion of normalized temperature7f(Xy ^f

)

in a dynamic MPZ (quenching)

(b) クエンチとリカバリーの境界の探索

クエンチとリカバリーの境界を 探るため，)JIl熱時IMJ Tl/lIと加熱長さXM11を同じに してlJmiの値を変化させながら慌度応答等を調べた. ここに，その境界を求めた

結果を1つの例と して示す. なお， 導体がクエンチに至るか，リカバリーとな るか は， 導体中心;昆度の時間変化， 無次兄混度がf壬Iの低机領域の導体ql心軸

より片側半分の長さ(以後九old

(τ)

^{/ 2 と}

記す)

の時間変化および、導体の除去エネ ルギー の時間変化 より判定できる.

ここに， 除去エネルギーについて定義する. MRZ平衡において は， 図2. 22に 示すように中心部分の温度が周囲よりも低い慌度分布を示す. この導体に蓄え られるエネルギーは 無限大と なり計算できない.そこで， 7;聞を各時刻における

導体の最高温度とすると ，導体が均一にTrr閣の温度の時に蓄えられるエネルギー から この時刻 の温度分布にある導体に蓄えられるエネルギーを差しヲ|し1た値を 考え る. このエネノレギー値を除去エネルギーと呼ぶことにして，その1/2をエ!

に表すと以下のようになる.

E

= foOJ f;m副〆'AdTdX

二ρ4(九一九'y:BXchO

c.， [七("(yl f'1

δ=ニ = ~ = l d r l m 出 c(tノdt

E。

ρ�(To一九ノCBXch

h L

(2. 106) (2. 107)

T -T，

ここで，^• tmaxは各時刻における導体の無次元最高温度であり ^{仁 max} βで

ある.

山

五一九

図 2. 25 (a) ， 図 2. 25 (b) お よび図 2. 25 (c)に ， それぞれ， 計算条件 e = 1，i

=

0.5，x'l1l二0.5， T'11l = _0.5 の

場

^合の(a)

導体中

^{心における無}

次

^{元 温}

度 : 巾

^，

Tτサ)

(ωbω)低温領域の長さの1ν/2上: I乙ιω叫 old

パ 付 ( (や

^T

サ )ν

^/2， (c) 無次元除去エネノレギーの1/2

:δ(τ)

の無次元時間τに対する変化を，ヴ1日川P

て， ヴq仇札1/川，川川li

=

^4.84255以kの場合がクエンチ，ヴ九刀二4.84254以 Fの場合がリカバリ一

62

(むのの∞のhh.OH) N広三c一ωLコパ干の」ωaEω判℃

Cω宝00

←

τ1m Xini =0.5，

戸\

ト4

�

^1.5

o

�

50 100 5 10

Normalized Time 7:'

T emperature at ^x二O

0 0.5 0.1

� fち

ω L

� コ

ro lo....

ω

E

^0.5

← ω

てコω

トJ ro E

lo....

Z 0

(OO寸OO∞ω寸.N川)

N庄三ECOB2200』0王切Cω一吉工

←

(a)

5 4

2 3 N\へい」ミ。d・co一切主主00』O工Ucω一』一市工

100 50

1 5 10

Normalized Time

Half length of cold region

0 0.5 0.1

τ

E、、』 〆{、、

o:: S?

� ;..二 4ー--E

E

m T一

"、..-­

cも. �

、lJ.hu rrtk

7:'im

=0.5， Xim二0.5， 7:'仰二0.5

Recovery

一一一ー一一-¹一一一一一一一^丸山アり-^一一一一 25

20 15 10

へと勺do一志刀むLωCU刀ω出一句ELOZ

5

50 100 5

1 5 10

Normalized Time 7:'

(c) Energy deficit

0 0.5 0.1

Fig.2.25 Excursions of interesting quantities

( ;=0.5， xinpO.5， �inFO.5)

63

と判定される. したがって， これらの値の問に境界値が存在することになる.

�-tお， 図中に'，mを縦破線として示す. また ， 横破線は静的安定性理論の1つで ある最小回復領域(MRZ)による(a)"-' (c)の値である. ヴ が境界値に近づくにつ れその分岐点は横破線のMRZにおける値に漸近する様子がわかる. 本研究の場合，

これら(a) "'-' (c)の値が最小回復領域(MRZ)による値に明確に収束するような結 果は得られなかった が， MRZタイプの熱擾乱に対する動的安全性基準と静的平衡 理論の一つであるMRZ平衡理論の関連は明らかに認められる.

(c)クエンチとリカバリーの境界近傍における計算結果

これまで クエン チとリカバリーの聞における境界の探りかたを例とともに 示してきた . 次に， この境界近傍におけるいくつかの加熱条件 における計算結 果を， 特性発熱をe ⁼ 1に対して示す. なお， 以下の結果は ， 先の図と同様にい ずれも(a)導体中心における無次元温度:巾ス)， (b)低温領域:仁old (τ) / 2および (c)無次元除去エネルギー:δ(τ)の無次元時間τに対する変化を同時に示す

( i ) 加熱条件τ1mの影郷

� 2. 26に ， 計算条件e ⁼ l，i二0.5，xi円1ニ0.5を共通に し てτ1mをτ1m二0.5^，

τzni ⁼ 1.0およびτini ⁼ 5と変えた場合の比較結果を示す.全体的な応答の様相は 大 差なく，時間τ1mのあた りで中心温度ゃんold (τ)/2が急に大きくなりしばらく横破 線のMRZにおける値に漸近した後τ=50近傍でクエンチとリカバリーに分岐する 傾向を示しているが， 横破線に漸近している時間はτ1111が大きいほど短くなって し1る.

6/1

(むのω∞のhh.OH)

N庄三c一ω」コパVEω丘Eω判℃C

ω七一00

十

7:';171エ5

τ;/7;=1む5τifJF1 1.5

F「unu

ヘiNGL判、OHNHmwωLコ一vmwLωaEω←刀hU2一のELoz (OO寸OO∞の寸.NN)NZEECOBE豆。こ。工Ucω一半一の工

←

50 100 5 10

Normalized Time ^7:' (a) T emperature at ^x二O

0.5

5 月X勺

e=1

i司.5

50 100 5 10

Normalized Time 7:'

Half length of cold region

0.5 0

0.1 約\ヘぃ、\OJ・COBE200半O工Ucω一い一の工

5 4 3 2

、、，sJLU fEK

ト.，J r句、

庄 0� �

� 0

.._ーこ に

m ...­

"， マ・・­

E勺 �

100 50 5 10

Normalized Time ^7:' (c) Energy deficit

i =0.5， X;/7;二0.5

0.5 25

20

5

0 0.1 10 15

ヘh)'も島村一ο一志℃〉凶LωCU勺ωN=のにとoZ

Fig.2.26 Excursions of interesting quantities

(

^{e = 1 ， /-}

0.5，

^XjnF

0.5 )

65

( ü )非加熱長さX，mの影響

計算条件e

= 1，ル=0.5を共通にして非加熱長さxtmを変えた場合の比較

結果を， 図2. 27 (動作電流i=0.5)， 図2. 28 (i二0.615)および凶2. 29 (i=0.475 ) に 示 す . いずれの動作電流 においても ， XIP71二0.5および X，l1i -1では全体的な応答の様相は大差ないが， XInI二5になると応答がかな り異なっており，非加熱長さXiniの影響はかなり大きいことがわかる. しか も，動作電流が異なる場合は，動作電流が大きいほどxmIの影響は大きくな

るようである.

(iü )動作電流jの影響

計算条件e

^{= 1，} Xim = 0.5ヲT，円i = 0.5を共通にして，動作電流をi=0.475， i=0.5お よびi=0.615と変えて場合の比較結果を図2. 30に示す. これらの結果より， 動 作電流の影響は大きいことがわかる. とくに， (c)の無次元除去エネルギー:

δ

(

^τ

)

^{の差が大きい} (差が大きすぎるので縦軸をlogスケールでとっている)

これらの違いは， 細線の横線(それぞれ破線， 実線および一点鎖線)のMRZに おける値がかなり異なることに関連しているようである.

66

(ωω的。めhh.OH) e=1

2

へいさ、む川Uヘ百ω」コさ包Eωト勺ωN=のE」OZ

500 0.5

(OO寸OO∞の寸.NH)NZ25coE2200』0工UE一吉工

←

5

4 3 2

N\下、。ナco一切ω」℃一oこo工Ucω一恥一の工

500

^{nu nU 4E---nu Fhd} _r

5 10

Normalized Time

Half length of cold region

0.5

ト、J ;-、

0::: 9.

E ニc ^r::. o ... r、

co 4・- '(五ご

勺 11、-._/

、、lJ仏Ufzk

Z" íní

と103

、

+-' 0

� 102

b ω

はJc 1

勺10'

_ω

トd

E ro

� 100

一 0.1 5 10 50 100 500

Normalized Time Z"

(c) Energy deficit

0.5

Fig.2.27 Excursions of interesting quantities

( i=0.5， ゲ♂0.5 )

(ω←∞∞め←門.OH) ト寸庄 三C

ω L

+J コ

f匂lo....

ω ♀

E ω

4噌一一一_てコ+J

C ω

て30 0

7:int

500 50 100

τ

5 10

Normalized Time (a) T emperature at x二O

0 0.5 0.1 0.2

QU

AHE nU

ハU

のω」コパFEω且Eωト℃ωN二mwELoZヘhOL?O川」ベパ干

0.6

(oomNOUNh←日)

ト寸Z E C C o

b.D ω

lo....

Tコ

。。 斗ー0 4咽一一一_....c

U C ω

斗­

工ro τJnl

5

4

3

2

内\へh当。J・cOBE宝00』O王切Cω一半一の工

500 5 10 50 100

Normalized Time 7:

Half length of cold region

0.5

、1J仏UJfk

ト、J ，，--句、

� 2 4・-� a，

E巴_くO

1万 m句o

Eむ とL

7: ini

1=0.615

l xml=05(万ini=3.98115)

片一一一一一一一一一ー一一一一-一一一

1 (5.70326) 一 一 一 一 -f .!.一 一 一 一 一一

;

:

50ト/ |

//

Zアini=0.5 nu

nv Fhd

nu へと'もどο一志万治」ωCUBSELoZ

500 50 100

5 10

Normalized Time (c) Energy deficit

0 0.5

0.1

r

Fig.2.28 Excursions of interesting quantities

( í =0.615，

l:

in;=O. 5 )

(ON∞寸∞O∞∞.OH) NZEC一ωLコ一石」ω己Eω

μ刀 「』ω 豆 00

7:'ini

500 5 10

Normalized Time 7:'

(a) T emperature at X

0 0.5 0.1

ヘしNOL判.ONN一干のω」コパVEω己Eω←刀む忠一のELoZ

7:' ini二0.5

Xil7lニO.5( 7J仰ニ5.13147) 1 (6.86489) i =0_.4 75，

θ二1

2

( OO的。∞∞-c . NH) NZ25 co一切 と℃一 00 恥O工Ucω一恥一句工

←

=0 5

4 3 2

N\ヘミ\。ア co一切ω 」刀一 oごO工普ω一恥 一の 工

^{500 5 10} Normalized Time ^7:'

Half length of cold region

0.5 0

0.1

、、IJLU ，，『‘、

ト.，J ...

庄 笠� è'í

c

「・、

-一 ぱコ

�一一 主的σコ

ヤ 11.， 、、../

cも τInl

3

2

1

0

0

nu

nu

nu

nu 4・・・・45・・a唱・・・a旬・・・

ヘ-NL勺， μ百一志勺〉凶LωCU刀ω旦古川ELOZ

50 100 5 10

Normalized Time (c) Energy deficit

0.5

r

Fig.2.29 Excursions of interesting quantities

( ;=0.475，

7;'

ini=0.5 )

N広三c一mULコ一石」ω己Eω一v-u

cω刀一00

(の←ωOH一LohFω←∞∞門←りOH)+

CコNr-、

coぱコ守+r、

∞^寸 co 11 Cコo αコーL O 門11、と )

I tg_

雪 山… .

司噌ーぷ0 ド11 0，，-11 0

、_.. ...

RU

「D

nU

ヘiNGL?OHNHmwω」コ百」ω己Eω←℃ωNこ

のELoz

5 10

Normalized Time Z:

(a) T emperature at ^{x =0}

0.5

NZEECOBE宝00』0王切C2半一の工

(の

.OM--』O

』00寸OO∞の寸NH)

Z: tnl ;� ; θ二1

3 2 5 4 利\ヘミ\。22220ごO工Ucω一』一の工

50 100 5 10

Normalized Time Z:

Half length of cold region

0.5 0 0.1

、lJ仏U，，，‘、 NZEC

一 ミ山 崎、

(のO H-』O』

ON←ohh←←H) dp (mE.OHこ￡O寸∞目的ω.0∞H) Z:，m

2

1

0

0

nu

nu

nU

ヘhL'もぷ一o一恥ω刀〉切・』ωCU刀ωN一一のELoZ

50 100

r

5 10

Normalized Time (c) Energy deficit

0.5

Fig.2.30 Excursions of interesting quantities

( xíní =O.5，

_"l'

íní=O.5 )

(iv) 安全性判別h'

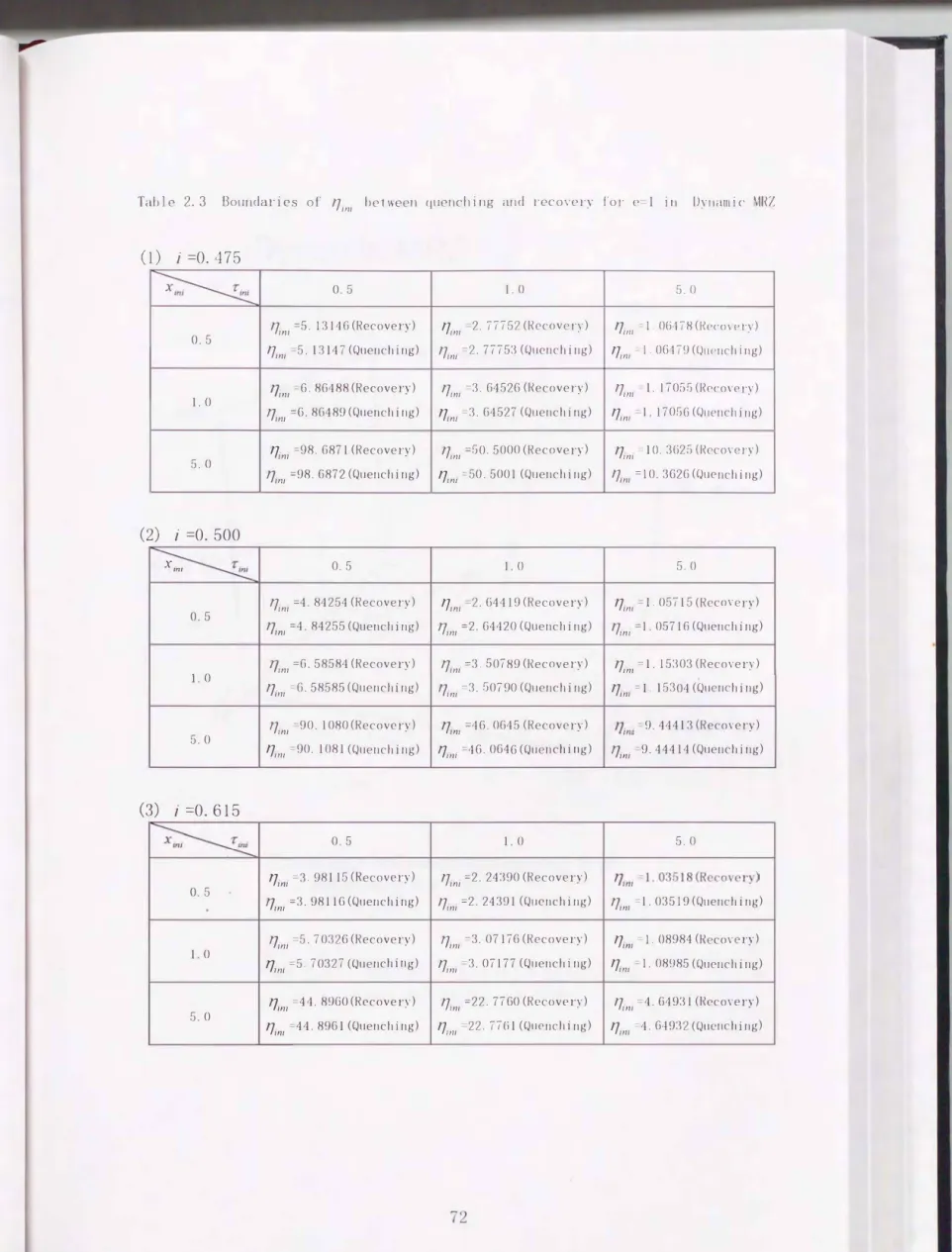
これまでにクエンチとリカバリーの境界近傍の計算例をいくつか示したが， こ れらのクエンチとリカバリーの問に境界があるとして， 発熱条件X九Iげ川P円11およひび、Tznげ川F円1 に対して求めたη化I川mの境界値近イ傍芳の値を表2.3に示す.

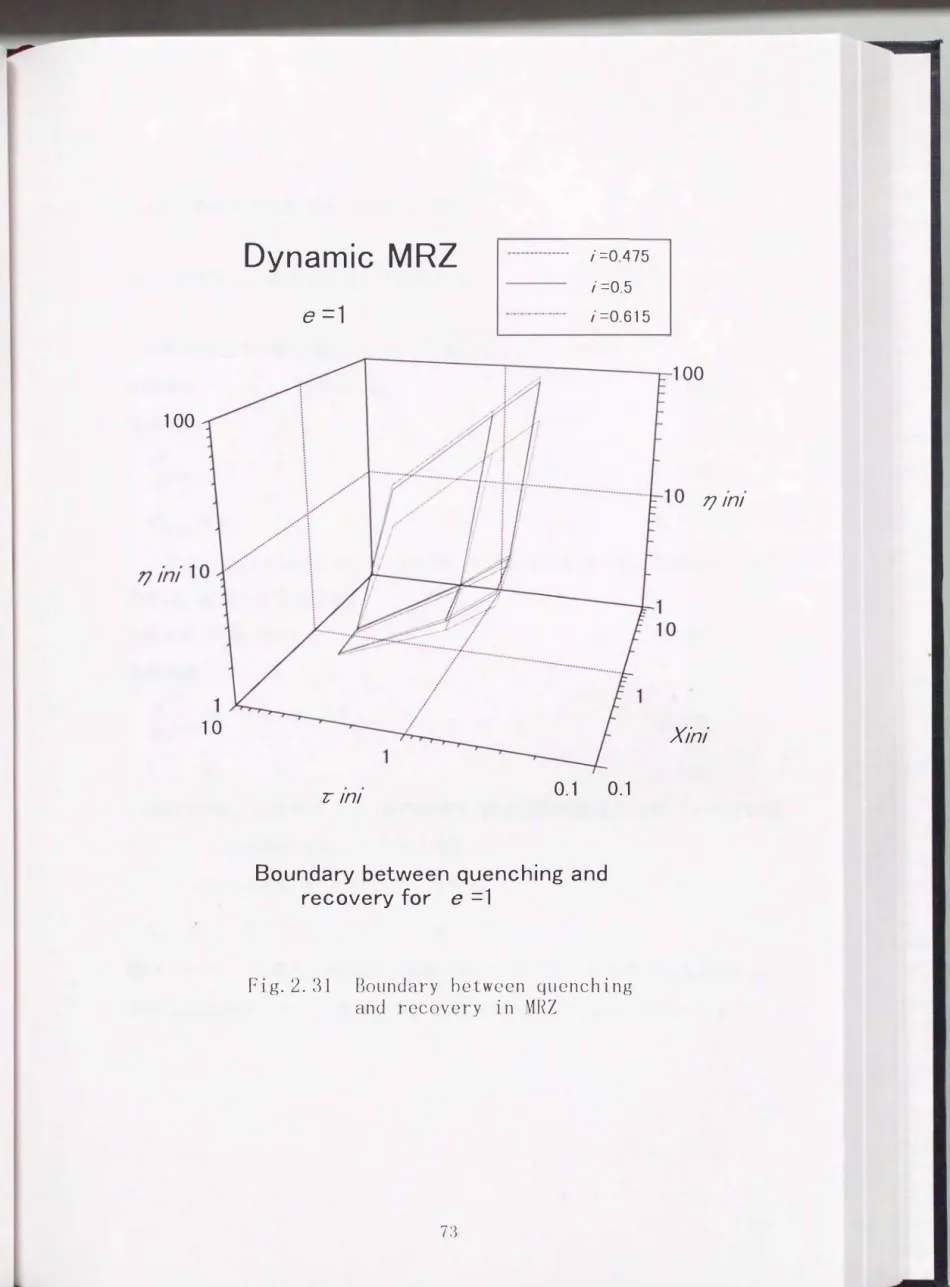
これらクエンチとリカバリーの境界の値を3次元の空間に境界面として図 2.31に示す. この図において， 境界面はら-X m一仇11空間に動作電流jをパラ メータとして表されており， 境界面より上の空間では，導体はクエンチの状態に なり危険であることを， 下の空間では超電導の状態に復帰し安全であることを 示している. したがって， 動作電流jが小さいほど， 非加熱長さXiniが大きいほ ど， またT，円1が小さいほど導体は安全であることがわかる.

以上の結果より， 液体ヘリウムのプール沸騰冷却超電導体の安全性は， 従来 の静的安全性の基準では判定できず， 本研究のような動的な安全性の基準が必 要であることがわかる.

71

Table 2.3 Boundaries o[ヴ1円; betwcen quellchillg éllld reco\'cry for e 1 _ill I)Yllélwic MRZ

(1) i二0.475

三メ吋に

O. ₅

1.0

5. 0

(2) i =0. 500

Xini �、-、、、^τini

O. 5

1.0

5.0

(3) iニ0.615

Xil1l 、、、.... 、、』 τ;n;

O. ₅

1.0

5. 0

O. ₅

ヴm;=5.13146 (Recovery) ヴ;111=5.13147 (Quenching)

ヴ'111;=6.86488 (Recovery) ヴ';n;=6.86489 (Quenching)

ヴ川=98.6871 (Recovery) ヴ';n;=98. 6872 (Quench i ng)

O. ₅

η川二4.84254(Recovery)

ヴ'm;=4.84255 (Quenching)

庁m;=6.58584 (Recovery) ヴ'/111=6. 58585 (Quench i ng)

lJm; =90. 1080 (Recovery) ヴ1円;=90.1081 (Quenching)

O. ₅

ヴtm=3 98115(Recovery) η';/1; =3.98116 (Quenching)

ヴ';n;=5.70326 (Recovery) ηint=5 70327(Quenching)

ヴ'//1;=44.8960 (Recovery) ヴ;/1;=44.8961 (Quenching)

1.0

ヴI円Iニ2.77752(Recovery) ヴ/111=2. 77753 (Quenching)

ヴ/111=3. 64526 (Recovery) ヴ川=3.64527 (Quenching)

ヴ1円;=50.5000 (Recovery) ヴ川=50.5001 (Quenching)

1.0

ヴ川=2.64419(Recovery) η'/n; =2.64420 (Quenching)

ηIP11=3 50789(Recovery) 庁'/111=3. 50790 (Quenchi ng)

ヴ'111;=46. 0645 (Recovery) ηI円，=46.0646(Quenching)

1.0

ヴ川=2.24390 (Recovery) ヴ/111=2. 24391 (Quenching)

lJ;11I =3. 07176(Recovery) ヴ/111=3. 07177 (Quenchj ng)

ヴ/111=22. 7760 (Recovery) ヴ/IJI二22.7761(Quenching)

5. 0

ヴIHI-1 0G478(!??COVPI-y) ヴInI-106479(Quenchi Ilg)

ヴI円/-1. 17055 meco\'C'ry) ヴ1nI-1 17056(Qlienclli ng)

ヴ/111= 1 O. 3G25 mecovcry) ヴ1円I=10.3626(Quenching)

5. 0

ヴInI=105715(Recovery) ヴm/=1. 05716(Quenching)

ヴ1円;= 1. 15303 (Recovery) ヴ1円I=1 15304(Quenching)

ヴ'm;=9.44413 (Recovery) ヴ';/1;=9.44414 (Quenching)

5.0

ヴ間二1.03518(Recovery)

ヴ'111;= 1. 03519 (QlIench i ng)

ヴImz1 08984(Recovery) ヴI円I二1.08985 (Quenching)

ヴ/111=4. 64931 (Recovcry) ヴ1111二4.64932(Quenching)

100

10

Dynamic MRZ

θ二1

τInl

i =0.475 j二0.5 /二0.615

0.1 0.1

Boundary between quenching and recovery for

e二1

Fig. 2. 31 Boundary beiween quenching and recovery in MRZ

73

100

ηInl

Xini

2. 2. 3 動的最小伝陪領域(Dynamic MPZ)

(1) 初期条件? 境界条件および発熱条件

初期条件および境界条件は， 以下の伎になる.

初期条件: T(X，O)

=ら

境界条件:

dT，

dX IX=O - ^v

(2. 108)

(2. 109)

Tlx→∞こら

^{(2. 110)}

こ こで， 式 (2.6)から， 式 (2.14)を用いて無次元化を行うと， 初期条件， 境界 条件は， 以下のようになる.

初期条件:

中，0)=0

(2.111)

境界条件:

ハU一一

d一依

(2. 112)

tl

x→∞二O (2. 113)

加熱条件は， 加熱長さXini， 加熱時間Siniおよび加熱量Hの加熱ノξターンを採 用した. これを無次元化して次式に示す.

O<x三XInI かっ 0<τ三τ η二ηln (2. 114)

x. < x 1111 または τ>τ1111

η=0

図2. 20に， この場合の典型的な温度分布を， 図2. 32に無次元加熱長さXInI，

無次元加熱時間Ti円1および無次元加熱量ヴI円1であらわした初期加熱条件を示す.

74

η

f

X

Fig. 2. 32 Normalized heat input introduced as disturbance η(x， τ) for dynamic MPZ

(2) 離散化

式(2. 79)を隣散化する7)が， 結果そのものは前節の式(2. 89)から式(2. 105)と 同様である. なお， m=2の点の温度は， 先に求めた格子点m= 1 における温度 および、m=3における温度より求めることができる• ^m =3以降の計算も出度が

10-7以下になるまで続ける (境界条件は1

1

…=0であるが， この数値計算で、は

温度が10-7以下になると計算を止めた• )このような計算を各時間ステップで混 度が収束するまで繰り返し行なった. ただし収束条件に関しては， この計算で は， 前回の計算値との温度差が10-4以下になると温度が収束したとみなした.

(3) 計算結果および考察

(a) 温度応答

( i ) クエンチ

� 2. 33 (a)に， 超電導体がクエンチした場合の温度応答の1例を示す. 計算条

件は， e二1，i=0.7，xini=0.5，τini = 5刀ini 二11 であり， 導体上の中心より片側半分の 温度分布の時間的変化を経過時間とともに示している. 図中， 計算時間はすべ ては記してはいないが， 時間の経過とともに温度が変化する様子がわかる. 特 に， 加熱時間がτini

=

5であるので， まずτini

=

5まで温度が急激に上昇し， そ の後一旦温度は下がるが， その後再度温度が上昇しクエンチに至る様子が確認 できる. また温度分布の様子に関しでも， 加熱長さがXini

=

0.5であるので， 加 熱時間中は狭い範囲で温度上昇が見られるが， その後高温の領域が時間経過と とともに広がっており興味深い. なお， この計算条件での導体の中心温度が時

間とともに変化する様子は後程示す.

76

本�

詰 � ³ 1f:ご人1J ^{40 Qtlending e} ₌₌₁

鴎ζミミど��

^ナ二川

^{i ==0.7}

C54 _{2 Xini 二0.5}

τznz二5

可- 4HN コ^A

1J ini二1 1 dl

Z 5

⁰

。 。 5 10 15

N ormalized distance from hot end

^x

Fig.2.33(a) Excursion ofnormalized temperature，

t(x， rノ

in a dynamic MPZ

、2 +d

4吐L=Lコ^J

A A

4 4

e ==1

Recovery i ==0.7

ι

E

^4A

χznz二0.5 τini==5

甘. 4P，4 A 4

�0.2 1J ini二3

，・c・t

4

z g

^o

。 。 2 3 4 5

Normalized distance from hot end

^x

Fig.2.33(b) Excursion of normalized telnperature，

1仇り

in a dynamic MPZ (recovery)

( ü ) リカバリー

超電導体が超電導状態に復帰する場合の例を， 図2. 33 (b)に示す. 計算条件 に関しては， e=1，i=0.7，xini=0.5，τJ円，=5は先の(i )クエンチでの条件と同じで

あるが， 加熱量が小さくなっておりれI 二3である IfuL度応答はこの場合も， 導 体上の中心より片側半分の温度分布の時間的変化を経過時間とともに示してあ る. この例でも， 加熱時聞がτ'/11二5であるので， まずτi/11⁼ 5まで温度が急激に上 升するが， その後急激に温度は下降し， 超電導体が超電導状態に復帰する様 が確認できる. また高温部の広がりかたに関しても， 先の例と同様に， 加熱長 さがXiniニ0.5であるので， 加熱時間中は狭い範囲で温度上昇が見られるが， その 後高温部が時間経過ととともに広がりながら， 全体としては温度が下がってい

る. また， この例の条件での導体の中心温度が時間とともに変化する様子も後 程示す.

(b) クエンチとリカバリーの境界の探糸F

前の(a)でクエンチとリカバリーの温度応答の例を示したが， クエンチとリ カバリーの計算条件の聞のどこかに存在するであろう境界を探るため， 加熱時 間τiniと加熱長さに11を同じにして九の値を変化させながら温度応答等を調べた.

ここに， 前の(a)におけるのクエンチとリカバリーの計算条件の問で境界を求 めた結果を1つの例として示す. なお， 導体がクエンチに至るか， リカバリー となるかは， 導体中心温度の時間変化， 無次元温度がf三lの高温領域の導体中 心軸より片側半分の長さの時間変化(以後/加t (τ) / 2と記す)および導体の蓄積エ

ネルギーの時間変化より判定できる. 以下に， 各計算結果を示す.

78

図2. ^3/1 (a)に，計算条件e二1，i=0.7，x1/11二0.5，τ1/11= 5における導体の中心温度の 無次元日年間τに対する変化を， ヴI円Iの値をパラメータとして示す. ヴln1= 11および

ヴ1/11 =9の場合の結果がクエンチと判定される. 一万， ヴ日l/ = 5およびヴi/11= 3の場

合がリカバリーの結果を示している. これらの問のある値引m二6.63の場合が，

この場合の境界に相当すると考えられる. この境界値の九= 6.63の場合に関し て興味深い結果は， 時間の経過につれてある一定の温度に収束しており， しか もこの一定の温度が静的平衡理論の一つであるMPZ平衡の温度分布と一致する ことである. したがって， 矩形状の熱擾乱に対する動的安全性基準に静的平衡 理論の一つであるMPZ平衡理論の関連が認められる.

図2. ³⁴ (b)に， 前節(a)の場合と同じ計算条件e = 1，i = 0.7，xlni = 0.5， rini = 5におけ る高狙領域('hol (τ) / 2 )の無次元時間τに対する変化を， ヴ1mの値をパラメータ として示す. なお， ここで高温領域とは， 導体の温度が臨界温度であるt= 1よ り高い領域の長さの半分(導体中心より片側半分の部分)を表す. この図の場 合もη川二11およびヴ1円I二9の場合の結果がクエンチと判定される. 一方， ヴini= 5

および庁1m二3の場合がリカバリーの結果を示していることも先の場合と同じ である. ηini= 6.63の場合が境界に相当するが， この境界値のηI円1二6.63の場合に 関しては時間の経過につれてある一定の値に収束しており， しかもこの一定の 値が静的平衡理論の一つで、あるMPZ平衡の場合のMPZ長さと一致している. なお，

この境界値(札i= 6.63の場合)が， 時間の経過につれてある一定の値に収束す ることは， (匂ωa心)の結果においてヴ1げ叩P

てある一定の値に収束していることから当然の結果と思われる. このことから も矩形状の熱擾乱に対する動的安全性基準に静的平衡理論の一つであるMPZ、Ir 衡理論の関連が確認できる.

79

ト吋 丘 三 C ω

lo....

..j...J コ

ro L ω 0..

4噌一-E

..j...J ① てコc ω fヘαコo co ..j...J -

2 ¹¹

... 、、__，

7:lnt

50 100 5 10

Normalized Time ^7:

(a) Temperature at ^x =0 0 0.5

0.1

ヘiNGL判.OH

NHmwω」コパFEω己EωトカωN=のにとoZ θ=1， Iニ0.7，xlnl =0.5， 7: ^，，71 =5.0

Boundary 6.63 4

3 2

ト寸Q_

E C C o

b.O ω

lo....

..j...J

�_g

4-0 ...c

u c ^，.-司、

� <õ

4-ー m つ;; C'J

工 」L 6

e = 1， í =0.7 xlf1l 司.5， 7: ^If1I

4

2

N\ヘhxd，coELH

O工ちもにω一恥一の工 ^{50 100 5 10}

Normalized Time ^7:

Half length of hot region

τJnl

0 0.5 0.1

、1J仏U/E、、

N Q_

E

c ，戸、、^co

・一 _「、

認め

今_� J ，...-

�' � 、--"

�一一

40 30 20 10

(ド)ωメ凶」ωcω刀mwLO一あちωN一

一のE」OZ

50 100

r

5 10 Normalized Time (c) Stored energy 0 0.5

0.1

Fig.2.34 Excursions of interesting quantities for ^θ= 1， i ⁼ 0 . 7， ^{Xù1i =} O. 5 a n d ^{7: ù1i=} O. 5

80

超電導体の安全性を評価する上で重要な因子の一つに導体に蓄積される訴積 エネルギーがある. この蓄積エネルギーεの無次元時間τ に対する変化を示した のが図 2.

34

(c) で あ る . なお ， 前の(a) の場合と同じく計算条件は

e = 1，i二0.7，Xini = 0.5，τini = 5であり， ヴ1111の(直をパラメータとしてある.

ここに， 蓄積エネルギーεは次式により定義される.

E(S)

=〆BAXch

(To

_-T B)c(τ) (2.

115)

Yん1d d'f d 、、.. z，ノ4'a 〆't\

c

f向iaE16

∞ mhEE，d

一一

、、.，ノτ 〆'E\ε (2.

116)

。 。

また， 図中横破線で示されているCsωは， MPZ平衡において導体に貯えられる 無次元蓄積エネルギーで、あり， 次式で定義される.

Estat二ρCBAXch(Ya

-T

B)cs附 (2.

11 7)

εstat二

f f c(t IMPZ

eq川 (2.

118)

。 。

これらの結果も(a)および(b)の結果と矛盾せず， ηlni ⁼ 6.63を境界として，

'7im = 11およびηlni = 9の場合の結果がクエンチ， ηini = 5およびヴ1m二3の場合が リカバリーの結果を示している.

最後に， これまで述べてきたe二1，i= 0.7，Xini ⁼ 0.5， Ti円i=5におけるクエンチ， 境 界およびリカバリーの例のうち， 代表的な九=11 ， ηini = 6.63および刀ini = 3にお ける導体の温度応答を， それぞれ図2.

35

_{(a)から図2.}

35

(c)に全体的な変化の 様子が捉えやすいように時間軸を加えてX- T-I空間において立体的に示す.

�

_2.

35

_{(a)は， クエンチの例(e}= 1， i二0.7，xi円i = 0.5， Tini = 5， '7ini = 11 )であり，

τini ⁼ 5まで温度が急激に上昇し， その後一旦温度は下がるが， その後再度温度 が上昇しクエンチに至る保子が確認できる.

図2.

35

(b)は， 境界の例(e二1，i⁼ 0.7，xillI = 0.5， T'11l二5， '7l1JI = 6.63 )であり，

81

Tini = 5まで温度が急激に上昇することは先の例と同様であるが， その後 -JL出 度は下がり時間の経過につれて静的平衡理論の一つであるMPZ、ド衡のrfuL度分布 に漸近している様子が確認できる.

、� 2. 35 (c)は， リカバリーの例(e=1，i=0.7スI円1= 0.5，τ川I二5， '71/J1二3 )であり，

τ1111 = 5まで温度は上昇するがその後急速に下がり， I巴7E導状態に|叶復してい

る

(c) クエンチとリカバリーの境界における計算結果および加熱条件の影響

これまで クエンチとリカバリーの境界の探りかたを例とともに示してきた.

次に， この境界値が得られるようなさまざまな加熱条件の場合の計算結果を，

特性発熱をe= 1として， 動作電流i= 0.7およびi= 0.635に対して示す. なお， 動 作電流を， i = 0.7およびi= 0.635の2種類選んだ訳は， i = 0.635に関しては， 前 立で、述べたMaddockの平衡が成り立つ動作電流i]Ii，W ( = 0.634)に出来るだけ近い値 ということからであり， i = 0.7に関してはこの値より大きな値で計算結果に違い が出やすいような値と考えて選んだ. さて， これから， 動作電流i= 0.7および i = 0.635の場合に分けてクエンチとリカバリーの境界での結果の例を示すが，そ の際のxI円i'Tiniおよひけ1mの組み合わせば多いので? これらのうちのどれかを固定

して計算し整理してみた. まず， xtniの値を定め， τ1mをパラメータとして整理す る.その際境界における札1の値を付記することにする.次にTlmの値を定め， XInI をパラメータとして整理する. また， その際境界における札1の値を付記する.

後に， 代表的なXiniおよび、τ1mに対して動作電流jの影響を調べる.

82

g二1， j二o. 7，

Xi刀i二O. 5， τ1刀l'=5， η 1刀1・二 11

3.5

3. 5

キJ

ω 3

いつ

�

_2.5

い(1)

� 日 (1) -f--) Fてコ(1) 'r→ Ñ r-I ro

白い z o

�

2

NOJ:llJali?' ハ J

hJ7711ce し el}d

QJ .々_hγ i-...J むも hγ ~ ヘyc1)'

~ �

々り

O. 1

r

10 ρU z --上 1i a m r o n ワL

ripi oM n e o --

・1 m

s a r n

uy pU1nu x

pu

\/ \lノ e --i n a r

ub f\ u n 「円U+し ・1ょ っda τhu -

r

c

つム e n - ny ρU σbm u

--i

ρu

n可

F十し/l\

η 1刀1・二6.63

。二1， j=O. 7，

Xi刀1・二O.5，

_τ

1刀1・二5，

4、主

3.5

. .é.吉む

100 ;:;

むも

~ ~ ヘvctt

~ �

「ラ

o. 1

々

3. 5 3

2

NOl.'llJali7 正 、 J

hJ7hce し el1d

4

キ心

むいつ戸

、のいω(山田ωザ

Fてコ(1) .rベÑ y---4

c古田 ト40 2三

of normalized

MPZ

__.r

n e o-- ・1 m s a r n uy c，d

x

pun

--i

Fig. 2. 35(b) temperature

(quenching)

84

η 1刀1・二3 θ二1， 1司. 7，

Xini二o. 5，

^τ

1刀1・二5，

4唱

3.5

.1$' む

100 . ;:;

むも

� ~

"-t

� '1J η ~

々

10 o. 1

. ・

. ・

. ・

. .

. ・ ・

. .

・・・Hトー・ ・ ・ . . . .i^. ーー・・ー ・・..;

. ・ ・. ・ .

ム .

・. ーチ^一一ー.

ー・.. . ・

^. .

.

^{.. ..}

一 ー

^.，

ー 一ー

^・'..ー今

一 占 . ・

^. .

‘ー一

^一一ー一

・

^・..ー

.・・ー ー

^・・^.ー

・ ・ ト ャ ・ ・

^{，--'・ー・・・・一一}

.'.・....

^A・

ー

^4.

・ . 一 .

^{. ・・}

. ー

^{. ・}

・

・ H ・ H・

H・{...

.;.

司 .

^. ._--

一一ー・..

^{一司・・・ 4ー}

・.

^ぞー・ー

・ 一一 ーー-'"

^{・・・・ー一}

ー. .

: :

・

^，

. ・ ?

. ・ ・

. .

. ^・

・

. ・

+日�

^r

1

^{. ...・.}

ヤ

^{・，・・・ ・ ー一一・._�}

ム

^{1: .}

. ・ ・

・ .

2

NOrrn - 4-.1_ 1 2ed d 勺 7 from h ・ n 匂 _{し el1d} ^l1Ce

3.5 3

キJ

むいつパザ吋'Hω(目白ωパザ

FてコG) .r-I Ñ r--I ro 白 い0 z

r

of normalized Excursion MPZ

in dynamic

\lノ ρu

r c

\/

/\UY

5tr qua e

r v つムe 0 ・ p c σbm e --

e r

ゎr+し/l\

85

( i )動作電流i= 0.7における計算結果(， の影響)

fJly節と|司係， 熱援1ïLに対する超電導体の動的な応答は， 導体中心温度の時間 変化， 高氾領域(^'ho/ (τ) / 2 )の時間変化および、蓄積エネノレギーの時間変化として 観察出来るので， それぞれ計算例を示す.

、� 2. 36 (a)に， e二1， i二0.7における加熱長さらi= 0.5における超電導体の導

体中心温度の時間変化を， τIIllをパラメータ('lI1i = 0.5，1，5，10，50)として示す. 超電 導体の導体中心温度は， 無次元加熱時間τ1mまでは一旦温度が上昇するが， その 後温度は下降しe= 1， Ì二0.7におけるMPZ平衡で、の導体中心温度に漸近するよう になる. その際の無次元加熱時間τ円1における最高到達温度は， パラメータであ るτ が大きいほど低い結果となっている.

つぎに， 図2. 36 (b)に， e = 1， Ì二0.7および加熱条件Xini二0.5における高温領 域( ^'ho/(τ) / 2 ) の時間変化を， 前図と同様にらIを パラメータとして示す.

'hO/ (，) / 2は， TH11が小さいほど早い時間より大きくなり始めるが， いずれの場合

も時間がたつにつれMPZ平衡におけるMPZ長さを表す破線に漸近するようになる.

なお， 'ho/ (τ)/2はτII1lが小さいほど早い時間より大きくなり始めているが， これ

は図2. 36 (a)において導体中心温度が， τmが小さいほど早い時間より高くなり

始める結果に対応している.

最後に， 図2. 36 (c)に， e=l， Ì=0.7および加熱条件XlI1i⁼ 0.5における導体の

蓄積エネノレギーεの時間変化を， 前図等と同様にτ1mをパラメータとして示す.

この図において? 導体の蓄積エネルギーは無次元加熱時間'imまでは急速に大き くなるが， その後次第に小さくなりe=l， Ì=0.7におけるMPZ平衡での蓄積エネ ルギ�&S({l(の値に漸近するようになる. これらの結果より， 図2. 36 (a)における それぞれの加熱条件での温度応答との対応がよく表れている.

(∞Oω.FH) N丘三亡一22悶」ω♀ES刀亡ω日0工 4

100 101 102 Normalized Time 0

10-1

τ

0.5

F円uqd

へい、O)NhOH〉ヘザ何ω」コ苛」ω丘Eωト刀ω出一句E」OZ

2.5 2 3

1.5

(a) Temperature at X =0

(←ωσ.NH) Nn比三c一co一回ω」日0工』050cω二一何工、\

i =0.7

Xini =0.5

e =1

6

0 10-1 5 4 3 2

内\へい)』oh九~，CO一切ω」VO工』O工戸市山Cω一』一閃工 、、.，，，hu ，，.‘、

(ド)ω

50

(ωトの?")

N丘三C一花百'w

/dF

e =1

i =0.7

Xini =0.5

30

0 10-1

ð> 40

L-Q) 比jc

てコ(J) _L- O (f) てコω N ro E

Z O 20

10

102 Normalized Time r

Stored energy

Excursions of interesting quantities for ^{e =}1， i ⁼0.7 _and xini ⁼0.5

(c) Fig.2.36

87