平成
28年
度
学位論文
数学的コ ミュニケー シ ョンを実現 させ るための
授業づ くりに関す る研究
一 グルー プによる話 し合い活動に注 目 して一
兵庫 教 育大学 大学 院学校 教 育研 究科 教 育 内容 ◆方法専攻
認識 形成 系教 育 コー ス
M1 5 1 4 9D
金 澤 文彦目次 第
1章
本 研 究 の 目的 と方 法 … … … ・ … … … … ・ … … 第1節 本研 究の 目的 と方法・・・・・・・・・ ・・・・・・ ・・・・・・ ・・・・1-1.本
研 究の 目的1-2.本
研 究の方法 第2節 本論 文の構成・・・・・・・ ・・ ・・ ・・・ ・・・ ・・・・・・・ ・・・・ 1 2 5 6 第2章
第1節 1 1 1 第2節 2 2 第3節 3 3 第3章
第1節 第2節
2 2 数 学 的 コ ミ ュ ニ ケ ー シ ョン に 関 す る先 行 研 究 … … … 。… … 金本氏による数学的 コ ミュニケー シ ョン・・ ・・・・・・・・・・・・・・-1.数
学的 コ ミュニケー シ ョンの定義-2.算
数数学 の表現-3.算
数数学 の表現の使用 の仕方 江森 氏 に よるコ ミュニケー シ ョン・・・・ ・・・・・・・・・・・・・・・-1.コ
ミュニケー シ ョンの定義-2.コ
ミュニケー シ ョン連鎖 ポジシ ョニ ング セ オ リー・・ ・・・・・・・・・・・・・・・・・ ・・・1-1.ポ
ジシ ョニ ング セオ リー ー2.ネ
ゴシエー シ ョン ムーブ 授 業 分 析 ・ … … ・ … 。… … … 。… … … … ・・ 、。…27
分析 の対象 と方法・・・・・ ・・・・・・・・・・ ・・・・ ・・・・・・28
既存デー タの分析・・・・・・・・・・・・・・・ ・・ ・・・・ ・・・ 。29
-1.公
開授 業 の概 要-2.分
析第
4章
実 践 授 業 ・ … … … ・ … … … ・ ・ … … … … ・35
第1節 実践授 業 の概 要・ ・・・・・ ・・・・・・・・・・・・・・ ・・・ ・・ 。36
1-1.題
材設定 の理 由1-2.授
業 の 目的1-3.時
期 と対象 第2節 考察・ ・・・・・・・・・・ ・・・・・ ・・・・・・・ ・・・ ・・・・・43
第5章
本 研 究 の ま と め と今 後 の 課 題 ・ … ・ … ・ … … … … ・ ・ …53
第1節 本研 究 のま とめ・ ・・ ・・・・・・・・ ・・・・・・・ ・・・ ・・ ・・・54
1-1.各
章のま とめ1-2.全
体 のま とめ 第2節
今後の課題・ ・・・・・・・ ・・ ・・・ ・・・・・ ・・・ ・・・・・・・56
引用0参
考文献 。… … … … ・ … … … ・ … 。57
付 録 付録①・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・60
付録②・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・66
付録③・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・69
第
1章
本研究の 目的 と方法
本章では本研究の目的と方法
,な
らびに本論文の構成を示す。
第
1節
本研 究の 目的 と方法
1-1.本
研究 の 目的
1…
2.本
研 究の方法
第
2節
本論文の構成
第
1節
本 研究 の 目的 と方法
1-1.本
研究の 目的
筆者はス トレー トの院生であるが,現
在,公
立中学校 で非常勤講師 として第1学
年の 数学科 を担 当 してい る。その授業では,学
習の手立ての1つ
と して,グ
ループによる話 し合 い活動 を取 り入れてい る。数学学習 においては,生 徒個人で考 えることも重要だが, 周 りの友達 と意見交流 を しなが ら考 える,い わゆるコ ミュニケー シ ョン活動が特に重要 となつて くる。なぜ な らば,コ
ミュニケー シ ョン活動 を通 して,生
徒が多面的な見方や 学習内容の本質 を追求 してい く方法 を学ぶ ことができるか らである。また,コ
ミュニケ ー シ ョン活動 は論理的思考力 を身 につ けるためのきつかけに もなる。この ことは,他
者 に 自分の意見を伝 える とき,筋
道 を立てて,分
か りやす く伝 えたい とい う動機 が伴 うこ とに起因す る。この よ うな コ ミュニケー シ ョン活動 は,生
徒 に 自信 をもたせ,数
学 を好 きに させ る効果が見込 まれ る。 コ ミュニケー シ ョン活動 の必要性 については,社
会的要請 とい う側面 をもつ。現行の 学習指導要領総則編 (平成20年
8月)で
は,「知識・技能 の習得 と思考力・判断力・ 表現力等の育成 のバ ランスを重視す るこ と」 を基本的なね らい と して改訂 が行われた。 また,「言語活動 の充実」が,
日標及び指導内容 に明示的に位 置づ け られ てい る。 さら に,OECD(経
済協力開発機構)の PISA調
査 な どか らは,我
が国の児童 。生徒 につい ては,表
現す ることや,自
信 の欠如 といつた課題が見 られ る。そ して,平
成26年
4月 4日,次
期学習指導要領の策定に向けて,育
成すべ き資質・能力 に関 して論点整理 され る中で生徒間の コ ミュニケー シ ョンについて述べ られている(教育新 聞,平成26年
4月17日
付[3272]号1面
掲載)。 次期学習指導要領 では内容ベー スか ら資質・能カベー ス ヘ とカ リキュラムの重点がシフ トされ る中で,生徒 間の コ ミュニケー シ ョンが強調 され ることになろ う。 以上の ことか ら,本
研 究は,生
徒間の コ ミュニケー シ ョンに注 目す る。また,生
徒間 の コ ミュニケー シ ョンは数学学習の様 々な場面で見 られ るので,本研 究では グループに よる話 し合い活動の場合 に しぼることとす る。これ らを踏 まえ,本
研 究の 目的は次の通 りである。 ・ グループによる話 し合い活動時にお ける, 数学的コミュニケーションを実現 させ るための授業づ くりの視点 を得 る数学的コミュニケーション とは,「数理的な事象 に関わ るコ ミュニケー シ ョンであ り,ま た
,算
数数学 の表現 を使用 してい るコ ミュニケー シ ョンの こ と」(金本,2014,p.39)
本研究では,こ
の金本氏の数学的 コ ミュニケー シ ョンの定義 に立つ こととす る。 ここで,算
数数学 の表現 とは,「算数数学の授業の中で,数
学的 な意味があ り,そ
の 意味が子 どもた ちの 中に構成 され てい る 目的意識 の中で使 われ てい るもの」 とされ る。 そ して,数
学的な問題解決の過程の中で,子
どもたちが作 り出 してい る表現は,全
体で 共有できるよ うな ものでな くて も,算 数数学の表現の範囲に含 めて捉 えるもの としてい る。また,算
数数学の表現 は,は
じめか ら厳密 に数学的な意味 に対応 して使用 されてい るのではな く,徐
々に適切 な使用 に変わつてい く。その使用 は,既
習の内容 をもとに考 え,そ
れ らを組み合 わせ る中で,よ
り数学的な意味 として適切 な ものに変わつてい く。 筆者の経験 になるが,算
数数学の授業 において,グ
ループに よる話 し合い活動 を取 り 入れた とき,そ
の場 が学力水準の高い児童・生徒の発言ばか りで終わって しま う傾 向に あった。また,学
習 内容 とは関係 のない話 を して しま う児童・生徒 がいて,指
導 に困る ことがあった。筆者 は,グ
ループによる話 し合い活動 に数学的 コ ミュニケー シ ョンを実 現 させ ることを 目指 してい るが,そ の際 グループのメンバー全員が参加 している状況を 想 定 している。1-2.本
研究の方法
本研究では,数学的 コ ミュニケー シ ョンが実現 しているのか ど うかを判断す るために, コ ミュニケー シ ョン連鎖 の枠組みを用い る。また,グ
ループの メンバー全員の話 し合い 活動への参加状況 を見 るために,ポ
ジシ ョニング セオ リー を用い る。 なお,コ
ミュニ ケー シ ョン連鎖 とポ ジシ ョニ ング セオ リーに関 しては第2章
で詳 しく述べてい る。 こ れ らの知見に基づ き,既
存の実践授業のデー タ (学習指導案,ビ
デ オ及び音声,指
導者 へのインタビュー)を
分析 し,数
学的 コ ミュニケー シ ョンを実現 させ るための授業づ く りへ向けた基礎事項 を抽 出す る。その基礎事項 に基づいて理論的枠組み を示 し,研
究授 業 を実施 し検証す る。以上の方法による結果 を踏 まえて,本
研 究の 目的 に応 じた授業づ く りの視′点をま とめる。第
2節
本論 文の構 成
本論文は, 5つ
の章か らなる。 第1章
では,本
研 究の 目的 を述べ,そ
の 目的 を達成す るための方法 を示す。グループ に よる話 し合い活動時の数学的 コ ミュニケー シ ョンを提 えるために,コ ミュニケー シ ョ ン連鎖 とポジシ ョニ ング セオ リーの知 見を用い ることや,実
践授業 を分析す るとい う こ とについて述べ る。それ らの結果か ら,数
学的 コ ミュニケー シ ョンを実現 させ るため の授業づ くりの視点 を得 よ うとす る,本
研 究の全体像 を示す。 第2章
では,先
行研 究 よ り,数
学的 コ ミュニケー シ ョンについて概観す る。まず,金
本(2014)の
先行研 究か ら,数
学的 コ ミュニケー シ ョン とは何 か,話
し合 い活動 にお け る算数数学の表現 は どの よ うな ものがあるのかについて考 える。次に,江
森 (2012) の先行研究か ら,コ
ミュニケー シ ョン連鎖 に着 日して,子
どもた ちの中で どの よ うなや り取 りがあれば,良
い話 し合 い活動になるのかについて考 える。 ここでは,3つ
の区分 規準 と4つ
の類型 (協応連鎖,共
鳴連鎖,超
越連鎖,創
発連鎖)に
ついて整理す る。 さ らに,Anna&Gloriana(2015)の
先行研究か ら,ポ
ジシ ョニ ング セオ リーに着 目し て,話し合い活動 時の グループ内での子 どもたちのポジシ ョンが コ ミュニケー シ ョンに どの よ うな影響 をもた らす のかについて考 える。ここでは,そ
れ ぞれ の会話 を3つ
のポ ジシ ョン (エキスパー ト,ノー ビス,フ
ァシ リテー ター)で
捉 え,ネ
ゴシエー シ ョン ム ー ブの コー ドを用い ることで,や
りとりを さらに分析す る。 第3章
では,先
行研 究の知見に照 らし合わせ,既
存の実践授業のデー タを考察 し,次
章 で提案す る理論的枠組みの基礎事項 を整理す る。 第4章
では,数学的 コ ミュニケー シ ョンを実現 させ るための授 業づ く りに向けた理論 的枠組み を提案す る。 その枠組みをもつて実践授業 を行 い,検
証す る。 第5章
では,本
研 究のま とめ と,今
後の課題 について述べ る。第
2章
数学的 コ ミュニケー シ ョンに関す る
先行研究
本章では
,本
論文における数学的コミュニケー ションを明確にするために
,金本
(2014)の数学的コミュニケーシ ョンの定義
,江
森
(2012)のコミュニケーシ
ョン連鎖,Anna&Glorlana(2015)の ポジショニング セオ リー を概観する。
第
1節
金本氏による数学的 コ ミュニケー シ ョン
1-1.数
学的 コ ミュニケー シ ョンの定義
1¨
2.算
数数学の表現
1-3.算
数数学の表現の使用の仕方
第
2節
江森氏によるコ ミュニケー シ ョン
2‐
1.コ
ミュニケー シ ョンの定義
2-2.コ
ミュニケー シ ョン連鎖
第
3節
ポジショニング セオ リー
3-1.ポ
ジショニング セオ リー
3-2.ネ
ゴシエーション ムープ
第
1節
金本 氏 に よる数学 的 コ ミュニケー シ ョン
本節 では,金
本(2014)の
先行研 究 をもとに,数
学的 コ ミュニケー シ ョンを どの よ うに捉 えてい くかを考察す る。1‐1で
は,数
学的 コ ミュニケー シ ョンの定義 を与 え られ ている研 究をもとに,数
学的 コ ミュニケー シ ョン とは どの よ うな ものなのかを捉 える。 1‐2で
は,数
学的 コ ミュニケー シ ョンを定義す るときに,検
討 しなけれ ばな らない問題 の1つ
である算数数学の表現 について検討す る。1‐3で
は,同
じく数学的 コ ミュニケー シ ョンを定義す る ときに,検討 しなけれ ばな らない問題 の1つ
である算数数学の表現の 使用の仕方について検討す る。1‐
1.数
学的 コ ミュニケー シ ョンの定義
金本(2014)は
数学的 コ ミュニケー シ ョンを次の よ うに定義 してい る。 数 学 的 コ ミュニ ケー シ ョン とは,数
理 的 な事 象 に関 わ る コ ミュニ ケー シ ョンで あ り,ま た,算
数数 学 の表 現 を使 用 して い る コ ミュニ ケー シ ョンの こ とで あ る。 (d≧冽ヽ, 2014, p.39) ここで,「数理的な事象 に関わ る」 とは数学的な意味での算数数学 の授 業 を構成 して い く活動 との関連 とい うことで制限 され る。また,数
学的 コ ミュニケー シ ョンを定義す る場合,検
討 しなけれ ばな らない問題 が2点
生 じる と次の よ うに述べている。 その第1の
点は,「算数数学の表現 を使用 している」といつた ときの 「算数数学の表現」 とは どこまでを指すか とい う点である。 また,第
2の
点は,「 算数数学の表現 を使用 し ている」 といつた ときの 「使用の仕方」 を どう捉 えるか とい う点である。 (d≧冽障, 2014, p.39) よって,次
項以降では,算
数数学の表現 と算数数学の表現の使用の仕方について検討 す る。 61-2.算
数数学の表現
「算数数学の表現」とは どこまでを指すか とい う点について,次 のよ うに捉 えている。 「算 数数学 の表現 」とは,算
数 数 学 の授 業 の 中で教 師 が数 学 的 な意 味 を子 ど もた ちの 中 に構成 してい くとい う目的意識 で もつて使 つてい る もの と考 え る。 (4≧冽ド, 2014, p.40) さらに,金
本(2014)は
具体的に どの よ うな ものが 「算数数学の表現」 に相 当す る のかについて,次
の3つ
を挙 げてい る。(i)学
習指導要領 (算数数学関係 の もの とす る)上
に記載 され てい るものはそれ に相 当す る(中
略) (五
)学
習指導要領 上に記載 されているものを発展 あるいは拡張 し た ものはそれ に相 当す る(中
略) (Ш
)算
数数学の学習指導上において教育的 価値 として教師に捉 え られているものはそれ に相 当す る (金冽に, 2014, p.40)(1)と
(五)に
ついては,算
数数学の授業は学習指導要領 によつて規定 され,成
立 しているため,学
習指導要領 に記載 され ている表現,あ
るいは学習指導要領 を基 に して 使 われている表現が 「算数数学の表現」 に相 当す る。 また,(面
)に
ついては,算
数数 学の授業 を構成す る上で必要であれ ば学習指導要領 には記載 されていないが,「算数数 学の表現」に相 当す るものがあることを示 している。例 えば,「違 う」「似てい る」 とい った よ うに,
日常言語 に も関連 した内容 であるものが挙げ られ る。 ただ し,(面
)は
ど こまで認 めるのかについての基準が 「教育的価値」 とあるよ うに,教
師の感覚,指
導観 に任 されて しま うところがあると考 え られ る。 金本(2014)は
「日常言語 による数学的な意味の表現が存在す ることを認 め,議
論 をすべ き場面に応 じて,ど の よ うな コンテクス トの上で使用 されてい るかを同定す るこ とが よい と考 える。」 (p.41)と 述べてい る。 この ことか ら,「違 う」「似 てい る」な ど日 常言語で数学的な意味の表現 に関わるものは多様 に存在 してお り,数学の授業以外の 日 常の会話で も,数
学的な意味の表現が使 われ ているはずである。つま り,そ
の表現が数 学的な意味 として用い られているのかについての議論 をす る ときには,そ の発言が出て きた,前
後の文脈 (コ ンテ クス ト)か
ら判断す ることになる。これ に加 え,金
本 (2014) は,「算数数学の授業の中で問題解決 に当たつて子 どもたち 自身が作 り出 した表現につ いて検討 してお く必要がある。」 (p.41)と 述べてい る。 この こ とよ り,日
常言語だけで な く,算
数数学の授業 において,特
に問題解決 している ときの子 どもたち 自身で作 り出 した表現 も含む ことが考 え られ る。以上の ことよ り,「 日常言語 による数 学的な意味の表現」 とは何 かについて
,次
の 2 点 に整理す ることができる。 ・算数数学の授業の中で,数
学的な意 味があ り,そ
の意味が子 どもたちの中に構成 さ れている 目的意識 の中で使 われてい るものである。 ・数学的な問題解決の過程の中で,子
どもたちが作 り出 してい る表現 は,全
体で共有 できるよ うな ものでな くて も,算
数数学の表現の範 囲に含 めて捉 えるもの とす る。1…
3.算
数数学の表現の使用の仕方
「算数数学の表現の使用の仕方」とは どこまでを指すか とい う点について,次
の2点
に着 目す る必要があると述べている。 第1の
点については次の通 りである。 第1に
,算 数数学の表現であつて もその使用はは じめか ら厳密 なもの として行われてい るのではない とい うことに着 目をす る必要がある。 (中略) 「算数数学の表現 を使用 している」 といつた ときの 「使用の仕方」は 「初期の使用」や 「漠然 とした意味の もとでの使用」を含 んで捉 えることが必要である。 (金冽ド, 2014, pp.41‐42) 金本(2014)は
日野(2002)の
先行研究を参照 して,「初期 の使用」 とは,「教室で 導入 された数学的表記 を使 い始 めるときにみ られ るものであ り,自 分な りの見方が投影 された独特の使 い方 として現れ る。ここでは,数 学的表記 は,思 考の道具 として よ りも, 教 師や 友 人 の期 待 に 沿 うよ うに 自分 の行 為 を表 示 す る道 具 と して の役 割 を持 つ 」 (pp.41‐42)と
述べてい る。また,「漠然 とした意味の もとでの使用」について,「すで に構成 された意味 と表現の援用 として,そ の数学的意味が確 定す ることな く,予 期的に, いわば漠然 とした意味の下で,表現の新 たな使用あるいは新 たな表現 の使用がな されて い ること」(p.42)と 述べてい る。 以上の ことよ り,算
数数学の表現の使用は,は
じめか ら厳密 な もの として行われてい るのではな く,数
学的に適切 な使用が徐 々に行われ るものである と解釈 できる。第
2の
点 につ いて は次 の通 りで あ る。 第2に
,既
習の表現 が援用 され る とい う点にも着 目をす る必要がある。 (中略) す でに構成 された意味 と表現の援用 として,そ
の数学的意味が確定す ることな く,予
期 的に,い
わば漠然 とした意味の下で,表
現の新たな使用 あるいは新 たな表現の使用がな されていることを明 らかに してい る。(金
本,2014,p.42)
この ことは,算
数数学の表現の使用 は,そ
の段階においては じめか ら数学的な意味に 対応 しているものではな く,次
々 と変化 してい くものである と解釈できる。 以上の ことよ り,「 算数数学の表現の使用の仕方」 については,次
の2点
に整理す る こ とができる。 ・算数数学の表現は,は
じめか ら厳密 に数学的な意味に対応 して使用 され ているので はな く,徐
々に適切 な使用 に変わつてい く。 ・算数数学の表現の使用 は,既 習の内容 をもとに考 え,その ことを組み合わせ る中で, よ り数学的な意味 として適切 な使用 の仕方 に変わつてい く。第
2節
江森氏によるコ ミュニケー シ ョン
2-1.コ
ミュニケー シ ョンの定義
江森(2012)は
「コ ミュニケー シ ョン」 を次の よ うに定義 してい る。 コ ミュニケー シ ョン とは,意思の伝達 を 目的に意図的に外化 された メ ッセー ジが存在す る情報伝達過程である と定義す る。(江
森,2012,p.21)
江森 (2012)は コ ミュニケー シ ョンを考える意義 について2つ
の視点 を挙げている。1つ
は,理
解・認知の変容 を動的なプ ロセス として捉 える研 究モデル を提示す ることで ある。 も う1つ
は,現
行の学習指導要領 で も明示 された 「思考力・判断力・表現力の育 成」とい う算数科や数学科教育の 目標 を具現化す る方法論 を提供す ることである。また, 「コミュニケーシ ョンは,単
なる情報伝 達ではな く,情
報伝達 に付随す る認知過程 を考 慮す ることによ り,個 々の学習者 の数学学習その ものに深 く関わ り合 う」(江森,2006a,p.4)と
述べ,こ
の コ ミュニケー シ ョンの捉 え方 を数学学習 に適用 している。 さらに,この コ ミュニケー シ ョンは 「問題解決
,推
論,情
報伝達,な
らびに,数
学的知識 を関連 づ ける とい う,数
学学習 の場 で展開 され てい る諸活動 を統合す る活動である」(江森,2012,p.46)と
述べてい る。 これ よ り,江
森氏の コ ミュニケー シ ョンの提 え方 を,本
論文にお ける数学的 コ ミュニケー シ ョンと捉 えて も差 し支 えない と判断す る。2-2.コ
ミュニケー シ ョン連鎖
江森(2012)は
,「数学学習 におけるコミュニケー シ ョンを理解す るためには,コ
ミ ュニケー シ ョンを連鎖 してい るもの として捉 える必要がある」(p.48)と 述べている。 また,そ
の コ ミュニケー シ ョンにおける連鎖 を協応連鎖,共
鳴連鎖,超
越連鎖,創
発連 鎖 の4類
型 に分類 してい る。 江森(2012)は
協応連鎖 と共鳴連鎖 の間を区分す るための もの と して第1規
準 を設 け,共
鳴連鎖 と超越連鎖 の間を区分す るための もの として第2規
準 を設 け,超
越連鎖 と 創発連鎖の間を区分す るための もの として第3規
準 を設 けた。 以下に,江
森(2012)の
示す4類
型 と3つ
の区分規準 を図1で
示す。 協応 連鎖 共鳴連鎖 超越 連鎖 創発 連鎖 図1:コ
ミュニケー シ ョン連鎖の4類
型 と区分規準 江森(2012)は
,こ
れ らの コ ミュニケー シ ョン連鎖 を分類す る3つ
の区分規準につ いて,次
の よ うに述べてい る。 第1規
準 「メ ッセージの解釈方法」 第2発
言者 による第 1メ ッセー ジの角峯釈が,コー ド解読 によつて行 われ る (コー ドモ デル)or推
論に よる省略 された情報の補完 によつて行われ る (推論モデル) 第2規
準 「メンタル・ スペースの包含 関係」 第2発
言者 のメンタル・スペースが第1発
言者 のメンタル・スペースを超越 していな いor超越 してい る 第3規
準 「メンタル・ スペースの構築方法」 第2発
言者の メンタル・スペー スの構築方法が第2発
言者の既存の知識 に依存 してい るor依
存 していない (江森, 2012, p.88) 10この ことに関 して
,筆
者 の考察 を加 える。 第1規
準の 「メ ッセー ジの解釈方法」 とは,第
1発
言者 のメ ッセー ジを第2発
言者が 解釈す るときに,メ ッセー ジの言葉通 りに解釈す る とい うコー ド解読 によるコー ドモデ ル なのか,あ るいはメ ッセー ジの内容か ら第1発
言者 が何 を伝 えたいのか とい うことを, 第2発
言者 が推論 して解釈 してい る推論モデル なのかを問 うものである と考 え られ る。 つ ま り,第 2発
言者が,第
1発
言者 のメ ッセー ジを言葉通 りに解釈 していれ ば,協
応連 鎖 であ り,第 2発
言者 が第1発
言者のメ ッセー ジの内容 を解釈す るために,第
1発
言者 が何 を伝 えたいのかを推論す ることで理解 していれ ば,共
鳴,超
越,創
発のいずれかの 連鎖 になる。 第2規
準の 「メンタル・ スペー スの包含関係」 とは,第
1発
言者 の メンタル・ スペー ス と第2発
言者 の メンタル・ スペー スの量的及び質的比較 に よるものである。 メ ン タル ・ ス ペ ー ス とは ,「 言 語 表 現 に よ つ て 心 の 中 に 作 り出 され る もの 」(Fauconnier,1994/1996)を
指す。江森(2012)は
これ を参照 し,メ
ンタル・ スペ ースを「数学 とい う複雑 に構造化 された知識体系 と数学 を使 う人々が数学的概念 を構成 す る能力や数学 をす ることに よつて共有 しているシェマな ど,私たちが数学 について思 考 し,コ
ミュニケー シ ョンす る際に用い る認知的な空間」(p.87)と した。 つま り,メ
ンタル・スペース とは,メ ッセー ジの内容に関す る知識や解決方法 を含んだ認知空間で ある。そ して,話
し手 と聞 き手の どち らがよ り多 くまたは よ り深 くといつた,そ
のメ ッ セー ジの内容 に関す る知識や解決方法 についての情報量や理解度 に よって メンタル ス ペースの包含関係 を判断す ることになる。第1発
言者の メンタルスペースが第2発
言者 の メンタル スペー スを包含す る場合 は共鳴連鎖であ り,第2発
言者 の メンタル スペース が第1発
言者の メンタルスペースを包含す る場合は超越連鎖 あ るいは創発連鎖 となる。 第3規
準の 「メンタル・スペースの構 築方法」 とは,第
2発
言者 のメンタル・スペー スが,第
1発
言者 か らメッセー ジを受 け取 る以前か ら,存
在 していたのか,あ
るいは第1発
言者の メ ッセー ジを受 けて,新たに生み出 されたのかを問 うものである と考 え られ る。つま り,第
1発
言者か らのメ ッセー ジを受 け取 る前か ら,第 2発
言者がそのメ ッセ ー ジに関す る知識や解決方法 を有 していれ ば,超
越連鎖 とな り,メ ッセー ジを受 け取つ た ことで,新
たな知識や解決方法が浮かんだのであれば創発連鎖 となる。 これ らの規準 によつて分類 された,「協応連鎖」,「共鳴連鎖」,「超越連鎖」,晴
J発連 鎖」 とい う4つ
の類型 について,以
下に事例の概要 を示す。 1協応連鋼
(江森
,2012,pp.60‐
63) ここでは,中
学校2年
の連立2元 1次
方程式の授業で行 われ た,「連立2元
1次
方程 式x+3y=-1…
①, 2x+y=-7…
② を解 け。」 とい う問題 に対 しての会話 が取 り上げ られている。 は じめに,生
徒Aか
ら次の よ うな解法が示 された。≪生徒
Aの
解法 ≫x+3y=-1…
①―
x+2y= 6
-)2x+ y=-7…
②
十
) x+3y=-1
-x+2y= 6 5y= 5
∴y=1, x=-4
これ に対 して
,複
数 の生徒 たちか ら,「 どち らの文字 を消去す るのか」,「 解法の意図 が明確 ではない」 とい う疑間の声が上がった。教師は生徒Aの
解法の意図を明確 に し よ うと,「なんで,①
か ら② を引 こ うと思 つたの?」 と生徒Aに
問いかけたが,生
徒A
は説 明できなかつた。そ こで,教
師は他 の解法はないか と学級全体 に尋ね る と,生
徒B
と生徒Cか
ら次の よ うな解 法が示 された。 ≪生徒Bの
解法 …xの
係数 を揃 えるや り方 ≫2x+6y=-2…
① ×2 y=1
―
)2x+ y=-7…
②
①式から
x=-4
5y= 5
≪生徒Cの
解法 …yの
係数 を揃 えるや り方 ≫6x+3y=-21…
・② ×3 x=-4
-) x+3y=- 1…
①
②式から
y=1
5x =-20
2つ
の解法が示 された後,教
師は さらに「2つ
の解法が出ま したが,同
じよ うな解 き 方,他
にはないで しょ うか」 と学級全体 に問いかけた。 この教師の問いかけに対 して, 生徒Dか
ら「-2を
① の式 にかけて② の式にたす と,-5y=-5に
なるか ら」とい う 発言が出た。 ≪生徒Dの
解法 》-2x-6y= 2…
① ×(-2) y=1
十
)2 x tt y=-7…
②
①式から
x=-4
-5y=-5
生徒Dの
解法が示 された後,「もう1つ
くらいあ りそ うですね」 とい う教師の問いか けに対 し,生
徒Eか
ら 「②の式に-3を
かければいいと思います」 とい う発言が出た。 ≪生徒Eの
解法 ≫x+3y=-1…
①x=-4
十
)-6x-3y=21…
②×
(-3)
②式から
y=1
-5x =20
, “ここで
,生
徒Fが
生徒Eの
発言 を聞いて,「や つぱ り出た。 これ しかないや」 とつぶ や いた。この とき,生
徒Eの
解法 しか残 されていない ことを,生
徒Fが
予期 していた と 考 え られ る。 この事例では,数式 とい うコー ドの操作によつて コ ミュニケー シ ョン連鎖が導 き出 さ れ ている。つま り, 1つ
の式 をa倍
(―a倍
)し
て,も
う一つの式 を引 く (足す)と
い うコー ド操作 を行 つてい ると考 え られ る。江森(2012)は,こ の よ うに メ ッセー ジ送信(コ ー ド操作)が
学習者 (第1発
言者 と第2発
言者)の
予測可能性 の範 囲内で起 こるコ ミュ ニケー シ ョン連鎖 を 「協応連鎖」 と呼んでい る。 1共鳴連釧
(江森
,2012,pp.64‐
68) ここでは,協
応連鎖 の事例 に引き続 く形で,次
の よ うな会話 が取 り上げ られ ている。 教 師:さ
つき,み
ん なが出 して くれた よ うに,加
減法 のや り方 には,文
字x, yの
どち らか を消去す るか,そ
の消去 を加 法で行 うか,減
法 で行 うかの,全
部 で4通
りあ ります。 教 師:そ
れ じゃ,さ
つきの,最
初 にA君
がや つて くれたのは ど うかな。 これ は,特
に係 数を揃 えていないね。①か ら② を引くと,一
x+2y=6で
, どちらの文字 も消 えていない。A君
の方法は, どうい う方法なんで しょうか。誰か, どうですか。 生徒G:上
のか ら下のを引いたのに,上
のをた したのは,あ
れ と同 じだと思います。 複数 の生徒 :え つ?(驚
きの声があが る) 教師:も
う一度言 つて,わ
か るよ うに。 生徒G
教 師 生徒G
教 師だから
,①
から②を引いて
,①
をたすと,… うつんん。わかんないかな。
ちょつと,ゆ つくり考えてみよう。まず,こ れ
,①
から②を引いたもの,こ れ。
じゃ,こ れを③としようか。それで。
それに①をたしたら,同 じになる。
うん
,待 つて
,待
って。これに①をたしたら,…
(間)。 教師:G君
の言 つてい ることわかるかい ? 他 の生徒 :(少 し緊張 した雰囲気 になる) 教師:(こ
こで教師が指名 した2人
とも 「わか らない」 と答 える) 教師:G君
。 も う一度 ゆっ く り言 つてみ て。 生徒G
教師 だか ら,上
のか ら下のを引いて,上
のをたす と… (沈黙)。 あつ,そ
うか。① ―②+①
だか ら,こ
れは2番
目の解答,①
×2-②
と同 じこと を しているつて言 うんだね ! ① ―②+① =①
×2-②
(2つ
の解法の同値性 を示 した板書) 生徒G:そ
う,そ
れが言 いたかつたんだ よ。 他 の生徒 :(笑 い=緊
張感 の解 消) 13教 師
:そ
うか,そ
うす る と,A君
の解答 も,実
は,加
減 法 でや つたBさ
んの方法 と同 じ こ とを していた ことになるんだね。(江
森,2012,pp.66-67)
この事例では,教
師の発言によつて生徒B,C,D,Eの
解法が加減法 とい う1つ
の 共通 した解法であること,xと yの 2つ
の文字のいずれかを消去す る方法は,2通
り(x とyの 2つ
の文字)× 2通
り (カロ法または減法)の
全4通
りとなることが告げ られた。 このことか ら,生
徒Aの
解法が他の生徒の解法 と異なつているとい う認識 を学級全体 で深めてい く。 ここで教師は,も
う一度,生
徒Aの
解法に注 目させ,「それ じゃ,さ
つ きの,最
初にA君
がやつて くれたのはどうかな。これは,特
に係数を揃 えていないね。 ① か ら②を引くと,一
x+2y=6で
,
どちらの文字 も消えていない。A君
の方法は, どうい う方法なんで しょうか。誰か,ど
うですか。」 と問いかける。 この問いかけに対 して,生
徒Gが
答 えたが,こ
の発言はす ぐに理解 されず,「えつ?」 とい う生徒たちの 驚 きの声が上がる。教師 も理解す ることができずに,「もう一度言つて,わ
かるように」 と指示 している。生徒Gは
再び説明を試みたが,
うまくできずに 「わかんないかな」 とつぶやいている。 教師は,「①か ら② を引いたものを③ としよ うか」 と提案 しているが,論
理関係 を整 理 しようと考えている教師 と,「① ―②+①
=①
×2-②
」 とい う内容 を説明 したい生 徒Gと
の間で,一
瞬ではあるがギャップが生 じている。つま り,生
徒Gが
「①―②十 ①=①
×2-②
」 となることか ら,生
徒Aの
解法は生徒Bの
解法 と同値であることを 説明 しようとしているにもかかわ らず,教
師が「① 一② 十①=③
十①」とい う考え方に 固執 して しまつた瞬間があつた。 この後,教
師は生徒Gの
発言の意図が理解でき,「① ―②十①=①
×2-②
」 とい う式にたどり着いて,教
師 と生徒Gの
間で,生
徒Aと
生 徒Bの
解法の同値性が共有 された。そ して,「① 一② 十①=①
×2-②
」 とい う式を板 書 したことで,生
徒Gの
意図が他の生徒に伝わつた。 この事例では,当
初生徒Gの
発言は教師を含 め,他
の生徒に理解 されなかつた。 し か し,教
師は生徒Gの
発言は重要な意味があるものだ と感 じ取つた。通常,誰
にも理 解 されない発言は,そ
のまま無視 されて しま うことが多いが,教
師はあきらめずに「ゆ っくり考えてみよ う」 と言い,
さらに生徒Gの
発言を促 している。 このよ うに生徒G
のメッセージ解釈には,コ ー ドの解釈だけではなく,関
連す る数学的知識 を用いた数学 的概念の再構成 とい う認知活動が必要 とされる。江森(2012)は,こ
のよ うに第2発
言者 (教師)が
第1発
言者 (生徒G)の
意図を首尾 よく解釈す ることにより成立す るコミュ ニケーション連鎖を 「共鳴連鎖」 と呼んでいる。に越連釧
(江森
,2012,pp.75‐
79)ここでは
,教
師Aが
教師Bと
教自雨Cに
対 して,「a2+b2+c2-ab一
bc―ca≧0
を証 明せ よとい う問題 は ど うです か。」 と尋ねる場面か ら始 める会話 を取 り上 げる。 この問題 は大学の新入生 を対象に その問題が適切か どうか と した学力調査問題であ り,教師
Aは
教師Bと
教師Cに
対 して, い う判断 を求 めている。 教 師A
教 師B
教 師B
教 自雨C
教 師A
教 師A
a2+b2+c2_ab bc―
ca≧0
を証明せ よとい う問題 は ど うですか。 これ,平
方の和にすれ ばいいんで しょ。 ち ょつ と簡単過 ぎるか ら,実
係数の3つ
の2次
方程式ax2+2 bxttc=0,
bx2+2 cx+a=0,cx2+2 axttb=0の
うち,少
な くとも1つ
は実数解 をも つ ことを証明せ よとい う問題 に した ら。 判別式 の和に分解 したんですね。 判別式 の和? (教
師Aは
3つ
の判別式 を書 き出 してい る) :そ うか,(b2_aC)+(c2-ab)+(a2_bc)だ
か ら。少 な くとも1つ
は実数 解 をもつな ら,判
別式の和は0以
上になれ ばいいんだ。これ,な
かなか面 白い 問題ですね。 0工森
, 2012, p.76) 教師Aの
発言 に対 して,教
師Bは
「平方の和」 とい う用語か ら,こ
の問題 がa2_卜b2+c2__ab ―bc―ca= : {(a――b)2+(b__c)2_十(c――a)2}≧
0
として角御することを理解 している。 さらに
,教
師Bは
,「 ち ょつ と簡 単過 ぎるか ら」 と言 つて,「実係数 の3つ
の2次
方程式ax2+2 bx+c=0,bx2+2 cxtt a=0,cx2+2 ax+b=0の
うち,少 な くとも
1つ
は実数解 をもつ ことを証明せ よとい う問題 に した ら」と言い,男りの問題 を提案 している。これ に対 して,教
師Cは
「判別式の和 に分解 したんですね」と言い, 教師Aが
示 した不等式が,教
師Bが
示 した3つ
の2次
方程式の判別式の和であること に気付いている。つま り,2つ
の問題 は同 じ構造を もつた問題 であることを理解 してい る と,教
師Cが
教師Bに
伝 える形 になつている。 しか し,教
師Aは
教師Bが
なぜ2次
方程式の問題 を提案 したのか,教
師Cが
なぜ 「判別式 の和」 といつたのかを理解でき ず に,「判別式の和?」 と教師Cの
言葉 を繰 り返 し, 3つ
の2次
方程式の判別式 を書 き 出す。 この行為 を もつて,教
師Aは
教師Bと
教師Cの
発言 を理解す るこ とがで きた。 この事例では,教
師Bの
前半の発言 「これ,平
方の和 にすれ ばいいんで しょ。」は, 教師Aが
想定 していた平方の和への式変形 とい う知識 の範 囲内で行 われ ていたため, 教師Aと
教師Bの
間には 「共鳴連鎖」 が見 られた。 しか し,教
師Bの
後半の発言 「ち ょっと簡単過 ぎるか ら,実
係数 の3つ
の2次
方程式ax2+2 bxttc=0,bx2+2 cx十
a=0,cx2+2 axttb=0の
うち,少
な くとも1つ
は実数解 を もつ ことを証明せ よとい う問題 に した ら。」は,教
師Aが
予期 していた以上の応答が含 まれていた。江森(2012) は,こ
の よ うに第2発
言者 (教師B)の
応答が第1発
言者 (教師A)の
理解 を超 える範 囲で行われ るコ ミュニケー シ ョン連鎖 を 「超越連鎖」 と呼んでい る。つ ま り,教
師A
と教師Bと
の コミュニケー シ ョン連鎖 は 「共鳴連鎖」か ら 「超越連鎖」へ と変わつて 15いった。 また
,教
師Bの
提案 に対 して,推
論 をもつて 「判別式の和 に分解 したんです ね。」 と発言 した教師Cと
の間には 「共鳴連鎖」があった こ とになる。愴
J発連錮
(江森
,2012,pp.80‐
86) ここでは,小
学校5年
生の事例 を取 り上げる。 この事例 は,「 家 と家の間 を直接電話 線で結ぶ ことに します。今,ど
の家 とどの家の間にも,ち
よ うど1本
ずつ電話線 を取 り つけます」 とい う文章 に対 して,児
童Aか
ら 「電話線 の結び方が分 か らない」 とい う 質問が出 され,教
師が児童Aに
「3軒
の場合 について黒板 に図をかいて考 えよ う」 と 指示す るところか ら始 まる。 まず児童Aは
, 2軒
の家で考 え始 めた。家 を○印で表 し, 2つ
の○印の間を1本
の 線で結んだ。その後,も
う1つ
○印を加 えて1本
の線 で結び,矢
印で指 してい る○印か らさらに線 を結 ぼ うとした (図 2)。 その とき,児
童Aは
「これ, ど うなるんだか,わ
か らない」 と言 つた。 図2
ここで,教
師の 「誰 か どうです か。3軒
の家 の間,こ
れでちやん と結ばれている じや ない」 とい う問いかけに対 して,児
童Bは
「家 と家の間を1本
ずつ結ばな くちゃいけ ないんだか ら,こ こも結 ばな くちゃいけない」と左右両端の○印を結ぶ線 を描 いた。(図3)
図3
児童Bの
説 明が終わるとす ぐに,児
童Cは
「これ じや,な
んだか変に見 えるか ら, これを動か して,こ
うすればいい」 と言つて次の①∼③の手順 を行 って見せた。(図4
∼図6)
①一部を手で隠す (網掛けの部分) 16 図4
②
O印
を下にかく 図5
図6
そ して,教
師 は,「 いいです か,わ
か りま したね。家 と家 とを結ぶ とい うことは, こ うい うことです よ」 と言い なが ら,児
童Aと
児童Bと
児童Cの
意見をま とめて次 のよ うな形 を示 した (図 7)。 図7
以上の ことか ら,児
童Aの
図は児童Bの
図を引き出す うえで不可欠であ り,児
童B
の図は児童Cに
よる3軒
目の家か ら2本
の電話線 が出 るとい う操作 を導 くために必要 なメッセー ジであった こ とが分か る。それぞれのメ ッセージは単独 では最終的な形 を生 み出 し得 ない とい う点で,構
成要素以上 のものをもた らし,か
つ,も
との要素に還元で きない ものを生み 出す とい うものになつている。江森(2012)は,こ
の よ うに第1発
言者 の送信 したメ ッセージが第2発
言者の思考を刺激 して,第2発
言者 の所有 している知識 な どと結 びつ くこ とに よ り,新
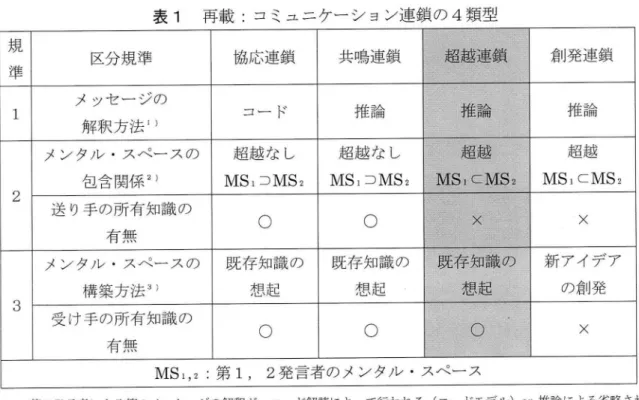
しいアイデアが創造 され るコ ミュニケー シ ョン連鎖 を 「創発連鎖」 と呼んでい る。 17規 準 区分規準 協応連鎖 共鳴連鎖 超越連鎖 創発連鎖 1 メ ッセー ジの 解釈 方法1) コー ド 推 論 推 論 推 論 2 メンタル・スペー スの 包含 関係2) 送 り手の所有知識 の 有無 超越 な し NIIS l⊃
MS2
○ 超越 な しMSl⊃
MS2
○ 超 越 DIIS l⊂IIIS2 × 超越MSl⊂
ⅣIS2 × 3 メン タル・スペ ー スの 構 築 方 法3) 既存知識 の 想起 既存知識 の 想 起 既 存知識 の 想 起 新 アイデ ア の創発 受 け手の所有知識 の 有無 ○ ○ ○ ×MSl,2:第 1, 2発
言者 の メンタル・ スペー ス 江森 (2012)は,こ
の4つ
の コ ミュニケー シ ョン連鎖 の内容 を整 理 し,以
下 の表1を
提 示 して い る。 表1:コ
ミュニ ケー シ ョン連 鎖 の4類
型 1)第 2発 言者による第1メ ッセー ジの解釈が,コー ド解読によつて行われ る (コー ドモデル)Or推論による省略 され た情報の補完によつて行われ る (推論モデル) 2)第2発 言者のメンタル・スペースが第 1発 言者のメンタル・スペースを超越 していない or超 越 している 3)第2発言者の メン タル・ スペ ー スの構築方法が 第2発言者 の既存の知識 に依存 してい る or依存 していない 0工森, 2012, p.89) また,コ ミュニケー シ ョンの レベルは,協
応連鎖→共鳴連鎖→超越連鎖→創発連鎖 と い うよ うに上がってい き,も
し,高
位 の レベルでの コ ミュニケー シ ョンが うま く成立 し なけれ ば,コ ミュニケー シ ョンは低位 の レベルに戻 るとい うコ ミュニケー シ ョンの再帰 性 について も指摘 してい る (p.89)。第
3節
ポ ジシ ョニ ング セオ リー
3¨ 1ポジショニング セオ リー
グループによる話 し合 い活動時,ポ
ジシ ョニ ング セオ リーは,生
徒 間の対人関係 を 理解す るための視点 とな る (Anna&Gloriana,2015,p.382)。 この ときのポジシ ョニン グ とは,話
し合い活動 を構造化 して捉 えるために,グ
ループ内の生徒 に何 らかの役割 を 割 り当てて,行
為 (action)ゃ発言 (speech)に ついて述べた ものである。Esmonde(2009)は ,グ
ループによる話 し合い活動時のポジシ ョン として,エ
キスパー ト,ノー ビス,ファシ リテー ターの
3つ
を設 け,こ
れ らのポジシ ョンのいずれかを生 徒た ちが とるとしたlAnna&Gloriana,2015)。
なお,エ
キスパー トは熟練者役,ノ
ー ビスは初心者役 ,フ ァシ リテー ターは促進者役 とい うよ うに 日本語訳 に言い換 え られ る が,本
稿 では英語表記 のまま使用す るこ ととす る。まず,エ
キスパー トとは,グ
ループ の他 のメンバーの活動 が正 しい ものか ど うかを決 めることがで き,数学的に認 め られた 権威 をもつポジシ ョンである。 そ して,エ
キスパー トでの動 きは “Kl move" (Kは
Knowledgeの
頭 文字で,1は
第1発
言者 とい う意味である。)と コー ド化 され る。次に, ノー ビス とは,自
分 自身 には十分な能力がない と考 え,エ
キスパー トに従い,し
ば しば 他者 に教 えて もら うとい うポジシ ヨンである。ただ し,エ
キスパー トの助言 を疑 うこと もある。 そ して,ノ
ー ビスでの動 きは “K2move" (Kは
Knowledgeの
頭文字で,2
は第2発
言者 とい う意味である。)と コー ド化 され る。最後に,ファシ リテー ター とは, い くつかの方法で グループでの話 し合い活動 に多 くのメンバー を参カロさせ,問 題解決を 促進す るポジシ ョンである。 そ して,フ
ァシ リテー ターでの動 きは “Al or A2 move"
(Aは
Actionの頭 文字 で,1は
第1行
為者,2は
第2行
為者 とい う意味である。)と
コ ー ド化 され る。 本稿では,グ
ループに よる話 し合い活動の 目指すべ き姿 として,生
徒 間の発言や行為 のや りとりによつて,生
徒一人ひ とりが これ ら3つ
のポジシ ョンを取 り,そ
のポジシ ョ ンが変動 してい くことだ と考 える。ただ し,こ
の変動 してい く中で,教
師の介入が必要 な場合 もあると思われ る。なぜ な ら,ノ ー ビスの生徒 はエキスパー トの生徒の意見を聞 くばか りで,受
動的な学習参加 にな ることが考 え られ るか らである。 この よ うな とき, 教師が介入 してフアシ リテー ターのポジシ ョンを取 り,ノ ー ビスの生徒 のポジシ ョン変 動 を促す ことになろ う。3-2.ネ
ゴシエーシ ョン ムープ
Anna&Gloriana(2015)は ,グ
ルー プによる話 し合い活動時,生
徒 たちの言葉 のや りとりをコー ド化す ることを通 して “ネ ゴシエー シ ョン ムーブ"と
い う視点 を与 えて い る。“ネ ゴシエー シ ョン ムーブ"と
は,グ
ループによる話 し合 い活動 の練 り上げ場面 について,生
徒 間のポ ジシ ョン変動 をもつて捉 えよ うとす るもので ある。彼女 らは,次
の課題 を用いて生徒 たちの話 し合い活動 を調査 した。【認長是夏 : The Going to Yellow Park Lesson】
Karlと 彼 らの友達は
,Yellow Parkで
キャンプをす るために旅行 を始 めま した。彼 ら は全員違 う場所 か ら出発 します が,Karlま
た は彼 の友 達 の誰 か が 午後8時
まで に Yellow Parkに 着かなけれ ばな りませ ん。 さもなけれ ば,彼
らは予約 が取 り消 され,約
東 と
100ド
ルの保証金 を失 うことにな ります。Karlと
彼 の友達はメ ッセー ジをお互い にや り取 りし,Yellow Parkの
担 当者 のLinnにも送 つています。Linnは
Karlと彼 の友 達 が午後8時
までに Yellow Parkに 着 くか どうかを,メ
ッセー ジの最新情報 を受 け取 る 中で判断 しなけれ ばな りませ ん。Linnは
あなたの手助 けを必要 としています。Karlと 彼 の友達は午後8時
までに Yellow Parkに 着 くことがで きるのか,ま
た Yellow Parkに 着 く順番 について見 当をつ けな さい。≪
Bryanか
らLinnへ
の ボ イ ス メー ル ≫PM5:47:“ こんにちは
,Linnさ
ん。 こち らKarlの友達のBryanで
す。Yellow Parkを 閉 園 しないで くだ さい。私 は午後8時
までに Yellow Parkに 着 くはず です。私 は今(5:47)で,Yellow Parkから
150マ
イル離れた ところにいます。私は安定 したペー ス(定速)で運転 しています。"
PM6:32:“ こんにちは
,Linnさ
ん。 こち ら再びBryanで
す。私は今 (6:32),Yellow Park か ら105マ
イル離れた ところにいます。私 はあなたにま もな く会 えるで しょ う。"≪
Karlか
らのeメ
ー ル ≫Date:8月
23日 (木)18:30:03
To:Bryan,Vidya,Isabel,Bryan
CC:Linn
Subject :On my way
こんにちは
,み
な さん。 私は問題 を抱 えて しまいま した。Isabel笑
わないで。私は こ の旅行の グラフを付 けています。私がいつ 目的地に着 けるのか どうかをあなたに知 って もらうためです。(私の家 はキャンプ場 か ら97.5マ
イル離れ ています。)私
はた くさん の準備物 (テン ト,寝
袋,懐
中電灯)を
忘れて しまいま した。私は6:00に
出発 したに もかかわ らず,2回
は家 に戻 りま した。すみ ません。私は間に合 うよ うに努力 したので す が.… しか し私は も う一枚 ス ピー ド違反のチケ ッ トをもら う余裕 はあ りませ ん。私は 時速65マ
イルで運転 しています。早 く会いたいです。 ≪Isabelの Facebookへ
の投 稿 ≫ Isabel Riley バイ クに乗 るには素晴 らしい 日だ。 時速 12マイル,歩
調 は一定。 8月 19日 午後 2:441sabel Rlley
雨は降つていない。 タイヤがパ ンク したが,修
理道具 を持 つていた。 8月 19日 午後 3:38 1sabel Riley 予想外の ことが起 こつた。私は速度 を上げ,時
速15マ
イルで行かなけ れ ばな らない。8月 19日 午後 4:14
1sabel Riley
ガ ソリンスタン ドにい る。 半分は過 ぎた。 8月 19日 午後 5:121sabel Riley
時速 10マイル。軽食 を食べて遅 くなったが,立
ち止 まってはいない。 8月 19日 午後 5:27 ≪Vidyaか
らLinnへ
の電 言舌≫ 午後 6:32:“Linnさ ん,Vidyaで
す。私 は今,家
を出発 しま した。午後6:32で
す。私 はモー ターバイ クで行 きます。 だか ら,私
は時速54マ
イル以上で向か うことはできま せ ん。私はsweet corn standへ到着 した時再びあなたに連絡 します。"午後 7:191“ こんばんは
,Linnさ
ん。私 はsweet corn standにいます。 ち ょ うどあ と 半分の距離 にな りま した。待 つていて くだ さい。" 【筆者による課題考察】 この課題は条件不足の問題 である。課題に取 り組む中で,生
徒 自身で条件を決めなけれ ばな らない。そのことで,グ
ループ内の話 し合い活動が活発になることが期待できる。 ま た,条
件 をどのよ うに決めるかで,学
習内容の レベルが上がることも考えられ る。Anna&Gloriana(2015)は
,こ
の課題 を3つ
のグループ(A,B,C)に
取 り組 ませ,そ
れ を以下の よ うに分析 した。 表2:各
グループの構成 メンバーGroup A Group B Group C
Bobby Bryce Addy
Eileen Chad Anton
」OSh 」ay Emily
」ulie Meg Kailey
【分析】 グループ
Aは
エ キスパー トとノー ビスが区別 され た グループであった。Eileenは一 貫 してエ キスパー トのポジシ ョンでKlの
moveを
行 い,ノ
ー ビスのポジシ ョンとなつ た他のメンバー(Bobby,Josh,Julie)に
対 して課題 の解決方法 を提供 した。 この解決方 法に対 して,他
のメンバーは疑いをもたなかつた。 グループBは
エキスパー トのポジシ ョンを取 る生徒 に対 して多 くの疑間を投げかけ た グループであつた。複数 の生徒がKlの
moveを
しば しば行 い,そ
の都度,他
のメン バーによつて疑われ た。 しか し,K2の
moveを
行 うメンバーはほ とん どいなかつた。 9 “グル ー プ
Cは
エ キスパー トとノー ビスのポ ジシ ョンが グル ー プの メ ンバー 間で共有 され た グル ー プで あ つた。あ る メ ンバ ー が決 ま った ポ ジ シ ョン を取 るの では な く,メ ン バ ー間で次 々 とポ ジシ ョンが変動 した。この グルー プで はアイデ ィアの ギブア ン ドテイ クが見 られ た。 グル ー プBと
グル ー プCで
は フ ァシ リテー ター のポ ジシ ョンを取 るメンバー が いた が,機
能 して い るの は グル ー プCの
フ ァシ リテー ター で あつた。 また,Anna&Gloriana(2015)は
,各
グル ー プで の メ ンバ ー 間のや りと りの様子 を表3と
表4の
よ うに数値 化 した。先 の分析 は この2つ
の表 に現れ た数値 に よつて裏付 け さ れ てい る。 表3:グ
ル ー プ活動 時 にお ける知識 と行為 のや りと りSulnlnary of Knowledge and Action Exchanges During GrOup Work
左端の上の項 目か ら
,グ
ループ活動 に費や した時間,教
師 (Mr.Taylor)が グループに 関わつた時間,知
識 のや りと りの数,行
為のや りとりの数,や
りとりの合計数 を表 して い る。この表か ら,教
師の介入が少 ない方が グループ活動のや りとりが多 く,一
人ひ と りが知識のや りとりが多い ことが分か る。教師の介入 は少ない方がいいのではないか と 考 える。また,少
ない介入の中でいかに話 し合いが活発 になるための助言ができるのか が大事になる と考 える。もちろん,教
師 の介入がまった くのないのではいけない。行為 のや りとりの数 は,教
師の関わつてい る時間によらない ことも分か る。この行為が起 こ るや りとりは他 の要因があることが考 え られ る。GrOupA
GroupB
GrOupC
Duration of group work 32:30 31:55 34:25 Tilne M■Taylor spent with group 9:10 4:20 1:35
Number of knOwledge exchanges 26(87%) 85(79%) 112(83%) Number of action exchanges 4(13%) 23(21%) 24(17%)
Total exchanges 30 108 136
(Anna&Gloriana,2015,p.398)
表
4:各
グル ー プ にお け るネ ゴシエ ー シ ョン ムー ブ の配 分Distribution of Negotiation Ⅳloves PerfOrlned by Each Group Member
(Anna&Gloriana,2015,p.399)
dAl…第1行為者,行為する
※Kl… 第1発言者,情報 を提 供す る
K2…
第2発言者,質問す る A2… 第2行為者,行為 に関 して要求す る Challenge・ …疑 うNumber of exchanges performing(発
言 と行 為 のや りと りの数)Kl
(%K exch。)K2
(%K exch.)dAl
(%A exch.)A2
(%A exch。) Challenge (%exch.) Group ABobby
4(15%) 5(19%) 0(0%) 0(0%) 0(0%) Eileen 14(54%) 2(8%) 0(0%) 3(75%) 2(6%)Josh
5(19%) 4(15%) 0(0%) 0(0%) 1(3%) Julie 3(12%) 6(23%) 0(0%) 1(25%) 0(0%) GrOup B Bryce 27(32%) 10(12%) 0(0%) 13(57%) 11(10%)Chad
16(19%) 8(9%) o(0%) 2(9%) 6(6%) 」ay
38(45%) 20(24%) 1(4%) 3(13%) 16(15%)Meg
7(8%) 4(5%) 0(0%) 0(0%) 2(2%) Group CAddy
41(37%) 24(21%) 0(0%) 6(25%) 11(8%)Anton
21(19%) 0(0%) o(o%) 0(0%) 0(0%) Kailey 26(23%) 17(15%) 0(0%) 1(4%) 6(4%)Emily
37(33%) 25(22%) 0(0%) 16(75%) 8(6%) 23さらに
,Anna&Gloriana(2015)は
,ネ
ゴシエーシ ョン ムーブの網羅 リス トを設け,それ らをコー ド化 して表
5を
示 している。表
5:ネ
ゴシエー シ ョン ムーブの網 羅 リス ト(Synoptic Moves)コー ド 動 き 描 写
例 (課題 :The Going to
Yellow Park Lesson
よ り) Kl 第1発言者 情報 を提供す る 彼 は 8:30に そ こに着 く。 Al 第1行為者 行 為 をす る 例 えば[計算す る] K2 第2発
言者 質 問す る 他 の誰 か に よつて確 認 され た情報 を提案す るKarlは
そ こに何 時 に着 き ます か?私
は,彼
はそ こに8:00に
着 くと思 うん だ け ど。 A2 第2行
為者 行 為 に関 して要求す る あなたは 97.5を 65で害1る こ とができますか ?dKl
第 1発 言者 に 遅れ て 情報 の提供 が遅れ る それ と,距
離 は等 しいけ どdAl
第 1行為者 に 遅れ て 行為す る ことを申 し出 る あ な た は私 がKarlの
状 況 を 分 か る こ と を 望 ん で い ます か?K2f
第2発
言者 に よ つて引き続いて 行われ る 第1発言者 の動 きの後 に 引 き続 いて行 う オ ッケー。=K1/K2
動 きの詳 述K1/K2の
動 きを言 い直す そ れ で,Karlは
そ こ に8:00の
30分
後 に着 きま す。+K1/K2
動 きの拡 張K1/K2の
動 きにい くつかの 情報 を追カロす る Karlはそ こに 8:30に 着 き ます。だか ら,彼
は遅刻す るで しょ つ。 x K1/K2 動 きの強化K1/K2の
動 きにい くつ かの 条件 を提 供 す る 彼 はそ こに 8:30に着 きま す。 なぜ な ら,彼
は 7:00 現在,ま
だ97.5マイル離 れ た地点 にい るか らです。 (AnnagこGloriana, 2015, pp.420‐ 421) 24ネ ゴシエー シ ョン ムーブの構造 を木 に例 えると
,表
5は
幹の部分 に当たる。Anna&
Gloriana(2015)は,枝
葉に当たる部分を表6の
ように整理 している。表
6:ネ
ゴシエー シ ョン ムーブの細部 リス ト(Dynamic Moves)
コー ド 動 き 描 写 例 鰈 題
:The Going to
Ye■
ow Park Lessonよ
り)保 留 に関す る もの(Suspending mOves)
cig
確認 を依頼す る 前 の発言 が正 しく聞 けて い るのか確認 を依頼す る あ な た は何 と言 い ま した か? Cf 確 認 を与 え る 前 の発 言 を確認 す る 私 は言 つた,Karlは
そ こに 8:30に着 くで しょう。 bch 相 づ ち を打 つ 主張 を認 める動 きか聞い てい るのか示す う―ん。 check 確認す る 話 し手は発言 が聞かれ て い るのか確認す る あなたは私の こと聞いてい た ? 未完に関す るもの(Aborting moves) Ch 疑 う 第 1の主張の妥 当性 を疑 つ(Karlは
そ こに8:30に
着 く。) いい え,彼
は着 きません。 rch 疑 い に対 す る 反 応 疑いに対 して反応する(Karlは
そ こに 8:30に着 く。) い い え,彼
は着 きませ ん。 はい,彼
は着 きます。 SCh 自身 を疑 うKlの
動 きの成果 を偏 ら せ るKlの
動 きを制 限す るKarlは
そ こに何時に着 きま す か?知
りませ ん。Karlは
そ こに8:30に
着 き ます が,私
は本 当に知 りま せ ん。 解 明 に関す る もの(Elucidating moves) cl取 明確 化 前の発言の意味を明 らか にすることを試みる あなたが意味す るのは 97.5 マ イ ル で す か,そ
れ と も 97.5分ですか ? rcl野 明確 化 に対す る 反 応 cl取 の動 きを解決する 私 は 97.5マ イル を意味 して い ます。 25持 続 に関す る もの(Sustaining moves) rp 繰 り返 す 前 の発言 を繰 り返す