プレゼンファイル・集中講義ノート Jun O'Hara

(1)

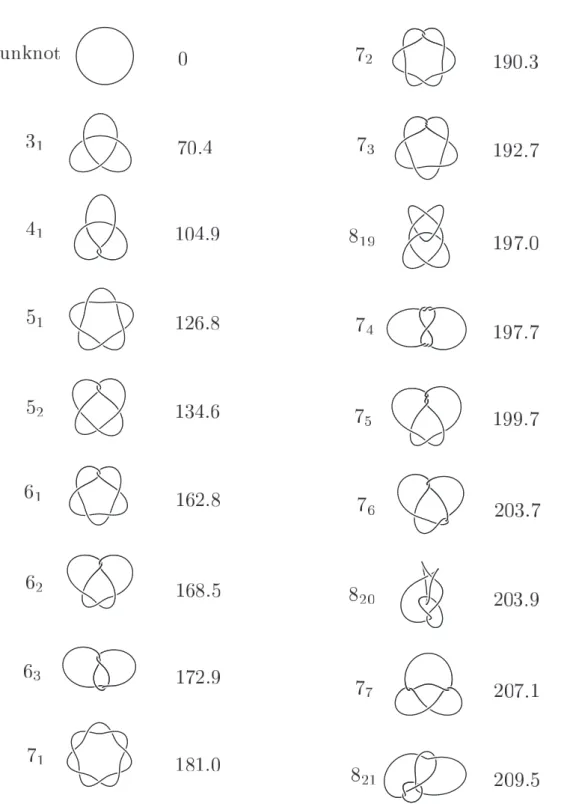
結び目のエネルギーとその周辺

今井淳

(首都大学東京)

平成

29 年

12 月

20 日

概要

結び目のエネルギーとは、荷電した結び目の静電エネルギーを繰り込んだものの一般化で、各結び目型の「最良の形」を定義するために導入された。このように、大域的な情報を持つ汎関数を見つけ、それを用いて最適問題を考える、という変分問題的な問題意識から幾何学的結び目理論と呼ばれる研究が始まった。「最良の形」の存在や滑らかさなどを示すため解析的手法が適用された。さらに数値実験を通してＤＮＡ研究・高分子科学などにも応用されている。一方、結び目のエネルギーの最初の例はメビウス変換で不変になることが分かり、そこからメビウス幾何学、特に大域的・積分幾何学的な側面との関連が生じた。また、結び目のエネルギーの定義で用いた繰り込みの手法を応用すると、ユークリッド空間のコンパクト領域のポテンシャルの１-パラメータ族を得るこ

とができ、ここから領域の中心の１-パラメータ族を得る。これは重心の一般化になっている。この部分には解析

のポテンシャル論や凸幾何学が関連する。最後に、このポテンシャルのあるものと、メビウス幾何学・積分幾何学を合わせると、平面領域や結び目に対する新しい量を得ることができる。

0 はじめに

平成２４年５月の埼玉大および東工大（情報）での集中講義の講義ノートです。修論のネタの提供が主な目的です。章建ての通り、大きく４つに分けられます。各々のトピックはかなり独立に読むことができます。とりあえず全貌を掴んでほしいので、証明は簡単なもの以外は省略しています。

以前に書いたものからの切り貼りを用いた部分も多々あるため、また、分量が増えてきたため、重複や、記号の不統一など様々な不都合があるかもしれませんので、ご了承ください。

1 結び目のエネルギー、繰り込まれた

_r

−2

-

エネルギー

1.1 結び目の基礎用語と記法

M をR3 _または_S3 _とする。_M _の_{アンビエント・イソトピー}_{とは、同相写像の}_1-_{パラメター族} _h

t:M →M

(t∈[0,1])で、次を満たすものとする：

(1) H(x, t) =ht(x)で与えられる写像H :M×[0,1]→M は連続である.

(2) h0 は恒等写像である.

結び目とはS1 からM つまりR3 _または _S3_{への埋め込み写像}

f、またはその像 K=f(S1) のこととする。

M を全空間という。Mの二つの結び目が同じであるとは、まわりの空間も込めて連続変形可能、ということとする。正確には、K と K′ _が_{イソトピック}_{であるとは、}_M _{のアンビエント・イソトピー}_h

t:M →M (t∈[0,1])

でh1(K) =K′となるものがあることをいう。後述のプルタイトは二つの結び目がイソトピックである必要十分条件は、K′ ₌_h(K)_{となるような}_M _{の向きを保つ同相写像}_h_{が存在することである。折れ線結び目とイソトピッ}

クなものを順な(tame)結び目という。微分可能な単純閉曲線とイソトピックとしても同じである。順でないものを野性的(wild)結び目という。以下、結び目といったら順なものを指すこととする。このとき、イソトピックという条件は、Reidemeister移動という局所変形を何回か繰り返せば互いに移りあう、という条件と同値である。イソトピックという関係は、結び目全体の集合の同値関係になる。結び目Kを含む同値類をKのイソトピー類、結び目型と呼び[K]であらわす。直観的にいえば、紐で作った結び目を紐を切ることなく変形して得られたもの同じと見なすのである。自明な結び目とは、平面内の通常の円（正円と呼ぶことにする）、またはS3の大円とイソトピックな結び目のことである。結び目理論では、余次元、つまり全空間の次元₋結び目の次元が2の場合を扱うが、これは余次元が大きいと全ての結び目がほどけてしまうからである。これは、任意の結び目の射影図は、交点の上下を何か所か変えると、自明な結び目の射影図になることから分かる。

(4)

図 1: 二つの結び目の合成図 2: 合成結び目の成分

合成して得られたものをK1♯K2とあらわす。K1,K2に対応する部分を成分と呼ぶ（図2）。自明でない二つの結び目の連結和となる結び目を合成結び目といい、合成結び目でない結び目を素な結び目という。

図2の丸で囲まれた部分のように、結び目の一部分を球面で切り取ったものをタングルという。以下では、球面の中に入っている曲線が1本のみで、その両端が球面上にあるもののみを指すものとする。

RからR3_{への埋め込み写像で、両端が同一直線に漸近的なようなもの、またはその像を}_{開いた結び目}_という。ここでは、開いた結び目という場合は、通常の結び目から、中心がその結び目の上にあるような球面に関する反転（後述）で得られるものに限ることにする。

記法R3_{の結び目が長さ}₁_{で弧長でパラメータ付されているときには、埋め込み写像を}_h_{で表すことにする。}

1.2 結び目のエネルギーとは∼幾何学的な最適問題

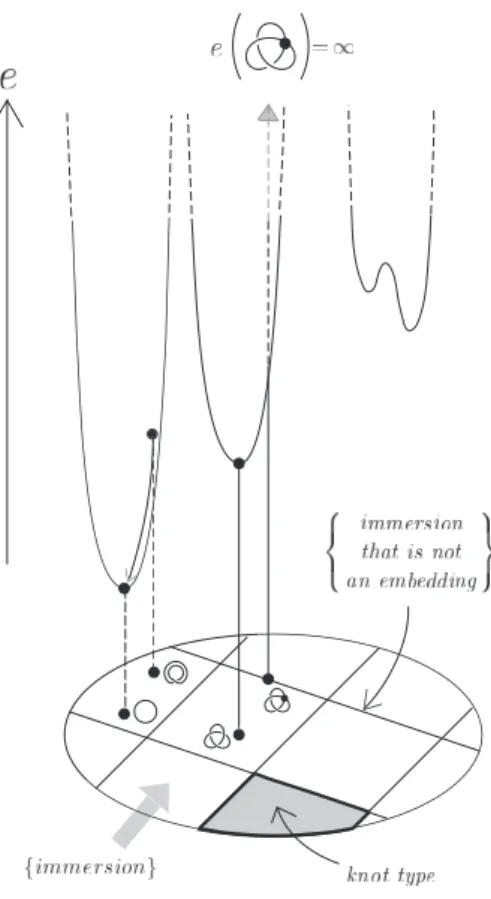
結び目のエネルギーのアイディアは、各々の結び目型（アンビエント・アイソトピーについての同値類）で、「最もよい形」の結び目を定義するために導入さた。この動機としては、以下のようにいくつかある：

• 与えられた結び目をエネルギーを用いて「最もよい形」に変形し、結び目の分類問題に使いたい。

• 平均曲率を用いれば、極小曲面という美しい曲面が得られる。このようなことを結び目で（トポロジーに留意しながら）やりたい。

• 結び目全体のなす空間でモース理論をしたい。

後で分かるように、与えられた結び目型の中に、「最もよい形」の結び目が存在するかどうかは、エネルギーの種類や、その結び目型が素であるかどうか、という位相的な条件や、結び目が入っている空間の計量といった、幾何学的な条件に依存する。また、「最もよい形」が存在する場合でも、一つの結び目型に「最もよい形」がいくつ存在するかは分かっていない。その最初の例は、荷電した結び目の静電エネルギーを一般化して、積分の発散を繰り込むことにより得られる。

問題 1.1 （福原、作間）

(1) 結び目の空間上に適当な汎関数（「エネルギー」と呼ぶ）E を定義する。

(2) 結び目型[K]に属する結び目のエネルギーの値の下限をE([K])と表す、すなわち、E([K]) = infK′_∈_[_K_]E(K′)。

これが、[K]に属する結び目K0で実現されるとき、すなわち、E(K0) =E([K])となるとき、この結び目 K0 を結び目型[K]のE-最小元と呼ぶ。

(3) 各結び目型に、（対称性をもつような）見た目のよい「代表的」な結び目を、「エネルギー」最小元として定義出来るような、「エネルギー」を与えよ。

(5)

図3: モチヴェーション.

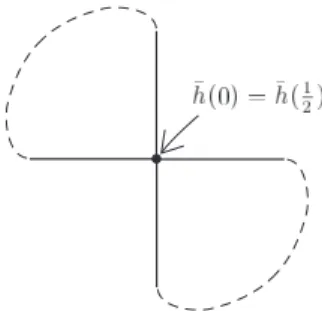
運良くエネルギー汎関数の極値に到達し、更に運良くそれがその元々の結び目型のエネルギー最小元になれば解決したことになる。（図3参照。下の空間にはC2_-_{位相を入れる。）（但し、この試みは実際には、数値実験でし} か出来ていない。）その為には、変形の途中で、結び目型が変わってしまっては困る。結び目が自己交叉すると、結び目型が変わってしまうかもしれないので、これが起こらないようしたい。その為に、

定義 1.2 結び目の空間上定義された汎関数は、結び目が自己交叉しようとすると（正確には、二重点を持つ“特異結び目”にCk_-_{位相で近づく（}_k_は₀_または₂_{とする）と）発散するとき、}_Ck_-斥自性_{を持つという。}

斥自性を持ち、ある位相（通常C2_-_{位相）に関して連続で、下に有界な汎関数のことを}_{結び目のエネルギー}_と呼ぶことにする。

定義 1.3 結び目KのGromovの distortion([G2])は

Distor(K) = sup

x,y∈K,x̸=y

dK(x, y)

|x−y| (1)

で与えられる。ただし、dK(x, y)は弧長。

Gromov のdistortionはC0_-_{斥自性を持つ。したがって、ある正の定数}_C_{が存在して、結び目の空間の上の汎関} 数eが、全ての結び目Kに対してe(K)_≥C_·Distor(K)を満たすならばeもC0_-_{斥自性を持つことになる。以下} 登場する汎関数においては、C0_-_{斥自性の証明は大抵このように} _distortion_{を経由して証明する。}

以下、結び目の空間上に、いろいろな幾何学的な量eを定義し、次の問題を考える：

• Ck_-_斥自性_(k_{= 0 or 2)}_{を持つか、つまり結び目のエネルギーになるか。}

• 各結び目型に、e-最小元が存在するか。

(6)

• 結び目K が非自明ならばe(K)_≥e(正円) +C となる定数C >0が存在する1_。

• eは正円において（のみ）最小値をとるか。

1.3 E

(α)

_の定義

この目標の為の、最も自然な候補は、荷電した結び目の静電エネルギーであろう。クーロン斥力のお陰で、エネルギーが有限なら、自己交叉しないと思われるからである。ところが、静電エネルギーそのままの定義

“E”(K) =

∫ ∫

K×K

dxdy

|x−y| =∞ (∀K) (2)

では、全ての結び目に対して、積分が対角成分_{△ ⊂}K_×Kの寄与のため発散してしまう。

1.3.1 繰り込み

ここで、一般に積分が発散するときに、そこから有限な値を取り出す方法を述べる。

(1) ∫_Mω を考えたいが ωが X _⊂M 上で発散するため ∫_Mω が発散するとする。ε >0に対し、Nε(X)をX

の ε-管状近傍とし、p(ε) := ∫_M_\_N

ε(X)ω とおく。するとlimε→+0p(ε) =∞である。そこで p(ε)を 1

ε の級数に

展開する： _∫

M\Nε(X)

ω=a0+ a1

ε + a2 ε2 +· · ·

各係数は意味のあるものになるが、このうちの定数項a0を取り出すことを、ここでは繰り込みと呼ぶことにする。つまり、

lim

ε→+0 (∫

M\Nε(X)

ω−(a_ε1 +a2 ε2 +· · ·

))

を考える訳である。−(a1

ε + a2

ε2 +· · · )

をcounter term (打ち消し項)と呼ぶことにする。

注 1.4 _• log1_ε項が必要となることもある。

• 級数は a0+ 1 εb

(

a′0+ a′

1 ε +

a′ 2 ε2 +· · ·

)

(b_̸∈N)の形になることもある。

• 我々が扱う場合には、級数の定数項以外の第一項の係数は局所的な幾何とは関係ない。第二項の係数は、曲線の場合は全二乗曲率になり、曲面の場合には（注2.19,未解決問題4.19でみるように）Willmore汎関数になるようである。つまり、曲面の場合には、曲面のエネルギーを考えても、それを境界とする3次元領域のエネルギーを考えても、第二項からは同じものが出てくると予想される。

このように、級数展開から、曲率などの局所的な幾何学的量が自然に現れる。

• counter term にlog項が現れるとき、それが定数項にambiguityを及ぼしてしまうことがある。

(2)上の級数展開で、曲率などの局所的な幾何学的量が現れない場合、基準となるM0 を一つ固定し、それとの差をとることにより、M, M0の式に現れるcounter termをキャンセルする。

(7)

1.3.2 rα-静電エネルギー

上述の繰り込みの方法を今の場合に適用すると、

(1) M =K_×K,X =_△=_{(x, x)_|x_∈K_}（対角成分）,ω=dx_∧dy/_|x₋y_|となり、counter termは2 log(ε)

のみ。（ε-近傍を取るときに弧長を使っているので、正確にはM =S1_×_S1_で_ω_{は引き戻しになる。）}

(2) 相対的なエネルギーを考える。すなわち、一つ基準となる結び目（例えば、正円K_◦）を決め、それとの差をとりE(K)−E(K◦) =∞ − ∞で有限な値にする。

すると、二つの方法で同じものE(1)_{が得られる。ところが、この}_E(1)_{は斥自性を持たない、すなわち、結び目} が自己交叉してもE(1)_{の値は有界となってしまい、我々の目的には適さないことが分かる。斥自性を持つ汎関数} を得る為の一つの方法は、被積分関数の中の|x−y|の冪（エネルギーの指数と呼ぶことにする）を大きくすることで、実は2以上にすると斥自性を持つことが分かる。そのための準備をしよう。

結び目Kは弧長sでK=_{h(s)_}とパラメータ付けされていて、x=h(s), y=h(t)とする。結び目の上で測った弧長をδまたはdKで表すものとする。つまり、

dK(x, y) =δ(s, t) = min{|s−t|,1− |s−t|} (s, t∈S1= [0,1]/0∼1).

定義 1.5 二つの点電荷間の Coulombの反発力が二点間の距離の α+ 1 乗(α≥1) に反比例するいう仮定の下で、結び目の上の点h(s)から弧長でε以上離れた部分が荷電しているとしたときの点h(s)における「電位」を

Vε(α)(h;s)とし、それを結び目上積分して得られるもの、すなわち対角成分の √ε

2 管状近傍の外での「静電エネルギー」の2倍をEε(α)(h)とする。

Vε(α)(h;s) =

∫

ε≤|s−t|≤1−ε

dt |h(s)₋h(t)_|α,

Eε(α)(h) =

∫

S1

Vε(α)(h;s)ds=

∫ ∫

ε≤|s−t|≤1−ε

dsdt |h(s)₋h(t)_|α.

Vε(α)をε排自r−α型修正電位、E(εα)を ε排自r−α型修正静電エネルギーと呼ぶことにする。

まずs_∈S1 _{を固定して、}_V(α)

ε (h;s)の ε→0での発散の様子を調べてみよう。その為に0< u≪1に対して

|h(s+u)₋h(s)_|−α_を_u_{でテイラー展開してみると、}_(h′_{, h}′₎_≡₁ _より_(h′_{, h}′′_{) = 0, (h}′_{, h}(3)_{) +}

|h′′_|2_{= 0}_等が成立することを使うと

|h(s+u)₋h(s)_|−α₌_u−α₊α|h′′(s)|2

24 u

2−α₊α(h′′(s), h(3)(s))

24 u

3−α

+

{

α 2

(

(h′′_{(s), h}(4)_(s))

40 +

|h(3)_(s) |2 45

)

+α(α+ 2)|h ′′_(s)_|4 1152

}

u4−α+· · ·

(3)

となる。

∫ 1 2

0

tn−αdt

{

= +∞ n−α≤ −1 <_∞ n₋α >₋1

(8)

定義 1.6 ([O10]) (3)の右辺

u−α+α|h ′′_(s)_|2 24 u

2−α₊α(h′′(s), h(3)(s))

24 u

3−α₊

· · · (4)

の内、 αに応じて uの肩の指数が₋1以下になる項全部を_|h(s+u)₋h(s)_|−α _{から引いたものを考えると、そ}

れはu を−1/2≤u≤1/2で動かして積分すると積分可能になることが分かる。これをK=h(S1₎_の_h(s)_におけるr−α_{型修正電位の正規化}_V(α)_(h;_s)_{とおき、それを} _S1_{上積分したものを}_r−α_{型修正静電エネルギーの正規}

化E(α) _とおく。

ここでt=s+u(|u| ≤1/2)とするとuはh(s)とh(t)の間の弧長の短い方δ(s, t)と等しいことに注意すると：

• 1_≤α <3 の場合：

V(α)_(h;_{s) =} ∫

S1 (

1

|h(s)−h(t)|α −

1 δ(s, t)α

)

dt

E(α)_{(h) =} ∫ ∫

S1_×_S1 (

1

|h(s)₋h(t)_|α −

1 δ(s, t)α

)

dsdt

(5)

被積分関数が非負で恒等的には零でないので、E(α) ₍₁

≤α <3) は常に正である。

• 3≤α <4 の場合：

E(α)(h) =

∫ ∫

S1_×_S1 (

1

|h(s)₋h(t)_|α −

1 δ(s, t)α−

α_|h′′_(s)_|2 24δ(s, t)α−2

)

dsdt

• 4_≤α <5 の場合：

E(α)_{(h) =} ∫ ∫

S1_×_S1

( ₁

|h(s)−h(t)|α −

1 δ(s, t)α−

α_|h′′_(s)_|2 24δ(s, t)α−2

−α(h′′(s), h (3)_(s))

24δ(s, t)α−3 )

dsdt

α≥5 の場合も同様に定義する。

αをE(α)_の_指数_、_E(α)_{の被積分関数の内}

|h(s)₋h(t)_|−α _{を積分の主要項、残りを積分の発散を打ち消す}_counter

termと呼ぶ。

積分の発散を打ち消す引き算項のε→0での発散のオーダーを計算すると、1≤α <3 のときは、

V(α)(h;s) =

     lim

ε→0(V (1)

ε (h;s) + 2 log 2ε) α= 1

lim

ε→0 (

V(α)

ε (h;s)−

2 (α−1)εα−1

)

+ 2

α

α−1 1< α <3

(6)

が成立する。α≥3の場合も同様の考察をすれば、次の定理が得られる。

定理 1.7 _• 1< α <3 の場合は、

E(α)(h) = lim

ε→0 {

Eε(α)(h)−

2 (α₋1)εα−1

}

+ 2

α

α₋1

• α= 3 の場合は

E(3)_{(h) = lim}

ε→0 {

E(3)

ε (h)−

1 ε2 +

log 2ε 4

∫

S1|

h′′(s)_|2_ds }

+ 4

このように α <3の場合は、ε→0の時のE(εα)(h)の発散のオーダーは結び目hに依らない。すなわちこの場

(9)

注 1.8 今までの話では、積分が発散する対角成分△のε-近傍を取るときに弧長を使っていたが、後述の曲面のエネルギーのAuckly-Sadun の定義では、全空間の距離を用いる。結び目で1_≤α_≤3の場合には、二つの方法で同じものがでる。

In defining voltages and energies one can use the distance in the ambient space instead of using arc-length to avoid the diagonal. Assume the knotK is charged outside the 3-ballBε(x) with centerxand radiusε. The

voltage Vε(K;x) =Vε(h;s) at pointx=h(s) is then given by

Vε(K;x) =Vε(h;s) =

∫

|x−y|≥ε

dy |x−y|α.

Define

Eε(K) =Eε(h) =

∫

K

Vε(K;x)dx=

∫ ∫

|x−y|≥ε

dxdy |x₋y_|α.

The order of blowing up of E(εα)(h) as ε→ 0 can be calculated similarly. When 1 ≤α ≤3 the order is the

same as that ofEε(α)(h). This is because if we put ¯ε=|h(s+ε)−h(s)|thenε= ¯ε+ |h

′′₍_s₎_|2 24 ε¯

3₊_O(¯_ε4_{), which}

impliesε−(α−1)_{= ¯}_ε−(α−1)₊_O(¯_ε3−α_{) and log}_ε_{= log ¯}_ε₊_O(¯_ε2_{). In particular, when 1}

≤α <3

E(α)(h) = lim ¯

ε→0 {

E(ε¯α)(h)− 2 (α₋1)¯εα−1

}

+ 2

α

α₋1

and whenα= 3

E(3)(h) = lim ¯

ε→0 {

E(3)ε¯ (h)− 1 ¯ ε2 +

log 2 ¯ε 4

∫

S1|

h′′(s)|2_ds }

+ 4 +

∫

S1

|h′′_(s)_|2 12 ds.

1.3.3 E(α)_{はいつ結び目のエネルギーになるか}

以下ではα <3の場合のみ E(α)_{を扱うことにする。この場合は被積分関数が簡単な形をしていて非負性が明} らかで扱い易いからである。

まず self-repulsivenessから確かめよう。α <2 のときには結び目が自己交叉を持ってもE(α) _{は発散しないこ} とが分かる。実際 ¯_h_{を８の字の形の平面曲線で点}_P _{で直角に自己交叉するような特異結び目とすると、}_P _の近

傍の積分への寄与は大体以下で与えられるからである。

図4: A planar figure eight singular knot.

∫ c

−c

∫ c

−c

dsdt (s2₊_t2₎α

2 ∼4 ∫ c′

0 ∫ π

2

0 dθdr rα−1

{

<_∞(α <2) =∞(α≥2).

このことからα <2ならばE(α)_{は結び目のエネルギーとはならない。逆に}

命題 1.9 2≤α <3ならばE(α)_{はグロモフの} _distortion_{を上から抑える（よって}_C0_-_{斥自性を持つ）。言い換え} ると、任意の実数 b に対して正の定数 C=C(α, b)が存在して、E(α)_(h)

(10)

証明: 下の補題より、α= 2の場合に示せばいいことが分かる。

β (0< β_≤ 1₂),d(0< d_≤β)に対し弧長でβ だけ離れた二点を距離dに近づけるような結び目のE(2) _の値の下界を求める。簡単の為

K0(β, d) ={h:S1→R3 埋め込み写像 (|h′| ≡1) : |h(0)−h(β)|=d}

とおく。infE(2)₍

K0(β, d))を直接求めるのは困難なので、次のような評価を考える。被積分関数は非負なので、積分における

[₋ε, ε]_×[β₋ε, β+ε]_⊂S1_×S1 (ε >0)

の部分の寄与のみ考えよう。例えばεとして (β−d)

8 をとるとs, t >0 に対して

|h(s)−h(β+t)| ≤d+s+t, δ(h(s), h(β+t)≥β−1₄(β−d) =d+3 4(β−d)

となることを用いると、infE(2)₍_K

0(β, d))を下からβ,dの関数で評価することが出来る。この不等式から命題が

導かれる。 ✷

補題 1.10 α >1とする。x, yを固定すると、E(α)_{の被積分関数}

|x₋y_|−α

−dK(x, y)−αはαの単調増加関数に

なる。

証明: 1/2_≥dK(x, y)≥ |x−y|より2≤dK(x, y)−1≤ |x−y|−1となることから

1 |x−y|α −

1 dK(x, y)α

=α

∫ |x−y|−1

dK(x,y)−1

ξα−1_dξ.

✷

また、連続性に関しては、

命題 1.11 E(α)_は_C2_-_{位相に関して連続である。}

E(α)_{の被積分関数は非負で、恒等的には}₀_{ではないので、}_E(α)_>₀_{となり、下に有界であることが分かる。以} 上のことから

定理 1.12 ([O2])E(α) ₍₁_≤_{α <}₃₎_は指数 _α_≥₂ _{のときに限り結び目のエネルギーになる。} 命題1.9よりE(α)_(h)_<

∞ならばh−1 _は_Lipschitz_{条件を満たす。}_h_{は元々弧長でパラメトライズされていたの} で、Lipschitz条件を満たすので、結局hは bilipschitz写像になる。

命題 1.13 E(α)_(h)_は_h_{が区分的に}_C1_ならば_d

K(x, y)が定義できるので意味をもつが、実際にC1ではなく「角」

（一階微分の不連続点）があれば、E(2)_{(h) =}

∞（したがってE(α)_{(h) =}

∞(2_≤α <3)）となる。

系 1.14 E(α)₍₂_≤_{α <}₃₎_は_C1_-_{位相では（よって}_C0_-_{位相でも）連続にならない。}

1.3.4 E◦(2)の定義

そこでまず、指数が2の場合を考えよう。距離rの点電荷の間の「クーロン斥力」がr−3_{に比例するという仮} 定の下での静電エネルギーとみなすことができる。

以下簡単のため、特に断らない限り、結び目は長さ１で、弧長でパラメトライズされているものとする。結び目

K の二点x, y の間の弧長をdK(x, y)で表す。

(11)

上の「クーロン力の逆3乗則」の仮定の下で、点xから弧長でεだけはなれた部分弧が荷電しているときのx

の「電位」をVε(2)(K;x)とする。つまり

Vε(2)(K;x) :=

∫

dK(x,y)≥ε

dy |x₋y_|2.

このVε(2)(K;x)はε→+0で発散するが、発散のオーダーは結び目Kと点xにはよらず、O(2/ε)である（式(6)

による）。そこで、

V◦(2)(K;x) := lim

ε→+0 (

Vε(2)(K;x)−

2 ε

)

= lim

ε→+0 (∫

dK(x,y)≥ε

dy |x−y|2 −

2 ε

)

,

E_◦(2)(K) :=

∫

K

V_◦(2)(K;x)dx= lim

ε→+0 (∫ ∫

{dK(x,y)≥ε}⊂K×K

dxdy |x₋y_|2−

2 ε

)

. (7)

とおくと([O1])、E◦(2)は斥自性を持つ結び目のエネルギーとなる2。これを結び目K の（繰り込まれた）r−2-エネルギーと呼ぶ3_。

例 1.15 正円K◦:t7→(21πcos 2πt,

1

2πsin 2πt,0)のエネルギーを計算しよう。対称性よりV

(2)

◦ (K◦;x)はxによら

いない。

V◦(2)(K◦;x) = lim

ε→+0 ( 2 ∫ 1 2 ε dt (1

πsinπt)2

dt₋ 2 ε

)

= lim

ε→+0 (

2[₋πcotπt]

1 2 ε − 2 ε ) = 0

となるので

E◦(2)(K◦) = 0.

この例が手で計算出来る唯一の例である。

エネルギーE◦(2)の定義方法２: K◦ を正円とすると、上の計算によりE (2)

◦ (K◦) = 0となるので、E(2)◦ (K) = E_◦(2)(K)₋E_◦(2)(K_◦)となり、上の(7)式の₋2

εがキャンセルする。KとK◦の対応する点をとると、次が成り立

つ：4

E◦(2)(K) =

∫ ∫

K×K

(

1 |x−y|2 −

1

(

2 sin(1₂dK(x, y)

))2 )

dxdy =₋4 +

∫ ∫

K×K

(

1 |x−y|2−

1 dK(x, y)2

)

dxdy.

(8)

ここから分かるように、E◦(2) は相似拡大・縮小で不変である。

E(2)◦ (K)は、「クーロン力の逆3乗則」の仮定の下での、荷電した結び目の“静電エネルギー”を、(全空間から

決まる）外在的なものから(結び目だけで決まる）内在的なものを引いて正規化したものと解釈できる。

2_E(2)

◦ の下の◦は、別にO’Haraの頭文字という訳ではなくて、正円○で値0を取る、という意味でつけた。

(12)

e

K が（両端が同一直線に漸近的なような）開いた結び目のときは、定数項−4を除いてE◦(2)(K)e を定義する：

E◦(2)(K) =e

∫ ∫

e

K×Ke

(

1 |x₋y_|2 −

1 dKe(x, y)

2 )

dxdy.

直線では_|x₋y_|=dKeK(x, y)なので、直線でのE (2)

◦ の値は0になる。常に|x−y| ≤dKe(x, y)つまり1/|x−y|2− 1/dK(x, y)2≥0なので、

命題 1.16 開いた結び目の中では直線のみがE◦(2)の最小値0を与える。

後述するように、（通常の閉じた）結び目の中では正円がE◦(2)の最小値0を与える。連続性に関しては、命題 1.11で述べたように、エネルギーE◦(2) はC2 位相に関して連続である.

命題 1.17 主張3.3後述の図1.5.1のプルタイトでE◦(2) の値は発散しない。このことからもE◦(2)はC0-位相では

不連続であることが分かる。

1.4 E

_◦(2)

のメビウス不変性

1.4.1 メビウス幾何学の基礎事項

T :R3

∪ {∞} →R3

∪ {∞}がメビウス変換であることは、Tが球面に関する反転の合成として表すことが出来ることと同じである。ここで、平面は無限遠点を通る球面とみなす。その場合、反転は平面に関する面対称とする。

メビウス変換全体のなす群をメビウス変換群と呼ぶ。メビウス変換群は回転、平行移動、および相似拡大・縮小を含むので、合同変換群、相似変換群を含む。

図5: 平面（直線）に関する対称の合成で回転・平行移動を得る。相似拡大・縮小は同心円に関する反転の合成で得られるAdd homothety

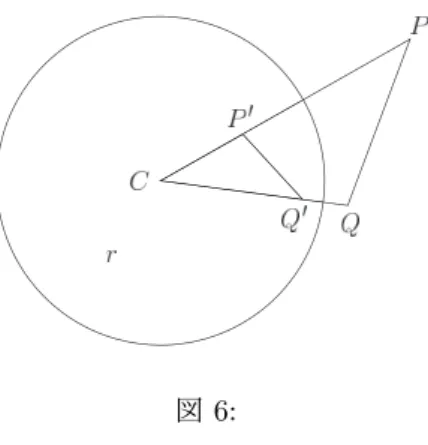
T を中心C半径rの球面に関する反転とし、P′ ₌_T_(P_{), Q}′₌_T_(Q)_{とする。このとき}

|CQ′_| |CP_| =

r2 |CP_{| · |}CQ_| =

|CP′_| |CQ_|

より△P CQと△Q′CP′は相似で相似比はr2/|CP| · |CQ|である。よって

|P′Q′|= r 2

|CP_{| · |}CQ_||P Q|

一般に T をRn

(13)

図6:

• p∈R3_に対して_|_T′_(p)_|₌_|_det_dT_(p)_|1/2n _{とおく。ここで}_det_dT(p)_は_T_の_p_{におけるヤコビアン。特に}_T

が中心Cで半径rの球面に関する折り返しの場合は、_|T′_(p)_|₌_r/_|_C₋_p_|_{となる。この時}_{p, q}_∈_R3 _および f :S1 _or_R_→_R3_に対して

|T(p)−T(q)|=|T′(p)||T′(q)||p−q|

|(T◦f)′(s)|=|T′(f(s))|2_|_f′_(s)_| (9)

となる。

• 上の式より、Rn_{の標準的なリーマン計量を}_g_{とすると、ある正値関数}_φ_{が存在して}_T∗_g₌_φg_{となる。こ}

れは角度を保つということと同値であるので、このときTは共形写像または共形的(conformal)であるという。

• k次元球面（平面を含む）(0_≤k_≤n)を同じ次元の球面（平面を含む）にうつす。

という性質を持つ。ただし、

• 距離を保たない。

• 球面を球面にうつすが、中心を中心にうつす訳ではない。

ことに注意しよう。

2次元の場合、平面を複素平面と同一視すると、R2_{∪ {∞} ∼}₌_C_{∪ {∞}}_{のメビウス変換は、一次分数変換と複素} 共役で生成される。一方、正則（複素解析的）関数は等角写像つまり共形写像となるので、2次元の場合、共形写像の集合とメビウス変換との間には大きな差がある。ところが、3次元以上だと事情は大きく異なる：

定理 1.18 (Liouville)n_≥3ならば、Snの開集合U からf(U)_⊂Snへの共形的な微分同相写像f はSnのメビウス変換の制限として得られる。

メビウス幾何学では、R3_{∪ {∞}}_と_S3_は_立体射影_{を用いて同一視するのが自然である。}_S3 _を _R4 _{の原点中心} の単位球面、 N = (0,0,0,1)を北極とし、R3_{を大円を通る}₃_{次元平面と同一視すると、立体射影は下で与えら} れる：

pN :S 3

\ {N} ∋(x1, x2, x3, x4)7→ (

x1 1₋x4

, x2 1₋x4

, x3 1₋x4

)

∈R3_,

pN−

1_:_R3_∋_m_{= (x}

1, x2, x3)7→ (

2m |m_|2_{+ 1},

|m|2₋₁ |m_|2_{+ 1}

)

∈S3\ {N}.

この立体射影自体、北極Nを中心とした半径√2の3次元球面に関する反転（R4

(14)

N

1.4.2 E_◦(2)のメビウス不変性

E(2)◦ の定義式の被積分関数の主要部である dxdy

|x₋y_|2 はK×K\ △上の2-formであるので、これをρKと書くことにすると、ρKは「メビウス不変」である、すなわち、ρK= (T×T)∗(ρT(K))が成り立つ。これは、K=f(S1) として、S1

×S1

\ △上の2-formとして、(9)より、

|(T◦f)′(s)| |(T◦f)′(t)| |T_◦f(s)₋T_◦f(t)_|2 dsdt=

|f′(s)| |f′(t)| |f(s)₋f(t)_|2dsdt

となることより分かる。

このことを用い、Freedman, He, WangはE(2)_◦ のメビウス不変性を示した。dxdy/_|x₋y_|2_{がメビウス不変で} あっても、繰り込みで用いる距離または弧長dK(x, y)はメビウス変換で不変ではないので、E◦(2)のメビウス不変

性は自明ではない。

定理 1.19 ([FHW])E◦(2)はメビウス不変である。すなわち、T をメビウス変換とすると、

E◦(2)(T(K)) =E◦(2)(K) ∀K.

これはT(K)が開いた結び目の場合も正しい。また、全空間の次元が何であっても成立する。

命題1.16より

系 1.20 （閉じた結び目の中で）正円のみがE◦(2)の最小値0を与える。

1.4.3 E◦(2)のコサイン公式

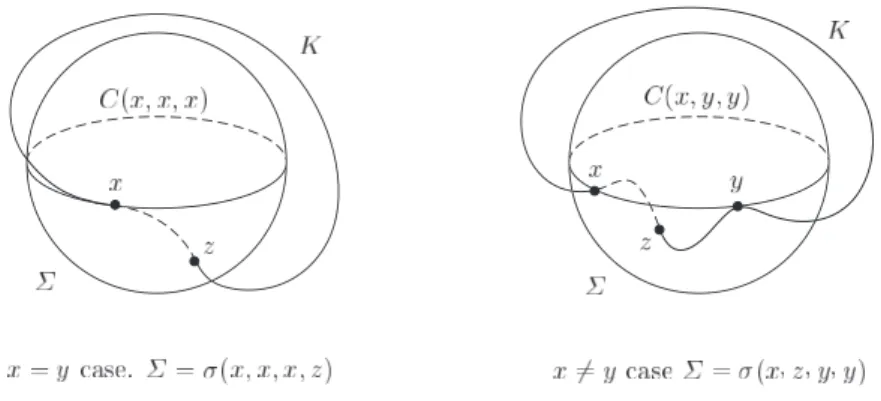
定義 1.21 (Doyle-Schramm, [KS2]で報告された) x, y を結び目K上の二点とする。Γ(x, x, y)を点xで結び目

K に接し点y を通る円、Γ(y, y, x)を点y で結び目Kに接し点xを通る円とする。Γ(x, x, y)とΓ(y, y, x)とが点xあるいは点y においてなす角をθ=θK(x, y)とし(0≤θ≤π)、これを(xとyの間の)共形角と呼ぶことに

(15)

この共形角θK(x, y)はx, yの連続関数だが、C1級関数ではない。その絶対値のような振る舞いをする。また、

対角成分近くでθK(x, y) =O(|x−y|2).5

Doyle とSchrammは、E◦(2)(K)は共形角によって、

E_◦(2)(K) =

∫ ∫

K×K

1₋cosθK(x, y)

|x−y|2 dxdy (10)

とあらわされることを示した([AS],[KS2]で報告された)。この式を E(2)◦ (K) のコサイン公式と呼ぶ。共形角と dxdy/|x−y|2_{ともにメビウス変換で不変であることから、コサイン公式は}_E(2)

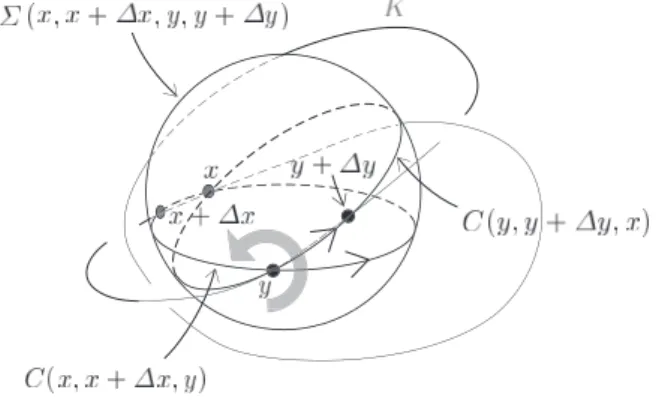
◦ のメビウス不変性の別証明になる。証明: 以下では、x=f(s),y=f(t)とおいて、

|f′(s)|ds|f′(t)|dt |f(s)₋f(t)_|2 =

|dx||dy| |x₋y_|2

と書くと分かりやすい。

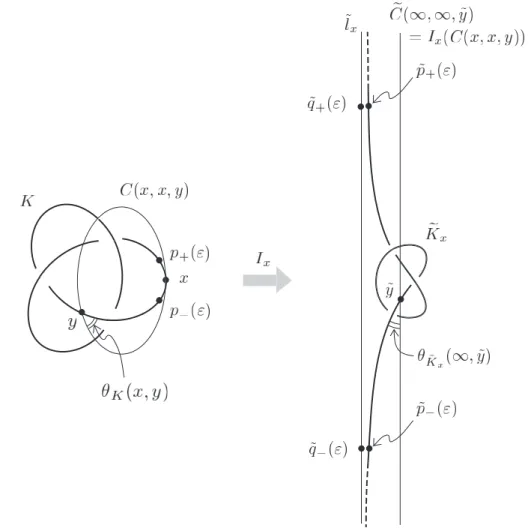
再びK=h(S1₎_{を弧長でパラメトライズされた結び目とする。} VK(x) =V◦(2)(h;s)とおくと、前に書いたように

V◦(2)(K;x) = lim_ε →0

(∫

y∈K,δ(x,y)≥ε

dy |x₋y_|2 −

2 ε

)

E◦(2)(K) =

∫

K

V◦(2)(K;x)dx

であった。0< ε≪1を固定する。Ixを点xを中心とする半径1の球面Sx に関する反転、K˜ =Ix(K)を反転

された開いた結び目、y˜=Ix(y),p±=p±(ε) =h(s±ε), ˜p±=Ix(p±)とおく。(a)より

|Ix′(y)|=

1 |x₋y_|

で

|d˜y_|=_|d(Ix(y))|=|Ix′(y)|2|dy|= |

dy_| |x₋y_|2. よって

∫

y∈K,δ(x,y)≥ε

dy |x₋y_|2 =

∫ p˜−(ε)

˜

p+(ε)

|d˜y_|

は反転された開いた結び目_K˜ ₌_I_x_(K)_の_p_˜₊_(ε)_と_p_˜₋_(ε)_{の間の部分の弧長に等しい。}

次に −→t =h′_(s)_を _x₌_h(s)_における_K ₌_h(S1₎_{の単位接ベクトル、}−→_n _{を単位法ベクトルとし、}_k₌ |h′′_(s)_|

をK の点xにおける曲率とすると、

p_±(ε) =x_±ε−→t +ε 2_k

2 −→n +O(ε 3₎

となるので p˜_±(ε) =x_±1 ε

− →_t ₊k

2−→n +O(ε).

従って

|p˜+−p˜−|= 2

ε +O(ε).

よって

∫

y∈K,δ(x,y)≥ε

dy |x−y|2 −

2 ε =

∫ p˜−(ε)

˜

p+(ε)

|d˜y_{| − |}p˜+(ε)−p˜−(ε)|+O(ε)

5_R3_{の曲線は合同変換を除いて（弧長}_s_{）曲率、れい率で決まるのと同様、}_R3_{の曲線はメビウス変換を除いて共形的弧長}_ρ_{、共形的曲率、}

共形的れい率で決まることが知られている。共形的弧長ρは lim |x−y|→0

√

6θK(x, y)

|x₋y_|2 =

dρ

(16)

はO(ε)を除いてp˜+(ε)とp˜−(ε)の間のK˜ の弧長とp˜+(ε)とp˜−(ε)の間の距離の差に等しい。（これは反転され

た結び目の「余分な長さ」と呼ばれている。）

Ix(Cx(y))はy˜を通る直線でε→0でp˜+(ε)と p˜−(ε)を通る直線と平行に近づく。一方Ix は共形写像で角度

を変えないのでy˜における_K˜ _の接線と_I_x_(C_x_(y))_{のなす角度は}_h′_(s)_と_h′_(t)_{のなす共形角}_θ₌_θ(K;_{x, y)}_と等

しい。

図 7: The inverted open knot, the conformal angle, and the exess-length.

以上から

V◦(2)(K;x) = lim_ε →0

(∫

y∈K,δ(x,y)≥ε

dy |x₋y_|2 −

2 ε

)

= lim

ε→0 ∫ p˜−(ε)

˜

p+(ε)

d˜y(1₋cosθ)

= lim

ε→0 ∫

y∈K

(1−cosθ)dy |x₋y_|2 . よって

E◦(2)(K) =

∫ ∫

K×K

1−cosθ

|x₋y_|2 dxdy(3.3)

=

∫ ∫

S1_×_S1

(1−cosθ(h;s, t))dsdt |h(s)₋h(t)_|2

(17)

1.5 エネルギー

E

_◦(2)

-

最小元について

1.5.1 E◦(2)-最小元の存在

Freedman, He, Wangは、メビウス不変性を用いて、次を示した。

定理 1.22 ([FHW])素な結び目型には、E◦(2)-最小元が存在する。

定理の「素」という条件の理由は以下の通り。_{Kn} ⊂[K]なる結び目の列で、

lim

n→∞E (2)

◦ (Kn) =E(2)◦ ([K]) = inf

K′_∈_[_K_]E

(2) ◦ (K′)

なるものをとる。C0_-_{位相に関しては、必要なら}_R3_{の相似変換をすれば、極限} _lim

n→∞Kn =:K∞が存在する。と

ころが、途中で結び目が交わらなくても、下図のように、タングルが１点に縮んで、K∞ の結び目型が変わって

しまうことが起こりうる。この現象をプルタイトと呼ぶ。

図8: プルタイト

ところが、もしも素な結び目型ならば、メビウス変換によって、タングル（一つしかないので）を大きくし、プルタイトを防ぐことにより、K∞∈[K]と出来る。

後は、Fatouの補題によりE_◦(2)(K_∞)_≤E_◦(2)([K])となり、K_∞はE_◦(2)-最小元となり、定理が証明される。

注 1.23 メビウス不変性から、ある結び目がその結び目型のE◦(2)-最小元だとすると、そのメビウス変換の像（必

要なら、その鏡像）もまたその結び目型のE_◦(2)-最小元となるので、自明でない素な結び目型には、非可算無限個のE◦(2)-最小元が存在することになる。

未解決問題 1.24 （素な）結び目型のE◦(2)-最小元のメビウス変換に関する同値類の（１つになるか、有限個か、

など）個数については、（自明な結び目型についても）分かっていない。

未解決問題 1.25 正円以外にE◦(2)の臨界点になるような自明な結び目はあるか？

もしなければ、S3の自明な結び目の空間は、大円の空間に変形レトラクトする、というHatcherの結果([Ha])の別証明になる。数値実験によると、M. Ochiai’s unknot ([KHG]) (図9)と“Freedman unknot”6 _([KS2])(_図₁₀₎

(18)

を、E◦(2)を減らすように変形すると正円になる。

図9: Ochiai unknot

図10: Freedman unknot

上の証明法は、素でない結び目型の場合には適用できない。[K1],[K2]を非自明な結び目型、[K] = [K1♯K2]をその連結和の結び目型とし、上と同じように結び目の列をとる。例えば [K1] の成分がプルタイトしないように M¨obius変換で膨らませると、[K2] の成分がプルタイトする可能性があるので、[K1],[K2] 両方の成分がプルタイトすることを同時に防ぐことが出来るとは限らない。実際にKusnerとJ.Sullivanによる数値実験[KS2]では、両方の成分がプルタイトする現象が観察されている。これは、結び目の上に中心を持つ球面に関する反転で開いた結び目にして考えれば、 [K1], [K2] 両方の成分がどんどん離れていくことに対応する（図11）。両方の成分が

図11: 合成結び目でエネルギーを減らす

十分に離れれば、積分での相互の影響は０に収束し、エネルギーはそれぞれの開いた結び目のエネルギーの和になると考えられるので、再びM¨obius変換で普通の閉じた結び目にすれば、以下の予想を得る。

予想 1.26 ([KS2])

(1) 素でない結び目型には、E◦(2)-最小元は存在しない。E◦(2) を減らそうとすると、素でない結び目は正円に退

化しようとする。

(2) [K1],[K2]を結び目型とすると

(19)

1.5.2 E◦(2)の勾配とE◦(2)-最小元である結び目の滑らかさ

f を（パラメータが必ずしも弧長とは限らない）C4 _{級の結び目とする。}_P

f(s):R3→R3 をf′(s)と直交する平面への直交射影とする：

Pf(s)(v) =v−

(v, f′_(s)) |f′_(s)_|2 f

′_(s).

命題 1.27 ([FHW])Gf:S1→R3を

Gf(s) = 2p.v.

∫

S1 {

2Pf(s)(f(t)−f(s)) |f(t)₋f(s)_|2 −

1 |f′_(s)_|

d ds

(

f′_(s) |f′_(s)_|

)}

|f′_(t)_| |f(t)₋f(s)_|2dt

ただし、p.v.は主値積分を表す、とおくと、C2 _級の_p_:_S1

→R3 _に対して

∇E◦(2)(f)(p) = lim_ε →0

E(f+εp)₋E(f)

ε =

∫

S1

Gf(s)·p(s)|f′(s)|ds

が成立する。ここで·は R3 _{の標準的な内積を表す。すなわち、}_G

f はE の L2-勾配である。

注 1.28 Cr _(r

≥4)級の結び目でのE(2)◦ の勾配はCr−2 級となって微分可能性が２つ落ちる。

Heは∇E◦(2)(f)(p) = 0 (∀p∈C∞(S1,R3))なるオイラー・ラグランジュ方程式を局所的に解くことにより、

定理 1.29 ([He])

(1) E◦(2)-最小結び目は滑らかである。

(2) 曲率が三乗可積分な平面閉曲線の中で正円のみが E◦(2) の臨界点である。

を示した。ただし、Heの用いた_∇E◦(2)のL2-gradientは積分が絶対収束していない（主値積分で求めている）た

め、解析からみると不完全であり、近年それの正当化がいくつかなされている（および石関-長澤）。

Refe

1.5.3 エネルギーの臨界点となるトーラス結び目について

三次元球面 S3 のClifford トーラス上のトーラス結び目のエネルギーに関するKimと Kusner [KK]の考察を紹介しよう。

ここではE(2) ₌_E(2)

◦ + 4とする。また、R4の距離を用いて、同様に定義したエネルギーをER(2)4 とする。

まず、S3_⊂_R4 _から_R3_{∪ {∞}}_{への立体射影を}_P _とすると_P _は_R4_{∪ {∞}}_上の_M¨obius_{変換に拡張する。}_E(2) R4

がR4

∪ {∞}のM¨obius変換で不変であることから、S3_の結び目_f _{に対して、}_E(2)_(P

◦f) =ER(2)4|S3(f)である。

S3_⊂_C2_の半径_r_の_Clifford _トーラス

Tr=

{

(z, w)_∈S3_⊂C2

|z_|=r,_|w_|=√1₋r2} ₍₀_{< r <}₁₎

上の(p, q)トーラス結び目

fr;p,q: [0,2π]∋θ7→

(

repθi,√1−r2_eqθi)

∈S3⊂C2 ₍₁₁₎

の ER(2)4 を計算すると、KusnerとStengle による留数を用いた次の公式を得る。

ER(2)4(fr;p,q) = 4 + 4π2

∑

|z|<1

Res −{r 2₍₁

−r2_)p2₊_q2 }

(20)

一方S1 _は_S3 _{に等長的に}

a:S1∋eit7→

(

at:S3∋

(

z w

)

7→

(

eipt_z

eiqtw

)

∈S3

)

で作用する。ER(2)4|S3 はその作用で不変で、a_t(f_r,p,q(s)) = f_r,p,q(s+t)よりf_r,p,q(S1) は１点の軌道になってい

る。このことからPalaisの対称的臨界性の原理[P] を用いると、

∂ ∂rE

(2)

R4|S3(f_r,p,q)

r=r0

= 0 (13)

となるならば、fr0,p,q はE

(2)

R4|S3 の臨界点となることが分かる。

(p, q)トーラス結び目は素な結び目であることから定理1.22によりエネルギー最小結び目が存在する。(13)により得られたE(2) _の臨界点_f

r0,p,q が、このエネルギー最小結び目と一致するかどうかについて、KimとKusner

は数値実験の結果から次のように予想している。

予想 1.30 ([KK])p= 2又はq= 2 の時、かつその時に限り(13)で得られた(p, q)トーラス結び目型のE(2) _の臨界点fr0,p,q はE

(2) _{の安定な極小点になる。}

実際p, q のどちらかが極端に大きい場合、トーラスの上に綺麗にのっているものよりも、ある部分が外れている方が、エネルギーが小さくなりそうではある。一方(3.6)式で(p, q) = (2,3)すなわち三葉結び目の場合を考えれば,ER(2)4(fr;2,3)は r0≈1.857で最小値約74.41204を取る。この値は数値実験で得られる三葉結び目でのE(2) の最小値とよく合う。

1.6 平均交点数との関係と結び目型の有限性

1.6.1 絡み目、ライズ、平均交点数

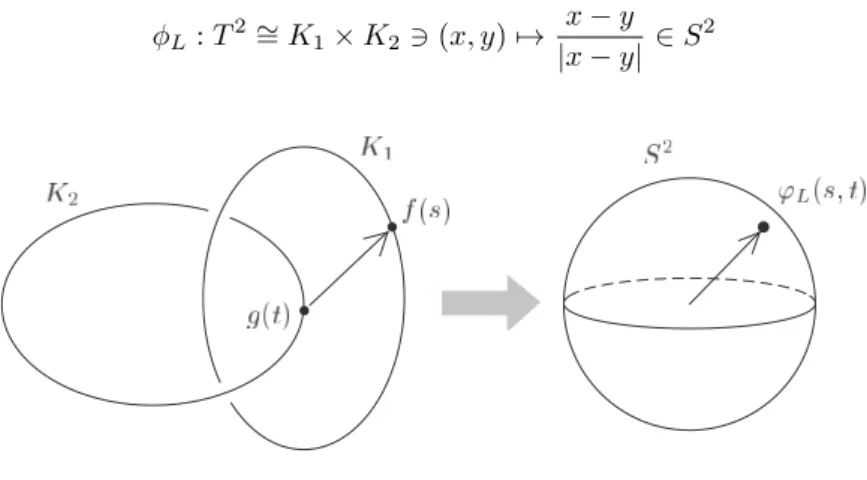
絡み目 L=K1∪K2 の絡み数lk(K1, K2)は、写像

ϕL:T2∼=K1×K2∋(x, y)7→ x−y |x₋y_| ∈S

2

図 12: The Gauss map.

の写像度であり（このことから整数値であることが従う）、このことからガウスによる積分表示

GI(K1, K2) := ∫

T2

ϕL∗dS2=

1 4π

∫

K1 ∫

K2

det(_|x_x−₋y_y_|, dx, dy)

|x−y|2 (14)

で与えられる。すなわち、像ϕL(T2)⊂S2 の符号付きの面積割るS2 の面積である。（絡み数の他の定義との同

(21)

この被積分関数をその絶対値で置き換えたものを平均交点数([FH])といい、⟨c⟩(K1, K2)で表すことにする。

⟨c_⟩(K1, K2) := 1 4π

∫

K1 ∫

K2

det(_|x_x−₋y_y_|, dx, dy)

|x−y|2 (15)

これは、像ϕL(T2)⊂S2 の幾何学的な（符号なしの）面積割るS2 の面積である。

⟨c_⟩(K1, K2) = 1 4π

∫

v∈S2

♯(ϕL−1(v))dS2(v)

となることから、⟨c_⟩(K1, K2)は、絡み目を射影する方向を動かしたときの、K1が K2 の上にくる交点の数の平均になることが分かる。定義より、_⟨c_⟩(K1, K2)≥ |lk(K1, K2)|である。

上の定義で K1 =K2=K とおくと、K×K の対角成分付近で、被積分関数の分子は |x−y| の4乗のオーダーになるから積分はwell-definedであることがわかる。GI(K, K)をK のwrithe といいWr(K)であらわす。

⟨c_⟩(K, K)を_⟨c_⟩(K)と書き、結び目K の平均交点数という。

Let us give another formulae of the Gauss integral in terms of angles. Let ¯θx = ¯θx(x, y) (or ¯θy = ¯θy(x, y))

(0 _≤θ¯x,θ¯y ≤π) be the angle between w and vx (or betweenw and vy respectively). Let ¯θxy = ¯θxy(x, y) be

the angle between the plane Span_⟨w, vx⟩, which containsΓ(x, x, y), and the plane Span⟨w, vy⟩, which contains

Γ(x, y, y), with a sign convention so that (w, vx×vy) = sin ¯θxsin ¯θysin ¯θxy. Then

GI(K1, K2) = 1 4π

∫

K1 ∫

K2

sin ¯θxsin ¯θysin ¯θxy

|x₋y_|2 dxdy,

⟨c_⟩(K1, K2) = 1 4π

∫

K1 ∫

K2

sin ¯θxsin ¯θy|sin ¯θxy|

|x₋y_|2 dxdy, (16)

which also hold in the case of a knotK1=K2. ¯

θxyが定義できないような対(x, y)に対しては、dim Span⟨w, vx⟩= 1またはdim Span⟨w, vy⟩= 1となるので、

¯

θxまたはθ¯y が0またはπとなり、上の被積分関数の分子が0となるので、定義には差支えない。

Since 2r(C(x, x, y)) sin ¯θx=|x−y|

Wr(K) = 1 16π

∫ ∫

K×K

sin ¯θxy(x, y)

r(C(x, x, y))r(C(x, y, y))dxdy (17)

([GM]).

1.6.2 エネルギーE◦(2)と平均交点数、結び目型の有限性定理 1.31 (平均交点数との関係)(Freedman-He-Wang [FHW])

(1) 勝手な開いた結び目_K˜ _に対して_⟨_c_⟩_{( ˜}_K)_≤ 1 2πE

(2)

◦ ( ˜K)。従って、結び目型 [K]の最小交点数をc([K])とす

ると、

c([K])_≤ 1 2πE

(2) ◦ ([K]).

(2) 勝手な（通常の閉じた）結び目K に対して

⟨c⟩(K)≤ _12π11 E◦(2)(K) +_3π14.

平均交点数はその結び目の属する結び目型の最小交点数より多く、非自明な結び目の最小交点数は3以上なので、

(22)

E(2)◦ (K)(正円) = 0 なので、非自明な結び目の E◦(2)(K) の値との間にギャップが存在することになる。但し、

非自明な結び目のE◦(2) の値の最小値は、数値実験によれば三葉結び目のときで約70となるので、上の系の値は

シャープではないと思われる。

系 1.33 (結び目型の有限性)([FHW]) 任意の実数bに対してE◦(2)(K)≤bとなる代表元K を持つような結び目

型は有限個である。その数はbの指数関数（2_·24(b+3)/(2π)_{）で抑えられる。}

1.6.3 自己絡み数

定理 1.34 ([Cˇa1]-[Cˇa3], [Po1]) 結び目Kの各点で曲率が消えないと仮定する。τ を K のれい率とする。すなわちK=f(S1₎_ならば_τ _{= det(f}′_{, f}′′_{, f}′′′_)/_|_f′_×_f′′_|2_. _Tw_{(K) =} 1

2π

∫

S1τ(t)dt とおくと,

Sl(K) =Wr(K) +Tw(K)

は整数値を取り、

(1) K を主法線方向に1≫ε >0 だけずらして得られるものを Kpε とすると、Sl(K) =lk(K, Kpε)。

(2) K を従法線方向に1_≫ε >0 だけずらして得られるものをKbε とすると、Sl(K) =lk(K, Kbε)。

(3) K のホモトピーでその途中で曲率がどの点でも消えないようなものを考える。このとき、途中で自己交差がなければSl(K)は不変。自己交差の度に Sl(K)は _±2ずれる。

定義 1.35 Sl(K)を K の自己絡み数という。

注 1.36 巻き（kink）を一つ作る事にSl は ±1ずれるので、自己絡み数は結び目不変量にはならない。自己絡み数については、他に[BT], [Po2], [Wh1]-[Wh3]を参照。

2 幾何学的結び目理論：幾何学的複雑さを測る量と最適な形

2.1 静電エネルギーの繰り込みの一般化の自然な拡張

2.1.1 Eα,p_{とエネルギー最小元の存在}

E(2)◦ に関しては、素な結び目型にはエネルギー最小元が存在することが証明されたが、合成結び目の結び目型

については、最小元が存在しないと予想されているので、元々の問題1.1に対しては半分しか有効でないことになる。似たようなエネルギー汎関数を用いて、全ての結び目型でエネルギー最小元が存在するようにするための方法として、次の二つが考えられる。

(1) 被積分関数の分母の距離の冪を大きくする。

(2) 結び目の入っている全空間の計量を変える

まず、(1)の方法を考える。∫_d

K(x,y)≥ε

dy

|x−y|α (α∈R)はα≥3のとき発散のオーダーが結び目Kと点xに依ってしまう（曲率が入った項が必要になる）ので、公式(8)はα≥3のときそのままでは成り立たない。

結び目 Kは長さ1 とする。α, p_∈Rに対し、

Eα,p(K) :=

∫ ∫

K×K

(

1 |x₋y_|α −

1 dK(x, y)α

)p

dxdy

(23)

定理 2.1 ([O2])Eα,p は、αと pが

α_≤2 または p < 1

α−2 (2< α <4)

のときに限り well-definedで、αとpが更にα >0 かつαp_≥2 を満たすときに、結び目のエネルギーとなる。この条件は

α >0, p >0, αp≥2, αp−1 2p <1

と同値。

タングルTが図1.5.1のようにプルタイトするとき、

(1) αp >2ならEα,p_→₊_∞_。₍_{従ってこのときは}_Eα,p _{はメビウス不変ではない。}₎

(2) αp= 2ならEα,p

→C(T)>0 。

(3) αp <2ならEα,p_→₀ _。

これは、エネルギーへのタングル部分の寄与（つまり、Tをタングル部分として、T_×T上の積分）を考えると、タングルの大きさが半分になると、被積分関数は2−αp_{倍になる一方、}_T

×Tの面積は1/4になることから従う。

αp >2ならEα,p_(K)_{が上から抑えられていれば}_K _{は急には曲がれない。}

まず、fがC1,a _(a_∈_R₎_{であるとは、}_f_が_C1_級で_f′_が_a_次の_H¨older_{条件を満たす、つまり、}

∃A >0 s.t. _|f′(s)₋f′(t)_|< Ad(s, t)a (_∀s, t_∈S1= [0,1]/_∼)

となることを言う。ここで、d(s, t) =dK(h(s), h(t)) = min{|s−t|,1− |s−t|}.

補題 2.2 αp >2 ならEα,p_(h)_{が上から抑えられていれば} _h_は_C1,αp−2

2p である。上の係数AはEα,p(h)を用いて表すことができる。

上の補題は、[O2]でC1,2(αpp+2)−2 であることを示していたが、後に_[B]で改良された。

命題 2.3 αp >2とする。b_∈Rに対し、有限個のソリッドトーラスTi∼=D2×S1が存在して、

(1) Eα,p_(h)

≤bならばR3_{の合同変換で} _h(S1₎_をある_T

iの中に入れることができる。

(2) Eα,p_(h)_≤_b_かつ_h(S1₎_⊂_T

iならば、h(S1)はTiの各メリディアンディスク（D2× {t}(t∈S1)）と1点

で交わる。

定理 2.4 ([O3])αp >2 なら任意の結び目型にEα,p_-_{最小元が存在する。}

Eα,p_-_{最小元の形は}_α_と_p_{に依存する。}

Abrams, Cantarella, Fu, Ghomi, Howardは

(24)

2.1.2 Eα,pに関する解析

まずSobolev-Slobodeskij 空間の定義をする。

θ∈(0,1), q∈[1,∞)に対し、

Wθ,q(S1,Rn_{) :=}

{

f _∈Lq(S1,Rn₎

∫

u∈S1 ∫ 1/2

−1/2

|f(u+w)₋f(u)_|q

|w|1+qθ dwdu <∞

}

とおき、そのノルムを

∥f∥Wθ,q₍_S1_,Rn₎:=∥f∥_Lq+ (∫

u∈S1 ∫ 1/2

−1/2

|f(u+w)₋f(u)_|q

|w|1+qθ dwdu

)1 q

で定める。W1+θ,q_(S1_,_Rn₎_を

W1+θ,q_(S1_,_Rn_{) :=}{_f

∈W1,q_(S1_,_Rn₎

|f′_∈Wθ,q_(S1_,_Rn₎}

で定める。ここで、W1,q_(S1_,_Rn₎_は通常の_Sobolev_{空間である：}

W1,q(S1,Rn_{) :=}{_f

∈Lq(S1,Rn₎

|f′_∈Lq(S1,Rn₎}_.

Blattは Eα,p_(h)_{が有界になるために埋め込み写像}_h_{が満たすべき必要十分条件を与えた。}

定理 2.6 ([B]) h_∈C0,1_(S1_,_Rn₎_{を、弧長パラメータをもつ埋め込み写像とする。}_{α, p}

∈(0,_∞)が

αp≥2, p≥1, θ:=αp−1 2p <1

を満たすとする。このとき、

Eα,p(h)<∞ ⇐⇒h∈W1+θ,2p(S1,Rn₎

で、あるC=C(α, p)>0が存在して、

∥h′_∥2_Wpθ,2p₍_S1_,_Rn₎≤C (

Eα,p_{(h) +}

∥h′_∥2_Lp2p )

.

このことから補題2.2が従う。

2.1.3 Normal energy

Let vx be the unit tangent vector toK at a pointx, νx be the orthogonal 2-plane to vx throughx, and let

Pvx⊥:R 3∼₌_T

xK⊕νx→νxbe the orthogonal projection.

Instead of considering a (modified) Coulomb repulsive force F(x, y) we can consider its normal projection Pvx⊥(F(x, y)) toνx.

Let ¯θx= ¯θx(x, y) (or ¯θy= ¯θy(x, y)) (0≤θ¯x,θ¯y≤π) be the angle between vxand the chord (y−x) joiningx

andy (or respectively, betweenvy and (x−y) ). We remark thatηx(x, y) =O(|x−y|) near the diagonal.

定義 2.7 (1) Thenormal projection energyof Buck and Orloff ([BO]) is given by

Enp(K) = ∫ ∫

K×K

sin2ηx(y)

|x₋y_|2 dxdy.

(2) Thesymmetric normal projection energy of Buck and Simon ([BS]) is given by Esnp(K) =

∫ ∫

S1_×_S1

sinηx(y) sinηy(x)

|x₋y_|2 dxdy.

ClearlyEnp(K)≥Esnp(K) for any knotK. The formula (16) of the average crossing number implies

命題 2.8 ([BS])The projection energies bound the average crossing number ⟨c⟩:

(25)

2.1.4 サインエネルギー

Under Construction

Esinθ については、被積分関数の間の簡単な不等式から、

Esinθ(K1, K2)≥4π⟨c⟩(K1, K2) Esinθ(K)≥4π⟨c⟩(K)

が分かる。

2.1.5 Brylinskiのベータ関数

BrylinskiはαエネルギーE(α) _の指数_α_{を複素数にして、主要項のみとったものを、この指数}_α_{の複素関数} と考え、結び目のベータ関数と呼んだ([Bry])。

定義 2.9 ([Bry])hを弧長でパラメトライズされた結び目とする。zを複素数として結び目のベータ関数Bh(z)を

Bh(z) =

∫ ∫

S1_×_S1|

h(s)₋h(t)_|zdsdt

で定義する。

S1 ×S1

∋(s, t)_{7→ |}h(s)₋h(t)_|z

∈C

は _ℜez >0で連続なので、積分は ℜez >0 で収束する。

例 2.10 h0 を正円とする。

Bh0(z) = 2π ∫ 2π

0 (

2 sin t 2

)z

dt= 2z+3π

∫ π 2

0

(sinx)zdx

ここで sinx=√y とおくと ∫ π

2

0

(sinx)zdx= 1 2

∫ 1

0

yz−21(1−y)− 1 2dy=B

( z 2+ 1 2, 1 2 )

但しB(p, q) はオイラーのベータ関数

B(p, q) =

∫ 1

0

xp−1(1−x)q−1dx

である。オイラーのガンマ関数

Γ(w) =

∫ ∞

0

tw−1_e−t_dt

との間の関数等式

B(p, q) = Γ(p)Γ(q) Γ(p+q)

を用いると _∫ _π

2

0

(sinx)zdx=Γ( 1 2)Γ(

z+1 2 ) Γ(z

2+ 1) となる。以上から、正円のベータ関数Bh0(z)はzの有理型関数で、その極はΓ(

z+1

2 )が極をとる

z+1

2 = 0,−1,−2,· · · すなわちz=₋1,₋3,₋5,_{· · ·} でとる。

定理 2.11 ([Bry])滑らかな結び目 hに対し C∋z_7→Bh(z)∈Cは C上の有理型関数に解析接続することが出

来る。極はz=₋1,₋3,₋5,_{· · ·} 以外ではとらない。z=₋2n₋1 における留数は、曲率、れい率およびそれらの微分の多項式をS1 _{上積分することにより具体的に計算することが出来る。}

プレゼンファイル・集中講義ノート Jun O'Hara

結び目のエネルギーとその周辺

今井 淳

(首都大学東京)

平成

29

年

12

月

20

日

目 次

0

はじめに

1

結び目のエネルギー、繰り込まれた

r

-

エネルギー

1.1

結び目の基礎用語と記法

1.2

結び目のエネルギーとは∼幾何学的な最適問題

1.3

E

の定義

1.4

E

のメビウス不変性

1.5

エネルギー

E

-

最小元について

Refe

1.6

平均交点数との関係と結び目型の有限性

2

幾何学的結び目理論：幾何学的複雑さを測る量と最適な形

2.1

静電エネルギーの繰り込みの一般化の自然な拡張

Under Construction

今井淳

目次

_r

_の定義