グラウバー模型を用いたハイパー核の反応断面積の研究

グラウバー模型を用いたハイパー核の反応断面積の

研究

著者

赤石 友秀

学位授与機関

Tohoku University

グラウバー模型を用いたハイパー核の反応断面積

の研究

Reaction cross sections for hypernuclei with

Glauber model

東北大学大学院 理学研究科

物理学専攻 原子核理論研究室

B0SM2002

赤石友秀

概要

論文題目

グラウバー模型を用いたハイパー核の反応断面積の研究

Reaction cross sections for hypernuclei with Glauber model

東北大学大学院 理学研究科 物理学専攻 原子核理論研究室 赤石友秀

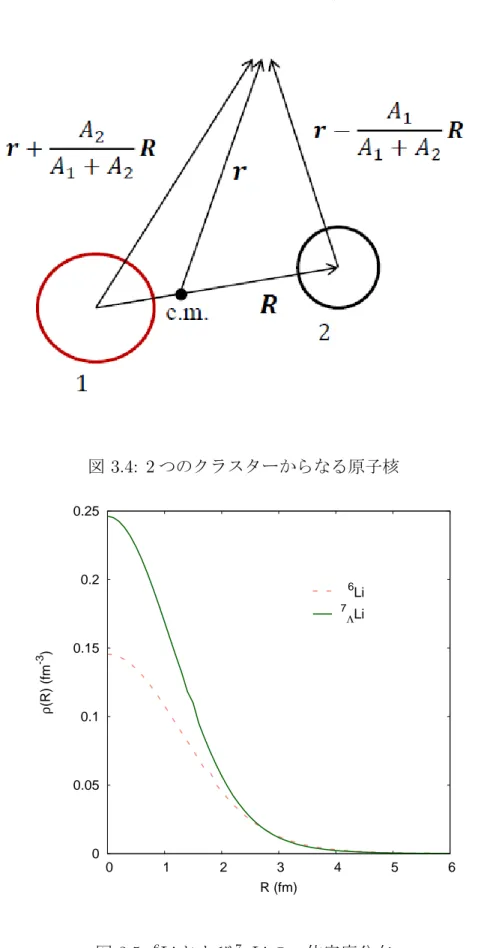
核子（陽子・中性子）からなる原子核にラムダ粒子が混入することによる不純物効果は、ハ イパー核研究の大きな興味の一つである。一般に、不純物効果は原子核の縮み（shrinkage） 効果として現れることが様々な理論的及び実験的研究から示唆されている [1-3]。これは ラムダ粒子が核子からのパウリ原理を受けないために原子核の中心部に入り込むことが でき、周囲の核子を引きつけるためである。特に、クラスター構造が発達しやすい軽い原 子核では、shrinkage 効果が顕著になることが期待できる。このような構造を持つ原子核 では、クラスター同士が弱く結合しているため、ラムダ粒子の引力によって原子核の構造 が大きく変化するためである。 本研究の目的は、中性子過剰核のハロー現象（中性子密度分布の大きな空間的広がり）の 発見において非常に重要な役割を果たした相互作用断面積の方法を用いて、ハイパー核の 不純物効果を調べることである。この方法により、高エネルギー重イオン衝突から原子核の 大きさを引き出すことができる。我々は、高エネルギーの散乱問題でよく用いられている、 グラウバー模型を理論的な解析に用いた。この模型では、原子核の基底状態の情報のみが必 要となる。具体的な系としては、基底状態が 2 体クラスター構造（core + deuteron, core =

α, 5ΛHe）を示すことで知られる、6Li 及び7ΛLi を入射核（入射エネルギー 100 MeV/A） とし、12_{C を標的核とする系を考え、ラムダ粒子による shrinkage 効果が相互作用断面積} に対してどのように影響を及ぼすのかを調べた。実際には、このエネルギー領域において 相互作用断面積とほぼ等しくなる、反応断面積 σ_Rを計算している。 まず、6_{Li 及び}7 ΛLi の基底状態の情報を引き出すために、半微視的なクラスター模型を 用いて 2 クラスター間の相対運動を調べた。（図 1）は、6_{Li 及び}7 ΛLi に対する、2 クラス ター間相対運動の基底状態（動径）波動関数である。ラムダ粒子の混入により7 ΛLi の相 対波動関数は6_{Li のものより中心に引き込まれていることがわかる。平均二乗半径にする} と、6_{Li が 4.342 fm、}7 ΛLi が 3.527 fm となっており、約 19% の縮みとなっている。次に、 このようにして求めた原子核の基底状態の密度を用いて、反応断面積の計算をする。一 般に、グラウバー模型の範囲内で近似なしに反応断面積の計算をすることは難しいので、 近似計算がよく用いられている。そこで我々は、入射核となる6_{Li 及び}7 ΛLi 内のクラス ター間の相関を取り入れることができる、少数系の方法（FB：few-body treatment）に基 づいて計算を行った。（図 2）は 2 つの系に対する反応断面積の計算結果である。横軸は、 グラウバー計算でインプットとなるラムダ-核子散乱の全断面積 σΛNである。例えば、現 実的に考えられる σ_ΛN = 10 mb では、7ΛLi の反応断面積は σR(7ΛLi) = 786.7 mb となり、 6_{Li に対する計算結果に比べて 40 mb ほど小さい。また、非現実的に大きな σ} ΛN = 100 mb

ることが期待できる。この結果は、ハイパー核の shrinkage 効果が反応断面積を通じて調 べられること、及びグラウバー計算を通じてハイパー核の密度の情報を引き出せることを 示唆するものである。 これまでハイパー核の shrinkage 効果は、実験的にはガンマ線分光によってのみ調べら れてきた [3]。これは Motoba らにより行われた、基底状態と励起状態の両方が関与する 電磁遷移の解析から、原子核の shrinkage 効果を探る方法である [1,2]。本論文で議論する 相互作用断面積の方法はこれと相補的な方法であり、原子核の基底状態の情報のみが必要 であることや、グラウバー計算を通じてハイパー核の密度分布が引き出せるなどの利点が ある。現状では短寿命のハイパー核を用いた衝突実験はほとんど不可能であるが、将来実 験が可能になった場合には、本論文の方法がハイパー核の大きさに関する研究で強力な方 法になることが期待される。 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0 5 10 15 20 u(R) (fm -1/2 ) R (fm) 6_Li 7 ΛLi 図 1: 7 ΛLi内の5ΛHe− dクラスター間（実 線）及び6_{Li内のα−dクラスター間（点線）} 相対運動の基底状態（動径）波動関数。u(R) はΨ(R) = u(R)_R Y00( ˆR)で与えられる。 780 785 790 795 800 805 810 815 820 825 830 0 20 40 60 80 100 σR (mb) σ_ΛN (mb) 6 Li 7 ΛLi 図 2: 12_{Cを標的核とした}6_{Li（点線）、}7 ΛLi （実線）の反応断面積。7 ΛLiについてはラム ダ-核子散乱の全断面積σΛNに対する依存性 を示す。現実的なσΛNの値は10∼20 mb程 度である。

参考文献

[1] T. Motoba, H. Band¯o, and K. Ikeda, Progress of Theoretical Physics 70, 189 (1983). [2] E. Hiyama et al., Phys. Rev. C 59, 2351 (1999).

i

目 次

第 1 章 序章 1 1.1 ハイパー核の研究 . . . . 1 1.2 不安定核の研究と相互作用断面積 . . . . 2 1.3 本研究の目的 . . . . 4 第 2 章 グラウバー模型 5 2.1 反応断面積と相互作用断面積 . . . . 5 2.2 アイコナール近似 . . . . 6 2.3 グラウバー模型 . . . . 8 2.4 光学極限近似 . . . 10 2.4.1 キュムラント展開 . . . 10 2.4.2 プロファイル関数 . . . 11 2.5 少数系の方法 . . . 13 第 3 章 クラスター間の相対運動 17 3.1 6_{Li（α− d） . . . 17} 3.2 7ΛLi（5ΛHe− d） . . . 19 3.3 ポテンシャルと波動関数の比較 . . . 20 3.4 一体密度 . . . 21 第 4 章 グラウバー模型の適用 23 4.1 6_Li+12_{C 系への適用 . . . . 23} 4.2 ハイパー核への応用 . . . . 24 第 5 章 結果と考察 27 5.1 入射エネルギー . . . 27 5.2 反応断面積 . . . . 27 第 6 章 まとめと今後の課題 29 付 録 A グラウバー模型 33 A.1 アイコナール近似での光学定理 . . . . 33

A.2 ガウス分布での光学極限近似の散乱行列 . . . . 34

A.3 光学極限近似での反応断面積 . . . . 35

A.3.1 一体密度 . . . . 35

A.3.2 反応断面積 . . . . 36

A.4 光学極限近似（フーリエ変換の方法） . . . . 36

付 録 B Semi-Microscopic Cluster Model 39 B.1 模型の方針 . . . . 39 B.2 ポテンシャルの導出 . . . . 40 B.2.1 V0(R) . . . . 41 B.2.2 V1(R) . . . . 42 B.2.3 V2(R) . . . . 43 B.3 相対運動の量子数 . . . . 44 付 録 C ラムダ粒子の扱い 45 C.1 ラムダ-核子に対するポテンシャル . . . . 45 C.2 ガウス型密度分布の幅パラメーター . . . . 46

1

第

1

章 序章

1.1

ハイパー核の研究

ラムダ・ハイパー核とは、核子（陽子と中性子）とラムダ粒子からなる原子核である。 ハイパー核研究の大きな興味の一つに、ラムダ粒子の不純物効果が挙げられる。ラムダ 粒子の混入による不純物効果は、原子核の縮み（shrinkage）効果として現れる。これは、 ラムダ粒子が陽子や中性子からのパウリ原理を受けずに原子核の内部に入り込むことが でき、周囲の核子を引きつけるためである。軽い核（A<_{∼30）における不純物効果の理論} 的研究はこれまで盛んに行われてきた。具体的には、3 体模型を用いた原子核の大きさの 研究 [1–3]（以下で概説）、相対論的平均場（RMF）計算や反対称化分子動力学（AMD） による変形度の研究 [4–6]、中性子ドリップラインの研究 [7, 8] などがある。その中でも 原子核の大きさの研究に関しては、ラムダ粒子が加わることによる6_{Li の大きさの変化に} 対して、高分解能のガンマ線分光による実験的検証 [9,10] が行われ、はじめてハイパー核 の大きさを引き出すとともに、ラムダ粒子の混入による原子核の shrinkage 効果が確認さ れた。 Motoba らのクラスター模型計算（6Li = α + d 及び7ΛLi = α + d + Λ）では、ラムダ 粒子の混入による原子核の縮みは、E2 遷移強度の減少によって確かめられることが指摘 された。これは、α− d クラスター間距離が E2 遷移強度の 1/4 乗に比例するためである。 そのため彼らは、 Rc−d Rα−d = [ B(E2 ; 5/2+_{→ 1/2}+₎ 7 9B(E2 ; 3+→ 1+) ]1/4 (1.1.1) という関係式に着目し、解析を行った。左辺分母・分子はそれぞれ6_Li,7 ΛLi の 2 クラス ター間平均距離であり、右辺は E2 遷移強度の比を表し、括弧内の各状態は（図 1.1）に 示されるように、ラムダ粒子のスピンによる分岐を無視すれば、基底状態と第 1 励起状態 に対応する。また右辺分母にある 7/9 は、6_{Li の 3}+ _{→ 1}+_{への E2 遷移強度が、}7 ΛLi では 7 9B(E2 ; 5/2 + → 1/2+_{) +} 2 9B(E2 ; 5/2 + → 3/2+_{) のように分配されることからくる。}6_Li の E2 遷移強度については実験値、Rα−dについては実験値と理論値に基づいた量 [3, 11] を用いることができるので、実験的には7 ΛLi の E2 遷移強度を測定できれば両原子核の大 きさが比較できることになる。ところで、（1.1.1）式は α + d クラスターを仮定している限 り、2 つのクラスター間の相対運動の励起のみを考えればもっともらしいが、5 ΛHe + p + n

図 1.1: 6_Li,7

ΛLi の基底状態、第 1 励起状態のエネルギースペクトルの実験値。文献 [9]

より

のような 3 体模型でもそのまま成り立つかどうかは自明でない。Hiyama らは、2 つの原子 核（6_Li, 7

ΛLi）に d クラスターを仮定しない 3 体模型計算（core + p + n、core = α,5ΛHe）

を行った。この模型の中で両辺を別々に計算した結果、（1.1.1）式が良い精度で成り立つ ことが示された。これは6_Li, 7

ΛLi 両原子核中において、valence 陽子・中性子間距離が基

底状態、第 1 励起状態におけるすべての場合でほぼ等しいためである。（2 つの原子核中 で同様の deuteron-like なクラスターが形成されている。）

Hiyama らの計算により、core と deuteron-like なクラスターの相対距離は約 25% 縮む ことが予言された。その 2 年後、Tanida ら [9] によるガンマ線分光実験（KEK での E419 実験）により、7 ΛLi の 5/2+ → 1/2+ への E2 遷移強度が測定され、（1.1.1）式を通して約 19% の縮みであることが確認された。 E2 遷移強度から原子核の大きさを引き出す上記の手法は、（1.1.1）式からわかるよう に、6_Li, 7 ΛLi それぞれの基底状態と第 1 励起状態の波動関数を必要とする。また、6Li と 7 ΛLi の変形度が違う可能性もあるため、以上の結果が正当化されるとは必ずしも限らな い。そこで次節では、ハイパー核物理とはやや分野が異なる不安定核のこれまでの研究を 概観しながら、そこで用いられた基底状態の情報のみ（原子核の密度）を用いて原子核の 大きさを引き出す方法を紹介する。

1.2

不安定核の研究と相互作用断面積

1980 年代、中性子過剰な不安定核のビームが、高エネルギー重イオン衝突での入射核破砕 過程により生成可能となった。1985 年、Tanihata ら [12] は Li アイソトープ（6−9_Li, 11_Li）な

どを入射核、4_He, 12_C, 9_{Be などを標的核とした衝突実験（入射エネルギー≃ 790 MeV/A）}

において、相互作用断面積 σ_Iの測定を行った。相互作用断面積とは、入射した核が元の 核以外となって出てくる断面積の和である。入射核と標的核をそれぞれ半径 RI(P ), RI(T )

1.2. 不安定核の研究と相互作用断面積 3 2 2.2 2.4 2.6 2.8 3 3.2 3.4 6 7 8 9 10 11 RI (fm) A 図 1.2: Li 同位体の相互作用半径の実験値 [12]。実線は安定核でよく知られる半径の式 R = 1.17A1/3_を表す。 の球体とし、高エネルギーの衝突では少しでも衝突すれば原子核は壊れると仮定すると、 σI= π [RI(P ) + RI(T )]2 (1.2.1) が成り立つ。RIは相互作用半径と呼ばれている量である。Tanihata らはまず、安定核同 士の衝突実験から相互作用半径を調べ、この量が原子核の大きさを表す適切な物理量で あることを確かめた。すると（1.2.1）式からわかるように、相互作用断面積とよく大き さの知られた標的核の相互作用半径から、入射核の大きさを引き出すことができる。(図 1.2) は入射核を Li アイソトープ、標的核を12C とした衝突実験での相互作用半径を表して いる。6−9_{Li については安定核で知られる半径の法則（R∝ A}1/3_{）がよく成り立っている} が、11_{Li はこれに比べて有意に大きな半径を示している。これは、今日では常識となって} いるハロー核の存在を示唆する最初の実験的証拠となった。ハロー核（別名、暈原子核） とは、芯核となる原子核の周りに非常に弱く束縛した核子を持ち、遠方まで密度がテール を引くような原子核である。11_{Li では}9_{Li が芯核に該当し、弱く束縛した 2 つの中性子を} 持つことが現在では知られている。（しかし Tanihata らが実験を行った段階では大きな変 形度をもつ原子核という可能性も捨てきれなかった。） Bertsch ら [13] は第 2 章で説明されるグラウバー模型による理論的な解析により、芯核 と薄く広がった密度分布を持つ valence 中性子という描像で、11_{Li の大きな相互作用半径} を再現した。この模型では原子核の基底状態の密度及び核子-核子散乱の全断面積がイン プットとなる。彼らは従来の Hartree-Fock 法による計算 [14] を現象論的に改良し密度を 求めることでこれを実現した。

後に入射核破砕片の鋭い横方向の運動量分布の測定 [15] から、この原子核が薄く広がっ た密度分布を持つという解釈が実験的にも正当化され、ハロー核の存在は確固たるものと なった。

1.3

本研究の目的

本研究の目的は、ハロー核の発見に重要な役割を果たした相互作用断面積の方法を用 いて、ハイパー核の不純物効果を調べることである。（1.2 節）で述べたように、高エネル ギーの散乱問題でよく用いられるグラウバー模型を用いると、原子核の基底状態の密度の みが必要となり、この方法により直接的にハイパー核の基底状態の大きさを探ることがで きる。これは、基底状態と励起状態の双方が関与する電磁遷移の解析と相補的な方法であ る。我々はこの方法を6_{Li 及び}7 ΛLi を入射核とする系に適用し、ラムダ粒子の混入による 原子核の shrinkage 効果が、相互作用断面積にどのように影響を及ぼすのかを議論する。 本論文は以下のように構成される。第 2 章では、グラウバー模型とその近似計算を概説 する。第 3 章では、グラウバー計算で必要となる原子核の内部波動関数を求める方法を、 クラスター模型に基づいて述べる。実際の系への適用は第 4 章で述べ、第 5 章ではその計 算結果を示し考察を行う。最後に第 6 章でまとめと今後の課題を述べる。

5

第

2

章 グラウバー模型

グラウバー模型は、1955 年に Glauber が提唱した高エネルギーにおける原子核衝突の 近似理論である [16]。この模型ではポテンシャル散乱の問題において、入射核の運動を 直線軌道で近似するアイコナール近似と、核子の配位を凍結する断熱近似（2.3 節）を組 み合わせることにより、核子-核子散乱の自由度から原子核衝突を記述することができる。 比較的容易な計算で多体系の散乱を微視的に記述できる点がこの方法の強みである。安定 核のみならず不安定核への適用（とりわけハロー核の発見に大きく貢献した）もしばしば 行われ、高エネルギーの散乱問題において有力な方法の一つとなっている。 この章ではまず、序章で触れた実験的観測量である相互作用断面積と、理論的に計算が 容易な反応断面積の関係を述べたあと、グラウバー模型の基礎となるアイコナール近似の 説明から、グラウバー模型の近似理論（光学極限近似、少数系の方法）まで順を追って説 明していく。

2.1

反応断面積と相互作用断面積

グラウバー模型では、相互作用断面積 σI（（1.2 節）参照）よりも反応断面積 σRの計算 が容易である。反応断面積とは、弾性散乱以外の全てのチャンネルの断面積の和である。 2 つの断面積には、 σR = σI+ σinel (2.1.1) という関係がある。ここで σinelは非弾性散乱の断面積である。高エネルギーの衝突では、 入射核と標的核の密度が少しでも重なれば、双方の原子核は壊れ他の核になることが期待 できるので、 σI≃ σR (2.1.2) が良い近似で成り立つことが期待される。特に本研究で扱う6_Li,7 ΛLi は基底状態がクラ スター構造を示すことが知られており、クラスター同士は弱く結合し安定な束縛状態の数 は多くない。そのため（2.1.2）式がよく成り立つことが期待される。

2.2

アイコナール近似

核反応が直線軌道に沿って起こるというアイコナール近似は、ポテンシャル散乱の問題 において次の 2 つの条件が整う場合によく成り立つ近似理論である。すなわち、入射粒子 の波長がポテンシャルの作用範囲に比べて十分短い場合 k0a≫ 1 (2.2.1) （a はポテンシャルの作用範囲）と、入射エネルギーがポテンシャルの深さよりもずっと 大きい場合 E ≫ |V0| (2.2.2) である。 Schr¨odinger 方程式 [ p2 2µ + V (r)− E ] Ψ(+)(r) = 0 (2.2.3) から出発し、これらの条件から導かれる波動関数を考察する。高エネルギーの散乱問題で あるので、入射粒子がポテンシャルの作用範囲を通過する時間は短く、（半古典的ではあ るが）軌道はほとんど直線であると考える。この時、波動関数を Ψ(+)(r) = eik0z_{ω(r) (2.2.4)} のように、平面波と平面波からのずれを表す関数 ω(r) の積に書いておく。これを Schr¨odinger 方程式（2.2.3）式に代入し、ω(r) に関する方程式 [ vpz− ℏ2 2µ∇ 2_{+ V (r)} ] ω(r) = 0 (2.2.5) （v =_{ℏk/µ）を得る。ω(r) が r に対してゆっくりとした関数とし、（2.2.5）式の第 2 項が} 第 1 項に比べて小さいとして無視する。この時、1 階の微分方程式 ∂ω ∂z =− i ℏvV (r)ω(r) (2.2.6) を解くと、 ω(r) = exp [ −_ℏvi ∫ z −∞ V (x, y, z′)dz′ ] (2.2.7) となり、アイコナール近似での波動関数は Ψ(+)(r) = exp [ ik0z− i ℏv ∫ z −∞ V (x, y, z′)dz′ ] (2.2.8)

2.2. アイコナール近似 7 となる。 （2.2.7）式を用いてアイコナール近似の妥当性を考察する。まず（2.2.5）式で無視し た∂2ω ∂x2 や ∂ 2_ω ∂y2 が小さいことは、波動関数の x, y 方向への変化がないこと、つまり直線軌道 を表すことになる。次に、（2.2.6）式を z で微分し、 ∂2ω ∂z2 =− i ℏv ( ∂V ∂z − i ℏvV2 ) ω (2.2.9) を得る。これと 1 階微分の場合の大きさを比べてみると、    −ℏ2 2µ ∂2_ω ∂z2 vpzω   = 1 2 v u u t(∂V∂z kV )2 + ( V 2E )2 ≪ 1 (2.2.10) となる。根号内の第 1 項は 1 波長におけるポテンシャルの変化とポテンシャルの大きさの 比であり、条件（2.2.1）式より十分小さい。また、第 2 項も条件（2.2.2）式より十分小さ い。これで、（2.2.5）式の第 2 項を第 1 項と比べて無視できることが正当化された。 ここで求めたアイコナール近似の波動関数は、散乱問題の境界条件を満たさない。しか し散乱振幅は f (θ) =−2µ ℏ2 1 4π ∫ dr e−ik′·rV (r)Ψ(+)(r) (2.2.11) で与えられ、遠方で十分小さくなるポテンシャルによる散乱を考える限り、ポテンシャル 中心の付近での波動関数の形がわかればよいので問題は生じない。（2.2.11）式に（2.2.8） 式を代入し z 積分を実行すると f (θ) = ik 2π ∫ db eiq·b(1− eiχ(b)) (2.2.12) となり、入射軸に対し垂直な面内での積分（衝突径数での積分）が残る。ここで q = k′_−k は運動量移行であり、 χ(b) =− 1 ℏv ∫ _∞ −∞ dz V (x, y, z) (2.2.13) は位相差関数と呼ばれる。（付録 A.1）で示すように、アイコナール近似では光学定理が 成り立つので、弾性散乱断面積、全断面積、吸収断面積（反応断面積）が求められ、それ ぞれ σel = ∫ db|1 − eiχ(b)|2 σtot = ∫ db 2(1− Re [ eiχ(b)]) σabs = ∫ db (1− |eiχ(b)|2) (2.2.14) となる。

2.3

グラウバー模型

この章のはじめに述べたように、グラウバー模型は前節で紹介したアイコナール近似と 断熱近似とを組み合わせることにより、高エネルギーでの原子核同士の衝突を核子-核子 散乱の自由度から記述する枠組みである。ここでは話を単純化するために、入射核と核子 の散乱を考える。原子核同士の衝突の場合に拡張するのは容易である。 核子-原子核散乱に対する Schr¨odinger 方程式 [ Prel2 2µ + H0({ri}) + U({Rj}) − E ] Ψ = 0 (2.3.1) を考える。ここで H0({ri}) は入射核の内部ハミルトニアン、U({Rj}) は入射核内の核子 と標的核子に働く相互作用 V_jt(Rj) を用いて、U ({Rj}) = ∑A j=1Vjt(Rj) で与えられる。こ こで入射エネルギーは内部励起に比べ十分に高いとし、内部ハミルトニアンを基底状態の エネルギー_−ϵ0に置き換える断熱近似を導入する。E0 = E + ϵ0とすると [ Prel2 2µ + U ({Rj}) − E0 ] ΨAD = 0 (2.3.2) となる。波動関数の添え字の AD は断熱（ADiabatic）近似を表す。アイコナール近似の 場合と同様に、 Ψeik = eiK0z_ω({r i}, R)ϕ (A) 0 ({ri}) (2.3.3) （R = (x, y, z)）と置いて、（2.3.2）式に代入し ω に関する 2 階微分を無視すると、 ∂ω ∂z =− iµ ℏ2_K 0 U ({Rj})ω({ri}, R) (2.3.4) を得る。これを解くと、 ω({ri}, R) = exp [ − i ℏv ∫ z −∞ U ({R′_j})dz′ ] = exp [ −_ℏvi A ∑ j=1 ∫ zj −∞ Vjt( √ b2 j + zj′2)dzj′ ] _(2.3.5) である。ここで bj は核子 j の衝突径数である。断熱近似していることを用いて、入射核 の重心座標による積分を個々の核子の積分に直した。 この波動関数を用いて、入射核が励起状態 α へ遷移する散乱振幅も計算できる。終状 態の波数の大きさを Kα ≃ K0として、散乱振幅 f (Kα) =− iK0 2π ∫ dbeiq·b ∫ _∞ −∞

dz⟨ϕ(A)_α |Uω|ϕ(A)₀ ⟩ =−iK0

2π ∫

dbeiq·b⟨ϕ(A)_α |S(A)({bj}) − 1|ϕ

(A)

0 ⟩

2.3. グラウバー模型 9 i j

b

r

i sr j s

r

projectile target 図 2.1: 原子核同士の衝突 を得る。q = Kα− K0は運動量移行であり、1 行目から 2 行目の変形で、（2.3.4）式を用 い部分積分を実行した。ここで S(A)({bj}) = exp [ i A ∑ j=1 χj(bj) ] = A ∏ j=1 Sj(bj) χj(bj) =− 1 ℏv ∫ _∞ −∞ Vjt(Rj)dzj (2.3.7) である。S 行列 S(A)_{は入射核中の各核子に対する S 行列 S} jの積で与えられる。入射核内 の核子と標的核子の散乱行列を決定すれば、（2.3.6）式により散乱振幅を求めることがで きる。標的が原子核の場合に拡張すると、 f (Kαβ) =− iK0 2π ∫ db eiq·b⟨ϕP_αϕT_β|ei∑APi=1 ∑AT j=1χ(b+si−sj)− 1|ϕP 0ϕ T 0⟩ (2.3.8) となる。ここで (図 2.1) に示すように b は衝突径数、si（sj）は入射核（標的核）の重心 から見た核子 i（j）の x, y 面内での位置である。 グラウバー模型の枠組みでも光学定理が成り立つこと [16] が知られている。これによ り、弾性前方散乱の散乱振幅の虚部と全断面積が結びつき、全断面積から弾性散乱の断面 積を引くことで反応断面積 σR = σtot− σel = ∫ db [ 1− |⟨ϕP₀ϕT₀|ei∑APi=1 ∑AT j=1χ(b+si−sj)|ϕP 0ϕ T 0⟩| 2] (2.3.9)

を得る。第 2 項は基底状態内部波動関数で期待値を計算する形となっており、モンテカル ロ積分法が適用できる [17]。これはグラウバー模型の範囲で近似なしに反応断面積を計算 できることを意味する。しかしながら計算は複雑であり、通常は次節で紹介する近似的な 方法が用いられる。

2.4

光学極限近似

グラウバー模型で得られた散乱振幅や各種断面積を計算しようとする場合、位相差関数 χ(b)≡ AP ∑ i=1 AT ∑ j=1 χ(b + si− sj) (2.4.1) の多体波動関数による期待値 ⟨eiχ(b)_{⟩ ≡ ⟨ϕ}P 0ϕ T 0|e i∑AP_i=1∑AT_j=1χ(b+si−sj)|ϕP 0ϕ T 0⟩ (2.4.2) を計算しなければならない。これに対する近似としては、

• 光学極限近似（OLA：Optical Limit Approximation）：位相差関数の期待値を、以

下で説明するキュムラント展開し、第 1 項までで近似する方法。多重散乱は考慮さ れない。 • 少数系の方法（FB：Few-Body Treatment）：光学極限近似をベースに、原子核内の 粒子（クラスター間やハロー核内の芯核と valence 核子など）の相関を正しく扱う ことができる方法。[18] • NTG：核子-核子散乱の多重散乱の効果を一部考慮した計算法。[19] • NTO：核子-原子核の光学ポテンシャルが利用できる場合の方法。[19] などが知られているが、6_Li,7 ΛLi はクラスタ構造を示すことが知られているため、本論文 では少数系の方法（FB）を用いる。まず、FB の準備として本節では光学極限近似の方法 を紹介する。

2.4.1

キュムラント展開

ある物理量 X の期待値⟨eX⟩ を考える。これを ⟨eX_{⟩ = e}⟨X⟩_⟨eX−⟨X⟩_{⟩ (2.4.3)}

2.4. 光学極限近似 11 と変形し、 ln⟨eX⟩ = ⟨X⟩ + ln(⟨eX−⟨X⟩⟩) =⟨X⟩ + ln ( 1 + 1 2⟨(X − ⟨X⟩) 2_{⟩ + · · ·} ) = ∞ ∑ n=1 κn n! (2.4.4) とすると、X のゆらぎで展開ができる。ここで最後の等号では ln(1 + x) のテイラー展開 をし、各 κnは κ1 =⟨X⟩ κ2 =⟨(X − ⟨X⟩)2⟩ · · · (2.4.5) などである。グラウバー模型において、 ⟨eX_{⟩ ≃ e}⟨X⟩ _(2.4.6) と、第 1 項までで近似するのが光学極限近似である。近似の妥当性は、グラウバー模型の 範囲内で近似なしの計算をしてみれば確かめることができるが、この近似で得られる反応 断面積は、高エネルギー領域では他の高次の項を考慮した計算よりも必ず大きく出ること が知られている [20]。 さて物理量 X として位相差関数 X = i AP ∑ i=1 AT ∑ j=1 χ(b + si− sj) (2.4.7) を考え、光学極限近似を適用すると

⟨eiχ(b)_{⟩ ≃ exp}

[ i ∫ ∫ drdr′ρP(r)ρT(r′)χ(b + s− s′) ] (2.4.8) を得る。この式は 1 体密度 ρP及び ρTを用いて表されているように、核子-核子の相関、つ まり多重散乱の効果は考慮されていない。これは（2.4.4）式の 2 次の補正項は 2 粒子密度 を用いて表され、原子核内の核子-核子相関に依存することによってもわかる。核子-核子 散乱の位相差関数 χ をどう決めるかという問題が残されるが、そのことについては次節 で述べる。

2.4.2

プロファイル関数

通常、複雑な核力から核子-核子散乱の位相差関数を直接計算するということは行われ ていない。その代わりに、核子-核子散乱全断面積の実験データに結び付けて考えるのが

よく用いられるやり方である。そのために、 ΓNN(b + si− sj)≡ 1 − eiχNN(b+si−sj) (2.4.9) で定義されるプロファイル関数を用いると見通しがよくなる。ここで下付きの NN は核 子-核子散乱を表す。プロファイル関数 ΓNNを用いて、核子-核子散乱のアイコナール近似 での散乱振幅を求めると fNN(θ) = ik 2π ∫ db eiq·bΓNN(b) (2.4.10) である（（2.2.12）式参照）。ここで最も単純に考えて、 ΓNN(b) = 1 2σ (NN) tot δ(b) (2.4.11) とすれば光学定理は成り立つ。σ(NN) tot は核子-核子散乱の全断面積である。実際、（2.4.11） 式を（2.4.10）式に代入すると fNN(θ) = ik 4πσ (NN) tot ∫ db eiq·bδ(b) = ik 4πσ (NN) tot (2.4.12) となり、 Im fNN(θ = 0◦) = k 4πσ (NN) tot (2.4.13) と光学定理が成り立つ。一般的には、プロファイル関数に虚部を持たせるものや、デルタ 関数ではなくガウス関数を用いる有限レンジのもの [21] ΓNN(b) = 1− iα 4πβ σ (NN) tot e−b 2_/2β (2.4.14) が用いられており、核子-核子の弾性散乱データなどからパラメータが決められている。な お、本研究では (2.4.11 式) のようなゼロレンジのものを用いる。 このように、プロファイル関数と核子-核子散乱の全断面積を結びつけることができた ので、光学極限近似をプロファイル関数を用いて書くことを考える。位相差関数の期待 値は ⟨eiχ(b)_{⟩ = ⟨} AP ∏ i=1 AT ∏ j=1 (1− ΓNN(b + si− sj))⟩ (2.4.15) と書けるが、 AP ∏ i=1 AT ∏ j=1 (1− ΓNN(b + si− sj)) = 1− AP ∑ i=1 AT ∑ j=1 Γij +O(Γ2) (2.4.16)

2.5. 少数系の方法 13 と展開し、Γ の 1 次までをとって 1− AP ∑ i=1 AT ∑ j=1 Γij ≃ e− ∑AP i=1 ∑AT j=1Γij _(2.4.17) とすると位相差関数を用いた場合と同様な方法でキュムラント展開が適用できる。プロ ファイル関数を用いた光学極限近似での表式は、

⟨eiχ(b)_{⟩ = exp}

[ − ∫ ∫ drdr′ρP(r)ρT(r′)ΓNN(b + s− s′) ] (2.4.18) となる。(2.4.11 式) のプロファイル関数を用いると、反応断面積は σR = ∫ db [ 1− exp [ −σ(NN) tot ∫ dsTρ(z)_P (−b + sT)ρ(z)_T (sT) ]] (2.4.19) と書くことができる。ここで、 ρ(z)(s)≡ ∫ dz ρ(r) (2.4.20) であり、2 次元ベクトル sTは標的の重心から見た核子の x, y 面内での位置である。この 表式は次のような見方をすると直感的に理解ができる [13]。原子核が入射軸（z 軸）方向 を向いた無限に細いチューブからなると考え、入射核と標的核のチューブが重なる部分を 核子-核子の断面積の重み（反応確率のようなもの）で足し合わせたものが、 σ(NN)_tot ∫ dsTρ (z) P (−b + sT)ρ (z) T (sT) (2.4.21) であり、 exp [ −σ(NN) tot ∫ dsTρ (z) P (−b + sT)ρ (z) T (sT) ] ≃ 1 − σ(NN) tot ∫ dsTρ (z) P (−b + sT)ρ (z) T (sT) (2.4.22) は反応しない確率を表すので、(2.4.19 式) は全体として反応確率をあらゆる衝突係数で足 し上げたものと見ることができる。

2.5

少数系の方法

この節では、弱く結合した複数のクラスターをもつ原子核やハロー核における芯核＋ valence 核子の構造のように、入射核が複数の粒子からできている場合に、粒子間の相関 を正しく取り入れることができる一種の光学極限近似の応用を示す。（2.4 節）で扱った光

br target projectile 1 br b2 r bn−1 r bn r ͙ Rr 図 2.2: n 体からなる入射核と内部構造を持たない標的核の衝突 学極限近似では反応断面積の表式からわかるように、入射核と標的核の密度を必要とす る。このような入射核の密度を作ろうとする場合、（3.4 節）で紹介するようにクラスター のあらゆる相対位置で平均をとるような操作をするため、断熱近似が破れてしまう。その ため弱く結合したクラスターからなる原子核や、遠方まで密度がテールを引くハロー核な どにおいて、通常の光学極限近似を適用することが良い近似になるとは考えにくい。 この扱いの第一段階では、（図 2.2）のような内部構造を持たない標的核と複数の粒子か らなる入射核の散乱問題を考える。(2.3 節) での多核子からなる入射核と標的核子の散乱 とのアナロジーで、散乱振幅は f (Kα) =− iK0 2π ∫ dbeiq·b⟨ϕ(n)_α |S(n)({bj}) − 1|ϕ(n)0 ⟩ (2.5.1) となる。ここで散乱行列は各粒子の散乱行列の積として与えられ、 S(n)({bj}) = exp [ i n ∑ j=1 χj(bj) ] = n ∏ j=1 Sj(bj) χj(bj) =− 1 ℏv ∫ _∞ −∞ Vjt(Rj)dzj (2.5.2) である。反応断面積は σR = ∫ db [ 1− |⟨ϕ(n)₀ |S(n)|ϕ(n)₀ ⟩|2 ] (2.5.3) で与えられ、入射核内の粒子と標的粒子の散乱行列 Sj（と入射核の内部波動関数）がわ かればこれらの量を計算できる。特に入射核が 2 体系である場合は、2 体クラスター間の

2.5. 少数系の方法 15 相対運動の波動関数 ψrel を用いて反応断面積は σR = 2π ∫ b db[1− |⟨ψrel|S1(b1)S2(b2)|ψrel⟩|2 ] (2.5.4) で与えられる。 ここで第二段階として、散乱行列 Sjを核子からなる複合粒子同士の衝突と見直すこと により、各々の散乱行列に光学極限近似を適用する。実際の系への適用は第 4 章を参照さ れたい。

17

第

3

章 クラスター間の相対運動

よく知られているように、軽い原子核はしばしばクラスター構造を示す。歴史的には、 1960 年代から始まった軽重イオン反応により、α クラスター構造を示す核が多く発見さ れた。もちろん α クラスターだけが核内のクラスターではなく、deuteron クラスターや 12_{C クラスターなども考えることができる。クラスター構造を示す状態は、その系のエネ} ルギーが各クラスターに分解するしきい値の近傍にある場合に現れる、という法則がよく 成り立っている [22]。理論的には、 • クラスターを構成する核子の自由度からクラスター間の相対運動を決定する、微視

的なクラスター模型である共鳴群法（resonating group method: RGM）[23, 24] や 生成座標法（generator-coordinate method: GCM）[25, 26]

• 上記の微視的クラスター模型の簡易版であり、核子間の反対称化を相対波動関数の直

交性によってのみ取り入れる直交条件模型（orthogonality condition model: OCM） [27, 28]

• 本章で紹介する、内部構造を持たない α クラスターを仮定し、その他の自由度をき

ちんと考慮する semi-microscopic cluster model [29]

などが考案され、原子核のエネルギーや α 粒子の散乱の位相差、四重極モーメント [30] などの説明に成功している。 本研究で扱う6_{Li と}7 ΛLi は基底状態がクラスター構造を示すことで知られている原子核 である。ここではそれらの原子核におけるクラスター間の相対運動を、semi-microscopic cluster model に基づき決定する。得られた相対運動の波動関数は、グラウバー模型にお ける少数系の方法で必要となる、内部波動関数（基底状態）での S 行列の期待値の計算 に用いられる。

3.1

6

Li

（

α

− d

）

Hiyama らの三体模型計算（core + p + n）[3] によると、6Li と7ΛLi 核内の valence 陽子・

中性子は真の deuteron クラスターとは陽子・中性子間の距離が違うものの、deuteron-like なクラスター構造を示す。（この計算では6_{Li と}7

ΛLi 中の deuteron-like なクラスターは 2

rr R r 2 / r R r r + 2 / r R r r − core p n 図 3.1: 半微視的な描像。deuteron の自由度のみきちんと扱う。 対運動の変化、あるいは core となっている原子核へのラムダ粒子の混入が反応断面積に与 える影響を調べることであり、以下では valence 陽子・中性子に真の deuteron クラスター （d）を仮定する近似を用いる。すなわち6_{Li と}7 ΛLi の構造として、α + d 及び5ΛHe + d を仮定する。

（付録 B.2）及び（付録 B.3）で示すように、semi-microscopic cluster model に基づく と、6_{Li における α}− d クラスター間の s-wave（基底状態）のポテンシャルは

V0(R) =−2

∫

drU0(r, R)χ2(r) (3.1.1)

で与えられる。（図 3.1）に示すように、R は 2 クラスターの相対位置、r は valence 陽子・ 中性子の相対位置である。χ(r) は deuteron の s-wave の波動関数である。U₀は、α 粒子と 核子に働く有効相互作用が中心力（実際には LS 力も存在するが、基底状態を考える限り 中心力のみを考慮すればよい（付録 B.3）） VαN =−U(|R ± r/2|) (3.1.2) である場合に、U を多重極展開 U (|R ± r/2|) = 4π∑ λ Uλ(r, R)Yλ(±ˆr) · Yλ( ˆR) (3.1.3) したときの係数である。 次に具体的な deuteron の s-wave の波動関数、α 粒子と核子の有効ポテンシャルなどを 考慮し、V0(R) を求め Schr¨odinger 方程式を解く。deuteron の s-wave の波動関数としては

文献 [30] と同様の Hulthen 型

3.2. 7 ΛLi（5ΛHe− d） 19 を用い、α 粒子と核子の有効ポテンシャルは文献 [31] のガウス型のパラメーターを再調 整 [32] した VαN(r) =−v0e−βr 2 , v0 = 40.45 MeV, β = 0.189 fm−2 (3.1.5) を用いた。V0(R) の具体的な形や波動関数の形は、（3.3 節）において7ΛLi のものと比較 する。

3.2

7_Λ

Li

（

5_Λ

He

− d

）

次に、（3.1 節）と同様な方法で7 ΛLi 核に対するポテンシャルや波動関数を求める。こ こでは、core となる核が5 ΛHe になる点において6Li の場合と異なる。α 粒子の重心とラ ムダ粒子の中心が一致すると仮定して話を進める。core と核子に働く有効ポテンシャルは 前節と同様、 VcN =−U(|R ± r/2|) =−UαN(|R ± r/2|) − UΛN(|R ± r/2|) (3.2.1) である。UΛNは ΛN 相互作用をラムダ粒子の密度で畳み込むことで作った。ラムダ粒子の 密度としてはガウス型 ρΛ(r) = 1 (√πbΛ)3 e−r2/b2Λ _(3.2.2) を仮定し、ΛN 相互作用もガウス型 [1] vΛN(r) = v0e−r 2_/b2 v _(3.2.3) にとった。v₀の値は文献 [32] で9 ΛBe の基底状態を再現するよう再調整されたもの v0 = −20.9 MeV を用いた。すると UΛNは解析的に求めることができ（付録 C.1）、 UΛN(rN) = ∫ drρΛ(r)vΛN(rN − r) = v0 ( b2_v b2 Λ+ b2v )3/2 exp [ − r2N b2 Λ+ b2v ] (3.2.4) となる。ここで bΛ= √ (4mN+ mΛ)/4mΛbα （mN : 核子の質量、mΛ: ラムダ粒子の質量） （付録 C.2）、bα = 1.358 fm [1] である。 以上で VcNを求めることができたので、（3.1 節）の場合と同様にクラスター間の有効ポ テンシャルを求めることができ、それによりクラスター間の相対運動に対する波動関数も 求められる。

-70 -60 -50 -40 -30 -20 -10 0 0 1 2 3 4 5 6 V0 (R) (MeV) R (fm) 6 Li 7 ΛLi 図 3.2: （クーロン力を除く）7 ΛLi 内の5ΛHe− d クラスター間（実線）及び6Li 内の α− d クラスター間ポテンシャル（点線） エネルギー（MeV） 平均二乗半径（fm） 6_{Li -1.475 4.342} 7 ΛLi -3.481 3.527 表 3.1: 基底状態のエネルギーと平均二乗半径

3.3

ポテンシャルと波動関数の比較

この節では（3.1 節）、（3.2 節）で得られたポテンシャルの比較、及び基底状態の波動 関数の比較を行う。 クラスター間の s-wave に働く中心力は（図 3.2）に図示されている。ラムダ粒子の混 入により、ポテンシャルは 5.98 MeV 深くなった。Schr¨odinger 方程式を解く際には、ク ラスター間のクーロン力も考慮した。クーロン力としては一様帯電球（core）と点電荷 （deuteron）の作るポテンシャルを用いた。得られた基底状態の波動関数を（図 3.3）に示 す。7 ΛLi の深いポテンシャルから予想される通り、7ΛLi の波動関数のほうが6Li のものよ り中心に引き込まれている。平均二乗半径は6_Li, 7 ΛLi それぞれに対し、4.342 fm, 3.527 fm であり、約 19% の縮みとなっている。（表 3.1）に結果をまとめる。

3.4. 一体密度 21 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0 5 10 15 20 u(R) (fm -1/2 ) R (fm) 6 Li 7 ΛLi 図 3.3: 7 ΛLi 内のクラスター間（実線）および6Li 内のクラスター間（点線）相対運動の 基底状態（動径）波動関数。u(R) は Ψ(R) = u(R) R Y00( ˆR) で与えられる。

3.4

一体密度

グラウバー計算に対する光学極限近似（2.4 節）の計算で必要な一体密度は、2 クラス ター間の相対波動関数を用いて ρ(r) = ∫ dR|ψrel(R)|2 [ ρ1 ( r + A2 A1+ A2 R ) + ρ2 ( r− A1 A1+ A2 R )] (3.4.1) で与えられる。ここで各変数は（図 3.4）の通りであり、ψrel(R) は 2 クラスター間の相対 波動関数、A₁, A2はそれぞれクラスター 1, 2 の質量数である。位置 r における各クラス ターの密度を、相対密度の重みであらゆる相対位置で平均化したような直感的な式となっ ている。ハロー核のように、十分に重い粒子（core）と核子からなるような系にこの模型 を適用すると、（3.4.1）式で A₁ >> A2及び ρ2(r) = δ(r) としてよく知られた密度の表式 ρ(r) = ρc(r) +|ψrel(r)|2 (3.4.2) となることもわかる。しかし、このようにして求めた密度で光学極限近似をしようとする 場合、相対位置で平均化していることから断熱近似を破り、グラウバー模型の良い近似に なるとは考えにくい。 （図 3.5）は（3.4.1）式を用いて求めた6_{Li および}7 ΛLi の密度分布である。文献 [12] に よると、相互作用半径 R_I は密度がおよそ 0.05 fm−3になる長さであることが経験的に知 られているので、6_{Li と}7 ΛLi の相互作用半径は、それぞれ約 1.9 fm、約 2.0 fm であること がわかる。

図 3.4: 2 つのクラスターからなる原子核 0 0.05 0.1 0.15 0.2 0.25 0 1 2 3 4 5 6 ρ (R) (fm -3 ) R (fm) 6 Li 7 ΛLi 図 3.5: 6_{Li および}7 ΛLi の一体密度分布

23

第

4

章 グラウバー模型の適用

以上で反応断面積の計算に必要な道具立てができたので、グラウバー模型（の近似で ある少数系の方法）を具体的な系へ適用することを考える。（4.1）節では具体的な系とし て、まず6_Li+12_{C 系を考える。ラムダ粒子を含む系への応用は（4.2 節）で述べる。}

4.1

6

Li+

12

C

系への適用

6_Li+12_{C のような、2 体からなる入射核（}6_{Li = α + d）と 1 体からなる標的核の衝突問} 題（図 4.1）は、少数系の方法（FB）の中でも最も単純な問題である。(2.5 節) に従いこ の系に FB を適用すると、反応断面積は σR = 2π ∫ b db[1− |⟨ψrel|S1(b1)S2(b2)|ψrel⟩|2 ] (4.1.1) となる。ここで S_i(bi) は粒子 i と標的核との散乱行列であり、(2.5 節) の最後で述べた通 り、光学極限近似を適用する部分である。また、ψ は α と deuteron の内部波動関数（相 対運動の波動関数）であり、(3.1 節) で求めたものを用いる。散乱行列 Siには光学極限近 似を用いるので、各クラスターの密度が必要となる。今回の計算には各クラスターに対し ガウス型の分布 ρi(r) = Ai (√πγi)3 e−r2/γi2 _(4.1.2) を仮定したので S_iは解析的に求まり（付録 A.2）、 Si(b) = exp [ −σNN 2 ∫ ds ρ(z)_i (−b + s)ρ(z)_T (s) ] = exp [ −σNN 2 AiAT π(γ2 i + γT2) e−b2/(γi2+γT2) ] (4.1.3) である。ガウス関数の幅パラメータは（表 4.1）にまとめた。 反応断面積を求めるには、(4.1.1 式) を数値積分すればよい。散乱行列の期待値 S(b)≡ ⟨ψ|S1(b1)S2(b2)|ψ⟩ = ∫ dr|ψ(r)|2S1 ( b− A2 A1+ A2 r_⊥ ) S2 ( b + A1 A1+ A2 r_⊥ ) _(4.1.4) の数値計算には極座標表示を用い、θ, ϕ 積分はガウス-ルジャンドルの方法で行った。動 径積分および衝突係数 b 積分は上限を 15 fm ほどにすれば十分に収束した。

クラスター γ (fm) α 1.358 d 1.595 12_{C 1.894} Λ 1.419 表 4.1: （4.1.2）式で与えられるガウス型密度分布の幅パラメーター 12 : C T 12 ₌ A 4 : α A1= 2 : d A2= rr br 1 br b2 r ⊥ r r 図 4.1: 6_{Li と}12_{C の衝突}

4.2

ハイパー核への応用

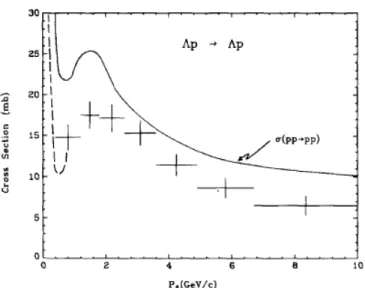
少数系の方法では、光学極限近似での散乱行列がわかれば反応断面積の計算ができるの で、そのような場合を考察すれば十分である。ここでは例として5 ΛHe と12C の衝突（図 4.2）を扱う。これまで取り扱ってきた核子だけからなる入射核の問題とは違い、ラムダ 粒子が混入するのでいくつかの修正が必要となる。それらは、 • 核子-核子散乱のプロファイル関数だけでなく、 ラムダ-核子散乱のプロファイル関数が必要となる • 核子とラムダ粒子の質量の違いによる入射エネルギーの違い などである。1 つ目の修正では、プロファイル関数 ΓΛN が入ってくるので散乱行列は変更 を受け、 S(b) = exp [ − ∫∫ drdr′ρα(r)ρT(r′)ΓNN(b + s− s′) − ∫∫ drdr′ρΛ(r)ρT(r′)ΓΛN(b + s− s′) ] (4.2.1)

4.2. ハイパー核への応用 25 C 12 He Λ 5 b r 図 4.2: 5 ΛHe と12C の衝突 となり、第 2 項がラムダ粒子が混入したことからくる寄与である。また、プロファイル関 数を核子-核子散乱に仮定したものと同様の形 ΓΛN(b) = 1 2σ (ΛN) tot δ(b) (4.2.2) に仮定すると、ラムダ-核子散乱の全断面積が必要となる。これについては実験値 [33] が あるので、（図 4.3）に示す。本研究では、核子あたりの入射エネルギーが 100 MeV でグ ラウバー模型を適用する。（図 4.3）は弾性散乱断面積であるが、このエネルギー領域では 核子-核子、ラムダ-核子散乱とも弾性散乱しか起こらず、 σtot= σel (4.2.3)

が成り立つ。2 つ目の修正を核子あたりのエネルギーが 100 MeV で行うと、E_{Λ≃ 118.8 MeV} （運動量にして pΛ = 514.9 MeV/c）なので、σΛN = 10∼20 mb 程度を計算に用いることに する。核子-核子散乱の全断面積 σNNの値としては、 σNN= σpp+ σpn 2 = 31.6 + 78.7 2 mb = 55.15 mb (4.2.4) を用いる [34]。 7 ΛLi+12C 系に少数系の方法を適用する場合は、（4.1.1）式における散乱行列 S1に（4.2.1） 式を用いればよい。

図 4.3: ラムダ-陽子の弾性散乱断面積の実験データ（点線及びエラーバー付きの点）。実 線は陽子-陽子の弾性散乱断面積である。横軸は実験室系でのラムダ粒子の運動量である。 文献 [33] より

27

第

5

章 結果と考察

5.1

入射エネルギー

ある一定の入射エネルギー以上（E >_{∼ 700 MeV）では、反応断面積 σ}Rは強いエネルギー 依存性を持たなくなり [19]、相互作用断面積 σ_Iと同様、原子核の大きさを表す良い物理 量となる（σI ≃ σR）。これをグラウバー模型の範疇で説明すると、反応断面積に対する 重要なインプットである核子-核子散乱の全断面積が、十分に高エネルギーならばほぼ一 定となるためである。 本研究では、ラムダ-核子散乱の全断面積の実験データが存在する、核子あたりのエネ ルギーが 100 MeV でグラウバー計算を行い、6_Li, 7 ΛLi の反応断面積を比較した。このエ ネルギー領域では、反応断面積から原子核の大きさそのものを直接引き出すことは難しい が、密度分布をインプットとするグラウバー模型を通じて間接的に情報を得ることができ る。このことは文献 [12] において、密度がおよそ 0.05 fm−3になる長さが相互作用半径を 表すことからもわかる。

5.2

反応断面積

第 4 章ではグラウバー模型の少数系の方法（FB）を具体的な系（6_Li+12_{C 系および} 7 ΛLi+12C 系）に適用した。この節ではその数値計算の結果を示す。結果は（表 5.1）お よび（図 5.1）にまとめられている。また（表 5.1）には、光学極限近似（OLA）による 計算結果も示す。 まず、相対運動の縮みによる反応断面積の減少を見るために σ_ΛN = 0 mb の計算を実行 した。6_{Li に対する反応断面積は σ} R = 825.9 mb であり、これがラムダ粒子の縮み効果に より σR = 781.6 mb と 45 mb ほど減少する。これは、各原子核を構成する 2 クラスター間 相対運動の平均二乗半径が、ラムダ粒子の混入により約 19% 縮むのに対し、反応断面積 が約 5% 減少することを意味する。次に、α クラスターへのラムダ粒子混入による反応断 面積の増加を見るために、現実的に考えられる σΛN = 10 ∼ 20 mb 程度を含め、非現実的 に大きい σΛN = 100 mb まで計算を行った。ラムダ-核子断面積が 10 mb 増加するごとに、 反応断面積は約 5 mb 増加することがわかる。また現実的には考えられないラムダ-核子断 面積 σΛN = 100 mb を用いない限り、一般的には6Li の反応断面積の方が7ΛLi の反応断面 積に比べて大きく出ることが期待できる。この計算は、ハイパー核の縮み効果が反応断面

σR(mb)（FB） σR(mb)（OLA） 6_{Li 825.9 880.6} 7 ΛLi(σΛN = 0 mb) 781.6 815.3 (10 mb) 786.7 819.9 (20 mb) 791.7 824.4 (30 mb) 796.5 828.8 (100 mb) 826.1 表 5.1: 少数系の方法（FB）と光学極限近似（OLA）による、12_{C を標的核とした}6_Li、 7 ΛLi の反応断面積。7ΛLi については σΛN の値を変えいくつかの計算を行った。 780 785 790 795 800 805 810 815 820 825 830 0 20 40 60 80 100 σR (mb) σ_ΛN (mb) 6_Li 7 ΛLi 図 5.1: 12_{C を標的核とした}6_{Li（点線）、}7 ΛLi（実線）の反応断面積。7ΛLi についてはラ ムダ-核子散乱の全断面積 σΛNに対する依存性を示す。現実的な σΛNの値は 10∼20 mb 程 度である。 積を通じて調べられること、及びグラウバー計算を通じてハイパー核の密度の情報を引き 出せることを示唆するものであり、今後の発展が期待される。 2 クラスターからなる原子核の密度の性質上、光学極限近似はグラウバー模型の良い近 似にならないことはこれまでに述べたとおりである。しかし（表 5.1）を見ると、定性的 な振る舞いは少数系の方法の場合と同様なことがわかる。そのため、計算の容易な光学極 限近似でおよその見積もりをすることが意味を持つことがわかる。

29

第

6

章 まとめと今後の課題

本研究では、高エネルギーでの原子核衝突に対するグラウバー模型を用い、6_{Li 及びハ} イパー核である7 ΛLi を入射核（入射エネルギー 100 MeV/A）とし、12C を標的核とする 衝突の反応断面積を評価した。序章および第 5 章で述べたとおり、この量は原子核の大 きさを引き出す可能性を与える。その結果、7 ΛLi については不定性が大きいが、ラムダ-核子散乱の全断面積 σΛNの、現実的に考えられる範囲で常に7ΛLi の反応断面積が6Li よ り小さく出ることが結論された。例えばインプットとなる σ_ΛNとして 10 mb を用いると、 7 ΛLi の反応断面積は σR(7ΛLi) = 786.7 mb となり、6Li に対する計算結果に比べて 40 mb ほど小さい。 これまでハイパー核の縮み効果は、ガンマ線分光によって調べられてきた。本論文で議 論したグラウバー模型を用いた反応断面積の方法はこれと相補的な方法であり、ハイパー 核の基底状態の情報のみが必要であることや、計算を通じてハイパー核の密度分布が引き 出せるなどの利点がある。現状では短寿命のハイパー核を用いた衝突実験はほとんど不可 能であるが、将来実験が可能になった場合には、本論文の方法がハイパー核の大きさに関 する研究で強力な方法になることが期待される。 将来の実験の発展に伴い、より定量的な計算が必要になる場合には、本論文で行ったグ ラウバー計算において例えば以下の 3 点について改良すればよい。 • 核子-核子散乱の全断面積の媒質効果を考慮する。 • ラムダ-核子散乱の全断面積のより詳しい情報を得る。（現在は、ラムダ-陽子散乱の 全断面積の実験値しか存在しない。） • 少数系の方法での原子核の扱い方を改善する。もしくは少数系の方法を超えた扱い や、グラウバー模型の範囲内で近似なしの計算をする。 核子-核子散乱の全断面積 σNNは、グラウバー計算において非常に重要なインプットであ る。本論文では、フリースペースでの σ_NNを反応断面積の計算に用いた。一般には、原 子核中において媒質効果が存在するので、なんらかの方法で考慮する必要がある。2 点目 については、現実的なラムダ-核子ポテンシャルを用いて散乱問題を解き、全断面積を得 ることが考えられる。また、核子-核子散乱の場合と同様に媒質効果も考える必要がある。 3 点目については、6_{Li 及び}7 ΛLi 核内の deuteron クラスターは弱く結合した陽子・中性子 からなるため、少数系の方法において 2 つの核子を別々に扱い、入射核を core + p + n の ような 3 体からなる核とすることが考えられる。また、少数系の方法と多重散乱を一部考

慮した NTG 近似を組み合わせた計算や、非常に複雑ではあるがグラウバー模型の範囲内 で近似なしの計算をすることが考えられる。

31

謝辞

本論文の作成にあたり、お世話になりました原子核理論研究室の皆様に感謝致します。 特に指導教官である萩野先生には、テーマの決定から研究の進め方、細かい計算や論文 を書く上での日本語の注意まで、幅広く御指導いただきました。また、スタッフや学生の 方々からはセミナーにおいて、有意義なコメントや質問を沢山いただきました。 最後に、精神面・経済面で支えてくれた家族に感謝します。

33

付 録

A

グラウバー模型

A.1

アイコナール近似での光学定理

ポテンシャル散乱の問題において、光学定理とは Im f (θ = 0) = k 4πσtot (A.1.1) のように、前方散乱の散乱振幅 f (θ = 0) の虚部と全断面積 σtotを結びつける関係式であ る。ここで k は入射粒子の波数の大きさである。一般にはフラックスの保存から導かれ る。アイコナール近似の場合でも光学定理が成り立つことを、アイコナール近似での散乱 振幅（（2.2.12）式） f (θ) = ik 2π ∫ db eiq·b(1− eiχ(b)) (A.1.2) を用いて示す。ただしここでは、ポテンシャルは実であり吸収は起こらないとして、全断 面積を求めるために弾性散乱断面積を計算する。 まず（A.1.1）式の左辺は、θ = 0 において q· b = 0 であるから Im f (θ = 0) = Im ik 2π ∫ db (1− eiχ(b)) = Im ik 2π ∫ db (1− Re [ eiχ(b)]− i Im [ eiχ(b)]) = k 2π ∫ db (1− Re [ eiχ(b)]) (A.1.3) である。（A.1.1）式の右辺の全断面積は σtot = σel = ∫ dΩ| f(θ) |2 = ∫ dΩ k 2 4π2 ∫∫ dbdb′eiq·(b−b′)(1− eiχ(b))(1− e−iχ(b′)) (A.1.4) から計算できるが、Ω 積分をはじめに実行する。この積分で実質的に考慮すべき部分は運 動量移行 q = k′_{− k 内の散乱後の波数 k}′のみなので、∫ dΩ eik′·(b−b′) を考える。ここで、

高エネルギーではほとんどの散乱が前方散乱であることを考慮し、単位球面上での面積分 を k′_x, k_y′ 平面の積分に置き換える近似 dΩ→ dk ′ xdk′y k′2 (A.1.5) をすると、 ∫ dΩ eik′·(b−b′) ≃ ∫ _dk′ xdky′ k′2 e ik′·(b−b′) ≃ 1 k2 ∫ dk_x′dk′_yeik′x(bx−b′x)+ik′y(by−b′y) = 1 k2(2π) 2 δ(2)(b− b′) (A.1.6) となる。2 つ目の等号では k′ _{≃ k であることから 1/k}2 _{を積分の前に出した。また 3 つ目} の等号ではデルタ関数の定義式を用いた。δ(2)_{は 2 次元のデルタ関数を表すものとする。} （A.1.4）式に（A.1.6）式を代入すると、 σtot = ∫∫

dbdb′e−ik·(b−b′)δ(2)(b− b′)(1− eiχ(b))(1− e−iχ(b′)) = ∫ db (1− eiχ(b))(1− e−iχ(b)) = 2 ∫ db (1− Re [ eiχ(b)]) (A.1.7) となり、（A.1.3）式と比較することにより光学定理が成り立つことがわかる。

A.2

ガウス分布での光学極限近似の散乱行列

光学極限近似において、zero-range のプロファイル関数 ΓNN(b) = 1 2σ (NN) tot δ(b) (A.2.1) を用いる場合、（2.4.18）式より原子核同士の衝突の散乱行列は Si(b) = exp [ −σNN 2 ∫ ds ρ(z)_i (−b + s)ρ(z)_T (s) ] (A.2.2) と表される。ここで入射核と標的核の密度分布をガウス型にとると、 ρ(r) = ρ(s, z) = A (√π γ)3 e −r2_/γ2 ρ(z)(s) = ∫ dz ρ(s, z) = A (√π γ)2e −(s2 x+s2y)/γ2 (A.2.3)

A.3. 光学極限近似での反応断面積 35 である。（A.2.3）式を（A.2.2）式に代入すると Si(b) = exp [ −σNN 2 AiAT π2_γ2 iγT2 ∫ ds e−γ21 (−b+s) 2₋1 γ2s 2] (A.2.4) となり、被積分関数の exponential の肩を − 1 γ2(−b + s) 2₋ 1 γ2s 2 ₌₋γ 2 i + γT2 γ2 iγT2 ( s− γ 2 T γ2 i + γT2 b )2 − 1 γ2 i + γT2 b2 (A.2.5) と変形するとガウス積分が実行でき、 Si(b) = exp [ −σNN 2 AiAT π(γ2 i + γT2) e−b2/(γi2+γ2T) ] (A.2.6) を得る。

A.3

光学極限近似での反応断面積

この節では、（5.2 節）で結果のみ示した 2 体クラスター模型における光学極限近似での 反応断面積の計算方法を紹介する。文献 [12] によると、グラウバー模型（光学極限近似） の計算では、反応断面積は密度のモデルに強く依存しない。そこで6_{Li の密度を作る際に、} 2 クラスター間相対運動の波動関数をガウス型にとることにより一体密度を作り、反応断 面積の計算に用いることにする。ただし正確な相対波動関数とガウス型とで、平均二乗半 径は一致させる。実際に我々の計算では、ガウス型の相対波動関数から求めた反応断面積 と、実際に Schr¨odinger 方程式を解いて求めた相対波動関数を用いた場合で、1% ほどの 違いしか出なかった。

A.3.1

一体密度

入射核（6_{Li）の一体密度は、（3.4 節）と同様な方法で作る。相対波動関数を} | Ψrel(R)|2 =  u(R)_R Y00( ˆR)  2 → 1 (√π γrel)3 e−R2/γrel2 (A.3.1) のようにとり、ガウス関数の幅パラメーター γrelを平均二乗半径が 4.342 fm（3.3 節）に なるよう調節したものを用いる。元の波動関数はノードを 1 つ持ち、ガウス型はノードを 持たない。（3.4.1）式に従い、 ρ(r) = ∫ dR|ψrel(R)|2[ρ1( r + c1R) + ρ2(r + c2R )] (A.3.2)