空間群のヒエラルキーと分類
ロレーヌ大学結晶学教室
ネスポロ マッシモ
Massimo NESPOLO: Hierarchy and Classification of
Space Groups
前回の記事1)でヘルマン・モーガン記号(国際記号) から対称性の導き方を説明した.結晶構造の対称操作 は全域操作と局所操作に分類される.前者は「群」とい う代数学概念を形成し,その群は「空間群」という.局 所操作も考慮すれば「亜群」というより一般の概念が必 要2)だが入門を超える内容なのでここでは省略する. 今回は空間群のヒエラルキーと分類を説明する.日常 的に利用される「晶系」というカテゴリーがあれば滅多 に出会わない「ブラべー群れ」などのようなカテゴリー もあるが簡単だと思われるものにも罠が隠れている. その罠を避けるために必要な理解を深めることを今回 の目的にする.以下で利用する定義と記号に関しては文 献1)を参照. 1.ヒエラルキーと分類図 1 はInternational Tables for Crystallography, Volume A (以下ITAと省略する)第6版第1章図1.3.4.1を拡張した ものである3)(ア:二次元空間;イ:三次元空間).二次
元の空間群は文様群か壁紙群(wallpaper groupの翻訳だ が英語では普通plane group)と呼ぶ.この図を日本語に 翻訳するに当たって問題が生じる.「晶系」と「空間群タ イプ 」はcrystal systemとspace-group typeに当て嵌まる がcrystal classは普通に「晶族」と翻訳されている.しか し,松本(1977)4)に説明があるように「晶族」という語
彙はcrystal familyを連想させるため英文のcrystal class の翻訳としては不適切である.したがって,本稿では松 本(1977)4)に基づきcrystal class を「結晶類」に訂正し, crystal familyを「結晶族」と呼ぶこととする*1.その他の カテゴリーは日本語になっていないようなので本稿では それらの翻訳を提唱する.近い将来に日本結晶学会に正 式な翻訳を決定するように希望している. 図 1 は左右2つの部分に分けられている.右の部分は 群(点群と空間群)のヒエラルキーを表示する.左の部 分は群の「類」,「系」,「族」への分類を表示する.この相 違を理解するために右には「モノ(object)」,左には「箱」 があると例えよう.あるモノ(object)をある基準によっ ていくつかの箱に分配する.別の基準を利用すると,別 の分配になる(箱の数も異なる). 強調のため,図1で「モノ(object)」は白色で,「箱」は 灰色で表示する.区分は下段のほうが細かく,上に行 くほど粗くなる.横の移動は「ある基準によってモノ (object)を箱に挿入する」という論理的な過程が行われ る.二重矢印(↕)は「モノ(object)」と「箱」の一対一 対応を示す.この関係が成り立っている場合でも「モノ (object)」と「箱」は同一の概念にならない.混乱を避け るためにできるだけ別の記号を採用するが,点群タイプ と幾何的結晶類のような例では同じ記号を利用する場 合もあるので注意すべき一点である. 2.群のヒエラルキー 対称操作は線型部分(行列W)と並進部分(ベクトル w)で表現する.結晶構造の周期性と互換性のある対称 操作を線型部分で分類すると二次元空間では6種類(1, 2,3,4,6,m), 三次元空間では10種類(1,2,3,4,6,1_,2_ ≡m,3_,4_,6_)がある.これらの行列Wのみで形成される 群は点群で,並進部分も含む操作(W,w)で形成される 群は空間群である.点群操作には並進部分は存在しない ため点群操作の表現はWのみである.図1の最右にある 操作の行列表現はこの違いを強調している. 2.1 群対群タイプ 連載企画 ヘルマン・モーガンの記号の解読では「空 間群」と「空間群タイプ」の相違を説明したが,*2点群に おいても同じ区別に注目する必要がある.二次元と三次 元空間ではそれぞれ10個と32個の点群が存在するとい う断言を頻繁に目にするが,実はこれらは点群タイプ (point-group types)である.対称要素の方位を考慮すれ ば「点」以外の幾何的要素(すなわち,「線」と「面」)に 無限の可能性があるので,1,2,3,4,6以外(二次元空間) *1 文献4)ではBravaisは「ブラーべス」と書かれているがフラン ス語の発音と合わないためここで「ブラべー」と訂正する. *2 著者によって,空間群タイプ,空間群型,空間群種という3 つの呼称が利用されている.
あるいは1と1_以外(三次元空間)の点群タイプには無限 個の点群が相当する.しかし,その中に特別な結晶学的 意味をもっている点群を同定することができる.最高の 位数の点群(二次元空間では4mmと6mm;三次元空間 では6/mmmとm3_m)を空間中に固定し,その可能な部 分群を考慮すれば全体的に二次元と三次元空間ではそ れぞれ21個と136個の点群を導くことができる.5)これ らを点群と呼ぶ.*3例えば,m3_mに3本の4回回転軸があ るが対称性の低下によって4/mmm点群タイプに相当す る3個の点群があり得る.単独で考えれば残存した4回 回転軸を正方のc軸と呼称するがそれは元のa,元のb, 元のc軸という3つの可能性があるので1個の点群タイ プに3個の点群が相当するという結論になる. さらに空間群の場合は同様な考察と同時に操作が原子 位置を関連付ける写像ということを考慮すると格子定数 も空間群の定義に含まれている.同じヘルマン・モーガン 記号でも無限の可能な格子定数があり得るので空間群の 数は無限である.1)結晶構造の格子定数を考慮せずに,対 称操作の種類を分類の基準とすると空間群タイプが得ら *3 厳密にいうと最高の位数の点群とその共役部分群のことであ るが共役という概念は今度の記事で紹介する予定なのでここ では省略する. 図 1 空間(文様)群タイプのヒエラルキーと分類.ITA第6版第1章図1.3.4.1を拡張したものである.3)(ア):文様群 (二次元空間).(イ):空間群(三次元空間). ソンケ 無限 第2種対称操作含有 第2種対称操作除外 無限 アフィン ビーベルバッハ ソンケ空間 (ア) (イ)
れる.二次元と三次元空間ではそれぞれ17個と230個の 空間群タイプが存在するが三次元空間ではそれらを結晶 空間群タイプ(crystallographic space-group type)という.
同様に,ブラベ ー 格子の定義に格子定数も含まれて いるのでその数は無限である.格子定数を考慮しない と5個(二次元空間)と14個(三次元空間)のブラベー 格子型が得られる.なお,格子型(lattice type)と格子系 (lattice system)の相違にも注意すべきである. 2.2 席対称群 空間中のすべてのx,y,z座標(原子位置)は各空間群 タイプでのワイコフ位置(Wyckoff position)に分類され る.各ワイコフ位置に空間群の対称操作で等価な無限個 の原子位置が属する.ITA3)では慣用単位胞内の原子位 置しか表示されず,その数は多重度(multiplicity)と呼称 するが,並進操作も適用すると同じワイコフ位置に属す る無限個の原子位置が得られる. 前述のように,対称操作は(W,w)という行列・ベクトル ペアで表現し,ベクトルwは位置に依存するwloc(location, 位置)と要素に平行な操作の並進wintr(intrinsic,本質)で 形成される.原子位置の席対称群(site-symmetry group)*4 はその位置を固定(不変に)する空間群の部分群であり, その対称操作はすべてwintr=0をもち,(W,wloc)で表現 する.一般ワイコフ位置に属する原子位置の席対称群は 恒等操作しか含まないが特殊ワイコフ位置に属する原子 位置の席対称群はそれ以外の操作も含む.P2221(17番, 図 2(ア))のワイコフ位置は表1に表示されている.2aの 特殊ワイコフ位置を分析してみよう.(x,0,0)位置を固 定(不変に)する対称操作は以下のとおりである. ( )I ; ( )II 1 0 0 0 1 0 0 0 1 0 0 0 1 x 0 0 = x 0 0 0 0 0 1 0 0 0 1 0 0 0 00 = x 0 0 x (I)は恒等操作,(II)はa軸に平行な2回回転操作で ある.(II)の対称要素は原点を通るので2x,0,0という 記号で表現する.この2つの操作の線型部分のみ取り出 すと点群操作を得るが並進部分(この場合はゼロ)も存 在するので,これは同型空間群(isomorphic)でもある. これらは位数2のP2221部分群を形成し,「席対称群」と いう.席対称群の操作は点群操作と同型なので席対称群 も2という点群と同型群(isomorphic group)である. 次に(x_,0,½)位置に上記の操作を適用すると以下の 結果となる. ( )I ; ( ) x x II 1 0 0 0 1 0 0 0 1 0 0 0 0 ½ 0 ½ 1 = 0 0 0 1 0 0 0 1 0 0 0 0 ½ 0 ½ = x x (II)の操作は(x_,0,½)を固定せずに(x_,0,½_)に関連 付けるのでこの操作は(x_,0,½)の席対称群に属さない. (x_,0,½)を固定する操作は以下のとおりである. ( )I ; ( ) x x II 1 0 0 0 1 0 0 0 1 0 0 0 0 ½ 0 ½ = 1 0 0 0 1 0 0 0 1 0 0 1 0 ½ 0 ½ = x x (I)は恒等操作,(II)は2回回転操作,その対称要素は z=½を通るので2 x,0,½という記号で表現する.この 2つの操作は(x,0,0)と別の席対称群を形成するが,こ れも2という点群と同型群である. 上記をまとめると下記の結論となる. (ア)席対称群は点群と同型の空間部分群である. (イ)同じワイコフ位置に属する原子位置の席対称群 は同型の操作で形成される.その対称要素は平 行であるが同一のものとは限らない.*5 *4 代数学では安定群(stabilizer)という. *5 厳密にいうと同じワイコフ位置に属する位置の席対称群は共 役群である.これに関しては今度の記事で詳しく説明する予 定である. (ア) (イ) 図 2 (ア)P2221と(イ)C2221空間群タイプのc軸に沿った 対称要素の投影(文献3)より,国際結晶学連合の 提供). 多重度 ワイコフレター 席対称群 座標
4 e 1 (x,y,z)(x_,y_,z+½)(x_,y,z_+½)(x,y_,z) 2 d .2. (½,y,¼)(½,y_,¾) 2 c .2. (0,y,¼)(0,y_,¾) 2 b 2.. (x,½,0)(x_,½,½) 2 a 2.. (x,0,0)(x_,0,½) 表 1 P2221(17番)空間群タイプのワイコフ位置.席対 称群と座標.
2.3 焦電群 焦電体(焦電効果を示す物質)は焦電群(pyroelectric groups)に結晶化する.焦電群は二次元と三次元空間 でそれぞれ 2個(1,m)と10 個(1,2,3,4,6,m,mm2,3m, 4mm,6mm)の点群タイプとそれに相当する4個と68個の 空間群タイプである.焦電群に1本以上の極方向(polar direction)が存在するため原点を対称性によって決定で きないものである.そのため,構造精密化に当たって1個 の原子での自由座標を固定しないと数多くの相関関係 (correlation)が現れる. 極線の存在によって焦電群はpolar groups(「極群」)と いう呼称も利用されている. 2.4 ビーベルバッハ空間群 特殊位置のない空間群タイプはビーベルバッハ群 (Bieberbach groups)という.一般位置に空間の次元と同 じ自由座標をもっているので一般位置しかない群は不動 点をもたない群(fixed-point free groups)またはねじれのな い群(torsion-free groups)とも呼ばれている.二次元と三 次元空間ではそれぞれ2個(p1,pg)と13個(P1,P21,Pc, Cc,P212121,Pca21,Pna21,P41,P43,P31,P32,P61,P65)の ビーベルバッハ空間群タイプが存在する. 2.5 キラル空間群,アキラル空間群,ソンケ空間群 連載企画 ヘルマン・モーガンの記号の解読では,対 掌性(chirality)の概念を紹介したが,結晶構造の対掌性 のみを解説した.実は,三次元空間群そのものも対掌性 の有無で区別できる.結晶構造は原子で形成され,その 原子を関連付ける第2種対称操作が存在するか否かに よって結晶構造がアキラルかキラルという2つのカテゴ リーに分類される.ここで,原子の場合と同様に空間中 の対称要素を考えてみよう.その対称要素を関連付ける 写像は空間群を超える正規化群の操作である.これらの 写像が第2種操作を含有するかによって空間群そのもの がアキラル(208タイプ)かキラル(22タイプ,11対)に 分類されている. 演習問題 1 キラルな空間群22タイプ(11対)を例示せよ. 構造の対掌性と群の対掌性の違いを強調する必要が ある.キラル結晶構造は第2種対称操作を含まない空間 群タイプに出現する.これらは二次元と三次元空間では それぞれ5個と65個であり,ソンケ群(Sohncke groups) という.三次元空間での22個のキラル空間群タイプは もちろんソンケ群であるが,ソンケ群はすべてキラルで はない.例えば,P42は第1種対称操作しか含まないので ソンケ群の1つではあるがキラル群ではない.なぜなら ば,左回転と右回転は同じ結果をもたらすからである. 文献でソンケ群をキラル群と呼ぶ誤りが頻繁に見られる ので注意すべきである.6) 2.6 アフィン空間群 キラル空間群の対は同じ性質をもち,螺旋操作の回転 方向で異なる.例えば,P31とP32のような空間群タイプ は同様な操作で形成されているが3回回転方向で区別で きる.その操作を適用するモノ(object)の左右性は逆にな るだけであるのでP31とP32の区別する重要性が乏しくな る.代数学者の視点を採用すれば群を抽象的に考えるの でキラル空間群の各対は1個の空間群タイプとして扱わ れる.三次元空間での11対のキラル空間群タイプを区別 しないなら219個(208アキラル+11キラル対)のアフィ ン空間群タイプ(affine space-group types)が得られる.
2.7 共型と非共型空間群 空間群は無限個の対称操作で形成されているため無限 群(位数が無限)である.一次元(「点」)以外の各幾何的 要素を無限個の対称操作が共有し,これらの操作の並進 部分で区別する.例えば,a軸に平行な2回回転(あるい は螺旋)操作は以下の行列・ベクトルペアで表現する. 1 0 0 0 1 0 0 0 1 p q r p,q,rは媒介変数なので無限の離散的並進を表示す る.表2はP222(17番)空間群タイプの場合の対称操作1 とそれに相当する幾何的要素を表示する.*6各幾何的要 素で無限の22n(nはゼロ以上の整数)操作が共存する.p =0の場合は操作は2(普通は2と省略)という2回回転0 操作なのに対してp>0の場合は22,24,26 などの2回螺 旋操作となる.全軸においても定義操作は回転操作なの で対称要素はすべて2回回転軸という. 一方,C2221(20番)空間群タイプの場合の(½,½,0) というC格子ベクトルも存在するので対称操作と対応す る幾何学的要素は表3のようになる.Cベクトルの存在に よって22nの操作とともに22n+1の操作が共存する.前者 の場合はP2221と同様にp=0だと操作は2(2回回転操 作),p>0だと操作は22,24,26 (2回螺旋操作)である のに対して後者の場合はpの値に関係なく,全操作は螺 旋操作(21,23,25 )である.したがって,前者の定義操 作は2回回転操作(p=0)なのに対して,後者の定義操 作は2回螺旋操作(p=½)という結果になる.C2221の 空間群タイプでa軸に平行な回転軸と螺旋軸が共存する がプライオリティの決まりに従って前者がヘルマン・ モーガン記号に現れる.b軸に関しては同じ結論になる が回転軸は原点を通らないのでr媒介変数は半整数であ る(図2).一方,両方の空間群タイプのc軸に平行な操 演習問題の解答はJ-Stageに付録として掲載してあります. *6 対称操作および幾何的要素に関しては,“連載企画 ヘルマ ン・モーガンの記号の解読”で説明した.
作はすべて螺旋操作であり,純粋な回転操作はないため 全対称要素は2回螺旋軸である. 上記の分析は共型(symmorphic)空間群タイプの定義 に必要である.以下の2つの条件を満たす空間群タイプ は共型という. 1.生成操作としてwintr=0をもっている操作を選ぶこ とができる; 2.生成操作の対称要素は共通の不変部分空間をもつ. この2つの条件の結果として,最小の多重度のワイコ フ位置の席対称群は点群と同型となる.17個(二次元空 間)と230個(三次元空間)結晶空間群タイプの中にそ れぞれ13個と73個の共型空間群タイプがある.P2221と C2221は2つの回転操作(aとbに平行なwintr=0操作) が生成操作として選択できるが,2番目の条件を満たさ ないので非共型(non-symmorphic)という.さらに,図2 に明らかなようにaに平行な2回回転軸はz=2n+½(n は整数)にある(z=0,±½,±1,±³/2など)のに対してb に平行な2回回転軸はz=2n+¼にある(z=±¼,±¾, ±5/4など)ので交点はない.正に,どちらの空間群タイ プにおいても最小の多重度のワイコフ位置の席対称性は 2..か.2.であり,aに平行な2回回転軸とbに平行な2回 回転軸の共通部分空間は存在しない. 逆に,P222(16番)とC222(21番)の場合は上記と同 じくaとbに平行な回転操作が生成操作として選ばれる が今度は交点があるためその交点は生成操作の共通部分 空間である.なお,cに平行な操作は生成操作の連続施 行で現れるが,生成操作の交点が存在するか否かによっ て回転操作か若しくは螺旋操作になる.P222とC222空 間群タイプの最小の多重度のワイコフ位置の席対称群 は222であり,点群と同型のものである.これこそ共型 空間群タイプの特徴である(これを考慮すると共型空間 群タイプは一般位置しかないビーベルバッハ空間群タ イプの正反対であることがわかる).222という席対称群 をもっているワイコフ位置は8個(P222)か4個(C222) 存在し,その1つが原点を含む. 222という点群に相当する空間群タイプがほかにも存 在する.単純(基本)格子をもっている空間群タイプだ けでも4つある:P222(共型),P2221,P21212とP212121 (ビーベルバッハ).最小の多重度(最高の位数の席対称 群 )の位置はそれぞれ1a,1b,1c,1d( 席対称群は222), 2a,2b,2c,2d(席対称群は2..あるいは.2.),2a,2b(席対 称群は..2)と4a(席対称群は1)である. 共型空間群タイプに関しては混乱が生じ,誤解を示す 定義が頻繁に見られる.7)特に多く見かける誤りは以下 のものである. ・「共型群に螺旋操作と映進操作は存在しない」.共型 空間群タイプのヘルマン・モーガン記号に点群記号が 見えることによって生じる誤解と思われる.対称操作 の行列・ベクトルペアにwintr=0という操作もあるが それ以外のものも無限個にあるので上記の断言は p1 (二次元空間)あるいはP1とP1_(三次元空間)にしか 当て嵌まらない.対称要素の定義操作はwintr=0に相 p q r 操作 幾何的要素 p q r 操作 幾何的要素 p q r 操作 幾何的要素 0 0 0 2 x,0,0 0 0 1 2 x,0,½ 0 1 0 2 x,½,0 1 0 0 22 x,0,0 1 0 1 22 x,0,½ 1 1 0 22 x,½,0 2 0 0 24 x,0,0 2 0 1 24 x,0,½ 2 1 0 24 x,½,0 .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. 0 1 1 2 x,½,½ 0 2 0 2 x,1,0 0 2 1 2 x,1,½ 1 1 1 22 x,½,½ 1 2 0 22 x,1,0 1 2 1 22 x,1,½ 2 1 1 24 x,½,½ 2 2 0 24 x,1,0 2 2 1 24 x,1,½ .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. p q r 操作 幾何的要素 p q r 操作 幾何的要素 p q r 操作 幾何的要素 0 0 0 2 x,0,0 ½ ½ 0 21 x,¼,0 0 0 1 2 x,0,½ 1 0 0 22 x,0,0 ³/2 ½ 0 23 x,¼,0 1 0 1 22 x,0,½ 2 0 0 24 x,0,0 5/2 ½ 0 25 x,¼,0 2 0 1 24 x,0,½ .. .. .. .. .. .. .. .. .. .. ½ ½ 1 21 x,¼,½ 0 1 0 2 x,½,0 ½ ³/2 0 21 x,¾,0 ³/2 ½ 1 23 x,¼,½ 1 1 0 22 x,½,0 ³/2 ³/2 0 23 x,¾,0 5/2 ½ 1 2 5 x,¼,½ 2 1 0 24 x,½,0 5/2 ³/2 0 25 x,¾,0 .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. 0 1 1 2 x,½,½ ½ ³/2 1 2 x,¾,½ 0 2 0 2 x,1,0 1 1 1 22 x,½,½ ³/2 ³/2 1 22 x,¾,½ 1 2 0 22 x,1,0 2 1 1 24 x,½,½ 5/2 ³/2 1 24 x,¾,½ 2 2 0 24 x,1,0 .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. 表 2 P2221(17番)空間群タイプの対称操作と幾何的要素 表 3 C2221(20番)空間群タイプの対称操作と幾何的要素
当するものので空間群タイプ記号に点群記号が現れ るが言うまでもなく同じ軸(幾何的要素)を回転操作 と螺旋操作が共有し,また同じ面(幾何的要素)を鏡 映操作と映進面が共有する.例えば,P4mmという共 型空間群タイプを分析しよう.00z軸と½½z軸(幾何 的要素)に4,44,48,412 .などの無限の操作があるが最 短並進部分はゼロなので定義操作は4である.0½zと ½0z軸の場合は2,22,24,26 .などの無限の操作がある が最短並進部分はゼロなので定義操作は2である.よ り高い位数の操作が空間群の記号に現れるので[001] 方向の記号に4回回転軸が選択される.また,{100}面 に鏡映操作があるが,p,q,r媒介変数の値によって無 限のg映進操作が同じ幾何的要素を共有する.定義操 作としてmが選ばれるので対称要素はmと定義され るが決して映進操作がない訳ではない.{110}に関し ては同じ結果になる.しかし,この場合はm(x,x,z)と m(x,x_,z)のほかに純粋なg映進面(x±½,x,z)も存在 するがヘルマン・モーガン記号に前者が優先されるの で空間群タイプの記号はP4mmとなる. ・「共型群ですべての対称操作が原点を通る」.空間群タ イプは周期のある結晶構造の群なので無限の対称操作 と対称要素があるがすべて原点を通ることはあり得な いし,もしそうなら空間群ではなく点群になる! この 誤解の原因はおそらく無限の対称操作の中でp=q= r=0という操作しか考えていないことにあると思わ れる. 2.7.1 非共型空間群の区分 非共型空間群タイプはフェドロフ8)によってさらに 2種類に区分されている.同じ点群と同じ格子型に相当 する空間群タイプ(すなわち,同じ代数的結晶類;下記 を参照)は1つ以上存在し,その中の1つは共型であり, それ以外は非共型である.ここで最高の位数の席対称群 Sを考慮しよう.非共型空間群タイプの席対称群をS非 と指定し,その位数をn非と書く.同様に共型空間群タ イプの場合はS共とn共と書く.n非はn共の除数であるが, 特にn非=n共/2の場合に注目しよう. ・S共は第2種対称操作を含むがS非は第2種対称操作を 含まない場合はその非共型空間群タイプを半共型空間 群タイプ(hemisymmorphic space-group types)と呼ぶ. ・その他の非共型空間群タイプを異共型空間群タイプ
(asymmorphic space-group types)と呼ぶ.
例.Pmmmは共型空間群タイプである.S共はmmmで, 第2種対称操作を含む.その位数はn共=8.同じ点群に 相当し,単純(基本)慣用単位胞をもっている空間群タ イプはほかに15個あり,すべて非共型である.そのうち n非=4で,S非=222(第2種対称操作を含まない)という 条件を満たすのは3個ある:Pnnn,PccmおよびPban.こ れらはフェドロフの定義に従って半共型空間群タイプと 呼ぶ.残りの12個は異共型空間群タイプである. フェドロフの分類では,空間群タイプは3種類(共型, 半共型,異共型)に分けることができる.その相違点は結 晶模様(crystal pattern)として観察できるので大切であ 図 3 共型,半共型,異共型空間群タイプの結晶模様の例.(ア)mmm点群ステレオ投影.左:対称要素.右:一般形態. (イ)Pmmm共型空間群タイプの一般位置.原点の周りのアキラル多面体は形態のステレオ投影に酷似している. (ウ)Pnnn半共型空間群タイプの一般位置.(イ)の多面体は2つのキラル多面体に分けられた.(エ)Pmna異型空 間群タイプの一般位置.(イ)の多面体は2つのアキラル多面体に分けられた.(オ)Pcca異型空間群タイプの一 般位置.(イ)の多面体は4つの多面体に分けられた(文献7)よりreproduced with permission.).(VESTAで作成9))
る.共型群に点群と同型の席対称群が存在するためその 位置の周りに一般形態の双対多面体が形成される.非ソ ンケ群の場合は席対称群の対称操作は半分が第1種,残 りは第2種であるので多面体の原子に左右性を当て嵌め ると半分は「左」,残りは「右」と呼称する(International Tables for Crystallographyでコンマあり・コンマなしで区 別される).非共型群ではその多面体は2つ以上に分け られてしまう.半共型群の場合は2つになり,これの部 分多面体は第2種対称操作に関連付けられているのでキ ラル多面体である.異共型群の場合はそれ以上の多面体 の数になる(席対称群の位数がさらに低下する場合)か アキラル多面体になる.図3は具体的な例を示す.(ア) mmm点群のステレオ投影.左:対称要素.右:一般形態 の斜方両錐体のステレオ極.(イ)Pmmm共型空間群タイ プの一般位置.mmmという席対称性をもつ原点の周り に8個の原子が斜方両錐体の双対多面体を形成する.こ の多面体を形成する原子の左右性を色で区別すると半 分は白,残りの半分は黒となる.(ウ)Pnnn半共型空間群 タイプの一般位置.222の席対称性をもつ原点の周りに 4個の原子(黒)が斜方両榍体を形成する.また,単位胞 の中心の周りに同じ多面体(白)が形成されるがこの2 つの多面体は第2種対称操作(色,すなわち左右性を変 更する操作)で関連付けられている.(エ).Pmna異共型 空間群タイプの一般位置.原点の席対称性は.2/m.であ る.半共型群に比べて席対称群の位数は同じなのでこの 場合でも元(共型群)の多面体は2つに分けられるがそ れぞれ白原子も黒原子も存在する.(オ).Pcca異共型空 間群タイプの一般位置.原点の席対称性は 1_である.元 (共型群)の多面体は4つに分けられる. 3.群の分類 これまでの分析で群のヒエラルキー(種類)を説明し た.これからは群の分類を説明する.上記の例えを再利 用すると「モノ(object)」から「箱」に移る.図4は4_2m という点群タイプを共通する空間群タイプの結晶類への 分類を示す. 3.1 代数的結晶類
代数的結晶類(arithmetic crystal class)は最も詳細な分 類である.同じ点群タイプと同じ格子型をもつ結晶構造 や空間群タイプは同一の代数的結晶類に属する.*7代数 的結晶類は共型空間群タイプと一対一対応である.混乱 を避けるために,代数的結晶類の記号に格子型の記号は 点群の記号の後ろに記載する. 例 え ば,P2/m,P21/m,P2/c お よ び P21/c と い う 4 つ の空間群タイプは同じ点群タイプ(2/m)と同じ格子型 (mP:単斜基本格子)をもつため2/mPという代数的結晶 類に分類する.この記号で共型空間群タイプのP2/mと 混乱することはない.また,C2/mおよびC2/cという2つ の空間群タイプは同じ点群タイプ(2/m)と同じ格子型 (mC:単斜底心格子)をもつため2/mCという代数的結 晶類に分類する.点群が同じであっても格子型は異なる ため別の代数的結晶類に分類される.代数的結晶類の数 は共型空間群タイプの数と同じ,二次元と三次元空間 ではそれぞれ13個と73個である. 演習問題 2 三次元空間の代数学的結晶類73個を記載 してみよう. 3.2 高調的結晶類
高調的結晶類(harmonic crystal classes)は現在は International Tables for Crystallography3)に採用されていな
いがSouvignier10)によって提唱されたものである.同じ 格子型と同じ点群タイプあるいは空間中での対称要素 の方向だけで異なる点群タイプという空間群タイプは 同じ高調的結晶類に分類される.例えば,P4_2mとP4_m2 の空間群タイプは同じ正方基本格子をもち,4_2mと4_2m という点群で異なるが前者を[001]方向で45度を回転 すれば後者に変換する.従って,上記の空間群タイプは 4_2mPという高調的結晶類に分類される.高調的結晶類 の記号は代数的結晶類と同じだがその数は二次元と三 次元空間ではそれぞれ12個と66個に低下する. 演習問題 3 三次元空間の高調的結晶類66個を記載し てみよう. 3.3 ブラベー類 格子の点群タイプに相当する5個(二次元空間)と14個 (三次元空間)の代数的結晶類があり,それらはブラベー 演習問題の解答はJ-Stageに付録として掲載してあります. *7 文献1)で説明したように,厳密にいうと「単純」,「底心」,「体 心」などの「格子型」は「その格子の慣用単位胞」の省略した 表現である. 図 4 空間群タイプの結晶類への分類の例.4_2mという 点群に相当する12個空間群タイプは4つの代数的 結晶類と2つの高調結晶類に分類される.幾何的 結晶類は点群と一対一対応するので12個の空間 群タイプはすべて同一の幾何的結晶類に属する.
類(Bravais classes)と呼ぶ.二次元空間では2p,2mmp, 2mmc,4mmpおよび6mmpで,三次元空間では1_P,2/mP, 2/mC,mmmP,mmmC,mmmI,mmmF,4/mmmP,4/mmmI, 3 _ mR,6/mmmP,m3_mP,m3_mI,m3_mFと表示される. 3.4 幾何的結晶類 同じ点群タイプをもつ結晶や空間群タイプが同一の幾 何的結晶類(geometric crystal class)に属する.同じ点群 タイプをもつ空間群タイプ,あるいは結晶構造(「モノ (object)」)を同一の幾何的結晶類(「箱」)に挿入し,そ の結晶類にラベルを貼る.分配の基準は「共通の点群タ イプ」なのでその点群をラベルとして利用するのは論理 的だろう.したがって,幾何的結晶類は点群と同じヘル マン・モーガン記号で同定されるが決して点群と同じ ものではない.二次元と三次元空間ではそれぞれ 10個 と32個幾何的結晶類があり,後者は1830年(天保1年) にヨハン・フリードリヒ・クリスチャン・エセル11)に よって最初に同定されたものである.幾何的結晶類はさ らに分類されている. ・中心対称(centrosymmetric)の11個の点群タイプと その非中心対称部分群は11個のラウエ結晶類(Laue class)を定義する.*8吸収が弱く,フリーデル則が有効 な場合はエックス線回折で同じラウエクラスに属する 点群タイプを区別できない. ・格子の完全対称性を示す点群は完面像(holohedry)と いう幾何的結晶類を同定し,それ以外の点群は上記 の部分群であり,欠面像(merohedry)という幾何的結 晶類を同定する.二次元と三次元空間ではそれぞれ 4個と7個の完面像がある(表4). 3.5 晶系 晶系(crystal system)に関しては文献に矛盾する複数 の定義があり,そのために混乱しやすい概念と言っても 過言ではないだろう.ITA3)に以下の定義が採用されて いる. 図 1 に示したように晶系は幾何的結晶類の分類であ る.そして,幾何的結晶類は点群の分類である(当然だ が同じ点群タイプに相当する空間群タイプや結晶構造 の分類でもある).同じブラベー格子型に作用する完面 像と欠面像は同一の晶系を形成する.例えば,cP,cF,cI という3つのブラベー格子型に作用する点群は23,m3_, 432,4_3m,m3_mである.m3_mは完面象で,その他はすべ て欠面像である.この5つの幾何的結晶類は立方晶系を 形成するのでこの5つの幾何的結晶類に属する空間群タ イプや結晶構造も立方晶系に属する. 一般 化すると,PとP'は点群であり,PはP'の部分 群とする.P'が作用するブラベ ー 格子型にPも作用す るが逆のことは必ずしも成り立たない. 例えば,3_m は6/m2/m2/mの部分群である.後者は六方格子型に作 用するので前者も同じ格子型に作用する.しかし,前 者は菱形格子型にも作用するが後者はそれに作用し ない.したが っ て,3_mとその部分群(3m,32,3_,3)は 同一の晶系( 三方,trigonal)に分類され,その他の群 (6,6_,622,6mm,62m,6/m,6/m2/m2/m)は別の晶系(六方, hexagonal)に分類される. 晶系という名はブラベー時代の前から存在し,ヨハン・ ヤーコブ・ベルンハルディが1808年(文化5年)に導入した もの12)だが実は現代の結晶族(crystal family)に相当す る.その後,1815年(文化12年)にクリスチャン・サミュ エル・ワイス13)は「結晶軸」という名前で結晶成長方向 の概念を導入した上で,結晶面と結晶軸の関係を基準 にし,結晶を分類した結果を「Krystallisationssysteme」と 呼称した.すべての結晶に直交基底を適用したためまず は結晶面の軸への切片によって4つのカテゴリーを導入 し,そして可能な形態が出現するかによって7つの晶系 に分けた.単斜晶系と三斜晶系を直方(斜方)晶系の欠 面象,また三方晶系を六方晶系の欠面象と不適切な解釈 したにもかかわらずワイスの分類は最高位数の回転操作 *8 二次元空間で反転操作は存在しないのでこの概念は当て嵌 まらない. 二次元空間 三次元空間 完面象 欠面象 完面象 欠面象 ラウエ結晶類 同じラウエ結晶類に属する非中心対称点群タイプ 2 1 1 _ 1 1_ 1 2/m 2,m 2/m 2,m 2mm m mmm 222,mmm mmm 222,mmm 4mm 4 4/mmm 4/m,422,4mm, 4_2m,44_,4 4/m 4,44 _ 4/mmm 422,4mm,44_2m 6mm 6,3m,3 3 _ m 3_,32,3m,3 33 _ 3 3_m 32,3m 6/mmm 6/m,622,6mm,6_2m,66_,6 6/m 6,6 _ 6/mmm 622,6mm,6_2m m3_m m3_,4_3m,432,23 m3 _ 23 m3_m 44_3m,432 表 4 幾何的結晶類の完面象,欠面象とラウエ類への分類.
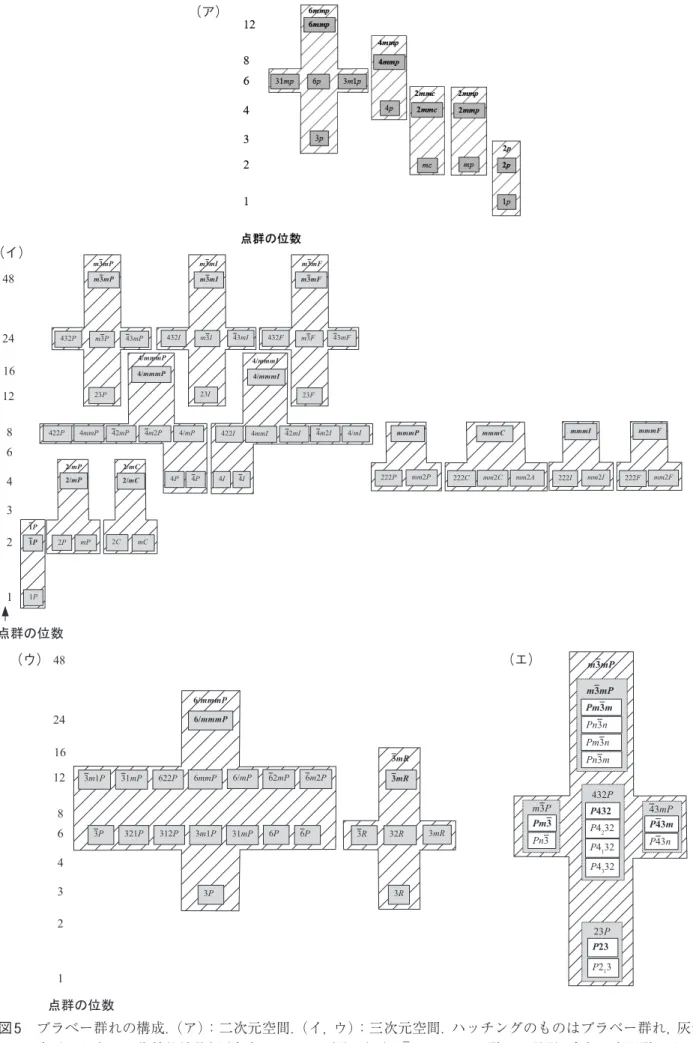
と矛盾のない結果となっている.後者は現代の晶系の定 義とも矛盾しないので晶系の概念はワイスに遡ると言え るだろう(表5). 3.6 格子系 格子系(lattice system)は格子の対称性によって定義 される.完面像と格子系は一対一対応となる. 二次元空間では晶系と格子型は一対一対応するが三 次元以上の場合はこの対応は成り立たなくなる. 三次元空間では三方晶系(trigonal)は3_mおよびその 部分群に相当する幾何的結晶類を内包する.しかし, これらの点群タイプは菱形格子にも六方格子にも作用 するため,三方晶系は2つの格子型に対応する: 菱形 (rhombohedral)と六方(hexagonal).文献に数多くの誤 りが次々に出てしまうのでここに注意すべき箇所があ る.「三方」は晶系を同定するので「三方格子」というも のは存在しないが文献によく現れる.同様に,「菱形」は 格子型を同定するので「菱形晶系」というものは存在し ないが文献によく現れる.このような混乱の原因は結晶 学の歴史にある. 結晶学は鉱物学から発展し,十九世紀に活発な研究 分野になった.この分野で特にフランスとドイツが重大 な貢献をしたが前者は格子による分類を重視し,後者は 形態による分類を優先した.その分類の結果はそれぞれ 現代の「格子系」と「晶系」に相当する.ところが当時両 方とも「晶系」と呼ばれていた(仏:système cristallin, 独:kristallsystem)ので混乱が生じ,その混乱は現在に 至る.特に三方と菱形は類語といまだに思う人が多いよ うである.フランスではtrigonal(三方)という語彙は英 語系,rhombohedral(菱形,仏語ではrhombohédrique)と いう語彙は仏語系と思い,前者を拒否する人が多い.実 は前者は古代ギリシャ語の「τρίγωνον(trígōnon 三角)」 から,後者はラテン語の「rhombus(菱形)」*9から生ま れた言葉である.上記の排外主義は結晶学と言語学の両 方の無知の証であろう. 3.7 結晶族 結晶族(crystal family)は一番粗い分類である.同じ値 の自由(対称性で制限されない)格子定数および同じ点 群が作用する空間群タイプは同一結晶族に属する. 例.2つの自由格子定数をもっている空間群タイプは 正方晶系,三方晶系および六方晶系で,それぞれの完面 像は4/mmm,3_m,6/mmmである.4/mmmは正方晶系の 空間群タイプにしか適用できないためこれらの空間群タ イプは正方結晶族に属する.しかし,3_mの対称操作は三 方晶系の空間群タイプにも六方晶系の空間群タイプにも 適用できるのでこれらの空間群タイプは同一の結晶族に 属する.3_mは6/mmmの部分群であるため,この結晶族 は六方結晶族という. 結晶族において複数の晶系を内包することは意外と 思われるかもしれない.二次元空間ではその例はない. 三次元空間の場合,六方結晶族は唯一の例である.しか し,空間の次元が上がるにつれてこの結果は一般であ る.14)すなわち,われわれが最も利用する空間の次元が 限られているため例外的な例が普通に見え,逆に普通の 状態が例外に見えている. 3.8 ブラベー群れ ブラベ ー 群れ(Bravais flock)はおそらく最も馴染み のない概念であろう.本稿では空間群タイプを「 モノ (object)」,代数的結晶類を「箱」に例えた.このイメージ を拡張するとブラべー群れを「箱の箱」に例えられる.同 じ点群タイプと同じ格子型をもつ空間群タイプを同一の 「箱」に挿入し,その箱を代数的結晶類と呼ぶ.「箱」のラ ベルとしてその類に属する共型空間群タイプの記号を取 り出し,格子型と点群の記号を逆にする.得られた代数 的結晶類の内5個(二次元空間)か14個(三次元空間)が ブラべー類である.同じブラべー類に相当する代数的結 晶類を同一の「箱の箱」に挿入し,それをブラべー群れ と呼ぶ.図5は二次元(ア)と三次元(イ,ウ)のブラベー 群れを表示する.ハッチングのものはブラベー群れ,灰 色で表示したものは代数的結晶類,である.図5(エ)で は1つのブラベー群れ(m3_mP)について説明する. ・白色で表示したのは空間群タイプである(モノ(object)). 太字で示したのは共型空間群タイプである. ・灰色で表示したのは代数的結晶類である(箱).記号は 共型空間群と同じものであるが区物のため慣用単位胞 の記号は最後にくる.太字で示したのはブラべー類で ある. ・ハッチングで表示したのはブラベー群れである(箱の 箱).記号はブラべー類と同じ. ブラベー群れはブラべー類と一対一対応のもので,ITA 第5版までは空間群タイプのヒエラルキーに明示的に利 用されていた概念(図8.2.1.1参照)が第6版(図1.3.4.1参 照)にはブラベー類が優先されている.その理由は英語 名のflockにあるようである.英語ではflockは普通鳥や 哺乳類の群れを意味し,代数的な概念を表すのに不適切 *9 実はこれの語源も古代ギリシャ語の「ῥóμβος(rhómbos)」に ある. 最高位数の回転操作 ITAによる晶系 1 三斜 2(単独) 単斜 2(3つ) 直方(斜方) 4 正方 3(単独) 三方 6 六方 3(3つ) 立方 表 5 回転操作に基づく分類およびITAによる晶系の比較.
図 5 ブラべー群れの構成.(ア):二次元空間.(イ,ウ):三次元空間.ハッチングのものはブラベー群れ,灰色で 表示したものは代数的結晶類(太字:ブラべー類).(エ)m3_mPブラべー群れの説明.白色:空間群タイプ(太 字:共型空間群タイプ).灰色:代数的結晶類(太字:ブラべー類).ハッチング:ブラベー群れ. (ア) (イ) (ウ) (エ)
という批判の声がある.ドイツ系の結晶学者に導入され た語彙だが英語系の学者には強い抵抗を受けているため 最新のITAでは目立たないように利用されている. 4.対称性による格子定数の制限 上記に説明したように晶系の定義に混乱が生じてい る.そのため,教科書に掲載されている晶系とそれに相 当する格子定数の制限には,誤りを含む場合が多い.そ の制限は一方では厳し過ぎて,他方では緩すぎる訳であ る.15)構造の対称性は格子定数に制限を課すが,構造の 非対称性は制限を課すことはない.これは当然だろうと 思われるかもしれないが実はこのような当たり前の事実 はほとんどの教科書で見逃されている. 単斜の結晶を考えよう.単斜晶系に属する結晶は1本 の対称方向をもっているためその方向は結晶軸の1つと される(普段b軸として選択されるがそれはあくまでも 決まりに過ぎない).この軸に垂直な結晶面が存在する が軸がbとされると結晶面は(010)というミラー指数 で表示される.その面内に対称方向はないので残りの2 本の軸(a軸とc軸)はある程度自由に選んでも構わない が,普通はできるだけその角度(β)は90度と120度の間 で好まれる.a軸とc軸をどう選んでも(010)面である限 りb軸に垂直なので単斜晶系の慣用単位胞は90度角度 (αとγ)を2つもっている.それ以外の格子定数は対称 性によって制限されないため自由変数となっている.し たがって,単斜晶系の場合は構造の対称性による格子定 数の制限はα=γ=90度のみである.*10その他の4つの 格子定数は制限されていないので自由変数は 4個ある. ほかの晶系にも同様な対称性による制限を適用すると 表 6 という結果になる. しかし,ほとんどの教科書に不要な制限が表示されて いる.例えば,上記の単斜晶系の例の場合は,a≠b≠c, β≠90°という制限も示されている.これは根本的な誤解 から生じる誤りである.β角度は対称性に制限されてい ないためどの値でも可能なので90度もその1つである. ある温度・圧力の範囲でβ=90度になっても,決して晶 系は直方(斜方)になる訳ではない.同様に,線型定数は 対称性に制限されていないためどの値でも可能で,ある 温度・圧力の範囲でその2つが(あるいは3つでも)同じ になっても(実験の誤差を考慮した上で)決して晶系が 上昇した訳ではない. 上記の制限は構造ではなく,純粋な幾何学概念である 「格子」にかかわる解釈も成り立たない.まずは格子の みの分類に集中するなら晶系が構造の対称性を反映す るのでそこに表示すると矛盾する.次に格子の対称性に よる制限は上記の条件は不充分である.単斜の例を再び 考えよう.直方(斜方)の格子に昇格されないためには a≠b≠c,β≠90°という制限では足りない. ・単純単位胞(mP)で,β=cos–1(a/2c)なら直方(斜方) のB底心単位胞を選択できるので格子は実際に直方 *10 対称方向がa軸あるいはc軸として選ばれた場合は対称性に 制限される角度はそれぞれβとγおよびαとβとなる. 結晶族(*) 制限ある格子定数(慣用単位胞) 自由格子定数の数 晶系 格子系 ブラベー格子型(**) a=anortic 三斜 (triclinic,asymmetric, tetartoprismaticなど) なし 6 Triclinic 三斜 Triclinic三斜 aP m=monoclinic単斜 (clinorhombic,monosymmetric, binary hemiprismatic, monoclinoedricなど)
α=γ=90° 4 Monoclinic単斜 Monoclinic単斜 mC,mA,mI,mF)mP(mB),mS(≡
o=orthorhombic直方(斜方) (rhombic,trimetric,terbinary, prismatic,anisometricなど) α=β=γ=90° 3 Orthorhombic 直方(斜方) Orthorhombic直方(斜方) oP,oS,oI,oF t=tetragonal正方 (quadratic,dimetric, monodimetric,quaternaryなど) a=b
α=β=γ=90° 2 Tetragonal正方 Tetragonal正方 tP(tC),tI(tF)
h=hexagonal六方 (senary,monotrimetricなど) a=b α=β=90° γ=120° 2 Trigonal (ternaryなど)(***) 三方 Rhombohedral 菱形 hR Hexagonal 六方 hP Hexagonal 六方 c=cubic立方 (isometric(等長),monometric, triquaternary,regular,tesseral, tessural...) a=b=c
α=β=γ=90° 1 Cubic立方 Cubic立方 cP,cI,cF (*)()で類語.(**)S=底心単位胞のこと.()で等しい格子型が表示されている.
(***)三方晶系の結晶格子は菱形または六方である.
(斜方)である. ・体心(mI)単位胞の場合は複数の条件を考慮しなけれ ばならない: ・β=cos–1(a/c)の場合は直方(斜方)のC底心単位胞 を選択できる. ・a2+ b2= c2お よ び a2+ accosβ = b2あ る い は b2+ accosβ=a2の場合は格子は菱形の対称性を待つ. ・c2+3b2=9a2およびc=3acosβあるいはa2+3b2= 9c2およびa=3ccosβの場合は,格子はまた菱形の 対称性を待つ. 上記の例が示すように,格子のみの対称性による制限 は数多くある(ITA 第6版第3章表3.1.4.1を参照3)).教 科書に載っている格子定数の制限は構造の対称性によ るものと解釈すれば不要なものもあり,格子の対称性に よるものとすれば不充分である.どちらにせよ不適切で ある. 5.議 論 これまでの分析では格子定数の特殊な関係(metric specialization)を考慮しなかった.その特殊な関係が存 在する場合に格子の対称性が上昇する. 特殊な関係は2つ以上の自由格子定数をもっている空 間群に存在する.二次元空間では単斜晶系および直方 (斜方)晶系に属する空間群のみである(正方晶系と六方 晶系の場合は1つの自由線型格子定数しかない).三次 元空間では立方以外の晶系に属する空間群はこの条件 を満たすので特殊な関係はあり得る.しかし,六方晶系 の場合には格子定数の特殊な関係は影響を及ぼさない. なぜなら,6/mmmは最大完面像の1つである(当然なが らもう1つはm3_mである)ため,c=aになっても格子の 対称性が上がらない.それ以下の晶系の場合は影響が見 られる. 例1.R3cでα=90度,60度,若しくは109.47度なら 格子の対称性はm3_m(立方)である. 例2.P2でβ=90度の場合は格子の対称性はmmm (直方(斜方))である. 例3.Pccmでa=bの場合は格子の対称性は4/mmm (正方)である. これらのような格子定数の特殊な関係は対称性による ものではないので相転移がなくても温度・圧力・電場な どの変更によって破れてしまう.しかし,測定条件の範 囲でこの格子定数の特殊な関係が実現されれば格子の 対称性は構造の対称性より高くなる.測定データから空 間群を決定するに当た っ て晶系を誤解し,構造解析が 困難になる場合がある.また,この格子定数の特殊な関 係があるからこそ双晶がでやすい.16) 格子の対称性が上昇したことによって試料はより高い 格子系に属すると誤想するおそれがある.ブラベー格子 は結晶の点群が不変にする計量テンソルの空間で決定す る.この空間には無限個の計量テンソルが存在し(格子 定数に無限の可能性があるから),その中に格子定数の 特殊な関係のため,より高い対称性をもっている計量テ ンソルもある.しかし,空間全体に同じ点群が作用する のでこれらの計量テンソルはすべて同じ格子型に属す る.例えば,P4mmという空間群タイプを考慮する.この 対称性をもつ結晶の計量テンソルは以下の形がある. a a c 0 0 0 0 0 0 この計量テンソルを不変にする点群は4/mmmなので 格子系は正方である.aとcに無限の値があり得るので上 記のものは1個の計量テンソルではなく無限個の計量テ ンソルの代表である.これらは計量テンソルの空間を定 義する.その中で,格子の特殊な関係c=aをもっている 計量テンソルもその空間の1つであるのでそれも正方格 子系に属する.立方格子系に属するのは対称性によって c=aと制限されるものなので立方の対称性を示してい る計量テンソル空間の全テンソルの場合のみである.格 子の対称性の上昇は空間群タイプに見られず空間群にの み影響があるという結論になる. 本稿で紹介したヒエラルキーと分類は格子定数の特 殊な関係に依存しないので空間(文様)群ではなく,空 間(文様)群タイプに提供する.図1で空間(文様)群か ら空間(文様)群タイプへの三角形の矢印は「格子定数 の特殊な関係を考慮しない」を意味する. 今 後 次回の連載企画の記事はミラー指数と消滅則との関 係を紹介する予定である. 謝 辞 ラドバウド大学ナイメーヘンのBernd Souvignier博士 との有義な議論,国際結晶学連合(図2の提供)とWiley 出版社(図3の再利用許可)に感謝する. 文 献 1) ネスポロ マッシモ:ヘルマン・モーガン記号の解読,日本 結晶学会誌 58, 251(2016). 2) 定永両一:“結晶学序説”,岩波書店(1986).
3) M. I. Aroyo, Ed.: “International Tables for Crystallography Volume A:Space-group Symmetry”, Sixth edition, Wiley(2016). 4) 松本崧生:四次元の結晶学, 鉱物学雑誌 13, 247 (1977). 5) M. Nespolo and B. Souvignier: Point groups in crystallography, Z.
Kristallogr. 224, 127 (2009).
6) M. Nespolo: A note on the notion of chirality, Cryst. Res. Techn. 50, 413 (2015).
Techn. 52, 1600129(2017).
8) B. K. Vainsthein: Fundamentals of Crystals. Symmetry, and Methods of Structural Crystallography. Second, Enlarged Edition. Springer, Modern Crystallography, 1(1994).
9) K. Momma and F. Izumi: VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl.
Crystallogr. 44, 1272 (2011).
10) B. Souvignier: Enantiomorphism of crystallographic groups in higher dimensions with results in dimensions up to 6, Acta
Crystallogr. A59, 210 (2003).
11) J. F. C. Hessel: Kristallometrie oder Kristallonomie und Kristallographie(Ostwald’s Klassiker der exacten Wissenschaften). Engelmann, Leipzig 1897, nos 88, 89(1830).
12) J. J. Bernhardi: Darstellung einer neuen Methode, Kristalle zu besischreiben, Gehlen’s J. Chem. Phys. Mineral. Berlin, 5, 157; 492; 625(1808).
13) C. S. Weiss: Übersichtliche Darstellung der verschiedenen natürlichen Abtkeilungen der Krystallisations-Systeme, Abhandlungen der Königlichen Akademie der Wissenschaften, Berlin, p.289(1815)
14) H. Brown, R. Bülow, J. Neubüser, H. Wondratschek and H. Zassenhaus: “Crystallographic groups of four-dimensional space”, John Wiley & Sons, New York, Chichester, Brisbane, Toronto, xiv +443(1978).
15) M. Nespolo: The ash heap of crystallography. Restoring forgotten basic knowledge, J. Appl. Crystallogr. 48, 1290 (2015). 16) M. Nespolo and G. Ferraris: Twinning by syngonic and metric
merohedry. Analysis, classification and effects on the diffraction pattern, Z. Kristallogr. 215, 77 (2000).
プロフィール
ネスポロ マッシモ Massimo NESPOLO ロレーヌ大学結晶学教室
CRM2 UMR CNRS 7036, Institut Jean Barriol, FR 2843, Faculté des Sciences et Technologies, Université de Lorraine
BP 70239, Boulevard des Aiguillettes, F54506 Vandoeuvre-lès-Nancy cedex France