小児循環器専門医に必要な統計学

はじめに 本シリーズでは小児循環器専門医が習得すべき知識 や経験を具体的に示す教科書的な総説として企画され ている．筆者が担当する統計学においては，小児循環 器学に特化したものはなく，本稿は「臨床専門医に必 要な統計学」という視点でまとめてみた． 臨床専門医に必要な統計学と一口にいうが，筆者は この中にも 3 種類のものがあると考える．ひとつは① 日常の臨床を行う上で直接必要な統計学，もうひとつ は②臨床の基礎となる他人の学会発表や学術論文を理 解するために必要な統計学，そして最後に③自らの経 験を学問として発信するための学会発表や論文執筆の ために必要な統計学である．①が極めて基本的な知識 であることについて異論はないであろう．②と③の関 係は微妙である．他人の学会発表や論文を理解するた めのものという意味では，ある程度の高度な統計学を 理解しておく必要があるが，これらを自分で使う必要 はないという考え方もできる．しかし，逆に学会発表 や論文執筆の立場になると，自分でも高度なものを使 うことができなければならない．しかし，統計学の専 門家に共同研究者として自らの研究に加わってもらえ ば，自分で統計を使いこなすことができなくても，こ とが足りるかもしれない．しかし一方で，統計解析を 統計学者に丸投げということであれば，臨床専門医と しての立場が研究に反映されなくなる． 以上のように考えると，②と③は同一レベルと考え ることもできるし，一方では①だけでは専門医と称す るには心許ない（そもそも「専門医とは何か」という根 源的な課題に行き着くが，ここではこれ以上は触れな い）．したがって，区分はあるが，臨床専門医としては すべてについて一定レベル以上の理解が必要であ ろう． 以下では，日本小児循環器学会が提示している「小 児循環器専門医修練目標」の中であげられている統計 学やその関連領域について解説していく．

小児循環器専門医に必要な統計学

statistics, statistical inference, estimation, test, data.

中村　好一

自治医科大学公衆衛生学教室

Basic Knowledge of Biomedical Statistics for Pediatric Cardiologists

Department of Public Health, Jichi Medical University, Tochigi, Japan

In this article, items concerning biomedical statistics according to the Aims of Training for Pediatric Cardiologists issued by the Japanese Society of Pediatric Cardiology and Cardiac Surgery are explained. The items are not only for pediatric cardiologists, however, but also for medical specialists in all the fi elds. Issues discussed in this article are; （1） characteristics of data, （2） representative values and variations, （3） descriptive statistics and analytic statistics, （4） estimations and tests, （5） methods of tests, （6） methods of estimations, （7） correlation and regression, （8） multiple comparison, and （9） charts and graphs.

要　　旨 日本小児循環器学会の「小児循環器専門医修練目標」で取り上げられている統計に関する事項を解説した．ただし， 紹介した事項は小児循環器専門医に特化したものではなく，すべての臨床専門医に必要な事項と考える．項目は以 下の通りである：（1）データの種類，（2）代表値とばらつき，（3）記述統計と分析統計，（4）推定と検定，（5）検定の実際， （6）推定の実際，（7）相関と回帰，（8）多重比較，（9）図の作成．

小児循環器専門医の

ための総説シリーズ

21

データの種類 データを大きく分けると数量データと質的データに 2 区分できる．数量データは数値で表すデータ（年齢， 体温，血清アルブミン値など）であり，質的データは性 別，職業など数値では表現しないデータを指す．数量 データは後述のような代表値とばらつきでその特徴を 示すが，質的データは全体に占める割合を示すのみで ある． 数量データの中にもいくつかの区分がある．連続 データは，観察の精度は置くとして，各種の検査値な どいくらでも細かな数値まで理論的には取り得るもの であるのに対して，離散データは，たとえば兄弟姉妹 の数など，理論的に特定の値しかとらないものを指す． 離散データの平均を求めると「兄弟姉妹数の平均は 1.8 人」といったあり得ない数値になることもあるが，気 にする必要はない．絶対値として 0 が存在するデータ を比尺度，そうでないものを間隔尺度という．摂氏や 華氏で表現した温度は間隔尺度であるが，絶対温度は 比尺度である．比尺度では「ある値はもうひとつの値 の x 倍である」と表現することができる． 質的データは順序尺度と名義尺度に区分することが できる．並び方に意味があるもの（たとえば重症度な ど）は順序尺度で，意味がないもの（職業など）は名義尺 度である．2 値データ（性別などの 0 － 1 データ）はす べて名義尺度である． 代表値とばらつき 1．代表値 集団を代表するデータを代表値という．前述の通り， 数量データで用いる． （1）平均（mean，average，算術平均，arithmetric mean） すべての値の合計を標本サイズ（n）で除した値を平 均（値）という．幾何平均（geometric mean，すべての値を 乗じた数値の n 乗根）と区別するために，算術平均とい うこともある．正規分布に近い分布であれば，観察さ れる個々の数値とそれほどかけ離れた値が平均になる ことはないが，極端な数値が含まれる場合や，分布が 歪んでいる場合（たとえば CRP 値など）には，個々の数 値とはかけ離れた平均が観察されることもある． （2）最頻値（mode） 以上のような平均の問題点を解除するために最頻値 や中央値が存在する．最頻値は頻度が最も多い値だが， 数学的には度数分布曲線が上向きに凸の変曲点の値と 定義される． （3）中央値（median） 個々の値を大きな順（小さな順でも可）に並べた場合 の中央に存在する値である．標本サイズ n が奇数の場 合には上から数えても下から数えても（n ＋1）/2 番目の 数値である．偶数の場合には n/2 番目と n/2 ＋ 1 番目の 値の算術平均を中央値とする． 2．散布度 代表値が同一でも個々のデータが幅広く分布するも のもあれば，代表値の周囲に集中しているものもある． このようなばらつきを示す指標として，各数値と平均 の差の 2 乗の合計を n － 1 で除した分散（variance）があ る．これを母集団の分散の推定値として「不偏分散」と 呼ぶことがある．エクセルでは関数 VAR.S を用いる． 一方で観察集団そのものを全体（＝母集団）と考えた場 合には n － 1 ではなく n で除した分散を用いる（この 場合のエクセル関数は VAR.P である）． 分散のディメンジョンは，個々の数値や平均の 2 乗 なので扱いにくい．そこで　分散の平方根を計算し， 標準偏差（standard deviation）を用いることも多い．エク セルでは分母が n － 1 の場合には STDEV.S を，n の場 合には STDEV.P を使う． 複数の変数の標準偏差の相互比較は変数の大きさが 異なるためにできない（身長と体重の標準偏差の比較 を考える）ので，標準偏差を平均で除した変動係数 （coefficient of variation）を用いて相互比較を行う． 記述統計と分析統計 統計の目的を 2 種類に分けて検討する．データを収 集した場合（たとえば，川崎病の全国調査で26,691 人［第 22 回全国調査報告患者数］の患者データが集まってい ると想起してほしい），これらのデータの集まりだけで は何もわからない．これをわかりやすく集計して示す のが記述統計である．一方で，データが得られた標本 の状況から，確率論に基づいて母集団の状況を推計す るのが分析統計である．平均を計算する記述統計より も t 検定を行う分析統計のほうが高度なことを行って いるようにみえるが，特に臨床医学で重要なのは患者 集団の状況を正しく的確に示すことであり，分析統計 よりも記述統計のほうが重要と筆者は考える．なお， 川崎病全国調査の結果はすべて記述統計である．

1．率（rate）と割合（proportion） 率（rate）には時間の概念が入っているのに対して，割 合は断面の現象を観察している．すなわち，率は一定 の期間に新たに発症したイベントの頻度を示すもので あるのに対して，割合はある 1 時点でのイベントの状 況を示す． 2．罹患率（incidence rate）と有病率（prevalence） 疾病の頻度の観察において，患者発生について率と 割合を用いるものが罹患率と有病率である．ここで注 意が必要なのは有病率は日本語表記では「率」を使っ ているが，率ではなく割合である． 罹患率は一定期間に発生した患者数を観察した人年 で除したものである．1 人年は 1 人の人間を 1 年間観 察したことを意味する．川崎病全国調査では罹患率は 0 ～ 4 歳人口 10 万対年間で表記するのが慣行だが，あ る年の罹患率はその年の 0 ～ 4 歳の小児を 1 年間観察 したと考えて，これを分母とし，この 1 年間に川崎病 に罹患した患者数を分子として算出している．なおこ の場合，分子の患者には 5 歳以上のものが含まれてい ても構わない． 一方で有病率は，ある時点での観察対象全体に占め る患者の割合である．集団の中での先天性心疾患を持 つ者の割合は有病率である． 3．記述統計（descriptive statistics） 以上のような指標を軸に集団の特性を示していく統 計手法を記述統計という． 4．分析統計（analytic statistics） 記述統計に対して，後述の統計学的推論（観察集団を 標本と捉え，母集団の状況を推論すること）を行うのが 分析統計である．推定や検定がこれに該当する． 5．相対危険（relative risk）と 寄与危険（attributable risk） 複数の集団間で疾病頻度を比較する方法を検討す る．話を単純化するために，比較する集団は 2 つ（たと えば，男と女，低出生体重児群とそうでない群，など） としよう．罹患率でも有病率でも構わないが，双方の 疾病頻度の比を相対危険という．他方に比べてどれだ け疾病頻度が高いかを示す指標である． 疾病頻度の差を寄与危険という．曝露群（たとえば低 出生体重児）と非曝露群（そうでない者）の疾病頻度を 考える場合，曝露群の頻度のうち非曝露群の頻度の分 は曝露とは無関係に発生したと考えて，寄与危険（曝露 群の頻度－非曝露群の頻度）は真に曝露によって発生 した頻度と考えることができる．曝露群の頻度全体に 占める寄与危険の割合を寄与危険割合（attributable risk percent）といい，曝露群の頻度の中で真に曝露によって 発生した割合を示している． さらに，曝露群と非曝露群の比較ではなく，集団全 体（＝曝露群と非曝露群で構成される）と非曝露群との 比較を同様に行った場合には，集団寄与危険（あるいは 人口寄与危険，population attributable risk），集団寄与危 険割合（人口寄与危険割合，population attributable risk percent）という． 推定（estimation）と検定（test） 前述の通り，観察した対象集団について統計学的に 記述するのを記述統計と称するのに対して，観察した 対象集団を母集団からの標本とみなして，母集団の状 況を確率論を用いて推論するのを分析統計という．推 定や検定は分析統計である． 1．推定と検定の違い いずれも母集団の状況を推論する手法である．推定に は点推定（point estimation）と区間推定（interval estimation） がある．点推定は標本で観察された値をそのまま母集 団の推定値とするものであり，たとえばある疾患患者の 血圧の平均が 110/75mmHg であったとすれば，母集団 （＝当該疾患の患者全体）の血圧の平均も 110/75mmHg と推定することである．理論的には，点推定はこれ以 外にはあり得ない．観察する群が複数の場合でも，2 群 間の平均の差の推定値などを計算する． 検定は推定よりも守備範囲が狭く，結論は「あり」か 「なし」かの判定結果である．たとえばある疾患の患者 の母集団の収縮期血圧の平均が 110mmHg である場合， 観察された標本にたまたま血圧が高い患者が多く含ま れていた場合，標本 100 人の平均が 115mmHg である こともありうるかもしれない．しかし，標本平均が 150mmHg ということは，直感的には考えにくい．これ を直感ではなく，確率論的に計算して，偶然発生した

のか，それともそうでない（統計学的に有意）のかを検 討するのが検定である．2 群間だと両群の間に有意 （significant）な差があるかどうかの検定となる． 2．帰無仮説（null hypothesis）と 対立仮説（alternative hypothesis） 検定は，仮定した母集団の状況のもとで観察された 標本の結果が出現する確率を計算し，その結果から一 定の判断を行うものである．前述の例だと，母集団の 血圧の平均が 110mmHg という仮定のもとで，標本の 平均は 115mmHg であったり，150mmHg であったりす る確率を計算する．この場合の仮定を帰無仮説と呼ん でいる．通常，帰無仮説は明らかにしたいこととは逆 のことを設定し，これが検定の結果として棄却（reject） された場合に，対立仮説を採用する．たとえば 2 群間 の有病率の差の検定では，帰無仮説として「2 群間に有 病率に差はない」を設定し，このような条件の下で観 察された結果（「事象（phenomenon）」という）が出現する 確率を求め，この確率が一定以下だと帰無仮説を棄却 して対立仮説である「2 群間の有病率は差がある」を採 用することになる． 3．第 1 種の過誤（type I error）と 第 2 種の過誤（type II error），有意確率（p） 母集団の真の状態（たとえば差がある／ない）と検定 結果（有意差あり／なし）において，母集団で差がある 場合の有意差ありの検定結果と，母集団に差がない場 合の有意差なしの検定結果は，母集団の状態と検定結 果が一致しているので問題はない．一方で母集団に差 がない場合の有意差ありの検定結果は問題であり，こ れを第 1 種の過誤と呼んでいて，その確率をαで表す． 逆に，母集団に差がある場合の有意差なしの検定結果 を第 2 種の過誤といい，確率をβで表す（表1）． 通常の検定では帰無仮説の元で観察された事象が出 現する確率を求める．これを有意確率といい，通常，p で表現している．そして，慣習として p が 0.05 以下（20 回に 1 回しかみられない稀な事象が観察されたと考え る）の時に，帰無仮説を棄却し，対立仮説を採用する． このことを逆に考えると，実は母集団では差がなく 誤って帰無仮説を棄却してしまった場合（第 1 種の過 誤）でも，その確率は 0.05 以下で，それほど大きなもの ではないということになる． なお，1 からβを減じた数値を検出力（power）という． 母集団に差がある場合に「有意差あり」という検定結 果が出てくる確率である．これが高い場合，検定の結 果で有意差がなければ，母集団で差がない可能性が高 い（ただし断定的なことはいえない）． 4．信頼区間（confidence interval） 区間推定では母集団の状況が一定の確率で取り得る 範囲を示す．通常は 95％信頼区間を提示するが，これ は有意確率を 5％（0.05）で区分することの裏返しであ り，95％を採用する理論的根拠はない．標本の状況か ら点推定値と標準誤差（standard error，たとえば平均の 場合には標準偏差を標本サイズの平方根で除した値） を求め，点推定値± 1.96 ×標準誤差を 95％信頼区間と している．たとえば母集団の収縮期血圧が「110.5, 95% CI: 100.3 ～ 120.7）」という場合，母集団の平均は 100.3 と 120.7 の間にあると考えて構わないであろう． 5．統計学的推論の解釈 いくつかのポイントがある．まず第 1 に，推定と検 定の結果は，手段は異なるが同じものを観察している ので，得られる結論は同じということである．たとえ ば相対危険の推定と検定を行った場合，相対危険の 95％信頼区間が 1.0（＝曝露群と非曝露群で差がない）を 跨ぐ場合には，「相対危険は 1.0」という帰無仮説を有意 水準 5％で棄却できない，ということと同等である．た だし，検定結果は統計学的に有意か否かという 2 者択 一の判断でしかないが，推定ではたとえば 95％信頼区 間が 0.95 ～ 3.44 であれば，「もう少しで有意である」と いったことがわかる．したがって，推定結果のほうが 表 1．母集団の真の姿と検定結果の関係 帰無仮説を棄却 （有意差あり） 帰無仮説を採用 （有意差なし） 母集団の真の姿 差がある 問題なし 第 2 種の過誤 差がない 第 1 種の過誤 問題なし 第１種の過誤の確率＝α，第２種の過誤の確率＝β，検出力＝１－β

得られる情報量が多く，このために検定よりも好まれ ることになる．検定は，①推定を行うことができない 場合（たとえば 3 群以上の平均の差の観察など）や，② 標本サイズが小さいために 95％信頼区間の幅が広すぎ て意味をなさないような場合に留めるべきであろう． 通常の検定では第 1 種の過誤の確率しか観察しない． そこで，得られた有意確率が 0.05 より大きく，帰無仮 説が棄却できない場合でも，「帰無仮説が認められた」 ということではない．「観察された結果は偶然に起こっ た可能性も十分にある」ということだけであり，「2 群 間に差がないことが確認された」といったことでは ない． 検定結果は標本サイズに大きく依存する．2 群間の 比較の場合，群間の差が大きくても標本サイズが小さ ければ有意とはならない．一方，差が医学的には意味 がないような小さなものであっても，標本サイズが大 きければ有意な結果が得られる．統計学的推論は観察 された結果が偶然発生したものかどうかを検討してい るだけであり，医学的に意味がある差かどうかについ ては統計学は何も情報を提供しない． 検定の実際 検定には大きく分けて 2 種類ある．一定の分布（t 分布， カイ 2 乗分布など）を仮定して，パラメータ（parameter） を用いて行うパラメトリック検定（parametric test）と，分 布を仮定する必要なく，したがってパラメータを用いな いノンパラメトリック検定（non-parametric test）である． 標本の分布が大きく外れている場合にはノンパラメト リック検定を使うのだが，標本サイズが大きいとパラメ トリック検定でもさほど問題は生じない． なお，誌面の関係でここではどのような場合にどの 検定を使うかに留め，実際の検定方法については本稿 の最後に示すような統計学の教科書などを参照してい ただきたい． 1．パラメトリック法 （1）対応のない t 検定 母集団が t 分布に従うことを想定した検定である．2 群間の差の観察に用いるが，たとえば男の患者群と女 の患者群の検査値の平均など，個々の値に対応がない 場合に用いる． （2）対応のある t 検定 治療前後の検査値の平均の比較のように，個々の値 に対応がある場合に用いる．たとえば 10 人の患者の治 療前後の収縮期血圧の比較を考える．治療前と治療後 でそれぞれ 10 ずつの血圧値があり，前後の値の平均を 算出するが，前後の値はそれぞれ独立ではなく，1 人の 患者で結びついている．そこでこの結びつきに配慮し た検定（あるいは，患者 1 人 1 人の治療前後の血圧の差 の観察と考えてもよい）が，対応のある t 検定である． 対応を崩して，対応のない t 検定を行うことも可能 だが，そうすると第 2 種の過誤を犯す（差があるものを 見逃す）確率が高くなる． （3）カイ 2 乗検定 m × n 分割表における一様性の検定である．最も単 純なものは 2 × 2 分割表で，表の縦・横とも 2 値のも の（ある／なし）で，基本的には 4 つのセルからなる． イェーツの補正項（カイ 2 乗値の公式の分子が｛｜ad － bc｜－ n/2 ｝2_{× n となっていれば，n/2 がイェーツの補} 正項である）を入れるかどうかについては，式からもわ かるように入れるとカイ 2 乗値は小さくなり，その結 果，検定の結果は有意に出にくくなるため，入れたほ うが無難である． （4）フィッシャーの直接確率法 これは厳密にいうとノンパラメトリック検定だが， 前項の 2 × 2 表に適用するので，ここで示す．2 × 2 分 割表で一部のセルの値が小さいと検定結果が正しく出 ないことがある．通常いわれているのはセルの期待値 （a のセルの期待値は｛ a ＋ b ｝×｛ a ＋ c ｝/n である）が 5 を下回るセルが 1 つでもあれば，カイ 2 乗検定ではな くフィッシャーの直接確率法を用いるとされている． 一方で，コンピュータの発達によりフィッシャーの直 接確率を計算することもそれほど困難ではなくなった ので，カイ 2 乗検定を用いずに，常にフィッシャーを 用いたほうがよいと主張する統計学者もいる． （5）分散分析 3 つ以上の群間の平均の差の検定の際に用いる．こ の際に注意しなければならないのは，分散分析の帰無 仮説は「すべての群で平均は等しい」であり，対立仮説 は「少なくとも 1 つの群では他の群と平均に差がある」 であり，「すべての群で差がある」ではないことに注意 しなければならない．通常はまず分散分析を行い，帰 無仮説が棄却された場合には群間の総当たりで差の有 無の検定を行う． 2．ノンパラメトリック法 前述の通り，観察する集団が特定の分布に従わない （ことが予想される）場合には，ノンパラメトリック法

を用いる．ノンパラメトリック法は母集団の分布に依 存しないのでどのような場合でも使用することができ るが，パラメトリック法と比較して検出力が落ちるた め，パラメトリック法が使える場合にはそちらを使用 するほうがよい． （1）マン・ホイットニーの U 検定 対応のない 2 群間の t 検定のノンパラメトリック検 定に相当する．紛らわしいのだが，ウィルコクソンの 順位和検定（次項のウィルコクソンの符号付順位和検 定とは別物）と同じである． （2）ウィルコクソンの符号付順位和検定 マン・ホイットニーの U 検定（ウィルコクソンの順 位和検定）が対応のない 2 群間の平均の検定なのに対 して，ウィルコクソンの符号付順位和検定は対応があ る 2 群間の平均の差の検定である． 推定の実際 推定には点推定と区間推定がある．点推定は標本で 観察された数値を，そのまま母集団の数値の推定値と するものである．一見乱暴にもみえるが，母集団の点 推定値はこれ以外にはあり得ない． 区間推定は通常，95％信頼区間で提示する．点推定 値± 1.96 ×標準誤差で求めることができる． 相関と回帰 1．相関係数（correlation coefficient） 2 つの数量データの関係を観察する際に用いるのが 相関係数である．相関係数は全く無関係の 0 をはさん で－ 1 ～＋ 1 の値をとる．相関係数が－ 1 または 1 で あるというのは 2 つの変数 x と y の間に y ＝ ax ＋ b という直線的な関係がある場合だが，人間を含めた生 体の観察ではあり得ない．相関係数の絶対値が 1 に近 いほど，2 つの変数の関連は強く，「高い相関がある」 と表現する． 相関係数を用いる場合に注意しなければならないこ とがいくつかある．まず第 1 に相関係数は 2 つの変数 の直線的な関係しか観察していないということを十分 に理解する必要がある．極端な外れ値があったり，複 数の集団が混在しているような場合には，変数間に関 連がなくても高い相関係数が観察されることがある． 逆に 2 つの変数の間に曲線的な関連がある場合には， 低い相関係数しか観察されない．単に相関係数を計算 するだけでは 2 変数間の関係の誤った解釈，あるいは 見逃しが起こる可能性があるので，必ず散布図（後述） を書いてみることを奨める． 相関係数ほど有意性と意義が誤って理解されている ものも少ないかもしれない．標本サイズが 50 ほどあれ ば，相関係数（絶対値）が 0.3 程度でも統計学的に有意な 結果となる（帰無仮説は「母集団の相関係数は 0」）．相 関係数の 2 乗の値を決定係数（coefficient of determinant） という．これは一方の変数の変動を他方の変数の変動 で説明できる部分を示す指標で，相関係数が 0.3 であ れば決定係数は 0.32_{＝ 0.09，すなわち変動の 1 割も説} 明できないということである．統計学的な有意性と意 義のある数値かどうかは別の視点であることを再度強 調しよう． （1）ピアソンの相関係数 通常「相関係数」というと，このピアソンの相関係数 を指している．パラメトリック法であり，2 つの数量 データが正規分布しているという仮定のものとで使用 される． （2）スピアマンの順位相関係数 ノンパラメトリック法による相関係数がスピアマン の順位相関係数である．観察する数量データが正規分 布することがあやしい場合には，こちらを用いる． 2．回帰分析（regression analysis） 相関係数と同様に複数のデータ間の関連を観察する 手法である．最も単純なものは 2 つの数量データ間の 直線的な関係を見るもので，y ＝ a ＋ bx（x と y が観察 するデータ）の関係を導き出す（具体的には a と b を求 める）ものである．この場合の x を独立変数（あるいは 説明変数），y を従属変数（あるいは目的変数）と呼ぶ． 相関係数でも x と y の関係は観察できるが，相関係数 と回帰分析は基本的には異なる解析方法であるし，同 じ変数に対して同時に異なる解析を行うのは感心し ない． 相関係数では 2 つの変数間の従属関係はない．わか りやすくいえば，一方の変数がもう一方の変数を規定 するということではなく，たとえば収縮期血圧と拡張 期血圧のように単純に関連を観察しているだけであ る．一方，回帰分析では x が y の値を決める（影響を与 える）という背景がある．たとえば，x が年齢で，y が収 縮期血圧のような場合である．この場合に変数の逆転 （x が収縮期血圧で y が年齢だとすると，収縮期血圧が 年齢の影響を及ぼすことになる）は，あり得ない．した

がって従属関係が明らかな場合には回帰分析を使用 し，明らかではない，あるいは従属関係の有無がわか らないような場合には相関係数を計算するのがよいだ ろう． 相関係数とは異なり，複数の独立変数を組み込むこ ともできる．このような場合を重回帰分析と呼ぶこと もある．また，独立変数は数量データだけでなく，性別 などの質的データを用いることも可能である．さらに， 従属変数は数量データだけでなく，2 値データ（あり／ なし，など）を用いるロジスティック回帰分析（logistic regression analysis）や，生存データ（観察対象者の観察期 間と観察終了時にイベントが発生しているかどうかの 2 つのデータを組み合わせたもの）を扱うコックスの比 例ハザードモデル（Coxʼs proportional hazard model）など も医学研究ではよく使用される． 医学研究における多変量解析の使用目的は，①モデ ルの形成，②交絡因子の制御のどちらかである．多変 量解析を行う際に悩ましいのは「どの変数を独立変数 としてモデルに投入するか」ということであるが，こ の 2 つの目的のどちらかで考え方も異なる．①の場合 には，モデルに組み込む独立変数の数は少ないほうが よい（少ない独立変数で従属変数の予測ができる）が， 独立変数の数が多いほどモデルの適合性はよくなる （予測値と実際の値が近くなる）という矛盾した背景が ある．そこで，単変量解析で従属変数と有意な関連が あった変数を独立変数としてモデルに投入する，とい う考えは十分に成立する．一方②の場合には単変量解 析の結果如何にかかわらず，交絡因子として作用する と考えられる変数はすべて独立変数として投入するの が正しい考え方である．しかしながら，数ある独立変 数すべてを投入することもできないということで，便 宜的に「単変量解析で有意なものを独立変数とする」 という処理方法も，完全に否定するわけではない． 多重比較（multiple comparison） 前述の通り，統計学的推定や検定は確率論に基づい て母集団の状態を推論するものである．そしてそこに は伝統的に有意確率 0.05 という基本原則がある．20 回 に 1 回程度以下のめずらしい事象であれば前提（帰無 仮説）が誤っていると判断してもよいだろう，という発 想である． ということは，逆に帰無仮説が正しくても 20 回に 1 回程度は統計学的に有意な関係が観察される，という ことである．7 つの数量データ間の相関係数を総当た りで観察することを想定しよう．合計 21〔＝ 7 × 6 ÷2） 個の相関係数が算出されるが，すべての変数間で関連 がなくても 1 つぐらいは p<0.05 で有意となる，という ことである． このように，数多くの検定を行い，その中で一部に 有意な結果が観察された時に，たとえ検定の結果は有 意であっても，偶然観察された可能性がある，という のが多重比較の問題である．これを解決する方法とし て，Tukey の方法や Dunnet の方法など種々の手法が提 唱されているが，決定的な方法はない．しかし，多重比 較の問題が存在するということは少なくとも頭の隅に 入れておいたほうがよいだろう． 図の作成 医学研究の成果を報告する際によく使う図を紹介す る．なお，用いたデータは 2011 年，2012 年の 2 年間の 患者を対象とした第 22 回川崎病全国調査である．一部 の図は既に報告書で示したが，本稿のために新たに作 成したものもある． 1．プロット〔箱ひげ図（ボックス・プロット：box plot）〕 図 1 に示すように，全体の分布を示すために用いる． 箱の下の辺は 25 パーセンタイル値（下から数えて 25％ 目に相当するものの値），中の線は中央値，上の辺は 75 パーセンタイル値である．箱から上下に延びた線の端 は最小値と最大値を示す． 2．棒グラフ（bar chart） 図 2 に示すように，分布を示すときに用いることが 多い． 3．折れ線グラフ（line chart） 図 3 に示すように，時系列の変化を示すときに用い るとわかりやすい． 4．ヒストグラム（histogram） 図 4 に示すように，分布を提示するときに用いる． 棒グラフと異なるのは横のバー同士は密着させ，間に 間隙を入れない．

5．帯グラフ 次の円グラフとともに構成割合を示すときに用いる （図5）．なお，欧米人には「帯グラフ」の概念は無く，「合 計を 100％にした横置き積み上げ棒グラフ」のようで ある． 6．円グラフ（pie chart） 帯グラフと同様に構成割合を示すときに用いる（図 6）．複数の集団を比較するときには帯グラフのほうが わかりやすい．一方，ひとつの集団の構成割合を示す ときには角度が視覚的にわかりやすい円グラフのほう がよい． 7．散布図（scatter diagram） 図 7 および図 8 に示すように，2 つの数量データの 関係を示すときに用いる．相関係数と回帰分析の項で 記載したように，2 つの変数間に従属の関係がない場 合（図7）には，どちらの変数を x 軸に持ってきてもよい が，一方の変数が一方の変数の値を規定する関係があ る場合（図8）には独立変数（図 8 の場合には日齢）を x 19640 2 4 6 8 年次別，性別患者数 10 12 14 千人16 川崎病全国調査 1966 1968 1970 1972 1974 1976 1978 1980 1982 1984 1986 1988 1990 1992 1994 1996 1998 2000 2002 2004 2006 2008 2010 2012 年次 男 女 図 2　棒グラフの例 全体 心後遺症あり 心後遺症なし 発病時の日齢（心後遺症の有無別） 0 1,000 2,000 3,000 4,000 5,000 6,000 7,000 （日） 第22回川崎病全国調査 図 1　箱ひげ図の例

年次別，月別，性別患者数 1,000 （人） 900 800 700 600 500 400 300 200 100 0 13 5 7 91113 5 7 91113 5 7 91113 5 7 91113 5 7 91113 5 7 91113 5 7 91113 5 7 91113 5 7 91113 5 7 91113 5 7 91113 5 7 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 2012 911（月） 年次 男 女 川崎病全国調査 図 3　折れ線グラフの例 図 4　ヒストグラムの例 初診時血清アルブミン値の分布 （g/dL） 第22回川崎病全国調査で初診時血清アルブミン値が報告された25,087人を集計 ∼1.9 16,000（人） 0 2,000 4,000 6,000 8,000 10,000 12,000 14,000 2.0∼2.9 3.0∼3.9 4.0∼4.9 5.0∼5.9 6.0∼

心後遺症の有無別初診時の白血球数の分布 ∼9,999 465 131 133 心後遺症あり 17,485 3,097 4,269 心後遺症なし 0 10 20 30 40 50 60 70 80 90 100（％） 10,000∼19,999 20,000∼29,999 30,000∼39,999 40,000∼49,999 50,000∼（mm3_） 第22回川崎病全国調査で初診時白血球数が報告された26,496人を集計 ∼19,999, 1,585 60,000∼, 609 50,000∼59,999, 1,305 40,000∼49,999, 4,293 30,000∼39,999, 9,967 第22回川崎病全国調査で初診時血小板数が報告された26,501人を集計 初診時血小板数の分析 20,000∼29,999, 8,742 図 5　帯グラフの例 図 6　円グラフの例

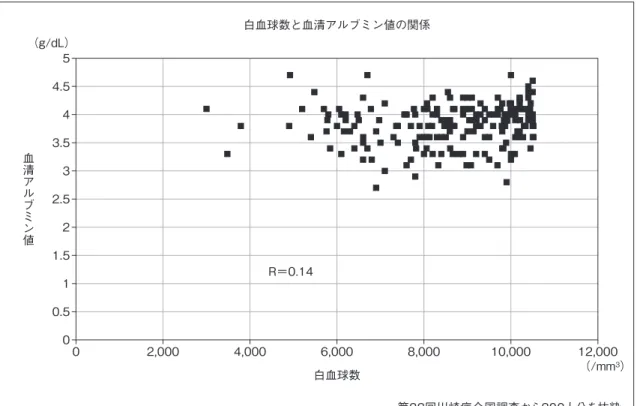
図 7　散布図の例（1） 図 8　散布図の例（2） 5 （g/dL） 4.5 R＝0.14 4 3.5 3 2.5 2 1.5 1 0.5 0 0 2,000 4,000 6,000 白血球数 （/mm3） 白血球数と血清アルブミン値の関係 第22回川崎病全国調査から200人分を抜粋 8,000 10,000 12,000 血清アルブミン値 80 （千/mm3_） 70 60 50 40 30 20 10 0 0 500 1,000 1,500 2,000 2,500 初診時日齢 初診時日齢と初診時血小板数の関係 第22回川崎病全国調査から200人分を抜粋 3,500 3,000 4,000 4,500 血小板数 Y＝−0.00404x＋34.3

軸に持ってくる．図 7 の場合，回帰直線（図 8 には記載 されている）を入れると，おかしなことになる． 【 参 考 文 献 】 以上，日本小児循環器学会「小児循環器専門医修練 目標」に準拠して統計（学）の概要を述べたが，誌面の 関係で項目としてあげたものでも十分に語り尽くせて いない．以下はすべて著者が関与している統計等に関 する著書だが，自信を持ってお奨めするので興味があ る方は参照していただきたい． 1） 福富和夫，永井正規，中村好一，ほか：ヘルスサイエンス のための基本統計学（第 3版）．東京，南山堂，2002 ※初心者用に執筆された統計学の入門書． 2） 中村好一編：医療系のためのやさしい統計学入門．診断 と治療社，2009 ※次の「論文を正しく読み書くためのやさしい統計学」 の姉妹編として，初心者向けに執筆された書籍． 3） 中村好一編：論文を正しく読み書くためのやさしい統 計学（第 2版）．診断と治療社，2010 ※医学論文をまず理解できるようになり，そして見よう 見まねで論文に統計の使用ができるようになること を目指した書籍． 4） 中村好一：基礎から学ぶ楽しい疫学（第 3版）．医学書院， 2013 ※第10章で主として疫学で使用する統計手法を提示し， エクセルで可能な手法を実例で示している．エクセル でもここまでできるという点を示すとともに，逆の見 方をするとエクセルの限界を提示している． 5） 中村好一：基礎から学ぶ楽しい学会発表・論文執筆．医 学書院，2013 ※第 17章は「図表の作成」． 【小児循環器専門医のための総説シリーズ】 項立て 掲載号 1 胎児循環生理 2 心血管系の身体所見　専門医に必要な循環器系理学所見のポイント 3 薬物について 3-1 利尿薬の使い方 3-2 血管拡張剤について 3-3 その他 4 鎮痛・鎮静 5 肺高血圧の治療戦略 6 失神について 7 呼吸と循環 8 超音波検査の原理から応用 9 心臓カテーテル検査によって得られた結果をどう解釈するか 10 心臓 CT 11 心臓 MRI 12 心臓核医学 13 運動負荷試験について 14 先天性心疾患の非手術歴（自然歴）1_{〃　　　　　　　2} 30-2 15 チアノーゼについて 16 ペースメーカのすべて 17 小児の心臓移植について 18 体外循環 19 代表的な手術法　その工夫と問題点 20 死亡心臓病学 21 小児循環器専門医に必要な統計学 30-2 22 臨床研究と倫理委員会と個人情報保護 23 川崎病 24 カテーテル治療 25 不整脈治療 26 感染性心内膜炎 27 学校生活，運動制限 30-1 28 心臓突然死