教科専門科目の内容を活用する教材研究の指導方法(II) : Team 2 プロジェクト (数学教師に必要な数学能力に関する研究)

教科専門科目の内容を活用する教材研究の指導方法

II

(Team

₂

プロジェクト

)

島根大学教育学部 青山 陽一 (Yoichi AOYAMA)

Faculty of Education,

Shimane

University

滋賀大学教育学部 神 直人 (Naondo JIN)

Faculty of Education, Shiga University 岡山大学教育学部 曽布川 拓也 (Takuya SOBUKAWA)

Faculty of Education, Okayama University

岐阜大学名誉教授 中馬 悟朗 (Goro CHUMAN)

Professor

Emeritus,

Gifu

University

\S 0.

まえがき

_by

_青山陽

-Team 2

_{プロジェクトの理念等に変化はない．}

[1,

_{\S 0]}

より引用する

:

「大学における教科専門科目の内容を体系的に把握して，小学校・中学校．

高等学校の数学を自ら構成し授業展開等を行える数学教師を養成する為に」

を掲げ，学生に備えさせるべき能力として

「小学校中学校・高等学校の数学の内容全てを，大学における教科専門科目

の内容を機能的に連携させて，捉え扱うことが出来る」 を目標にし，具体的方策として

「大学における教科専門科目の内容を活用する教材研究の指導」

に取組む．従って，プロジェクトの名称を 「教科専門科目の内容を活用する教材研究の指導方法」

と設定する．なお，ここに言う

‘

教材研究

’

とは，教育現場で如何に提示するかではなく，

我々の目指す教員を養成をするため，学生に教材を深く理解させるものと捉えている．

我々は，小学校中学校・高等学校における算数・数学教育を基軸として捉える立場を

採る．各校種におけるものではなく，12 年の教育課程に於いて．これが確りしていれば，

他の教育課程や課程から外れてしまった場合にも対応可能である．教師は，教育課程が

どのように成立っていて，その何れの部分を担当しているのかを把握していなければな

らない．なお，ここで言う教育課程は学習指導要領で規定されるものではなく，それを

形成する元のもの

-

文化

-

に基づくものと理解して貰いたい．

また前回に述べたことに加え，児童生徒に学力を付けさせることの出来る教師を，学

力とは何かを (学力とは．．．云々．．．と垂れるのではなく) 身を持って示すことの出来る

教師を育成したいとの意図を明記しておきたい．学期・学年等を通して，児童生徒にど

れだけ学力が付いたかが重要であり，個々の授業はその一連の流れの中で捉えられなけ

ればならないと考える．そういうことの出来る教師を養成する為のものとしても，上述

の理念スローガンがある．

今回は，大学における教育課程

$\sim$授業履修の仕組及び教育実習時期との関係一につ

いても触れなければならないと感じている．特に教育実習時期との関係は重要であろう．

教育実習までに何をどこまで学んでおくべきか．教育実習を終えた後に何を学ばせるべ

きか．大学における教育課程は，各教員が決められる事柄ではなく，また大学学部等毎

に異なる故，一括に論じることは困難であるが避けて通ることは出来ない． 前回の

[1] において，(\S 1

by 神’ は教育実習直後に実施されるものの事例報告となって

いる．今回は敷衛されたものが載せられている．一方，

$\grave{}$

\S 2

by 中馬-青山’ と

‘\S 3

by 青 山’

_{は扱う内容のみから成っている．今回，\S 2 では著者の一人である青山の事例を絡め}

て述べることとした．

“

三角形の合同相似．

．

，

，に対応するものは割愛した．今回の

\S 3

では，青山

-

曽布川で “数概念の取扱に関して” と題して取組みの方向性を極めて簡単で はあるが，述べさせて頂くこととした．

最後になりましたが，大津での研究集会

$(2009Nov30Mo.-DEC3Th.)$ から新たに参加 された曽布川拓也氏 (岡山大学教育学部) が

Team2

_{のメンバーとして加わり，当面数に}

関することを担当することになった (\S 3参照) ことを報告しておきます． [References] [1]RIMS

_{共同研究数学教師に必要な数学能力形成に関する研究，数理解析研究所講}

究録1657,

_{京都大学数理解析研究所，2009}

July. p.105-p.127

6.

教科専門科目の内容を活用する教材研究の指導方法 (Team2 プロジェクト).

\S 1.

「折って作る放物線」

の教材研究指導について

II

by

神直人

11

はじめに

1.1.1

報告する授業と受講生について 著者は滋賀大学教育学部で数学 (解析学)_{の講義を担当している。本学部における中学} 校の数学科教員志望者は主に教員養成課程. _{理数教育コースに在籍している。理数教育}

コースでは中学校数学科免許取得に必要な「指導法に関する科目」として次の

4

科目が

開講されている: 中等数学科教育法 I,II (3回生に配当、 _各2単位

;

数学教育教員が担当) 中等数学科教材内容論I,II (3回生に配当、各2単位 ; 教科専門教員が担当) 理数教育コースに在籍し、 中学校数学科 1 種免許を取得して卒業する学生の多くが上記

4

科目をすべて履修している。

著者は中等数学科教材内容論

II

の1/2

(

秋学期

7

回

)

を担当している。 ここで報告する のはこの科目で実施した授業である。 この科目は3回生の秋学期に配当されており、受 講生の多くはその直前の9月に中学校で教育実習を経験している。 9 月の実習期間中に中学 3 年では 2 次関数を学習しており、受講生はそのグラフであ る放物線を教えている。 しかし、 受講生の半数近くは高校で物理を履修しておらず、放 物体の描く軌跡が2次関数のグラフとして表される理由すら理解していない。 そこで中等数学科教材内容論 I垣こおいて放物線を主テーマにする授業を実施しようと 計画していたところ、平成20年度滋賀県小中学校教育研究会算数数学部会研究発表 会(高月大会) で、 中学

3

年数学の課題学習の実践例として発表があった研究授業「折っ て作る放物線」をもとに、授業を構成することにした。

1.1.2

Mathematical Knowledge for Teaching (MKT)

前年、 受講生に教育実習と大学での数学数学教育の授業との接点についてアンケー トを取ったところ、何名かは教育法などの授業が実習でも役に立った、 あるいは参考に したと答えた。 しかし、 大学で学ぶ数学 (教科専門科目)、 たとえば微積分、線形代数、 群論などに言及したものはほとんどいなかった。 その一方で受講生の多くは、 将来教員として算数数学を指導する際に必要なものは、 0 指導する内容の数学的理解 O 指導法 O 生徒の実態理解 であると考えている。つまり、「指導する内容の数学的理解」 といっても、 自らが教わ る側として

(

高校までの

)

数学を理解していること、即ち演習問題が解けることが必要で あると考えている。 しかし、 大学で学ぶ数学

(

教科専門科目

)

と将来教師として教える数 学につながりがあるとは捉えていない。 このことは、 私自身が彼らに『数学教師に必要 な数学能力』という特別なものがあることを伝え切れていないこと、そして『数学教師 に必要な数学能力』と大学で学ぶ数学 (教科専門科目) のつながりを明示できていないこ とに原因があると考える。 この『数学教師に必要な数学能力』に関わって、

Ball&Bass

は [Bass, 2005] において

「数学指導のための知識 (Mathematical Knowledge for Teaching : MKT)」 として次の

前述の「指導する内容の数学的理解」は、「一般的な数学的知識」の一部に対応し、「指 導法」 は「数学と教授法に関する知識」、「生徒の実態理解」 は「数学と生徒に関する知 識」 に対応している。 では、特殊専門的な数学的知識とは何か、 [Bass, 2005] では次のように述べられてい る

([RIMS1657, p.30])

:

特殊専門的な数学的知識は、 熟練した教師が必要とする (生徒についてではなく、 教授法についてでもない)「厳密な意味での数学的知識」である。 しかし、数学的 な訓練を受けた多くの専門家、例えば数学研究者、にはいまだに知られていない知 識なのだ。 つまり、一般に信じられているのとは反対に、「 $MKT$の純粋に数学的 な部分は、数学者が知っている知識の真に小さな部分集合ではない」 のである。 具体的な例として小学校の算数で学習する複数桁の掛け算が挙げられている。上記

4

つ のカテゴリーはそれぞれ次のようになる: 示法

1.2

実施した授業について

1.2.1 授業の目的 この授業の目的の 1 つは、大学で学ぶ数学(教科専門科目) と将来教師として教える数学 の間のつながりを伝えることである。青山はつぎのように述べている [RIMS1657,$pp.105-$ $106]$

:

小中高における数学の内容を山脈のように捉え，ここにはこのような小山脈があり 他の小山脈と如何につながり大山脈を形成しているか$\searrow$ 一方小山脈ひいては大山 脈を形成する素となる個々のものがどのような意味を持っているかを考察しよう， というような立場で理解する能力を身に付けてこそ “ 良い” 数学教師になり得るの ではないだろうか。 また，このとき注意しなければならないのは，『小中高の数学 を“体系的地図” で示し，各々の位置付けを教えることをすればよい』では，能力 とならないことを明確にしておくことである。 受講生の高校までの知識では、 放物線は2次関数のグラフと同一であり、 どのような 山脈に位置ついているのかは不明である。 しかし、放物線には、文字通りの放物体の軌 跡、 円錐曲線、 あるいは2次曲線などの捉え方もあり、受容の歴史も興味深いものがあ る。 このことを受講生に体験させるのが

1

つの目的である。

もう 1 つの目的は、「数学指導のための知識 $(MKT)$ 」 の中で受講生には意識されてい ない「特殊専門的な数学的知識」 とはどういうもので、それを身に付けるためにはどう いうことに気をつければいいかを考えさせることである。 前回 [RIMS1657, pp.107-113] で報告した授業においては

1

つ目の目的を中心に授業 を組み立てていたが、 今回は「特殊専門的な数学的知識」 も考察するために中学校で行 なわれた研究授業「折って作る放物線」のビデオを利用することにした。この研究授業 の簡単な記録は本文の後に付録として掲載する。 1.2.2 授業の構成 1時限目

:

受講生が生徒として、 研究授業とほぼ同じ内容の授業を受ける。 2時限目: 研究授業「折って作る放物線」のビデオを見る。 3時限目: 実際の授業の場面で必要な教師の数学を学ぶ。 4時限目: 放物線に関する数学の体系的理解を学ぶ $\mathscr{L}1\#_{\backslash }$ 研究授業「折って作る放物線」 (50 分) の流れは以下の通りである: (1) 導入: パラボラアンテナの実物を見せてその仕組みを探ることが授業のテーマであ ることを伝える。 (2) 「地表面に垂直に交わる平行線群を

1

点に集めるにはどう反射させればよいか」を 考えさせる。 次に、 1 辺に垂直に交わる 5mm 間隔の平行線を描いた長方形の用紙を配布して 焦点 $F$ を生徒各自に決めさせ、長辺上の垂線との各交点が焦点 $F$ に重なるように 折らせる。 (3) 用紙に浮かび上がる曲線が放物線であることを確かめる方法を話し合う。 焦点 $F$ がのっている垂線を $y$軸にし、$y$軸と長辺の交点 $P$ を $F$ に重ねるように 折ったときできる折り線を $x$軸とする。 lcm

を 1 として曲線上の点の座標屋

y) をいくつか実測する。 今回は、用紙から実測した長さを元に表を書いて、$y=ax^{2}$ _{の関係を見つけること} により確かめさせる。 (4) まとめ

:

パラボラ$=$parabola が放物線を意味することを伝える。

私の実施した1時限目の授業でもほぼ上記の流れの通りに行なった。そして、受講生 に次回までの課題として (3) の表を基にエクセルを利用してグラフを描くこと、そして 表を利用して浮かび上がった曲線が2次関数のグラフになっていることを確かめる方法 を考えること、 の2点を指示した。 研究授業においては、表から $y=ax^{2}$ _{の関係を見つける方法として、} $\lceil_{X}$ の値が

2,3,4

$n$ 倍になれば、$y$ の値は $2^{2},3^{2},4^{2},$ $\cdots,$ $n^{2}$ 倍になる」 ことを利用していた。 しかし、 この方法では $a$ の値に言及しないため、実際のデータが どのくらい $y=ax^{2}$ _{の関係からずれているのかが判定しにくい。 一方、 表から} $\frac{y}{x^{2}}$ を計 算すれば $a$ の値を求めることになるので、実際のデータがどのくらい$y=ax^{2}$ の関係か らずれているのか理解しやすい。 このことに受講生が思い至るかどうかを調べる目的でこのような課題を出した。その 結果、 およそ四分のーの者が $\frac{y}{x^{2}}$ の値を計算することに気づいていた。 $\mathscr{T}2\#_{\backslash }$ 研究授業「折って作る放物線」 のビデオを見る。 受講生には下記のことを指示した

:

『研究授業のビデオを見て次のことをまとめよ。

(箇条書きで構わない)』

1. 教師の気になった発問，発言 2. 生徒の気になった発言，つぶやき 3. 中学校以降，つまり，高校，大学以上で学ぶ数学的知識が教師に必要とされる場面 4. シミズさんとミホさんの表

5.

この授業のよい点

6.

この授業の改善点と改善策

7.

その他の意見 ここで注目したいのは上記の3. の質問への回答である。 しかし、 約半数の受講生が白 紙回答で、 回答の中では 「放物線であることを確かめる$\rfloor$ 、「紙を折って放物線が見える 理由」、「焦点と準線による放物線の定義」 などに約三分のーの受講生が言及したにとど まった。

3

樹川

1

研究授業の簡単な記録を書いたプリントを配布した。 授業記録のプリントに 「数学」 欄を加えそこに番号をつけ、 この研究授業で必要な数学的知識として下記の10点を具 体的に挙げ、 それらを解説した (付録の数学欄の番号にも対応している)

:

1.

パラボラアンテナのしくみ。電波とはどのようなもので，なぜ

1

点に集めるのか。

2.

焦点の位置の取り方でどのように放物線の形が変わるのか。焦点の位置をクラス全 体で統一するか，各個人に任せるかの判断。

3.

紙の下の端点を 1 点に集める理由。

4. 折っていったら曲線が見える理由。

5.

美術でやったのは何か。 それは放物線だったのか。

6.

$y$軸対称を確かめる方法。

7.

放物線の性質と放物線の定義の違い。必要条件と十分条件の違い。

8.

表から $y=ax^{2}$ _{の関係を確かめる方法。}

9.

シミズさんの表のどこがミスなのかを見つけだす方法はなにか。

10.

パラボラアンテナのどこが放物線なのか。パラボラアンテナはどのようにできてい るのか。 パラボラ$=$parabola のもともとの意味は何か。なぜパラボラが放物線に なったのか。 上記の中から、 (A) 折ってできた曲線が放物線であることの確認 (B) 折れ線から曲線が見える理由 (C) 表から $y=ax^{2}$ _{の関係を確認} それぞれの場面において必要になる数学指導のための知識 (MKT) を具体的に考えると 以下のようになる: このうち、 (C) の特殊専門的な数学的知識に関して以下のような説明を加えた。 研究授業のビデオにおいてシミズさんは下記のような表を発表していた:

この表で $x=1,2,3,$$\cdots$ と変わると、$y$ の値は4倍、9倍、 . . . になることを確認しよう としたが、 これはうまくいかなかった。そこで、 教師はもう一人のミホさんの表を利用 して上記のことを確認した。 つまり、 シミズさんの表を活用することに失敗したわけである。 では、シミズさんの表を活用するには、教師はどういう対処をすればよいであろうか。 シミズさんの表で $y$ の階差をとってみると、 となっているが、理想的には1:3:5:7:9:11:13:15:17:19 となるはずである。す ると、最初の2つの値が例えば、

03,03

ならば階差が

$0,0.1,0.3,0.5,0.6,0.8$

,0912

となって、 $(x, y)$ _{の各点は大体同じ放物線上にのる。} つまり、 $x=0,1$ あたりの $y$ の値を読み取る際に誤差が多く出た可能性が高いことが推 測でき、 そのことをシミズさんに伝えて測りなおさせればシミズさんの表を用いて授業 を進めることも出来るはずである。 この場面で教師に必要な数学的知識は、 $『_{}y=ax^{2}$ _{の関係があるとき、}$x=0,1,2,3,$ $\cdots,$ $n$ の値に対応する $y$ の値の階差をと ればその比が、 $1:3:5:7:\cdots:2n-1$ になること』 である。 この知識は、 生徒の作った表のどこがおかしいかを判断するのに重要な役割を 果たす、 まさに特殊専門的な数学的知識である。 UH 川巨 この時間は、 MKT における「一般的な数学的知識」 に焦点を絞って放物線の様々な 性質の同値性などについて授業を行なった。 具体的内容は、 (a) 放物体が描く軌跡 (b) $y=\alpha x^{2}$ のグラフ (c) 焦点 $F$ と準線$l$ からの距離が等しい点の描く軌跡 (d) 1本の母線と軸を含む平面に平行な母線の法線ベクトルを法線ベクトルにする平 面で，直円錐を切ったときにできる切り口の曲線 (e) 折ってできる放物線 (f) 「美術の時間に作った曲線」 2 点 $(0, n),$ $(10-n, 0)$

ただし，

$n\in \mathbb{Z}$ 、 を結ぶ直線 族から作られる曲線 の間で、

$(a)\Rightarrow(b),$ $(c)\Rightarrow(b),$ $(d)\Rightarrow(c),$ $(e)\Rightarrow(c),$ $(e)\Rightarrow(b),$ $(f)\Rightarrow(b)$

を証明すること、 特に $(e)\Rightarrow(b)$ においては中学校の範囲内の初等幾何学的に証明する

こと、 また、包絡線の一般論を用いずに、 (e), (f) で曲線が浮かび上がって見える理由を

中学校、高校の範囲内で説明すること、であり授業中に扱え (扱わなかった) ところは最

13

終わりに

研究授業「折って作る放物線」を構成する数学の内容は次の

2

点である

:

i$)$ 準線と焦点を用いた放物線の定義 ii) 包絡線の理論 数学研究者はこれらの一般化、抽象化された理論を十分に理解すれば、その具体例へ の応用として「折って作る放物線」 の授業を中学校、 高校で実践することができると考 えるであろう。 しかし、 これまで詳しく見てきたようにこの研究授業で教師に必要な数学は、主に次 の 3 点である:

1.

中学校

(

あるいは高校

)

の範囲で、曲線が放物線であることを証明する。

2.

中学校 (あるいは高校) の範囲で、直線の集まりから曲線が見えることを説明する。

3.

生徒の表から間違っているところを見つける。 これらの内容は通常の数学の講義では触れられない。 確かに数学研究者ならば、 ある命 題を条件を変えて証明しなおすことはよく出会っていることであり、 その点では1,

2

のような考え方には違和感がないであろう。また，

3.

のような生徒の間違いの理由を 推測することも試験の採点では通常行っていることである。つまり、 数学研究者から見 れば i), ii) のような一般化、抽象化された理論をよく学べば、いい中学校の数学教師が 出来上がることになる。 しかし、実際に中学校の数学教師を目指すものの多くは数学の研究をしようと考えて いるわけではない。彼らは「数学という教科」を MKT で表される 「数学」を使いなが ら生徒に教えることを目標にしている。いわば数学のユーザーである数学教師あるいは 数学教師を目指す学生は、教師の数学利用法に適した 「数学」 を学ぶべきであり、 その ような「数学」を作り出すことは教員養成に関わっている数学研究者の責務であると考 える。 このような教師のための 「数学」 のあり方は多様であろうが、 ここで報告したような 実際の中学校高校での授業をもとにして、 そこで必要となる数学について考え深めて いくという授業形態の可能性をこれからも探っていきたいと考えている。 参考文献

[Bass, 2005] Bass, H. : Mathematics, Mathematicians, and Mathematics Education,

Bull. of AMS, vol. 42(2005), No. 4,

417-430

[RIMS1657] 数理解析研究所講究録1657 「数学教師に必要な数学能力形成に関する研

\S 2.

正多角形の作図に関する教材研究の指導について

II

by

青山陽一-

中馬悟朗

21

はじめに

前回 [1,

\S 2]

_{は，初等幾何学における作図問題が教材として適切なものであることを述}

べ，定木とコンパスによる作図 (ユークリッド作図，略して $E$-作図) について記述した． $E$

-

作図可能な場合として正五角形を，不可能な場合として正七角形を扱った．更に，ガ ロワ理論により正$n$角形の$E$-作図可能性が解明できることを材料に授業を組立てること について触れた．今回も同じ思想の下に話を進めるが，正五角形に関することを主要話 題とする．模擬授業及び並行して行った講義と教材研究としての正五角形の作図につ いて述べることにしたい． 次へ進む前にちょっと． [1,

_{\S 3]}

_{において，次の様な主旨の事を述べた}

:

『生徒の方法が正しいかどうかを判定す

るように．

』，

『自分の方法で遣らせようとするのは困る．

』，

『生徒の考え方で解くため

にはどうすれば良いかを考え，対処するように．』等々．

これは，本稿

\S 1

にも触れられている

[Bass,2005] (in

\S 1)

における特殊専門的な数学的知 識’(例えば，生徒の標準的でないものの正誤を分析する方法など) と関係がある． 今回事例で述べている講義の最初で，次の問題を出した:

二直線 $y=ax,$

$y=bx(a<b)$

のなす角の二等分線を

$y=mx(a<m<b)$

とするとき，$m$ を $a,$$b$ を用いて表わせ． 期待していたように何通りかの解法が示された: 二等辺三角形の頂点角の二等分線は， 対辺の中点を通る或いは対辺に垂直であるを使ったもの．三角形の一つの角の二等分 線は対辺をどの様な比に分けるかを使ったもの．直線の傾きは $x$軸となす角の正接であ ることより正接関数の加法公式半角公式を使ったもの． 次の三通りの解が得られた: $m= \frac{b\sqrt{a^{2}+1}+a\sqrt{b^{2}+1}}{\sqrt{b^{2}+1}+\sqrt{a^{2}+1}}$ (2.1) $m= \frac{\sqrt{b^{2}+1}-\sqrt{a^{2}+1}}{b\sqrt{a^{2}+1}-a\sqrt{b^{2}+1}}$ (2.2) $m= \frac{a(\sqrt{b^{2}+1}+1)+b(\sqrt{a^{2}+1}+1)}{(\sqrt{a^{2}+1}+1)(\sqrt{b^{2}+1}+1)-ab}$ (2.3) (21) と (22)

_{が同じものを表わしていることを確かめるのは，高校生にとっても難しく}

はないだろう．しかし，

(23)

と他の二つが同じものを表わしていることは，直ぐに判る

だろうか．また，互いに他に変形することは，生徒にとって易しいことだろうか．どの

表現を

‘

正解

’

とするのか或いはどれも

‘

正解

’

とするのか．

‘

正解∵不正解

’

とする基準は

何なのか．“これらの事が自分で根拠を持って判断出来るようになる為に” が，‘難しい’ 数学を勉強する理由の一つなのだと言う事を伝えたかった訳であるが．

22

事例

:

_{講義，学生による模擬授業}

青山が所属する島根大学教育学部では，教育課程に

‘1000

時間体験学修

’

なるものが採 り入れられている．子供との触合いの機会や学習支援活動など多彩な体験が出来るよう になっている．教育実習も含まれており，それは単位に換算される．その中で専攻別体 験学修プログラムを主専攻生に提供することが課されている．青山の属する数理基礎教 育専攻では，その一つとして [教材等の調査学習及びロールプレイ模擬授業」なるも のを実施している．2009年度は青山が担当し，代数学の講義と結び付けて初等幾何学を

題材にして実施した．学生に，[3],[4]

を勉強してきて模擬授業として説明をして行くこ とを課すというやり方である．代数学の講義は，[4] を読ませていることもあり，[4, 第 6 章]

_{を種本にして行った．標識定木とコンパスによる角の三等分線と正七角形の作図も}

含めたが，これに関しては次回に廻すことにする． 体験学修プログラムについて 先ず体験学修プログラムについて簡単に説明する．ここで報告する「教材等の調査学 習及びロールプレイ模擬授業」は，各専攻で体験学修プログラムを提供せよとの要請 により設けられた．学生は，取組むか否かは自由である．内容は次の通りである． 適当な数学のテキストをもとに，学生が順番に先生役になり，他の学生が生 徒役となって，模擬授業を行う．この活動を通して， (1) _{きちんと準備をして授業をする事} (2) _{きちんと授業を聞き，判るまで質問議論をする事} (3)

_{授業の内容，数学，を楽しむ事}

を体験し，教師としての能力を培う． 後期に模擬授業を週一コマ行い，その為の準備練習等のため同等の時間を要する，特 に先生役のときは倍位必要，として時間数を認定することにしている．適時課題を課す こともある．最後にレポート (感想等を含む) の提出がある．また，学内資格取得のため の基礎知識を修得するものとしての位置付けも持たせている．

2009

年度は青山が担当者になったので，我々が取組んでいる「正多角形の作図に関す る教材研究の指導」と合致させることが可能であるとの判断で，[3L[4] をテキストにし

て実施することにした．幸

$l$), 特色

GP

予算と体験学修用予算で書籍 [3],[4] と教師用定 規 (マグネット付) _{コンパスを購入して貰うことが出来たので，大いに活用した．} 対象とする学生について 上記プログラムは

2

年生 (及び3年以上で未体験の者) を対象としている．代数学幾 何学解析学分野では次が既修である: 線型代数学

4

単位，微分積分学

6

単位，代数学 2単位，幾何学4単位．行おうとしている内容に対しては十分である．教育実習関係で は，附属学校における授業観察を 1 年次から行っており，2 年次前期には研究授業を行い 教壇に立った者も居り，研究授業協議会も経験済である．模擬授業の意義は理解してい ると考えて差支えないだろう．

募集したところ，数理基礎教育主専攻生

2

年生

10

名全員が応募した．代数学の講義の

直前の時限が空いているとのことなので，その時限で模擬授業を行い，続いて講義を行

うという都合の良い次第となった．しかも同じ教室で実施可能であった． 講義について

1

年次に線型代数学を学ぶことになっている．前期で行列と行列式，後期で線型空間

の基礎理論を教えている．これらは

2

年次の代数学を学ぶ上で必須である．行列と行列

式については自由に扱えることが必要であり．線型空間の基礎理論では，線型独立・基 底次元に関することは常識となっている必要がある．(現実は，覚束無い感じだが．)

2

年次前期で，群環体の基礎理論をやる．講義ノートの

pdf

file

の入った

CD-ROM

を受講生に渡し，要点を講義で行うようにしている．全てをかっちりと遣ることはしな いことにしている．(全てをかっちりと遣ることは，非常に厳しいらしい．)2009年度は， それらの概念が生み出されてきた経緯等を述べ，この理論により，角の三等分線と立方 体倍積の $E$

-

作図不可能性が証明されたことを述べた．

“

この代数学的解釈が，古典的な

作図問題の不可能性を厳密に証明する道具を，初めて提供したのである．もしこれらの

証明が今日やさしく見えるとすれば，それは私たちが当然のこととしている現代代数学 すべてのためである．

”([4,

第6章最初]).

こういうことは強調しておきたい．先ず，正

の実数 $a$

に対しその平方根轟の

$E$

-作図法を問題として遣らせる．まあ大体出来るよう

だ．そうすると，座標平面上で

(0,0) と (1,0) から，1から加減乗除と正の平方根を取 ることを有限回繰返して得られる実数を成分とする点が全て $E$-作図で得られることを示 す．これが判ると，正五角形が$E$

-

作図可能であることは簡単に判る．具体的に正五角形 を $E$-作図することを課題にする．大体支障なくこなせる．実際に黒板でも遣って見せる 力$\searrow$

学生に遣らせる．実行内容については，

232

節，

233

節を参照されたい．次にガロ

ワ理論を生み出した 4 次以下の方程式には解の公式があり，5 次以上の方程式には存在 しないことを述べ，4次以下の方程式の解き方を示す．そしてレポート問題にする．通常 は

1

次から始めて

4

次に至るのであるが，たまに

4

次から始めてそれに必要だから

3

次

をやりとするのが居る．

1

次，

2

次は大前提であり書く必要がないらしい．高校までのこ

とは既知で

3

次，

4

次を新しく学ぶのだからということらしい雰囲気である．

1

次方程式 に触れない者が結構居る．

1

次方程式 $ax+b=0$ の解が $x=- \frac{b}{a}$ である，というのは

解の公式ではないらしい．

2

次方程式

$ax^{2}+bx+c=0$ の解が $x=\underline{-b\pm\sqrt{b^{2}-4ac}}$ で

ある，というのが解の公式の資格ありという感じか．こういうことも頻繁

$F$

It

ポートな

どで調べておく必要があるかも知れない．等式

$(\cos\theta+i\sin\theta)^{n}=\cos n\theta+i\sin n\theta$ を利

用して，$\cos n\theta$ を $\cos\theta$ の整数係数多項式で表わせを同時にレポート問題にする．これ

には期待を裏切られた．ウーン．一般の $n$ にするとこんなものなのか．

模擬授業と並行して行った代数学の講義(2 年次後期) について述べよう．最初に行っ

たことについては

21

節を参照．標識定木に関すること

([4,

\S 30])

は次回に廻す．体の拡

はこんなものかで良いのだが，具体例を扱うとキョトンとするのが結構居る．

$\mathbb{Q}(\sqrt{2})$ の

$\mathbb{Q}$

上の基底として

1,

〉うが取れ，

$\mathbb{Q}(\sqrt{2})$ の $\mathbb{Q}$

上の拡大次数は

2

である．と言うとキョト

ン $(\begin{array}{l}11\end{array}),$ $(\begin{array}{l}12\end{array})$

が線型独立であるというのは納得出来るが，

1,

$\sqrt{2}$ が $\mathbb{Q}$上線型独立であ

るというのには抵抗感を感じる者が居るらしい．その証明となると

ウー

ン．

$\sqrt{2}$ が無理

数であることと同値だよと教えると，

「面が無理数であるから，

1,

$\sqrt{2}$ は $\mathbb{Q}$上線型独立

である」と書いて終わりにする．

「而が無理数であることを証明し，上記を示せ」にき

ちんと答えられた学生はどの位居たでしょう．と言う訳でかなり丁寧に説明し，証明を 示さないとならなかった．でもメゲズに頑張ろう．で，$E$-作図可能であるためには，そ の点に対応する数が充たす既約 $\mathbb{Q}$係数方程式の次数が2の票であることが必要である， を示した．これにより，角の三等分問題と立方体倍積問題に否定的解決が得られたこと

を述べる．更に，正

$n$角形が$E$

-

作図可能であるための条件を与えた．

(cf.

[1, 2.5 節]) 途

中でアイゼンシュタインの既約性定理を示す．これを使って

$\sum_{k=0}^{n-1}X^{k}$ が$\mathbb{Q}$上既約 $\Leftrightarrow n$

が素数” を示すことを問題にする．最後に体裁を整えるために，ガロワ理論の基本定理 を記述し，可解性の概略を述べた．ここらは教員の自己満足か．でも述べておきたい． 模擬授業について 学生を三つのグループに分ける: 原論 [3] を読むグループ (4名), [4, 第2章] を読む グループ (3名), _{[4, 第 1 章]} を読むグループ (3 名). 先ず，有名ではあるが読んだ事はないであろうユークリッド幾何学原論に触れること

から始める．座標幾何を知っているのでその視点が入ってしまうだろうが，当時のもの

そのままの形に忠実に再現することを心掛けていくのが肝要であることを伝えておく． 巷間で言われているのとは違うものも多いので，気を付けないと．と言う訳で，最初か

ら読み始めた．定義

(23個), 公準 [要請](5個), 公理 [共通概念](9個). 黒板に列挙し て行き説明を試み，「訳判らない」 と．「そんなこと．気にせず進もう」．図も交えなが ら解釈を披歴しながら何とか遣り終える．「根気が必要．訳が判らなくても続けることが 出来るのは若者の特権 $($?$)$ とか$\searrow$ どこかの本で読んだことがあります」

と．続いて命題

に入る．命題やその証明には少しは慣れなどがあるので，割と遣り易くなったようであ る．が，何を何処でどの様に使ったのかを必ず説明する様に要請する．こうして，原論 を読むグループは終わった．行き着いたのは，第

1

巻命題

12.

正五角形の作図なんて遥 か先．でもこれで良いのである．兎に角，原論に触れ，

–

っづっ積み上げて行く操作を 学ぶ事が重要なのですよと．ここで次のことを注意する: 量というのは第5巻からで ある．従って，全ては図形の操作多くは作図の形で表現されていることに注視して欲し い．方罵の定理やピタゴラスの定理も数値で表現されているのではなく，例えば「二つ の正方形の和が他の正方形に等しい」と言う様に表現されている．この調子で正五角形 の作図まで遣ってしまうのである．これを追いかけて正五角形の E 作図に挑戦して欲し いものです．(例えば，231節にあるように．)「使えるものはそれまでに済ませたことの みである」 と言ったが，実は当時は余りにも当たり前とされたのか$\searrow$ 何の説明もなく使

われている事柄が在る事にも注意するように．

次に，ハーツホーンの本

[4]

_の第

₂

_{章を読むグループに移る．原論は長い間完全なもの}

と思われていた，一方その公準・公理の立て方などに対する省察が多くの人によってな

され続けた．そうしてヒルベルトによりユークリッド幾何学を打ち立てるに必要十分な

ものが与えられた．ユークリッド原論ができたのが紀元前

300

年頃とのこと，ヒルベル

トの幾何学の基礎が出たのが紀元後

1900

年頃，実に

22OO

年の隔たりがある．これを現

代数学の視点から解説した教科書がハーツホーンの本

[4] であることを述べる．

[4]

の第

2

章を最初から遣り始める．ユークリッド原論よりもこちらの方が読み易いと感じてい

るようだ．当然のことではあるが，これは自分で気付いてもらわないと．進み方は前の

グループと同様にして

3

名が終えた．読んだのは，

\S 6

と

\S 7

の途中まで．現代数学の厳密

さと理論構成の方法を少しでも学べれば上出来である．

最後にハーツホーンの本[4]

_の第

1

章を読むグループの番となった．

[4,

第1章] では作

図することが求められるものが多くあり，その標準手順回数も記されている．公理系や

基本的な事柄ばかりでは

‘

味気ない

’

だろうとのことで，

[4,

第

1

章

]

の中からトピックを

選んで説明するようにと指示した．結局私が選ぶことになってしまったが，全体に軽く

目を通すこと，オイラー線と九点円の定理について解説することを提案した．正五角形

の作図についての

\S 4

_{ではなく．}

\S 4

_{を読むのなら，きちんと全部を読むのが良いだろう}

し，これは多分時間的に無理だろうし，少し毛色の違うのを遣っておくのも良いだろう

しという訳である．結構皆が興味を持ったようである．並行して幾何学の講義で初等幾

何の諸定理を扱っていた時期とも重なったことでだそうだが．ここら辺りになると，余

り

‘

違和感，は感じないようだ．だが，循環論法などに陥らないように気を付けるべしと

注意．

体験学修プログラムの最後に次の課題を出した．

次の問いに応えよ (註 :(‘答えよ” _でなく “応えよ”) ＾燭觧 とは，何時か

?

燭訃貊蠅箸蓮げ申茲

?

０燭訖 (講演者)

_{とは，誰か}

_?

げ燭砲弔い討旅岷蕕

?

ス岷蕕鯤垢 に来た人は，何人か

?

ν儖佞靴芯弘愡劼蓮げ慎咾

?

課題．上記 ァきΔ砲弔い;

(ア) 算数の範囲 (文字式等を用いない)

_{で，図などを使って，解答を与えよ．}

(イ) 中学 1 年の範囲 (使える文字-未知数-は1つ) で解答を与えよ．(二通り) (ウ) _{中学2年の範囲 (}連立一次方程式，使える文字-未知数- は 2 つ) で解答を与えよ．

文章は附属中学校での教育実習の際に出されたものである．対象学年は

1

年，従って

(イ)

_{が扱われたものである．この模擬授業で扱ってきた内容とは関係がないが，授業の}

仕方と各々の範囲での解法についての意見を聞きたかったので． ， ら い泙任六賛堯

数学ではないが，文章を読んで疑問を持つかも知れない事柄にどう対処するかを伝えた かったのである．

(cf.

[1, 2 ページ目

3

つ目の黒丸

])

$($ァ$)$ , (イ),(ウ) すべてを授業のつも

りで遣らせたところ，どの学生も，説明図も良く，満足のいく結果であった．だが比較

検討になると，議論が進まなくなる傾向がある．中学

1

年で扱っているから

(イ) の方法

が妥当であると思ってしまっている感もあるようだ．説明図が上手く出来ていれば

(ア) で良く理解出来る (文字を使った方程式 (なんか) を考えなくてもよい)

_{し，方程式を使う}

のなら (ウ)_{の方が見易いと思わないかと言うのが伝えようとしたことであり，扱ってい}

る数学の内容に対してどのような題材を使うのかについての見識を持つ為にも大学で習

う数学を勉強して欲しいという訳である． 青山の感想反省 模擬授業では原論 [3] を読んで行くのであるから当然数値計算や文字式を使用したり しない．一方，講義ではガロワ理論というのがテーマであるから多項式が活躍する．図形

だけの操作と式を用いた分析の違いについては，意図的に明確な説明はしなかった．学

生がどの位感じるかに興味があったのである．あまり高望は良くないことは承知の上で．

模擬授業を通して良い意味での

‘

素朴

’

な幾何の雰囲気を味わって欲しいと願っていた

が，学生は教育実習に向けての練習としての捉え方が主であった．もう少しこちらの意 図を伝えて，模擬授業の中でもそちらに注意を向けさせるのが良かったかなと思ったり している．

最近は，何を目的としているのかを説明して実施することが推奨され，良いこととさ

れているが，反面

“

それさえやればよいのだ

”

との風潮が支配的になるのは好ましいこと とは思えない．それ以上のものを吸収してやろうという気概を持たせるにはどうすれば 良いかも考えなければならないだろう．

中学校数学で扱われる問題を題材として模擬授業をすると，結構

‘

上手い

’

授業をする

のであるが，分析となると，既習の教科内容で行えるのに，そういう発想は持たないら しく，こちらの意見を聞いて覚えようとする者が殆どになってしまう．ここら辺りにも 我々が取組んでいる課題の必要性が見て取れると思う．

全般的に見て，青山の意向が成功したとは言い難いと感じている．次年度も担当する

ことになれば，今回のものを踏み台として

‘

良い

’

ものにして行きたい．

2.3

正五角形の作図について

23.1

原論における正五角形の作図 この小節では，模擬授業で目指したユークリッド原論における正五角形の作図を学ぶ ために必要な命題を順に簡潔に述べることにする．こういう構成が出来るようになるこ

とを目指して，大学で数学を学び教材研究を行うのである．原論は

[2] から引用している

が参考のために，簡単にかつ学校数学に適するような表現で翻訳する．なお，作図だけ

にとどめて証明は省略する．

[Book4-Proposition11]

In

a

given

circle

to inscribe

an

equilateral

and

equiangular pentagon.

[第

IV

巻．命題

11]

与えられた円に内接する正五角形を作図すること．

図21:

作図．(図 21) 底角 G, H がそれぞれ頂角 F の 2 倍である二等辺三角形

FGH

を

[IV-10] を用いて描く．次に，[IV-2]

を用いて，円

ABCDE

に内接するように

ACD

を

$\triangle ACD\infty\triangle FGH$ _{となるように描く．角}

ACD

_と角

ADC

_{の二等分線と円}

ABCDE

_との

交点をそれぞれ E, B

とする．このとき，円

ABCDE

に内接する五角形

ABCDE

は正五

角形である 口

上の作図で用いた命題の作図，作図法を順に述べる．

[Book2-Proposition11] To cut

a

given straight line

so

that the rectangle

contained

by the whole and

one

of the segments is equal to the square

on

the remaining segment.

[第II

巻．命題

11(

黄金分割

)]

与えられた線分を次のように (二つに) 分ける点を求める． 線分全体と 1 つの部分によって囲まれる長方形 (の面積) が残りの部分を一辺とする正方 形 (の面積) と等しい． 作図．(図 22) 与えられた線分を

AB

とし，線分 AB を一辺とする正方形

ABDC

を作 る．線分

AC

の中点を点 E とする．点 E を中心，半径 EB の円と線分

EA

の点

A

側の 延長と交わる点を点 F とする．点

A

を中心とし，半径

AF

の円と与えられた線分

AB

との交点を点 H とすれば良い．

この点

H を黄金点といい，線分

AB

を点

H

で黄金分割するという． 略解

:

AB

$=$

AC

$=1$

とする．

AE

$=$

 だ 分

BE

$=$

EF

$= \frac{\sqrt{5}}{2}$, 線分

AF

_$=$

AH

$= \frac{\gamma_{5-1}}{2}$.

AH

$=x$ とおくと

BH

$=1-x$ であるから命題は $x^{2}=1(1-x)$ であるからこの方程式 を解いて $x= \frac{\sqrt{5}-1}{2}$

を得る．

$F$ 口 図22:

[Book4 - Proposition2] In

a

given circle to inscribe

a

triangle equiangular with

a

given triangle.

[

第

IV 巻．命題 2]

与えられた三角形と相似な三角形を，与えられた円に内接するように

作図すること．

作図．(図23) 与えられた円を円 ABC, 与えられた三角形を $\triangle DEF$ とする．点

A

_で

円 ABC と接するように GH を引く．次に線分 AH 上の点 A において $\angle DEF$ _と等しい

角 $\angle HAC$ _{を作図し，さらに}

AG

_上の点

A

_において $\angle DFE$ _と等しい $\angle GAB$ _を作図し

て，BC を結べば，$\triangle ABC$ が求める三角形である．ロ

[Book4-Proposition 10]

To construct

an

isosceles triangle havingeach

of

the angles

at the base double of the remaining

one.

[第

IV

巻．命題

10]

二つの底角が残りの角 (: 頂角) の2倍となる二等辺三角形を作図す

ること．

作図．(図 24) _{図において，まず任意の線分}

_AB

_{を引き，点}

_C

で二つの部分に分け，

AB,

BC

を2辺とする長方形の面積と

AC

を一辺とする正方形の面積が等しいように分

の円 BDE(:円 A)

_{が描かれ，円}

BDE

上の点 $D$ を

BD

$=$

AC

となるようにとる．

BD,

CD,

_{AD を結ぶ．このとき，}

$\triangle ABD$

が求める二等辺三角形である．口

図24:

2.3.2

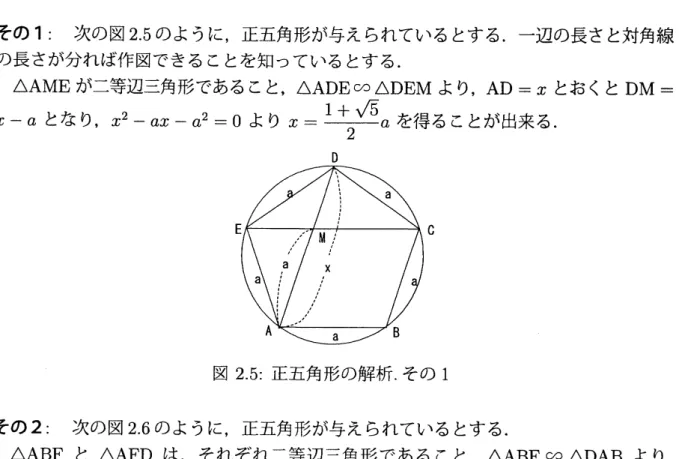
正五角形の解析 この小節と次の小節では，主に講義で行った正五角形の作図に関することを述べるこ とにする．(実際に行ったのは一部である．) その1:

_次の図

₂₅

_{のように，正五角形が与えられているとする．一辺の長さと対角線}

の長さが分れば作図できることを知っているとする．

$\triangle AME$

_{が二等辺三角形であること，}

$\triangle ADE\infty\triangle DEM$

より，

AD

_{$=x$ とおくと}

DM

_$=$

$x-a$ となり，$x^{2}-ax-a^{2}=0$ _より $x= \frac{1+\sqrt{5}}{2}a$ _{を得ることが出来る．}

図25: 正五角形の解析．その1

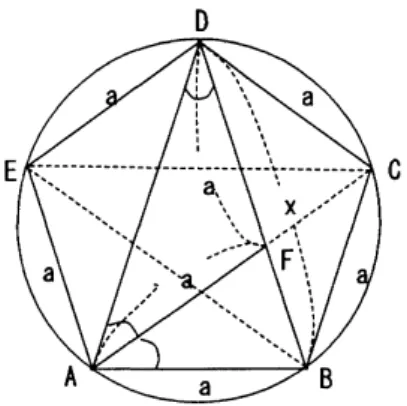
その 2: 次の図

26

のように，正五角形が与えられているとする．

$\triangle ABF$ _と $\triangle AFD$ _{は，それぞれ二等辺三角形であること，}$\triangle ABF$ co $\triangle DAB$ _より，

BD $=x$ とおくと BF $=x-a$ となるから，$x^{2}-ax-a^{2}=0$ _より $x= \frac{1+\sqrt{5}}{2}a$ _を得る

図26: 正五角形の解析．その2 解析から正五角形の一辺の長さと対角線の長さは (一辺の長さ) :(対角線の長さ) $=1$ : $\frac{\sqrt{5}+1}{2}$ であることが分る．また (一辺の長さ) :(対角線の長さ) $= \frac{\sqrt{5}-1}{2}$ :1 も良く用いられている． これは「黄金比」とか「外中比」「中末比」とか呼ばれている．原論において黄金比は 第2巻命題11, 第6巻定義3及び命題30である． 正五角形に関するその他の性質について．

(

一辺の長さ

):(

対角線の長さ

):(

外接円の半径

):(

内接円の半径

)

$=$ 1 : $\frac{\sqrt{5}+1}{2}$ : $\frac{\sqrt{10(5+\sqrt{5})}}{10}$ : $\frac{1}{2}\sqrt{\frac{5+2\sqrt{5}}{5}}$

$=$ $\frac{\sqrt{10-2\sqrt{5}}}{2}$ : $\frac{\sqrt{10+2\sqrt{5}}}{2}$ : 1 : $\frac{1+\sqrt{5}}{4}$

であることがわかる．

仝凝

O

を中心，半径

1

の円を描き，座標軸との交点を図

27

のようにおく．

PO の中点を M とし，M

_{を中心，半径}

MS の円を描き X 軸の正の方との交点を

$N$ とする．

このとき，次のようになっている．

MS

_$=-$

$\sqrt{5}2$ ,

ON

$= \frac{\sqrt{5}-1}{2}$ ,

RN

$= \frac{\sqrt{10-2\sqrt{5}}}{2}$ , PN $= \frac{\sqrt{5}+1}{2}$.

黄金比を求めるには，図 27 を利用する方法は基本的であるが，次の図 28 のように

「円と割線の関係」を利用したものもある．

すなわち，与えられた線分を

AB とし点 $B$

において，AB

に垂線 BO,

BO

$=$

lBA

を引

く．点 O を中心とし，半径 OB の円を描く．点 A

と点

O 結び，円 O

との交点を P, Q

図27:

$\backslash \backslash \backslash \backslash ..\tau$

$\wedge^{/}$’

$\backslash _{L}---,-$

,

図28:

AB:AQ

$=1: \frac{1+\sqrt{5}}{2}$ ,

AB: AP

$=AB:AR=1$ : $\frac{\sqrt{5}-1}{2}$ となる点 $R$ を黄金点とい$b^{\backslash }$, 線分

AB

を点 _$R$ で黄金分割するという．

233

正五角形の作図 「一辺の長さが与えられたとき」 その 1: まず，図

28

を利用して正五角形を作図すると (cf. 図 29) 点

B

_{を中心として，半径}

AB

の円と点

A

を中心として，半径

AQ

の円を描き，交点を

C

とする．点

A

と点 B

を中心として，半径

AQ の円を描き，AB の上側の交点を D と

する．点

A

を中心として，半径

AB

の円と点 B

を中心として，半径

AQ

の円を描き， 交点を

E

とする．このとき，出来ている五角形

ABCDE

は正五角形である． 図 29:

その 2: 図

27

において，点 P を A, 点

O

を B とする．点

O

すなわち点 B を中心， 半径

OP

の円と点

A

を中心，半径

PN

の円との交点を

C

とする．点

A

と点 B を中心 とし半径

PN

の円を描き，その交点を

D

とする．点

A

を中心，半径

OP

の円と点

B

を 中心，半径

PN

の円との交点を

E

とするとき，出来ている五角形

ABCDE

は正五角形 である．

「半径の大きさが与えられたとき，円に内接する正五角形の作図」

その1: 図27で考える． 点

R

を点 D とする．その点

D

を中心として半径

RN

の円を描いて，円

O

との交点を E,

C

とする．ただし，左側が E とする．点

E

中心とし，半径

RN

の円と円

O

との交点 を A, 点

C

を中心，半径

RN

の円と円

O

の交点を

B

とするときできる五角形

ABCDE

は正五角形である． $D$ 図 210: その2: 図27で，与えられている円を線分

ON

を一辺とするように切って出来る図形 は正十角形である．正十角形の頂点を

1

点おきにとって正五角形とする方法．

[References]

[1]RIMS

_{共同研究数学教師に必要な数学能力形成に関する研究，数理解析研究所講}

究録 1657,

_{京都大学数理解析研究所，}

2009

July. p.105-p.127

6.

教科専門科目の内容を活用する教材研究の指導方法 (Team2 プロジェクト).

[2]

Sir Thomas

L.

Heath

訳:The Thirteen Books

of

theElements (Euclid $s$Elements),

2nd ed. Cambridge

Univ.

Press, 1925,

repr.

New York Dover,

1956.

[3] 中村幸四郎-寺坂英孝-伊東俊太郎-池田美恵訳:

ユークリッド原論，共立出版，

1971.

[4] ロビンハーツホーン著 (難波誠訳): 幾何学 I,II,

_{シュプリンガー．ジャパン，}

\S 3.

数概念の取扱に関して

by

青山陽一

-

曽布川拓也

数に関することは，算数・数学教育において大きなテーマである．小学校入学から高等

学校卒業まで，数えることから始まり複素数に至る．理論的には，ペアノ公理系を出発

点として自然数整数有理数・実数・複素数と構築していく方法で教授するのが通常

であろう．しかし，小学校から高等学校に至る数概念の拡張はこの順序でなされていな

いことは周知であろう．また，四則演算の導入も理論的構築におけるものと一致してい

るとは限らない．用語等についても然りである．従って，教員養成機関において理論的

構築方法だけで数概念を教えることには問題があると思われる．更に，中学校・高等学校

(数学)

_{の教員免許状取得のためには，数学の単位が必須であるが，小学校の教員免許状}

取得のための算数科内容に関する単位数は

2

であり，しかも必修ではない．一方，履修

のさせ方は大学学部等毎に異なる．小学校教員を目指す学生にも中等系の専門科目を課

しているところもあれば，中等系の専門科目を修得する必要のないところもある．等々，

状況は極めて多岐に亘る．数の概念を修得していくうえで，小学校で扱われる事柄は根

源的であり，非常に重要である．中学校では，負の数の導入，無理数の認識などの飛躍が

なされる．このような環境の中で教員養成に携わる数学者は，小学校から高等学校まで

の数概念の取扱われ方をしっかりと把握しておく必要がある．

例を挙げてみよう．数を初めて認識する或いはさせることはどの様なプロセスなのか．

数の表し方については．足し算の導入そして引き算はどういうものか．掛け算はどの様

に定められるのか．計算方法は．割り算とはどういうものか．約数・倍数・最大公約数な

どの初等整数論の初歩的部分はどの程度の扱われ方が妥当か．小数分数の導入方法とそ

の計算についてはどの様な考え方で行われるのか．大小関係に関することは．四則演算

との両立性についてはどうか．負の数の導入とその計算，大小関係との両立性．無理数

の認識，実数の捉え方．複素数については．

この問題に対し一つのプログラムを提起したいというのが，我々の目標である．明確

に全体像を持っている訳ではなく，それを形造ろうというのが目論見である．今の段階

では，先ず小学校から高等学校までの算数・数学の教科書における数概念の取扱われ方と

指導についての調査から取掛る計画であることしか報告し得ないが，上記目標に向かっ

て進んで行くことを述べて終わらせて頂きます．

なお執筆者の一人である曽布川が同僚の平井氏と共同で，小数・分数の乗法・除法の指

導法について考察した論考 [1]

_{が次に載せられているので，是非参照して貰いたい．}

“

我々数学者が忘れてしまいがちな要素

”

に触れている [1, 第 3 節] には目を通して欲しい．

[References]

[1] 平井安久-曽布川拓也

:

数学者からみた 「算数教育」

について，本講究録所収．