3次元弾性基本解(線対称解)の有限要素解析 : 有限要素法による弾性基本解の解析に関する研究(その2)

【論　 文】 UDC ：624

．

042 ：519

．

6 日本 建 築 学 会構 造系論文報告集 第407 号

・

1990 _年 1月

3

次 元

_弾性

基

_{本 解 （}

_線

対 称

解

）

の

_有

_{限 要}

_素

_{解 析}

有 限要 素法

に よ る

弾

性 基 本解

の

_解析

に

_関

する

_研

_{究 （}

その

2

_）

正 会 員

　

藤

　　

谷

　　

義

　　

信

＊ 　 1

．

序 　無 限 領 域 中の

一

点に集中荷 重を受 ける場 合の荷 重 点 近 傍の弾 性 応 力お よび変位の解は弾性 基 本 解とよ ばれ てお り

，

境 界 要素法等の_{解 析}法の なか で重 要な役 割 をす る。 前 報1） で は，

2

次元 領 域 内の弾 性 基 本 解 を 有 限要 素法に より数 値 的に_求め る方 法を提 案し

，

良 好な解が得ら れ る こと を示し た

。

こ の_方法では

，

荷 重 点 近 傍の応 力特異 性 が r

−

1 _（r は荷重点か らの距 離 ）

，

変 位の特 異 性 が 苴og r で ある こと に着目 し 理論 展 開を行い

，

最 終 的に荷 重 点近 傍 を半 無限 長 く さ び 形要 素に分 割し た と き の_要素剛 性マ トリックス を導い て いる。 こ のよ うに

，

2次 元弾性 基 本 解 を求め る問題は

，

有限要素法で定 式 化さ れ て連 立 方程 式 を解 く問 題に帰 着され るが， 3 次元 弾 性 基 本 解の 場合は，

3

節で説 明 するように

2

次元問 題と は異なっ _た 定 式化が 必要とな る

。

　

2．

基本解の解 析 法

　

基本解を求め る方 法と して

，

解 析 領 域 内の

一

点に単位 の大き さの_集中力が作 用し た とき のつ り合い方程 式 を作 り， これ をフ

ー

リエ 変換により解 析する方 法が

一

般に行 わ れ ている

。

この方 法により

，

た と え ば

，

松 岡 と勅 使 川 原は_，

Transversely

・

isotropy

に お け る

Kelvin

解 を求

め2）

，

さ ら に

，Boussinesq

_解3 ）

_，

　Cerruti_解4） ，　Mindlin 解 5｝ を 求め ている

。

この フ

ー

リエ 変_換を解 析 的に行うこと が 難しい 場 合は

，

数値的に近 似 解を求める こと が行わ れて い る

。

こ のよ う な 基本 解の数 値 漸 近 解の_求め方お よび解 析 例につ いて は文献6＞で議 論 されて いる

。

　

本 論 文で提案す る 3次 元 弾 性 基 本 解の解 析手 法 は

，

基 本 解の応 力， 変 位の 解の形 が球座標 軸 r のべ き乗 項を 有 する変 数 分離形 で あ ること に着 目して解 を求め よ う と す る手 法であり， これ までの基本解を求め ようとする手 法とは異な る独 自の手 法で あ る。 　r の べ _{き乗 項 を有す る解を求め る手 法は}

_，

_すでに

2

次元， お よ び3次 元 領 域 中の クラッ ク先 端近傍の解を求 める手法 として提案さ れて お り

，

以下に示す よ う な研 究 が_{報 告}さ れ ている。 まず

，

Williams ’） は， 任意の開き角 を もつ 2_{次元 ク ラックに}つ い て

，

2つの ク ラック 辺 が自 1 _{広 島 大 学} 　教授

・

工博 　〔1989_年3月2e日 原稿 受理

，

1989 年10月17日採 用 決 定 ） 由 辺と固定辺の組み 合わ せ に よ る 3と お り の場 合につ き， 極 座標 系に お けるエ ア リ

ー

の 応 力 関 数を用い て ク ラック先 端 近 傍の応 力 特異解を解析的に導い ている

。

こ の _問題は特 異 性の大き さを固有値と する固 有 値問 題 と な る

。

ま た

，Williams

は

，

古 典 板曲 げ 理論に よる_{板 曲}げ 問 題におけるクラッ ク先 端の応力特異 解 を 求め， 面内変 形 問 題の特 異 解との間に解の双対性が ある こと を確か め て い る8｝ 。 3次 元 問 題と して は， Benthem9 ）_が ， 物 体表 面 近 傍の クラック先 端の応 力特異 解を求 めて い る

。

これ は球座標 軸r のべ _{き乗 項 を 有す る解を}

_，

_{3次元弾性 論} にお け る 7つ の

basic

　_{solution で組み} 合わせ て導い た も の であ る。 こ の 3次 元 表 面ク ラッ ク問題につ いて は

，

筆 者が

，

3っ の

basic

　solution _{を 用}い る い わ ゆる

一

般 化 さ れ た

Boussinesq

関 数 を用い て解い て い る10）

_。

　

一

方

，

これ らの r のべ _{き乗項 を有 す}る特 異 解 を解 析 的に では な く数 値 的に求め る方法につ い てもい くつ か報 告さ れて い る

。Bazant

と

EstenssoroM

は 3次元表面ク ラックの応 力 特 異 解 を有 限要素法で定 式 化し， 固有値解 析に よ る応 力 特 異 性の大き さ を求め

，

Benthem の_解と 良い_対応を示す こ とを確か め てい る

。

筆 者12Jは_， こ の_表 面ク ラッ ク問 題 をRayleigh

−Ritz

法で数 値 的に解い てい る。 ま た

，

筆 者は

，Bazant

ら が提案し た有 限要 素 法を

，

2次元 クラッ ク の応 力 特 異 解の_{解析問 題}に適 用し，

Wil・

liams

の面 内 変 形お よび板曲げ問 題の特 異 解 が 数値 的に 容易に得ら れる こと を報 告 して い る13 ）

・

14 ）

。

筆 者は

_，

この 数 値 解 析 手 法に よ り， 異方 性 材 料 中 15 ） ， 異 種 材料境界 線 上13 ）_お よび弾 塑 性 材料 中16） の

2

次 元ク ラック先 端近傍の 応 力特異 解 を求めてい る

。

　

ところで

，Kelvin

解と 呼 ば れて い る 3次元弾性基 本 解も

，

球 座 標 系で表すと r のべ _{き乗項を有 する解 とな} っ ている。 こ の基 本 解 を， 上で述べ た よ う な特 異な 固有解 の中の

一

つ _とし て位 置づ け られ ること を議 論し た_論文は 見 あたら ない

。

_{本 論 文}は

，

ク ラッ ク 問 題の特 異 解 を求め る手 法 を 用いて，

3

次元弾性 基 本 解 を求め よ う とし たも の である

。

こ の場 合

，

変位の 解につ い て は

_，

r の _{関 数} はべ き乗の形 をし てい るの で

，

こ の べ _き乗の _大き さ λ を固 有 値と し

，

r 以 外の θ

，

　epの関 数を固 有 関 数と する 固有値 解 析を行おうと するもの であ る。 こ の と き

，

基本

一

₇₁

一

解の解 析 問題 は

，

ク ラッ ク 問題と異な り

，

固 有 値 λ の 値が

一

1で あ ること が あ ら か じ め わ かっ て い る問 題 とな る

。

　静 的 問 題の基 本 解に対して

，

_点加 振解と呼 ばれる動 的 問題の基 本 解 が ある。 こ の点 加 振 解を有限要素法を 用い て半 解 析 的に求め る方 法と して 3次元薄 層 法 が知ら れて いる17｝

・

］S）

_。

_{こ の} 手 法は

，

円筒座標 系（r

，

ep

，

　z）におい て

，

r 方 向に

Hanke1

変 換

，

　_ep方向に

Fourier

級 数展開さ れ たz 方 向の み の関 数である解を有限要 素法に よっ て離 散化する_方法である

。

本 論 文で提 案す る3次 元弾性基 本 解を求め る方 法 も

，

変 数 分 離さ れ た解に おいて

，

r 方 向の 項 を 取 り出し

，

残りの項に_対し て_有限要素法 を適 用 す る点で3 次元薄層法と類 似し た解 析法であ る

。

　

3．3

次 元弾性 基 本 解に つ いて

　

3次元弾 性 基 本 解は図

一

1に示す よ う な無限

領

域 中の

一

_点に単 位 荷 重 を受ける場 合の

解，

す な わ ち

1

（elvin 解 の ことであるが， 前 報の 2次 元 弾 性 基 本 解の場合と同様 に し て， 本 論 文で も図

一

_2に示す

_B6ussinesq

_解

_，

_図

一

₃ に示す

Cerruti

解を も3次 元 弾 性 基 本 解に含め る

。

た だ し

，

本 論文で は

，

こ のう ちの線 対 称 解で あ る

Kelvin

解

y

y

　 　 　 z 図

一

1Kelvin 解 　 　 z 図

一

2Boussinesq 解 X X と

Boussinesq

解 を解 析し

，

面 対 称 解で あ る

Cerruti

解 につ い て は次 報で取 り扱うことにする。 　いま

．

図

一

一

4a

，

　

b

に示 す よ うな

，

半 無 限 領域の_表面に 垂 直な力が作 用する場 合を考え

，

荷 重 点を座標の原 点と す る球 座 標 系 （r， θ， ¢）をと る。 こ の 領 域か ら任 意の半 径 を もつ半 球を切 り出す と

，

この半球面に作 用す る応 力 σ

。

，

τ

．

θと荷重 1 との間に は

，

荷重線に関して軸対 称 応 y 　 　 z 図

一

3Cerruti 解 図

一

4a 球座標系

φ

　 　 　 r 図

一

4b　半 球 面上 応 力 と外 力のつ り合い X sin θ

力状態に あ ること か ら

，

荷 重 方 向に対し て次のつ り合い 関 係が成立す る。

　　

　

∬

ノ

℃

（・r・ ・s ・

−

Tr・s… ）r ・ s…

d

・

d

・

− 1

　 　 　 　

………・

………・

……・

（1） この式が成 立する た めに は

_，

_{応 力 成 分}が r

−

2 の項 をも た なけれ ば な ら ない

。

そ して， ひず み成 分 も また r

”

2 の項 を もつ ことにな り

，

その た め

，

変位は （3）式を参 考にする と r

−

1 の_項をもつ こ_とにな る

。

し た がっ て

，

応 力 も変 位も r のべ _{き乗 解と な るの で} ， この種の 解析 問 題は文 献13 ）と 同様の_{手 法}が適 用で き る

。

す な わ ち

，

以 下に説 明す る よ う に変位の r の べ _きの 大き さ を ひ と まず未 知 数λとし て定式化す る方 法で ある

。

4．

解 析 法 　4

．

1　仮 想 仕 事 方 程 式の _{誘 導} 　r の べ _{き乗 項 をも}つ 変_{数 分}離_形の 軸 対 称 変 形 問 題に おける変 位 式は

，

次式で_表さ れ る

。

　 　　Ur_（r_，θ_，ψ）； rλuf_（θ_）

　　　

Ue（r，θ，ψ）＝ r λ_u 彦（θ｝

　　

・

冒

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

…

　『

（

2

） 　 　　Up（r

，

θ

，

9）＝ O こ れ か ら ひずみ式を求 める と次の よ うに な る

。

Er

一

警

≒

r・

−

1_λ ・

f

・・

一

 

号

留

一 广 ・

侮

＋

鬱

）

・_・

一

 

＋

舞

一 rA

一

亘

（

uf_＋

多

・：

）

　 　 　 ∂Ur 　 　 　 ∂Ue 　 　 l 　 　 　 uθ γ・θ

＝

下

Tt

・

＋万

7

−

7

一

州

離

・（・

一

凋

　 　 　7ep

＝

O

，

　 7Ptr

＝

0 こ こ に

，

p

＝

cos θ

，

万

＝

sin θ である

。

・

…

_（3） 応 力 成 分 も等 方 性 材 料の場 合 次式の形で表さ れ る。

　

　

・

Kr

・

θ）

「

1＋ ．）

言

．

、の

1

（1

一

_帰 … ＋・_・ 。【 　 　 　

＝

＝

　_rλ

一

置_{σ梦（θ）}

　

　

・

alr

・

・）

「

、＋の

晉

一

翫 レ・・＋（ト の・・＋・・，｝ 　 　 　

＝

rA

−

ia 蜜（θ）

　

　

・・（・r

・

・）

一

（、＋ の

署

一

，

n1

・Er ・ vεθ＋（1

−

v）・。

1

　　　 　　

−

rλ   渉（θ）

　

　

T・e（・

，

e）

−

₂ （

i

气

の衿・イ

ー

・ τ

rale

） 　 　Tθe（r

，

θ）

＝0，

　 rgKr

，

θ）

＝

0 　 　 　 　

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

…

　（4 ） つ り合い方 程 式は

，

軸 対 称 変形問題の_{場 合}

，

r 方 向と θ 方向につ き

，

_次の よ うに表さ れ る

。

謡

（r2ar）・

誡

（・rr・・

一

÷

（ae ・・_．

1

−

・

　

　

　

謡

・rSr・e・・

誡

  ・・

一

ち

・．

一

・ 　 　 　

一呷

’

’

’

”・

・

・

・

・

…

　

一・

・

・

・

…

　

『

・

…

　

一・

・

（5） ま た

，

軸 対 称 変 形 問題の_{物 体 表 面}にお け る応力境界 条 件 は次式で与え られ る

。

　 　 　τ，ene ＋τ9

，

np ＝

0

　 　　 　　　 　　　 　　　

’

’

’

”・

・

一・

・

・

・

・

・

・

・

・

・

・

・

・

・

…

　

一

…

　｛6 ） 　 　 　σ ene ＋τeipnPt＝

0

こ こ に

，

n は境 界に立て た外 向 きの法線で

，

_本問題の境 界では nθ

＝

1， ne ＝ 0である

。

　

いま

，

つ り合い方 程 式 （5_）の残 差 をそ れ ぞ れR。

，

Re，

境 界 条 件 （6）式の_残差を

T

．

，

τθとして

，

次の よ うな 仮想仕 事 方 程 式 を考え る

。

　　

　

f

，

　

c

°

xaf

：

（

R

・

aUr

＋

R

。δ・，晦

d

・

d

_伽

　　

　

　

・

_J

（

’

”

fl

（・

，

・・．＋T，δu。）・

d

・

d

・・一 ・

……・

（・） こ こ に

_，

_{解 析 領 域}は 0≦r＜。 。

，0

_{≦ θ≦α≦} π，

一

π≦g ≦ π であ る。 （5）

，

（6 ）式を （7 ）式に代入 し

，

部 分 積分 を行っ て整理 す ると

，

境界 積 分 項は_相殺さ れ

，

〆 の無 限領 域 積 分を含むこ の_式が0になるた め に は

，

次の θ に関す る積 分 式 が 0にな ら な け れ ばなら ない

。

なお

，

ψに_関する積 分 値は 2π で あ る か らこ の式か ら除くこ _と が で き る

。

　　

　

∬［

κ・＋1）

P

・誉う （・

z

・・：）｝・ur

　　

　

　

−

_）・：e∂

3

笋

・

1

（・＋・鵬

一

・・：・u：

　　

　

　

−

_P

_・：∂

蓉

笋］

・・

一

…

…・

……・

……・

……

_（・） こ の式は次の よ うにマ ト リッ ク ス表現 す ること がで き る

。

　　

　

∬

剛 ・

万

］

1

酬

d

・

一

・

………一 …・

…・

…

_（・_） こ こ に

，

1

σ孝

1

＝

ホ r 　 零 θ 　 拿 P σ 　 σ 　 σ 　 θ ゆ

『

τ ， ［∂

B

］； （λ十1）

P

，　　0 　

_一

−

　 　 　

＿

∂ ρ



・

−

P 房 　

一

ρ 　 ，　

−

P う

晶

，

（・＋ ・｝

P

　

　

　

1

_州

_謝

…………・

…・

……・

一 ・

…・

一 ・

_（

₁

_・

₁

また， ひずみ

一

変位関 係は

，

ε肇 ε言 E_名 γ靄e λ　 　 　01

晶

1

　

亘 　 　 　 ρ ∂ 　 　 （λ

一

1） ∂θ

圜

…・

…一 …

_（1ユ）

i

ε

n

＝

［∂亅3Jlu＊ト

・

・

・

…

　

一・

・

・

・

・

・

・

・

・

・

…

　一・

…

　9幽

・

…

　一

…

　

_（12_）

一

₇₃

一

であ り， 応 カ

ー

_{ひず み関係 は次 式}で与え ら れ る

。

ホ 7 常 θ 購 O σ 　 σ 　 σ 　 θ 宰

γ

τ

＝

_万 1

−

v 　 」ノ 　y0 ε

1

ε育 ε毒 τ裘e レ

一

レ ー 0 　 ン 　 レ 1

一

レ

0

　

0

　 0 　 01

−

_2v2

，

万一 （、＋の

言

＿

2の

・

・

：

…

（

13

）

　　　

1

σ

r

＝

［D ］亅・宰ト

……・

一 …………・

・

…………

（

14

） （

14

），（

12

） 式 を （9 ）式に代入 すると

，

最 終 的 に次 式 の よ う なマ トリックス方程式 が 得 られ る。

　　　∫

「

・u・

lr

［・

B

］T［・］［・B ］・

1

・’

1

・・一 ・

…一 ・

…

（15）

　4．

2　

有 限要素法に よる定式 化

　

い ま

，

図

一

5に示 す ように， θの領 域 を放 射状に有 限 個の_{要 素 （}半 無 限 長く さび形 要 素 〉に分 割 する。

一

つの 要素 内で， uT〔θ），　u言（θ）は線形に変化する もの と し て， 次の よ うに θ の 1次 式で近 似する

。

　　　u裘（ξ）

＝

（

1一

ξ＞u裘t＋ξu肇，

　

　

　

ul・

e

… （

1−

・

1

・＃t・・u・」・ξ一

混

…

豊

’

一一

_（

₁₆

_｝

　　　

lu

寧 ｝＝ ［

N

］

ld

＊｝

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

・

…

　

一

・

一・

…

　

（17） た だ し， 　 　 　 　嘘

　

　

　

・胡

一

［

（1

_石

ξ）

_ag

，、

ll

］

…

畷

　　　　　　　略

k

，，

−

fi

（1

−

・）

｛

（

1一

ξ） ・ （・＋ ・）（・

−

1〕

一

， ’

1

，

｝

図

一

一

5 領 域の有 限要 素分割

j

Urj こ こに

，

ld

＊

1

は要 素 両 端の節点変位で あ る

。

　

（17）式 を （15）式に代入 す る と

，

一

つ の要 素に関 す る次の _{仮 想 仕 事 方 程式}が得ら れ る

。

　

　

　

∫

】剛 丁 囲 7［・

B

］「 ［

D

］［・

B

］［・］

ld

’

lld

ξ

一

・ 　　　　　　

…………・

・

……・

………

（

18

） こ こ に_，

1＝

　

eJ− e

_，で要素長 （要 素 角 ）を 表 す

。

こ の （18）式を全要素につ い て総 和 する と

，

次の よ う な 同 次 方程 式が得ら れ る

。

　　　

［

K

〔λ）］

lu

｝

＝

0

・

・

・

・

・

・

・

・

・

・

・

・

・

・

…

　

∵

・

・

・

…

　

t・

・

t・

・

・

・

・

・

・

・

…

　

（19 ） こ こ に

，

　　　

［・］−

4

∫

t ［k］ldξ

　　　　　

一

￥

f

， ’ ［

N

］T［・

吾

r

［・ユ［・・ユ［

N

］

ld

ξ

…・

・

（・・） Σ は全 要 素に関する もの の総 和を表す

。一

つ の要 素に e 関す る各 剛性マ ト リックス ［

h

］の成 分の具体的な形は次 の よ うに な っ て いる

。

た だ

．

し

，

（13）式の

E

をか け る

。

h

、，

− P

（1

一

ξ）（・

− 3

λ・＋

1−

・）

h

・ ・〔1

一

ξ）・

1

（・・1）・

− 11

1

・13

−

P

（1

一

の

｛

ξ（・

一

ξ）（・＋ ・）（・

−

1）・

嗣

h

、．

−

Pl

（・＋1）・

− lli

・

P

ξ（・

一

・ λv＋1

−

_・｝

痘

・_・ξ〔1

一

ξ）

1

（・＋

1

）v

−

ll

k

，、

一一

・（1

一

ξ） ・_（・ v ＋1）・

P

〔1

一

ξ〕（・ λ・

一

・＋ ・・）

毒

h、、… ｛1

−

・）

｛

（・

一

ξ） ・ （・＋ ・）（・

−

1）

去

一

圭

｝

・ ・ρ・1

一

ξ）・

1

一

努

（

1一

ξ）’（1

一

の

lt

、、

− Pl

ξ（・λ・

一

・＋ ・・）・（1

−

_{・）（・＋ ・）}

_t

距

・ξ（

1一

ξ〉（

1

… ）

h

、、一 ・（1

−

・）

｛

ξ（1

一

ξ）（・＋・｝（・

− 1

・

去

咽

… （・ξ

一

_1）

5

一

窒

ξ（1

一

ξ｝（・

一

・・

k

、，・

P

（・

一

・）

｛

ξ（1

一

ξ）（・＋・）（・

−

_1）・ ， ’ 1，

｝

k

、

、

一

一

ξ

1

（・＋ ・）v

−

・

li

−

T

（

1−

・

X1

一

ξ）（・

−

1＞

痘

・Pξ（1

一

ξ｝

1

（・＋1）v

−

ll

h

．−

P

（1

一

の

｛

ξ ・ （・＋ ・）（・

−

1〕

一

、 ’ 1、

｝

… ……・

……・

…・

・

……

_（21）

h

・・一 ・ξ21（・＋1）・＋

T

_ξ（・

−

3λ・＋1

−

・）

毒

k

“一 ＋ ξ）（・＋ ・・）

（

_・ξ・

写）

_う ξ（_・＋・）（

1一

蝪

k

・

−

P

・・

一

・・

｛

・・1

一

ξ）〔・＋ ・…

−

1

齢

i

・_{・ v}・・ξ

十

誓

…

一

・…

一

・

h

・一

一

ξ（1＋ ・・｝

（

_・ξ・

7

）

・_・ξ（・＋ ・・（

1−

・）

h

k

・

＝

P

（

1．

−

v）

｛

・ ’ ・A

−

1｝（・＋ ・・

S

一

吉

ト

・_…

1

−

；

・…

一

・ 　4

．

3 計 算 法 　まず， 領 域を適当に要素分 割 し

，

要 素 剛 性マ ト リッ ク ス を 求め

，

（19）式の係 数マ ト リッ クスを 作 成す る。 そ し て そ の 固有 値 λを 求 め る

。

こ の λ の値の

一

つ は2節 の _{考 察}より

一

1とな る はずであ る。 また

，

こ の固有値に 対応 する固 有 変位ベ _クトルが求め るべ き変 位 解 となり

，

（3 ）

，

（14）式 を用い ると 応 力解が求めら れ る_。 た だ し

，

こ の ように し て_求め た解はモ

ー

_{ド解 （応 力， 変位}の最 大 値を

1

として正 規 化し た解 ）を与え るもの であ るの で

，

確定 値とし て の_{基 本 解}を求め るに は_， た と え ば

，

応 力 解 の _{場 合}

，

_{応 力}モ

ー

ド解に_{次 式}か ら決 定さ れ る x を 乗 じ なくて は な ら ない ［（1）式 参照］。

　　　

1

−

2　_{n・Σ ［（σ曇cos θ}

一

τ袤。　sin θ）sin θ］尸

O

　 　 　 i

＝

1 　 　 　　 　 　　 　 　 　

’

’

’

””

’

”……’

…・

・

…………・

・

（22 ＞ こ こ に

_，

n は領 域0≦ θ≦α の要 素 分 割 数で ある

。

なお， （20）式の _ξに関 する積 分は ガ ウス_{積 分 を用}い た

。

固有 値 を求め る方 法と して は行列 式の値が

0

と な る λ の_値 を試行錯誤 的に探 す 方 法 をとっ て い る

。

　

5．

計算例 　 5

．

1Boussinesq 解

　

要素分 割 数の増 加に_伴う固 有 値 λ の収束性を図

一6

に 示す。 た だ し

，

こ こ で はガウスポイン ト数 を 3で計算し ている

。

Boussinesq _{問 題}の _{変 位} ， 応 力モ

ー

ドの解析 結 べ Φ ” 富 ｝ 口 Φ 恤 畠

一

1

．

03

一

1

．

02

一

1

．

01

一

1

．

00 8　　　12　　16 　　20　　

24

　 　 　 　 Number 　ef 　Element ＄ 図

一

S 　固有 値 λの収 束 性 （Boussinesq解 ） 3

．

0

（

鵠

）

』 o 勘 』 国 02 1

。

0

1

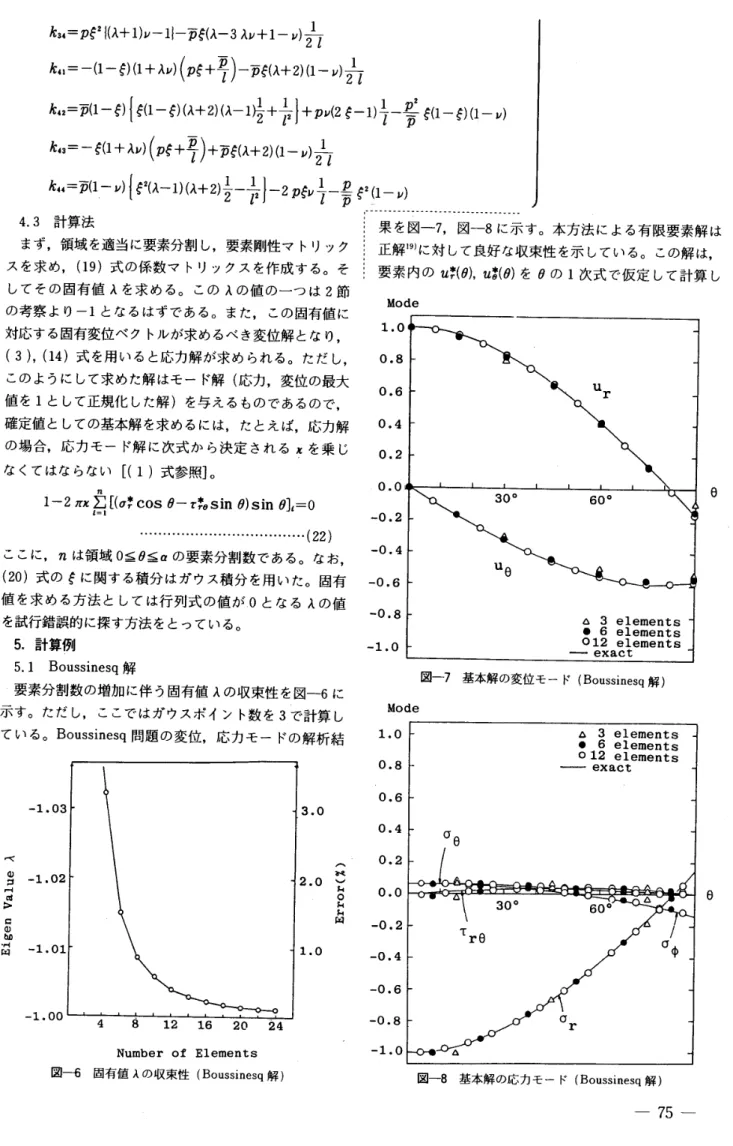
果 を 図

一

7

，

図

一

8に示す

。

本 方法に よる有 限要 素解は

i

正解19 ）に_対して_良好な収 束 性 を示 して いる。 こ の解は

，

i

要 素 内の 罅（θ）， u：（

e

｝を θの 1次式で仮定し て計 算し 　 Mode1

．

00

．

8 0

．

6 0

．

4 0

、

2 0

．

0

一

〇

．

2

一

〇

．

4

一

〇

．

6

一

〇

．

8

一

₁

_．

₀ Mode1

．

0 0

．

8 0

．

6 0

．

4 0

．

2 0

．

0

一

〇

。

2

一

〇

．

4

一

_〇

_．

₆

一

〇

．

8

一

1

．

0 図

一7

基 本解の変 位モ

ー

ド （Boussinesq解 ） 図

一

8 基 本 解の応力モ

ー

ド （Boussinesq 解） θ θ

一 75 一

べ   コ 霊 〉 口 o 切 州 国

一

1

．

一

1

．

一

1

一

1

一

1

一

₁

一

₁ Mode

　 　 　 Nurnber 　of 　Elements 図

一

9　固有 値 λの_収束性 （Kelvin解）

．

Q

．

0

．

o

．

0

．

0

．

0 1

．

₀ ム　3elements ●　6elements 0

．

8 012　　 elements exact ur 0

．

6 0

．

4 0

．

2 0

．

0 60

°

120 °

一

〇

．

2

一

〇

．

4 ム

一

〇

。

6

．

一

〇

．

8 u θ

一

1

。

0 図

一

10

　

基 本 解の 変位モ

ー

ド （Kelvin解 ）

（

裡

）

臼 O 猟 臼 国 e た解で あ る が

，

解 析 結 果よ りわ か る よ うに

，

3要素分割 とい う少ない分 割で工学的に使 用で き る解が得ら れ てい るの で_， 工学 的に は この 1次 式の仮定で よい こ と がわ か る

。

な お

，

単位荷 重に対す る応 力 解は

，

4

．

3節で説明し たよ う に倍 率 x を乗じ な くては な らな い。 　5

．

2Kelvin 解zo ）

　

要素分割 数の増 加に伴う固有値 λ の収束性を図

一

9に 示す

。Kelvin

問題の変 位

，

応 力モ

ー

ドの解析 結 果を図

一

₁₀

_，

_図

一

₁₁に示す。 　

6．

結　 論

　

3次 元 領 域に お け る弾性基 本 解を有限要 素 法に よっ て 数 値 的に解 析 する方法 を提 案し た

。

この計 算 法 を用いれ ば

，Boussinesq

解や

Kelvin

解 が 同じ手法で求め られ

，

解の収 束 性は良 好であ るこ と が わ かっ た

。

Mode1

．

0 0

．

8 0

．

6 O

．

4 0

．

2 0

．

0

一

〇

．

2

＿

0

．

4

一

〇

．

6

一

〇

．

8

＿

1

．

0 図

一

11　基 本 解の 応 力 モ

ー

ド （Kelvin解 ） θ

　

前 報で示 し た よ うに 2次 元 弾 性 基 本 解の解 析 問題が連 立 方 程 式を解く問 題になっ た の に対して， 3次 元 弾 性基 本 解の 解 析 問 題は本 論 文で示し た ように固 有値問 題に なっ てい ることは興 味 深い

。

この よ うな違いが生 ずる理 由は

，3

次元弾 性 基 本 解が変位解 が r

−

’ t 応力解が r

−

2 で あ り

，

と もに 〆の べ き乗 項を 有 する の に対し て， 2 次 元弾性 基 本解は変 位 解が 且ogr と r°

，

応 力 解が r

−

1 で

あ

り

，

完全な r のべ

ぎ

_乗解で は ない た めに数学的に 異な っ た定 式 化が行わ れた た めである。

　

本 論 文で は， 3次 元 等 方性弾 性 材

料

中の基 本解を有 限 要素法で解析す るための定式化を行っ たが

，Transvers

−

ly

・

isotropyの よ うな異方 性材 料の場 合は

，

応 カ

ー

ひずみ 関 係に

，

その_異方 性の材 料 特 性を代入 し

，

同様な定 式 化

を

行えばよい

。

こ の場 合

，

応カ

ー

ひずみ関 係 式が円筒座 標 系ま た は直交 座 標系で与え られ る の で

，

これ を球 座 標 系に_変換し て用いる 必 要 が ある

。

こ の点に関し て は

，

文 献

15

）の 2次 元 異 方 性材料の ク ラッ ク特異解の解析と 同じ手順で解析 し て い けばよい 。

　

ま た，本論文の解 析に おい て

，

λ≠

−

₁の_解につ い ては

，

集 中荷重 以 外の荷 重

，

た と えば 集 中モ

ー

メ ン ト荷重など を 受 ける場 合の解に対 応する もの であ り， こ の よ う な解 につ い ては

，

別 稿で報 告する。 　 謝 　 辞

　

本 研究をま と め るに あ たっ て， 広 島 大 学 吉 田長行助 教 授

，

同助 手 藤 井 大地君

，

学 生 坂 田 邦 宏 君 （現鈴 与 建 設 ） の_協力 を得た。 こ こ に感 謝の意を 表しま す

。

参 考 文 献 1） 藤谷義 信：2次 元 弾 性基本解の有 限要 素 解 析

一

有 限 要 素 　 法によ る 弾 性基 本 解の解 析に関す る研 究

1

その 1）

，

日本

　　 建 築 学 会 構 造 系 論 文報告集

，

第393 _号

_，

_pp

．

54

−

61

_，

昭和 　 　 63年ll月 2） 松 岡 　 理

，

勅 使 川 原 誠 司 ：TRANSVERSLY

−

ISO

．

　　

TROPY

の集 中荷 重の問 題 （そ の 1

．

基 本 解 ｝

，

日本 建 築 　　 学会論文報告集

，

第256_号

_，

_pp

．

7

−

14

_，

_昭和52年6月 3＞ 松 岡 理

，

勅 使 川 原 誠 司 ；TRANSVERSLY

−

iSO

．

　 　TROPY の集 中 荷重の問題 （そ の 2

．

　Boussinesqの問 題 ）

，

　　 日本建築 学 会 論文報告集

，

第261号

，

pp

．

71

−

78

_，

昭 和52 　 　 年11月 4） 松 岡 理

，

井 波 隆

，

勅 使 川 原 誡 司 ；TRANSVERS

．

　　LY

−

ISOTROPY の_{集 中荷}重の_{問 題 皿 （}CERRUTI の問 　　題 ）

，

日本 建 築 学 会 学 術 講 演 梗 概 集 （北 陸 ）Tpp

，

741

−

742

，

　 　 昭和49年 IO月 5） 松岡 理

，

加 藤 和 幸

，

杉 山 武 ：TRANSVERSLY

−

　　ISOTROPY の BOUSSINESQ とMINDLIN （1）の_問

　　題 の解

，

日 本 建 築 学 会 学 術 講 演 梗 概 集 （東 海）， 　 　 pp

．

925

−

926

，

昭和51年10月

6）Walker

，

　 S

．

：Fundamental　 Solutions

，

progress　 in 　　 Boundary　Elernent　Meth（〕

ds

_（Edited　by　C

．

A

．

　Brebbia）

，

　　 Pentech　Press

，

　_pp

．

13

−

44

，

1981

7）Williams

，

　M

．

　L

．

；Stress　Singlllarities　resulting 　

froM

　　 Various　Bounda【y　Conditions　in　Angular　CorneTs　of 　 　 Plates　in　Extension

，

　

J．

　of 　Applied　Mechanics

，

　Vo且

．

　lg 　 　 （4）

，

　pp

．

526

−

528

，

　1952

8） Williams

，

　M

．

L

．

：Surface　Stress　Singularnies　resulting 　　 frorn　Various　Boundary 　Conditions　in　Angular　Corners　of

　　

．

Plates　under 　Bending

，

　Proc

．

　of 　the　first　

U

　S

．

　National 　　 Congress　of　Applied　Mechanics　ASME

，

　_pp

．

325

−

329

，

　 　 195］

9＞　Ben山em

，

　J

．

P

．

；Three

．

Dimensiona ［State　of　Stress　at

　　 the　Vertex　of　a　

Quarter

．

lnfinite　Crack　in　a 　Half　Space

，

　　 Report　nr

．

563

，

　Laborate［y　Qf　Engineerlng　Mechanics

，

　　 Department　of　Mechanlcal　EngineeTing

，

　De］ft　Universト

　 　 ty　of　Technology

，

　September　l975 10） 藤 谷 義 信 ；直 線 状の前 縁 を もつ 3次元弾 惟 体 表 面ク ラッ 　　 ク の応 力 特異解の解析

，

日本建 築 学会論 文 報 告 集

，

日本 　　 建 築 学 会 論 文 報 告 集

，

第350号

，

pp

．

28

−

36

，

昭和60年 　 　 4月 ll_） 12） 13＞ 14） 15） 16） 17） 18〕 19） 20｝

Bazant

_，

　Z

．

　P

．

　and 　EstenssorD

，

　L

．

_：Genera且Numerical

Method　for　Three

−

dimensional　Singularities　in　Cracked

or　No亡ched 　ElasticSol｛ds

_，

　Fracture　1977

，

　Vol

．

3

，

　ICF　4

，

Waterloo

_，

　

Canada，

　pp

．

37］

−

385

，

1977

藤谷義信：Rey且eigh

・

Ritz法による 3次 元 表 面クラッ ク問 題の応 力 特 異 解の_解析

，

広島大学工学 部 研 究 報 告

，

第Z8 巻

，

第2号

，

pp

．

129

−

137

_，

昭 和55_年3_月 藤 谷 義 信 ：有 限 要 素法による 2次 元ク ラッ ク先 端の応 力 特異解の解析

，

構 造1学 論 文 集

，

Vol

．

31B

_，

　_pp

．

103

−

114

，

昭 和50年3月 加藤巨 邦

，

藤 谷 義 信 ：板 曲げ変 形 問題にお け る ノッチ先 端の 応 力 特異解の_{有限 要 素 解 析}

，

_{構 造}T

．

_{学 論 文 集}

_，

Vo且

．

33B

_，

　pp

．

9

−

16_， 昭 和62_年3_月

Fujitani

_，

　Y

．

：Analysis　of 　Stress　Singularities　 of 　the

Notch　in　theTwo

・

Dimensienal 　 OrthotropicElastic

Body

，

　Memoirs　of　_theFaculty_ofEngineering

，

Hiroshi

・

ma 　University

，

　Vol

．

　g

，

　No

．

3_（Serial　No

．

29_）

，

　_pp

．

39

−

441

January

，

1987

藤 谷 義 信 ：2次元弾 塑 性 材料中の ノッ チ先 端の応 力特異 性の解析

，

広 島大 学T

．

学 部 研 究 報 告

，

pp

．

　43

−

54

，

第36巻

，

第1号

，

昭和62 年12月

Tajimi

_，

　H

．

；AContr｛bution　to　Theoretical　Prediction　of

Dynamic 　Stiff【Less 　of　Surface　Foundations

，

　Proceedings of　the　7th　World　C〔）nference 　on 　Earthquake　Engineering

，

Istanbul

，

　Turkey

，

　Vo旦

、

5

，

　pp

．

105

−

112

，

1980

Tajimi

，

　H

．

　and　Izumikawa

，

　M

，

：Dynamic　Analysis　of

Embedded　Mat　Foundatlons　by　Applicati〔〕n 　 of 　Point

．

Load　Solution　in　a　Thin　Layered　Medium

，

　Proceedings

of　the　6th _亅apan 　Earthquake　Engineering　Symposium

，

pp

．

1745

−

1752

，

　1982

S

．

P

．

　Timoshenko　and 　

J．

　N

．

　GoQdier：Theory　of 　Eiasti

−

city

，

　Thi【d　Edition

，

　McGraw

．

Hill

，

　pp

．

99

−

106

，

413

−

417

，

1977

．

8C

，

A

．

　Brebbia：The　Boundary　Element　Method　for　En

−

gineer

，

　Pentech　Press

，

1978

，

_神谷紀 生

，

出巾⊥E隆

，

田 中 喜 久 昭共著 ：境 界 要 素 法入門

，

培 風 館

，

pp

．

108

−

109

_，

昭和55 年9月

SYNOPSIS

UDC 624.042:519.6

FINITE

ELEMENT

ANALYSIS

OF

THREE-DIMENSIONAL

ELASTIC

FUNDAMENTAL

SOLUTION

(AXI-SYMMETRICAL

SOLUTION)

(Studies

on analysis of elastic

fundamental

solutions

by

finite

element method,

Part

2)

byDr._{YbSHINOBU FUJ]TANI,} Pref.,Hiroshima University,Member of A.I.

J.

Inthis _paper,themethod of finiteelement analysis

for

an elastic

fundamental

solution

is

_proposed.

The

three

dimensional

fundamental

solution treatedinthis_papercontain the

Kelvin's

solution defined inan infiniteregeon and the axi-symmetric

Boussinesq:s

solution

defined

in

a semi-infinite region.

Inthe case of three

diinefisional

region, the

displacement

cornponents must

be

cornposed

by

using r"

singular-ity

(r

means the

displacement

from

the

loading

point),

for

the reason thatthe stress components

have

r'2 sing-ularity.

By

discretizing

thevirtual work equation at the radial nodal

line

in

thevicinity of the

loading

_point.the

element stiffness matrix with respect tothe nodal unknown

displacement

can

be

obtained.

It

isneted thatthethree

dimensional

elastic

fundamental

solutions are analysed as an eigenvalue _problem. The results

by

the _present

finite

e!ement analysis of the

Kelvin's

and

Boussinesq's

solutions show a goed convergence