第1章 微分方程式と近似解法

第

1

章 微分方程式と近似解法

畔上 秀幸

名古屋大学 情報科学研究科 複雑系科学専攻

§1.2

数値解析の考え方

数値解析における問題処理のプロセスを図 1.1 に示す． 近似方程式 数値解 数理モデル化 離散化 (有限差分法, 有限要素法, 境界要素法, 有限体積法, 粒子法) コンピュータ による数値計算 熱伝導 熱伝導方程式(偏微分方程式) 有限差分方程式 近似関数による弱形式 (連立方程式) 記述方程式 現象 図1.1:数値解析における問題処理のプロセス

偏微分方程式の境界値問題の基本問題として Poisson 問題が使われる． Poisson 問題は静的なつり合い状態にある様々な場の現象を表す数理モデルとし て用いられる．ここでは，熱伝導現象を例に挙げて，Poisson 問題がその定常的 な熱のつり合い状態を表していることをみてみよう．最初に，1 次元連続体の時 間発展型熱伝導問題について考えてから，d∈ {2, 3} 次元連続体の時間発展型熱 伝導問題に拡張していくことにする．

§1.3.1 1

次元問題

a u(t,x) x=l b(t,x) u,b x=0 図1.1:1次元熱伝導問題 図 1.1 のような 1 次元連続体を考えよう．(0, tT) を時間の領域，(0, l) を 1 次 元連続体の領域とする．a を断面積を表す正の実定数とする． b : (0, tT)× (0, l) → R を単位時間, 単位体積あたりに内部で発熱する熱量， u : (0, tT)× (0, l) → R を温度とする．このとき，b に対して，u を求めるため の熱伝導方程式が得られるまでをみてみよう． まず，熱と温度は次のように関連付けられると仮定する．

定義 1.3.1 (熱と温度の構成方程式)

u (t, x) を (t, x)∈ (0, tT)× (0, l) における温度とする．熱が伝わる物体の単位体 積あたりの熱量は w (t, x) = cV(x) u (t, x) (1.3.1) で与えられる．ここで，cV: (0, l)→ R は体積熱容量を表す正値をとる関数で ある． 次に，熱の移動は，次のようなFourier の熱伝導法則に従うと仮定する (図 1.2)．

定義 1.3.2 (Fourier の熱伝導法則 (1 次元領域))

u (t, x) を温度とする．x における断面を単位時間，単位面積あたりに通過する 熱量 (熱流束) は q (t, x) =−λ (x)∂u ∂x(t, x) (1.3.2) で与えられる．ここで，λ : (0, l)→ R は熱伝導率を表す正値をとる関数である． x u(t,x) q(t,x) u 図1.2:Fourierの熱伝導法則

∈ (0, t × (0, l) に対して，微小な adxdt における熱 量の変化は， (w (t + dt, x)− w (t, x)) adx = (b (t, x) dx − q (t, x + dx) + q (t, x)) adt となる (図 1.3)．ここで，dx→ 0, dt → 0 の極限をとれば， ∂w ∂t (t, x) = b (t, x)− ∂q ∂x(t, x) が成り立つ．さらに，式 (1.3.1) と 式 (1.3.2) を用いれば， cV ∂u ∂t − ∂ ∂x ( λ∂u ∂x ) = b

–q(t,x)adt q(t,x+dx)adt b(t,x)adxdt dx a 図1.3:熱量のつり合い 熱伝導方程式は空間に関して 2 階，時間に関して 1 階の微分方程式である．u を一意に決定するためには，二つの境界条件と一つの初期条件が必要となる．例 えば，次のような条件が考えられる． 1 uD: (0, tT)→ R を既知の温度として，x = 0 において u (t, 0) = uD(t) が満たされているとする．このような u を指定する条件は基本境界条件あ るいは第 1 種境界条件，Dirichlet 条件とよばれる．

2 pN: (0, tT)→ R を既知の熱流束 (定義 1.3.2) として，x = l において λ∂u ∂x(t, l) = pN(t) が満たされているとする．このような u の導関数を指定する条件は自然境 界条件あるいは第 2 種境界条件，Neumann 条件とよばれる． 3 u0: (0, l)→ R を既知の温度として，t = 0 において u (0, x) = u0(x) が満たされているとする．このようなある時刻における u を指定する条件 は初期条件とよばれる．

初期条件は時間領域の境界条件とみなすことができる．そこで，初期条件も含 めた境界条件と偏微分方程式が満たされるような u を求める問題は，偏微分方 程式の境界値問題とよばれる．熱伝導方程式は線形 2 階偏微分方程式に分類され る．その中でも，熱伝導方程式は放物型偏微分方程式に分類される (1.4 節)．定 常状態のときは，b (t, x) = b (x) および u (t, x) = u (x) となり， − d dx ( λdu dx ) = b (1.3.3) となる．式 (1.3.3) は定常熱伝導方程式とよばれる．この定常熱伝導方程式を d 次元領域に拡張したときは，後で示される式 (1.3.5) のような偏微分方程式とな る．これは楕円型偏微分方程式に分類されることになる (1.4 節)．

次に，d∈ {2, 3} 次元物体における熱伝導現象を考えよう．図 1.4 に 2 次元も 場合を示す．Ω をRd _{上の区分的に滑らかな領域として，ΓDを Ω の境界 ∂Ω の} 部分集合とする．ΓN= ∂Ω\ ¯ΓD とおく．b : (0, tT)× Ω → R を単位時間, 単位体 積あたりに内部で発熱する熱量，u : (0, tT)× Ω → R を温度とする．このとき， Fourier の熱伝導法則は次のようになる． Γ νp(t,x) u(t,x) b(t,x) uD x2 u,b Ω

定義 1.3.3 (Fourier の熱伝導法則 (d 次元領域))

u : (0, tT)× Ω → R を温度とする．単位時間，単位面積あたりに物体を伝わる熱 量 (熱流束) q : (0, tT)× Ω → Rd _は q =    q1 .. . qd    = −    λ11 · · · λ1d .. . . .. ... λd1 · · · λdd       ∂ ∂x1 .. . ∂ ∂xd    u = −Λ∇u を満たす．ここで，Λ = (λij)_ij : Ω→ Rd_{×dは熱伝導率を表す正定値実対称行列} (定義 2.4.5) 値をとる関数である．

熱伝導率が等方的であれば，正の実数値をとる関数 λ : Ω→ R を用いて，

Λ = λI (I は単位行列) とかくことができる．このとき，

q =−λ∇u (1.3.4)

任意の (t, x)∈ (0, tT)× Ω に対して，微小な dx1· · · dxddt における熱量の変 化を考えれば，ei を xi 軸方向の単位ベクトルとして， (w (t + dt, x)− w (t, x)) dx1dx2· · · dxd =   b (t, x)− ∑ i∈{1,··· ,d} (qi(t, x + eidxi)− qi(t, x))   dt となる (図 1.5)．ここで，dx1,· · · , dxd→ 0, dt → 0 の極限をとれば， ∂w ∂t = b− ∑ i∈{1,··· ,d} ∂qi ∂xi が成り立つ．

q(t,x+e1dx1)dx2dx3dt dx2 dx3 –q(t,x)dx2dx3dt b(t,x)dx1dx2dx3dt q(t,x+e2dx2)dx1dx3dt –q(t,x)dx1dx3dt q(t,x+e3dx3)dx1dx2dt –q(t,x)dx1dx2dt x1 x2 x3 dx1 図1.5:3次元の熱量のつり合い

さらに，式 (1.3.1), 式 (1.3.4) を用いれば， cV ∂u ∂t − ( ∂ ∂x1 · · · ∂ ∂xd )       λ11 · · · λ1d .. . . .. ... λd1 · · · λdd       ∂ ∂x1 .. . ∂ ∂x3       u = cV∂u ∂t − ∇ · (Λ∇u) = b を得る．この方程式は d 次元の熱伝導方程式とよばれる．熱伝導率が等方的で あれば， cV ∂u ∂t − ∇ · (λ∇u) = b となる．さらに，λ が実定数であれば， cV ∂u ∂t − λ∆u = b

となる．ただし，∆ =∇ · ∇ はLaplace 作用素，調和作用素あるいは発散作用

素とよばれる．∆ は∇2_{とかかれることもあるが，本書では ∆ を用いることに}

d 次元の熱伝導方程式を満たす u を一意に決定するためには，次のような境 界条件が必要となる． 1 uD: (0, tT)× ΓD→ R を既知の温度として， u = uD on (0, tT)× ΓD が満たされているとする (基本境界条件)． 2 pN: (0, tT)× ΓN→ R を既知の熱流束として， ν· (Λ∇u) = pN on (0, tT)× ΓN が満たされているとする (自然境界条件)．熱伝導率が等方的であれば， λ∂νu = pN on (0, tT)× ΓN となる．ただし，∂ν(· ) は (∂( · )/∂x) · ν を表すものとする． 3 u0: Ω→ R を既知の温度として，ある t0∈ (0, tT) に対して u (t0, x) = u0(x) in x∈ Ω が満たされているとする (初期条件)．

定常状態のときは，b (t, x) = b (x) および u (t, x) = u (x) となり，熱伝導方 程式は −∇ · (Λ∇u) = b (1.3.5) となる．また，∂Ω 全体で自然境界条件の場合は，定数分の不定性が残る．u を 一意に決定するためには，ΓD の大きさが零ではない必要がある． 以上をまとめると，熱伝導問題は次のように定義される．Ω を d∈ {2, 3} 次 元領域とする．また, ΓD⊂ ∂Ω および ΓN= ∂Ω\ ¯ΓD とする．cV: Ω→ R は正 値をとる関数とする．Λ : Ω→ Rd_{×d は正定値実対称行列値をとる関数とする．}

問題 1.3.4 (熱伝導問題)

b : (0, tT)× Ω → R, pN: (0, tT)× ΓN→ R, uD: (0, tT)× ΓD→ R, u0: Ω→ R が与えられたとき， cV ∂u ∂t − ∇ · (Λ∇u) = b in (0, tT)× Ω, ν· (Λ∇u) = pN on (0, tT)× ΓN, u = uD on (0, tT)× ΓD, u = u0 in Ω at t = 0 を満たす u : (0, tT)× Ω → R を求めよ．

定常状態のとき，熱伝導問題は次のようになる．

問題 1.3.5 (定常熱伝導問題)

b : Ω→ R, pN: ΓN→ R, uD: ΓD→ R が与えられたとき， − ∇ · (Λ∇u) = b in Ω, ν· (Λ∇u) = pN on ΓN, u = uD on ΓD を満たす u : Ω→ R を求めよ．

§1.4

線形

2

階偏微分方程式の分類

1.3 節でみたように，熱伝導問題は時間発展問題としてみたときに放物型に分 類され，定常問題としてみたときに楕円型に分類された．ここでは，定数係数の 2 階偏微分方程式 (線形 2 階偏微分方程式) の標準形に基づく分類法についてま とめておこう．

偏微分作用素 ∂/∂xi (i∈ {1, · · · , d}) を ξi と表して，階数の和が最大の項 (主要 項) の特性方程式が f (ξ1, ξ2,· · · , ξd) = 0 であるとする．このとき，次のように いう． 1 特性方程式が (ξ1, . . . , ξd) = (0, . . . , 0) 以外の実数解をもたないとき，楕円 型偏微分方程式という． 2 特性方程式が (ξ1, . . . , ξ_d)̸= (0, . . . , 0) に対して，常に２つの異なる実数解 をもつとき，双曲型偏微分方程式という． 3 特性方程式 f (ξ1, ξ2,· · · , ξd) = 0 が ξ1− f1(ξ2,· · · , ξd) = 0 とかくことが できて，f1(ξ2,· · · , ξd) = 0 が (ξ2, . . . , ξd) = (0, . . . , 0) 以外の実数解をもた ないとき，放物型偏微分方程式という．

である．実際，

f (ξ1,· · · , ξd) = ξ21+· · · + ξ 2 d= 0

となり，(x1, . . . , xd) = (0, . . . , 0) 以外の実数解をもたない．Laplace 方程式の他 に Poisson 方程式 ∆u = b や Helmholz 方程式 ∆u + ω2_{u = 0 なども楕円型に分} 類される．ただし，b と ω は実数とする．これらの特徴は • つり合い型であること • 閉じた境界条件が必要であること である．ただし，閉じた境界条件とは，偏微分方程式が定義された領域の境界上 のすべての点において第 1 種境界条件 (Dirichlet 条件)，第 2 種境界条件 (Neumann 条件) あるいは第 3 種境界条件 (Robin 条件) が与えられていることを 示す．例として，定常熱伝導 (温度)，静電場 (電位)，静的線形弾性体 (変位)， 理想流体の流れ場 (ポテンシャル)， Stokes 流れ場 (流速と圧力) などが挙げら れる．

一方，双曲型偏微分方程式の典型は波動方程式 ¨ u− c2∆u = ∂ 2_u ∂t2 − c 2 ( ∂2 ∂x2 1 + ∂ 2 ∂x2 2 + ∂ 2 ∂x2 3 ) u = 0 である．ただし，c は正の実数で波の速度とよばれる．実際， f (ξ1,· · · , ξd) = ξ21− c 2(_ξ2 2+· · · + ξ 2 d ) = 0 となり，(x1, . . . , xd)̸= (0, . . . , 0) に対して，常に二つの異なる実数解をもつ． 双曲型偏微分方程式の特徴は • 時間発展型であること

である． さらに，放物型偏微分方程式の典型は拡散方程式 ˙ u− a∆u =∂u ∂t − a ( ∂2 ∂x2 1 + ∂ 2 ∂x2 2 + ∂ 2 ∂x2 3 ) u = 0 である．ただし，a は正の実数で拡散係数とよばれる．実際， f (ξ1,· · · , ξd) = ξ1− a ( ξ22+· · · + ξd2 ) = 0 となる．放物型偏微分方程式の特徴は • 時間発展型であること • 閉じた境界条件と一つの初期条件が必要であること である．

定義 1.5.1 (線形性 )

1 関数 u :Rd→ Rn が，任意の α, β∈ R, 任意の x, y ∈ Rd に対して u (αx + βy) = αu (x) + βu (y)

を満たすとき，u を線形関数 (linear function) , あるいは 線形作用素 (linear operator) という．

2 同様に，U , V をノルム空間として，写像D : U → V が，任意の α, β ∈ R,

任意の x, y∈ U に対して

微分作用素は線形であることを確認しよう．関数 u :R → R の微分は du dx(x) = limϵ→0 u (x + ϵ)− u (x) ϵ で定義される．任意の α, β∈ R, 任意の関数 u, v に対して d dx(αu + βv) = limϵ_→0 αu (x + ϵ) + βv (x + ϵ)− αu (x) − βv (x) ϵ = lim ϵ_→0 αu (x + ϵ)− αu (x) ϵ + limϵ_→0 βv (x + ϵ)− βv (x) ϵ = αdu dx+ β dv dx が成り立つ．

線形性の利点: 線形性が成立すれば微分方程式の解を解析的に得ることがで きる．

非線形微分方程式の例

µ

図 1.1 のような単振り子の運動方程式は ld 2_θ dt2 + g sin θ = 0 となる．sin θ は θ = 0 周りで sin θ = θ−θ 3 3! + θ5 5! +· · · と展開できる．そこで， θ≪ π のときには sin θ ≈ θ より，線形化できる．

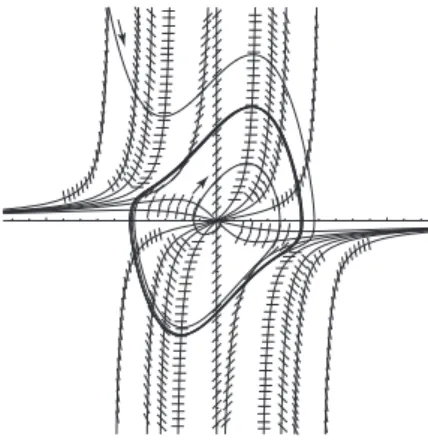
Van der Pol の運動方程式 d2_u dt2 − µ ( 1− u2) du dt = 0 を満たす u は，図 1.2 のように，任意の初期条件に対して，あるリミットサイ クルに落ち込む．この現象は本質的に非線形であると考えられる．

運動方程式を非線形にする例をいくつか挙げてみる． u f(u) u f(u) u f(u) (a)硬化ばね (b)軟化ばね (c)がた 図1.3:非線形ばね

mg θ l l(1–cosθ) (a)軟化ばね (b)硬化ばね 図1.4:大変形による剛性の非線形性

u˙ f(u˙) u˙ f(u˙) (a) Coulomb摩擦 (b)動摩擦 図1.5:摩擦による減衰の非線形性

§1.6 Poisson

問題

この教材では，次のような Poisson 問題を取り上げて，数値解析の原理を考え ていこう．

問題 1.6.1 (1 次元 Poisson 問題)

ある b : (0, 1)→ R, uD∈ R, pN∈ R を固定する．このとき， −d2u dx2 = b in (0, 1) , u(0) = uD, du dx(1) = pN を満たす u : (0, 1)→ R を求めよ．

ΓD⊂ ∂Ω および ΓN= ∂Ω\ ¯ΓD とする．

問題 1.6.2 (d 次元 Poisson 問題)

Ω⊂ Rd, d∈ {2, 3}, ΓD⊂ ∂Ω, b : Ω → R, pN: ΓN→ R, uD: ΓD→ R を固定と する．このとき， − ∆u = b in Ω, ∂u ∂ν = pN on ΓN, u = uD on ΓD を満たす u : Ω→ R を求めよ．

§1.7

有限差分法の考え方

数値解法の典型として有限差分法の考え方をみておこう． 有限差分法では，問題 1.6.1 を次のように解く． m ある自然数として，(0, 1) 上に節点{x0, x1, x2,· · · , xm}, x0= 0, xm= 1, を等間隔に配置する．節点間の長さを h = 1/m とする．近似関数を uh: (0, 1)→ R と表して，uh(xi) = ui とかく． u1 u0=uD ui{1 ui ui+1 um um{1 x x0=0 x1 xi{1 xi xi+1 xm{1 xm=1 h 図1.1:近似関数uh(x)

Taylor の公式より， uh(xi+1) = uh(xi) + h duh dx (xi) + h2 2 d2uh dx2 (xi) +h 3 6 d3_u h dx3 (xi) + O ( h4) uh(xi−1) = uh(xi)− h duh dx (xi) + h2 2 d2uh dx2 (xi) −h3 6 d3_u h dx3 (xi) + O ( h4) が成り立つ．2 式の和をとれば

が成り立つ．両辺を h2 _{で割って，O}(_h2)_{を省略すれば} −d2uh dx2 (xi) =− uh(xi+1)− 2uh(xi) + uh(xi−1) h2 が成り立つ．

自然境界条件について，Taylor の公式より， uh(xm₋₁) = uh(xm)− h duh dx (xm) + O ( h2) が成り立つ．両辺を h で割って，O (h) を省略すれば duh dx (xm) = uh(xm)− uh(xm₋₁) h が成り立つ．

したがって，uh(xi) = ui, b (xi) = bi とかけば，問題 1.6.1 に対して，未知変 数 u0, u1, u2,· · · , umに対する m + 1 元連立 1 次方程式 u0= uD, −ui+1− 2ui+ ui₋₁ h2 = bi i∈ {1, 2, · · · , m − 1} , um− um₋₁ h = pN を得る．この連立 1 次方程式は一意に解ける．

m と n をある自然数として，Ω を含む領域 D 上に節点 {x00, x01, x02,· · · , xmn} を等間隔に配置する．節点間の長さを h = 1/m = 1/n とする．近似関数を uh: D→ R と表して，uh(xij) = uij とかく． x xij h xmn ¡D D xij xi j+1 xi+1 j xi{1 j x

Taylor の公式より， uh(xi+1 j) = uh(xij) + h ∂uh ∂x1 (xij) + h2 2 ∂2_u h ∂x2 1 (xij) +h 3 6 ∂3uh ∂x3 1 (xij) + O(h4) uh(xi−1 j) = uh(xij)− h ∂uh ∂x1 (xij) + h2 2 ∂2_u h ∂x2 1 (xij) −h3 6 ∂3uh ∂x3 1 (xij) + O(h4) uh(xi j+1) = uh(xij) + h ∂uh ∂x2 (xij) +h 2 2 ∂2_u h ∂x2 2 (xij) +h 3 6 ∂3uh ∂x3 2 (xij) + O(h4) uh(xi j₋₁) = uh(xij)− h ∂uh ∂x2 (xij) +h 2 2 ∂2_u h ∂x2 2 (xij)

が成り立つ．4 式の和をとって，両辺を h2 _{で割って，O}(_h2)_{を省略すれば，} ∂2uh ∂x2 1 (xij) +∂ 2_u h ∂x2 2 (xij)

=−uh(xi+1 j) + uh(xi j+1) + uh(xi−1 j) + uh(xi j−1)− 4uh(xij) h2

が成り立つ．

基本境界条件については，ΓD 近傍の節点 xij を選んで

uh(xi j+1) = uh(xij) + h ∂uh ∂x2 (xij) + O ( h2) が成り立つ．両辺を h で割って，O (h) を省略すれば， ∂uh ∂x1

(xij) = uh(xi+1 j)− uh(xij) h ∂uh ∂x2 (xij) = uh(xi j+1)− uh(xij) h が成り立つ． したがって，Ω 上と Ω に隣接する節点 xij に対して，uh(xij) = uij, b (xij) = bij, pN(xij) = pNij, uD(xij) = uD ij とかいて，さらに，境界付近の 節点 xij における法線 νij の情報が与えられれば，問題 1.6.2 に対して，未知変 数_{uij}_ij に対する未知変数個の連立 1 次方程式 uij = uD ij, −ui+1 j+ ui j+1+ ui−1 j+ ui j−1− 4uij h2 = bij,

ui+1 j− uij h νij1+

ui j+1− uij

h νij2= pNij を得る．この連立 1 次方程式は一意に解ける．

有限差分法について，次のことがいえる．

• 境界付近の節点 xij における法線 νij の評価は容易ではない．

• 一方，有限要素法は微分方程式の弱形式 (weak form) に基づく近似解法で，

1 微分方程式で表させる現象を一つ挙げて，その微分方程式と境界条件で構成 された境界値問題 (初期値問題，初期値境界値問題も含む) を示せ．また， その境界値問題は，線形 / 非線形，線形 2 階偏微分方程式の場合は楕円型 / 双曲型 / 放物型のどれに分類されるのかを示せ． 2 1 次元 2 階微分方程式の境界値問題 −d2u dx2 + u = b in (0, 1) , u(0) = uD, du dx(1) = pN に対して，有限差分法による連立 1 次方程式を示せ．ただし，(0, 1) 上に節 点_{x0= 0, x1, x2,· · · , xm= 1} を等間隔に配置して，節点間の長さを

§1.9

まとめ

数値解析の考え方を概観した． 1 数値解析における問題処理のプロセスでは，現象を偏微分方程式などで数理 的にモデル化し，差分方程式などで離散化し，コンピュータによる数値計算 により連立 1 次方程式を解いて，数値解を得る． 2 熱伝導現象は，熱量と温度の関係式 (構成方程式)，Fourier の熱伝導法則か ら，発熱と温度分布の関係を表す 2 階偏微分方程式の境界値問題として数理 モデル化される． 3 2 階偏微分方程式は，楕円型，双曲型，放物型に分類される．これらは線形 微分方程式である．非線形微分方程式の例として，単振子の運動方程式と Van der Pol の運動方程式をみた．

4 有限差分法によって 1 次元 2 階微分方程式の境界値問題と Poisson 問題の近

[1] 菊地文雄. 有限要素法概説: 理工学における基礎と応用. サイエンス社, 1980. [2] 藤田宏,ほか. 数理物理に現われる偏微分方程式. 岩波書店, 1977. [3] 草野尚. 境界値問題入門,復刊. 朝倉書店, 2004.