卒業研究論文
中央大学後楽園キャンパスにおける
消費電力量の分析と予測モデル
学籍番号
08D8101024E
齋藤 宏
中央大学理工学部情報工学科 田口研究室
2012 年 3 月
あらまし
本研究では,後楽園キャンパス5 号館の消費電力量の分析および予測を行う.まず消費 電力量を重回帰モデルで表し,消費電力量の要因とその影響の大きさを調べる.次に,予 測精度を上げるために重回帰モデルによる残差を時系列モデルで表す.これにより得られ た消費電力モデルを用いて前後の年度における消費電力量の予測シミュレーションを行う. さらに,1 日の授業時間が消費電力量に与える影響を分析し,授業時間を変化させたときに 消費電力量がどのように変化するのかシミュレーションを行う. キーワード:消費電力量予測,重回帰モデル,時系列モデル目次
第 1 章 はじめに ... 1 第 2 章 重回帰モデル ... 2 2.1 回帰モデルと最小二乗法 ... 2 2.2 重回帰モデル... 3 2.3 数量化理論Ⅰ類モデル ... 4 2.4 決定係数 ... 5 第 3 章 時系列モデル ... 6 3.1 時系列データ... 6 3.2 定常的な時系列に対するモデル ... 7 3.2.1 一変量自己回帰モデル ... 7 3.2.2 多変量自己回帰モデル ... 10 3.3 非定常的な時系列に対するモデル ... 11 3.3.1 自己回帰和分移動平均モデル ... 11 3.3.2 季節自己回帰和分移動平均モデル ... 12 3.4 赤池情報量基準(AIC) ... 13 第 4 章 モデリングと予測シミュレーション ... 16 4.1 中央大学後楽園キャンパス5 号館 ... 16 4.2 使用するデータ ... 16 4.3 5 号館の消費電力量モデル ... 19 4.3.1 要因に着目したモデリング ... 20 4.3.2 残差に着目したモデリング ... 24 4.4 予測シミュレーション ... 31 4.4.1 完全な予測 ... 31 4.4.2 モデルの検証 ... 32第 5 章 授業時間の変更による節電対策 ... 35 5.1 授業時間が消費電力量に与える影響 ... 35 5.2 節電対策のシミュレーション ... 38 5.2.1 春季および夏季の授業1 時間繰上げ策 ... 39 5.2.2 春季および夏季の授業平均化策 ... 40 5.2.3 春季および夏季の授業3, 4 限カット策... 42 5.2.4 授業動的割当て策 ... 43 5.3 4 つの節電対策の比較 ... 45 第 6 章 おわりに ... 46 6.1 まとめ ... 46 6.2 今後の課題 ... 46 謝辞 ... 47 参考文献 ... 47
第 1 章 はじめに
2011 年 3 月 11 日,東北地方太平洋沖地震が日本に大きな被害をもたらした.内閣府の 発表によると,この震災による被害額の推計は約16 兆 9000 億円であり,阪神・淡路大震 災のときの被害額推計約9 兆 6000 億円 [12] と比較してもその規模の大きさがうかがえる. この震災によって,関東の一部地域で数回にわたって計画停電が実施された.これは,発 電所や変電所等の電気供給力の低下により需要量が供給量を上回ることを未然に防ぐため である. 計画停電の実施に加え,政府や東京電力,その他さまざまな方面からの呼びかけにより 例年に増して節電への意識が高まった.夏季の一般家庭においては「室温28℃を心がける, “すだれ”や“よしず”を利用して室内の温度を調節する,エアコンを無理のない範囲で 消す」をはじめとした節電に対する取り組み [10] がなされ,さらに企業の節電努力もあっ て,東京電力の今夏の最大電力は昨夏の5999 万 kW を大きく下回る 4922 万 kW にとどま った [11]. 節電を考える際には,まずその消費実態を把握することが大切である.中央大学後楽園 キャンパスにおいては,コスト削減のため,消費電力量の計測機器の設置・使用が最小限 に抑えられているので,消費電力の詳細を知ることが困難である.しかし,消費電力量の 周期性に注目したり,関連のある要因を調べたりすることで,消費電力量を予測すること ができる.本研究ではまず,中央大学後楽園キャンパス5 号館の電力使用量を気温や曜日, 空調の運転期間などが与える影響をふまえてモデル化し,電力使用量の予測を行う.その 後,1 日の授業時間と消費電力量の関係式を求め,授業時間を変更した場合の節電効果のシ ミュレーションを行う.第 2 章 重回帰モデル
本章では重回帰モデルについて説明する.2.1 回帰モデルと最小二乗法
回帰分析とは,目的変数(従属変数)である と説明変数(独立変数)である との 関係を調べる手法である.目的変数がひとつの説明変数で表されるとき,その関係式をと くに単回帰モデルと呼び,ふたつ以上の説明変数で表されるとき,重回帰モデルと呼ぶ. 表 2.1 のような 個の系列からなるデータが与えられたとする.ここでは, と の 関係が (2.1) という 1 次式のモデルで表せると仮定し,このときの適切なパラメタ を求めたい. 図 2.1 のように,それぞれの系列は誤差項 を含み (2.2) で表される.この誤差項の平方和を とおくと, はパラメタ からなる 2 変数関 数 ( ) ∑ ∑* ( )+ (2.3) であり,この関数値を最小化するための連立方程式 { (2.4) を解くことでパラメタの推定値 , ̂ ∑ ( ̅)( ̅) ∑ ( ̅) ̂ ̅ ̂ ̅ (2.5) を得る.ここで ̂ ̂ は の推定値を表し, ̅ ̅ は の平均値を表す. このように,データ‐モデル間の誤差の平方和を最小にすることでモデルのパラメタを 推定する方法を,最小二乗法という.表 2.1 サンプルデータ 系列 目的変数 説明変数 1 2 図 2.1 プロットの例と 1 次式のモデル
2.2 重回帰モデル
目的変数 と説明変数 の関係が (2.6) という重回帰モデルで表せると仮定する.このときの適切なパラメタ につ いても最小二乗法により推定することができる.それぞれの系列は (2.7) で表される.ここで,この先の式展開を簡易化するために,式 (2.7) を行列・ベクトルを 用いて表す.まず, ( ) (2.8)( , ( ) ( ) を定義する.ここで,ベクトル の転置を と表す.このとき,式 (2.7) は (2.9) となる.誤差の平方和は ( ) ( ) ( ) (2.10) であり,この関数値を最小化するための方程式 (2.11) を解くことでパラメタの推定値 ̂ ( ) (2.12) を得る.
2.3 数量化理論Ⅰ類モデル
データは量的データと質的データの2 つに分類される.表 2.2 に例を示す.数量化理論 Ⅰ類によると,回帰モデルの説明変数として,質的データと量的データの両方を同時に取 り入れることができる. 例えば,質的データである「性別」は「“男である”または“女である”」のふたつの 値をとりうる.このような質的データの場合は,表 2.3 のように「“0(男でない)”また は“1(男である)”」をとる「男」と,「“0(女でない)”または“1(女でない)”」 をとる「女」の新しい変数に分ければよい.ただし,男でなければ女であることが明らか なように,「男」か「女」のどちらかひとつの変数で「性別」を過不足なく表すことがで きる.一般に, 種類の値をとりうるデータは 個の「0 または 1」をとる変数で表 現することができる. 表 2.2 量的データと質的データの例 量的データ 気温,湿度,従業員数,客動員数, 売上金額,売場面積,… 質的データ 性別,曜日,セールを行うかどうか, 満足度の5 段階評価,…表 2.3 質的データの変換 性別 男 女 女 0 1 男 1 0
2.4 決定係数
回帰分析により得られたモデルについて,データとのあてはまりのよさを知る指標とし て決定係数(R 二乗値)がある. 次の恒等式 ∑( ̅) ∑( ̂ ̅) ∑( ̂) (2.13) は,平均からのデータのばらつきがモデルで説明できる部分の平方和と,説明しきれない 部分(誤差)の平方和に分けられることが示されている.ここで ̂ は, による の 予測値である.決定係数 は,平均からのデータのばらつきのうち,モデルにより説明 できる部分の割合を表し, ∑ ( ̂ ̅) ∑ ( ̅) ∑ ( ̂) ∑ ( ̅) (2.14) で定義される.よって,この値が 1 に近いほどモデルのあてはまりがよいと解釈できる.第 3 章 時系列モデル
本章では時系列モデルについて説明する.3.1 時系列データ
時刻の経過に則して観測されたデータを時系列(あるいは時系列データ)という.時系 列について,統計的な性質が時刻により変化しないものを定常的であるといい,図 3.1 の ように系列の平均値が変化するものや,図 3.2 のように分散が変化するものを非定常的で あるという. 表 3.1 のような時系列 が与えられたとき,その定常性を仮定すると,期待値 ( ) と 分散 ( ) は時刻によらず一定である.すなわち, ( ) ( ) (3.1) と表せる.また, と の自己共分散 ( ) および自己相関係数 ( ) は,ラグ の大きさにのみ依存する.それぞれを ( ) ( ) (3.2) で表すとする.ここで, と のあいだには,次の関係 ( ) ( ) √ ( )√ ( ) (3.3) が成り立つ. 図 3.1 平均値が変化する例 図 3.2 分散が変化する例表 3.1 サンプルデータ 時刻 観測データ 1 2
3.2 定常的な時系列に対するモデル
3.2.1 一変量自己回帰モデル
自己回帰モデル 前節と同様に表 3.1 の定常的な時系列が与えられたとする. が,これまでに観測され た 期前までのデータ を用いて (3.4)と表されるとき,これを 次の自己回帰モデル (Autoregressive model) といい,AR( ) と 記す.ここで, は期待値がゼロ,分散が一定であるホワイトノイズを表し,次の性質を もつ. ( ) ( ) { ( ) (3.5) さらにここで, ( ) を仮定する.もし時系列 について ( ) ならば, とする新しい時系列 について考えることで, ( ) となる.したがっ て,以降定常的な時系列 については, ( ) とする. このとき,式 (3.4) の適切なパラメタ を求めたい.そのためにまず,式 (3.4) の両辺にそれぞれ をかけると (3.6)
となり,それぞれ期待値をとると (3.7) となる.ここで, ( ) ,* ( )+* ( )+- , - の関係 を用いている.式 (3.7) の第 1 式以外のものについて,自己相関係数の関係式 (3.8) を連立方程式として解くことで,パラメタの推定値 ̂ ̂ ̂ を得る. また, となるようなラグをとるオペレータ を導入すると,式 (3.4) は ( ) (3.9) と表すことができる. 移動平均モデル AR(1) を考える.AR(1) は (3.10) で表されるが, 以降についても次々と代入を行っていくことで, (3.11) のように,無限項からなるホワイトノイズの線形和で表すことができる.この式を 期前 までで打ち切ったもの (3.12)
を 次の移動平均モデル (Moving Average model) といい,MA( ) で記す.式 (3.9) と 同様の形式で表すと ( ) (3.13) となる.このときの適切なパラメタについても,式 (3.6) から式 (3.8) までのものと同様 の手順を踏むことで,方程式を立てることができる.まず,式 (3.12) の両辺にそれぞれ をかけると (3.14)
となり,それぞれ期待値をとると ( ) ( ) ( ) (3.15) となる.式 (3.15) の第 1 式以外のものについて,自己相関係数の関係式 (3.16) を連立方程式として解くことで,パラメタの推定値 ̂ ̂ ̂ を得る. 自己回帰移動平均モデル AR( ) および MA( ) をふまえると,定常的な時系列 は ( ) ( ) (3.17) と表すことができる.これを ( ) 次の自己回帰移動平均モデル (Autoregressive Moving Average model) といい,ARMA( ) と記す.このときの適切なパラメタについても,式 (3.6) から式 (3.8) までと同様の手順を踏むことで,方程式を立てることができる.一般に, ARMA( ) の場合における式 (3.7) および式 (3.15) に対応する方程式は複雑な構造を しており, ∑ ∑ ( ) ∑ ∑ ( ) ∑ ( ) (3.18) で表される.
3.2.2 多変量自己回帰モデル
表 3.2 のような 個の変量からなる定常的な時系列 について,自己回帰モデルを 考える.まず,時系列 と係数行列 ,ホワイトノイズ を ( ) ( ) ( ) (3.19) と定義する.すると,この自己回帰モデルは一変量のときと同様に (3.20)と表される.これを多変量自己回帰モデル (Vector AR model,Multivariate AR model) と いう.ホワイトノイズ について,次の性質をもつ. ( ) ( ) ( + ( ) ( ) (3.21) ただし は対称行列である.時系列 と の自己共分散行列 に関して, ( ) ( , - [ ] [ ] [ ] ) ( ) ( ) ( , - [ ] [ ] [ ] ) (3.22) である.このときの適切なパラメタ を求めたい.
表 3.2 サンプルデータ 時刻 観測データ 1 2 まず,式 (3.20) より ( ) *(∑ ) + ∑ , - , -(3.23) であるから,式 (3.21) より ∑ ∑ (3.24) となる.式 (3.24) の について (3.25) となるので,これを連立方程式として解くことで,パラメタの推定値 ̂ ̂ ̂ を得る.
3.3 非定常的な時系列に対するモデル
3.3.1 自己回帰和分移動平均モデル
図 3.1 のように,系列の平均値が時刻により変化するとき,各系列の階差に注目すれば 定常的であると見なせることがある.図 3.3 から図 3.5 までに,非定常的な時系列が階差図 3.3 非定常的な時系列 図 3.4 1 階の階差 図 3.5 2 階の階差 をとっていくごとに定常的なものに近づいていく例を示した.いま,ラグをとるオペレー タ を用いると,時系列の 1 階の階差は ( ) で表されるの で,階差を 回とったときに定常的であるような,非定常的な時系列のモデルは ( )( ) ( ) (3.26) で 表 さ れ る . こ れ を ( ) 次 の 自 己 回 帰 和 分 移 動 平 均 モ デ ル (Autoregressive Integrated Moving Average model) といい,ARIMA( ) と記す. ( ) と する新しい時系列 を考えれば,式 (3.26) は ARMA( ) と一致する.したがって,式 (3.18) と同様にしてパラメタを推定することができる.
3.3.2 季節自己回帰和分移動平均モデル
例えば,あるチョコレート会社におけるチョコレートの月次売上のデータが,今年 1 月 分まで手元にあるとする.チョコレートは,年間を通してバレンタインデーを含む 2 月に もっとも売上が伸びることはよく知られている.手元にある売上データから今年 2 月の売 上を予測するとき,1 月,12 月,11 月,… の売上の推移を見るのが,これまでの時系列 モデルであったが,去年の2 月,おととしの 2 月,… の売上の推移をふまえることも妥当 である. 時系列において,時間単位に関する明らかな周期的変動(例えば,月次データであれば 12 ヶ月,日次データであれば 7 日を 1 サイクルとする変動)が見られる場合,その差分や 自己回帰,移動平均を考慮したモデルは ( ) ( )( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) (3.27) で表される.ただし, は周期の長さ, はそれぞれ非周期部分の自己回帰の次数, 階差の次数,移動平均の次数, はそれぞれ周期部分の自己回帰の次数,階差の次数,移 動 平 均 の 次 数 を 表 す . 式 (3.27) を 季節 自己 回 帰和 分移 動 平均 モデ ル (Seasonal Autoregressive Integrated Moving Average model) といい,SARIMA ( ) ( ) と記す.このモデルは,次の変換 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) (3.28) を行うと ARMA( ) と一致するため,パラメタを推定することができる.
3.4 赤池情報量基準(AIC)
時系列モデルでは,過去の何期前までデータを用いるかの判断が必要である.モデルの あてはまりのよさの指標である決定係数については前章で触れたが,決定係数には,説明 変数を単に増やすだけで,あてはまりが見かけ上よくなるという問題点を抱えている.こ こでは,モデルのあてはまりのよさに対する別の指標である赤池情報量基準(AIC)につい て述べる. まず,尤度について説明する.データ の背景にある確率分布について,未知のパラメ タを ,確率密度関数を ( ) とするとき,データの尤度は ( ) ∏ ( ) (3.29) で表される.統計学においては,尤度を最大にするパラメタが,真のモデルにもっとも近 いと考え,このときのパラメタ ̂ を最尤推定量という.式を扱いやすくするために,その 対数をとったものが対数尤度であり, ( ) ∑ ( ) (3.30) で表される.ここで,データが正規分布にしたがうと仮定すれば,データ はある一定の 分散 で与えられる誤差を含み,期待値が ̂ で観測されるから,この確率密度関数 ( ) は ( ) √ ( ( ̂) ) ( ) ( ̂) (3.31) となる.いま,パラメタの推定値が得られたとき,AIC は ( ̂) (尤度のパラメタ数) (3.32)で表される.この値は,尤度が高いほど小さくなるが,データを表現するパラメタが多く なると大きくなっていく.よって,なるべく尐ないパラメタで効率よくデータを表現する モデルがよいという考え方を反映している. 重回帰モデルに対するAIC まず重回帰モデル (2.9) に対する AIC について述べる.与えられたデータについて正規 分布を仮定しているので,式 (3.30),式 (3.31) より対数尤度は ( ) ( ) ( ) (3.33) となる.最尤推定量を求めるには,次の連立方程式 { ( ) ( ) (3.34) を解けばよい.これを解くと, , ̂ ( ) ̂ ( ̂) ( ̂) (3.35) となり,このときの最大対数尤度は ( ̂ ̂ ) ̂ (3.36) となる.尤度に対するパラメタは の ( ) 個であるので,AIC は ( ̂ * ( ) ̂ ( ) ̂ ( ) ( ) (3.37) となる.第3 項はモデルによらない定数なので,省略される. 時系列モデルに対するAIC AR( ) (3.4) に対する対数尤度は ( ) ∑ ( ∑ ) (3.38) であり,最大対数尤度は ( ̂ ̂ ̂ ̂ ) ̂ (3.39) となるので,AR( ) に対する AIC は
̂ ( ) (3.40) と表される.AR( ) 以外の定常的な時系列に対するモデル MA( ),ARMA( ), 変量 AR( ) に対しては,それぞれ ̂ ( ) ( ) ̂ ( ) ( ) | ̂| 変量 ( ) ̂ ( ̂ ̂ ) (3.41) と表される.
第 4 章 モデリングと予測シミュレーション
本章では,使用するデータについて述べ,その後モデリングを行う.さらに作成したモ デルをもとに,将来および過去の消費電力量を予測するシミュレーションを行う.4.1 中央大学後楽園キャンパス 5 号館
中央大学後楽園キャンパスにおける主な建物には,1 号館から 6 号館までの 6 棟と 8 号館 (附属高校校舎) の計 7 棟があり,なかでも 5 号館は授業や昼食で多くの学生が利用する建 物である.5 号館地下 1 階には生協と食堂があり,昼のピーク時には学生で溢れ返る.1 階 から3 階までには全部で 27 部屋計 2300 平方メートルの実験室および準備室,41 部屋計 800 平方メートルの研究室,14 部屋計 2800 平方メートルの教室があり,履修人数の多い 科目の授業の大半がこれらの教室で行われる.そして4, 5 階は保健体育教員室と吹抜けの アリーナ,2 つの大教室からなっている.5 号館の消費電力量の内訳は,各部屋の照明およ びコンピュータ機器や,生協の冷蔵庫,食堂の冷蔵庫および調理器具のほか,まわりの建 物を含む,空調をはじめとした設備の動力である.それぞれについての計測データは存在 しないので,(データから得られる)間接的な要因により電力使用量を分析する.4.2 使用するデータ
今回使用するデータを表 4.1 にまとめた.観測期間はいずれも 2010 年 4 月 1 日から 2011 年3 月 31 日までの計 365 日間である.表 4.2 に使用するデータの一部を記し,図 4.1 か ら図 4.9 までにデータ全体をグラフで示す.ただし,図 4.7 から 図 4.9 までについては 質的データのグラフであるので,数値の種類にのみ意味があり,数値の大きさには意味が ない.横軸はいずれも日付であり,2010 年 4 月 1 日から 1 日刻みで 2011 年 3 月 31 日ま である.それぞれの縦軸の表すものと単位は表 4.1 のとおりである. なお,変数「電力量」は後楽園キャンパスにおける2010 年度の「受変電日報」より抜粋 しまとめたものである.この日報には1 時間ごとの計測値が記録されており,24 時間の合 計値をとり,データとして使用する.2010 年 12 月 17 日の 7 時から 19 時までのあいだは, 全館停電日によりデータが欠損している.よって,この日のデータについては,「電力量」 は停電時間外に観測された12 時間のデータの合計値とした.変数「気温」「湿度」「降水」 「風速」「日照」は気象庁の統計データ [9] にもとづいている.変数「空調」は 2010 年度 に管財課が発行した「後楽園キャンパス空調運転予定表」にもとづいている.ただし,とくに行事のない日曜日(「行事」が“0”,“1”,“2”,“3”かつ「曜日」が“0”)に おいては空調が使用できないため,その日は停止運転(「空調」は“0”である)とする. 変数「行事」は2010 年度講義要項における「授業実施確認表」にもとづいている.ただし, 夏休みおよび冬休み前後の休業日(2010 年 8 月 5 日,8 月 6 日,9 月 19 日,12 月 26 日, 2011 年 1 月 6 日,1 月 7 日)は,休業日(「行事」は“0”である)と表記されているが, それぞれ長期休業期間内である(「行事」は“1”または“3”である)と仮定した. 表 4.1 使用するデータの説明 変数 分類 説明(カッコ内は単位) 電力量 量 5 号館の 1 日の消費電力量 [kWh] 気温 量 1 日の平均気温 [℃] 湿度 量 1 日の平均湿度 [%] 降水 量 1 日の降水量 [mm] 風力 量 1 日の平均風速 [m/s] 日照 量 1 日の日照時間 [h] 曜日 質 その日の曜日を表す; 0:日曜日,1:月曜日,2:火曜日,3:水曜日, 4:木曜日,5:金曜日,6:土曜日 空調 質 その日の空調運転を表す; 0:停止運転,1:換気運転,2:暖房運転, 3:冷房運転 行事 質 その日の授業の有無および行事などを表す; 0:休業日,1:冬休み,2:春休み, 3:夏休み, 4:試験期間,5:授業日,6:入試期間,7:他 表 4.2 使用するデータの一部 日付 電力量 気温 湿度 降水 風速 日照 曜日 空調 行事 4/1 6790 14.7 56 0.0 4.8 4.9 4 2 7 4/2 6840 15.2 71 0.0 5.7 0.0 5 2 7 4/3 6400 11.1 40 0.0 3.0 6.5 6 0 0 4/4 5900 8.8 55 0.0 2.3 1.2 0 2 7 4/5 5480 9.4 83 16.0 2.0 0.0 1 1 7 4/6 5360 14.8 72 0.0 3.0 8.0 2 1 7
図 4.1 2010 年度の消費電力量 [kWh] のグラフ 図 4.2 2010 年度の 1 日の平均気温 [℃] のグラフ 図 4.3 2010 年度の 1 日の平均湿度 [%] のグラフ 図 4.4 2010 年度の 1 日の降水量 [mm] のグラフ 図 4.5 2010 年度の 1 日の平均風速 [m/s] のグラフ 図 4.6 2010 年度の 1 日の日照時間 [h] のグラフ 0 8000 16000 4/1 5/1 6/1 7/1 8/1 9/1 10/1 11/1 12/1 1/1 2/1 3/1 0.0 20.0 40.0 4/1 5/1 6/1 7/1 8/1 9/1 10/1 11/1 12/1 1/1 2/1 3/1 0.0 50.0 100.0 4/1 5/1 6/1 7/1 8/1 9/1 10/1 11/1 12/1 1/1 2/1 3/1 0.0 60.0 120.0 4/1 5/1 6/1 7/1 8/1 9/1 10/1 11/1 12/1 1/1 2/1 3/1 0.0 4.0 8.0 4/1 5/1 6/1 7/1 8/1 9/1 10/1 11/1 12/1 1/1 2/1 3/1 0.0 8.0 16.0 4/1 5/1 6/1 7/1 8/1 9/1 10/1 11/1 12/1 1/1 2/1 3/1
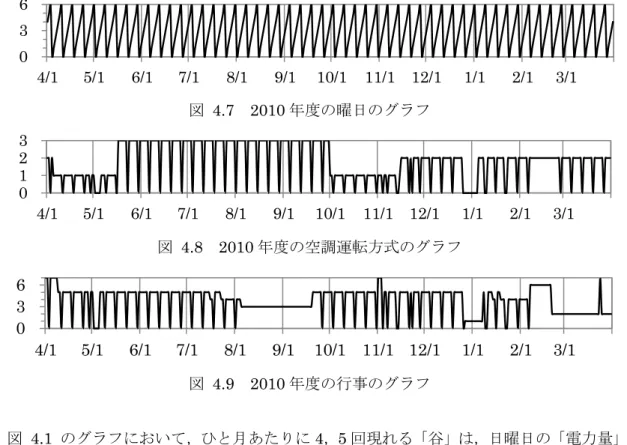
図 4.7 2010 年度の曜日のグラフ 図 4.8 2010 年度の空調運転方式のグラフ 図 4.9 2010 年度の行事のグラフ 図 4.1 のグラフにおいて,ひと月あたりに 4,5 回現れる「谷」は,日曜日の「電力量」 の値であり,前後の平日との差を見ると約4000 から約 8000 キロワット時あり,日曜日と それ以外の曜日では消費電力量がかなり異なる.1 週間を周期としたこの「山」の高さは, 時期により尐しずつ変化し,夏季においては高く,冬季においては低い傾向がある.この ことは,学生の活動に関する電気設備にかかる負荷がとくに夏季において大きくなること を示していると考えられる.
4.3 5 号館の消費電力量モデル
ここでは,4.2 節で示したデータをもとに,実際にモデリングを行う.まず 4.3.1 節では, 要因となりうる変数群から,消費電力量と関連のある変数のみを残して重回帰モデルで表 すことを考える.そのために,あらかじめ消費電力量と各変数の関連の強さを計算し,要 因としての優先度を与える.そして,優先度の低いものから省いていき,そのつどモデリ ングを行ったときのAIC を求め,最適なところで省くのをやめる.続く 4.3.2 項では,要 因では説明しきれなかった残りの部分について,時系列モデルで表すことを考え,モデリ ングを行う. 消費電力量を 2 つのモデルを用いて表すことについていえば,重回帰モデルで表される 部分は,目的変数である消費電力量の要因が明らかであるため,削減のための対策が立て やすくなる.一方,時系列モデルで表される部分については,この特性ははっきりとして 0 3 6 4/1 5/1 6/1 7/1 8/1 9/1 10/1 11/1 12/1 1/1 2/1 3/1 0 1 2 3 4/1 5/1 6/1 7/1 8/1 9/1 10/1 11/1 12/1 1/1 2/1 3/1 0 3 6 4/1 5/1 6/1 7/1 8/1 9/1 10/1 11/1 12/1 1/1 2/1 3/1おり,制御も可能であるが,この原因には別途解明が必要である.現段階においてはデー タが不足しているため,この内容を明らかにすることはできない.とはいえ,要因を変化 させるような節電対策の効果予測には,時系列モデルは十分に役立っているといえる. なお,モデルのパラメタの推定には統計解析ソフトSPSS Statistics Version 19 [8] を用 いた.
4.3.1 要因に着目したモデリング
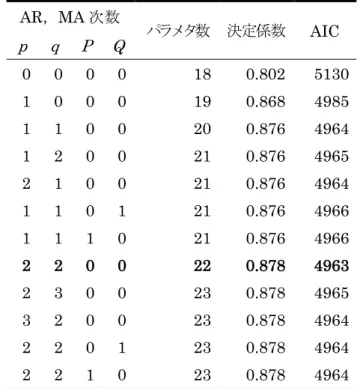
まず,それぞれの変数間の関係を調べるために相関係数を計算した.この結果を表 4.3 に示す.ここで,5% 水準で有意に満たないもの(統計的に見て,その値の期待値が尐なく ともゼロではない確率が95% 以下のもの)は青字で記してある. これによると,「電力量」に対して,「空調」「行事」はそれぞれ相関があり,「気温」 は弱い相関があり,「湿度」「曜日」はそれぞれかなり弱い相関があることがわかった. しかし「降水」「風速」「日照」はいずれも直接的な相関関係はなかった. 「気温」については,この変数は「電力量」以外にも,「湿度」と正の相関があり,「空 調」とも相関があった.湿度との相関関係については,気温が上昇し飽和水蒸気量が上が ることで湿度が下がるといった効果よりも,平均気温の高い時期(夏季)は平均湿度が高 く(蒸し暑い),平均気温の低い時期(冬季)は平均湿度が低い(乾燥している)という 効果のほうが大きいことを示している.空調運転との相関関係についても同様に,四季の 変化によるものであると考えられる.次に,「湿度」「降水」「日照」の 3 つの変数間の 相関関係は「天気」にあることが考えられる.1 日のなかで悪天候が続くと日照時間が短く, 降水量が大きくなるために 1 日の平均湿度が大きくなる.一方晴天が続くと日照時間が長 く,降水量が小さくなるために 1 日の平均湿度が小さくなる.次に,「曜日」と「行事」 の 2 つの変数の弱い相関関係については,毎週日曜日が休業日であるという部分に相関関 係が現れたものだと考えられる.実際,データから日曜日の系列をすべて除いたものにつ いて改めて相関係数を求めると,「0.35」から「-0.01」へ変化した.なお,「風速」につ いては,どの要因とも相関が弱く,間接的にも「電力量」に影響を与えていないと考えら れる. 以上をふまえて,表 4.4 に示す 6 つのモデルを考えた.このそれぞれのモデルに対する 決定係数およびAIC の計算結果を 表 4.5 に示す.ただし「天気」は「湿度」「降水」「日 照」の3 つの変数について主成分分析を行い取り出した第 1 主成分であり,事前に 天気 湿度 (湿度) √ (湿度) 降水 (降水) √ (降水) 日照 (日照) √ (日照) (4.1) という結果を得た.表 4.3 相関係数 電力量 気温 湿度 降水 風速 日照 曜日 空調 行事 電力量 1.00 0.44 0.25 0.04 0.09 0.00 0.27 0.79 0.54 気温 1.00 0.43 -0.04 0.12 0.06 -0.03 0.36 0.03 湿度 1.00 0.46 -0.05 -0.64 -0.08 0.21 0.20 降水 1.00 0.06 -0.38 -0.01 0.07 0.10 風速 1.00 0.15 0.14 0.18 0.00 日照 1.00 0.08 0.01 -0.15 曜日 1.00 0.38 0.35 空調 1.00 0.49 行事 1.00 表 4.4 6 つのモデル モデル 目的変数 説明変数 1 電力量 気温,湿度,降水,風速,日照,曜日,空調,行事 2 電力量 気温,天気,曜日,空調,行事 3 電力量 気温,湿度,曜日,空調,行事 4 電力量 気温,曜日,空調,行事 5 電力量 気温,空調,行事 6 電力量 空調,行事 表 4.5 6 つのモデルに対する決定係数および AIC モデル パラメタ数 決定係数 AIC 1 22 0.803 5136 2 19 0.802 5131 3 19 0.802 5131 4 18 0.802 5130 5 12 0.785 5148 6 11 0.763 5171
表 4.5 の結果によると,6 つのモデルのなかでは,決定係数の性質上パラメタ数の多い モデル1 がもっともよくデータを表しているが,モデル 2,モデル 3,… とパラメタを減 らしていっても決定係数はほとんど変化しないため,その結果AIC は改善していった.し かし,変数「曜日」を省いたとき決定係数は大きく下がり出し,その結果,モデル5,モデ ル6 に関しては AIC が悪化した.したがって,以下では,モデル 4 をさらに詳しく分析す る.モデル 4 について,そのパラメタ推定値(係数)および変数のスケールをそろえた場 合のパラメタ推定値(標準化)を表 4.6 に示し,このモデルにより得られた消費電力量の 予測値と実測値の比較を図 4.10 および図 4.11 に示す.ここで,表 4.6 において 5% 水 準で有意に満たないものは青字で記してある.この表を見ると,冷房および暖房の標準化 相関係数が高かったことから,要因としてもっとも影響のあるのは「空調」であるとわか る.また「曜日」について日曜の係数は0.00 を仮定しており,土曜のほうがやや小さい負 の係数を示しているが,これは「電力量」のグラフに現れる「谷」が「曜日」の影響では なく,「空調」が停止運転であることと「行事」が休業日であることに大きく影響される ためであると考えられる.さらに表 4.6 より予測値を占める要因の割合を求めることがで きる.この結果を図 4.12 および図 4.13 に示す. 表 4.6 モデル 4 の係数 変数 係数 標準化 変数 係数 標準化 定 数 3166.83 曜日 月曜 656.57 0.10 気 温 75.25 0.25 火曜 638.45 0.09 行事 冬休 -1538.83 -0.11 水曜 704.77 0.10 春休 -847.70 -0.11 木曜 848.75 0.12 夏休 303.11 0.04 金曜 966.73 0.14 試験 2301.16 0.26 土曜 -57.67 -0.01 授業 1660.12 0.34 空調 換気 2.11 0.00 入試 1063.01 0.09 暖房 2179.00 0.42 他 346.04 0.03 冷房 2782.65 0.54
図 4.10 電力量の実測値と予測値の比較(前半) 図 4.11 電力量の実測値と予測値の比較(後半) 図 4.12 要因の占める割合(前半) 図 4.13 要因の占める割合(後半) 0 4000 8000 12000 16000 4/1 5/1 6/1 7/1 8/1 9/1 実測値 予測値 0 4000 8000 12000 16000 10/1 11/1 12/1 1/1 2/1 3/1 実測値 予測値 0 4000 8000 12000 16000 4/1 5/1 6/1 7/1 8/1 9/1 気温 曜日 行事 空調 定数 実測値 0 4000 8000 12000 16000 10/1 11/1 12/1 1/1 2/1 3/1 気温 曜日 行事 空調 定数 実測値
図 4.12 および図 4.13 を見ると,「電力量」の成分である 1 週間の周期をもつ波形を, 説明変数「気温」「曜日」「行事」がうまく追いかけており,「電力量」の年間にわたる 緩やかな平均値の変化を,説明変数「行事」「空調」がおおよそ追いかけていることがわ かる.またこれにより,時期ごとの消費電力量に占める要因の割合が異なることもわかる. 例えば空調の冷房運転期間(5 月第 3 週から 9 月末まで)において,「電力量」の約 20% が 「気温」によるものであり,これとは反対に,暖房運転期間(冬休みを除いた11 月第 3 週 から 3 月末まで)においては,「気温」によるところが尐ない.よって,夏季において高 い気温に対する消費電力行動を我慢すると消費電力量を削減することができるが,削減量 が20% を超えることはない.一方,冬季は寒いのを我慢しても省エネの効果は得にくいと 考えられる. しかし,このモデルでは細かい部分でうまく表せていないところがある.まず,図 4.10 を見ると4 月の予測値は実測値のピークをとらえていない.これは 4 月が年度の切替え時 期であり,履修科目の確定していない学生がいたり,教科書販売,サークルの勧誘活動等4 月特有のイベントがあったりするように,キャンパス内の学生の行動がまだ習慣化してい ないことが原因であると考えられる.次に,5 月の第 3 週から 8 月あたまの夏休みに入るま での冷房運転期間を見てみると,実測値における週のピークが時間をかけてだんだん高く なっていることがわかるが,予測値ではその部分の感度が悪い.これは「気温」がパラメ タ推定値よりもっと大きい値をとるべき可能性を示している.しかし,この期間以外の実 測値を見てみると,ピークがあまり変化しないことから,夏季ほど気温が大きな要因とな っていないとわかる.よって夏季とそれ以外の季節とのバランスをとっているので,夏季 の週のピークをうまくとらえきれていないのだと考えられる.また,図 4.11 において,入 試期間の終わる2 月の第 4 週から春休みが始まる 3 月末までの期間についても,目的変数 「電力量」の平均値の変化をとらえられていない.これも上記の5 月の第 3 週から 8 月 4 日までの冷房運転期間と同様のことが原因であるとも考えられるが,むしろ3 月 11 日の震 災発生を境に登校を控える学生が多くいたことが主な原因であると考えられる.
4.3.2 残差に着目したモデリング
4.3.1 節における実測値とモデル 4 の違いを明確にするために,実測値から予測値を引い た残りをグラフで表したものを図 4.14 および図 4.15 に示す.この図によると,5 月から 6 月までの期間と 9 月から 12 月までの期間においてモデルのあてはまりが比較的よく,そ れ以外の期間では,ばらつきが大きいことがわかる.このグラフは,消費電力量のうち「気 温」「曜日」「空調」「行事」では説明することのできなかった残りを表し,時期(時刻) に依存したモデルの誤差の大きさ,あるいは要因として分解できない変量であるととらえ ることができる.よって,消費電力量を,「気温」「曜日」「空調」「行事」の4 つの要図 4.14 重回帰モデルによる残差(前半) 図 4.15 重回帰モデルによる残差(後半) 因からなる重回帰モデルで表し,このモデルによる「残差」を時系列モデルで表すことを 考えていく.図 4.14 および図 4.15 を見ると「残差」がゼロのまわりで変化しているので, この時系列モデルは,階差 および をゼロとおいた季節自己回帰和分移動平均モデル, すなわち SARIMA ( ) ( ) であると仮定する.したがって,時刻 における 「電力量」の実測値を (電力量) で表し,「電力量」を占める要因の大きさを (要因) で 表すとすると,「電力量」を表す新しいモデルとして (電力量) (定数) (気温) (曜日) (空調) (行事) (残差) (残差) ( ) ( ) (4.2) を考える.ここで,(残差) ( ) ( ) は「残差」が SARIMA ( ) ( ) にしたがうことを表す. モデルの最適な自己回帰の次数 および移動平均の次数 を決めるために,モデ ル4 で得られた「残差」について,その自己相関係数 および偏自己相関係数 を図 4.16 および図 4.17 に示す.これらの図は,横軸にラグの大きさ ,縦軸にそれぞれ自己相関 係数 および偏自己相関係数 をとったものである.なお,偏自己相関係数 は,時 系列 と の自己相関係数 のうち による影響をとりのぞ いた相関係数であり,式 (3.8) と同じ式で与えられる方程式の解そのものである.この図 を見ると,「残差」は 1 時点前の値ととくに相関関係が強く,ラグが大きくなるにつれて 相関関係は弱くなっていくことがわかる.これは,「残差」が最近の過去の実績により推 -8000 -4000 0 4000 8000 4/1 5/1 6/1 7/1 8/1 9/1 誤差 -8000 -4000 0 4000 8000 10/1 11/1 12/1 1/1 2/1 3/1 誤差
図 4.16 残差の自己相関係数 図 4.17 残差の偏自己相関係数 定できることを示している.よって「残差」の次数は低いと見当をつけることができる. そこで,まずは表 4.7 に示すモデル間の決定係数を比較し,パラメタ数ごとにもっとも決 定係数の高かったモデルを選択する.図中の太字は,選択したモデルを表す.さらに選択 したモデル間のAIC を比較したものを表 4.8 に示す.このなかでもっとも AIC の小さい モデルを採用する. 採用されたモデルについて,そのパラメタ推定値(係数)および変数のスケールをそろ えた場合のパラメタ推定値(標準化)を表 4.9 に示し,このモデルにより得られた消費電 力量の予測値と実測値の比較を図 4.18 および図 4.19 に示す.ここで,表 4.9 において 5% 水準で有意に満たないものは青字で記してある.表 4.9 により得られた係数により, 重回帰残差の自己相関性を考慮した消費電力量モデルは (電力量) (気温) (曜日) (空調) (行事) (残差) (残差) ( )(残差) ( )(ノイズ) (気温) ( 日の平均気温) (曜日) { ( 日曜日 のとき) ( 月曜日 のとき) ( 火曜日 のとき) ( 水曜日 のとき) ( 木曜日 のとき) ( 金曜日 のとき) ( 土曜日 のとき) } (空調) { (停止運転のとき) - (換気運転のとき) (暖房運転のとき) (日曜運転のとき) } (4.3) -1.0 -0.5 0.0 0.5 1.0 1 11 21 31 41 自己相関係数 rk ラグk -1.0 -0.5 0.0 0.5 1.0 1 11 21 31 41 偏自己相関係数 r'k ラグk
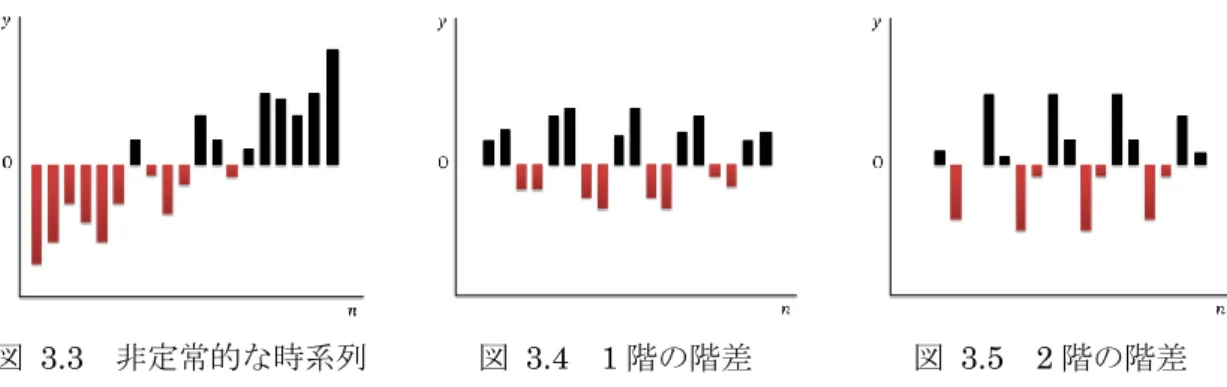
(行事) { ( 休業日 のとき) - ( 冬休み のとき) - ( 春休み のとき) ( 夏休み のとき) (試験期間のとき) ( 授業日 のとき) (入試期間のとき) (他の行事のとき) } と表すことができ,消費電力量の推定値は (電力量推定値) (気温) (曜日) (空調) (行事) ( )(残差) ( )(ノイズ) (4.4) により求められる.さらに表 4.9 より予測値を占める要因の割合を求めることができる. この結果を図 4.20 および図 4.21 に示す.この図の凡例である「1 次」は 1 次の自己回帰 成分と移動平均成分の和を表し,「2 次」は 2 次の自己回帰成分と移動平均成分の和を表し ている. 表 4.7 決定係数による最適なモデル候補を決めるための比較 p q P Q p q P Q p q P Q 0 0 0 0 18 0.802 1 1 1 0 21 0.876 1 4 0 0 23 0.876 0 1 0 0 19 0.847 2 0 1 0 21 0.873 2 3 0 0 23 0.878 1 0 0 0 19 0.868 0 1 1 1 21 0.850 3 2 0 0 23 0.878 0 0 0 1 19 0.804 1 0 1 1 21 0.869 4 1 0 0 23 0.876 0 0 1 0 19 0.805 0 4 0 0 22 0.865 5 0 0 0 23 0.876 0 2 0 0 20 0.858 1 3 0 0 22 0.876 0 4 0 1 23 0.865 1 1 0 0 20 0.876 2 2 0 0 22 0.878 1 3 0 1 23 0.876 2 0 0 0 20 0.873 3 1 0 0 22 0.876 2 2 0 1 23 0.878 0 1 0 1 20 0.849 4 0 0 0 22 0.876 3 1 0 1 23 0.876 1 0 0 1 20 0.868 0 3 0 1 22 0.865 4 0 0 1 23 0.876 0 1 1 0 20 0.850 1 2 0 1 22 0.876 0 4 1 0 23 0.866 1 0 1 0 20 0.869 2 1 0 1 22 0.869 1 3 1 0 23 0.876 0 0 1 1 20 0.806 3 0 0 1 22 0.875 2 2 1 0 23 0.878 0 3 0 0 21 0.864 0 3 1 0 22 0.865 3 1 1 0 23 0.876 1 2 0 0 21 0.876 1 2 1 0 22 0.876 4 0 1 0 23 0.876 2 1 0 0 21 0.876 2 1 1 0 22 0.876 0 3 1 1 23 0.866 3 0 0 0 21 0.875 3 0 1 0 22 0.875 1 2 1 1 23 0.877 0 2 0 1 21 0.859 0 2 1 1 22 0.860 2 1 1 1 23 0.877 1 1 0 1 21 0.876 1 1 1 1 22 0.876 3 0 1 1 23 0.875 2 0 0 1 21 0.873 2 0 1 1 22 0.873 0 2 1 0 21 0.859 0 5 0 0 23 0.872 決定 係数 AR,MA次数 パラメ タ数 決定 係数 AR,MA次数 パラメ タ数 AR,MA次数 パラメ タ数 決定 係数
表 4.8 AIC による最適なモデルを決めるための比較 AR,MA 次数 パラメタ数 決定係数 AIC p q P Q 0 0 0 0 18 0.802 5130 1 0 0 0 19 0.868 4985 1 1 0 0 20 0.876 4964 1 2 0 0 21 0.876 4965 2 1 0 0 21 0.876 4964 1 1 0 1 21 0.876 4966 1 1 1 0 21 0.876 4966 2 2 0 0 22 0.878 4963 2 3 0 0 23 0.878 4965 3 2 0 0 23 0.878 4964 2 2 0 1 23 0.878 4964 2 2 1 0 23 0.878 4964 表 4.9 採用したモデルの係数 変数 係数 標準化 変数 係数 標準化 AR ラグ1 0.03 MA ラグ1 -0.47 ラグ2 0.80 ラグ2 0.45 定数 3900.63 曜日 月曜 1063.56 0.15 気 温 25.99 0.08 火曜 1076.75 0.16 行事 冬休 -1249.01 -0.09 水曜 1179.79 0.17 春休 -305.93 -0.04 木曜 1270.03 0.19 夏休 681.51 0.09 金曜 1433.68 0.21 試験 1033.48 0.12 土曜 386.99 0.06 授業 1726.85 0.36 空調 換気 -65.41 -0.01 入試 166.01 0.01 暖房 1591.12 0.30 他 276.17 0.02 冷房 2266.25 0.44
図 4.18 電力量の実測値と予測値の比較(前半) 図 4.19 電力量の実測値と予測値の比較(後半) 図 4.20 要因の占める割合(前半) 図 4.21 要因の占める割合(後半) 0 4000 8000 12000 16000 4/1 5/1 6/1 7/1 8/1 9/1 実測値 予測値 0 4000 8000 12000 16000 10/1 11/1 12/1 1/1 2/1 3/1 実測値 予測値 0 4000 8000 12000 16000 4/1 5/1 6/1 7/1 8/1 9/1 気温 曜日 行事 空調 1次 2次 定数 実測値 0 4000 8000 12000 16000 10/1 11/1 12/1 1/1 2/1 3/1 気温 曜日 行事 空調 1次 2次 定数 実測値
表 4.8 で決定係数が向上したことからもわかるように,図 4.10 および図 4.11,そして, 図 4.18 および図 4.19 を比較すると,モデルのあてはまりがさらによくなったことがわか る.4.3.1 節の重回帰モデル(図 4.10 および図 4.11 の赤実線)でうまく表せていなかっ た4 月の年度切替えの期間,5 月の第 3 週から 8 月あたまの夏休みに入るまでの冷房運転期 間,2 月の第 4 週から春休みが始まる 3 月末までの期間を見てみると,改善した様子がよく わかる.図 4.20 および図 4.21 を見ると,1 週間の周期をもつ「山」の部分を「気温」「曜 日」「空調」「行事」の和で表し,「山」が立つ土台となる部分を「定数」「1 次」「2 次」 の和で表していることがわかる. また,図 4.22 および図 4.23 に推定した「ノイズ」を示す.図 4.14 および図 4.15 に 示した重回帰モデルの残差と比較すると全体的に波形のふれが小さくなるため,時系列モ デルをとりいれた方が,うまく予測できていることがわかる.図 4.24 および図 4.25 は「ノ イズ」の自己相関係数と偏自己相関係数を表しているが,どのラグに対しても相関性が低 くなっていることがわかるので,「電力量」の自己相関性をうまくモデルのなかに取り込 むことができたと考えられる. 図 4.22 モデル (4.3) のノイズ(前半) 図 4.23 モデル (4.3) のノイズ(後半) -8000 -4000 0 4000 8000 4/1 5/1 6/1 7/1 8/1 9/1 ノイズ -8000 -4000 0 4000 8000 10/1 11/1 12/1 1/1 2/1 3/1 ノイズ
図 4.24 ノイズの自己相関係数 図 4.25 ノイズの偏自己相関係数
4.4 予測シミュレーション
4.3 節で得られたモデル (4.3) をもとに,将来の消費電力量について完全な予測シミュレ ーションを行う.また,過去の消費電力量について予測シミュレーションを行い,モデル (4.3) の検証を行う.4.4.1 完全な予測
2010 年度のデータから推定したモデルの係数(表 4.9)を用いて,2011 年 4 月から 2011 年9 月までの半年間における 5 号館の消費電力量を予測する.使用するデータは気象庁の 統計データ(2010 年 4 月 1 日から 2010 年 9 月 30 日まで)と 2011 年度に発行「後楽園キ ャンパス空調運転予定表」にもとづいている.2011 年 4 月以降のデータについては,「電 力量」の時系列は推定値のみなので,2010 年度とは「残差」および「ノイズ」を推定する 方法が異なり, (残差推定値) (電力量) { (気温) (曜日) (空調) (行事) } (ノイズ推定値) (電力量) (電力量推定値) 年 月 日から 年 月 日まで (4.5) および (残差推定値) ( )(残差推定値) ( )(ノイズ推定値) (ノイズ推定値) 年 月 日から 年 月 日まで (4.6) -1.0 -0.5 0.0 0.5 1.0 1 6 11 16 21 26 31 36 41 46 自己 相関 係数 ラグ -1.0 -0.5 0.0 0.5 1.0 1 6 11 16 21 26 31 36 41 46 偏自 己相 関係 数 ラグ図 4.26 モデル (4.3) による予測 で与えられる.これにより2011 年 4 月 1 日から 2011 年 9 月 30 日まで逐次計算すること ができるが,予測する期間において「ノイズ」をゼロとおいているので,予測期間が長く なるにつれ,「残差」の効果もゼロに収束していく性質がある. この結果を 図 4.26 に示す.図中の赤実線は推定した 2011 年度の消費電力量を表し, 赤点線は 95% の信頼区間,すなわち,95% の確率でこの上下区間内に実測値がおさまる 幅を表す.参考として,2010 年度における消費電力量の実測値を黒実線で示す.
4.4.2 モデルの検証
ノイズをゼロとおいた場合 モデル (4.3) の係数を用いて,2009 年度における 5 号館の消費電力量を予測する.使用 するデータは気象庁の統計データ(2009 年度)および 2009 年度の「受変電日報」にもと づいている.2010 年 3 月以前の「残差」についてはこれまでのように,過去の値から推定 することができないので,ここでは後ろ向きの予測,すなわち,翌日,2 日後,… の値か ら今日の値を予測することを考える.式 (4.2) に対応する式は (電力量) (定数) (気温) (曜日) (空調) (行事) (残差) (残差) ( ) ( ) (4.7) である.2010 年度のデータをもとに「残差」の最適な次数およびパラメタを推定した結果, 2009 年度における「残差」と「ノイズ」の推定するためのモデルとして (残差推定値) ( )(残差推定値) ( )(ノイズ推定値) (ノイズ推定値) 年 月 日から 年 月 日まで (4.8) 0 4000 8000 12000 16000 4/1 5/1 6/1 7/1 8/1 9/1 2010年度 2011年度図 4.27 モデル (4.3) による予測値と実測値の比較(前半) 図 4.28 モデル (4.3) による予測値と実測値の比較(後半) を得た.これにより2010 年 3 月 31 日から 1 日ずつ戻っていき 2009 年 4 月 1 日まで逐次 計算することができる.この結果を図 4.27 および図 4.28 に示す.図中の赤実線は推定し た2009 年度の消費電力量を表し,黒実線は 2009 年の実測値である.この図を見ると,予 測開始して半年間の3 月 31 日から 10 月 1 日までの予測値は,冬休み期間である年末年始 を除いて,波形の山のピークをうまくとらえている様子がわかる.しかし,2010 年度予測 における要因の占める割合を調べた(図 4.20 および図 4.21)際に,自己回帰および移動 平均成分の大きかった6 月から 8 月までについては,図 4.27 からわかるとおり,山のピ ークが大きくずれている.これは,2009 年度予測ではノイズをゼロとして計算を続けたこ とによって,自己回帰成分および移動平均成分の影響がほとんど現れなくなったためであ る.上記期間を除いては,おおむねあてはまっているように見える.決定係数は 0.733 で ある. ノイズを逐次更新した場合 2009 年度のデータについては「電力量」の実測データが得られているので,「電力量」 の推定値を (電力量推定値) (気温) (曜日) (空調) (行事) ( )(残差) ( )(ノイズ) (4.9) 0 4000 8000 12000 16000 4/1 5/1 6/1 7/1 8/1 9/1 実測値 予測値 0 4000 8000 12000 16000 10/1 11/1 12/1 1/1 2/1 3/1 実測値 予測値
により求め,式 (4.5) と同様に (残差推定値) (電力量) { (気温) (曜日) (空調) (行事) } (ノイズ推定値) (電力量) (電力量推定値) 年 月 日から 年 月 日まで (4.10) として「残差」の推定値および「ノイズ」の推定値を計算していくことで,より精度の高 い予測値を得ることができる.この結果を図 4.29 および図 4.30 に示す.図中の赤実線は 残差およびノイズを逐次更新しながら推定した 2009 年度の消費電力量を表し,黒実線は 2009 年の実測値である.この図を見ると, 図 4.27 および図 4.28 では実現できなかった 夏場のピークをうまく表している様子がわかる.予測開始から11 か月後である 4 月におい ても,不規則な波形をとらえられている.決定係数は,ノイズをゼロとおいたモデル (4.8) と比べ,0.733 から 0.797 まで向上している. 2010 年度のデータより得たモデル (4.3) は,消費電力量の変動が比較的大きい時期や, ピークの安定しない時期については,つねに新しいデータを入手しながら「残差」「ノイ ズ」を更新する必要がとくにあるものの,2010 年度以外の年度においてもうまく予測する ことができると考えられる.2011 年度の予測に関しても,4 月 1 日からの消費電力量のデ ータを入手できれば,さらなる予測値の向上が期待できる. 図 4.29 モデル (4.3) によるノイズを修正した予測値と実測値の比較(前半) 図 4.30 モデル (4.3) によるノイズを修正した予測値と実測値の比較(後半) 0 4000 8000 12000 16000 4/1 5/1 6/1 7/1 8/1 9/1 実測値 予測値 0 4000 8000 12000 16000 10/1 11/1 12/1 1/1 2/1 3/1 実測値 予測値
第 5 章 授業時間の変更による節電対策
本章では,前章で推定したモデルを用いて,授業時間が 5 号館の消費電力量に与える影 響を調べる.さらに,4 つの節電対策を提案し,それらを比較検討する.5.1 授業時間が消費電力量に与える影響
図 5.1 は 2010 年 7 月 15 日(木)の 24 時間における 1 時間ごとの気温および 5 号館の のべ授業時間の推移を表したものである.木曜日は5 号館において 6 限の授業がないので, 授業時間は9 時から 18 時までに収まっている.この日の 2 限(10 時 40 分から 12 時 10 分まで)は 5 階にある大教室のひとつを除き,すべての教室が講義に使用されており,11 時台のピークとして図中に現れている.また,12 時については,1 時間のうち 50 分は昼休 みを含んでいるので,授業が行われず,グラフの谷として表れている. このグラフからわかるとおり,授業時間のピークは,太陽が昇り気温の高い時間帯に近 い.実際,2010 年度の授業時間割は 2,3,4 限に集中し,1 限や 6 限があまり使われてい ない.冷房を使う前期において,気温の高い時間帯にとくに集中して授業を行い,学生を 登校させている現状は,消費電力量を無駄に増加させており,その改善をはかることによ り消費電力量を減らす可能性があると考えられる.このとき,(1) 暑さ(寒さ)に対する不 快さを抱えた学生人数が多くなるのに比例して,5 号館の消費電力量が大きくなること,(2) のべ授業時間と5 号館にいる学生人数には強い相関関係があることの 2 つを仮定し,クラ ス分け授業の合併などにより授業時間を縮小したり電気設備等の使用を控えたりすること なく,時間割の構成のみで消費電力量を削減することを目的とする. まずは,気温を考慮した授業時間の分布が,その日 1 日の消費電力量にどのように影響 するかを考える.日付 における時刻 (単位は [h] である)に観測された気温を ( ), 時から ( ) 時までの 5 号館におけるのべ授業時間を ( ) とするとき,この日 に おける気温を考慮した授業時間を代表する値として,累積加重授業時間を (累積加重授業時間) ∑| ( ) | ( ) (5.1) と定義する.ここで,| ( ) | は,寒暖分岐点とされる摂氏 18.3 度(華氏 65 度)を 授業時間に対する重みゼロとして,この気温から何度離れているかを重みとしている.暖 房が必要な寒いときや冷房が必要な暑いときに授業が多いと,累積加重授業時間の値は大 きくなる.図 5.1 2010 年 7 月 15 日の授業時間と気温の推移 累積加重授業時間と消費電力量の関係を推定するために,2010 年 4 月から 2011 年 3 月 までの365 日間のうち,「行事」が授業日である 168 日間のデータを使用する.さらに「空 調」の運転方式をもとに168 日間を 4 つの区間 ▼ 春季(換気運転):04 月 09 日から 05 月 15 日までの 28 日間 ▼ 夏季(冷房運転):05 月 16 日から 09 月 30 日までの 66 日間 ▼ 秋季(換気運転):10 月 01 日から 11 月 15 日までの 34 日間 ▼ 冬季(暖房運転):11 月 16 日から 01 月 18 日までの 40 日間 に分ける.4 章で求めたとおり(図 4.20 および図 4.21),それぞれの区間ごとに「行事」 「空調」の与える影響の大きさは一定であり,消費電力量の変動の主な要因は「気温」「曜 日」であると考えられる.前日,前々日から影響される「残差」の部分については,回帰 モデルで抽出することはできないので,消費電力量から 4 章で求めた「残差」成分を取り 除く.この「残差」を取り除いた値を目的変数とし,累積加重授業時間を説明変数とする, 区間に応じた 4 つの単回帰モデルで表す.これにより,それぞれの区間(暑い時期,寒い 時期,寒暖切替わりの時期)における,気温を考慮した授業時間の影響を,単回帰モデル の「傾き」として得ることができる. 24 26 28 30 32 0 5 10 15 20 0 2 4 6 8 10 12 14 16 18 20 22 気温 [℃ ] 授業時間 [h] 時刻 授業時間 気温
図 5.2 累積加重授業時間と残差成分を除いた消費電力量のプロット 図 5.2 に累積加重授業時間と残差を除いた消費電力量に関する散布図を示す.図中に上 記区間ごとに色分けした計 168 日間のデータをプロットし,それぞれの区間に対する単回 帰モデルをプロットと同様に色分けした直線として示す. この図によると,それぞれの区間における単回帰モデルは (消費電力量) (残差) (累積加重授業時間) 春季 (消費電力量) (残差) (累積加重授業時間) 夏季 (消費電力量) (残差) (累積加重授業時間) 秋季 (消費電力量) (残差) (累積加重授業時間) 冬季 (5.2) となる.これにより得られた消費電力量の推定値と実測値の決定係数は 0.868 となった. また,夏季では消費電力量が最低でも約9000 キロワット時は必要であり,授業時間や過ご しやすい気温の条件により,(残差を除いた)1 日の消費電力量が 9000 から 11500 キロワ ット時変動することがわかる.春季については授業時間や過ごしやすい気温の条件により 6000 から 9000 キロワット時で変動することがわかる.冬季については,夏季と比べると 累積加重授業時間に対する負荷が小さいので,気温に鈍感であることがわかる. これに関連して,気温による重みを考慮しない場合について述べる.単純に授業時間の 累積をとったものと,残差を除いた消費電力量の散布図を図 5.3 に示す.縦軸は図 5.2 と 同様に残差を除いた消費電力使用量を表すが,横軸は単純な累積授業時間を表す.この累 積授業時間は,1 日ののべ授業時間を表すため,授業の行われる曜日ごとに決まった値をと る. y = 2.27 x + 6163.93 R ² = 0.46 y = 1.94 x + 8659.49 R ² = 0.56 y = 2.01 x + 6509.96 R ² = 0.24 y = 1.18 x + 8011.30 R ² = 0.22 3000 6000 9000 12000 0 500 1000 1500 消費電力 量 [ kW h ] 累積加重授業時間 [℃・h] 春季 夏季 秋季 冬季
図 5.3 累積授業時間と残差成分を除いた消費電力量のプロット 図 5.3 を見ると,秋季および冬季におけるあてはまりは比較的よいものの,夏季および 春季のあてはまりは悪い.このことは,図 4.12 および図 4.13 で見たように,冬季では気 温による影響の大きさが小さい結果と関連していると考えられる.これにより得られた推 定値と実測値の決定係数は0.781 となった. 図 5.2 得られた累積加重授業時間を用いたモデル (5.2) と,図 5.3 で得られた累積授業 時間を用いたモデルでは,消費電力量の推定に関して,決定係数を比較すると前者のほう があてはまりはよいが,これらのモデルについて単純に優劣を与えることは難しい.とは いえ,本章においては,暑さ(寒さ)に対する不快さを抱えた学生人数が多くなるのに比 例して,5 号館の消費電力量が大きくなることを仮定しているので,節電効果のシミュレー ションにおいては,累積加重時間を用いたモデル (5.2) のほうを用いる.
5.2 節電対策のシミュレーション
5.1 節で得られた区間ごとの消費電力モデル (5.2) を用いて,授業時間の変更を行ったと きに消費電力量がどのように変化するか,シミュレーションを行う. y = 21.18 x + 5406.42 R ² = 0.28 y = 20.31 x + 8200.65 R ² = 0.26 y = 21.95 x + 5443.20 R ² = 0.47 y = 21.61 x + 7033.79 R ² = 0.55 3000 6000 9000 12000 0 40 80 120 消費電力量 [ kW h ] 累積授業時間 [h] 春季 夏季 秋季 冬季5.2.1 春季および夏季の授業 1 時間繰上げ策
まずは,夏の時期は気温のピークである 14 時から,授業時間のピークをずらすために, 春季および夏季の授業時間割を全体的に 1 時間繰上げる節電対策を考える.時間割は従来 通りなので,方法としては単純であり,ただ1 時間早く 1 限が開始し,6 限が終わるだけで ある. 図 5.4 に授業日のひとつである 2010 年 7 月 15 日の例を示した.この授業 1 時間 繰上げ策を行った場合の累積加重授業時間を計算し,これと式 (4.3) で求めた残差を式 (5.2) に代入して消費電力量を計算した結果を図 5.5 に示す.図 5.5 は従来と授業 1 時間 繰上げ策を比較した,5 号館消費電力量の度数分布であり,例えば,消費電力量が 5000 か ら6000 キロワット時の区間に含まれる度数は,従来と授業 1 時間繰上げ策のいずれも 168 日間のうち11 日であることを示す. この結果より,授業 1 時間繰上げ策による明確な節電効果は見られない.このことは, 授業時間の重みである気温が前後1 時間で急激に変化することがなく,授業時間を 1 時間 早めたところで,過ごしやすい気温になるわけではないと考えられる.1 時間早く来なけれ ばならなくなる学生の負担を考えると,むしろデメリットのほうが目立つといえる. 図 5.4 授業 1 時間繰上げ策による授業時間の変化(2010 年 7 月 15 日の例) 24 26 28 30 32 0 5 10 15 20 0 2 4 6 8 10 12 14 16 18 20 22 気温 [ ℃ ] 授業時間 [h] 時刻 従来 繰上げ策 気温図 5.5 授業 1 時間繰上げ策による消費電力量の変化
5.2.2 春季および夏季の授業平均化策
次に,春季および夏季の授業を各時限へ均等に配分できたと仮定し,授業平均化策によ る節電の効果を推定する.各時限の開始および終了時刻は従来のままである.図 5.6 に授 業日のひとつである2010 年 7 月 15 日の例を示した.5 号館における授業は 1 週間計で 282 コマ(423 時間)あるので,1 日の各時限において,のべ平均で 11.75 時間分の授業が行わ れているものとしてシミュレーションを行った.実際の時間割構成を考えるのであれば, 別途スケジューリング計画を立てる必要がある.この授業平均化策を行った場合の比較を 図 5.7 に示す. 図 5.7 を見ると,消費電力量の分布に変化が現れたことがわかる.1 日 10000 から 11000 キロワット時の区間における度数が減尐し,代わりにひとつ下の 9000 から 10000 キロワ ット時の区間における度数が増加している.これにより,春季および夏季において消費電 力量のピークを一部カットすることができたことがわかる.しかし,12000 キロワット時 以上の区間の度数は変化しなかった. 授業平均化策により,授業の行われる168 日間の消費電力量の平均は 8362 キロワット時 から8329 キロワット時へ,1 日あたり約 30 キロワット時減尐し,最大値は 12942 キロワ ット時から12622 キロワット時へ,約 300 キロワット時カットされる. 11 35 18 51 23 15 12 3 0 15 30 45 60 40 00~ 50 00~ 60 00~ 70 00~ 80 00~ 90 00~ 10 000 ~ 11 000 ~ 12 000 ~ 13 000 ~ 度数 消費電力量 [kWh] 従来 繰上げ策図 5.6 平均化策による授業時間の変化(2010 年 7 月 15 日の例) 図 5.7 平均化策による消費電力量の変化 24 26 28 30 32 0 5 10 15 20 0 2 4 6 8 10 12 14 16 18 20 22 気温 [ ℃ ] 授業時間 [h] 時刻 従来 平均化策 気温 11 35 18 51 23 15 12 3 12 33 19 53 19 21 8 0 15 30 45 60 40 00~ 50 00~ 60 00~ 70 00~ 80 00~ 90 00~ 10 000 ~ 11 000 ~ 12 000 ~ 13 000 ~ 度数 消費電力量 [kWh] 従来 平均化策


![図 4.1 2010 年度の消費電力量 [kWh] のグラフ 図 4.2 2010 年度の 1 日の平均気温 [℃] のグラフ 図 4.3 2010 年度の 1 日の平均湿度 [%] のグラフ 図 4.4 2010 年度の 1 日の降水量 [mm] のグラフ 図 4.5 2010 年度の 1 日の平均風速 [m/s] のグラフ 図 4.6 2010 年度の 1 日の日照時間 [h] のグラフ 08000160004/15/16/17/18/19/11](https://thumb-ap.123doks.com/thumbv2/123deta/8084053.850744/22.892.131.770.164.1161/グラフ年度平均℃グラフグラフ年度グラフグラフ年度グラフ.webp)