筑波大学大学院博士課程

筑 波 大 学 大 学 院 博 士 課 程

システム情報工学研究科修士論文

ピアノ弦振動の測定とその等価回路表現

亀 倉 崇 寛

（知能機能システム専攻）

指導教官 水谷 孝一

２００６年１月

目次

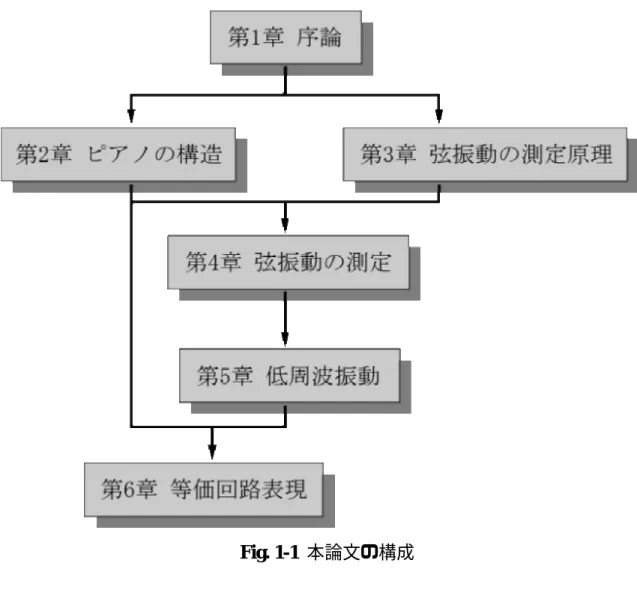
第 1 章 序論 ··· 3 1.1 研究の背景 ··· 3 1.2 研究の目的と概要··· 4 第 2 章 ピアノの構造・発音機構と打鍵装置 ··· 6 2.1 ピアノの構造 ··· 6 2.2 人工打鍵装置 ··· 7 2.3 まとめ ··· 8 第 3 章 弦振動の測定原理··· 9 3.1 光プローブの構造と測定原理 ··· 9 3.2 光プローブの出力電圧の静的特性 ··· 13 3.3 光プローブの出力電圧の動的特性 ··· 13 3.4 まとめ ··· 16 第 4 章 弦振動の測定 ··· 17 4.1 測定系の構成 ··· 17 4.2 二点同時測定 ··· 17 4.3 ピアノ弦振動測定結果と考察 ··· 21 4.4 まとめ ··· 21 第 5 章 弦振動における低周波振動 ··· 25 5.1 低周波振動の定義··· 25 5.2 低周波振動の抽出··· 25 5.3 低周波振動の特徴と考察··· 31 第 6 章 等価回路表現 ··· 40 6.1 波動方程式表現 ··· 40 6-2 等価回路表現 ··· 43 6.2 波動方程式計算結果と計測された結果との比較··· 44 6.3 長時間計算結果 ··· 46 6.4 結果による考察 ··· 47 第 7 章 結論 ··· 48 謝辞··· 49 参考文献 ··· 50 著者文献 ··· 51

第 1 章 序論

1.1 研究の背景 音楽は古来より世界中の人々によって愛されてきた。音楽とは、リズムのみ、 もしくはリズムと音階、音色の組み合わせなどが複雑に組み合った芸術である。 楽器の改良はルネサンス期に入ると次第に行われるようになったが、楽器の改 良は職人の経験的なものにおいて行われており、決して理論に基づいたもので はなかった。そして現在、楽器は科学的な解析が行われるようになったが[1]、 楽器とは複雑な要素が絡み合い発音しているために、解析が困難な部分が多大 に存在する。そのため、未だに楽器の設計は経験的な、古くからの方法のまま である。 全ての物理的な楽器を発音の仕組みによって分類すると、弦楽器、打楽器、 管楽器の 3 つに分けられる。ピアノは、その前身といわれるクラヴィコード、 チェンバロなどのさらに源をたどると、すべて１本の弦をもつ弦楽器に突き当 たる。つまりピアノは、鍵盤を叩いて発音するという意味では鍵盤楽器とされ ているが、原理的な部分では弦楽器と捉えることができる。 ピアノは、現在でも幅広い音楽分野で使用されており、一部のピアノ演奏家 などはグランドピアノなどを使用している。しかしピアノを置く場所やコスト 的な問題から、多くの音楽愛好家は一般による音楽の音源はシンセサイザーに よるものであることも少なくない。現在のシンセサイザーは、実際のピアノの 音を数段階のベロシティーで分けて録音されたものをコンピュータから出力さ れたベロシティー（打鍵の強さ）に合わせて振幅を調整し、それに周波数変調 を施して音を出力するものであり、完全なピアノ音を再現して出力するもので はない[2]。また、ピアノにも一台一台に個性があり、一般的に音が良いとされ るグランドピアノからローファイピアノまで、ピアノという一括りでもその音 の個性というものは無段階的に存在するものである。現在のシンセサイザーで は、その無限に近く存在するピアノの音質を任意に決定できる物は存在しない ということである。 このことの理由としては、ピアノは弦楽器の中でも最も幅広い音域を持って おり、その独特な音色はピアノが非常に複雑な内部機構を有しているからであ る。特に弦の振動は系全体の振動のエネルギー源となるものであり、弦の挙動 に微小な変化が起こっても聴音上大きな変化が現れたりもする。この複雑な内 部機構を解明するために、現在でも数多くの研究がなされている[3-10]。 ピアノ音をリアルタイムでシンセサイズする筐体は、コストや設置場所の点 から見ても非常に有用である。また、複数のパラメータを個別に設定すること によって、無段階的に音色を変えられることにもなるので、無限の音色を持つ

ピアノとして新しい楽器が生まれるとも言えるであろう。 1.2 研究の目的と概要 これまでには、ピアノの打鍵の方法による音色の変化や弦、駒、響板の振動、 発生音のスペクトル解析など、ピアノに関する多数の研究がなされてきた。特 にピアノ弦の振動を把握することは、振動の出力源を把握することにもなり、 非常に重要視されている。[11-12]しかし、これまでに報告されてきた弦の振動 に関する測定結果では歪みゲージ[5]や静電誘導プローブ[13]など、弦に直接接触 して計測するタイプのものもあり、弦の振動自体に影響を与える測定法が多か った。そこで本研究では、非接触・非破壊で測定可能な光プローブを用いた。 光プローブは、50kHz までの平坦特性を有し[8]、プローブに光を利用している ので応答速度も非常に高い。欠点としてダイナミックレンジが限られる、また は狭いことなどが挙げられるが、今回は打鍵強度を少し弱めることで対応した。 そして、本研究では多点同時測定を行うことで弦振動の 3 次元的な像をつかん だ。その結果、通常の振動よりも非常に低い周波数の振動が存在し、それが特 徴的なものであることが確認された。今まで細かく多点測定を行った例は無く、 本研究で細かく測定することにより初めてその特徴に注目されたのであろう。 本研究では、その振動を低周波振動とし、それが駒や可聴音にまで与える影 響を調査するために、発生する原因の解明と、等価回路表現で低周波振動を再 現することを目的とした。発音に大きな影響を及ぼす弦振動に着目し、高精度 な測定装置による実験と計算機シミュレーションの双方から、この低周波振動 の特徴とその発生原因を明らかにすることを試みた。その結果、低周波振動が 存在する原因と考えられるものが確認された。低周波振動はおよそ 0.6Hz 程度と 低かったために、計測できる範囲のサンプリング周波数では十分な周波数分解 能が得られず、高精度な低周波振動を抽出することが出来たとは言えないが、 決まった特徴を有していることは確かである。そこで複数の考えられる原因か ら一つを選び、それを踏まえたモデル化を行い、計算を行った。最終的に等価 回路表現で低周波振動を再現することは出来なかったが、予想していた原因の 一つは低周波振動の発生には関係していないということが判明した。 第 1 章では、序論としての本研究の背景、目的と概要を示す。第 2 章ではピア ノの構成要素と発音の仕組み、および打鍵装置について示す。第 3 章では、光 プローブを使用した測定原理および測定方法について示す。第 4 章では、光プ ローブを使用して実際に計測を行い、ピアノ弦振動の基本的な特徴について示 す。第 5 章では、測定により確認された低周波振動とその特徴について示す。 第 6 章では、第 5 章で示した低周波振動の再現を目的とした等価回路表現につ い て 示 す 。 最 後 に 第 7 章 で は 、 研 究 の ま と め と し て 成 果 を 示 す 。

第 2 章 ピアノの構造・発音機構と打鍵装置

2.1 ピアノの構造 ピアノ内部の構造を簡略化して Fig. 2-1 に示す。鍵盤は、ピアノ内部に張られ ている弦を直接打つためのハンマーと弦の振動を抑えて音を減衰させるダンパ ーに連動している。実際には、てこの原理を用いた連動になっており、複雑な 打弦機構となっている。また、この機構はアクションと呼ばれている。本研究 において使用しているピアノはグランドピアノ（Type C3/YAMAHA）で、弦に ついては 1 つの音程、つまり 1 セットの弦とハンマーに対して単弦と複弦が存 在していて、全 88 鍵のうち巻き線 1 本弦(A0~F#1)、巻き線 2 本弦（G1∼A#2）、 裸線 3 本弦（B2~C8）で構成されている。鍵盤を叩くと、先ほど述べた打弦機構 によって、ハンマーが上がりハンマーヘッドによって弦に振動を与える。この 時に弦が変形し、その歪みがパルス波となって弦上を左右に伝搬する。このパ ルス波が弦上を一往復する時間が基本周波数である。そうして生まれた振動エ ネルギーが弦に接している駒を通して響板へと伝わり、音エネルギーへと変換 され、放出される(Fig. 2-2)。つまり、弦の挙動はピアノの音色や減衰特性を決定 付ける重要な要素であって、その測定も重要視されている。 Keyboard Hammer Damper String _Bridge Soundboard Sound Fig. 2-1 ピアノの発音の仕組み Fig. 2-2 ピアノの発音機構モデル

Fig. 2-3 鍵盤側の留め金 2.2 人工打鍵装置 打鍵装置について、簡略化した図を Fig. 2-4 に示す。鍵盤を叩いていない状態 では、図に示す電磁石によってハンマーが上がっているが、電磁石に流す電流 を切ることによって自身の重みで鍵盤を叩く構造になっている。また、このハ ンマーの初期位置を変えることによって、ベロシティーを変えることが出来る ようになっている。 また、電磁石の電源は約 14V であるが、電磁石の電源を落とした瞬間に電圧 を分圧回路を用いて 5V に落とし、0-5V のトリガとして使用することにより、 電流を切ったと同時に測定を開始できるようになっている。 また、打鍵装置によるベロシティー安定性を確かめた。試行回数は 10 回で、 弦の変位の最大値を測定した。その結果、最大値は 0.42 mm、最小値は 0.40 mm、 平均値は 0.41 mm となった。標準偏差は平均値の約 1.6%となり、信頼できる結 果が得られた。以下、この打鍵装置を使用して測定する。また、弦の変位の測 定方法は後に説明する。

Electromagnet

Keyboard

Hammer

Fig. 2-4 打鍵装置の概略図 2.3 まとめ 本章では、ピアノがいかにして発音しているかを示した。ピアノはハンマー から弦に与えられたパルス波が両端で反射しながら形成する常在波が駒を介し て響板へと伝わり、発音する。また、測定の際に使用する打鍵装置についても 示した。打鍵装置は十分な再現性を持っており、多点同時測定にも使用できる ことがわかった。

第 3 章 弦振動の測定原理

3.1 光プローブの構造と測定原理 このプローブは、1 個のフォトトランジスタと 1 個の LED (TLRH180P/Toshiba) と 1 個のレンズ (f = 7.17mm, φ = 4.0mm, AJ45225G/Edmund) の組を 2 組使用し たものになっており、それぞれの軸は直行している。また、ピアノ弦に垂直に なるように設置する。間に入っているレンズは計測範囲を広げるためのもので、 このレンズとフォトトランジスタとの距離がレンズの焦点距離に等しくなると ころに設置されている。こうすることで、フォトトランジスタに集光される光 量が増えるので、S/N 比が改善されるとともに、ダイナミックレンジを広げるこ とができる。このプローブは、弦の上に平行に設置されたレールに取り付ける 仕組みになっており、構造上可能な範囲で弦の任意の点へ移動させることがで きる。Fig. 3-1 に示すように、弦が静止している状態で LED が照射する光の半分 を遮る位置に LED とフォトトランジスタを向かい合わせて設置する。これは弦 の変位とほぼ比例関係にあり、電圧の変動を見ることで、相対的に弦の変位を 計測することができる。それぞれの組は、響版に対して左右 45 度に向かせ、互 いに直行している。また、弦はそれぞれの光軸の交点から上下左右の 4 箇所に 配置することが可能で、ピアノ本体の構造的な問題があり、プローブの配置や 測定ができない場合は、他の場所で測定することで測定可能範囲を広げること ができる。またこの場合は座標変換処理を行い、x-y 座標平面での振動を得る場 合に、それぞれに適した計算に変える必要がある。

y

x

Photo transistor

Piano string

LED

Lens

Uy

Ux

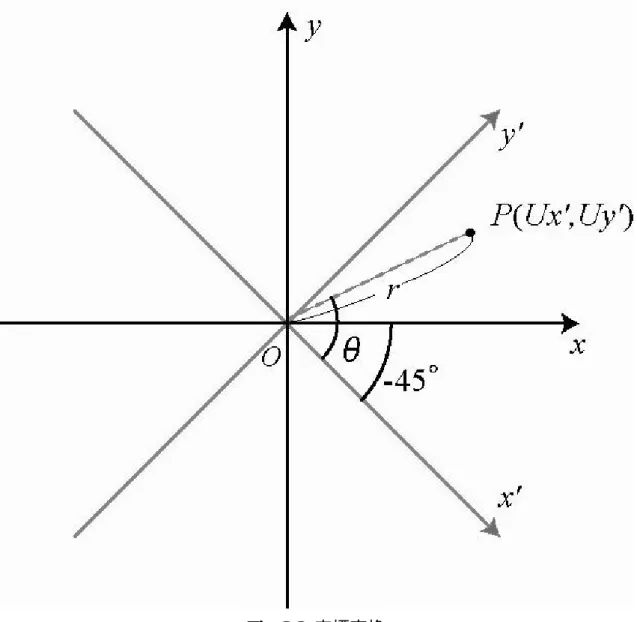
Fig. 3-1 光プローブの概略図 弦が振動すると、フォトトランジスタに届く光量が増減し、それを電圧の変 化として AD/DA ボードを通してコンピュータにて取得する。また、以下のよう に座標変換する。

Fig. 3-2 座標変換 Fig. 3-2 に示すように、座標系 x’-y’ 平面を 2 つの光プローブの光軸に一致さ せ、弦の変位を P(Ux’,Uy’)とする。それぞれのフォトトランジスタで取得される 電圧を Vx、Vy とすると、比例定数 A を用いて以下のように表される。

.

'

,

'

y x

AV

Uy

AV

Ux

=

=

(3-1) ここで、

,

'

'

tan

,

'

'

1 2 2

x

y

y

x

r

−

=

+

=

θ

(3-2)

とおくと、響版に対して水平な x 軸と垂直な y 軸をもつ座標系 x-y 平面におい て、P 点の座標は次のように表される。

).

45

sin(

),

45

cos(

°

−

=

°

−

=

θ

θ

r

Uy

r

Ux

(3-3) よって、式(1)と式(2)を用いて、式(3)は以下のように表される。

).

(

2

),

(

2

y x y x

V

V

A

Uy

V

V

A

Ux

+

−

=

+

=

(3-4) このようにして光プローブの光軸の座標から水平・垂直方向の座標へと変換 と、電圧から変位への校正を行う事ができ、同時に弦の挙動を知ることができ る。同様にして、弦の初期位置を光軸の上側に配置した場合は、

).

(

2

),

(

2

y x y x

V

V

A

Uy

V

V

A

Ux

+

=

+

−

=

(3-5) 光軸の左側に配置した場合は、

).

(

2

),

(

2

y x y x

V

V

A

Uy

V

V

A

Ux

−

=

−

−

=

(3-6) 光軸の下側に配置した場合は、

).

(

2

),

(

2

y x y x

V

V

A

Uy

V

V

A

Ux

−

−

=

−

=

(3-7) と表すことができる。

3.2 光プローブの出力電圧の静的特性 以下に、光プローブの出力電圧の静的特性を示す。Fig. 3-3 は、フォトトラン ジスタからの出力電圧の半分の電圧が出力される位置を静止位置とした弦の変 位と、フォトトランジスタから出力される電圧との関係を表すグラフである。 電圧、変位の両者がほぼ比例関係にあるのは、上下およそ 0.85 mm の範囲であ り、これを光プローブのダイナミックレンジとする。このグラフから式(3-1)に おける比例定数 A を求めると、およそ A = 0.4387 mm/V となることがわかる。

Displacement (mm)

Output (V)

0

-1.5

-1.0

-0.5

0

0.5

1.0

1.5

0.5

1.0

1.5

2.0

2.5

3.0

3.5

4.0

4.5

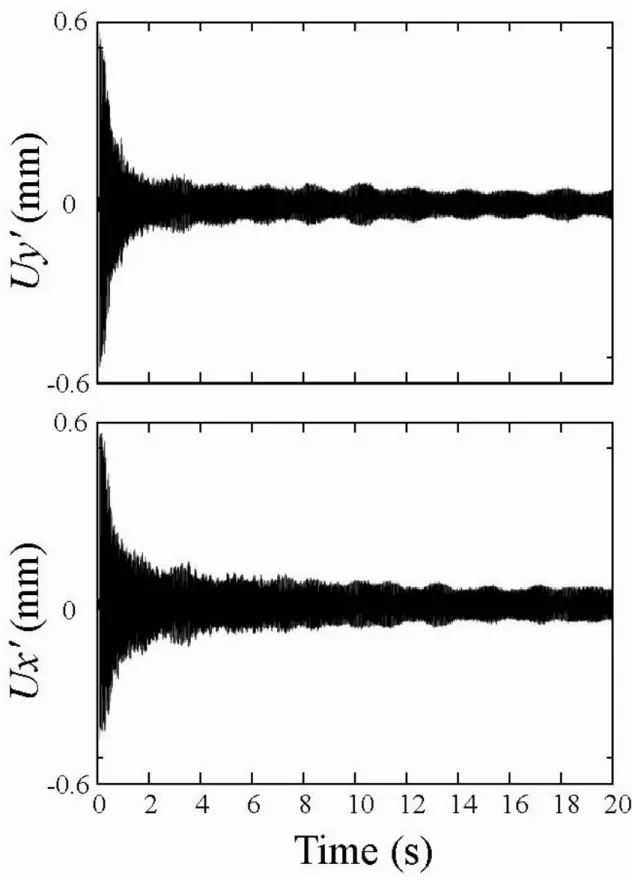
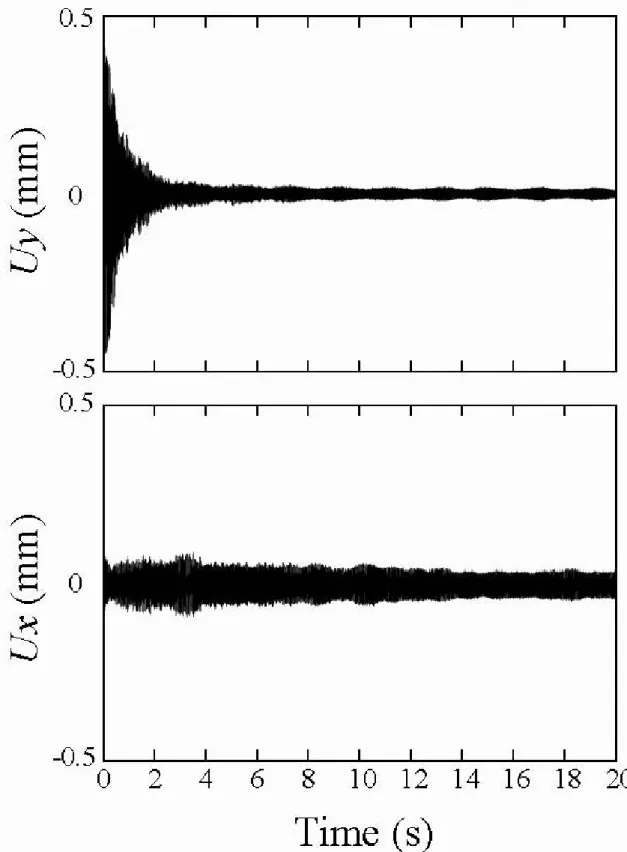
Fig. 3-3 光プローブの変位-出力電圧特性 3.3 光プローブの出力電圧の動的特性 以下に、光プローブの動的特性を示す。対象弦は、E1（基本周波数 約 41.2Hz） である。Fig. .6 は、Fig. .7 における z=637 mm の点で測定したものである。 Fig. .6.1 に示すグラフは、x’-y’ 座標系での弦の挙動の様子を示すグラフで、 Fig. .6.2 に示すグラフは、そのデータに式(3-4)に示す座標変換を行った結果であ る。グラフを見てわかる通り、正常に座標変換できていることがわかる。

3.4 まとめ

本章では、それぞれ斜め 45 度に配置された 2 対の光プローブの原理と、その 測定方法、座標変換方法を示した。そして、このプローブを用いて測定し、正 しく 2 次元振動が取得できていることを示した。

第 4 章 弦振動の測定

4.1 測定系の構成 以下に、測定系の構成を示す。Fig. 4-1 は、測定系の簡略化した図である。ピ アノ弦の静止位置を x=0 mm、y=0 mm とし、鍵盤側の留め金の位置を z=0 mm とする。対象弦は E1 で、基本周波数は約 41.2Hz である。測定系は、対象弦と 2 対の光プローブから成っており、片方は測定対象となる位置に動かすことがで きるようになっていて、もう片方は z=300 mm の位置に固定しておくものとする。 また、打鍵装置のハンマーを振り下ろした瞬間に、その電圧降下をトリガとし て測定を開始する。 測定した範囲は、ピアノと計測装置の構造の関係上 z=452∼772 mm が測定可 能範囲であり、20 mm 間隔で 17 点の挙動を調べた。また、サンプリング周波数 は 50kHz である。 4.2 二点同時測定 ここでは、固定プローブと可動プローブの 2 つを使って、ピアノ弦上を伝わ る波の速さを求める。現在では、ピアノ弦上を伝わる波の速さは 104(m/s)である ことがわかっているが、それは基本周波数成分の波の速さである。 Fig. 4-2 は、(a)可動プローブと(b)固定プローブの垂直方向の挙動を表したグラ フである。可動プローブは、z=772 mm の位置に設置して測定した。グラフにお ける破線がグラフに最初に現れた波の頂点での時間であり、一点鎖線がブリッ ジで反射してきた波の頂点での時間である[10]。 基本周波数成分を考えると、2 点間の距離が L=0.472 (m)であるから、波の伝 わる速さは、

).

m/s

(

9

.

104

0045

.

0

≈

L

(4-1) となる。 また、図における一点鎖線が反射波であるが、ブリッジによって固定端振動 になっているので波が反転している。2 点間における波の到達時間の差が破線の それと完全に一致しており、同じ波であることとともに正確に測定できたこと がわかる。 また、同一時間帯で測定した結果を並べたものを Fig. 4-3 に示す。破線は、同 一の波であると思われるもののピーク値を結んだものである。このグラフから、 ハンマーによる打弦によって生じた波が一定の速度で進行し、弦の両端で反射 しながら常在波を形成していることがわかる。

Agraffe

Hammer

Optical Probe

Bridge

Wound String

z

y

x

Fig. 4-1 ピアノ弦振動の測定系

-0.8

0

0.8

75

80

85

90

95

100

105

-0.8

0

0.8

18.5

4.5

4.5

Time (ms)

Uy

(mm)

z=300

z=772

79.8

98.3

93.8

84.3

Fig. 4-2 打鍵直後の z=300, 772 (mm)点における時間推移

0

0.01

0.02

0.03

772

752

732

712

692

672

652

632

612

592

572

552

532

512

492

472

452

1275

Time (s)

z (mm)

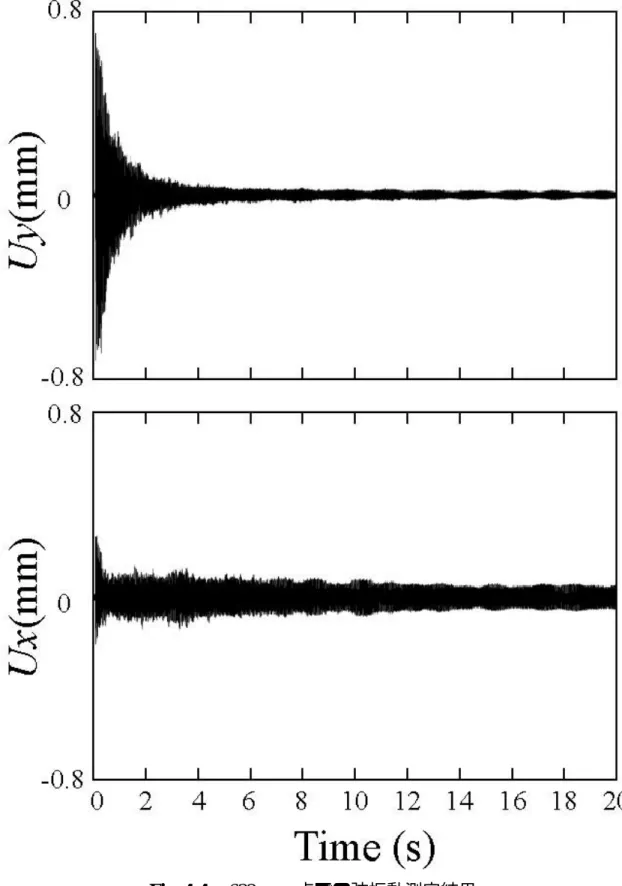
Fig. 4-3 波の進行する様子

4.3 ピアノ弦振動測定結果と考察 第 3 章にて説明した光プローブを用いて測定した結果を示す。対象弦は E1（基 本周波数 約 41.2Hz）である。サンプリング周波数は 50kHz であり、測定点は z=452~772 mm で 2 cm 刻みに測定した。ここでは、弦の全長の中点に近い点で ある z=632 mm の点について解析を行う。 Fig. 4-4 は z=632 mm 点での弦の垂直振動、水平振動の時間変化をグラフ化し たものである。垂直振動は立ち上がりから急激に減衰しているが、水平振動は 立ち上がりから少し減衰した後は振幅があまり変化せず一定であることがわか る。また、この点において周波数解析を行った結果が Fig. 4-5 である。波の開始 点から約 10 秒間で FFT を施した。グラフの上は垂直振動、下は水平振動である。 水平振動のほうが基本周波数と他のいくつかの周波数成分が高くなっているが、 これは先ほどにも述べたように水平振動はあまり減衰せずにほとんど一定の振 幅を長い時間保っているからである。このグラフから、偶数番目の部分音成分 が奇数番目の部分音成分より低くなっていることが見て取れる。これは、測定 した点が z=632 mm と、弦の全長 1275 mm の中心に近い場所で測定したことが 原因と考えられる。第 1 モードの振動は弦の中心が山になるので基本周波数成 分は大きく確認でき、他の奇数番目のモードでも同様に山になるので振幅が大 きくなるが、逆に偶数番目のモードだと中心が谷になるので振幅が小さくなる のである。また、第 8 モードの振動において谷となる点の一つである z=478 mm 点に最も近い測定点 z=472 mm 点でも周波数解析を行った結果を Fig. 4-6 に示す。 グラフを見ると、第 8 部分音成分が周りの周波数成分よりも低くなっているの が確認できる。 また、垂直成分よりも水平成分の相対振幅のほうが大きくなっている。これ は、Fig. 4-4 の 4 秒以降を見てもわかるとおり、ピアノ弦振動の余韻の部分では 垂直成分よりも水平成分の振幅のほうが大きくなるという性質から来ているも のである。 4.4 まとめ 本章では、始めに測定対象弦について座標系を定義した。そして二点同時測 定について示し、第 3 章で示した光プローブを用いて実際に弦の振動を測定し た結果を示した。弦の上を伝わるパルス波は、弦の両端で固定端反射して常在 波を形成していることが確認された。また部分音成分について、そのモードで 振動している場合に節にあたる位置で計測した結果では強度が小さくなってい ることも確認された。

-60

-40

-20

0

20

0

500

1000

1500

-60

-40

-20

0

20

Frequency (Hz)

Relative Amplitude(dB)

Vertical

Horizontal

Fig. 4-5 z=632 mm 点での周波数解析結果

-60

-40

-20

0

20

0

500

1000

1500

-60

-40

-20

0

20

Frequency (Hz)

Relative Amplitude

(dB)

Vertical

Horizontal

Fig. 4-6 z=472 mm 点における周波数解析結果

第 5 章 弦振動における低周波振動

5.1 低周波振動の定義

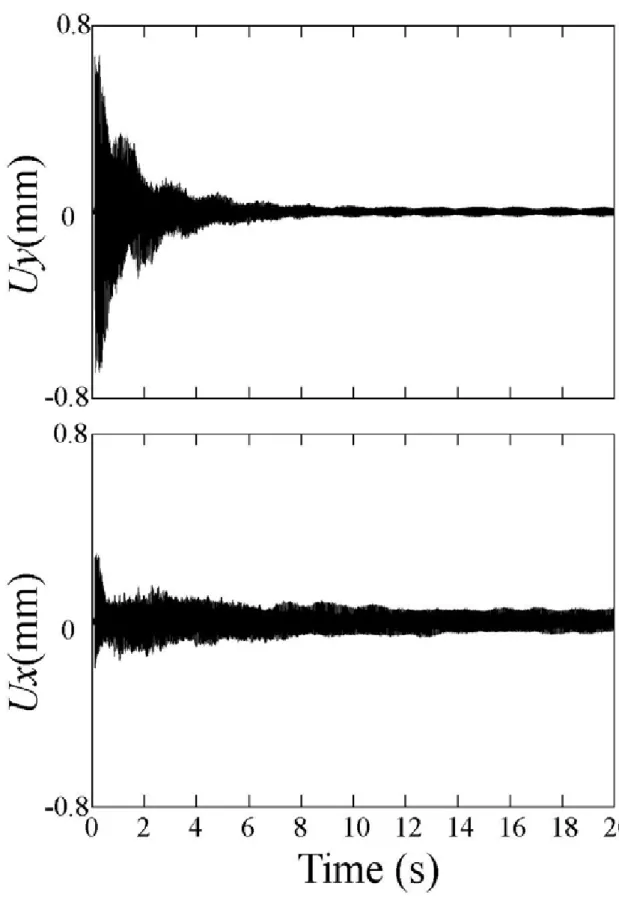
Fig. 5-1 の振動の垂直成分を見ると、若干上下に揺れながら減衰していること

がわかる。また、Fig. 4-4 と比べると、Fig. 4-4 には低周波振動が見られない。同 時に周波数が非常に低く、通常の振動とは完全に違った特性を有している可能 性が高いので、部分音成分の振動の変位を(UxAC,UyAC)、低周波振動の変位を(UxDC,

UyDC)とし、弦振動(Ux,Uy)を以下のように分けて定義する。[14]

(Ux,Uy) = (Ux

DC

,Uy

DC

) + (Ux

AC

,Uy

AC

)

(5-1)

5.2 低周波振動の抽出

この低周波振動の挙動を調べるために、振動の上下の包絡線をとり、これら の中心を求めた。そのグラフが Fig. 5-2 である。この低周波振動の周波数を求め るために、10 秒間の FFT を施した。窓関数はハミング窓を用いた。その結果を 以下のグラフ(Fig. 5-3)に示す。

-0.1

0

0.1

0

1

2

3

4

5

6

7

8

9

1

-0.1

0

0.1

0

Time (s)

Ux

(mm)

DC

Uy

(mm)

DC Fig. 5-2 z=772 mm 点での低周波振動抽出結果

-50

-40

-30

-20

-10

0

0

0.5 1

1.5 2

2.5 3

3.5 4

4.5 5

-50

-40

-30

-20

-10

0

Relative Amplitude

of (dB)

Frequency (Hz)

Uy

DC

Relative Amplitude

of (dB)

Ux

DC Fig. 5-3 z=772 mm 点における低周波振動の周波数解析結果

グラフによると、垂直成分ではこの低周波振動はおよそ 0.6 Hz であることが わかるが、水平成分の低周波振動では Fig. 5-2 と併せて見ても低周波振動は確認 しづらいので、以下の解析では垂直成分の低周波振動について行う。 このままだと、周波数分解能が約 0.1 Hz と、この低周波振動の周波数を決定 するには不十分であるので、田部井らの示す方法[15]によって周波数を高精度に 決定する。田部井らによると、入力系列 x(i)に窓関数を乗じたものの離散フーリ エ変換を G(k)とおき、G(k)系列の中で絶対値が最大のものの添え字を kmax とす ると、 (ⅰ)

G

(

k

max

−

1

)

>

G

(

k

max

+

1

)

の時

max)

(

)

1

max

(

k

G

k

G

r

=

−

_(5-1) とおくと、

r

r

k

f

+

−

+

=

1

2

1

max

_(5-2) (ⅱ)

G

(

k

max

−

1

)

<

G

(

k

max

+

1

)

の時

max)

(

)

1

max

(

k

G

k

G

s

=

+

_(5-3) とおくと、

s

s

k

f

+

−

−

=

1

2

1

max

_(5-4) として周波数を高精度に求めることができる。この計算法を用いて低周波振動 の周波数を求めた結果、周波数は約 0.616 Hz となった。

-0.04

0

0.04

0

1

2

3

4

5

6

7

8

9

1

-0.04

0

0.04

0

Time (s)

Displacement of (mm)

Ux

DC

Displacement of (mm)

Uy

DC Fig. 5-4 ローパスフィルタ処理後の低周波振動

また、水平成分の低周波振動についても 1 Hz 以下の同様の低周波振動が存在 すると仮定し、1 Hz 以上の周波数をローパスフィルタを用いてカットした波形 を Fig. 5-4 に示す。 5.3 低周波振動の特徴と考察 Fig. 5-4 を見る限りでは、水平成分の低周波振動に関しては、垂直成分ほどは っきりしたものは確認できない。また、Fig. 5-5 は横軸が水平方向の低周波振動、 縦軸が垂直方向の低周波振動で、低周波振動の x-y 平面上における軌跡を表した ものである。図中の矢印は軌跡をたどった方向を示している。水平方向の低周 波振動は垂直方向の低周波振動と比べて小さいので、図上では水平方向を 2.5 倍 に拡大して表している。Fig. 5-5 を見ても、通常の振動のようなきれいな回転運 動は見られない。垂直方向、水平方向ともに近い周波数で周期的な運動をして いるのであれば、このリサージュ曲線では短期的に円を描くように運動するは ずである。こういったことから、低周波振動は主に垂直成分に現れることがわ かった。

-0.02

-0.005

-0.05

0

0.05

-4

1

x 10

-5

0

5

-3

x 10

x 10 x 10

-12

-7

-5

0

x 10 x 10 x 10x 10

-0.01

0

0.01

-8

-2

-3

x 10

-1

-2

-10

x 10

-3

0

2

-0.02

0

0.02

-0.04

0

0.02

-15

0

5

-0.04

0

0.02

-3

x 10

-3

x 10

-3

x 10

x 10

-3 -3

x 10

-8

-2

-0.01

0

0.01

-3

x 10

5

Horizontal Vibration (mm)

V

ertical V

ibration

(mm)

0.0-1.0(s)

1.0-2.0(s)

3.0-4.0(s)

5.0-6.0(s)

7.0-8.0(s)

2.0-3.0(s)

4.0-5.0(s)

6.0-7.0(s)

Fig. 5-5 低周波振動のリサージュ曲線（x-y 平面での軌跡）

ただ、打弦から 1 秒間までの間は水平成分についても大きな低周波振動が確 認できる事がわかる。しかし、Fig. 5-5 の右下の図を見てわかる通り、ある程度 時間がたった後では垂直成分よりも水平成分のほうが大きいことがわかる。こ れは通常の振動にも共通して言えることで、水平方向の減衰が小さいというこ とである。 さらに、この低周波振動はある特徴を持っていることがわかった。Fig. 5-6,Fig. 5-7 は、低周波振動の波形を測定位置ごと、時間ごとに並べたものであり、それ ぞれの左側が垂直成分、右側が水平成分に対応している。また、Fig. 5-7 は□印 が実際に計測されたデータ点であり、実線がそのデータにスプライン補間をか けたものである。Fig. 5-6 を見ると、まず垂直成分についてであるが、弦の全長 の中心付近（z=638 mm）から離れるに従って振幅が大きくなる傾向がみられる。 さらに、z=592 mm と z=572 mm の間で位相が逆転していることがわかる。また、 水平成分については、弦の中心付近から離れるに従って振幅が大きくなる傾向 は弱冠みられるが、ほとんど一定であるといってもよい。しかし、垂直成分の ように位相が逆転しておらず、垂直成分とはまた違った挙動を示していること がわかる。また Fig. 5-7 では、垂直成分については、時間の早い段階では弱冠ず れが生じているものの、その後のデータでは計測範囲の両端で変位が逆になっ ていることがわかる。水平成分については、垂直成分と比べてもあまり目立っ た特長は見られないが、複数の節を持って振動している可能性も見受けられる。

0 2 4 6 8 10 0 2 4 6 8

Time(s)

Vertical

Horizontal

Position in

z axis(mm)

452 472 492 512 532 552 572 592 612 632 652 672 692 712 732 752 772 U DC 10 0 50 -50 Displacement of (Ǵm) Fig. 5-6 測定位置ごとの低周波振動

Vertical

Horizontal

Time (s)

1

2

3

4

5

6

1

2

3

4

5

6

Position in

z axis (mm)

452

472

492

512

532

552

572

592

612

632

652

672

692

712

732

752

772

-50 0 50

Displacement of

U

DC

(

Ǵm)

Fig. 5-7 測定位置ごとの低周波振動

この特徴的な挙動を示す低周波振動の存在は、ピアノ弦の挙動の解明におい て重要なものであると思われる。この低周波振動が存在する原因として考えら れるものを挙げると、対象弦が巻き線であることが考えられる。巻き線は、裸 線に銅の弦を巻きつけた構造になっている。また、この弦は端から端まで均一 な巻き線ではなく、Fig. 5-8 に示すような構造になっている。鍵盤側の裸線部の 長さは 15 mm、反対側は 17.5 mm となっており、両端の裸線部の長さが異なっ ていた。先ほど述べたように、低周波振動の節は z=572∼592 mm 間に存在する が、これは弦全体（長さ 1275 mm）に対する割合で示すと、鍵盤側の留め金か ら 44.86∼46.43 % の位置に相当する。また、裸線部の長さの比をこれに対応さ せると 46.15 % となり、弦全体での位置に置き換えると z=588.46 mm の位置に 相当することになる。このことから、巻き線部の両端の裸線部の長さの比が低 周波振動の節の位置に関係している可能性が高い。 Fig. 5-8 対象弦の構造 Fig. 5-9 推定される弦全体の低周波振動の様子 Fig. 5-9 は低周波振動の弦全体の様子（推測含む）である。Fig. 5-9 のように低 周波振動が存在していると仮定すると、巻き線部が自由端振動をしているとい うことができる。パルス波が巻き線部を往復して定在波を形成しているとする と、巻き線部の往復路長が 2.485 m、低周波振動の周波数が 0.616 Hz であるので、

巻き線上を伝わる波の進行速度は2.485×0.616=1.531 m/s となった。この速度は、 基本周波数成分の波がピアノ弦上を伝わる速度 104 m/s と比べてみても、はる かに小さいものである。[10] この低周波振動について、弦ではなくフレームやピアノ本体自身が振動し、 弦振動に乗って測定された可能性もあるため、対象弦 E1 を打鍵したときの隣の 弦（F1）の変位を測定した。ここで、F1 はミュートした（ダンパーが下りた） 状態で計測した。その結果を Fig. 5-10 に示す。グラフからはほとんど振動して ないことが見てとれ、ピアノ本体またはフレーム自体の振動が低周波振動とな っている可能性は無いことがわかる。 また、z = 583∼590 (mm) にて再度測定を行い、低周波振動の節を詳しく求め てみたところ、Fig. 5-11 のグラフを得ることができた。先ほど述べたように、 低周波振動の節は弦の両端の裸線部の長さの比と一致すると仮定した場合、節 の位置は z = 588.46 mm となる。そこで Fig. 5-10 の z = 588 mm の振幅を見てみ ると、前後の振幅と比べて小さくなっており、その前後で位相が逆転している。 このことより、z = 588 mm が節であることとともに、低周波振動の節は弦の全 長を両端の裸線部の長さの比で分けた点と一致することが証明された。

-0.8

0

0.8

0

2

4

6

8

10

-0.8

0

0.8

Time (s)

Ux

(mm)

Uy

(mm)

Fig. 5-10 E1 を打鍵したときの F1（ミュート状態）の測定結果

0

z=583

z=584

z=585

z=586

z=587

z=588

z=589

z=590

0.5

1

1.5

2

2.5

3

3.5

4

4.5

-0.02

0.02

0

-0.02

0.02

0

-0.02

0.02

0

-0.02

0.02

0

-0.02

0.02

0

-0.02

0.02

0

-0.02

0.02

0

-0.02

0.02

0

Time (s)

Uy

(mm)

Fig. 5-11 低周波振動の節近辺の測定結果

第 6 章 等価回路表現

6.1 波動方程式表現 本章では、低周波振動が発生する原因と、駒や響板への影響を調査するため に、計算機上で低周波振動をシミュレートすることを目的とした。そこで、考 えられる原因として第 5 章で弦の両端の裸線部の長さの比が低周波振動の節と 一致している件に着目し、弦を三つのそれぞれインピーダンスの異なる領域に 分割し、それぞれの境界面で波が反射すると仮定し、モデル化する。 まず、等価回路表現を実現するために波動方程式で弦の振動を表すことにす る。弦振動を波動方程式で表現すると、以下のようになる。 2 2 2 2 2

z

y

c

t

y

∂

∂

=

∂

∂

(6-1) ここで、c は波の速さである。ここで、

v

t

y =

∂

∂

u

z

y =

∂

∂

とおくと、

⎟

⎠

⎞

⎜

⎝

⎛

∂

∂

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∂

∂

u

v

z

c

u

v

t

1

0

0

2 (6-2) と書ける。

⎟⎟

、 とおき、ラックス-フリードリクス法[16]

⎠

⎞

⎜⎜

⎝

⎛

=

u

v

Y

_⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

0

1

0

c

2

A

τ

2

2

Y

_{i,j 1}

Y

_{i 1,j}

Y

_{i 1,j}

t

Y

_≈

+

−

+

−

−

∂

∂

(6-3)

h

Y

Y

z

Y

i j i j

2

, 1 , 1 − +

−

≈

∂

∂

(6-4) で近似すると、

h

Y

Y

A

Y

Y

Y

_{i j i j i j i j i j}

2

2

, 1 , 1 , 1 , 1 1 , +

−

+

−

−

₌

+

−

−

τ

(6-5) となり、

h

τ

λ

=

_とおくと

}

)

(

)

{(

2

1

, 1 , 1 1 ,j i j i j i

E

A

Y

E

A

Y

Y

₊

=

+

λ

₊

+

−

λ

_{− (6-6)} から

⎪⎭

⎪

⎬

⎫

⎪⎩

⎪

⎨

⎧

+

+

−

−

+

+

=

− + − + − + − + +

)

(

)

(

)

(

)

(

2

1

, 1 , 1 , 1 , 1 , 1 , 1 2 , 1 , 1 1 , j i j i j i j i j i j i j i j i j i

u

u

v

v

u

u

c

v

v

Y

λ

λ

(6-7) が得られる。初期条件は、

⎩

⎨

⎧

+

=

0

)

2

.

0

5

sin(

)

,

0

(

z

z

y

)

1

4

.

0

,

2

.

0

0

(

)

4

.

0

2

.

0

(

≤

<

<

≤

≤

≤

z

z

z

(6-8) ここで、

y

を三つの領域

y

₁ 、

y

₂ 、

y

3 に分けて考える。 3 2 1

y

y

y

y

y

y

=

=

=

)

1

(

)

(

)

0

(

2 2 1 1

≤

<

≤

≤

<

≤

z

l

l

z

l

l

z

とする。境界条件は、

0

)

0

,

1

(

)

0

,

0

(

0

)

0

,

1

(

)

0

,

0

(

=

=

=

=

v

v

y

y

(6-9) t t l t t l t t l t t l

v

v

y

y

v

v

y

y

, 0 , , 0 , , 0 , , 0 .

3

2

3

2

2

1

2

1

2 2 1 1

=

=

=

=

(6-10) とする。ここで、

0

)

,

0

(

)

,

0

(

₌

∂

∂

=

∂

∂

t

t

v

z

t

u

(6-11) より

0

2

, 1 , 1

−

₌

≈

∂

∂

−

h

u

u

z

u

j j j j

u

u

_1,

=

_1,

∴

₋ (6-12) が得られるのでこれを(6-7)式に代入すると

⎪⎭

⎪

⎬

⎫

⎪⎩

⎪

⎨

⎧

+

+

−

−

+

+

=

− − − − +

)

(

)

(

)

(

)

(

2

1

, 1 , 1 , 1 , 1 , 1 , 1 2 , 1 , 1 1 , 0 j i j j j j j j j j

u

u

v

v

u

u

c

v

v

Y

λ

λ

(6-13) より j j

v

v

_−1,

=

_1, (6-14) j j j

v

u

u

_{0, +1}

=

λ

_1,

+

_1, (6-15) が得られる。同様に (6-16) j N j N j N j N j N j N j N

u

v

u

v

v

u

u

, 1 , 1 1 , , 1 , 1 , 1 , 1 − − + − + − +

+

=

=

=

λ

(6-17) (6-18) である。求める

y

はフリードリクスの式より j i j i j i j i j i j i j i j i

v

y

y

y

y

y

y

v

, , 1 , 1 1 , , 1 , 1 1 , ,

)

(

2

1

2

2

τ

τ

+

+

=

∴

−

−

≈

− + + − + + (6-19) である。 次に、境界面での反射・透過を考える。反射波は j L

y

c

c

c

c

, 2 1 2 1 1

1

+

−

(6-20) 透過波は

j

y

c

c

c

, 0 2 1 2

2

2

+

(6-21) であるので、これらの重ね合わせを考えると j j l j l

y

c

c

c

y

c

c

c

c

y

_0, 2 1 2 , 2 1 2 1 1 ,

2

2

1

1

1 1

+

+

+

−

=

+ _(6-22) j j l j

y

c

c

c

c

y

c

c

c

y

_0, 2 1 1 2 , 2 1 1 1 , 0

1

2

2

2

1

+

−

+

+

=

+ _(6-23) となる。同様に、 j j l j l

y

c

c

c

y

c

c

c

c

y

_0, 3 2 3 , 3 2 3 2 1 ,

3

2

2

2

2 2

+

+

+

−

=

+ _(6-24) j j l j

y

c

c

c

c

y

c

c

c

y

_0, 3 2 2 3 , 3 2 2 1 , 0

2

3

2

3

2

+

−

+

+

=

+ _(6-25) が得られる。 6-2 等価回路表現 本節では、(6-1)式を等価回路表現に変換する。(6-1)式 2 2 2 2 2

z

y

c

t

y

∂

∂

=

∂

∂

は、弦の張力

T

、弦の断面積

S

、密度

ρ

を用いて表すと 2 2 2 2

z

y

S

T

t

y

∂

∂

=

∂

∂

ρ

(6-26) となる。これは、二階の偏微分方程式で表せる。すなわち

⎪

⎪

⎩

⎪⎪

⎨

⎧

∂

∂

=

∂

∂

−

∂

∂

=

∂

∂

−

t

f

T

x

v

t

v

x

f

1

σ

(6-27)

ここで、

f

=

T

∂

y

/

∂

x

は弦の張力の垂直成分、

σ

=

ρ

S

は線密度である。 この(6-27)式において、Table 6-1 のインピーダンス類推の対応関係を用いると

⎪

⎪

⎩

⎪⎪

⎨

⎧

∂

∂

=

∂

∂

−

∂

∂

=

∂

∂

−

t

i

L

x

e

t

e

C

x

i

(6-28) となる。そして、この(6-28)式をそれぞれ波の速度の異なる 3 つの領域に分けて 等価回路表現で表したものが Fig. 6-1 である。Eh = sin(t) で、t = 0 から電圧を出 力し、Eh = 1 となった瞬間にスイッチ S を切る。 Table 6-1 機械系、電気系での類推パラメータ Mechanical System

v

f

r

1

/

T

Mobility Analogy

e

i

_G

_L

Electrical System Impedance Analogy

i

e

_R

C

L C 1 1 L C 2 2 L C 3 3 Uy E S h Fig. 6-1 等価回路表現を用いたモデル 6.2 波動方程式計算結果と計測された結果との比較 本節では、6.1 節で得られた式をもとにシミュレートした結果を示す。Fig. 6-2 は、上のグラフが光プローブで測定した結果、下のグラフがシミュレーション 結果である。ともに、z = 772 mm の点で y 方向の弦変位の時間的変化を表した ものである。ともに特徴の異なる点が多数みられるが、弦上の空間パルス波の 挙動は周期的にみても同様である。下のグラフのシミュレーション結果を見て みると、時間が経つにつれ歪みが大きくなっていることがわかる。

-0.6

0

0

0.05

0.1

Time (s)

Uy

(mm)

0.6

0

0

0.1

0.05

-0.6

0.6

Time (s)

Uy

(mm)

Fig. 6-2 z = 772 mm での結果 上：光プローブでの測定結果 下：シミュレーション結果

6.3 長時間計算結果 本研究で弦をモデル化した式には減衰項は含まれていないため、振幅は時間 によって減衰しないが、低周波振動が弦の両端の裸線部が存在し、境界面でそ れぞれの領域のインピーダンスの違いから生まれるものであるという仮説が正 しいのであればこのシミュレーション結果にも低周波振動が現れるはずである。 Fig. 6-3 は 6.1 節で得られた式に関して長時間観測した結果である。結果を見 る限り、低周波振動は再現されていない。すなわち、低周波振動は弦の巻線部 と裸線部とのインピーダンスの違いによって生じる透過・反射波に起因するも のではないことが判明した。

0.0

0.5

1.0

1.5

2.0

2.5

-0.6

0

0.6

Time (s)

Uy

(mm)

Fig. 6-3 波動方程式出力の時間的変位

6.4 結果による考察 本章をまとめると、低周波振動は弦の両端の裸線部の存在が起因しているこ とが予想されるものの、その裸線部と巻線部とのインピーダンスの差によって 生じるものではないことが判明した。 他に原因として、弦の両端の裸線部の存在が関係していることを考えると、 ①裸線部と巻線部のスティフネス（剛性）が異なるために、裸線部と巻線部と の境界で折れが発生していること ②単位長さあたりの質量がそれぞれ異なるために、質量の大きい巻線部が振れ ていること ③巻線自体がバネのような構造をしているために、外周の巻線のみを往復する ようなパルス波が発生していること ④それら複数の要因の組み合わせ が考えられる。

第 7 章 結論

本研究は、ピアノ弦振動上に発生する低周波振動の発生原因の解明を目指し て、想定される原因を含めたモデルを計算機上で再現する研究をまとめたもの である。 第 2 章ではピアノの発音機構と打鍵装置の仕組みと、ピアノの弦の振動を測 定することの意味や、測定装置の有効性を示した。 第 3 章では弦振動の測定に使用する光プローブの測定原理について示した。 光プローブの中心に設置する遮蔽物の変位を細かく変え、出力の変化を見る実 験を行った。そして、測定系の軸を垂直・水平方向の軸へと変換する方法につ いても示し、遮蔽物の変位が正しく測定されていることを示した。 第 4 章では測定対象弦に対する座標を定義し、実際に測定した。また二点同 時測定についても、その有効性について示した。そして、実際に位置を変えて 測定し、波が弦の両端で反射しながら伝達し、それが定在波を形成しているこ とを示した。また、ある部分音成分について振動をモードで考えた時に、その 節にあたる位置では強度も低くなっていることがわかった。 第 5 章では、対象弦の測定可能領域を 20 mm ごとに測定した結果、基準音成 分と部分音成分の他に、とても低い周波数の振動が存在することを示し、それ を低周波振動と定義した。低周波振動は、ある測定点を境に位相が逆転してお り、その点を詳細に調べた結果、弦の両端の裸線部の長さの比で弦の全長を二 分する点であることが判明した。その結果から、低周波振動は弦の両端の裸線 部が何らかの形でその発生に関係していると思われる。 第 6 章では、第 5 章での結果を踏まえて、裸線部と巻線部との境界で双方の インピーダンスが異なることから発生するものであると仮定し、モデル化を行 い計算機上でシミュレートした。結果、低周波振動を確認することではなかっ たが、数多く考えられる原因のうちの一つに関して、原因ではないものである ことを確認した。 以上より、低周波振動の発生原因についての調査に進展があったと言える。 今後、低周波振動の可聴成分への直接的・間接的な影響について解明されれば、 高精度なピアノ音リアルタイム生成への貢献があると考えられる。また、本研 究では打鍵強度が一定な状況で測定を行ったが、打鍵強度を変化させたときの 影響についても調べる必要があると思われる。

謝辞

研究を進めるため多くのご指導・ご進言を頂いた、指導教官である筑波大学 システム情報工学研究科知能機能システム専攻 水谷孝一教授には大変お世話 になりました。2005 年 3 月まで指導教官としてお世話になり、退官された筑波 大学永井啓之亮名誉教授には、本研究の主題を与えていただき、また、音楽音 響に関しての多くの知識やご指導を頂き、感謝しております。音響システム研 究室の皆様には研究に関する多くの相談に乗って頂くなど、多大な支援に感謝 しております。

参考文献

[1] Fletcher, "The Physics of musical instruments”, Springer-Verlag(1998)

[2] 生 方 則 孝 , YAMAHA: “ ボ ー ド で 復 活 生 方 則 孝 の FM 音 源 講 座 ,” http://www.yamaha.co.jp/product/syndtm/read/fm/

[3] D.W. Martin: “Decay rates of piano tones,” J. Acoust. Soc. Am., 19, pp.535-541 (1947).

[4] H. Flecther, E.D. Blackham and R. Stratton: “Quality of piano tones,” J. Acoust. Soc. Am., 34, pp.749-761 (1962)

[5] I. Nakamura: “Fundamental theory and computer simulation of decay characteristics of piano sound,” J. Acoustic. Soc. Jpn. (E), 10, pp.289-297 (1989). [6] 高澤嘉光: “レーザ変位計を用いたピアノ弦の測定とその解析,” 日本音響学 会音響研究会資料, MA93-11, pp.15-20 (1993) [7] 水谷孝一, 渋谷 啓, 江連朝寛, 永井啓之亮: “スペクトロメータを用いる固 液二相流の流速測定”, 光波センシング論文集, LST26-6, pp.45-50 (2000) [8] 水谷孝一, 岩佐 修, 永井啓之亮: “ピアノ弦における過渡的振動の測定,” 日本音響学会音楽音響研究会資料, MA00-9, pp.21-26 (2000) [9] 井上慎一郎, 水谷孝一, 永井啓之亮: “同時計測されたピアノ 2 本弦の挙動解 析” (2003) [10] 岩佐修 “ピアノ音響特性の定量的測定” (2000) [11] 井上慎一郎, 水谷孝一, 永井啓之亮: “同時計測されたピアノ 2 本弦の挙動 解析” (2003) [12] 井上慎一郎, 江連朝寛, 水谷孝一, 永井啓之亮: “ピアノ 2 本弦の 2 次元振動 同時測定用光プローブ,” 日本音響学会 2003 年度春季研究発表会公演論文 集 I, 2-7-12, pp.827-828, (2003.3)

[13] H.Fletcher, E.D.Blackham and R.Stratton: “Quality of piano tones,” J. Acoust. Soc. Am. 34, pp.749-761 (1962)

[14] 亀倉崇寛, 永井啓之亮, 水谷孝一: “ピアノ 1 本弦の 2 次元振動測定とその 解析” (2004)

[15] 田部井誠, 上田光宏: “FFT を用いた高精度周波数決定法,” 電子情報通信学 会論文誌, A Vol. J70-A No.5 pp.798-805 (1987)

[16] 大江戸太郎: “周期的外力を持つ非粘性バーガース方程式の倍周期解の自 動判別法” (1998)

著者文献

亀倉崇寛, 水谷孝一, 永井啓之亮: “ピアノ 1 本弦の 2 次元振動測定,” 日本音響 学会音楽音響研究会資料, MA2005-24, pp129-132 (2005)