二相探索形式の最適性と目標のパッチ状分布との関係についての共進化ゲームモデル(カオスをめぐる力学系の諸問題)

Coevolutionary

Game

Modelling

Consideration

on

The Relation Between the Optimalities

of

Two-mode Searching Behavior and the Target’s Patchy Distribution Hiromi

SENO

Department ofMathematics, Faculy ofScience, HiroshimaUniversity

Kagamiyama 1-3-1, Higashi-hiroshima, 724Hiroshima JAPAN 二相探索形式の最適性と目標のパッチ状分布との関係についての

共進化ゲームモデル

広島大学理学部数学教室 瀬野裕美

ABSTRACT

We consider mathematically the relation between the efficiency of two-mode searching behavior

and the target’s patchydistribution. Two-mode searching includes patch-searching and target-catching.

Fourinmitivemodelsarepresented: Model 1 constructedbyaWienerprocesson$\mathbb{H}^{D1}$;Model2bya

time-discreteMarkovprocesson$\ovalbox{\tt\small REJECT}^{1}$,thatis,on acircle;Model3bya time-discretestochasticprocesson$\ovalbox{\tt\small REJECT}^{1}$.

InMoxlel3,differently from Model2,thesearcher’s present location isassumedto beinfluencedby the

pastpassageconfiguration. Model4isdifferentfrom theothers,applied the fractal concept for the

trajectory pattern made by the target. The optimality of thetrajectorypattemagainst the searcher is

analyzed. Thesedifferent modelsgive a varietyof resultsdepending onthecharacteristics ofeachmodel.

Weapplyourresultstoacoevolutionarygamebetween thesearcher’s searching behavior and thetarget’s

distribution. Compared withasimple mode searching, thesuperiorityoftwo-mode searchingisshown to

dependseriouslyonthe target’s distribution.

INTRODuCTION

Itiswell-known thatvarious speciesofinsectsbehave in

a

two-mode

way

to

search the target (e.g.,food, mate,

or

host)distributed patchily in

space.

Such

a

behavior isfrequently called “area-concentrated search”. An insectsearchesapatchof

targets with

a

relatively large motion whichis adaptabletothe spatial scaleof patch

distribution; then,after finding the frst target;itreducesitsscale ofmotion tosearch

another target in

a

relatively

near

region. Successively, obeying

some

criteria,the

searcher re-changesitsbehaviortosearch another patch. Such

a

criteriontypically

belongsto

one

of thefollowing three types: (a) fixed-time strategy,i.e., thesearcher

staysfor

a

fixedperiod of time ineachpatchencountered; (b) fixed-number strategy,

i.e., the searcher stays untilitcatches

a

fixednumber of targets ineachpatch

encountered

as

long

as

thetimeinterval between

a

catchandthenextcatch doesnot

exceed

a

fixed value. Avarietyofmathematical models havecontributedtothe

understanding of such

a

behavior within the framework of evolutionary

strategy.1),

2), 6),

7), 8), 9), 10)

Inthis

paper,

we

mathematically demonstrate that

a

two-mode searchingis

possibleto become

an

adaptable strategy of searcher in

a

coevolutionary

game

between

thesearching behavior and the target’s distribution. Thesearcherisassumedtobehave

alwaystorealize thepossible highest

mean

searching efficiency. If thetarget

distributionisassumed tobedirectedtomaketheefficiency

as

low

as

possible, this

coevolutionary

game

can

becalled

a

minimax

game

between the searcher and the

target.11)

Ifthedistributionis assumedto bedirectedtomakethe

mean

efficiency

as

high

as

possible, this

game

can

beregardedcooperative. We call the former type of

target “the counter-behaving target“ andthelatter “the cooperative-behaving target“.

Wedeal withthreemodels: Model 1 constructed by

a

Wienerprocess;Model2

by

a

time-discrete Markov

process;

Model

3

by

a

time-discrete stochastic

process.

Model

3

can

beregarded

as a

modification of Model

2

ofthequoted

paper.

The

searcher’s present location is assumedtobe influenced by thepast

passage

configuration, whichis

an

essentially differentassumptionfromthatfor Model

2.

Model4is different from theothers,applied thefractalconceptfor thetrajectorypattem

made by thetarget. Theoptimality ofthetrajectorypattemagainstthe searcheris

analyzed.

MODELLING ASSUMPTIONS

Targer Both patches and targets

are

respectively assumedtobeuniformly, that is,

regularlydistributed

on

the

space

and in the patch, and allidenticaltoeach other. We

set$\Delta S$thedistancebetween the nearest-neighbor patches and$\Delta L$ between the

nearest-neighbor targets and $l$thelength of patch

zone

(thepossiblelongest distance between

two targets in

a

patch). Each patchcontains$N$individuals of target. Thus,itisnaturally

assumedthat$N\Delta L=l$

.

We

assume

a

restrictionforthetargetdistribution:The

area

available forthe

targetdistribution islimited. Thus, thelargeristhesizeof patch, the smalleris the

distance between patches. Moreover,thelargeris the size of patch, the largeristhe

distance between targets for

a

fixed number oftargetsin the patch. In this

paper,

this

$\Delta S+N\Delta L=A$, (H)

where$A$

can

be regarded

as a

shareofspace

per

patch. The targetmust selectits

distribution pattern under thisrestriction.

Wealsotake account of thetarget size,

say

$b$

.

Theexistenceof

a

non-zero

target

sizeexcludesthat the patch size

can

be

zero.

That is,when

we

discuss the effect of the

targetsize,the sizewill be

seen

toplay

a

role inrestrictingthe target’sselectionof$\Delta L$

:

Moreprecisely $b\leq\Delta L$

.

Thesize$b$

may

be regarded

as a

minimal

necessary

share of

space per

target, too.

Searcher. In

our

model,thesearcher’s searchingconsistsoftwo

processes:

patch-searching

process

and target-catching

process.

The switchingrule betweentwo

processesis

as

follows: Thepatch-searching

process

is terminatedwhenthe searcher

encounters

a

certain point

or

enters

a

certain regionof thegiven

space.

Itisregarded

as

themomentwhenthe searcher finds

a

patch andcatches

a

target. Ontheotherhand, the

target-catching

process

continuesfrom thismomentuntil thesearcher’sgain satisfies

a

givencriterionin this

process.

The searching efficiency$E$is defined

as

follows:

$E \equiv\frac{M}{T_{1}+T_{2}}$

where$T_{1}$ denotesthetimetaken in the patch-searching

process,

$T_{2}$thetimetaken in the

target-catching

process

for catching$M$targets. Ahigherefficiency

means

a

better

searching behavior for the searcher. Weinvestigatethe optimal stIategytorealizethe

highestefficiencyfor

a

fixed patch’s quality (distancesbetween nearest-neighbor

$\ovalbox{\tt\small REJECT}:_{T^{2}=t_{1}^{\iota}+t_{2}^{2}+1_{3}}I_{:}^{0}\exists_{1^{T_{2}=0_{1}}}^{:_{T=1+t}}!^{:}\dot{i:::::}T_{2^{1}}=tT_{2}$

$\overline{\Phi^{o}\ \Theta E}$

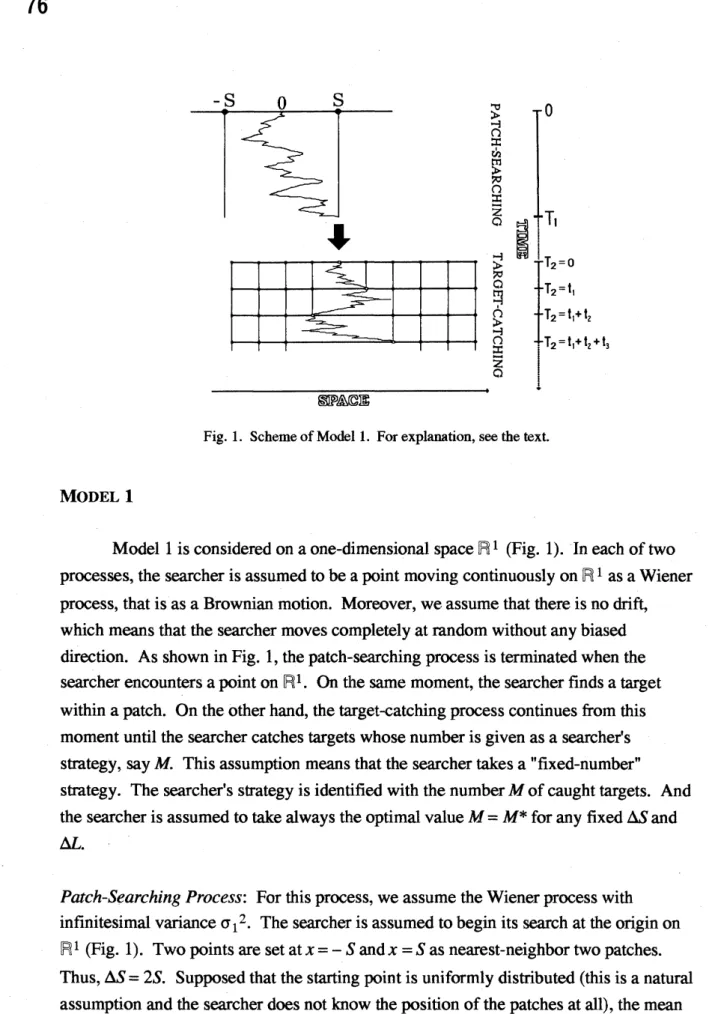
Fig. 1. Scheme ofModel 1. Forexplanation,seethe text.

MODEL 1

Model

1

is considered

on

a

one-dimensional

space

$H^{D1}$ (Fig. 1). Ineachof two

processes,

the searcheris assumed tobe

a

point movingcontinuously

on

$\mathbb{H}^{D1}$

as a

Wiener

process,

thatis

as a

Brownian motion. Moreover,

we

assume

that there is

no

drift,

which

means

that the searcher

moves

completelyatrandom without

any

biased

direction. As shown in Fig. 1, the patch-searching

process

is terminatedwhenthe

searcherencounters

a

point

on

$\mathbb{H}^{D1}$

.

On the

same

moment,the searcher finds

a

$ta^{r}get$

within

a

patch. On the otherhand, thetarget-catching

process

continuesfrom this

moment until the searcher catchestargetswhose numberis given

as a

searcher’s

strategy,

say

$M$

.

Thisassumption

means

that the searcher takes

a

“fixed-number“

strategy. Thesearcher’s strategyisidentified with the number$M$of caught targets. And

thesearcheris assumed to take alwaystheoptimal value$M=M^{*}$for

any

fixed$\Delta S$and

$\Delta L$

.

Patch-Searching Process: For this

process, we

assume

theWiener

process

with

infinitesimalvariance$\sigma_{1^{2}}$

.

Thesearcherisassumedtobeginitssearch attheorigin

on

$R^{D1}$ (Fig. 1). Twopoints

are

set at$x=-S$and$x=S$

as

nearest-neighbortwopatches.

Thus,$\Delta S=2S$

.

Supposed thatthestartingpoint is uniformly distributed(thisis

a

natural

assumptionandthe searcher does notknow thepositionof the patches atall),the

mean

The momentgenerating function (m.g.$f.$) of$T_{1}$ is given by that of the

first-passage-timewithsymmetricabsorbing boundaries (L. M.Ricciardi,private

communication), from which

we

can

obtain the

mean

time $\langle T_{1}\rangle^{9)}$;

$q_{1} \}=(\frac{\Delta S}{2\sigma_{1}})^{2}$

.

(1.1)

Target-Catching Process: The searcherisassumedtocatch

one

targetat$T_{2}=0$,that is,

atthemoment whenthe searcher begins the target-catching

process.

The searcher

searches thenextneighbor target by theWiener

process

with

an

infinitesimalvariance

$\sigma_{2^{2}}$whichis lessthan $\sigma_{1^{2}}$

.

The caught targetisassumedtobe removed. Thus, after

repeatedlytargets

are

caught, there willbe

a

wideregion with

no

target(seeFig. 1). Sincethesearcher undergoes the Wiener

process

in thisregion, the

mean

period

$\langle t_{j}\rangle$forcatching the$(j+1)$-th targetafter thej-this shorter than$\langle t_{j+1}\rangle$ forcatching the

$(i^{+} 2)$-thafter the$(j+1)- th$

.

The

m.g.

$f$

.

of period

$t_{j}$forcatching the $(j+1)$-th target

after the j-th

one

isgivenby that of the first-passage-time with absorbingboundariesat

$x=\Delta L$and$x=j\Delta L$ (L. M.Ricciardi,privatecommunication),which givesthe

mean

time$\langle t_{j}\rangle^{9)}$;

$p_{J}\}=j(\frac{\Delta L}{\sigma_{2}})^{2}$

.

(1.2)

Then,

we

can

find the

mean

time$\langle T_{2}\rangle$ tocatch$M$targets:

$q_{2} \}=\{\sum_{j=1}^{M-1}t_{j}\}=\sum_{j=1}^{M-1}\{t_{j}\}=\frac{1}{2}(\frac{\Delta L}{\sigma_{2}})^{2}M(M-1)$

.

(1.3)

Efficiency: Making

use

of theaboveresults,

we can

find the

mean

efficiency:

$\omega_{M}=\frac{M}{q_{1}\}+(T_{2}\}}=\frac{M}{\frac,41(\frac{\Delta S}{\sigma_{1}})^{2}+\frac{1}{2}(\frac{\Delta L}{\sigma_{2}})^{2}M(M-1)}$

.

(1.4)

Analysis: Calculating$\alpha E\rangle_{A}/\partial M$,

we

find thatthereis

a

unique$M^{*}$, whichmaximizesthe

$M^{*}= \frac{1}{q}\frac{\Delta S}{\Delta L}\frac{\sigma_{2}}{\sigma_{1}}$

.

(1.5)

When $M=M^{*}$, theefficiency becomes

$\Theta M^{*}=a\}\frac{\Delta L}{\sigma_{2}}(\frac{\Delta S}{\sigma_{1}}-\frac{1\Delta L}{a\sigma_{2}})_{1}^{1^{-1}}$

.

(1.6)

Seno(1991) analyzed(1.6) and showed the followings$9)_{;}$ The

counter-behaving target,

whichtends toreducethesearchingefficiency, always adopts

a

patchydistributionat

thecoevolutionary goal. In

case

of the cooperative-behaving target, which tends to

increasethesearchingefficiency,

a

targets’ uniformdistribution is

very

likely to be

adopted

versus

a

simple mode searching behavior of searcher. Searcher’stwo-mode

searchingbehaviorisalways adoptedagainstthecounter-behaving target, whileitis

adaptable against the cooperative-behaving target only when the target sizeandthe

patchsize

are

sufficiently small and the target density is sufficientlyhigh in thepatch.

Sufficiently large target size leads the searcher’s behaviorto

a

simple mode searching.

MODEL

2

Model

2

isconsidered

on

$\ovalbox{\tt\small REJECT}^{1}$, thatis,

on a

circle(Fig. 2). We

assume

that the

searchercannotdistinguish thevisited patch from the unvisited

one.

Moreover,

as

the

foundtargetis notassumedtobe removed in Model2, it is assumed that thesearcher

cannotdistinguish the found target from the encountered

one.

Thus, themodelling

spaoe

$\ovalbox{\tt\small REJECT}^{1}$ for Model

2

can

be regarded

as a

mathematicaltranslation of the

spaoe

$\mathbb{H}^{D1}$

where patches

are

uniformly distributed. Ineachof two

processes,

following

a

discrete

time, thesearcherdiscretely changesits site

on

$\ovalbox{\tt\small REJECT}^{1}$ ateach step. Thesearcher’s

siteis

selectedateach step

on

$\ovalbox{\tt\small REJECT}^{1}$atrandom

independently of the previous site. Thesearcher

mn@m\Leftrightarrow er[iloN@

Fig.2. Scheme ofModel2. Forexplanation,seethe text.

Patch-Searching Process: We consider this

process

on a

circle of length$A$

.

Onthis

spaoe,

thereis

a

connectedregion (an arc)of length$l(<A)$,which represents the

zone

of

patch. This situationcorrespondstothat when thepatch (segment)oflength$l$is

uniformlydistributed

on

$\mathbb{H}^{o1}$ withdistanoe$\Delta S=A-l$between the nearest-neighbor

patches. Notethat,

as

in the

case

of Model 1,$A$

can

beregarded

as a

share of

spaoe per

a

patch. We

use

thefollowingnotations for Model

2:

$P_{1}^{in}$

:

probabilityof thesearcher’sentlanceby

one

stepinto the patch. From

theassumption for the

process,

we

easily find$P_{1}^{in}=(l/A)(bNP)$

\langle$n_{1}\succ$; expectednumber ofstepsforthesearcherto enter thepatch,

where$b$

can

be regarded

as

thetargetsize

or

the

necessary space

share

per

target

as

in

Model 1, whileit

can

be regarded

as

thesearcher’s searching capacity. With these

notations, the following is easily found:

{

$n_{1}$)

$= \sum_{k=1}k\cdot P_{1}^{in}(1-P_{1}^{in}f^{-1}=\frac{1}{P_{1}^{i\mathfrak{n}}}$

Target-Catching Process: We

use

the followingnotations:

$P_{2}^{in}$

:

probability of the searcher’s catching the target in

one

step. From

theassumption for the

process,

thisprobability is given by$P_{2}^{in}=$

$b/\Delta L=bN/l$

.

$P_{2,k}^{in}$

:

probabilityofthesearcher’s catching thenexttargetby$k$ steps

after catching

a

target

$P_{2,cI}^{in}$ probability that after catching

a

targetthesearcher’s catches

the

nexttargetby

a

numberof stepslessthan

or

equalto$n_{c}$

$\langle n_{2}\rangle$

:

expected total number of steps in the target-catching

process

before thesearcher gives it

up

$\langle M\rangle$; expectednumberof targetscaughtin the target-catching

prooess

before the searchergives it

up.

Withthese notations, the followings

are

found:

$\{M\}=\sum_{k=1}k\cdot(P_{2,c}^{in})^{k-1}\cdot(1-P_{2,c}^{in})=\frac{1}{1-P_{2,c}^{in}}$

.

(2.2) $\{n_{2})=\sum_{M=1}^{\infty}\sum_{k_{j}=1}^{n_{c}}(k_{1}+k_{2}+\cdots+k_{M-1}+nd(\prod_{j=1}^{M-1}P_{2,k_{j}}^{in}\int 1-P_{2,c}^{in})$ (2.3) $= \frac{1}{P_{2}^{in}}\frac{1}{(1-P_{2}^{in})^{n_{c}}}+n_{c}$

.

Efficiency: With the aboveresults,theefficiency is givenby

$\emptyset_{tn_{1})}^{\ovalbox{\tt\small REJECT}_{+\phi_{2}\}^{=}}}=(\frac{1}{P_{1}^{in}}+n_{c}l^{1-p_{2}^{in}\gamma+}c\frac{1}{P_{2}^{in}}J^{-1}$

Analysis: Remark thatit isbeneficial for the searchertotake

a

simple mode searching,

onlywhen the efficiency with

a

simple mode searching (i.e.,$n_{c}=0$) islargerthan that

with the two-mode searching for$n_{c}\geq 1$

.

Sincethe simple mode searching of this model

is

a

simple Bernoulli

process,

theefficiency is easily obtained

as

follows:

$\otimes\iota_{imple}=\frac{bN}{A}=P_{1}^{in}$

.

(2.5)

Thecondition$\otimes|_{n_{c}=n_{c}}<\not\in’$)$|_{simple}$

can

beobtained from (2.4) and(2.5):

$\frac{1-(1-P_{2}^{in}1\gamma c}{n_{c}(1-P_{2}^{in})+/P_{2}^{in}}<P_{1}^{in}$

.

(2.6)

Consequently from the analysis

on

(2.6), Seno (1991) shows thatthe coevolutionary

goalconsists of

a

simple mode searching behaviorand the counter-behaving targets’

uniformdistribution,

or

of

a

two-mode searching behavior and the

cooperative-behaving targets’patchy distribution.9) With

some

additional conditions, Seno(1991)

consider suchpossibility that

a

two-mode searching

may

be selected by the searcherat

the consequentsituation in the coevolutionary

game

againstthe counter-behaving

target,too.9)

MODEL

3

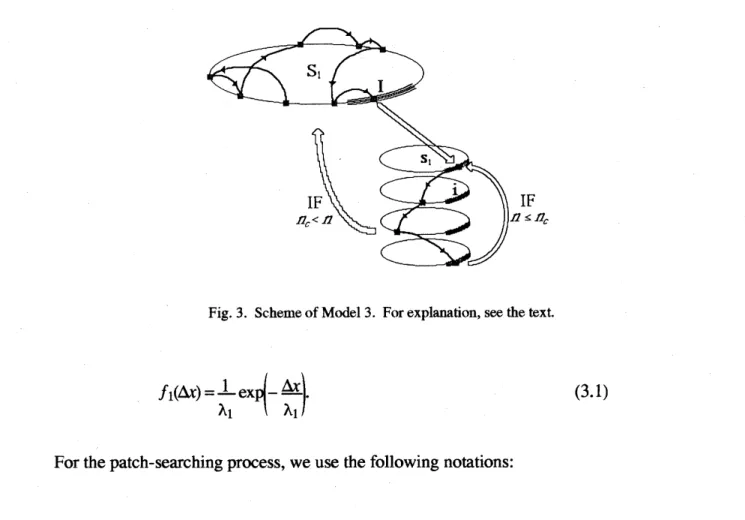
Thisisthe modelmodified from Model

2

(Fig. 3). Differently from Model2,

thedistancebetween

a

siteand the followingsite isassumedtobe

an

exponential

randomvariable. Thedirectionofeach stepis selectedatrandom,that is,with the

probability 1/2_{thesearcher jumpstothenextsitein theclockwise}

or

_{in theanti}

clockwise direction.

Patch-Searching Process: Atfrst,

we

must selecttheinitial $sitex_{0}$of the searcherout

of the patch. Itis assumed thattheinitial site isuniformly distributedoutof the patch.

Thenextsearcher’s stepis subjectedtotheexponential distribution with expected value

Fig. 3. Scheme ofModel3. Forexplanation,seethe text.

$f_{1}( \Delta \mathfrak{r})=\frac{1}{\lambda_{1}}ex+\frac{\Delta\kappa}{\lambda_{1}})$

.

(3.1)

For the patch-searching

process,

we

use

the followingnotations:

$x\in S_{1}\equiv[0, A]mod A$

I:

zone

of patch, $S_{1}\supset I\equiv(A-l, A)mod A$

$G$

:

zone

outof patch,$S_{1}\supset G=S_{1}-I\equiv[0,$ $A-lImod A$

$P_{x}(\eta)$

:

probability of the searcher’$s$entranoeby$n$steps intothepatch

from theinitialpoint$x_{0}$ outof thepatch with

a

configuration$x\equiv$

$(\eta, x_{1}, \ldots,x_{n-1})$ in$G$, independently of thepointreached in the

patch

$\langle n_{1}\rangle$; $\exp\infty ted$numberof steps for the searchertoenterfirstlythe

patch, averaged with respecttothe initialpointand the

configuration of searching.

$\prec n_{1}>=\sum_{n=1}^{+\infty}\int_{G^{dx_{0}}}\int_{G^{d\mathfrak{r}_{1}}}\int_{c^{dx_{2}}}\cdot\cdot\int c^{dx_{n-1}n\cdot P_{x}(\eta)}$

.

(3.2)

$P_{x}^{n}( \eta)=(\frac{1}{2\text{\‘{A}}_{1}})^{n-1}\}s\infty h(\frac{A}{2\lambda_{1}})\{n\sinh\{\frac{l}{2\lambda_{1}})co\mathbb{A}(\frac{2x_{n-1}-A+l}{2\text{\‘{A}}_{1}})\prod_{k=0}^{n-2}\infty\Phi(\frac{A-2|x_{k}-x_{k+1}|}{2\text{\‘{A}}_{1}})$

.

(3.3)

Target-CatchingProcess: Thesearcher’sinitialsite in the target-catching

process

isthe

centerof target’sregionwhich has length$2b$ (seeFig. 3). Now

we

regardthe center

pointoftarget’sregion

as

theorigin

on

$\ovalbox{\tt\small REJECT}^{1}$

.

Further, after catching

a

target,the searcher

isassumedtobegin alwaysitsnexttarget-catching

process

from thecenterof target’s

region. Thesearcher’sstepissubjected to the exponentialdistributionwith expected

value$\lambda_{2}$, that is,with probability density function:

$f_{2}( \Delta \mathfrak{r})=\frac{1}{\lambda_{2}}ex\phi-\frac{\Delta\kappa}{\lambda_{2}})$

.

(3.4)

Thesearcher is assumedtotake

a

fixed-giving upstepstrategy. Innature, thesearcher

may

stochastically

go

outof the patch, and the smaller the patch sizeis, the larger such

probabilitymustbe.

Below

we

list

up

thenotationsfor the target-catching

process:

$z\in s_{1}\equiv[0, \Delta L]mod \Delta L$

$i$

:

target’sregion,$s_{1}\supset i=i_{1}\cup i_{2}\equiv[0, b$) $\cup(\Delta L-b, \Delta L)mod \Delta L$

$g$

:

regionoutoftarget,$s_{1}\supset g=s_{1}-i\equiv[b, \Delta L-b]mod \Delta L$

$n_{c}$

:

fixed-giving

up

step,i.e.,the behavior-switching step number in

the target-catching

process

$\mu_{z}$; probability of thesearcher’scatching the target by$n$steps with

a

configuration$z\equiv(\triangleleft)’ z_{1},$

$\ldots,$$z_{n-1}$) in$g$

$F_{\langle z\rangle}$

:

probability of the searcher’scatching

a

targetby less than$n_{c}$

\langle$n_{2}\leq n_{c^{\rangle}}$

:

expectednumberof steps for thesearchertocatch another target

after catching one, averaged with respecttothe configuration of

searching, conditional

on

thenumberof steps being equal to

or

lessthan the fixed-giving

up

stepnumber$n_{c}$

$\langle n_{2}\rangle$

:

$\exp\infty ted$total number of steps inthe target-catching

process

beforethesearchergivesit

up

$\langle M\rangle$; expected number oftargetscaught in the target-catching

process

before the searchergives it

up.

With thesenotations, the following relations

are

found$10)_{;}$

$\langle M\rangle=\frac{1}{1-P^{c_{\emptyset}}}$ (3.5)

$\langle n_{2}\rangle=\{\langle M\rangle-1\}\langle n_{2}\leq n_{c^{\rangle}}+n_{c}$

.

(3.6)

$P_{z}^{n}=2( \frac{1}{2\lambda_{2}})^{n}\{\varpi h(\frac{d}{2\lambda_{2}})\}^{n_{\dot{\Re}11h}}(\frac{r}{\lambda_{2}})\cosh(\frac{d-2z_{1}}{2\lambda_{2}})coffi(\frac{d-2_{k- 1}}{2\lambda_{2}})\prod_{k=1}^{n-2}\cosh(\frac{d-2|_{4+1}-*\}}{2\lambda_{2}})$

.

(3.7)

Efficiency: With the aboveresults,the

mean

efficiencyisgiven by

(3.8)

Analysis: Made

use

oftiresomenumericalcalculations,the results obtained by Seno and

Buonocore(1991) 10)

are

thefollowings: Ifthereis

no

constraint

on

thedistribution, the

counter-behaving target takes $\iota*(<A)$

as

itspatchsizeatthe goal ofcoevolutionary

game

with the searcher’s searchingbehavior, whilethe cooperative-behaving target

takes

a

densepatchy distribution(every nearest-neighbor targets toucheach other in

eachpatch)

or a

uniformdistribution. If thereis

a

constraintfor the patchsize$l:h_{in}\leq l$

$\leq\iota_{nax}$, and$l_{\min}\leq l^{*}<l_{\max}$, then the counter-behaving target

can t&e

$\iota*$

as

itspatch size

atthe goal ofcoevolutionary

game,

while thecooperative-behaving target takes$l_{\min}$

or

thecoevolutionary

game

leads the patch sizeto$l_{\min}$

.

If$l_{\max}<l^{*}$, the

game

leads the

patch sizeto$l_{\max}$

.

Inthis case,

a

simple model searching

can

become

a

coevolutionary

goalfor the searcher against the counter-behaving target.

MODEL

4

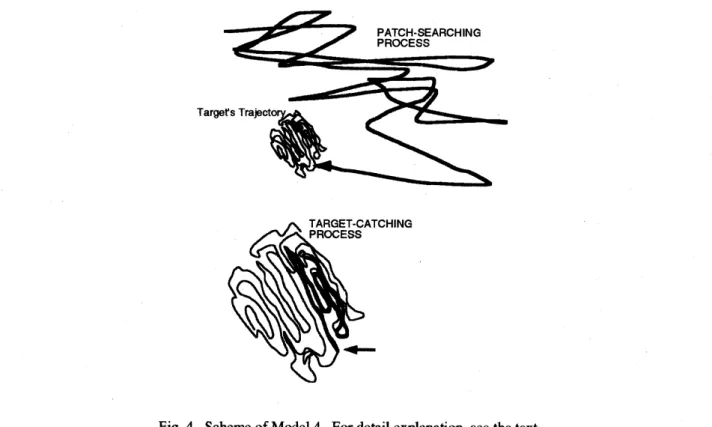
Model4considers

a

$sp\infty ific$ situation,differentlyfrom three models presented

above. Only

one

targetisconsidered,which makes

a

trajectoryin the2-dimensional

space

forthe searching

process

(Fig. 4). Thetrajectory corresponds tothe patch

considered for the other models. The searcher’s patch-searching

process

isassumed to

encounterthetrajectory. Aftertheencounter,bytracingthetrajectory the searcher is

assumedtosearch the target. This$COlTesponds$tothe target-catching

process.

This type

of searchingbehavior is observed for the predatoragainst

some

leaf-miner.3),4)

The target’s

trajectory

is assumedtoexpand the diameter$l$,whichisdefined

as

theminimaldiameter of the disc that

can cover

the wholetrajectory. Thetotallengthof the

trajectory

is assumedtobe$J$

.

Theexpectedtime $T_{1}$ for the searchertoencounterthetrajectoryin the

patch-searching

process

isassumed to beinversely proportionaltothe

area

expanded by the

trajectory,

1

2.

On the otherhand, the$\exp\infty ted$time$T_{2}$ for the searcherto fmd the target

in the target-catching

process

is assumedtobeproportionaltothetotal length of the

trajectory,$J$

.

The above argumentgives theprobability for the searcherto catch the

target

per

unittime:

$p \propto l^{2_{+}}\frac{Y}{J}$

ヲ (4.1)

where$Y$is

a

positiveconstant. The expected searching efficiencyiscorresponding to

$1/p$

.

Weconsider theapproximation forthetarget’sfractal trajectoryby

a

numberof

line segmentswith thelength$w$

.

Then,the required number$m$of segments is

approximatedlygivenby$J\wedge v$

.

Following Katz and George(1985) 5)

Fig. 4. Schemeof Model4. For detail explanation,seethetext.

where$D$isthefractal dimensiontocharacterize the spatialpatternof the

trajectory.

Assumethat the segmentlength$w$is characterizedby the mechanism for the target to

make thetrajectory. Thus,$w$is assumedtobedetermined, for example, bytherelation

between thephysiologyof targetorganismandthe structureof

spaoe.

Inthissense, the

trajectoryconstructedby

a

number of line segments with the length$w$

can

realize the

essential nature of thetrajectory. Now,made

use

of the relations (4.1) and(4.2),the

catching probability$p$is expressed

as

$p= \alpha J^{2}m^{2(1-Dy_{D}+}\frac{\beta}{J}$, (4.3)

where$\alpha$ and$\beta$

are

positiveconstants. Analyzed_{$\partial p/\partial J,p$}takes theminimalvalue when

$J=P$

:

$J^{*}=( \frac{\beta}{2\alpha})^{1\mathcal{B}}m^{2(D-1p_{D}}$

.

This$J^{*}$

can

be regarded

as

the optimal strategy for the targettoreduoe the searching

efficiency

as

low

as

possible. If$m$

can

beconsidered

as

thetimelength for the targetto

makethetrajectory,theexistenoeoftheoptimum$i^{*}$

means

that theoptimaltimelength

tomake thetrajectory exists. In

case

of theprey-predatorrelation,the length

may

be

deternined with

some

additional conditions for the prey’s survival

or

reproduction.

REFERENCEs

[1] Cowie,RJ.andKrebs, J.R.,Optinal foraginginpatchyenvircmnents. inPopulation Dynamics (eds.R. M. Anderson,B. D. Turner and L. R.Taylor),$Black_{We}n$ScientificPublications,New

York, 1979,183-205.

[2] Iwasa, Y.,Higashi, M. andYamamura, N.,Preydistributionas afactor$detern\dot{u}ning$the choice of

optimal foraging strategy. Am Nat.117(1981),710-723.

[3] Kato, M.,Min$\dot{n}g$pattem of the honeysuckle leaf-miner Phytomyza lonicerae. Res. PopuL Ecol.

26(1984),84-96.

[4] Kato, M.,The adaptivesignificance of leaf-nunmg pattemasananti-parasitoid strategy: A

theoreticalstudy. Res. Popul.Ecol 27(1985),265-275.

[5] Katz,M.J.,and George,E.B.,Fractals and the analysis of growth paths. Bull. Math. Biol. 47

(1985),273-286.

[6] Knoppien, P. andReddingius,J.,Predators with twomodes ofsearching:Amathematical model.

J.theor. $BioA114$(1985),273-301.

[7] Murdie, G.,Simulation of the effects ofpredator/parasitemodelsonpreylhost spatialdistribution.

inStatistical EcolOgy(eds.G. P.Patil,E.C.Pielou andW.E.Waters),Penn. State Statistical

Series,Pennsylvania, 1971,215-233.

[8] Murdie,G. andHassell,M.P.,Fooddistribution,searchngsuccessand predator-preymodels. in

The Mathematical Theory_ofTheDynamicsofBiologicalPopulations(eds.M.S. Bartlett and R.

W.Hiorns),AcademicPress, London, 1973,87-101.

[9] Seno, H.,Somemathematicalconsiderationsontwo-mode searchng I. Japan J. Indust. Appl.

Math.8(1991),325-344.

[10] Seno,H.,andBuonocore, A.,Somemathematical considerationsontwo-mode searchng11.

JapanJ. Indust. $AppL$Math8(1991),505-523.

[11] Stewart-Oaten,A.,Minimax strategiesforapredator-preygame. Theor. Popul. Biol.22(1982),