Numerical Simulation for Abrupt Contraction Flow of Fiber Suspensions in Polymeric Fluid Kazunori Yasuda, Taro Nishimura* and Kiyoji Nakamura Departme

論

文

繊維懸濁高分子流体 の急絞 り流 れ の数値解析

大阪大学工学部

保

田

和

則(会 員)

京都工芸繊維大学

西

村

太

良(会 員)

大阪大学工学部

中

村

喜 代 次(会 員)

Numerical

Simulation

for Abrupt

Contraction

Flow

of

Fiber

Suspensions

in Polymeric

Fluid

Kazunori

Yasuda, Taro Nishimura*

and Kiyoji Nakamura

Department

of Mechanical

Engineering,

Osaka University,

Suita, Osaka

*Kyoto Institute

of Technology

_{, Sakyo-ku,}

_Kyoto

Abstract

Flow pattern and fiber orientation of fiber suspensions in polymeric fluid through a two-dimensional abrupt contraction are calculated using the Giesekus model and the Dinh-Armstrong model.

The flow pattern of fiber suspensions in polymeric fluid is different from that of polymeric fluid ; a vortex near the salient corner in the suspension flow becomes larger than that in the polymeric fluid flow. The dependence of the vortex length on a mobility parameter a in the Giesekus model and a characteristic parameter of fiber suspensions in the Dinh-Armstrong model are discussed.

(ReceivedJune7,1994) (Accepted for Publication October 3,1994)

摘

要

目的 二 次元 急絞 り流 路 にお いて,高 分子 流 体 と繊維 とか らな る繊 維懸濁 高分 子流 体 の流れ を数 値計 算 に よ り明 らか にす る. 構 成 と して,高 分子 流体 に対 して はGiesekusモ デル,繊 維 懸濁 液 に対 して はDinh-Armstrongモ デ ルを用 い る. 成 果(1)繊 維 懸 濁液 で は絞 り角 部 に発生 す る循 環二 次流 れが,繊 維 を入 れな い場 合 よ り も長 くな った. (2)循環 二次 流れ の長 さ とGiesekusモ デルの流 動 パ ラ メー タ,繊 維 懸濁 液のパ ラメー タ との 関係 を明 らかに した. (平成6年6月7日 受 理) (平成6年10月3日 審 査終 了)

1.緒

言

近 年,さ まざ まな複 合材 料 が用 い られて い る.特

に短 繊 維 を高 分子 物 質 に分 散 させ た繊 維 複 合 材 料

は,軽 くて強度 的 に優 れて い るとい う特 徴 を持 ち,

需 要 が多 い.し か し,そ れ らを成形 す ると きの高 分

子 流 体 の流動 状態 はニュ ー トン流 体 とは異 な って お

り,ま た,短 繊維 を含 有す れば さ らに流 れ は複 雑 に

な る．

この 分野 の一連 の研 究 と して,現 在 まで ニ ュー ト

ン流 体 中 の短繊維 懸濁 液 を対象 と した流動 の研 究 が

な さ れ て き た.Givlerら1)は 繊 維 懸 濁 液 の 流 速 場 が ニ ュ ー トン流 体 の流 速 場 と 同 じで あ る と い う仮 定 の も と に,繊 維 の 配 向 に っ い て 研 究 した.Lipscomb ら2)は希 薄 な 繊 維 懸 濁 液 に 対 す る 構 成 式 を 提 案 し, 急 絞 り流 路 に お け る実 験 と解 析 か ら繊 維 懸 濁 液 の流 れ 場 が ニ ュ ー トン流 体 の 場 合 と は異 な る こ と を 示 し た.ま たChibaら3)は こ の 構 成 式 を 用 い,差 分 法 で 円 管 急 絞 り流 路 内 の 流 れ の 数 値 解 析 を 行 い,,ニ ュ ー トン流 体 と繊 維 懸 濁 液 と で 循 環 二 次 流 れ の 大 き さ が 異 な る こ と を 示 した. 一 方_{,や や 濃 厚 な 繊 維 懸 濁 液 に 対 して は,Dinh}

とArmstrong4)が 構 成 式 を 提 案 し,中 村 ら5,6)は二 次 元T型 分 岐 ・合 流 流 路 で 数 値 解 析 を 行 い,ニ ュ ー ト ン流 体 と の流 れ の 違 い を 検 討 した. しか し,実 際 の 複 合 材 料 で は高 分 子 流 体 が 分 散 媒 で あ り,分 散 媒 そ の も の の 流 れ が ニ ュ ー ト ン流 体 と は大 き く異 な る.高 分 子 流 体 の流 れ に 対 す る研 究 は 活 発 に行 わ れ て お り,現 在 ま で に さ ま ざ ま な 構 成 式 が提 案 さ れ て き た.本 研 究 で は こ れ ら の 中 か らGie-sekusモ デ ル7)を用 い る.Giesekusモ デ ル に 関 して は,い くつ か の 研 究 が 行 わ れ て い る. Leonov-likeGiesekus流 体(1モ ー ドのGiese-kusモ デ ル で,流 動 パ ラ メ ー タ α が0.5で あ る も の)に 対 し てDebbautら8)は 有 限 要 素 法 を 用 い, Choiら9)は 差 分 法 を 用 い,急 絞 り流 れ を 解 析 し た. ま たYooとChoi10)は,定 常 単 純 せ ん 断 流 れ 場 で の Giesekusモ デ ル を 解 き,Hulsenら11)は8モ ー ドの Giesekusモ デ ル を 用 い,流 動 パ ラ メ ー タの 値 を 変 え て 軸 対 称 急 絞 り流 れ を 有 限 要 素 法 で 解 い た. SchleingerとWeinacht12)は,定 常 ボ ア ズ イ ユ 流 れ で のGiesekusモ デ ル の 解 を 求 め た. ま た,高 分 子 流 体 を 分 散 媒 と した 繊 維 懸 濁 液 に 対 す る研 究 は極 め て 少 な く,Ausiasら13)が ガ ラ ス短 繊 維 強 化 ポ リプ ロ ピ レ ンに 対 して 構 成 式 を 提 案 して い る. 本 研 究 で は,短 繊 維 を 含 有 した 高 分 子 流 体 の急 絞 り流 れ を 数 値 解 析 に よ って 解 明 す る こ と を 目的 とす る.そ の た め に,1モ ー ドGiesekus流 体 を分 散 媒 の モ デ ル と し,繊 維 懸 濁 液 の 構 成 式 と し てDinh-Armstrongモ デ ル を 用 い て 繊 維 懸 濁 高 分 子 流 体 を モ デ ル 化 し,差 分 法 で 数 値 解 析 し て,流 れ 模 様 と 循 環 二 次 流 れ に つ い て 検 討 す る.

2.繊 維懸濁高分子流体 の流れ と繊維

配 向の基礎式

非 圧縮 性流 体 の場 合,連 続 の式 とCauchyの

運動

方程 式 か ら圧 力pを 消去 し,ψ を流 れ 関数,ω を渦

度 と して,次 の渦 度輸 送方 程 式 を得 る.

(1)

(2)

また本研 究 で は,繊 維 懸 濁高 分子 流 体 の構成 式 と

して次 式 を用 い る.

(3)

こ こで,ηs:ニ ュ ー トン流 体 の 粘 度,D:変 形 速 度 テ ン ソ ル,Tp:高 分 子 の 寄 与 を 表 す 偏 差 応 力 テ ン ソ ル,Tf:繊 維 の 寄 与 を 表 す 偏 差 応 力 テ ン ソ ル で あ る． 偏 差 応 力 の う ち,高 分 子 寄 与 分 と繊 維 寄 与 分 と は本 来 複 雑 に 関 係 しあ っ て い る と考 え られ る が,こ こ で は簡 単 に 両 者 の 和 を 用 い た. (3)式の 偏 差 応 力 の う ち,高 分 子 が 寄 与 す る応 力Ｔｐ をGiesekusモ デ ル7)を用 い て 求 め る.

(4)

こ こ で,λ:緩 和 時 間,ηp:粘 度 パ ラ メ ー タ,α:流 動 パ ラ メ ー タ(0<α ≦0.5),(＝):上 対 流 微 分15)を 表 す. さ ら に,(3)式 の 偏 差 応 力 の う ち,繊 維 が 寄 与 す る 応 力Tfを 求 め る た め に,DinhとArmstrong4)が 導 い た,ニ ュ ー ト ン流 体 を 分 散 媒 と す る や や 濃 厚 な 繊 維 懸 濁 液 に 対 す る構 成 式 を 用 い る.

(5)

こ こ で,ηs:ニ ュ ー ト ン流 体 の粘 度,β:繊 維 の パ ラ メ ー タ,P:繊 維 配 向 を 表 す 単 位 ベ ク トル で あ る. 繊 維 の パ ラ メ ー タ β は,l:繊 維 の 長 さ,d:繊 維 直 径,n:単 位 体 積 当 た りの 繊 維 本 数,ん:繊 維 間 の 平 均 距 離 を 用 い て,

(6)

と表せ る.hは,繊

維 が一 方 向に配 向 して い る場合

に は1/√2nl偏

とな る.(5)式 中の<∼>は,繊

維 の配

向分 布関 数 に関 す る確 率平 均 を表 して い るが,こ こ

で扱 うよ うな流 れ に対 して は繊維 の配 向分 布関 数 を

決定 す る こと は困 難 なの で,こ こで は考慮 しなか っ

た.従 って繊 維懸 濁液 の構成 式 は

(7)

と な る16). こ こ で 配 向 テ ン ソルS=PPを 導 入 す る.繊 維 の 配 向 テ ン ソ ルSの 計 算 に は(8)式を 用 い る.

(8)

こ こ で ω:渦 度 テ ン ソ ル,ra:繊 維 の ア ス ペ ク ト比 で あ る.こ の 式 は,配 向 ベ ク トルPを 用 い て 表 現 さ れ て い るJeffery14)の 式 を,配 向 テ ン ソ ルSを 用 い て 書 き 直 した もの で あ る.今 回 の 計 算 で は 繊 維 の ア ス ペ ク ト比raを 無 限 大 と した(任 意 のraに つ い て

計 算 可 能 で あ る).(1),(2),(3),(4),(7),(8)式 が,繊 維 懸 濁 高 分 子 流 体 の流 れ と繊 維 の 配 向 を 表 す 基 礎 式 で あ る.

3.数 値計算法

基礎 式 を解 くため に差 分法 によ る数値 計 算 を行 っ

た.ま ず 高分 子寄与 応 力 は,ニ ュー トン流 体 の速度

場 を初期 値 と して与 え,(4)式 を流 線積 分法5,6)に

よ り

計算 して求 め た.す なわ ち,ま ず差 分点(i,j)を

通

る流 線 と上流 側 の差 分 格子 の交点 にお け る応 力Tpo

を求 め る.次 に,そ の交 点 か ら差分 格子 点(i,j)ま

で の流体 の移動 時間 △tを求 め,差 分 点(i,j)に

お

け る応 力Tpを 次 式 に よ り計 算 す る.

(9)

こ こ で ∂T,/∂tを 計 算 す る た め に.座 標 を 流 線 方 向e1と そ れ に 直 交 す る方 向e2に と る.そ して,(4)式 を 成 分 表 示 した と き の 対 流 項u∂/∂x+υ∂/∂yをe1成 分 とe2成 分 に 書 き 直 す.こ の と き,例 え ばTpのxx 成 分Tpxxに 関 す る 対 流 項u∂Tpxx/∂x+υ∂Tpxx/∂yのe1 成 分 は√u2+υ2dTpxx/de1と な り,e2成 分 は 零 と な る.こ こ で√u2+υ2/de1=1/dtと お く と,dtは 流 線 方 向 を 移 動 す る 時 間 を 表 し,

(10)

とな る.す なわ ち,(4)式 の対流 項 が(10)式

で ∂Tpxx/∂t

に置 き換 え られ る ことが分 か ったので,(9)式か らTp

を求 め る こ とがで きる.

応 力 の入 口境界条 件 は,流 路 の入 口で平 行平 板 間

の発 達 した流 れ の応力 分布 を与 えた.

次 に繊 維 の配 向テ ンソルSの 計 算 で は,繊 維 の重

心 が流線 上 を流速 と同 じ速度 で 移動 す る と仮定 し,

(8)式を差分 化 した式 を用 いて,先 の高 分子 寄 与応 力

の計算 と同様 の方 法 で行 った.繊 維配 向 の入 口境 界

条 件 は,流 路 の入 口です べて の繊維 が流線 方 向 を向

いて い る と した.繊 維 に よる寄 与応 力 は,繊 維配 向

テ ンソルが分 かれ ば(7)式か ら計 算 で き る.

次 に,速 度場 の計 算 に は,(1)式 の境界 値 問題 か ら

ω が,(2)式 の境界 値 問題 か らψが計算 で きる.こ こ

で は両 境 界値 問題 の計 算 に はSOR法

を用 い,収 束

解 を求 め た.境 界 条件 は,流 路 の入 ロで は平行 平板

間 の発達 した速度 分布 を与 え,出 口で は流 路軸 方 向

に速度 が変 化 しな い とい う条件 を与 え た.

以上 の計 算 を繰 り返 し,収 束解 を求 めた.計 算 の

収 束条 件 は,流 れ関 数 の値 につ いて,1回

前 の計 算

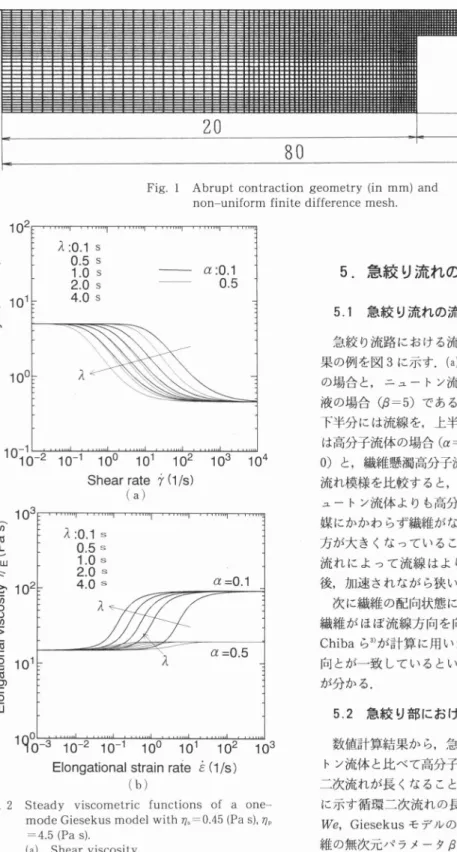
値 と の残 差 が 現 在 の 値 の1×10-3倍 以 下 と し た. 計 算 領 域 は,流 れ の 対 称 性 を 考 慮 し,流 路 の1/2 と した.図1に 数 値 計 算 に 用 い た 流 路 形 状 と差 分 格 子 を示 す.流 路 は,4:1の 急 絞 り流 路 で あ り,広 い 方 の流 路 の 流 れ 方 向 の 長 さ(20mm)は,そ こ の流 路 幅(10mm)の2倍 と し た.ま た狭 い方 の流 路 の 流 れ方 向 の 長 さ(60mm)は そ こ の 流 路 幅(5mm) の12倍 と し,応 力 が 十 分 緩 和 す る よ う に 考 慮 した. 差 分 格 子 に つ い て は,凸 状 角 部 付 近 で の 流 れ の 急 激 な 変 化 を予 想 して,図1に 示 す よ う な不 等 間 隔 の 差 分 格 子 を 用 い,で き る 限 り細 か い メ ッ シ ュ を 採 用 し た. ま た,流 体 の 粘 性 力 に対 す る弾 性 力 の 比 と して ワ イ セ ン ベ ル ク 数Weをwe=λU/Hと 定 義 し た.こ こで,U:幅 の 広 い上 流 側 で の 平 均 流 速,H:そ の 流 路 幅 で あ る. な お,本 研 究 で は,流 れ は ク リー ピ ン グ流 れ を想 定 し,粘 度 パ ラ メ ー タを ηs=0.45(Pas),ηp=4.5 (Pas),流 量 を1×10-4(m3/s)と し た.

4.流

体 の レ オ ロ ジー 物 性

高 分 子 流 体(Giesekusモ デ ル)の 単 純 せ ん 断 流 れ と伸 長 流 れ に つ い て,そ の レオ ロ ジ ー 物 性 を 検 討 す る.図2(a)か ら,定 常 せ ん 断 粘 度 はshear-thinning 性 を 示 し,緩 和 時 間 λ ・流 動 パ ラ メ ー タ α の 値 に よ って,粘 度 曲 線 が 左 右 に 移 動 す る.し か し,ゼ ロ粘 度 と第2ニ ュ ー ト ン粘 度 に は 変 化 は な い.図 中 の 矢 印 は,そ の 方 向 に λ が0.1(s),0.5(s)… と大 き く な る こ と を示 して い る. 次 に 定 常 伸 張 粘 度 を 図2(b)に 示 す.α が 小 さ い と, 伸 長 速 度 の 増 大 に 伴 っ て 伸 長 粘 度 が 増 大 す る stretch-thickening性 が 顕 著 に現 れ る.ま た 緩 和 時 間 λ が 大 き い と,よ り小 さ な 伸 長 速 度 で 伸 長 粘 度 が 増 大 す るよ うに な る.Leonov-1ike Giesekus流 体 (α=0.5)で は,こ のstretch-thickening性 が 小 さ い. 一 方_{,繊 維 懸 濁 液(Dinh-Armstrongモ デ ル)の} せ ん 断 粘 度 η,一 軸 伸 長 粘 度 ηEUは

(11)

で あ る.こ の こ とか ら,本 計 算 に 用 い た 繊 維 懸 濁 液 の 構 成 式 で は せ ん 断 粘 度 に つ い て は ニ ュ ー トン流 体 と変 わ らな い が,一 軸 伸 長 粘 度 は繊 維 の 影 響 に よ っ て ニ ュ ー トン流 体 よ り も βηsだけ 増 加 す る こ と が 分 か る.し か し,高 分 子 流 体 と は 異 な り,伸 張 速 度 に よ らず 一 定 値 を と る.

(a)

(b)

5.急 絞 り流れの数値計算結果

5.1急

絞 り流 れ の流 れ 模 様 と繊 維 配 向

急 絞 り流 路 に お け る 流 線 と繊 維 配 向 の 数 値 計 算 結 果 の 例 を 図3に 示 す.(a)は ニ ュ ー ト ン流 体(β=0) の場 合 と,ニ ュ ー ト ン流 体 を 分 散 媒 と し た繊 維 懸 濁 液 の 場 合(β=5)で あ る.繊 維 懸 濁 液 で は,流 路 の 下半 分 に は 流 線 を,上 半 分 に は 繊 維 配 向 を示 す.(b) は高 分 子 流 体 の 場 合(α=0.1,λ=1.0,We=1.0,β= 0)と,繊 維 懸 濁 高 分 子流 体 の 場 合(β=5)で あ る. 流 れ 模 様 を 比 較 す る と,角 部 の 循 環 二 次 流 れ が,ニ ュ ー ト ン流 体 よ り も高 分 子流 体 の 方 が,ま た,分 散 媒 に か か わ らず 繊 維 が な い場 合 よ り も繊 維 懸 濁 液 の 方 が 大 き く な っ て い る こ と が 分 か る.こ の 循 環 二 次 流 れ に よ っ て 流 線 は よ り ゆ る や か に 曲 が り,そ の 後,加 速 さ れ な が ら狭 い 流 路 に 流 れ 込 む. 次 に 繊 維 の配 向 状 態 に つ い て み る と,主 流 部 で は 繊 維 が ほ ぼ 流 線 方 向 を 向 い て お り,Lipscomb2)や Chibaら3)が 計 算 に 用 い た.繊 維 配 向 方 向 と流 線 方 向 と が 一 致 して い る と い う仮 定 を 満 足 して い る こ と が 分 か る.

5.2急

絞 り部 にお ける 循 環 二 次 流 れ の長 さ

数 値 計 算 結 果 か ら,急 絞 り流 れ に お い て,ニ ュ ー ト ン流 体 と 比 べ て 高 分 子 流 体 や 繊 維 懸 濁 液 で は 循 環 二 次 流 れ が 長 く な る こ と が 分 か っ た.そ こ で 図3(a) に示 す 循 環 二 次 流 れ の 長 さLvと ワ イ セ ンベ ル ク 数 We,Giesekusモ デ ル の 流 動 パ ラ メ ー タ α お よ び 繊 維 の無 次 元 パ ラ メ ー タ β と の 関 係 を 調 べ た.た だ し 以 下 で は,渦 の 長 さを,広 い 方 の 流 路 幅Hで 無 次 元 Fig. 1 Abrupt contraction geometry (in mm) and

non-uniform finite difference mesh.

Fig. 2 Steady viscometric functions of a one mode Giesekus model with ās,=0.45 (Pa s), āp =4.5 (Pa s).

(a) Shear viscosity. (b) Elongational viscosity.

(a)

(b)

化 した 渦 長 さLv*=Lv/Hで 表 した. 図4(a)(b)にWeとLv*と の 関 係 を 示 す.図 中 の 矢 印 は,そ の 向 き にβ が0,1,5,10と 大 き くな る こ と を示 して い る.い ず れ の α に お い て も,Weが 零 か ら大 き く な る と,循 環 二 次 流 れ は 急 激 に 長 く な り,We=1前 後 で ほ ぼ 一 定 した 長 さ と な る.ま た, α が 小 さ い と循 環 二 次 流 れ は長 く,循 環 二 次 流 れ の 長 さ に対 す る β の 影 響 が 小 さ い こ と が 分 か る. 図 中 の 記 号(●:β=0,○:β=1,△:β=5, □:β=10)は ニ ュ ー トン流 体(We=0)を 分 散 媒 と した と きの 循 環 二 次 流 れ の 長 さ を 示 して い る.こ れ を み る と,ニ ュ ー ト ン流 体 の 場 合 は,β が 大 き くな る と,循 環 二 次 流 れ は 急 激 に長 く な って お り,循 環 二 次 流 れ の 長 さ に 対 す る繊 維 の影 響 が 高 分 子 流 体 に 比 べ 七 大 き い こ とが 分 か る.

(a)

(b)

βの変 化 に対 す る循 環 二 次流 れ の 長 さの 変 化 を

Ｗe=2の

と き につ いて 図5に 示 す.α の 小 さい 方

が,曲 線 の傾 きが小 さ い ことか ら,β の影 響 を受 け

に くい こ とを示 し,ま た高分 子流 体 に比 べて,ニ ュ

ー トン流体 の方 が繊 維 の影響 が大 きい こ とを示 して

いる.

5.3急

絞 り部 にお け る伸 張 流 れ と伸 長 応 力

今 回 の 計 算 で は,中 心 線 上 の最 大 伸 張 速 度 が 約13 (1/s)で あ る.図2(b)か ら,We(す な わ ち λ)が 大

Fig. 3 Streamlines and fiber orientations. Lv de notes vortex length.

(a) Newtonian fluid ([ƒÀ=0) and fiber sus pension in Newtonian fluid (ƒÀ=5). (b) Polymeric fluid (ƒ¿=0.1, We=1) and

fiber suspension in polymeric fluid (ƒ¿=

0.1, We=1, ƒÀ=5). Fig. 4 Dependence of vortex length L‚–* on We for various values of ƒÀ. •œ•shows Lv* of Newto nian fluid, •› ; fiber suspension in Newtoni an fluid with ƒÀ=1, •¢ ; ƒÀ=5, • ; ƒÀ=10. (a) Mobility parameter ƒ¿=0.1 in Giesekus

model.

(b) Mobility parameter ƒ¿=0.4 in Giesekus model.

き くな る と,伸 長 粘度 が変 化 しつつ あ る伸 長速 度 の

範囲 が左 に移動 す るこ とが分 か る.従 って,特 に急

絞 り部付近 の伸 張 流れ場 にお いて,そ の付 近 の流体

の伸 長粘度 が大 き くな るため に伸 長応 力 が大 き くな

り,循 環 二次 流 れ も長 くな って い る(図4参

照).ニ

ュー トン流 体 で は,せ ん断粘 度 を大 き くす る と,伸

長応 力が大 き くな るが,循 環 二次 流 れの長 さに は変

化が な い.ニ ュ ー トン流 体 で は,伸 長 速度 によ って

伸長 粘度 が変化 しな いので,高 分 子流 体 の よ うに絞

り部 での応 力 が周辺 と比較 して増 大 しな いか らだ と

考 え るこ とが で きる.

次 に,α と循 環 二 次 流 れ の 長 さ の 関 係 に つ い て 述 べ る.図2(b)か ら,α が 小 さ く な る に つ れ て 伸 長 粘 度 が 大 き くな って い る こ とが 分 か る.こ れ に よ り絞 り部 の 応 力 が 局 所 的 に 増 大 し,そ れ に つ れ て 循 環 二 次 流 れ も長 く な っ て い る. 次 に 繊 維 の パ ラ メ ー タ β と循 環 二 次 流 れ の 長 さ に つ い て 述 べ る.図5か ら,β が 大 き い ほ ど循 環 二 次 流 れ も長 く な っ て い る こ と が 分 か る.す な わ ち, 繊 維 懸 濁 液 の 繊 維 含 有 率 が 大 き く,繊 維 の 長 さ が 長 く,ま た 直 径 が 小 さ く な る ほ ど循 環 二 次 流 れ が 長 く な る とい え る.こ れ は,(11)式か ら分 か る よ うに,β が 大 き くな る こ と に よ って 伸 長 粘 度 が 大 き くな る た め と考 え る こ とが で き る.

5.4応

力 場＝ 速 度 場 に お け る繊 維 の 影響

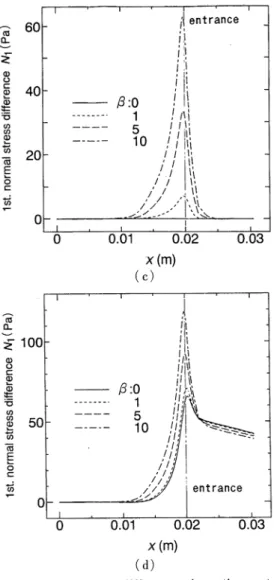
応 力 場 に 対 す る繊 維 の 寄 与 を 考 察 す る.図5か ら,β=1の と き は,α に か か わ らず,繊 維 懸 濁 ニ ュ ー トン流 体 よ り も繊 維 懸 濁 高 分 子 流 体 の 方 が 循 環 二 次 流 れ が 長 い こ と か ら,応 力 場 は 高 分 子 流 体 の 応 力 が 支 配 的 で あ る こ とが 考 え られ る.ま た β=10の と き は,繊 維 懸 濁 ニ ュ ー ト ン流 体 で も循 環 二 次 流 れ が か な り成 長 し,繊 維 懸 濁 高 分 子 流 体 の 循 環 二 次 流 れ の 長 さ と近 い こ と か ら,絞 り部 で の 応 力 場 は繊 維 の 寄 与 が 支 配 的 に な って い る こ と が 考 え られ る. そ こで,流 路 の 中 心 線 上 で の 繊 維 懸 濁 高 分 子 流 体 の 法 線 応 力 差 を 図6に,流 速 分 布 を 図7に 示 した. 図6(a)に は 中 心 線 上 の 法 線 応 力 差(α=0.2,We= 2)の う ち,ニ ュ ー トン流 体 に 関 す る成 分,2ηsDか ら 求 ま る 応 力 差,を 取 り 出 して 示 した.横 軸 に は入 口 (χ=0(m))か ら下 流 の0.03(m)ま で の 分 の み を 示 した.χ=0.02(m)が 絞 り部 に相 当 す る.β の 増 加 に よ り,循 環 二 次 流 れ が 長 くな り(図5参 照),伸 長 速 度 の 変 化 が 抑 え られ る こ と が 分 か る(図7参 照).そ れ と と も に 法 線 応 力 差 の 変 化 が 小 さ くな っ て い る.

(a)

(b)

Fig.5 Dependence of vortex length Lv*. on β for various values of α(We=2).

(c)

(d)

ま た,極 大 値 を と る位 置 は 絞 り部 上 流 で,こ れ は繊 維 の 有 無 に は依 存 しな い.伸 長 速 度 が 零 に な る と 法 線 応 力 差 も零 に な る. 図6(b)に は,高 分 子 が 寄 与 す る法 線 応 力 差 成 分, Tpに 基 づ く応 力 差,を 取 り 出 して 示 した.こ こ で も,β の増 加 に よ り,法 線 応 力 差 の 大 き さ と変 化 率

が抑 え られ ると ともに,循 環二 次流 れ が長 くな る.

ま た,絞 り部 の下 流 に あ る極大 値 を と る位置 はさ ら

に下流 に移動 す るこ とが分 か る.ニ ュー トン流体 の

寄与応 力成 分 と は異 な り,絞 り部下 流 の伸長 速度 が

零 にな る領 域 で も応 力 は残存 す る.

図6(c)に は,繊 維 が 寄与 す る法線 応力差 成分,Tf

に基 づ く応 力差,を 取 り出 して示 した.β が増加 す

る と急激 に法線 応力 差 が増大 す る ことが分 か る.繊

維 の寄与 す る成 分 の場合 は,極 大 値 は絞 り部 上流 に

現 れ,β が変化 して もその位 置 は移動 しない.ま た,

伸長 速度 が零 に な ると法 線応 力差 も零 にな る.よ っ

て繊 維 の影響 は絞 り部付 近 に集 中 して現 れ る.

図6(d)には,(3)式 に基 づ き三 っ の寄 与応 力 を合計

した法線 応力 差 の分 布 を示 す.β が増 加 す る と繊維

の寄与 が大 き くな るので,そ の分 最大 値 が大 き くな

り,絞 り部上 流 で法線 応力 差 が急激 に増加 し,絞 り

部 下 流 で 急 激 に減 少 す る.ま た極 大 値 を と る位 置

は,上 流へ と移動 して い く.

図7か らは,高 分子 流体 の ときに はみ られ る流 速

の オーバ ー シュー ト現 象 が,β が大 き くな る に従 い

小 さ くな って い くこ と,流 速 の変化 の割 合 が抑 え ら

れて い る ことが分 か る.

6.結

論

繊 維 懸 濁 高 分 子 流 体 の 急 絞 り流 れ を 数 値 計 算 に よ り検 討 した.分 散 媒 と して の 高 分 子 流 体 の モ デ ル と してGiesekusモ デ ル を,繊 維 懸 濁 液 の モ デ ル と し てDinh-Armstrongモ デ ル を 用 い た.高 分 子 流 体

Fig. 6 Normal stress difference along the center line for various values of ƒÀ (ƒ¿ = 0.2, We= 2). (a) Newtonian term of normal stress

differ-ence in fiber suspension in polymeric fluid.

(b) Viscoelastic term of normal stress dif-ference in fiber suspension in poly-meric fluid.

(c) Fiber suspension term of normal stress difference in fiber suspension in poly-meric fluid.

(d) Normal stress difference

in fiber

sus-pension in polymeric fluid.

Fig. 7 Velocity profile along the center line for fiber suspension in polymeric fluid for var-ious values of ƒÀ (ƒ¿ =0.2, We=2).

で は 循 環 二 次 流 れ が ニ ュ ー ト ン流 体 よ り も長 く な り,繊 維 懸 濁 高 分 子 流 体 で は,さ ら に 長 くな った. そ れ は,絞 り部 の 伸 長 応 力 と 関 係 し て い る と考 え る こ と が で き る. ま た,繊 維 の パ ラ メ ー タが 増 加 す る と,応 力 に 占 め る繊 維 の寄 与 が 大 き くな る の で,絞 り部 の よ う な 伸 長 速 度 の大 き な と こ ろ で は繊 維 の 影 響 が 現 れ,伸 長 速 度 の 小 さ な と こ ろ,特 に絞 り部 下 流 で は 高 分 子 の 影 響 が 現 れ た. (謝 辞)こ の 研 究 を進 め る に 当 た り,(社)日本 繊 維 機 械 学 会 学 術 奨 学 金 の 援 助 を受 け ま した.謝 意 を 表 し ま す.

参考文献

1) R. C. Givler, M. J. Crochet and R. B. Pipes ; J. Composit Materials, 17, 330 (1983)

2) G. G. Lipscomb II, M. M. Denn, D. U. Hur and D. V. Boger ; J. Non-Newtonian Fluid Mech., 26, 297 (1988) 3) K. Chiba, K. Nakamura and D. V. Boger ; J.

Non-Newto-nian Fluid Mech., 35, 1 (1990)

4) S. M. Dinh and R. C. Armstrong ; J. Rheol., 28, 207 (1984)

5)中 村 ら他5名;繊 維 機 械 学 会 論 文 集,45,T147(1992) 6)中 村 ら他5名;繊 維 機 械 学 会論 文 集,45,T165(1992)

7) H. Giesekus ; J. Non-Newtonian Fluid Mech., 11, 69 (1982)

8) B. Debbaut, J. M. Marchal and M. J. Crochet ; J. Non-Newtonian Fluid Mech., 29, 119 (1988)

9) H. Ch. Choi, J. H. Son and J. Y. Yoo ; J. Non-Newtonian Fluid Mech., 29, 347 (1988)

10) J. Y. Yoo and H. Ch. Choi ; Rheol. Acta, 28, 13 (1989) 11) M. A. Hulsen and J. V. D. Zanden ; J. Non-Newtonian

Fluid Mech., 38, 183 (1991)

12) G. Schleiniger and R. J. Weinacht ; J. Non-Newtonian Fluid Mech., 40, 79 (1991)

13) G. Ausias ‚瑼5–¼; J. Rheol., 36, 525 (1992) 14) G. B. Jeffery; Proc. Roy. Soc, A 102, 161(1922)

15)中 村 喜 代 次;繊 維 工 学,47,P167(1994)

16) S. G. Advani and C. L. Tucker III ; J. Rheol., 34, 367 (1990)