二進GCD法によるワードベース逆元計算の改良とその効率

全文

(1)Vol.2010-CSEC-50 No.9 2010/7/1. 情報処理学会研究報告 IPSJ SIG Technical Report. 1. はじめに. 二進 GCD 法によるワードベース逆元計算の改良とその効率. 近年，情報技術の進歩にともない，電子商取引などの様々なサービスが身の周りで提供されている．それらのサービスが安全に運用される為に，様々なセキュリティ対策がなされているなか，暗号技術はその中心的な役割を果たしている．近年では RSA 暗号にかわり楕. 石. 田. 努†1. 長. 瀬智行†2. 円曲線暗号が注目されている．楕円曲線暗号では，RSA 暗号と同等の安全性をより少ない. 吉岡良雄†2. 鍵長 (ビット数) で実現されることより，通常のコンピュータより少ない計算資源しかもたない組込みシステム上での実現も期待されている．. 楕円曲線暗号等1) では，曲線上の 2 点の加算や倍点を求める計算を有限体上で行う．体上の四則演算のなかでは，逆元の計算を求める必要があるため除算の演算コストが高い．逆元を求める方法としては，拡張ユークリッド互除法2) や二進 GCD 法2) らがあり，それらについて改良されたワードベースの逆元計算アルゴリズム3) が提案されている．本論文では，その逆元計算アルゴリズムを事前計算されたテーブルを用いることにより，より高速計算を行うとともに，組み込みシステムのような低い演算環境でも動作できる手法を提案する．. 楕円曲線暗号では，曲線上のある点の k 倍点を効率よく求めることが，暗号化，復号化の高速化につながる．曲線上の k 倍点を求めるには，異なる 2 点の加算，及び点の倍点計算を組み合わせて計算することになるが，それらの方法としては二進展開法，NAF(non. adjacent form) 表現に基づく移動窓法など効率的なアルゴリズムが提案されている．ところで，曲線上の点の加算，及び倍点を計算する過程では，除算を行うために有限体上での逆元を求める必要がある．この逆元を求める計算は他の演算に比べ大きなコストが必要となるため，k 倍点を求める場合は出来るだけ除算を含まないように，射影座標へ変換し計算す. Improvement and Speeding up of Word-based Inversion Algorithm based Extended Binary GCD Method. る等の工夫がなされている．反面，除算の回数を減らす代償として，点の加算や乗算の演算回数が増加してしまう．そのため，逆元計算をより効率よく実装することは，楕円曲線暗号. Tsutomu Ishida,†1 Tomoyuki Nagase†2 and Yoshio Yoshioka†2. の高速化につながる．本報告では，有限体上の逆元計算について，小林らが提案しているワードベースの拡張二進 GCD 法3) を事前計算されたテーブルをもちいて改良するアルゴリズムを提案し，コンピュータ上での数値実験をおこなった結果について報告する．. On the elliptic curve cryptosystem (ECC)1) , the addition of two points on the curve and the multiple computation of a point are calculated over the finite fields. Among all arithmetic operations on a field, the cost of operations for division is high since it is necessary to calculate the inversion. For calculating the inversion, there are traditional methods such as the extended Euclidian algorithm2) and the extended binary GCD method2) . And also a kind of advanced word-based inversion calculation algorithm is presented3) . Based on it, in this paper, by using pre-calculated table, we propose a kind of faster and more suitable method compared with the inversion calculation algorithm. This method can be implemented and running on simple operation environments such as embedded systems.. 2. 逆元計算アルゴリズム 2.1 拡張ユークリッド法逆元を求める代表的なアルゴリズムとしては，拡張ユークリッド法や拡張 2 進 GCD 法などがある．図 1 に示す拡張ユークリッド法は，a と b の最大公約数を求める過程で，. xa + yb = gcd(a, b) となる整数の組 (x, y) を求めるアルゴリズムである．このアルゴリズ †1 青森大学 Aomori University †2 弘前大学 Hirosaki University. 1. c 2010 Information Processing Society of Japan ⃝.

(2) Vol.2010-CSEC-50 No.9 2010/7/1. 情報処理学会研究報告 IPSJ SIG Technical Report. Input: Output:. X, N (X < N かつ (X, N ) = 1) X −1 (mod N ). Input: Output:. X, N (X < N かつ (X, N ) = 1) X −1 2k (mod N ). Step1:. 初期設定 (U1 , U2 , U3 ) ← (1, 0, N ), (V1 , V2 , V3 ) ← (0, 1, X) 終了判定 if (V3 = 0) X −1 ← U3 , 終了除算，乗算など q ← ⌊U3 /V3 ⌋ (T1 , T2 , T3 ) ← (U1 , U2 , U3 ) − (V1 , V2 , V3 )q (U1 , U2 , U3 ) ← (V1 , V2 , V3 ) (V1 , V2 , V3 ) ← (T1 , T2 , T3 ) Step 2 へ. Step1:. 初期設定 (U, V ) ← (N, X), (S, T ) ← (0, 1), k ← 0 終了判定 if (V = 0) then Step4 へビット単位の計算 U, V の値によって 1. ∼ 4. へ 1.U が偶数ならば U ← U/2, T ← 2T, k + + 2.V が偶数ならば V ← V /2, S ← 2S, k + + 3.U, V が奇数でかつ U > V ならば U ← (U − V )/2, S ← (S + T ), T ← (2T ), k + + 4.U, V が奇数でかつ U ≤ V ならば V ← (V − U )/2, T ← (S + T ), S ← (2S), k + + Step2 へ最終計算 X ← −S (mod n) U が 1 でないならば，計算不能 U が 1 ならば，return(X, k). Step2: Step3:. Step2: Step3:. 図 1 拡張ユークリッド互助法 Fig. 1 Extended Euclid Method. Step4:. ムでは，図 1 の Step3 毎に１回の多倍長整数の除算，乗算が必要となるため，合計繰り返し回数分の多倍長整数除算を計算しなくてはならない．. 図 2 拡張 2 進 GCD 法 Fig. 2 Extended Binary GCD Method. 2.2 拡張 2 進 GCD 法それに対し，拡張 2 進 GCD 法は図 2 に示すとおり，Step 3 で演算の対象となる整数の下位 1 ビットの値を調べ，その値によって 2 倍あるいは 1/2 倍を基本的に繰り返すアルゴ. み合わせとなるが，すべて単精度整数演算であるため，計算コストは低い．また Setp3 で. リズムである．コンピュータでは，2 倍や 1/2 倍は左シフト，右シフトを 1 ビット行うこと. は w 回の 2 × 2 の行列のかけ算を行っている．これは，Step4 で行う w ビット分の単精度. であり，除算が必要な拡張ユークリッド法に比べ，各演算のコストは低い．しかしながら，. 整数 × 多倍長整数の計算を行うための係数行列を求める過程である．Step4 では，単精度. Step3 の反復回数は入力データのビット長より多くなり，多倍長整数のシフト演算，加算. 整数である 2× 2 行列 g との乗算を行うことによって，多倍長整数である U,V,S,T の値を. が比例して多くなる．. 更新している．. 2.3 改良 2 進 GCD 法. この手法により拡張 2 進 GCD 法にくらべ単精度計算の演算回数が増加するが，多倍長. この拡張 2 進 GCD アルゴリズムに対して，小林らによって改良提案された手法3) を図 3. 演算の回数はおよそ 1/w ほどになる．. に示す．以下本報告では，この提案された手法を従来法と呼ぶことにする．従来法は，拡張. 3. 提案手法. 2 進 GCD 法の Step2, Step3 の過程を，Step2 において多倍長整数のうち 1 語 w ビット単位の整数部分をそれぞれ取り出し，Step3 でそれらについて拡張 2 進 GCD 法を用い部. 3.1 従来法の単精度整数演算回数について. 分解を求めて，Step4 で多倍長整数を w ビット分だけ更新する方法である．Step2 では，. 従来法は拡張 2 進 GCD 法に比べ，単精度整数の演算回数が増加，多倍長整数の演算回数. 多倍長整数 U, V からそれぞれ上位 w ビット，下位 w ビットを取り出す処理をおこなう．こ. が減少する特徴をもつ．我々は従来法の Step3 における単精度整数の計算過程をあらかじ. れらは Step3 で行う単精度演算の繰り返し処理における初期値を設定している．Step3 に. め準備されたテーブルを用いることで，大幅に減少させる手法を提案する．従来法 Step3 では，次の 2 つの処理が行われる．. おける u, v, s, t の演算は拡張 2 進 GCD 法と同じく 2 倍，1/2 倍のシフト演算と加算の組. 2. c 2010 Information Processing Society of Japan ⃝.

(3) Vol.2010-CSEC-50 No.9 2010/7/1. 情報処理学会研究報告 IPSJ SIG Technical Report. ある．. Input : Output :. X, N (X < N かつ (X, N ) = 1) X −1 2k (mod N ). Step1 :. 初期設定 (U, V ) ← (N, X), (S, T ) ← (0, 1), k ← 0 単精度整数 (w ビット) の初期化 i = max(⌊log2 V ⌋ + 1, ⌊log2 U ⌋ + 1, w) v ˆ = ⌊V /2i−w ˆ = ⌊U/2i−w ⌋, v ¯ = V mod 2w , u ¯ = U mod 2w , ! ⌋, u. s0 =. Step2 :. 1 0 0 1 w ビット分の繰り返し (単精度計算) u ¯, v ¯, u ˆ, v ˆの値によって 1. ∼ 4. 1. u ¯が偶数 u ˆ ← ⌊ˆ u/2⌋, u ¯←u ¯/2, g = 2.. 3.. 1 0. 0 2. Step5 :. 2. , s1 =. !. 2. 0. 0. 1. Ã , s2 =. !. 1. 1. 0. 2. Ã , s3 =. !. 2. 0. 1. 1. これらの行列 s0 , s1 , s2 , s3 は，各要素が 0,1,2 であることとそれらの要素の配置より，こし合わせる演算を行っているこになる．. 2 0. 0 1. !. g, k ← k + 1. (1). u ˆ, vˆ, u ¯, v¯ の更新, 演算回数 (除算 2 回，加算 2 回). (2). 係数行列の更新, 演算回数 (乗算 8 回，加算 4 回). Step3 では w 回の繰り返しが行われるため，演算回数の合計は乗算 w × 8 回, 除算 w × 2 g, k ← k + 1. u ¯, v ¯共に奇数かつu ˆ>v ˆ 1 0. 1 2. 2 1. 0 1. u ¯, v ¯共に奇数かつu ˆ≤v ˆ v ˆ ← ⌊(ˆ v−u ˆ)/2⌋, v ¯ ← (¯ v−u ¯)/2, g =. Step4 :. 0. Ã. 高々次のようになる． !. u ˆ ← ⌊(ˆ u−v ˆ)/2⌋, u ¯ ← (¯ u−v ¯)/2, g = 4.. 0. 次に，従来法の Step3 における，繰り返しの中の 1 回分について演算回数を計算すると，. v ¯が偶数 v ˆ ← ⌊ˆ v /2⌋, v ¯←v ¯/2, g =. !. 1. れらと乗算することは，対象になる行列 g のある要素を 2 倍する，あるいは要素同士を足. g=. Step3 :. Ã. !. !. 回，加算 w × 6 回となる．ちなみに，1 回の乗算，除算は 1 ビットのシフト演算で行うことができるため，演算回数の合計はシフト演算 w × 10, 加算 w × 6 となる．これらのなかで，係数行列の更新に関わる演算がその中心であることがわかる．. g, k ← k + 1. 3.2 係数行列のテーブル化従来法の Step3 で求められた単精度整数を要素とする行列は Step4 で多倍長整数. g, k ← k + 1. U, V, S, T の更新に用いられる．Step4 で用いられる係数行列 g は次のようになる．た. 多倍長の計算 ! U′ ← 2−w g −V ′. ! ! ! U S′ S , ← g −V T′ T U ← |U ′ |, V ← |V ′ |, S ← (U ′ /U )S ′ , T ← (V ′ /V )T ′ V = 0 ならば Step5 へ，それ以外は Step2 最終計算 X ← −S (mod n) U ̸= 1 ならば，計算不能 U = 1 ならば， return(X, k). だし，各 gi は Step3 の i 回目の繰り返しの時に選ばれた行列であり，s0 , s1 , s2 , s3 のいずれかである．係数行列 g = gw−1 gw−2 . . . g0 g1 g0. 係数行列 g は Step3 で掛け合わせた s0 , s1 , s2 , s3 の w − 1 回の乗算したものとなる．つ. 図 3 従来法 (改良 2 進 GCD 法) Fig. 3 Improved Binary GCD Method. まり，s0 , s1 , s2 , s3 を w 個並べる組み合わせの中の 1 つとなる．そこで s0 , s1 , s2 , s3 から k 個並べ，順に乗算した行列を k ビット係数行列 g(k−1)(k−2)...210 とすると次のようになる．. (1). u ˆ, vˆ, u ¯, v¯ の更新. (2). 2 行 2 列の係数行列の更新, g = sk g. k ビット係数行列 g(k−1)(k−2)...10 = gk−1 gk−2 . . . g1 g0. このうち (2) の係数行列の更新作業は，w ビット毎に単位行列として初期化されている行列 g に，次の 4 つの行列 s0 , s1 , s2 , s3 のいずれかと乗算を行い，行列 g を更新することで. 3. c 2010 Information Processing Society of Japan ⃝.

(4) Vol.2010-CSEC-50 No.9 2010/7/1. 情報処理学会研究報告 IPSJ SIG Technical Report. この k ビット係数行列 g(k−1)(k−2)...10 がとり得る値は入力 X, N の値に関わらず，すべ. s0 , s1 , s2 , s3 のいずれかが選択された順を記憶する必要がある．そのため Step3 では w. て事前計算することができる．この係数行列 g を k ビット毎に分割し，事前計算した k ビッ. 回繰り返しが行われるため，大きさ w の配列 m を用意し，mw−1 mw−2 . . . m2 m1 m0 に. ト係数行列を次のように利用し，計算することができる．. s0 , s1 , s2 , s3 にそれぞれ対応した 0,1,2,3 のいずれかの値を確保し，w 回分の演算行列順を記憶させる．step4 では，mw−1 mw−2 . . . m2 m1 m0 から順に k 個分を取り出し，該当する. g = gw−1 gw−2 . . . . . .. |. k. {z. g2k−1 . . . gk. }. ビット係数行列. |. k. {z. k ビット係数行列が格納されているテーブルの位置を計算する必要がある．k ビット係数行. gk−1 . . . g1 g0. |. }. {z. }. 列は事前計算により配列に順に格納されているため，次の計算で配列の位置を計算すること. ビット係数行列 k ビット係数行列. ができる．その場合，約 ⌊w/k⌋ 回に行列乗算回数を押さえることができる．そのため k は w を割り. . index = mk−1 × 4k−1 + . . . m2 × 42 + m1 × 41 + m0. 切るような値をとることが望ましい．また，k ビット分係数行列をテーブルとして保存するには，4 × 4k 個の単精度整数が確保できるメモリが必要となる．. この index を計算するためには k − 1 回の乗算と加算が必要である．ここでの乗算はビッ. 例として，k = 2 の場合は，2 ビット係数行列 g10 は次の 16 通であり，これらをテーブ. ト積とシフト演算の組み合わせで置き換えることができる．. ルとして保存するためには 4 × 42 = 32 個の単精度整数が確保できるメモリが必要となる．. Ã s0 s0 =. 1. 0. 0. 4. 2. 0. 0. 2. Ã s0 s1 =. Ã s0 s2 =. 1. 1. 0. 4. 2. 0. 2. 2. Ã s0 s3 =. !. Ã =. !. 1. 0. 0. 2. 1. 0. 0. 2. Ã =. !. Ã =. !. 1. 0. 0. 2. 1 0. Ã =. !Ã 1. 0. 0. 2. 2. 0. 0. 1. !Ã !Ã. 1. 1. 0. 2. 0. 2. 0. 2. 1. 1. !Ã. 3.4 提案手法のアルゴリズム. !. 本報告で提案する拡張 2 進 GCD 法への改良法について，図 4 にそのアルゴリズムを示す．. 3.5 提案アルゴリズムの単精度整数演算回数について. !. 単精度整数演算回数について，提案手法と従来法を比較する．比較する部分は Step3 および Step4 である．提案法では Step3 において，各繰り返しのなかで u ˆ, vˆ, u ¯, v¯ の更新を. !. 行う過程で 2 回の除算が行われる．これは従来法と同じく 2 度のシフト演算となる．提案法では，この Step3 において，係数行列の更新を行わないため，これ以上の演算は行われ. !. ない．. Step4 では，係数行列の計算においてテーブルを用いて計算できる場合と，用いることができない場合の処理がある．ここでは k は w を割り切る値であるため，テーブルを用い. s1 s0 = . . . .. .. ることが出来ない場合は Step3, Step4 の繰り返しのなかで，最後の数回である．そのため，テーブルを用いることが出来ない場合の単精度整数演算回数は，全体のなかでごくわず. s3 s2 = . . .. かであるため，無視できる．よって，Step 4 における単精度整数演算の回数は (1).1 の処. s3 s3 = . . .. 理回数とする．. k ビット係数行列のテーブルを利用するためには，テーブルの index を計算する必要があ我々は，k ビット係数行列を 4k 個 (1 個には行列の 4 つ要素) の配列に順に格納した．. り，この演算回数は前節で述べた通り，それぞれ k − 1 回の乗算 (ビット積とシフト演算の. 3.3 テーブル参照位置計算. 組み合わせ) と加算が必要である．また，k ビット係数行列から係数行列を更新する演算と. 係数行列 g を k ビット係数行列を用いて計算する場合，Step3 の各繰り返しにおいて. して 2 行 2 列の行列積をもとめるため，8 回の乗算と 4 回の加算が必要である．なお，従来. 4. c 2010 Information Processing Society of Japan ⃝.

(5) Vol.2010-CSEC-50 No.9 2010/7/1. 情報処理学会研究報告 IPSJ SIG Technical Report Input : Output :. X, N (X < N かつ (X, N ) = 1) X −1 2k (mod N ). Step0 :. 係数行列の事前計算, 係数行列のビット数 k を決める係数行列 gk−1...10 を配列テーブル T ABLE[4k ] へ初期設定, (U, V ) ← (N, X), (S, T ) ← (0, 1), k ← 0 単精度整数 (w ビット) の初期化 i = max(⌊log2 V ⌋ + 1, ⌊log2 U ⌋ + 1, w) v ˆ = ⌊V /2i−w ⌋, u ˆ =!⌊U/2i−w ⌋, v ¯ = V mod 2w , u ¯ = U mod 2w ,. 表 1 単精度演算回数の比較 Table 1 Comparison of operation times for Single-Precision 提案法. Step1 : Step2 :. 1 0 0 1 w ビット分の繰り返し (単精度計算) u ¯, v ¯, u ˆ, v ˆの値によって 1. ∼ 4. 1. u ¯が偶数, u ˆ ← ⌊ˆ u/2⌋, u ¯←u ¯/2, mj = 0, k ← k + 1 2. v ¯が偶数, v ˆ ← ⌊ˆ v /2⌋, v ¯←v ¯/2, mj = 1, k ← k + 1 3. u ¯, v ¯共に奇数かつu ˆ>v ˆ, u ˆ ← ⌊(ˆ u−v ˆ)/2⌋, u ¯ ← (¯ u−v ¯)/2, mj = 2, k ← k + 1 4. u ¯, v ¯共に奇数かつu ˆ≤v ˆ, v ˆ ← ⌊(ˆ v−u ˆ)/2⌋, v ¯ ← (¯ v−u ¯)/2, mj = 3, k ← k + 1 j ←j+1 多倍長 U,V の更新係数行列を求める (単精度整数) 1.テーブルを利用する (⌊w/k⌋ 回の繰り返し) index ← mk−1 × 4k−1 + · · · + m1 × 41 + m0 g = T ABLE[index] × g 2.残りの計算 (w − k × ⌊w/k⌋) 回の繰り返し g = smj g. Step3. 乗算加算. Step4. 乗算加算. w×2 0 ⌊w/k⌋ × (k + 7) ⌊w/k⌋ × (k + 3). 従来法 w × 10 w×6 0 0. j ← 0, g = Step3 :. Step4 : (1) :. (2) :. Step5 :. 4. コンピュータによる数値実験提案法と従来法の比較を行うため，コンピュータ上で数値実験を行った．プログラムは基本的に C 言語で記述し，多倍長演算演算部分については GMP ライブラリを利用した．使用したコンピュータ環境としては CPU:Intel Pentium4,1.6G, メモリ:768MByte,OS:Linux である．実験データとしは，160 ビット整数 (X,N) を 1000 組用意し，1000 個の逆元計算を行う時間と，各手法において Step3, Step4 の乗算回数の比較である．また，事前計算する k ビット係数行列として，8 ビット係数行列 (メモリ:65536 × 4)，4 ビット係数行列. (256 × 4) を用意した．上の条件のもと，コンピュータ上での数値実験結果を表 2 と表 3 に示す．表 2 より，Step3, Step4 の?単精度整数演算処理に関して，提案法が従来法より約 16%ほ. U, V, S, ) ! ! T の更新 (多倍長整数 ! ! U′ U S′ S −w ←2 g , ←g ′ ′ −V −V T T U ← |U ′ |, V ← |V ′ |, S ← (U ′ /U )S ′ , T ← (V ′ /V )T ′ V = 0 ならば Step5 へ，それ以外は Step2 最終計算 X ← −S (mod n) U ̸= 1 ならば，計算不能, U = 1 ならば， return(X, k). ど処理が早くなっていることがわかる．一方，逆元をもとめる全体時間については，差は. 4%程であった．これは逆元を求める処理において、多倍長整数演算がその中心を占めるため、単精度整数演算より多くの処理時間を必要としているためである．多倍長整数演算，主に加算，乗算については，いくつもの専用のハードウェアによる提案があるため，それらを用いることで，本提案を利用した逆元計算の全体処理も効果的になると推測できる．また，表 3 より単精度の乗算回数は提案方法が従来法の約 1/10 と大幅に減少した．ただし，従来. 図 4 テーブルを用いた改良 2 進 GCD 法 Fig. 4 Binary GCD Method with Table. 法は乗算が全てシフト演算により計算できるのに対して，提案法はシフト演算，ビット演算，乗算の組み合わせからなる点が異り，このことが表 2 の単精度部処理時間が 16%程度. 法と異なる点は行列積で行う乗算は単純なシフト演算ではないことも注意する必要がある．. しか減少しないことに現れている．. これらより，Step4 の単精度整数演算は乗算が ⌊w/k⌋ × (k + 7), 加算が ⌊w/k⌋ × (k + 3). 5. まとめ. 回数必要である．従来法と提案法の単精度演算回数の比較を表 1 に挙げる．. 本報告では，事前計算された係数行列をテーブル化し，拡張 2 進 GCD 法による計算過程でそのテーブルを参照することにより，単精度整数演算を減少させる手法について提案し. 5. c 2010 Information Processing Society of Japan ⃝.

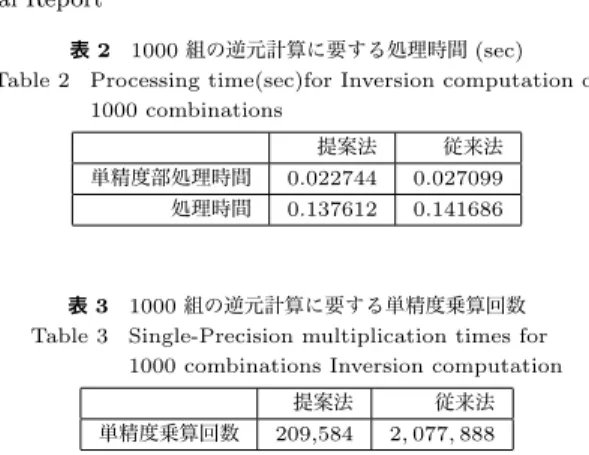
(6) Vol.2010-CSEC-50 No.9 2010/7/1. 情報処理学会研究報告 IPSJ SIG Technical Report 表 2 1000 組の逆元計算に要する処理時間 (sec) Table 2 Processing time(sec)for Inversion computation of 1000 combinations 提案法 0.022744 0.137612. 単精度部処理時間処理時間. 従来法 0.027099 0.141686. 表 3 1000 組の逆元計算に要する単精度乗算回数 Table 3 Single-Precision multiplication times for 1000 combinations Inversion computation 単精度乗算回数. 提案法 209,584. 従来法 2, 077, 888. た．数値実験の結果からは，単精度整数演算回数，処理時間については，十分な効果が得られたが，逆元を求める一連の処理としては僅かな効果しか得られなかった．これは，全体処理のなかで多倍長演算の時間が大きいことと，実験したコンピュータ環境では単精度乗算に必要とする時間が他の命令にくらべ，それほど大きな違いがなかったことに起因すると考えられる．しかしながら，計算リソースが限られている組み込みシステムなどでは，乗算のコストは他の演算より大きく，このようなシステムでは本提案法が効果的であると推測している．今後の課題として，組み込みシステム上で本提案を実装し，その効果について検証してゆきたい．. 参. 考. 文. 献. 1) N. コブリッツ, 数論アルゴリズムと楕円暗号理論入門, シュプリンガーフェアラーク東京,1997. 2) D.E. クヌース,The Art of Compuer Programming,Volume2，株式会社アスキー,2004. 3) H. Kobayashi, H. Morita, Fast modular inversion algorithm to match any operation unit, pp.733-740,IEICE Trans. Fundamentals,Vol.E82-A, No5, May 1999. 4) I.F. ブラケ, G. セロッシ, N.P. スマート, 楕円曲線暗号, ピアソンエデュケーション,2001. 5) J.H. シルバーマン, J. テイト, 楕円曲線論入門, シュプリンガーフェアラーク東京, 1995. 6) N. コブリッツ, 暗号の代数理論, シュプリンガーフェアラーク東京, 1999. 7) 辻井重男, 笠原正雄ら, 暗号理論と楕円曲線, 森北出版, 2008.. 6. c 2010 Information Processing Society of Japan ⃝.

(7)