阪大物理学オナーセミナー (担当:久野、長島):Note 3 平成 19 年 12 月 13 日
8
ニュートリノの性質
ここではいわゆる標準理論の枠組み内で議論をする。従ってニュートリノは質量を持たず右巻きのニュートリノ は存在しないという前提で話を進める。標準理論を越える現象であるニュートリノ振動現象については、次回改 めて議論する。8.1
3種のニュートリノ
電子 (e−)、ミューオン ( µ−)、タウレプトン (τ−)の3種の荷電レプトンは、質量を除けば全く同じ性質を持って いる。種々の反応率なども質量値を置き換えるだけで正確に再現できる。この3つのレプトンを区別する性質は 全くない。にもかかわらず付随するニュートリノとともに固有の量子数 (レプトンの香りといい、(νe, e−)は e-数、 (νµ, µ−)は µ -数、(ντ,τ−)は、τ-数と名付ける) を持っており、互いに混じることはない。弱い相互作用には左巻 きの粒子が、ペア (2重項) で関与する。弱い力は、2種類の”弱 (電) 荷”により生じると言い換えてもよい (SU(2) 対称性)。電磁相互作用の力の伝達子は一種類のフォトンのみであるのに反し、弱い相互作用では3種の伝達粒子 (W+, Z0,W−)があるのはこの理由による。右巻きの粒子は弱荷を持たず弱い相互作用に関与しない* 1) 。弱い相互 作用の仕方により、レプトンを分類すると以下のようになる。3 種類あり香りが違うという言い方で区別をする。 それぞれペアを組むレプトンとは同じ香りを持つ。全ての反応で香りは保存することが知られている* 2) 。 レプトン [ νe e− ] L [ νµ µ− ] L [ ντ τ− ] L , eR, µR,τR (1a) 同じ電荷を持つならば、電磁力の強さが物質の種類によらず全て同じであるのと同じように、弱い力の強さもま た物質の種類に依らず (普遍相互作用)、力の示す性質もよく似ている。実際、電磁力と弱い力は力の源の電(弱) 荷の数が違うだけで、共にゲージ理論という数学的な枠組みに従う* 3) 。2重項が、W ボソンを放出もしくは吸収 することによって弱い力を伝える時は、電荷が変わるので粒子種も変化する。しかし変わる相手は必ず2重項の パートナーである。Z ボソンの吸収放出の場合は、電荷はそのままであり変身はしない。 レプトン数保存則 クォークやレプトンはスピンが 1/2 のフェルミオンであり、粒子と反粒子で数の数え方が違 う。あらゆる反応で、クォーク数とレプトン数 (粒子数-反粒子数) および香りが保存することが知られている。例 えば次のベータ崩壊とミューオン崩壊で眺めてみれば、全て保存していることが判ろう。 ベータ崩壊 d → u + e− + ν¯e クォーク数 1 1 0 0 レプトン数 0 0 1 − 1 ミューオン崩壊 µ− → e− + νe¯ + νµ レプトン数 1 1 − 1 1 µ数 1 0 0 1 e数 0 1 − 1 0 * 1) 中性のゲージボソンは、一部フォトンと混合しているので、その分だけ右巻き成分にも結合する。なお、この章で右巻き左巻きという時 は、ヘリシティではなく、カイラリティが正負の意味で使う。 * 2) 後述のニュートリノ振動は香りが変わる反応である。 * 3) 強い相互作用は3種の色荷により生じ、SU(3) 対称性に従うゲージ理論である。歴史的経緯 ニュートリノの種類は、歴史的には最初はベータ崩壊に関与するニュートリノのみが知られていた。 (A, Z)→ (A,Z − 1) + e++νe (2a)
(A, Z)→ (A,Z + 1) + e−+ ¯νe (2b) このニュートリノは電子と相伴って生成されるので電子ニュートリノと呼ぶことにする。ニュートリノは電気的 に中性で相互作用が弱く、当時の検出器にはかからなかったので、信号としてはエネルギーを持ち去るのみの見 えない粒子であった。ミューオンもまた崩壊して、電子の他にエネルギーを持ち去る見えない粒子を生成してい た。ミューオン崩壊での電子スペクトルが連続分布することから、2個のニュートリノが放出されることが判り、 これが第2のニュートリノの存在を示唆するはじめの徴候であった。 µ−→ e−+ ¯νe+νµ (3) ここで、もし二つのニュートリノが同種ならば、このニュートリノはミューオンにも電子にも結合するわけであるから、 図 1 の様な過程により、µ→ eγ崩壊反応が存在しなければならないが、この反応は現在に至るまで観測されていない。 図 1: µ→ eγ反応。ミューオンに結合す るニュートリノと電子に結合するニュート リノが同一粒子であれば、この過程が存在 する。 µ→ e +γ 分岐比 < 1.2× 10−11 (4) しかし、もし第 2 のニュートリノが電子ニュートリノと違う粒子であるなら ばこの過程は存在しないことが説明できる。この仮説は、πメソンからの崩 壊ニュートリノを使って、物質と反応させ、電子が生成されるか、ミューオ ンが生成されるかを見れば検証できる。πメソンは π+→ µ++ν µ によりミューオンとニュートリノに崩壊するが (図 2(b))、このニュートリノ は定義によりνµである。これがベータ崩壊からのニュートリノ (νe) (図 2(a) 図では反電子ニュートリノ) と違うならば、電子ニュートリノは物質と反応 して電子のみを生成し、ミューニュートリノはミューオンのみを生成するはずである (図 2(c)(d))。実験的にまさ にそうなっていることが、レーダーマン・シュタインバーガー・シュワルツ等により 1962 年に確かめられた。 図 2: (a) ベータ崩壊、d クォークは原子核の中の中性子の中にいる。(b) パイオン崩壊。π+は u クォークと反 d クォークの複合体であり、合 体して消えると共に仮想的に W+に変わり、さらに µ+νµの対に崩壊する。(c)(d)(e) は νe,νµ,ντを物質 (クォーク) と反応させたとき対応 するレプトンを生成する。また生成レプトン種を見れば入射ニュートリノの種類が判明する。 タウレプトンは、 e−+ e+→τ−+τ+ (5a) τ→ e + ¯νe+ντ µ + ¯νµ+ντ (5b)
反応で発見され、崩壊パターンがミューオンと全く同一であることから、第3番目のニュートリノντが確認され た。ντ,νe(νµ)は、τ→ e(µ) +γがないことから、あるいは、νe(νµ)ビームではタウレプトンが作れないこと から言える。香りの保存は標準理論では前提として組み入れられている。標準理論の範囲では香りの混合、例えば µ→ eγ, τ→ µγや e + X→ µ +Y などの異種のレプトンを崩壊生成する過程は観測されていない。ただし、ニュー トリノの混合は存在することが判っており、標準理論の枠組みを越えた取り扱いを必要とする (後述)。 ニュートリノは3種類だけか? 標準理論では、ニュートリノは3種類のみである。実験的には次のようにして 確かめられる。電子衝突型加速器で、ゲージボソン Z を作り、次いで粒子対に崩壊する次の反応を起こす。 e−+ e+→ Z → (qi+ ¯qi) or (ℓ−i + ¯ℓ+i ) or (νi+ ¯νi) (6) iは香りの種類を表すが、クォークの場合はカラーの自由度を入れ 3 倍する。終状態はエネルギー保存則から各 粒子・反粒子対の質量が mZ/2以下のみ可能である。従って、トップクォーク対へは崩壊できない* 4) 。終状態の クォーク対は、ハドロンとして観測される。終状態のニュートリノは直接観測にはかからない。 図 3: e−+ e+→ Z → ハドロンの全断面積。Nν=3,4,5につ いての計算値と実験値を比較している。 しかし、余分の香りを持つニュートリノが存在すれば、全崩壊 率が変わるので、観測可能な過程、例えばハドロンへの崩壊率 の全崩壊率の中に占める割合 (分岐比) BR =Γ(Z→ ハドロン) Γ(Z→ all) (7) が変わる。e−と e+2体重心系での全エネルギー E(e−e+)≡ √ s = mz領域でのハドロンの生成断面積は σ(e−e+→ hadrons) =σ(e−e+→ Z)BR(Z → hadrons) (8) である。実験値はトップを除く5種類のクォークと3種類の荷 電レプトン、3種類のニュートリノに崩壊すると仮定したとき の計算にぴったり一致した (図 3)。 Nν= 2.994± 0.012 (9) mz/2を越える重いニュートリノが存在した場合、この実験で は検知できないが、非常に軽い3種類のニュートリノがあって 4番目から突然重くなるシナリオは考え難いので、標準理論で はニュートリノを3種類に限定する。
8.2
ニュートリノの検出
ニュートリノは、強い相互作用と電磁相互作用を持たない唯一の粒子である。弱い相互作用は文字通り物質と弱 くしか反応しないので、検出は困難を極め、予言 (1930) から 30 年近く経過して、ようやくライネス・コーワン らにより検出 (1956) されたのであった。今日、ニュートリノは加速器、原子炉で大量生産され、大気ニュートリ ノや太陽ニュートリノも日常的に観測されているが、ライネス・コーワンの方法は今日でも低エネルギー反電子 ニュートリノ検出に使われる標準的手法であるので、詳しく解説しておこう。検出反応は ¯ νe+ p→ e++ n (10a) e++ e− →γ+γ n +Cd → Cd∗→ Cd + (3 ∼ 4) ×γ′s (10b) * 4) mZ= 91GeV, mtop= 185GeVである。他は mu∼ 3MeV, ms∼ 6MeV, ms∼ 120MeV, mc∼ 1.3GeV, mb∼ 4.2GeV レプトンは me∼ 0.51MeV, mµ= 105.7MeV, mτ∼ 1777MeV, mνi= 0である。
ここに、Cd はカドミウム原子核、Cd∗はカドミウム同位体の励起状態を示す。原子炉で作られるニュートリノは 正確には反電子ニュートリノであり、レプトン数保存、レプトンの香り保存則を考慮すると、反ニュートリノが W−ゲージボソンを仮想的に放出して陽電子 e+となり、W−ボソンが陽子 p(実際は u クォーク) に吸われて、中 性子n (d クォーク) なる。陽電子は反電子であるから直ちに物質中の電子と対消滅して、エネルギー和が 2meと なる2個のガンマ線を放出する。中性子は遅い速度で飛び出て、あちこちふらふらしながら最後にはカドミウム 原子核に吸収され、3-4 個のガンマ線を放出する。この間、10−4秒位の時間が経過して∼ 1m ほども動く。γ線は 物質中の電子を跳ね飛ばしたり (コンプトン散乱)、原子核近傍の強い電場を通過すると制動放射をおこして電子・ 陽電子対を生成するので、これらの電子が原子を励起して放出する光をシンチレーションカウンターで検出する。 反応時に陽電子が出す信号と中性子捕獲時の遅延同時計数 (コインシデンス) が望む事象の信号となる。 実験は、米国南カロライナ州にあるサバンナ原子炉の近傍に、図 4 のような検出装置を置いた。検出装置は信号 図 4: 始めてのニュートリノ検出 Reines-Cowan(1954):原子炉からの反ニュートリノが、陽子と反応して陽電子と中性子を作る。陽電子は物質 中の電子と対消滅を起こし、2個のγ線を放出する。中性子はカドミウム (Cd) 原子核に遅れて吸収され、X線を放出する。 の光を出す塩化カドミウムを含む水の層を液体シンチレーターではさみ、光電子増倍管でシンチレーション光を 検出する。原子炉の 1kW あたり 2× 1014個のニュートリノが放出されると計算され、実際に検出器を置いた場所 では 1013/sec/cm2のフラックスがあると推算された。これは太陽ニュートリノの約 100 倍の強度であるが、何分 にも反応頻度が小さく宇宙線による偽信号 (バックグラウンド) と区別を付けにくい。宇宙線バックグラウウンド は、今日の最先端実験でも未だにつきまとうやっかいな問題である。この最初の実験では特に深刻であった。結 局、原子炉運転時とオフの値の差を取り、ようやく平均して 20 分に一回真の反応が起きていること確認した。
8.3
ニュートリノの質量
8.3.1 電子ニュートリノの質量測定 原子核ベータ崩壊を考える。これは原子核内のクォークが d→ u + e−+νe (11) のように変換する過程である。崩壊率は遷移振幅を自乗してスピンについて始状態の平均、終状態の和を計算し て得られる。非相対論的量子力学では Wf i= 2π|Hi f|2ρ, ρ=位相空間体積 (12) と表される式である。静的近似で計算した原子核の遷移行列は定数であり、|Hf i|2部分は電子とニュートリノの運 動量を含まない。したがって、電子とニュートリノの運動量分布は位相空間のみで決まる。電子のエネルギー以外は全て積分してしまうと、崩壊率Γは、 ρ=δ(E0− Ee− Eν) d3pe (2π)3 d3pν (2π)3 (13a) dΓ= G 2 β 2π3|
M
| 2F(Z, E)p eEepνEνdEe (13b) pνEν= (E0− Ee) √ (E0− Ee)2− m2ν, E0= M(Z, A)− M(Z + 1,A) − mν= Ee, max (13c) |M
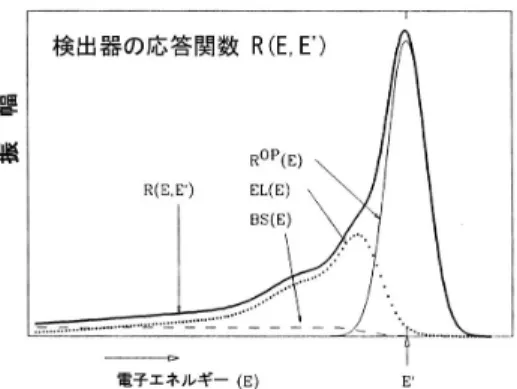
|2=| < 1 > |2+|CGT|2| <σσσ>|2 (13d) F(Z, E)はクーロン波動関数による補正項で計算可能な量である。 K(E) = [ dΓ dEe F(Z, E)peEe ]1/2 (14) と置くと、mν= 0であれば、K(E)∝E0− Eeと直線になるはずである。これをカーリー・プロットという (図 5)。 mν, 0 ならば、終端付近で直線性からのずれとして観測されるはずである。 図 5: トリチウムベータ崩壊のスペクトル (下図) と終端部のカーリープロット。mν, 0 ならば、電子の最高エネルギーが mνだけずれて、ス ペクトルが終端で垂直になる (上左図)。しかし、実験誤差を入れると上右図のような分布となる。 実験的考察 (1) E0が小さいほど小さな mνの値が測定できるので、通常 E0の最も小さいトリチウム (3H, E0= 18KeV )が選ばれる。質量値測定に有用な領域は、エネルギーが Ee= E0−∆∼ E0の区間であり、ここの事象の統 計を上げることが望ましい。全体の位相空間に対する Ee> E0−∆空間の割合を求めてみると ε= RE0 E0−∆E 2(E 0− E)2dE RE0 0 E2(E0− E)2dE = 10 (∆ E0 )3 (15) ∆= 1eV とすれば、ε∼ 2 × 10−13となる。mνの精度を上げるに従い急速に効率が落ちることが判る。図 6: 応答関数とその振る舞いの分析 (2) 検出器の解像力は有限であり、エネルギー E’ を持っ た電子のエネルギー観測値は、E’ の付近に分布する。こ の分布関数を検出器の応答関数といい、例を図 6 に示す。 ROP(E)が、エネルギー E’ の電子の放出する光量分布で 通常正規分布をする。EL(E) は、ベータ電子放出源の物 質中でのエネルギー損失、BS(E) は放出源支持構造から の後方散乱による。真のスペクトル分布を N(E′)とすれ ば実際に観測される電子のエネルギースペクトルは、 N(E)obs= Z
N(E′)R(E, E′)dE′ (16) で与えられるので、真のスペクトルの形が崩れる (図 5 のカーリープロット図)。 (3) また、トリチウム原子は、原子核とクーロン力により束縛状態のエネルギー状態を作るが、ベータ崩壊電子 放出前後で、束縛状態が変わる。通常は終状態が基底状態におさまるが、中には励起状態に行くものもある。そ の場合余分のエネルギー∆V が失われる。従って上のスペクトルは pνEν =
∑
i Pi(E0−∆Vi− Ee) √ (E0−∆Vi− Ee)2− m2ν) (17) と変更される。Piは、励起状態 i に行く確率である。これは、カーリー・プロットスペクトラムの傾斜を減少さ せ、終端で平坦にする効果を持つ。 東大核研の実験* 5) を、図 7 に示す。2重収束の磁石を使うスペクトロメター例。右側の首の所にある3Hアイソ トープよりベータ崩壊で放出された電子が、円弧を描いて左側の口にある面に比例計数箱とシンチレーション・カ ウンターに捕らえられる。∆p/p = 0.02%(∆E = 8eV )を実現し、磁石の設定を固定したまま、終端エネルギー E0 付近で 1600eV の範囲の粒子を計測した。図の右側にカーリー・プロットを示すが、mν= 0とする曲線に最も良 く適合し、mν< 13eVと抑えられた。最新の実験データでは mνe< 2eV である。8.3.2 ミューニュートリノとタウニュートリノの質量 ミューニュートリノの質量 ミューニュートリノの質量は π+ (p)→ µ+(q) +νµ(k) (18) の反応において、エネルギー運動量が保存することを使うと、πの静止系において mπ= √ q2+ m2 µ+ √ k2+ m2 ν, k =|k| = | − q| = q (19a) から、パイオンとミューオンの質量が既知であれば、ミューオンの運動量 q を測定する事によって、ニュートリ ノの質量が求まる。 mπ= 139.56995± 0.00035MeV mµ= 105.658389± 0.000034MeV q = 29.79200± 0.00011MeV ⇒ m2 ν=−0.016 ± 0.023 (20a) mνµ < 0.17MeV (90%CL) (20b) が得られている* 6) 。 * 5) Phys. Lett. B187(1987)198-204 * 6) K.AssamaganPhys. Rev. D53(1996) 6065
図 7: 左側に測定装置、右側にデータのカーリープロットを示す。データは mν= 0とする曲線に最も良く適合し、mν< 13eVと抑えられた。 タウニュートリノの質量 e−e+反応でタウペアを作り、タウの多重πメソン+ニュートリノへの崩壊を使う。 e−+ e+→τ−+τ− (21a) τ±→π±+π++π−+ν τ (21b) m2ν= E(ν)2− p(ν)2= (mτ−
∑
i E(πi))2− (∑
i p(πi))2, E(πi) = √ p(πi)2+ m2 π (21c) から計算する。上のエネルギー運動量はタウの重心系での測定量である。タウニュートリノの質量精度は、タウ 自身の質量精度に依存する。 mτ= 1777+0.30−0.27MeV ⇒ mντ< 18.2MeV (95%CL) (22) シーソーメカニズム ニュートリノ振動発見 (1998) により、ニュートリノの有限質量が確定したが、質量の値 が他のフェルミオンに比べて非常に小さく (図 8)、他のフェルミオンとは異なる特別な扱いを必要とする。 図 8: フェルミオン質量。ニュートリノ質量は mj=√|∆mi j|。mtop∼ 175GeV,mb∼ 4.3GeV,mc∼ 1.25GeV,ms∼ 105MeV,md∼ 6MeV,mu∼ 3MeV,mτ= 1777MeV, mµ= 105.7MeV, me= 0.511MeV
mtop≃ 175GeV に比べると
mν
mtop
一番軽い電子に比べても mν me < 10−7 (24) もの差がある。標準理論では質量はヒッグスとの相互作用により生じると考えられ、ヒッグスの真空期待値を v= 250GeVとするとき、各粒子の質量は m∼ gv (25) と表される。すなわち、質量の差はヒッグスとの結合力の差であり、ニュートリノだけ極端に小さいことは不自然 であると考えられる。しかし、ニュートリノが粒子と反粒子の区別のないマヨラナ粒子であれば、シーソーメカ ニズムにより極端に小さい質量値の説明を割に自然な形で提供できる。 ニュートリノを何故マヨラナと考えるか? まず第一に、右巻きのニュートリノが見つかっていない。ニュートリ ノを検出する手段は弱い相互作用しかなく、右巻きニュートリノは弱い相互作用をしないから、検出してないから といって存在しないとは限らないという考えもある。しかし、宇宙の軽元素 (水素・重水素・ヘリウムなど) 存在 比の予言値と観測値の比較から、数 MeV 以下の軽い質量のニュートリノは (左巻きと右巻きを独立に数えて) 3-4 種類以下と制限されている。宇宙論ではニュートリノの持つエネルギーで議論していて、上の結論は弱い相互作 用が右巻きに作用するかしないかには関係なく成立する。Z→ NνLν¯L実験で正確に N = 3 ときめられたことと合 わせて、質量の軽い右巻きのニュートリノは存在しないと考えるのが妥当である。 第 2 に、ディラック方程式に従う粒子は4成分 (粒子・反粒子、ヘリシティが正・負) を持つ。質量がゼロであれ ば、2成分のワイル方程式でよく、左巻き右巻き成分は独立な粒子となるが、ニュートリノ振動の発見により質量 のあることが証明されたから、ワイル粒子の可能性は除外される。質量が有限であっても、粒子と反粒子の区別 がないとすれば、やはり2成分のマヨラナ方程式が成り立つ。この場合、左巻きニュートリノνLと右巻ニュート リノνRは独立な方程式を充たすから、質量が同じである必要はなく、右巻きニュートリノの質量 mRが大きくて まだ発見されていないという解釈が成立する* 7) 。 そこで、標準理論を少し拡大して質量の大きい右巻きのマヨラナ粒子が存在し、左巻きニュートリノと混合する と仮定しよう。この場合、νL, νRを基底とする質量行列 M の一般形は M = [ mL 0 0 mR ] → [ mL mD mD mR ] (26) のように非対角要素を持つ。(26) を対角化して得られる二つの新たなニュートリノを、ν′, N、その固有値を mν, mN とする。この質量固有状態は、L 成分と R 成分を共に含み、決まったカイラリティ状態にない。今、質量の大き なνRを導入する以外は標準理論の枠内で考えることにし、mL= 0、mDは標準理論の質量スケール、mR≫ mDと する。この時固有解は容易に求められて、md/mRの高次項を無視すれば |ν′>≃ |νL>−mD mR| νR>, |N >≃ |νR> + mD mR| νL> (27a) mν′≃ −m 2 D mR , mN≃ mR (27b) 質量が負であることは問題ではない。|ν>=γ5|ν′>と置けば質量を正にできるからである。上式から mν· mR= m2D (28) となり、mRを大きくすることにより mν を小さくできる。これがシーソーメカニズムという名の由来である。 mD∼ mW, mR∼ 1016GeVとすれば、mν∼ 10−3eVとなって、ニュートリノ振動から推測されるニュートリノ質量 * 7) 左巻きマヨラナニュートリノを荷電変換すると右巻き反マヨラナニュートリノとなるが、マヨラナニュートリノでは粒子と反粒子の区別 がないので、単なる右巻きニュートリノとなる。これは (νL)cの様に表記して、ここで述べた右巻きニュートリノν Rとは区別する。4 成分 ディラック方程式の解、{νL, (νL)c= (νc)R}, {νR, (νR)c= (νc)L} が、マヨラナ方程式では2成分ずつに分離し、それぞれ独立な質量を持つ のである。
をほぼ再現する。1016GeV は、大統一理論のエネルギースケールであり、シーソーメカニズムは、大統一理論の 範囲ではごく普通の値のみ扱う自然な議論であり、特に奇抜なアイデアも導入してはいない。ニュートリノの質量 起源を追求することにより、大統一理論への足がかりがつかめると考える理由はここにある。 以上に述べたようにマヨラナニュートリノであれば、右巻きニュートリノが観測されていないことの説明や、 ニュートリノ質量を小さくする自然なメカニズムの導入が可能である。ディラックニュートリノの場合は、小さ な質量を自然に導入することが難しいので、現在はマヨラナニュートリノ説が有力である。
8.4
ニュートリノのヘリシティ
弱い相互作用、特に荷電カレント反応は左巻き粒子にのみ作用する。その顕著な事実を如実に示す例としてπメ ソン崩壊を考察する。 π+→ µ++ν µ, π+→ e++νe (29) 電荷の保存とレプトン数保存より、電荷が正のπメソンからはニュートリノ、電荷が負のπメソンからは反ニュー トリノが生成される。崩壊粒子はカイラリティ負の固有状態である。ニュートリノは質量がゼロであるから、純 粋なヘリシティ負状態、反ニュートリノは純粋なヘリシティ正状態で放出される。一方、µ+(e+)は質量を持つ反 粒子であるので、ヘリシティの優勢成分は正であるが、負のヘリシティ成分をもわずかに含む。πメソンのスピン はゼロであるから、πメソンの静止系では、運動量と角運動量保存則により µ+(e+)のヘリシティは負でなければ ならない (図 9 参照)。µ+(e+)の劣勢な負ヘリシティ量は、1− v ∼ (1/2)(m2/p2)程度であるので、もし質量がゼ ロであれば崩壊は起こらないが、質量がある分だけ崩壊が許される。したがって、πメソンの µ と電子への相対 図 9:πメソンの2体崩壊。崩壊粒子は共に左巻き (カイラリティ負) の状態にある。ニュートリノは質量ゼロであるから、ヘリシティ負の純粋 状態にある。角運動量保存則により、 µ+のヘリシティは負でなければならない。左巻き反ミューオンの持つヘリシティ負の成分により崩壊 が起き、それは質量の自乗に比例する。 分岐比は質量の自乗に比例する。より詳しい計算によれば、 Γ(π→ µ +ν) ∝ m2µ(m 2 π− m2µ)2 m5 π (30) であるので Γ(π→ e +ν) Γ(π→ µ +ν)= m2 e(m2π− m2e)2 m2 µ(m2π− m2µ)2 = 1.284× 10−4 (31) 放射補正値をも考慮すると理論値は 1.233× 10−4となり、実験値 1.218± 0.014 × 10−4と良く合う。終状態の差は µ と電子の質量差しかなく、ナイーブに考えれば、位相体積の大きい eνの方が崩壊率も大きいと推測されるが、 弱い相互作用が左巻き粒子にのみ作用するために、このような大きな差が出る* 8) 。 ニュートリノヘリシティの測定 歴史的にはベータ崩壊のニュートリノ、すなわちνeのヘリシティが最初に測ら れたが、ここではνµが左巻きであることを示した実験を紹介する。πメソン崩壊反応におけるミューオンのヘリ シティが測れれば、ニュートリノのヘリシティが判る。ミューオンのスピンの向きは、原子核に当てて電磁気散 乱 (モット散乱) をさせれば、散乱分布に左右非対称が出るので測定できる。モット散乱には電気散乱 (クーロン散 乱) と磁気散乱があり、クーロン散乱は電荷のみによるので散乱は左右対称である。一方、ミューオンの静止系で * 8) 弱い相互作用が右巻き粒子に作用しても同じ結果となるが、次に述べるように、ミューオンの偏極を調べて左巻きと判る。は、近づいてくる原子核が電流として見えるから、ミューオンの磁気能率 (⃗µ = (e/2mµ)⃗s;すなわちスピンに比例 する) は、コンパスが触れるのと同じく回転力を受け、磁場勾配があれば力を受ける。電流が左側にある場合引力 とすれば、右側にある場合は逆の斥力になる。結果的にどちらの場合も右側に散乱されることになるので、非対 称が生じるのである (図 10 左)。 図 10: 左図:クーロン散乱は非対称を生じないが、磁気散乱はミューオンのスピンの向きにより散乱される方向が異なる。右図:ミューオン がπの重心系で生成されたときの縦方向スピンは、実験室系では横方向スピンとなる。 ただし、磁気相互作用は磁場のスピン方向成分により生じるので (H =−µµµ ·B)、スピンの向きが電流に、言い変え ればミューオンの運動量方向に垂直な成分のみが関与する。π崩壊で生成される正のミューオンはヘリシティが 負の状態であるからスピンは縦成分のみである。πを飛ばして前方かつ有限角を持つて崩壊するミューオンを拾 えば、スピンは回転して (と言うよりはミューオンから見て走っている観測者からは、スピンは変わらず運動量方 向が変わって見える (図 10 右) と考えると良い)横偏極を生じる。実験装置を図 11 に示す。左方から運動量エネ 図 11: 実験配置図。ミューオンはカウンター #1, カウンター #2 の穴、カウンター #3(鉛シートの直前) を通り抜け、鉛で散乱されてカウンター #4に捕らえられる。さらに #4 で崩壊電子の遅延信号を捕らえてミューオンであることを確認する。#3 と #4 の相対配置で右方向もしくは左 方向散乱の区別をする (Phys.Rev.Lett.7(1961)23)。 ルギー 43MeV の負パイオンが入り、崩壊して生成された負ミューオンが前方円形状にならべた 10 個の鉛シート のどれか (例えば3番) に当たり、後方大角度散乱をして、鉛のシートに垂直に配置したカウンター 4 で止められ る。ミューオンは、ビーム線と鉛シートの直前に配置されたカウンター 3 の作る平面内に、かつビーム軸にはほ ぼ垂直方向に偏極している。止まったミューオンはさらに崩壊して電子を放出するので、遅延信号が存在すれば ミューオンと同定できる。右側の鉛シートからは右方散乱、左側の鉛シートからは左方散乱したミューオンを拾 い出せる。この設定が円対称に 10 組配置してある。 計算によれば、左右の非対称度は横偏極度を Pyとして A =L− R L + R=±0.09, f or Py=∓1 (32) 実測では、A =−0.09 ± 0.031 を得て Py= 0.9、すなわち、µ−がほぼ 100% 正のヘリシティを持つこと、従って反 ミューニュートリノが、右巻きであることが実証された。
8.5
二重ベータ崩壊
レプトン数非保存のテスト ニュートリノがマヨラナ粒子であれば、レプトン数は保存しない。レプトン数非保存 を検証する実験で重要なのは2重ベータ崩壊である。現時点では、レプトン数保存検証可能な唯一の実験といって も良い。2重ベータ崩壊とは、原子核が電子を2個放出して原子番号が2大きい原子核に変わる反応で、2νモー ドと 0νモードの2種類がある (図 12(a),(b))。 2νモード : (Z)→ (Z + 2) + 2e−+ 2 ¯νe (33a) 0νモード : (Z)→ (Z + 2) + 2e− (33b) 2νモードは、通常のベータ崩壊が核内で2重に起きるもので、弱い相互作用の高次効果として当然期待される 図 12: 2 重ベータ崩壊の三つの過程:(a) 2νモード、(b) 0νモード、(3) マヨロン放出モード。マヨロンはレプトン数保存が自発的に破れた時 に生じる未発見のゴールドストーンボソンである。 ものである。0νモードは反応の前後でレプトン数が2変化していて、レプトン数保存則が破れて始めて起きる反 応、すなわちニュートリノがマヨラナでないと起こらない反応である。弱い相互作用はカイラリティを保存する ので、図 12(b) のヴァーテックス (1) に注目すると、電子とペアで生成されるニュートリノはνLの反粒子、マヨ ラナであれば右巻き粒子でなければならない。一方、ヴァーテックス (2) の反応が起きるためにはニュートリノは 左巻き状態でなければならない。従ってこの反応が起きるためには、まず第一に反粒子と粒子とが同一でなけれ ばならない。第 2 に質量がゼロの場合は、角運動量保存則によりこの過程は起こらない。この過程が起きるため には、ニュートリノがマヨラナでありかつ質量を持つ(この場合は、異なるヘリシティ成分が (mν/me)2程度存在 する) か、もしくは弱い相互作用が標準理論と違って、右巻き粒子に作用する成分もあるとしなければならない。 図 13: 左図:2重ベータ崩壊おける電子のスペクトル。(a) 2νモード、(b) 0νモード、(c) マヨロン放出モード。 中図:ゲルマニウム検出器によるベータ活性のアイソトープのスペクトル。種々のピークの鋭い山は検出器のエネルギー分解能を示している。 測定時間 1.29kg y。しかし、2重ベータ崩壊が検出されるはずのエネルギー領域のデータ (右に拡大図を示す) に信号の山は見られない。点線 は統計的に 90%CL で除外できる信号の大きさを示す。実験的には、0νモードと 2νモードは、2個の電子のエネルギー和が一定の値をとるか、連続値をとるかで区 別できる (図 13 左図)。2重ベータ崩壊は 1018∼ 1024年もしくはそれ以上の崩壊寿命を持ち、自然環境による背 景雑音 (宇宙線や測定器を構成する物質内に含まれるアイソトープ) の影響の除去が困難な実験である。ゲルマニ ウムはそれ自身が精密なエネルギー検出器であるので、ゲルマニウム内で生じた 2 重β崩壊に対しては、100% の 立体角検出効率を持つ。ゲルマニウム検出器のエネルギー情報のみを使った実験例を図 13(中・右図) に示す。2ν モードは観測されていて* 9) 100Mo→100Ru + 2e− + 2 ¯νe τ1/2= 7.1± 0.4 × 1018年 (34a) 76Ge→76Se + 2e−+ 2 ¯νe τ1/2= 1.5± 0.1 × 1021年 (34b) 等を与えるが、0ν モードはまだ観測されていない。0νモードの崩壊電子は、互いに 180 °方向に放出されるの で、背景雑音を減らすためには軌跡をも検出するのが望ましい。現時点で進行中の実験ではこのような装置を使 う (説明省略)。現在最良の上限値はゲルマニウム (Ge) アイソトープから得られていて τ0ν> 1.9× 1025年 (35) この値をニュートリノ質量の上限値に換算するには、原子核行列の知識が必要であるが、理論の精度は余り良く なく、一桁くらいの不定性を伴う。種々の計算を総合して、マヨラナニュートリノの質量の上限値は mν< 1eV (36) となる。
A
補足:カイラリティとガンマ行列
A.1
カイラリティ
カイラリティやガンマ行列は、素粒子物理学の教科書では頻出するので、ここで基本を解説しておく。そのために はディラック方程式を導く必要があるが、深入りはしない。古典力学から量子力学に移行する簡単な一つの方法は E→ i∂ ∂t, p→ −i∇ (37) の変換 (第 1 量子化) を行い、波動関数ψに作用させることである。非相対論的なエネルギー運動量の関係式 E = p2/2m +Vからは、シュレーディンガー方程式 i∂ ∂tψ= Hψ= [ −∇2 2m+V ] ψ (38) が得られるが、相対論的関係式 E2= p2+ m2 (39) からは、クライン・ゴードン (KG) 方程式が得られる。 [∂2 ∂t2−∇ 2 + m2 ] φ= 0 (40) しかし、クライン・ゴードン方程式の波動関数をシュレーディンガー方程式にならって、確率振幅と見なすと負 の確率など種々の矛盾が生じ、歴史的には一度は捨てられた方程式であった。波動関数を確率振幅ではなく古典 的な場と再解釈し、場の量子化 (第 2 量子化) によってクライン-ゴードン方程式は復活したが、整数スピンの場し か記述できない。反奇数スピン場を記述するにはスピノール表現が必要となる。 ディラックは、相対論的方程式もシュレーディンガー方程式と同じように、時間微分に関し一階でなければなら ないと考えた。相対論では、時間成分と空間成分を同等に扱わねばならないから、この場合空間的にも一階微分 しか許されない。しかし、相対論の基本式である式 (39) を要求すれば、運動方程式の中に 2 階微分が入ることは 必然であろう。そのためには波動関数ψを多成分{ψ= (ψ1,ψ2,···)T; Tは転置を表す} とすれば良いのではない かと考えた* 10) 。そうすると、自由なシュレーディンガー方程式を相対論的に拡張した場合 i∂ ∂tψ= Hψ= [ α·∇ i +βm ] ψ ↔ Eψ= [α· p +βm]ψ (42) と書けるであろう。これをディラック方程式という。{α= (αi, i = 1∼ 3),β} は行列である。これはいわば (39) を E2= (α· p +βm)(α· p +βm) (43) と因数分解したような形になっている。相対論的方程式は条件 (39) を充たすという要請から E2= p2+ m2=∑
i, j (αiαj+αjαi)pipj+∑
i (βαi+αiβ)pim +β2m2 (44) ∴ α2i =β2= 1, αiαj+αjαi= 0 (i, j), βαi+αiβ= 0 (45)
* 10)多成分の一階微分方程式から、2階の微分方程式が得られる例として、調和振動方程式 ¨q =−ω2qを考えてみよう。p≡ ˙q を定義すれば、 ˙ p =−ω2qである。そこで、ψ= (q, p)T と置けば、 idψ dt = Sψ, S = [ 0, 1 −ω2 0 ] (41) は元の調和振動方程式を再現する。
この条件を充たす行列をディラック行列という。すなわち反交換関係を充たす 4 個の行列が必要であるが、2× 2 行列には 3 個しか存在しない。しかし、m = 0 であればβは不要であり、αi=±σiは上式を充たすので方程式が 成立する。 σ1= [ 0 1 1 0 ] , σ2= [ 0 −i i 0 ] , σ3= [ 1 0 0 −1 ] , (46) はパウリ行列である。符号± に対応するディラック方程式の解をφR,Lと置けば EφL=−σσσ· pφL, EφR= +σσσ· pφR (47)
となる。(E, p) は微分演算子であるが、エネルギー運動量の平面波解をφ(t, x) =φ(E, p)eip·x−iEtと置けば* 11) 、普 通の数として扱えるので φR=|p| E σ· p |p| φR, φL=− |p| E σσσ· p |p| φL (48) である。ここで h =σσσ· p |p| (49) は運動方向のスピン成分を表し、ヘリシティ演算子と言う。ヘリシティが正の状態は右に回転しながら進む状態で あるので右巻き、同様にヘリシティが負の状態は左巻きと言う。 演習問題 A.1. pの方向を、(θ,φ)とすると、ヘリシティ演算子は σσσ· p |p| = [
cosθ sinθe−iφ sinθeiφ −cosθ
] (50) と書ける。この固有解を求めよ。 解答: χ+= [ cosθ2e−iφ/2 sinθ2eiφ/2 ] , χ−= [ −sinθ 2eiφ /2 cosθ2e−iφ/2 ] (51) m = 0であるから|p|/E = ±1 である。ヘリシテイの固有状態χ±が、ハミルトニアンの固有状態φL,Rの解になる ことが判る。φRの固有解は、E≷ 0 に対応して φR=χ+ E > 0, φR=χ− E < 0 (52) すなわち、m = 0 のディラック方程式の固有解φRは、粒子ではヘリシティ正の固有状態であり、反粒子ではへリ シティ負の固有状態である。まとめて右巻き状態もしくはカイラリティ正の状態と呼ぶことにする。すなわち、カ イラリティとは粒子・反粒子の区別を採り入れたヘリシティの相対論的拡張概念とみなせる。φLは左巻き (カイラ リティが負) の状態である。φRとφLは二つの独立な解であり、ワイル解と呼ぶ。しかし、(47) の二つの方程式は、 パリティ変換 x↔ −x, p ↔ −p でφRとφLが互いに移り変わるので、パリティを保存する電磁相互作用や強い相互作用をする粒子では、この解 はあり得ない。しかし、弱い相互作用のみをするニュートリノに関しては、これが解となり得る。* 12) パリティの保存している世界では、二つの解φRとφLが混合する。そこでパリティ正負の両方の解をまとめて 一つの粒子の違う状態と見なすためには、4 成分に拡張して ψ= [ φL φR ] , α≡ [ −σσσ 0 0 σσσ ] , β≡ [ 0 1 1 0 ] (53) * 11)一般的には、ψ(t, x) = √1 (2π)3 #
φ(E, p)eip·x−iEtd3pとフーリエ変換した量を考察する。
と置く。βはφLとφRを入れ替える演算子である。こうして導入したααα,βは、質量を持つ粒子のディラック行列 の条件 (45) を充たすので、 Eψ= [α· p +βm]ψ (ααα,βは 4× 4 行列) (54) が 4 成分のディラックの方程式であり、望みの相対論的シュレーディンガー方程式を与える。4成分のディラック 方程式を、改めて元の2成分の方程式に書き直すと、 EφL=−σσσ· pφL+ mφR (55a) EφR= σσσ· pφR+ mφL (55b) すなわち、質量が混合の原因になっていることが判る* 13) 。この方程式は、(47) とは違う方程式であるので、φL,R はもはやヘリシティの固有状態ではない。しかし、p >> m であれば、違うヘリシティの成分は小さい。 演習問題 A.2. φL,R= aχ++ bχ− (56) と置いて (55) に入れ、a,b を決めよ。また、φL,Rのヘリシティ期待値が、速度 (を光速度で割った数:∓v,v=|p|/E) となることを示せ。 解答: φL= √ E + p 2E χ−+ √ E− p 2E χ+= √ 1±v 2 χ−+ √ 1∓v 2 χ+ (57) φR= √ E + p 2E χ++ √ E− p 2E χ−= √ 1±v 2 χ++ √ 1∓v 2 χ− (58) ± はそれぞれ粒子・反粒子に対応する。 この解は E の正負の符号に関わらず成立し、m = 0 すなわち|E| = p の時に (48) の解に一致する。ヘリシティh の 期待値は < h >=<φL,R|h|φL,R> <φL,R|φL,R> = |a|2− |b|2 |a|2+|b|2=∓ p E =∓v (59) m, 0 であっても、相対論的粒子では E = √p2+ m2≃ p + m2/2p, m << pであるので、この近似式を使うとφL のヘリシティ状態は、 φL≃ χ−+2pmχ+, E > 0 χ++2pmχ−, E < 0 (60) すなわち、相対論的な意味での左巻き状態 (カイラリティが負) は、ヘリシティが負で定義した左巻き状態を優勢 項として持つが、逆のヘリシティ成分をも∼ m/p だけ持っていることが判る。反粒子の場合は逆のヘリシティを 持つこととする。弱い相互作用をするのは、カイラリティが負の粒子であることに留意して欲しい。 * 13)質量があると、左右成分が混合することは次のように考えれば判る。質量が有限であれば、運動速度は光速度より小さいので、この速度 を超える観測系に移ることが可能である。そのような座標系で眺めれば、粒子の回転方向は変わらないが、運動方向が逆向きになるのでヘリ シティが逆転する。逆成分の振幅混入率は∼ m/p である。m = 0 であれば粒子を追い越す座標系は存在しないから、左巻き右巻き成分の混合 は起こらない。
A.2
ガンマ行列
さて、シュレーディンガー形式のディラック方程式は、時間成分を特別扱いしていて、相対論的な観点からは不 満である。そこで、両辺にβを掛けて、 γ0=β, γi=βαi, (61) を定義し整理すると [Eγ0− p ·γ− m]ψ= [iγ0∂0+ iγi∂i− m]ψ= [iγµ∂µ− m]ψ= 0* 14) (62) これが相対論的ディラック方程式である。γµはディラックのガンマ行列と言い、条件として γµγν+γνγµ= 2gµν, g00=−g11=−g22=−g33= 1, gµν= 0 ( µ,ν) (63a) γ0†=γ0, γi†=−γi, γ0γi†γ0=γi (63b) を充たす。 ψ≡ψ†γ0 (64) をψの共役 (adjoint) と呼ぶ。ディラック行列の性質 (63) を使えば、ψが式 i∂µψγµ + mψ≡ψ(iγµ ←∂µ+m) = 0 (65) を充たすことは容易に証明できる。(62) に左からψを掛け、(65) に右からψを掛けた量を相加えれば ∂µ(ψγµψ) = 0 (66) これはカレント保存則と見なせる。またψγµψがローレンツ・ベクトルの様に振る舞うことをも示している。実 際にψγµψがローレンツ・ベクトルであることも証明できる (証明略)。一般に、定数行列Γを間に挟む双 2 次型 式ψΓψがベクトルまたはテンソルのように変換する量であるとき、ψをスピノールと呼ぶ。スピノールはいわば ベクトルの平方根のような量であるとみなせよう。スピノール場を量子化することにより、半奇数スピンを持つ粒 子を表すことができる。 カイラリティ演算子 γ5≡ iγ0γ1γ2γ3=−iα1α2α3= [ −1 0 0 1 ] (67a) をカイラリティ演算子と呼ぶ。 演習問題 A.3. (γ5)2= 1, γ5γµ+γµγ5= 0 (68a) を示せ。 さらに ψL=1−γ 5 2 ψ= [ φL 0 ] , ψR=1 +γ 5 2 ψ= [ 0 φR ] (69) を定義すれば γ5ψL=−ψL, γ5ψR=ψR (70) を充たすので、ψL,Rはカイラリティ演算子の固有状態である。ψψ,ψγ5ψはローレンツ変換に際して、それぞれス カラー、疑スカラーのように振る舞う* 15) 。カイラリティはローレンツ変換で不変な量である (証明略)。 * 14)相対論でのベクトルは時間成分を加えて4成分とする。反変ベクトル Aµ= (A0; A)、共変ベクトル Aµ= (A0;−A) を定義すれば、ローレ ンツ不変なスカラー積は A· B = A0B0− A · B = AµBµ と書く慣例である。同じ指標が上下に現れたときは和をとるものと約束する (アインシュ タイン縮約)。 * 15)類似の量ψ†ψ=ψγ0ψは、スカラー量ではなく、ローレンツベクトルの第ゼロ成分であることに注意を喚起しておく。A.3
パリティ変換と荷電共役変換
ディラック行列の条件式 (63) は、変換γ→ SγS−1で変わらないから、条件を充たす行列の表示形式は多数ある。物 理観測量は、行列に対するディラックの条件 (63) のみにより表示に依存しないが、表示を明白に書いた方が計算 が容易であることが多い。 パウリ・ディラック行列 今までは、相対論的粒子すなわち|E|, p >> m を想定して議論を進めてきた。非相対論 的粒子 (p << m, E≃ m + p2/2m)を扱う場合は、ハミルトニアンの中のβを対角化する表示の方が、物理的な対 応が付けやすい。βを対角化する表示をパウリ・ディラック表示と言い、これまでの表示をワイル表示もしくはカ イラル表示と言う。変換行列をSと書き、表示に指標 D,W を付けて表すと ψD= SψW, S = √1 2 [ 1 1 −1 1 ] , γDµ= SγWµS−1 (71a) αD= [ 0 σσσ σσσ 0 ] , βD= [ 1 0 0 −1 ] , γ5D= [ 0 1 1 0 ] (71b) 歴史的にはパウリ・ディラック表示が先に導入された。ディラックは、相対論的方程式を導いた上で、非相対論的 近似を使い、電子の持つスピンや磁気能率を導いた。またディラック方程式にクーロンポテンシャルを入れた方 程式 i∂ψ ∂t = [ α·∇ i +βm− α r ] ψ (72) を解いて水素エネルギー準位の微細構造や超微細構造を再現すると共に、反粒子の存在をも予言したのである。 反粒子のパリティ 演習問題 A.4. ディラック方程式 (54) は、x→ −x, p → −p, ψ→βψの変換で不変であることを示せ。 すなわち、ディラック方程式のパリティ変換は、空間座標を反転すると共に、ψ→βψという演算を同時に行わな ければならない。多成分の状態に対しては、パリティ演算は成分の入れ替えをも考慮する必要があるということ である。パウリ・ディラック表示では、静止している粒子に対して H = mβ= m 0 0 0 0 m 0 0 0 0 −m 0 0 0 0 −m (73) であるから、ハミルトニアン H とパリティ演算子が比例関係にある。従って、ハミルトニアンの固有状態とパリ ティの固有状態が一致し、エネルギー正の粒子は正のパリティ、エネルギーが負の反粒子は負のパリティを持つ ことが判る。実際にはパリティ固有値には位相の不定性があるので、粒子と反粒子は相対的に逆のパリティを持 つというのが正しい言い方であるが、慣例として粒子のパリティを正にとる。 荷電共役変換 m=0の場合の二つの独立な方程式 (47) は、パリティ変換で入れ替わったが、実はもう一つ入れ替 える方法がある。(47) の左の式の複素共役を取り、左から−iσを掛けて iσ2σ∗i =−iσiσ2を使うと、 E(−iσ2φL) =−σσσ· (−iσ2φL) (74)すなわち、(−iσ2φL)は、φRと同じ方程式を充たす。同様にして +iσ2φRは、φLの方程式を充たす。この演算 φL→ (φL)c=φcR≡ −iσ2φ∗L, φR→ (φR)c=φcL≡ iσ2φ∗R (75) 4成分では ψ∗→ψc≡ [ 0 iσ2 −iσ2 0 ] ψ∗= iβα2ψ∗= iγ2ψ∗ = iγ2γ0ψT≡ CψT (76) を荷電共役変換 (C 変換=charge conjugation 変換) と呼び、粒子と反粒子を入れ替える演算となっている* 16) 。これ を簡単に見るには、運動量方向を z 軸に取り、ヘリシティ固有関数を (1, 0)T, (0, 1)Tとし、エネルギー正負の状態 を分けると φL(t) = a [ 1 0 ] e−i(−|E|)t+ b [ 0 1 ] e−iEt (77) 従って上の変換は、エネルギーの符号を変えると共に L と R を入れ替えることも判るであろう。エネルギーの符 号を変えることは、おおざっぱに言えば粒子と反粒子を変換することに対応する。より正確には粒子と反粒子は 電荷を持つとき、電荷により識別可能であり、粒子と反粒子を入れ替えると電荷も変わる。すなわち、C 変換とは 電磁相互作用をする粒子の方程式を、電荷が変わるように書き換える手続きと言える。電磁相互作用は、自由場 の方程式でエネルギー・運動量演算子を
p→ p − eA, E → E + eφ まとめて ∂µ→∂µ+ ieAµ Aµ= (A0,−A) (78)
に置き換えることにより得られるから、(47) に電磁相互作用を入れると (i∂t− eφ)φL,R=∓σσσ· (∇ i − eA ) φL,R (79) 上の式から電荷を変えた次の方程式を充たす [φL,R]cは、φL,Rの反粒子を表す場である。 (i∂t+ eφ)[φL,R]c=∓σσσ· (∇ i + eA ) [φL,R]c (80) 式 (79) の両辺の複素共役を取り、左から∓iσ2を掛けた式は、式 (80) を充たす。すなわち、φLが電荷 e を持つ左 巻き粒子を表すならば、[φL]c=φcR=−iσ2φ∗Lは電荷-e を持つ右巻き反粒子を表す。 マヨラナ粒子 L成分の反粒子を R 成分と同一視してみよう。 φR=−iσ2φ∗L, φL= iσ2φ∗R (81) と置いて (55) に入れると、 (E +σσσ· p)φL=−imLσ2φ∗L (82a) (E−σσσ· p)φR= imRσ2φ∗R (82b) となる。すなわち、4 成分有限質量の充たす連立方程式 (55) が、粒子と反粒子を同一視する事により、2 成分有限 質量の二つの式に分離されたことになる。φLとφRは、それぞれ独立な方程式を充たすので、質量が同じである 必要はなく、mLと mRとを区別して書いた。既知のニュートリノは左巻きであるので、式 (82a) を充たし (左巻き マヨラナ粒子)、(82b) を充たす粒子 (右巻きマヨラナ粒子) は存在しないか、もしくはあっても大きな質量を持ち、 未発見と考えることが可能であり、ニュートリノに右巻き成分がないことへの自然な解答を与える。 この方程式を充たす粒子は、L 成分の反粒子を R 成分と同一視するのであるから、粒子・反粒子の区別はなく、LR の区別があるのみである。つまり左巻きマヨラナ粒子を荷電共約変換すると右巻きの反粒子にならず単なる右巻 * 16)荷電共役変換により L と R も入れ替える。(75) 第 2 式の下付き指標はこの事実を反映させた表記である。φ LとφRとの変換式で符号を 変えたのは、2 回演算もしくは逆演算すれば元に戻るべきだからである。
き粒子になる。これは左巻きマヨラナ粒子の右巻き成分であり、右巻きマヨラナ粒子と混乱しないようにしよう。 従う方程式が違うため、便宜上質量 mLを持つ左巻き粒子、および質量 mRを持つ右巻き粒子という名前を付けた のである。パリティ演算を行っても LR が入れ替わることは既に述べた。質量がゼロの極限では、マヨラナ方程式 (82)は方程式 (47) に一致するから、ゼロ質量のマヨラナ粒子とワイル粒子は区別できない。 要約すると、電荷を持つ粒子はマヨラナ粒子ではあり得ないが、ニュートリノは電荷では粒子と反粒子とを識別 できないので、マヨラナ粒子である可能性がある。通常のスピン 1/2 の粒子は、粒子と反粒子、L と R の 4 成分 を持ち、ディラック方程式を充たすが、マヨラナ粒子は粒子・反粒子の区別が無く左巻きとその荷電変換粒子 (= 右巻き粒子) があるのみであり、2成分の方程式を充たす。そのかわり質量の異なる 2 成分左巻きマヨラナ粒子と 2成分右巻きマヨラナ粒子がある。逆に考えるとディラック粒子は質量の同じ二組のマヨラナ粒子 (φ1,φ2)と同等 である。この場合 (ψ,ψ†) ={φ1+ iφ2)/√2, (φ1− iφ2)/√2} は、互いに粒子・反粒子として区別ができるので、4 成分の自由度を持つ粒子となるのである。