在必要性が高い多倍長整数のビット数は高々数千ビット程度である. そこで本論文では, 筆算に基づく O(n 2 ) 時間の乗算を並列計算に適した積表と名付けたデータ構造を用いて GPU 上で高速に並列実行する手法を提案する.FFT 乗算とちがって, 提案手法では乗数と被乗数のビット数が異なる場合に長い

GPU による多倍長整数乗算の高速化手法の提案とその評価

北野 晃司

_†

藤本 典幸

_†

A Method for Multiple Precision Integer Multiplication on GPUs

KOJI

KITANO†

_and

_NORIYUKI

_FUJIMOTO†

†

Graduate School of Science, Osaka Prefecture University

1. はじめに

多倍長整数演算は，公開鍵暗号系で重要となる大 きい桁数の素数判定などに応用がある．多倍長演算 の中でも応用範囲の広い乗算に関する研究は多数 あり，Karatsuba 法[8]，Toom-Cook 法[20]，4-way 法[23]，5-way 法[23]，FFT を用いた Strassen の 乗算アルゴリズム（_{FFT 乗算）[17]などの手法が知} られている．これらの手法の時間計算量は，_{n ビッ} ト×_{n ビットの乗算の場合，それぞれ O(n}1.585_)，

O(n1.465_)，O(n1.404_)，O(n1.365_{)，O(n log n log log n)}

であるが，文献[23]で Zuras は，HP-9000/720 上 で C 言語とアセンブリ言語を用いたこれらの手法 の実装を比較し_{, 桁数が小さい場合はナイーブな} 筆算に基づく_O(n2_{)時間の乗算が最速であること，} 桁数が大きい場合は(37M ビット以上と極端に大き い場合であっても)，計算量的に有利な FFT 乗算よ りも，他のより単純な手法のどれもが高速であると 報告し，桁数が大きい場合でもFFT 乗算が必ずし も最速ではないと結論づけている_. 一方，近年，グラフィクス処理用プロセッサであ るGPU を汎用計算の高速化に用いる GPGPU に関 する研究が盛んであり，GPU を用いた多倍長整数 乗算の高速化に関する研究もいくつか報告されて いる（既存研究の概要については_{2 章参照）．これ} らの既存研究の中で最も高速なものは文献_[3]の FFT 乗算の GPU による高速化である．この手法は 多倍長整数を2393216_{進数で表現し，2}393216_進数の1 桁×1 桁を FFT を用いて行なうサブルーチンを Karatsuba 法から呼び出しながら多倍長整数の乗 算を行うものである．この手法はビット数が同一， かつ，393216 の倍数である多倍長整数同士の乗算 は高速に行えるが，乗数と被乗数のビット数が異な る場合は短い方の数のビット数を長い方の数のビ ット数に合わせ，かつ，393216 の倍数に切り上げ て乗算を行うことになるため，乗数と被乗数のビッ ト数が同一かつ_{393216 の倍数でない場合は効率が} 著しく落ちる_{[3]．また，暗号計算などの分野で現} 本論文では，筆算に基づく多倍長整数乗算を並列計算に適した積表と名付けたデータ構造を用い てGPU 上で高速に並列実行する手法を提案する．提案手法を CUDA を用いて実装し，2.93GHz Intel Core i3 CPU と NVIDIA GeForce GTX480 GPU を用いて評価したところ，CPU 用シング ルスレッド多倍長演算ライブラリのNTL と GMP に比べてそれぞれ最大 71.4 倍，12.8 倍の速度 向上率を得た．

This paper addresses multiple precision integer multiplication on GPUs. In this paper, we propose a novel data-structure named a ‘product digit table’ and present a GPU algorithm to perform the multiplication with the product table. Experimental results on 2.93GHz Intel Core i3 CPU and NVIDIA GeForce GTX480 GPU show that the proposed GPU algorithm runs maximum 71.4 times and 12.8 times faster than NTL library and GMP library respectively, two of common libraries for single thread multiple precision arithmetic on CPUs.

在必要性が高い多倍長整数のビット数は高々数千 ビット程度である． そこで本論文では，筆算に基づくO(n2_{)時間の乗} 算を並列計算に適した積表と名付けたデータ構造 を用いて_{GPU 上で高速に並列実行する手法を提案} する．FFT 乗算とちがって，提案手法では乗数と 被乗数のビット数が異なる場合に長い方のビット 数に切り上げて計算を行う必要はない．また多倍長 整数を232_{進数で表現するため，数千ビット程度の} 多倍長整数を扱う場合でも無駄は比較的少ない． 以降の論文の構成は次の通りである．第 _{2 章で} GPU を用いた既存アルゴリズムについて簡単に説 明する．第3 章で提案手法の詳細を示す．第 4 章で 評価実験について述べる．第5 章でまとめと今後の 課題について述べる．スペースの制限のため，本論 文では_{GPU のアーキテクチャおよびプログラミン} グの概要については述べない．これらに不慣れな読 者は文献[1,5,9,12,14,15,16]を参照されたい． 2. 関連研究 CUDA を用いた多倍長整数乗算に関する既存研 究は我々の知る限り以下のみである． 文献[3]は，同じ著者らによる文献[2]の結果をさ らに改善して，_{Karatsuba 法で分割した部分問題に} FFT を用いた Strassen の乗算アルゴリズムを適用 する手法を CUDA 上に実装し，2.93GHz Intel Core i7 870 の 1 コアと NVIDIA GeForce GTX480 を用いた実験で255Kbit～24.512Mbit の整数乗算 で最大4.29 倍の速度向上率を報告している．

文献_{[7]は，3GHz Intel Core2 Duo E8400 と} NVIDIA GeForce 9800GX2 を用いた 160～384bit 整数の乗算で，_{SSE2 命令を用いる CPU 用ライブ} ラリmpFq [6]に比べて 2.9～0.8 倍の速度向上率を 報告している． 文献_{[22]は，多数の並列実行可能な多倍長四則演} 算があることを前提として，各々の多倍長四則演算 を_{CUDA の１スレッドで実行する多倍長演算ライ} ブラリを提案し，2.80GHz Intel Core i7 の 1 コア 上で実行したCPU 用ライブラリ GNU MP [4]に比 べて NVIDIA GeForce GTX280 を用いた場合， 2048bit×2048bit の整数乗算 30720 個でおよそ 4 倍程度の速度向上率を報告している． 文献_{[19]は，n ワードの多倍長整数をモジュラー} 表現に変換することにより，変換と復元にはO(n2₎ 時間かかるが乗算自体はO(n)時間で実行できるモ 図 1 筆算と積表の対応例 図 2 a 桁×b 桁の筆算に対応する積表の形状 ジュラー算法[10]を CUDA で実装している． 文献[21]は，Karatsuba 法を用いた 1024bit× 1024bit の多倍長乗算の CUDA 実装の最適化につ いて報告している． 文献_{[13]は，FFT を用いた多倍長乗算の CUDA} 実装で_{10 倍の速度向上率を報告しているが，用い} たCPU と GPU についての記載はない． 3. 提案手法 3.1 積表 整数の積は図 _{1 左のような筆算により求められ} る．この例では基数を_{10 としている．この筆算を} 図1 右のような表を用いて計算することを考える． 図中の表の要素1 つは被乗数の 1 桁と乗数の 1 桁の 積を基数で割った商もしくは剰余であり，各要素は 独立に計算できる．例えば表で赤く塗られた要素 「_{2」は 8×4 を基数 10 で割った剰余であり，緑色} に塗られた要素「_{4」は 5×9 を基数 10 で割った商} である．表の各列の和を求めて桁上げ処理を行うと 積が求まる．このような表を積表と呼ぶことにする． 一般の場合の積表の形状を図2 に示す．図 2 は，基 数_{BASE で a 桁の多倍長整数 A と b 桁の多倍長整} 数_{B (ただし a≧b)の積に対応する積表の形状であ} る．赤・黄・緑色の要素に値が入っている．図_{2 か} らもわかる通り，積表は以下の特徴を持つ．

図 3 積表構成アルゴリズム ・ 赤と緑の部分は列数が等しく，その数は _B の桁数に等しい．またこれらの行数は図_{2 の} ように増減し，その変化量は 1 列ごとに 2 行ずつである． ・ 黄の部分の列数はA と B の桁数の差になり， 行数はB の桁数のちょうど 2 倍となる． 一般の場合の積表を求めるアルゴリズムを図 ₃ に示す．このアルゴリズムは_{BASE 進数 a 桁およ} び_{b 桁の多倍長整数 A，B の各桁の値がそれぞれ配} 列A[0..a-1]および B[0..b-1]に格納されている(A[0] およびB[0]が最下位桁)とき，A×B の積表を 2 次 元配列_{T に求める．値が代入されない T の要素は} don’t care である．A が 5 桁，B が 3 桁の場合に図 3 のアルゴリズムが構成する積表の例を図 4 に示す． 3.2 データ構造 積表の_{1 要素の計算には A の 1 桁と B の 1 桁の} 積の計算が必要となる．これを効率的に行えるよう BASE＝232_{と定める．このように定めると1 桁×1} 桁の積の演算結果が64bit に収まるため，GPU で unsigned long long 型を用いてその商計算を 32 ビ ット右シフトによりでき，なおかつその剰余計算は 1 桁×1 桁を unsigned int 型として求めることでで きる．そのため本実装では積表の要素を求める際に 商計算はビット演算により行い，剰余計算は明示的 には行っていない． 提案手法は，基本的には，積表の各列に1 スレッ ドを割り当て，列ごとの総和計算と桁の繰り上がり 処理を積表の列数のスレッドを用いて並列に計算 する．しかし図2 の積表をそのまま用いると，赤と 緑の部分においてスレッド間の計算およびメモリ 図_{4 図 3 のアルゴリズムによる積表の構成例} （_{A が 5 桁，B が 3 桁の場合）} 図_{5 負荷バランスを考慮した積表の再構成} アクセス量の負荷バランスが悪くなる．そこで積表 を図2 のような(a+b)×(2b)の 2 次元配列で表現す るのではなく，図_{5 のような a×(2b)の 2 次元配列} で表現する．以降ではこの表現における黄色の長方 形を長方形_{Y，赤色の三角形と緑色の三角形が合わ} さった長方形を長方形RG と呼ぶ．5 桁×3 桁の場 合の長方形RG の具体的な構成は図 6 のようになる． ただし，赤，緑それぞれの中では要素の上下の順番 は結果に関係無いので，これを次に述べる性質を満 たすように並べ替えている．図_{5 の長方形 RG の計} 算領域は以下の特徴を持つ． ・ 横の長さはb，縦の長さは 2b である． ・ 右からα列目における2α行目と 2α+1行 目の間に赤と緑の部分を分ける境界線が 存在する． ・ β 行 目 で は 全 列 に お い て _{B の 添 字} ⌊β/2 ⌋の要素が参照され，α列目では A の 添字αの要素の参照から始まり下に行く につれて 2 行間隔で参照する添字が１減 る(0 の次は最後尾になる)．

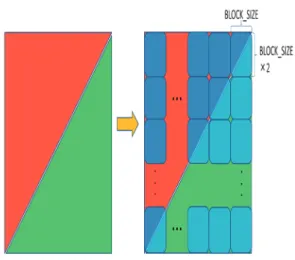
図 6 負荷バランスを考慮して再構成した 積表の例（5 桁の多倍長整数 A と 3 桁の多倍長整数 B の場合） 3.3 アルゴリズム 図 7 の よ う に 長 方 形 RG を 1 つ が 横 (BLOCK_SIZE)要素×縦(BLOCK_SIZE×2)要素 と な る 水 色 の 領 域 に 区 分 け す る ． こ こ で BLOCK_SIZE とは，CUDA での実装において 1 スレッドブロック（以降，ブロック）が持つスレッ ド数のことである．そして，1 ブロックにこの水色 の領域1 つの列の総和を求めさせる． この区分けした水色の領域は赤のみを含む・緑の みを含む・境界を含むという_{3 種類に分けられる．} 以降ではこれらの領域をそれぞれ領域_{R，領域 G，} 領域RG と呼ぶ．領域 RG では条件分岐が必要とな り実行効率が落ちるが，領域RG の列総和計算の計 算量は全領域の計算量から見れば小さいため最適 化されたプログラムではほとんど性能に影響しな くなる．また，領域_{R または領域 G ではブロック} の並列性は計算の最後まで保たれる． 水色の領域1つを1ブロックに割り当てることで， 領 域 内 の 列 総 和 計 算 に 必 要 な A の 要 素 が BLOCK_SIZE×2 要素，B の要素が BLOCK_SIZE 要素で済む．これにより_{1 つの領域内の計算では，} 一度これらの計算に必要な要素を共有メモリに載 せ，各スレッドが共有メモリ上の値のみを使い列総 和計算を行える．また，図6 で見たようにこのとき 参照するA や B の要素は配列内で連続したもので あるため，共有メモリに載せる際のデバイスメモリ へのアクセスはコアレスに行える． 図7 積表計算に対するスレッドブロックの 割当方法 3.4 実装の詳細 まず長方形 RG に対し具体的にブロックが行う 計算がどのようなものかを示す．担当する領域が領 域R か領域 G か，もしくは領域 RG かによらず， まずブロックが行うことは計算に必要なデバイス メモリの要素を共有メモリに載せることである．そ してブロック内の各スレッドはその値を使い，自分 が計算すべき列col における領域内での総和を求め る．このとき領域RG を担当するブロック内の各ス レッドは赤と緑の部分の総和を個別に求めておく． その後，赤の部分の総和は答えを格納する配列の添 字_{col へ，緑の部分の総和を添字 col+a へとそれぞ} れ足し込む．ここでa は A の桁数である．ここま でが長方形RG に対する計算となる．この計算を長 方 形 RG を す べ て 計 算 で き る ブ ロ ッ ク 数 =⌈b/BLOCK_SIZE⌉ × ⌈b/BLOCK_SIZE⌉で 計 算 す る．このとき _{x=blockIdx.x，y=blockIdx.y とする} と，x>y は領域 R，x=y は領域 RG，x<y は領域 G を示す指標となる．長方形RG に対するカーネル関 数の具体的なコードを図8 に示す．関数の引数は多 倍長整数を表す整数型配列 A と B，解を格納する ための整数型配列_{C，そして A の桁数 Alen と B の} 桁数_{Blen の計 5 つである．関数内の変数 Alen2 は} 条件分岐を減らすためのもので，領域R なら 0，領 域G なら Alen となる．

図_{8 長方形 RG に対するカーネル関数} 次に長方形 Y に対するカーネル関数について述 べる．この関数は長方形RG に対する関数と比べ， 参照する_{A や B の配列の添字や，総和を足し込む} 配列_{C の添字が異なるだけでほとんど同じである．} ブロック数は ⌈(a-b)/BLOCK_SIZE⌉×⌈b/BLOCK_SIZE⌉ である．具体的なコードを図9 に示す． ここまでの関数により解を格納する配列 _{C へと} 適切な総和を足し込んできたが，計算する桁数が十 分に多い時，配列 _{C はこの段階でほぼすべての要} 素が基数 232_{を超えていると言ってよい．これを，} すべての要素が基数より小さくなるように桁の繰 り上げ処理をする．それを効率的に行うため２つの 処理に分ける．１つは配列 C の要素で基数を超え ているものについて，超えた値を_{C2 という配列に} 覚えさせ，C のその要素を基数で割った剰余を新た 図9 長方形 Y に対するカーネル関数 図_{10 配列 C から配列 C2 を求めるカーネル関数} な要素とする処理である．そしてもう１つは多倍長 整数の和としてのC+C2 を最終的な結果 C として 求める処理である．１つ目の処理を行う関数は ⌈(a+b)/BLOCK_SIZE⌉ブロックで実行され，図 10 に示すようにシンプルなものである．引数の _{1 つ} Clen は C の桁数で，a 桁×b 桁では(どちらかが 0 である場合を除き)結果は a+b-1 桁または a+b 桁と なるので，今回のアルゴリズムでは配列 C を大き さa+b で確保しておき，予め Clen=a+b-1 としてい る．結果が_{a+b 桁になるなら最後に Clen に 1 を足} す．

図11 多倍長整数の和を求めるアルゴリズム ２つ目の処理，多倍長整数の和を求めるアルゴリ ズムについて説明する．多倍長整数の和を求める過 程で注意しなければならないのは，桁の繰り上がり の伝播である．最悪の場合，すなわち伝播が配列の 頭から最後まで続く場合には強い遂次性が生まれ， 1 スレッドが配列の頭から最後まで処理するのと 同等の計算時間がかかってしまう．今回実装するア ルゴリズムはハードウェアの全加算器の実装方法 の一つであるcarry skip adder[11]と本質的には同 じであり，これをCUDA を用いて実装した．ただ し，今回は伝播が少ない場合にほとんど無駄なく高 速に計算を行えるよう，実装を次に述べるように工 夫した．これは基数を232_{としていることで，そも} そも伝播 1 つが起こる可能性すら低いことを利用 している．図11 がこのアルゴリズムを図示したも ので，ここでは簡単のために基数を10 としている． まず初めに，足し合わせる_{2 つの多倍長整数から} 図のように繰り上がり情報を格納する配列を生成 する．繰り上がり情報とは，それぞれの要素の和が 基数を超えていれば1，基数-1（図では 9）であれ ば2，いずれでもなければ 0 のことである．次に， 繰り上がり情報が 2 である要素について，その 1 つ右が繰り上がりを示す_{1 なら 2 を 1 に変え，0 な} ら_{2 を 0 に変える．2 が連続している部分がある際} には，図のようにその部分の右端に処理をした後に 次々と左へ処理を繰り返していく．そして，2 つの 多倍長整数の要素同士と，対応する繰り上がり情報 の計３要素の和を求めて解を格納する配列へと格 納する．最後に，その配列のすべての要素を基数で 図12 多倍長整数の和を計算する 3 つのカーネル 関数 割った剰余にすればそれが和を表す配列となる．こ の処理過程はブロック間の同期が必要なため，3 つ の関数に分けて実現する．そのコードを図12 に示 す． 4. 評価実験

CPU は 2.93GHz Intel Core i3（1 コアのみ使用）， GPU は NVIDIA GeForce GTX480 を用いた．OS とコンパイラは原則64bit Windows7 Professional SP1 と Visual Studio 2008 Professional を用いた が，GMP は Windows を公式にはサポートしてい な い た め ，_{GMP プログラムのみ 64bit Linux} (ubuntu 11.04)と g++ 4.5.2 を用いて評価した． CUDA は Ver 3.2，ディスプレイドライバは Ver 285.62 を用いた． 共有メモリは 48KB 用いた．用 いた NTL と GMP のバージョンはそれぞれ 5.5.2 と5.0.4 である．NTL は SSE 命令などの SIMD 演 算命令を用いないが，_{GMP は SSE2 命令および} MMX 命令を用いる．

表_{1 提案手法を用いた場合の GPU による多倍長} 整数乗算A×B の実行時間（msec） まずは，_{CPU による既存の多倍長演算ライブラ} リ_{NTL[18]との比較実験の結果を示す．多倍長整数} の大きさは_{1024byte～32768byte の間における 6} 種類を対象とし，提案手法とNTL よる 36 通りの 乗算の実行時間を表1 と表 2 にまとめた．今回作成 した関数はすべての場合において_{NTL の速度を上} 回る結果を示した．具体的な速度向上率は表_{3 の通} りで，最大で_{70 倍を超える速度向上が見られた．} 次に，一般にNTL よりも高速として知られる多 倍長演算ライブラリ GMP[4]との比較を行った． GMP による多倍長整数乗算の実行時間を表 4 にま とめ，また，NTL と同様に速度向上率を表 5 にま とめた．_{NTL に対しての結果には及ばないものの，} 最大で_{10 倍を超える速度向上が見られた．} 最後に， GPU を用いた多倍長整数乗算の既存研 究の中で最も高速な，文献_{[3]の FFT 乗算を GPU} により高速化したものとの速度比較を行なった．文 献_{[3]では 255Kbit×255Kbit を GTX 480 で実行し} た結果は0.207 ミリ秒であると報告されている．ほ ぼ同条件の乗算の提案アルゴリズムによる実行時 間を測定したところ，文献[3]の FFT 乗算は提案ア ルゴリズムより約_{3 倍速いことがわかった．しかし} これは 255Kbit という今回我々が対象としている 多倍長整数の大きさの中でも極めて大きいものに 対する結果である．また_{1 章で述べた通り，彼らの} 実装は383Kbit の FFT に基づくため，乗数・被乗 数が _{383Kbit よりも小さい場合やそれらの大きさ} が異なる場合でも，383Kbit×383Kbit の計算によ り積を求めることになる．これに対して，我々のア ルゴリズムでは表1 で示した通り，乗数と被乗数の 両方，もしくはそれらの一方の大きさが小さくなる と実行時間は短くなる．例えば32768byte 同士の 乗算に対し，32768byte と 1024byte の乗算の実行 時間は約13 倍速い． 表2 NTL ライブラリを用いた場合の CPU による 多倍長整数乗算A×B の実行時間（msec） 表3 提案手法の NTL に対する速度向上率 表_{4 GMPを用いた場合の CPUによる多倍長整数} 乗算A×B の実行時間（msec） 表_{5 提案手法の GMP に対する速度向上率}

5. まとめ 積表というデータ構造を提案し，これに基づいて 多倍長整数乗算をGPU を用いて高速に実行するア ルゴリズムを提案した．提案アルゴリズムは筆算ア ルゴリズムをベースとしているため，同一ビット数 の多倍長整数の乗算ではFFT 乗算に劣るが，2 つ の多倍長整数のビット数が異なり，かつ，それらの ビット数が極端に大きくない場合は_{FFT 乗算より} も優れていることがわかった． 今後の課題としては，実装のさらなる最適化や， 公開鍵暗号系など実際の問題を想定した数千ビッ トの乗算に対してのより効率的なアルゴリズムの 実装などが挙げられる． 参 考 文 献 [1] 青木尊之, 額田彰, “はじめての CUDA プログラミン グ,” 工学社, 2009.

[2] Emmart, N. and Weems, C., “High Precision Integer Addition, Subtraction and Multiplication with a Graphics Processing Unit,” Parallel Processing Letters, Vol.20, No.4, pp.293-306, 2010.

[3] Emmart, N. and Weems, C., “High Precision Integer Multiplication with a GPU,” IEEE Int'l Parallel & Distributed Processing Symposium (IPDPS), pp.1781-1787 , May 2011.

[4] Free Software Foundation, “The GNU Multiple Precision Arithmetic Library, ”, http://gmplib.org/ , 2011.

[5] Garland, M. and Kirk, D. B., “Understanding Throughput-Oriented Architectures,” Communications of the ACM, Vol.53, No.11, pp.58-66, 2010.

[6] Gaudry, P. and Thomó, E., “The mpFq Library and Implementing Curve-based Key Exchanges,” Software Performance Enhancement for Encryption and Decryption Workshop, pp.49–64, 2007.

[7] Giorgi, P., Izard, T., and Tisserand, A., “Comparison of Modular Arithmetic Algorithms on GPUs,” Int'l Conf. on Parallel Computing (ParCo), http://hal-lirmm.ccsd.cnrs.fr/docs/00/43/06/89/PDF/artic le-parco09.pdf , Sept. 2009.

[8] Karatsuba, A. and Ofman, Y., “Multiplication of Multidigit Numbers on Automata,” Doklady Akademii Nauk SSSR, Vol.145, No.2, pp.293-294, 1962. (in Russian). English translation in Soviet Physics-Doklady, Vol.7, pp.595-596, 1963.

[9] Kirk, D. B. and Hwu, W. W., “Programming Massively Parallel Processors: A Hands-on Approach,” Morgan Kaufmann, 2010.

[10] Knuth, D. E., “The Art of Computer Programming,” Vol.2, Seminumerical Algorithms, 3rd _Edition,

Addison-Wesley, 1997.

[11] Lehman, M. and Burla, N., “Skip Techniques for

High-Speed Carry Propagation in Binary Arithmetic Units”. IRE Trans. Elec. Comput., Vol.EC-10, pp.691-698, 1961.

[12] Lindholm, E., Nickolls, J., Oberman, S., and Montrym, J., “NVIDIA Tesla: A Unified Graphics and Computing Architecture,” IEEE Micro, Vol.28, No.2, pp.39-55, 2008.

[13] Liu, H. J. and Tong, C., “GMP Implementation on CUDA : A Backward Compatible Design with Performance Tuning,” http://individual.utoronto.ca/haojunliu/courses/ECE1724 _Report.pdf

[14] NVIDIA, “CUDA Programming Guide Version 4.0.,” http://www.nvidia.com/object/cuda_develop.html , 2011. [15] NVIDIA, “CUDA Best Practice Guide 4.0. ,” http://www.nvidia.com/object/cuda_develop.html , 2011.

[16] Sanders, J. and Kandrot, E., “CUDA by Example: An Introduction to General-Purpose GPU Programming,” Addison-Wesley Professional, 2010.

[17] Schönhage, A. and Strassen, V., “Schnelle Multiplikation grosser Zahlen,” Computing, Vol.7, pp.281-292, 1971. [18] Shoup, V., “NTL: A Library for doing Number Theory,”

http://www.shoup.net/ntl/ , 2009.

[19] 田中雄大，村尾裕一，“GPU を用いた多倍長整数演 算 法 の 設 計 ，” 情 報 処 理 学 会 研 究 報 告 ， Vol.2010-HPC-124，No.2，pp.1-7，Feb. 2010. [20] Toom, A. L., “The Complexity of a Scheme of

Functional Elements Realizing the Multiplication of Integers,” Soviet Math., Vol. 3, pp.714-716, 1963. [21] Zhao, K., “Implementation of Multiple-precision

Modular Multiplication on GPU”, http://www.comp.hkbu.edu.hk/~pgday/2009/10th_paper s/kzhao.pdf , 2009.

[22] Zhao, K. and Chu, X., “GPUMP: A Multiple-Precision Integer Library for GPUs,” IEEE Int'l Conf. on Computer and Information Technology (CIT), pp.1164-1168, June 2010.

[23] Zuras, D., “More on Squaring and Multiplying Large Integer,” IEEE Trans. Computers, Vol.43, No 8, pp.899-908, Aug. 1994.