アルミ合金板の耐荷力に関する実験的研究-香川大学学術情報リポジトリ

アルミ合金板の耐荷力に関する実験的研究

宵 和 彦 Ⅰま え が き 本研究は既報「アルミ合金桁の終局強度に関する研究」（1，2）の−・環として行ったものである、すなわち大型構造物で は桁断面は薄肉平板要素で構成され，その強度を評価する場合，結局り．ェ．ブヤフランジ板の座屈問題に帰することが 多い．板の座屈に関する研究は従来より少くないが，その実験的資料については鋼材でも意外と少く，アルミ合金材 に至っては我国では現在皆無に近いと思われるい 著者はアルミ合金材を大型構造物に積極的に使用するための基礎資 料を得ることを目的として，構造用アルミ合金A5083の板をとらえ，4辺を単純支持しこれに−・軸の面内等分布圧 縮荷重を作用させ，結果生ずる弾性域及び非弾性域での座屈強度と，座屈後の挙動並びにその終局強度に注目して考 察を加えた、また合せて鋼材SS41との比較を試みたので，これらの結果をまとめて報告する．． ⅠⅠ理 論 強 度 1．板の座屈強度 1）弾性領域 面内に一・方向の等分布圧縮荷重を受ける矩形板の座屈強度は，板が荷重辺に沿って単純支持されるとき，GいH BIyan（8）の次式 か（妥・2蒜＋穿）芦−−P笛 ここで， ／ノ＝ 戯＄ I‥ごミ E，リ：弾性係数，ポアソン比，と：板厚 ひ：坂中立面の微小たわみ P：板辺単位長当りの圧縮荷重 を満足・す−る固有伐として次の如く表わされる。 （1） がガ

小

（2） ♂。γ＝ゐ・ 12（1−巧 Tablcl．Minimum Values of k

Restraint Condition l a／b k

ここで，烏：板座屈係数 あ／才：幅膵比 板が荷重に平行な側辺で，i）単純支持（4〉（4辺単純支持），ii）固定支持（4）（2辺単純支持，2辺固定支持）されると き，板座屈係数kは縦横比a／bの函数として表わされ，a／b＝1のときのkの最小値はTablelの値となる． 2）非弾牲領域 非弾性座屈強度が（2）式で与えられる強度曲線に，♂。γ＝♂pで接線をなすような直線的変化をなすものと仮定する と，♂。γ＝グpに対応する幅厚比スβは， スβ＝ ∈＝げp／げy

βた＝て一

（3） ここで， α。γ＝♂yに対応する幅膵比スAは， ん＝ ・ 従ってAB区間（スA≦ス≦スβ）の非弾性座屈強度は次式で表わされる． q汀＝［3ト2挿絵・封αy A）A50＄3の場合 a）ATPL4（Table8参照） TablelO（t＝4mm）から， ぞ＝ヱ孔＝0．72 ♂y かた＝て終「＝688肋 ノ盲；■＿0．0474 〟）庵 Jゐ これらを（5）式に代人すると， ♂eγ＝3333−89い3・ 枝盛屈係数ゐに対しTablelの値を用いると，板の座屈強度は， i） 4辺単純支持のとき グcγ＝3333一仏69・

スβ・＝50

ん＝・＝40

ii）2辺単純支持，2辺固定支持のとき， αcγ＝3333−32い23− （4） （5） （6） （7） （8）

スβ＝69，ん＝56 （7），（8）式を図示したものがFig、1であるい −一 ム／王 Fig．1．げ。γVS小招（ATPL外 b）ATPL6 TablelO（t＝6mm）から， ∈＝0．71 ノ♂y＿0．0470 Jβた イゐ 故に（5）式から ￠”＝3189−84・1・ i）4辺単純支持のとき， ♂eヶ＝3189−42・10・ スβ＝50，ん＝40 ii）2辺単純支持，2辺固定支持のとき， ♂け＝3189一犯36・ スβ＝70，ん＝56 （10），（11）式を図示したものがFig2である．また（2）式を非弾性領域まで拡張したFLBleich（5）の次式， 苦＝彪・霜雪町（‡）2 ここで， （9） （10） （11） （12）

（13） ＝ 丁￣ （♂y−♂p）♂p を用V）ると，TablelO，（13）式から次表を得る… Tablc2。DeterminationofCriticalStressq。 げ。（Kg／cm2） で ♂eγ／J㌻（Kg／cm2） 1064 l．000 1064 1368 O 383 0−120 4205 1460 0．117 4269 E＝7、50×105kg／cm2，ン＝03，み／f＝35のとき（12）式の右辺は， i）4辺単純支持のとき，右辺＝2211kg／cm2＞げp ii）2辺単純支持，2辺固定支持のとき，右辺＝4251kg／cm2＞αp 従ってTable2からi）のとき 6。r＝1368kg／cm2，ii）のときq。γ＝1460kg／cm2 となるい これらの補正座屈強庶 （♂欝di）をFig．2にプロットしてある． ▲ 〉7 10

）0 ▲ ‡ ￣￣￣「 n 軌 ふ再 四 l 柏 Eq（10 症（11） u 9 0 「丁 口 u 司 H −一一一，一1 山 口 ＼ ＼ u Ⅰ −・−ト 0 0 t 〝＿＿】＿‡．▲．＿ J l ヽ ヽ ＼ ＼ ＼ ユ ＼ ＼ 0 “】岬l−￣ l 0 Ⅰ 】 ▲：ふ」‡㍗ 0

0 20 3540 6 0 80 100 12

0 0 0 642 ︵㌔U＼叫ゴト。bl ＋＼ム／∼ fig・2グ。γVS・坤（ATf■L6） c）ATPL9 TablelO（t＝9mm）から， ぞ＝0い75

J石￣＿0．0466

〟）克 イゐ 故に（5）式から

♂eγ＝3202一弘14 i）4辺単純支持のとき， ♂eγ＝3202−43小07・ ス月＝50，ん＝41 ii）2辺単純支持，2辺固定支持のとき， ♂￠ア＝3202−31l06 スβ＝69，ん＝57 （15），（16）式を図示したものがFig．3であるい またここでゐ〃＝16い7であるから（12）式の右辺は， i）4辺単純支持のとき，右辺＝9415kg／cm2＞♂p ii）2辺単純支持，2辺固定支持のとき，右辺＝18099kg／cm2＞♂p 従って（13）式を用いるとTablelOから次表を得る． Table3．DetcrminationofCriticalStress6c （15） （16） げ。（Kg／cm2） 丁 ♂。γ／J㌻（Kg／cm2） 1リ000 1062 0．004 23311 この場合，i）のとき♂。γ＝1417kg／cm2，ii）のときげ…＝1421kg／cm2とをる．これらの座屈強度をFig・3にプロッ トしてある． 120 げ♪＝106 100 80 0 0 0 642 ︵NluU＼如ぷ︶“。bl ＋ ＼ム／f Figい3．．￠打VS．研（ATPL町

B）SS41の場合 a）STPL4（Table8参照） Tablell（f＝4mm）から， ぞ＝0．74 石㌔＿0．0407 Jかた イゐ 故に（5）式から げeγ＝7100−165・7 i）4辺単純支持のとき， αeγ＝710…2・86・ スβ＝57，ん＝47 ii）2辺単純支持，2辺固定支持のとき， ♂￠γ＝7100−59・76− スβ＝79，ん＝65 （18），（19）式を図示したものがFig，4である．．またこの場合あ〃＝70であるから（12）式の右辺は， i）4辺単純支持のとき，右辺＝1577kg／cm2く♂p ii）2辺単純支持，2辺固定支持のとき，右辺＝3032kg／cm2＞♂p 従ってii）の場合のみ補正すればよいル Tablell，（13）式から次表を得るから， Table4… DeterminationofCriticalStresso・。 （17） （18） ‥（19） q。（Kg／cm2） T O。，ノ√（Kg／cm2） 2376 1…000 2376 2637 0リ757 3030 2638 0“756 3033 ii）のときα￠γ＝2638kg／cm2となる巾 Fig…4にこの借をプロットしてある． b）STPL6 Tablell（t＝6mm）から， ∈＝0小65 J♂y＿0．0420 〟）た イ烏 故に（5）式から ♂￠γ＝6135−138・49＝ i）4辺単純支持のとき， ♂eγ＝6135−69・25・ （20） （21）

34 32 ♂，＝319 30 400 6 15テ「 ▲；㌶認’ 00 8 6 2 2 0 00 211 ︵㌔U＼ゼてざ1−−1 ＼ム／￡ Figい4u ♂。γVS‖研（STpL4）． ん＝59，一㍍＝43 ii）2辺単純支持，2辺固定支持のとき， αeγ＝6135−491・94 スβ＝82，ん＝60 （21），（22）式を図示したものがFig．5である．またみ／f＝35であるから（12）式の右辺は， i）4辺単純支持のとき，右辺＝5837kg／cm2＞♂p ii）2辺単純支持，2辺固定支持のとき，右辺＝11223kg／cm2＞♂♪ Tablell，（13）式から次表を得るから， Table5．DeterminationofCIiticalStressor。 （22） ♂￠（Kg／cm2） T ♂￠γ／、信（Kg／cm2） 2052 1…000 2052 2951 0…256 5832 2952 0い255 5846 3090 0．077 11115 3091 0い076 11240 i）のときOr。，＝2951kg／cm2，ii）のときqc，＝3091kg／cm2とをる．Fig．5にこれらの値をプロットしてある．

3400 3200 ♂一γ＝3146 3000 2800 2600 2400 2200 】 〟 2 1 1

㌃看＼孝吉1

O O O 0 0 ∧U O OO 6 100 120 0 20 3540 60 80 −・・・・−・・・一んJ Figい5．q。γVS小b／i（STPL6）小 c）STPL9 Tablell（よ＝9mm）から， ぞ＝0．．62 ノげy＿0．0391 〟）た イ点 故に（5）式から ♂eグ＝5372−110い2 i） 4辺単純支持のとき， ♂eγ＝5372堀13 ん＝65，ん＝45 ii）2辺単純支持，2辺固定支持のとき， ♂eγ＝5372−39・7 スβ＝90，ん＝62 （24），（25）式を図示したものがFi各．6である．またゐ〃＝16．7であるから（12）式の右辺は， i）4辺単純支持のとき，右辺＝27065kg／em2＞♂p ii）2辺単純支持，2辺固定支持のとき，右辺＝52033kg／cm2＞qp Tablell，（13）式から次表を得るから， （23） （24） （25）

Table6DeterminationofCriticalStressq。 0。（Kg／cm2） で 0。γ／斤（Kg／cm2） 1000 1L792 0い012 26667 0．010 28525 2885 0‖004 43712 2886 0．003 53444 i）のとき♂。ケ＝2880kg／cm2，ii）のとき♂。γニ2886kg／cm2となるいFig・6にこれらの倍をプロットしてある． 3 3 打、丁■2 ： 2 222 ㌃∈U＼澄︶ヒビバーーーーー一・ ＋＼ ム／‡ F短．6い ♂。γVS−帥（STPL9） 2．板の終局強度 座屈発生後，板の支持緑（荷重に平行な側辺）の近傍ではたわみが拘束され，座屈後も板の耐力は上昇する KaIman（8）により提唱された有効幅の仮定を用いると，板の終局強度（平均応力度）は次式で表わされる． 如 α…＝怒＝地ユ＝告げy ここで，‰：有効幅 板が4辺単純支持の場合，有効幅としてKま‡man（8）の次式 ＝∴＿ とWinteI（7）の次式 （26） （27）

（28） 告＝ノ吾［ト01・25J吾］ を用いると，各校の終局強度は次表の如くになる〃 Table7。TheoreticalUltimateStrengthofTestPlates ⅠⅠⅠ供託体及び実験方法 1．試 験 板 a）分 類 計13体で便宜上次表の如く分類した．我荷型式を合せ示す．

Table8”Classi丘cations ofTest Plates

Table9… Dimension Ratios of Test Plates．

Test Plate l a／b b／i

ATPL4−1，2 STPL4−1，2，3 1 70 ATPL6−1，2 STPL6−1，2 1 35 ATPL9−1，2 STPL9−1，2 1 161．7 where，b／t：SlendeIneSSratio

b）材 質 −・般構造用アルミ合金材A5083（AトMg系2元合金，非熱処理）と，一腰構造用圧延鋼材SS41である。その化 学成分については既報（1）を参照されたい‖ またその機械的性質は，TablelO，Tablellに示す如ぐである‖ C）寸 法 正方形板でその寸法をFigh9に示す．寸法比はTable9の如くである． 2．実験方法 a）載荷方法 200ton圧縮試験機を使用した… 仮の4辺を単純支持とするためFig。7，Fig8に示す如き支持装置（材質SS41） を考案し，板の寸法に応じて支持間隔を調節出来るようにした小職荷に際しては試験枚に端ヒンジ（棒鋼をり形，0 形に加工）を取り付け，装置に挿入し，載荷辺に充分剛をる我荷板を用いて試験板に等分布圧縮荷重が作用するよう に努めた Fig”8．Viewofsetup。 Fig17・・Testsetup． b）試験板の支持条件 試験坂の荷重辺並びに側辺はヒンジ構造ををし，概ね4辺単純支持条件に近いものと考えられる． C）測点及び測定方法 荷重の段階ごとに板の応力及び水平変位を測定した．その測定位置をFig．9に示す．．図中，−印は歪ゲ・−・ジの貼 布位乱 △印はダイヤルゲ・−ジでの測定位置を表わすぃ 変位の測定は支持装置の底板を基準とした．また応力測定に 当っでアルミ合金板では弾性係数の小なることから，塑性歪ゲ・−ジを用いた．

280 4一 ﹁ ．﹁ 「一一￣】」」￣￣】 ﹁1 二 〇山 、 ．い ． 、・→・

矧卑

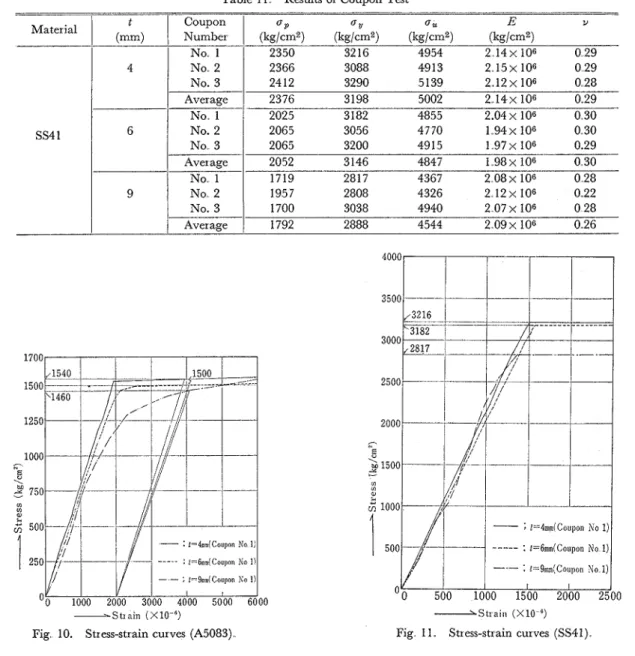
﹂↓60十料州 吾 川 霊 γ＝）19aIl（】Sll）19 lト1‘】）Ⅰ▲．6 aIl（lSl■1）Ⅰ。6 Fig，9McasuredpolntS ⅠⅤ 実 験 結 果 1．引張試験 各試験板から切り取って作成した引張試験片は，A5083がJIS5号，SS41がJISl号試験片である… これらの試 験片の引張試験結果並びに応力ー歪曲線をTablelO，Tablell，Fig10，Fig”11に示す TablelOResultsofCouponTest A5083

Table 11. Resultsof CouponTest

）0 l−−ルーー ；拝4叩（Col■l）OnN01）

l l 00 500 10001500 2000 250

0 0 0 0 ＜U O O O O 5 0 5 0 5 7 5 2 0 7 5 2 1111 ㌃∈＼M豊ss巴㌫1 ：l＝4mm（Coup肌No1j ：ま＝6mm（Co叩OnNol） ；ト9mm（CouponNol） 0 0 0 0 5 ハリ 0 5 1 1 2 ︵N∈U＼茸レSS巴㌫1 0 1000 2000 3000 4000 5000 6000 ＋、Stlain（×10￣6） ＋ ＼Stl−aill（×106） Fig・11… Stress−Straincurves（SS41）． Fig・10．Stress−Straincurves（A5083）l 2．座屈試験 a）荷重一板の面外変位 荷重の増大につれ板が座屈して面外に変位する様子を，A5083について，Fig，12に，SS41についてFig．13に 示す．図中縦軸は板の単位南街当りの荷重（jγ如，P：荷重，如：板断面療）を，横軸は板中央の面外変位盈（∂）を 表わす．．ここで∂は，荷重と直角な方向につき，板中央の面外変位から，両端近傍の変位の相加平均値を差し引い た値である．また図中に4辺単純支持の条件で算出した座屈強皮（げ…ク）と，補正座屈強度（α欝dl）を合せ図示した． b）板中央の歪変化 板が座屈し南外変位を発生すると，その位置における歪は，面内圧縮応力による歪と，面外変位に基づく盃で速成 されるけ 従って面内圧縮応力による歪が静出されれば，これを速成歪から差し引くことにより面外変位に基づく歪が 取り出せる筈である．このような意図で各板の両面中央における測定歪から，面内平均圧縮応力度による計算歪を差 し引き，面外変位に基づく歪のみを取り出したものを，A5083についてFig・14に，SS41についてFig．15に示す．

2250 2000 些牲 ㌃1500 ム壁弼1 ／♂主】1 ∈ ） ＼ 軸 ；些壁」 ＿ ゴ1000 di くく 亡 ＝） 準星抽 焉500 J 1 A、T −0．5 0 05 0 05 0 05 1 4000 豊増 り竺l ・（3000 U 田 叫

．！こし＿ 空 巴

さ ・lJ ニー 票2000 ・く 士 i＝ ：⊃ こ ；ユ 葛1000 C〉

ailllle） 7T￣ ∈ 田 日 「 1 ロ 2り5】 ￣‖−「￣r ♂野 面 ∩（1i ケ■ 惑 ‘Y■■−￣ 協 写′♂c 十け「ヤ・ 泊 肘 田 l 圭 S−1■P Ⅰ一4・1 n SトrP 1．6小2 SllPL9・2 n ∩

】05 0 05 0 0。5 0 0り5 1．0 ＼Deflection∂（mm） Fig．13り Loadvs．deflection（SS41） ＋Deflection∂（mm） Fig．12．Loadvs．・denection（A5083） なお面内平均圧縮応力度による歪の穿出に当っては，各板につき対応する弾性係数（TablelO，Tablell）を用いたが， 非弾性領域では圧縮応力皮の段階掛こ，かかる歪を界出することは極めて煩雑であるので，精確を歪の取り出しにこ だわらず弾性係数をそのまま用いた． C）板幅の応力分布 板の荷重方向と直角を中央断面につき，低荷重の時点と歪の測定が可瀧を範囲内での最大荷重の時点で，生じた板 幅の応力分布をFig‖16，Fig．17に示す．．ここで各応力皮の算出に当っては，枚両面の測定歪の相加平均をとり，弾 性域では板馴こ対応する弾性係数を用い，非弾性域では応力ー歪曲線に基づき非弾性応力を連絡する方法をとった・ 2000−2000−1000010002000 −2000−1000010002000「2000−100001000 ど（×10￣6トー ーE（×10￣6）e（×10￣6）」 ■一e（×10￣‘）亡（×10￣6）」・−⊥∈（×Ⅳ6） Fig．14．，Stressvs…Strain（A5083）・

︵N∈U＼茸︶sS巴︸S誌巴空々1′ S TPI。9・・2 −2000−1000010002000−2000−1000010002000−2000−1000010002000 e（×10−6）」 −ゝど（×106）ど（×10￣6）」 一！（×10￣‘）e（×10−6）」 一ど（×肝‘） Figh15 Stressvs．strain（SS41） 3000 ∈ ・ミ2000 如 1000 0

仁‥ − − ‥、−．−：−∴

Fig．16StTeSSdistributions（A5083） 巴禦ご呈基竺讐巴讐豊茫 んご二280 んご210 Fig17、StTeSSdistributions（SS41）・ d）座屈強度と終局強度 僅かを初期変形等の影響のために，同材質同寸法の板においても，座屈による面外変位発生の状態は一機となるこ となく，−・部の板では低荷重の時点から変位の発生するものもみられ，座屈強皮の把握は困難である・然しながら Fig．12，Fig．13（荷重一板の面外変位），FigP14，Fig・15（板中央の盃変化）を参照すれば，非弾性領域での座屈現象 が目立ち始める時点は，A5083，SS41共に4辺単純支持として許出した座屈強度（♂き彗）と補正座屈強度（♂欝dりの 間に存在するか或はその近傍であると思われる． またかかる時点に至っても板の平衡状態は存在し，更に若干の荷重の増加をみたが遂には平衡状態を保ち得なくな り，急速な変形を伴って荷重の低下をきたす．この時点をもって面外座屈による板の終局強度と判断した・・板が終局 強度に到達したのち，更に載荷を続けて座屈変形を目立たたせたものを，A5083についてFig‖18に，SS41につい

てFig19に示す． Fig”19Buckledplate（STPL4）・ Fig．18Buckledplate（ArPL4）r e）実験強度と理論強度の比較 実験座屈強度の判定が困難であるため，ここでは各板の実験終局強度と，理論座屈強度並．びに理論終局強度を対比 させ，一・括次表に示す

Table12．RatiosofExperimentalValuestoTheoreticalValues

Ⅴ 考 察 考察に先立ち当実験に関する二，三の問題点を挙げてみる．i）初期変形：当実験では試験板の作成に際しその初 期変形を出来るだけ少くする努力が払れ，A5083，SS41共に6rnm厚，9mm停の板ではその存在が一児認め難い程 度となっている然しながら4mm厚の薄肉板では両材質共に僅かの初期変形が目撃された．．ii）支持装置：Fig・7 から判断される如く板の漑荷辺の両端部付近は職荷不能である．従って厳密には荷重条件として，仮の載荷辺全体に わたって等分布荷重が作用するとは云い難い．また実験中測定した板の荷重方向中央部の歪分布は，必ずしも中央に っいて対称形を示さない．このことば初期変形の存在にも関連をもつが，応力伝達の面でかかる支持装置にも問題が 残ると思われる，また強度計糾こ当っては上記の影響を全く加味せず，これらの影響の度合いもここでは定かでない。 以上のことから早急を結論ははばかられるが，この試験の範囲内で次のことが考察される 1）Fig一12，Fig。13から判断される如くA5083，SS41共に板は初期変形等の影響を受け座屈強皮を明らかに把握

することは出来をい．．然し凌がら両材質共に座屈現象発生後も耐荷カは増加し，若干の後座屈強度を保持した．これ は座屈後発生した膜応力のうち，荷重と直角方向の膜応力が頁献するためであろう．A5083とSS41では座屈後終

局強度に到達するまでの挙動は異なり，後塵屈強庶は前者が後者より大であるu

2）Table12から判断される如く終局強度の理論座屈強皮に対する増分は，A5083，SS41共に弾性域が非弾性域 より大で，且つ非弾性域では板の幅厚比（あ／わが小なる程大である．これらの点は部材設計に当って安全率を導入す る際に考慮すべき点と考えられる．． 3）KaImanの方法で静出した終局強度は，A5083，SS41共に幅厚比み／f＝70∼35の領域で実験結果と良く近イ以 する．然しながらWinter法のアルミ合金材への適用は検討を要するように思われる。またb／t＝16．7の領域に至る とKarm孟n，Winter法共に適用は無理となる．この理由はFig．16，Fig…17に示した如く厚肉板（b／t＝16．7）では座 屈後も板幅の応力は直線的分布を示すが，蒋肉枚（ろ／わ＝70）では座屈後の応力分布は凹形となって応力の多くが板 の支持縁に近い部分で分担される様子が認められ，有効幅の概念に近い状態が発生するのは，この場合4mm厚（ろ／f ＝70），6mm厚（あ／g＝35）の坂に限られるためであろう． ⅤⅠむ す− び 当研究ではA5083に注目しその座屈領域として弾性域（げ。γくびp），並．びに非弾性域（げp＜♂。γ＜♂γ域と，♂。γ≒♂y 域）の3カ所を狙った‖ 引張試験結果による弾性係数Eが当初想定した倍と若干興った結果，所期の狙いを充分に 果し得なかったが，アルミ合金羽と鋼材との板座屈後の挙動，後塵屈強度の相異，有効幅概念適用可能な幅厚比の限 界等について或る程度明らかになし得たと思う． 本研究に当って，神戸製鋼所建設工事開発本部，梶本改良氏に多大の御協力を戴いたことを記し，ここに謝意を表 する． 引 用 文 献 （1）三宮和彦：番犬農学報，25，25ト262（Ma！

1974）

（2）∴

：番犬虚学報，26，15【24（Oct1974）

（3）BRYAN，G．H∴ On the Stability of a Plane

Plate under Thrustsinits own Plane，With

Applicationstothe‘Buckling’0董the Sides of

York，McGraw−Hill（1961）

（5）BLEICH，F‖：BucklingStrengthofMetalStruc− tures，330p331，NewYork，McGraw−Hill（1952）

（6）KARMAN，T、，SECHLER，E。E，＆DoNNELL，L．H．．：

TheStrength of Thin Platesin Compression，

Trans一ASME．，54，53（1932）

aShip，Proc”LondonMath．Soc．−，22，54（1891） （7）WINTER，G。：StrengthofThinSteelCompres− （4）TIMOSHENKO，S．P。，GERE，J。M．：Theory of sion Flanges，Trans…ASCE．．，112，534，（1947）．

Elastic Stability，2nd Edition，355，367，New

EXPERIMENTAL STUDY ON ULTIMATE STRENGTH OF ALUMINUM ALLOY PLATES

Kazuhiko SANNOMIYA

SⅦmmary

Thepapercontainsthercsultsof’theexperimentalstudyofthcelasticandtheinelasticbuckling

Strengthandtheultimatestrengthoftheplatcs，materialofwhichareA5083（binaryalloyof

AトMgsystem）and SS41，and the number ofwhich are7and6respectively．At the test，

theendrestraintconditionof．theplatesloadedbytheequallydistributedloadar・e丘Ⅹedsupport

Fromthesetests，thefo1lowlngmaybeconcluded：

1）TheplateswillcarrylargerloadthanthebucklingStrengthafterthebucklingoccurred

andtheratioofthestrengthafterbucklingtOthebucklingstrengthofA5083platesarelarger

thanthatofSS41plates・

2）The ratio ofthe experimentalultimate strength to the theoreticalbuckling strength

intheelasticrangearelarger♪thanthatintheinelasticrange

3）TheultimatestrengthcalculatedbyKarmantheoryarefairlyinagreementwiththe

testresultsintherangeofb／t＝70−35，butthevaluescalculatedbyWintertheorymaybenot

inwellagreementwiththetestresultsinthesamerang・e

4）ThevaluescalculatedbyKまrmantheoryandWintertheoryaredi飴r・entfiOmthetest

resultsin therange ofb／t＝16l7，because theconception ofthe e鮎ctivewidthwi11beinapq

Plicabletothethickplateslikeb／t＝16∩7・