2
変量確率分布に従う位相スペクトルをもつ
2
信号間の位相限定相関関数の統計的性質
Statistical Properties of Phase-Only Correlation Functions Between Two Signals
With Phase Spectrum Following Bivariate Probability Distributions
鈴木亮
†八巻俊輔
‡川又政征
†吉澤誠
‡† 東北大学大学院工学研究科
‡ 東北大学サイバーサイエンスセンター
Ryo Suzuki
†Shunsuke Yamaki
‡Masayuki Kawamata
†Makoto Yoshizawa
‡†Graduate School of Engineering, Tohoku University
‡Cyberscience Center, Tohoku University
アブストラクト 位相限定相関関数 (POC 関数:Phase-Only Correlation Functions) の性質に数学的根拠を与え るため,POC 関数の統計的解析を行う.本稿では,2 信 号の位相スペクトルがともに確率的に変化する場合を考 え,2 信号の位相スペクトルが 2 変量確率変数であると仮 定する.2 信号の位相スペクトルが 2 変量確率分布に従う とした時の POC 関数の期待値と分散を導出する.このと き,POC 関数の期待値と分散の一般式は 2 次元の特性関 数を用いて導出できることを証明する. 1 はじめに 2 つの信号の類似度を評価する方法の一つとして,信 号のもつ位相情報を用いる位相限定相関関数(POC 関 数:Phase-only-Correlation Functions)を用いる方法があ る.POC 関数は振幅スペクトルを 1 に正規化した信号(位 相限定信号)に対して相関を計算することで求められる. 2 つの信号が類似しているときに,POC 関数は鋭いピー クが観測される.また POC 関数は,2 信号間の幾何学的 な関係を求めることができる.例えば,POC 関数のピー クの出現する位置のずれを信号の位置ずれに変換して表 現することができる.これらの特徴から,POC 関数は指 紋認証技術 [1] や画像マッチング技術 [2],周期性のある DNA 配列の探索 [3] などに応用されてきた. 2 つの評価したい信号が等しいときは,それぞれの信号 の持つ位相情報は等しく,2 つの信号の位相スペクトル差 は 0 である.位相スペクトル差が 0 となる時の POC 関数 はデルタ関数になる.また,2 つの信号の位相スペクトル 差が 0 ではない時,POC 関数はデルタ関数と異なる.し かし,これまでの研究では,2 信号間の位相スペクトル差 が 0 ではない時に,POC 関数がどれだけデルタ関数と異 なるかについて数学的な根拠が与えられていなかった. 著者らのグループでは,これまでに 2 信号間の位相ス ペクトル差を 1 変量確率変数と仮定して,POC 関数の統 計的解析を行った [4].また,位相スペクトル差が直線上 で与えられる 1 変量確率分布に従うと仮定して POC 関数 の期待値と分散を導出した. これらに対して本稿では,2 信号の位相スペクトルを 2 変量確率変数と仮定して,POC 関数の統計的解析を行う. 具体的には,2 信号の位相スペクトルが平面上で与えられ る 2 変量確率分布に従うと仮定して POC 関数の期待値と 分散を導出する.その結果,POC 関数の期待値と分散の 一般式は 2 次元特性関数を用いて導出できることを証明 する. 2 POC 関数の統計的解析 2.1 POC 関数の定義 まず最初に位相限定相関関数 (POC 関数) を定義する. 信号長が N の 2 つの複素信号を x(n) と y(n) とする. こ れらの信号 x(n) と y(n) の 1 次元離散フーリエ変換は以 下の式で表される. X(k) = DFT [x(n)] = N∑−1 n=0 x(n)WNnk=|X(k)|ejθk (1) Y (k) = DFT [x(n)] = N∑−1 n=0 y(n)WNnk=|Y (k)|ejϕk (2) ここで k = 0, …, N−1 は離散周波数インデックスであり, WN = exp(−j2π/N) は離散フーリエ変換の回転因子を 表す.また|X(k)| は信号 x(n) の振幅スペクトルであり, θkは x(n) の位相スペクトルである.同様に|Y (k)| は信 号 y(n) の振幅スペクトルであり,ϕkは y(n) の位相スペ クトルである.POC 関数は 2 つの信号の正規化クロスパ 第30回 信号処理シンポジウム 2015年11月4日∼6日(いわき)
ワースペクトルの離散フーリエ逆変換として以下の式で 与えられる. r(m) = IDFT [ X(k)Y∗(k) |X(k)||Y (k)| ] = 1 N N∑−1 k=0 X(k)Y∗(k) |X(k)||Y (k)|WN−mk = 1 N N∑−1 k=0 ejαkW−mk N (3) (m = 0, 1, ..., N− 1) ここで‘∗ ’は複素共役を表し,αk= θk− ϕkは 2 つの信 号の位相スペクトル差を表す.つまり位相スペクトル差 αkがわかると POC 関数を求めることができる. 2.2 POC 関数の期待値と分散の一般式 著者らのグループでは,文献 [4] で,位相スペクトル差 αkを確率変数と仮定して,POC 関数の期待値と分散を導
出した.POC 関数の期待値 E[r(m)] および分散 Var[r(m)] の一般式は以下の式で表される. E[r(m)] = Aδ(m) (4) Var[r(m)] = 1 N(1− |A| 2) (5) ここで位相因子 ejαkの期待値を A = E[ejαk] (6) とおいている.ここで,位相スペクトル差 αkは,すべて の周波数インデックス k に関して独立かつ同一な確率分 布に従うと仮定している.式 (4) と (5),(6) より位相ス ペクトル差 αk の確率密度関数を与えることで,POC 関 数の統計的性質を表すことができる. 2.3 特性関数を用いた POC 関数の期待値と分散の 導出 位相スペクトル差 αk の確率密度関数が与えられたと き,式 (6) の計算にその特性関数を用いることができる. 確率変数 αkの確率密度関数 p(αk) の特性関数 ψα(t) は以 下で定義される. ψα(t) = E[ejαkt] = ∫ ∞ −∞ ejαktp(α k)dαk (7) ここで t = 1 とすることで,位相因子の期待値を以下の ように求めることができる. ψα(1) = E[ejαk] = ∫ ∞ −∞ ejαkp(α k)dαk = A (8) 従って,位相スペクトル差 αkの確率密度関数が与えられ たとき,式 (8) を用いることで POC 関数の期待値と分散 を導出することができる. 3 2 信号の位相スペクトルが 2 変量確率分布に従う場合 の POC 関数の統計的性質 3.1 2 信号の位相スペクトルにおける仮定 著者らのグループがこれまでに行ってきた POC 関数の 統計的解析では,信号 x(n) の位相スペクトル θkを確定 信号とし,一方,信号 y(n) の位相スペクトル ϕkを確率 信号であると仮定をおいていた.しかし,実際の信号処 理においては,2 信号 x(n) と y(n) の位相スペクトル θk と ϕkがともに確率信号である場合も考えられる.本研究 では,2 信号の位相スペクトル θk と ϕk が確率的に変動 すると仮定して,POC 関数の統計的解析を行う.この時, 2 信号の位相スペクトル (θk, ϕk) は,2 変量の確率変数で あると仮定している. 3.2 POC 関数の期待値と分散の一般式 αk = θk− ϕkの関係式を式 (6) に代入すると,以下の ように位相因子 ejαkの期待値を表すことができる. A = E[ejαk]= E [ ej(θk−ϕk) ] (9) ここで,2 信号の位相スペクトル (θk, ϕk) は,すべての周 波数インデックス k に関して独立かつ同一な確率分布に 従うと仮定している.式 (9) と (4),(5) より位相スペクト ル (θk, ϕk) の 2 変量確率密度関数を与えることで,POC 関数の統計的性質を表すことができる. 3.3 2 次元の特性関数を用いた POC 関数統計的性質 の記述 2 信号の位相スペクトル (θk, ϕk) の確率密度関数が与え られたとき,2 次元の特性関数を用いて POC 関数の期待 値と分散を表すことができる.2 信号の位相スペクトルの 確率密度関数を p(θk, ϕk) としたとき,その 2 次元特性関 数 ψθ,ϕ(t1, t2) は以下の式で与えられる [5]. ψθ,ϕ(t1, t2) = E [ ej(θkt1+ϕkt2) ] = ∫ ∞ −∞ ∫ ∞ −∞ p(θk, ϕk)ejθkt1ejϕkt2dθkdϕk (10) 次に,式 (10) において t1 = 1, t2 =−1 を代入すること で,以下のように位相因子の期待値を導出することがで きる. ψθ,ϕ(1,−1) = E [ ej(θk−ϕk) ] = ∫ ∞ −∞ ∫ ∞ −∞ p(θk, ϕk)ejθke−jϕkdθkdϕk = A (11) 従って,2 確率密度関数 p (θk, ϕk) の 2 次元特性関数を導 出できる場合には,式 (11) を用いることで POC 関数の
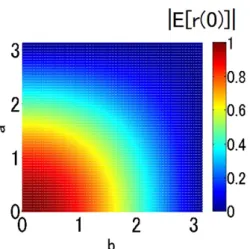
期待値と分散を以下の式で導出することができる. E[r(m)] = Aδ(m) (12) Var[r(m)] = 1 N(1− |A| 2) (13) ここで位相因子 ejαkの期待値を A = E[ejαk]= E [ ej(θk−ϕk) ] = ψθ,ϕ(1,−1) (14) とおいている. 3.4 2 信号の位相スペクトルが独立な場合の POC 関 数の統計的性質 2 信号の位相スペクトル (θk, ϕk) の 2 変量確率密度関数 を p (θk, ϕk) とし,θkと ϕkの周辺確率密度関数をそれぞ れ p (θk) と p (ϕk) とおく.このときに p (θk, ϕk) = p (θk) p (ϕk) (15) が成り立つ場合,2 信号の位相スペクトル (θk, ϕk) は互い に独立であるといえる.式 (10) において,p (θk, ϕk) に式 (15) が成り立つとすると,その 2 次元特性関数は以下の ように導出することができる. ψθ,ϕ(t1, t2) = E [ ej(θkt1+ϕkt2) ] = ∫ ∞ −∞ ∫ ∞ −∞ p(θk, ϕk)ejθkt1ejϕkt2dθkdϕk = ∫ ∞ −∞ ∫ ∞ −∞ p (θk) p (ϕk) ejθkt1ejϕkt2dθkdϕk = ∫ ∞ −∞ p (θk) ejθt1dθk ∫ ∞ −∞ p (ϕk) ejϕkt2dϕk = ψθ(t1)ψϕ(t2) (16) ここで,ψθ(t1) とψϕ(t2) は,それぞれ周辺確率密度関数 p(ϕk) と p(θk) の特性関数である.従って,式 (16) に t1= 1, t2 =−1 を代入することで,以下のように位相因子の 期待値を導出することができる. A = E[ejαk]= E [ ej(θk−ϕk) ] = ψθ(1)ψϕ(−1) (17) ここで,式 (17) を式 (4) と式 (5) に代入することで POC 関数の期待値と分散を導出することができる. 4 計算例 4.1 2 変量正規分布に従う場合の POC 関数の統計的 性質 2 信号の位相スペクトル (θk, ϕk) が 2 変量正規分布に 従うと仮定する.この時,平均 µ,共分散行列 Σ の 2 変 量正規分布 N (µ, Σ) の確率密度関数は以下の式で与えら れる. p(θk, ϕk) = 1 2π|Σ|12 e−12(Θ−µ)Σ−1(Θ−µ) t (18) Θ = ( θk ϕk ) µ = ( µθ µϕ ) Σ = ( σ2 θ ρσθσϕ ρσθσϕ σ2ϕ ) σ2 θ, σ2ϕはそれぞれ 2 信号の位相スペクトル (θk, ϕk) の分散 を表している.このとき,σθ, σϕは σθ > 0 と σϕ> 0 を 満たす.また,ρ は相関係数と呼ばれ,−1 ≤ ρ ≤ 1 を満 たす.相関係数 ρ = 1 の時は,θk = ϕkであり,ρ =−1 の時は,θk =−ϕkとなる.p (θk, ϕk) が式 (18) で与えら れる場合,その 2 次元特性関数は以下のように導出する ことができる. ψθ,ϕ(t1, t2) = ej(µθt1+µϕt2)e− 1 2(σ 2 θt 2 1+2ρσθσϕt1t2+σ2ϕt 2 2)(19) ここで,式 (19) に t1= 1, t2=−1 を代入することで以下 のように位相因子の期待値を導出することができる. ψθ,ϕ(1,−1) = ejµe− σ2 2 = A (20) σ2 = σθ2− 2ρσθσϕ+ σ2ϕ µ = µθ− µϕ 式 (20) を式 (4) と式 (5) に代入すると,以下のように POC 関数の期待値と分散を導出できる. E[r(m)] = ejµe−σ22 δ(m) (21) Var[r(m)] = 1 N ( 1− e−σ2 ) (22) 一例として,位相スペクトル (θk, ϕk) の分散 (σ2θ, σ 2 ϕ) が それぞれ (1, 1) であるとき,相関係数 ρ 及び平均差 µ の 変化に対する POC 関数 r(m) のピークの期待値|E[r(0)]| と分散 Var[r(m)] を図 1 と 2 に示す.分散 (σ2 θ, σ 2 ϕ) がそ れぞれ (1, 1) である場合は,POC 関数のピークの期待値 |E[r(0)]| と分散 Var[r(m)] は以下の式で表わされる. |E [r(0)]| = e−σ2 2 = e(ρ−1) (23) Var[r(m)] = 1 N ( 1− e−σ2 ) = 1 N ( 1− e2(ρ−1) ) (24) 式 (23) と (24) より,POC 関数のピークの期待値と分散 は平均差 µ に依存しないことがわかる.また相関係数 ρ が-1 から1に増加するに従い,位相スペクトル差のばら つきが小さくなるため,POC 関数のピークの期待値は増 加し,分散は減少する.図 1 と 2 にもその傾向が表れて いる.
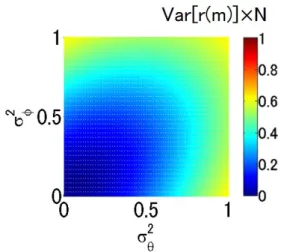
図 1: 2 信号の位相スペクトルの相関係数及び平均差が変 化した時の POC 関数のピークの期待値の挙動 図 2: 2 信号の位相スペクトルの相関係数及び平均差が変 化した時の POC 関数の分散の挙動 図 3: 2 信号の位相スペクトルの分散が変化した時の POC 関数のピークの期待値の挙動 図 4: 2 信号の位相スペクトルの分散が変化した時の POC 関数の分散の挙動 次に,相関係数 ρ = 0.5 であるとき,位相スペクトル (θk, ϕk) の分散 (σθ2, σ 2 ϕ) の変化に対する POC 関数 r(m) の期待値|E[r(0)]| と分散 Var[r(m)] を図 3 と 4 に示す. 相関係数 ρ = 0.5 である場合は,POC 関数の期待値と分 散は以下の式で表される. |E [r(0)]| = e−σ2 2 = e− 1 2(σ 2 θ−σθσϕ+σϕ2) (25) Var[r(m)] = 1 N ( 1− e−σ2 ) = 1 N ( 1− e−(σ2θ−σθσϕ+σϕ2) ) (26) 式 (25) と (26) より,POC 関数の期待値と分散は平均差 µ に依存しないことがわかる.また,σ2の値が大きくな るに従い,POC 関数の期待値は減少し,POC 関数の分 散は増加する.図 3 と 4 にもその傾向が表れている. 4.2 2 変量一様分布に従う場合の POC 関数の統計的 性質 2 信号の位相スペクトル (θk, ϕk) が 2 変量一様分布に従 うと仮定すると,その確率密度関数は式 (27) で定義する. p(θk, ϕk) = 1 2a 1 2b ( −a < θk < a −b < ϕk< b ) 0 otherwise (27) ここで,θkと ϕkは独立であると仮定している.式 (27) の 2 次元特性関数は以下のように導出することができる.
ψθ,ϕ(t1, t2) = sinc (at1) sinc (bt2) (28)
ここで sinc 関数は以下の式で与えられる. sinc(x) = 1 (x = 0) sin(πx) πx (x̸= 0) (29)
図 5: a と b が変化したときの POC 関数の期待値の挙動
図 6: a と b が変化したときの POC 関数の分散の挙動 よって,位相因子の期待値は式 (28) に t1= 1, t2=−1 を
代入することで以下の式のように導出できる.
A = ψθ,ϕ(1,−1) = sinc (a) sinc (−b)
= sinc (a) sinc (b) (30) ここで式 (30) を式 (4) と式 (5) に代入すると,以下のよ うに POC 関数の期待値と分散を導出できる.
E[r(m)] = sinc (a) sinc (b) δ(m) (31) Var[r(m)] = 1
N
(
1− |sinc (a) sinc (b)|2 ) (32) 一例として,a と b の変化に対する POC 関数 r(m) の ピークの期待値|E[r(0)]| および分散 Var[r(m)] を図 5 と 6 に示す.図 5 と 6 をみると,a と b の値が 0 から π に増 加するに従い,POC 関数のピークの期待値|E[r(0)]| は減 少し,分散 Var[r(m)] は増加していることがわかる. 5 まとめ 本稿では,2 信号の位相スペクトルを 2 変量確率変数 と仮定して,POC 関数の統計的解析を行った.具体的に は,2 信号の位相スペクトルが平面上で与えられる 2 変量 確率分布に従うと仮定して POC 関数の期待値と分散を導 出した.その結果,POC 関数の期待値と分散の一般式は 2 次元特性関数を用いて導出できることを証明した. 参考文献
[1] H. Nakajima, K. Kobayashi, T. Aoki, and T. Higuchi,“Pattern collation apparatus based on spa-tial frequency characteristics (USP 5915034), ”US patent, May 1995.
[2] C. D. Kuglin and D. C. Hines, “ The Phase Cor-relation Image Alignment Method, ” Proc. IEEE, Int. Conf. on Cybernetics and Society, pp. 163-165, 1975.
[3] A. K. Brodzik, “ Phase only filtering for the masses(of DNA data): A new approach to sequence alignment, ”IEEE Trans. Signal Processing, VOL. 54, NO. 6, pp. 2456-2466, June 2014.
[4] S. Yamaki, J. Odagiri, M. Abe and M. Kawamata, ”Effects of Stochastic Phase Spectrum Differences on Phase-Only Correlation Functions Part I: Sta-tistically Constant Phase Spectrum Differences for Frequency Indices,” Proceedings of IEEE 3rd Inter-national Conference on Network Infrastructure and Digital Content, pp. 360-364, September 2012. [5] A. Papoulis, S. U. Pillai, ”Probability, Random
Variables and Stochastic Processes,” McGraw Hill, 2002.