5
分布定数系解析基礎
連続体の振動,たとえば図5.1に示す張力をもって両壁間にピーンと張られ た柔軟で均一な弦の振動を考えよう.弦は一応断面を有して質量が連続的に分 布している連続体である.この弦の振動を解析する場合に,分布質量の連続体 として素直に何らかの連続関数でモデル化し厳密解を得ることができるモデル 化がある.これを分布定数モデルという.図5.2に示すように,実際の質量の 連続分布に対応して,その任意の位置の弦の微小部分について運動方程式を立 てて解析する方法である.ニュートンを始めとする学者によって確立された微 分学に基づいて17世紀に研究された方法であり,その解は環境媒体(空気な ど)の影響は考慮しない条件での“ 厳密解 ”となる.このモデル化で解析でき る対象物は幾何学的に単純な構造物,たとえば弦,均一な梁,矩形や円形の膜 や平板やシェルなどであるので,今日の実機について直接的に実用できる範囲 は制限される.なお,別のモデル化としては図5.3に示すように実際の弦の分 布質量に対応させて適当に多数の質点が質量無しの弦で等分布に取り付けられ た多自由度系として近似モデル化して解く考えがある.1700年代中頃にJean Le Rond d’Alembert, (1717-1783)が有限個の質量が取り付けられた弦の運動 の解析で,多自由度の連立運動方程式を適切な係数乗算と方程式間の加減算か ら非連成化して解いた研究活動を見つけることができる〔カッツ著,上野他訳, 「数学の歴史」共立出版,2005〕.この種のモデルを集中質量モデルとか有限離 散モデルという.集中質量モデルではその自由度よりも低次の固有振動数まで の低い周波数帯域しか精度を保った解析はできない.しかし,そこから発展し た現代の有限要素法は,任意形状の構造物の解析が可能なコンピュータを使った実用的近似数値解析法となっており,世界的に汎用プログラムが普及して多 くのエンジニアや研究者に利用されている. 本章では,分布定数系の振動解析法の基礎として,梁と弦の曲げ振動の固 有振動数解析について解説する.これらの基礎的例題の学習をふまえれば,膜 や平板の振動や,直方体閉空間やチューブ内に発生する音響の共鳴周波数解析 など容易に応用できる. 図 5.1 弦の振動 図 5.2 微分法に基づく弦の運動方程式導出法
124 5. 分布定数系解析基礎
図 5.3 弦の集中質量モデル化(lumped mass modeling)
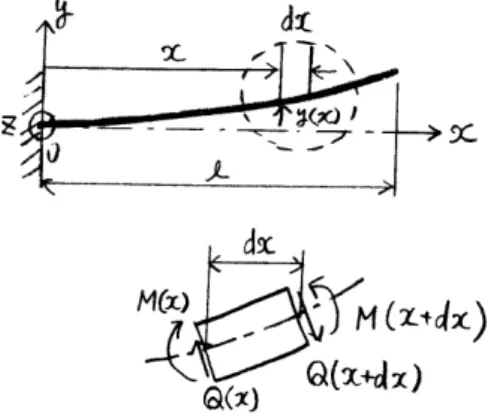
5. 1 梁 の 振 動 解 析 図5.4に示す片持ち梁の曲げ振動を考える.梁の張り出し方向をx座標,梁 の静的釣り合い位置がx軸上で直線状態として曲げのたわみ方向にy座標を定 義する.梁は均一断面で,その断面積をA,張り出し長さを`,材料密度をρ とする.梁の断面形状は梁の長さに比べて十分小さいとして,かつ,曲げ振動 の振幅(最大たわみ)も十分小さいものとする(梁の最大振幅時にどの部分の 図 5.4 片持ち梁の曲げ振動のモデル化
傾きもx軸に対して約10度程度までならば十分にこの条件は成立する). さて,同図に示すように固定端からの梁の任意の位置xのところの微小長さ 要素について考える.梁振動のたわみは時間と位置の関数となるので,y(x, t) と丁寧には表すことにし,簡略化してはyと記すことにする.その微小要素 の自由体図を考えれば両端断面に外部から曲げモーメントM (x, t)とせん断力 Q(x, t)が外力として作用している.なお,重力の作用は,梁の静的釣り合い位 置からたわみを定義すれば運動方程式から消去されるのでいまの場合考慮する 必要はない. 梁の曲げ剛性は,梁の縦弾性係数(ヤング率)Eと断面形状から決定される 断面2次モーメントIの積となる.曲げに関する応力とひずみはそれぞれ曲げ モーメントと曲率である.曲率は梁のたわみ角度の変化率であるので∂2y/∂x2 と表せる.曲率と曲げモーメントの関係式は M = −EI∂ 2y ∂x2 (5.1) である.位置xにおける曲げモーメントは,図に示されるように,いま注目し ている微小要素の左側断面に作用しz軸回り負方向となるのでマイナス符号を 付けている. せん断力は,Qで表して Q = −∂M ∂x = EI ∂3y ∂x3 (5.2) と記述できる.微小要素の右側断面に作用するせん断力Q(x + dx)は微分論理 から−{Q(x) + ∂Q(x)/∂x · dx}と計算できるので,結局のところ Q(x + dx) = − µ Q(x) +∂Q(x) ∂x dx ¶ = −EI∂ 3y ∂x3 − EI ∂4y ∂x4dx (5.3) と求められる.以上の結果を利用して注目している微小要素のy方向の運動方 程式をたてれば,質量がρAdxであるから
126 5. 分布定数系解析基礎 ρAdx∂ 2y ∂t2 = EI ∂3y ∂x3 + µ −EI∂ 3y ∂x3 − EI ∂4y ∂x4dx ¶ (5.4) ⇓ ρAdx∂ 2y ∂t2 = −EI ∂4y ∂x4dx ⇓ ∂2y ∂t2 + EI ρA ∂4y ∂x4 = 0 (5.5) となる.これが梁の曲げ振動の基礎運動方程式である.数式展開の便宜から c2= EI/ρAとパラメータを置き換えて解説を進める.梁の自由振動解は y(x, t) = φ(x)ejωt (5.6) とおいて式(5.5)に代入して c2d4φ(x) dx4 − ω 2φ(x) = 0 ⇓ d4φ(x) dx4 − ³ ω c ´2 φ(x) = 0 (5.7) を得る.もはやxだけに関するφの微分方程式なので常微分を用いる.式(5.7) の解は式の形式からφ(x) = Desxと設定して代入することでsが s4−³ ω c ´2 = 0 ⇓ s = ± r ω c, ±j r ω c (5.8) と計算できる.そこで,φ(x)の一般解は φ(x) = C1e √ω cx+ C2e− √ω cx+ C3ej √ω cx+ C4e−j √ω cx (5.9)
と得られる.ここで,C1∼C4は梁の境界条件で決定されるべき未定係数(積 分定数)である.数学的には式(5.7)はxに関する4階微分方程式なので,そ の解のφ(x)を求めるためには4階積分することと解釈できるから積分定数が 4つ現れる. 【例題】 両端単純支持の長さ`の梁の固有振動数と固有モード形を求めなさい. なお,梁は材料密度ρで縦弾性係数はE の材料で作られ,断面は一様形 状で断面積をA,その断面2次モーメントはIで表すこととする. 【略解】 境界条件を考える.片方の端点の座標をx = 0としてもう一方をx = `と座 標設定する.両端単純支持の境界条件であるから,どちらの支点でも,たわみ がゼロ,曲げモーメントがゼロ(すなわち,曲率がゼロ)の条件である.した がって,次のように,4つの境界条件式を設定できる. φ(0) = 0 (5.10) d2φ(x) dx2 ¯ ¯ ¯ ¯ x=0 = 0 (5.11) φ(`) = 0 (5.12) d2φ(x) dx2 ¯ ¯ ¯ ¯ x=` = 0 (5.13) 式(5.9)とその2階微分の式に境界条件式を当てはめると次の未定係数C1 からC4についての4元連立方程式を構成できる. C1+ C2+ C3+ C4= 0 (5.14) C1+ C2− C3− C4= 0 (5.15) C1e` √ω c + C2e−` √ω c + C3ej` √ω c + C4e−j` √ω c = 0 (5.16)
128 5. 分布定数系解析基礎 C1e` √ω c + C2e−` √ω c − C3ej` √ω c − C4e−j` √ω c = 0 (5.17) 式(5.14)と(5.15)の連立よりC1 = −C2とC3 = −C4を容易に得て, それらを残りの式に代入すると −C2e` √ω c + C2e−` √ω c − C4ej` √ω c + C4e−j` √ω c = 0 (5.18) −C2e` √ω c + C2e−` √ω c + C4ej` √ω c − C4e−j` √ω c = 0 (5.19) を得る.式(5.18)と(5.19)の加算からは C2 ³ −e`√ωc + e−` √ω c ´ = 0 (5.20) を得るが,左辺カッコ内がゼロとなるにはω = 0とならなければならず,その 解は振動学的には無意味である.そこで,C2= 0が解となる.したがって,C1 もゼロとなる. 式(5.18)と(5.19)の減算からは C4 ³ ej`√ωc − e−j` √ω c ´ = 0 (5.21) を導出できる.この式が成立するためにはC4= 0またはカッコ内がゼロとな らなければならない.C4 = 0では4つの未定係数がすべてゼロとなり振動学 的には無意味な解となるので,カッコ内がゼロとならなければならない.カッ コの内を三角関数で表現すると 2sin µ ` r ω c ¶ = 0 (5.22) であるので,これより,求めるべき固有角振動数Ωsは
` r ω c = π, 2π, 3π, 4π · · · ⇓ Ωs= ³ π ` ´2 s EI ρA, µ 2π ` ¶2s EI ρA, µ 3π ` ¶2s EI ρA, µ 4π ` ¶2s EI ρA· · · (5.23) である. その振動モード形は式(5.9)に上記の解を代入することで, C4 ³ ej`√Ωs c − e−j` √ Ωs c ´ ⇓ Csin à ` r Ωs c ! ⇓ sin à ` r Ωs c ! ⇓ sin µ iπx ` ¶ (i = 1, 2, 3 · · · ) (5.24) と得られる.正弦波状のモード形となり,両端のところで変位ここで未定の係 数Cは振幅を表す.固有モード形ではそれは決定できず,初期条件(振動開始 時の初期たわみなど)を与えての自由振動の振幅として具体的に決定される. 【例題】 図5.4の片持ち梁の固有振動数を求めなさい. 【略解】 境界条件について考える.固定端x = 0においては,変位とたわみ角ともに ゼロであるので,
130 5. 分布定数系解析基礎 φ(0) = 0 (5.25) dφ(x) dx ¯ ¯ ¯ ¯ x=0 = 0 (5.26) が設定できる. 自由端側x = `においては,曲げモーメントがゼロ,すなわち曲率がゼロ, およびせん断力もゼロであるから d2φ(x) dx2 ¯ ¯ ¯ ¯ x=` = 0 d3φ(x) dx3 ¯ ¯ ¯ ¯ x=` = 0 (5.27) が設定できる.すなわち,式(5.25)から式(5.27)の境界条件は具体的に同 順で C1+ C2+ C3+ C4= 0 (C1− C2) + j(C3− C4) = 0 C1e` √ω c + C2e−` √ω c − C3ej` √ω c − C4e−j` √ω c = 0 C1e` √ω c − C2e−` √ω c − C3ej` √ω c + C4e−j` √ω c = 0 (5.28) と連立できる.これらを行列表現すると 1 1 1 1 1 −1 j −j e`√ωc e−` √ω c −ej` √ω c −e−j` √ω c e`√ωc −e−` √ω c −jej` √ω c je−j` √ω c C1 C2 C3 C4 = 0 0 0 0 となる.そこで,
" −12(1 + j)e`√ωc +1 2(−1 + j)e−` √ω c − ej` √ω c 1 2(−1 + j)e` √ω c −1 2(1 + j)e−` √ω c − e−j` √ω c −1 2(1 + j)e `√ω c −1 2(−1 + j)e −`√ω c − jej` √ω c 1 2(−1 + j)e `√ω c +1 2(1 + j)e −`√ω c + je−j` √ω c # " C3 C4 # = " 0 0 # ⇓ " a11 a12 a21 a22 # " C3 C4 # = " 0 0 # ⇓ a11a22− a12a21= 0 (5.29) の条件式を得る.式(5.29)に関しては残念ながら解析的には解けそうもない 難しい非線形方程式である.そこで数値計算によって求めることになる. 定性的には,梁の固有振動数は,一般的に梁の長さの二乗に反比例し,材 料密度と断面積の平方根に反比例し,縦弾性係数と断面二次モーメント の平方根に比例する.そして,さらに境界条件に影響されて決まる. 5. 2 弦 の 振 動 解 析 図5.2に示す線密度 が均一の弦の振動を考える.なお,弦は曲げ剛性を無視 できるほど十分柔軟性を有すると仮定する.弦は張力Tでピーンと距離`の2 点に張られている.その弦の長さに比べて振動振幅は十分に小さく,そのため に振動中の張力の変化分は初期張力Tに対して無視できるほど小さいと仮定す る(現実的に妥当な場合が多い). 弦の左端をx座標の原点,右端を`として,その間の任意の位置xにおける 微小長さdxの弦要素を考え,その要素の時刻tでの振動変位をy(x, t)と表す. すなわち,振動変位は時間と位置の関数である.ただし,これ以降の数式展開 では便宜的にy(x, t)を省略してyと記述することにする.
132 5. 分布定数系解析基礎 この微小要素の質量は,ρを線密度とするとρdxと表せる.y方向の加速度 は∂2y/∂t2と表せる.位置xにおける微小要素の左端に作用する張力をTと すると,そのy成分は弦の傾きの幾何学を考えることで −T∂y ∂x (5.30) と求められる.sの微小要素の右端(位置はx + dx)に作用する張力のy成分 は次のように求められる.y座標の正方向となることを考慮して,位置xにおけ る弦の傾きが∂y/∂xであるので,そこからxの正方向に微小量dxだけ移動し たところでの傾きは位置xとは変化する可能性があり,その増分は∂x∂ ³ ∂y ∂x ´ dx と表現できるので, ∂y ∂x + ∂ ∂x µ ∂y ∂x ¶ dx (5.31) と表現できる.そこで,微小要素の右端に作用する張力T (x + dx)のy成分は µ T +∂T ∂xdx ¶ ½ ∂y ∂x+ ∂ ∂x µ ∂y ∂x ¶ dx ¾ ≈ T ½ ∂y ∂x+ ∂ ∂x µ ∂y ∂x ¶ dx ¾ (5.32) と求められる.以上より,この微小要素についてのニュートンの運動方程式(質 量×加速度=外力)を作成する.すなわち, ρdx∂2y ∂t2 = T ½ ∂y ∂x + ∂ ∂x µ ∂y ∂x ¶ dx ¾ − T∂t ∂x ⇓ ρ∂ 2y ∂t2 = T ∂ ∂x µ ∂y ∂x ¶ ⇓ ρ∂ 2y ∂t2 = T ∂2y ∂x2 (5.33) と得られる.式(5.33)は
ρ∂ 2y ∂t2 = T ∂2y ∂x2 ⇓ ∂2y ∂t2 = T ρ ∂2y ∂x2 ⇓ ∂2y ∂t2 = c 2∂2y ∂x2 (5.34) と変形できる.この式(5.34)は波動方程式(wave equation)である.c =pT /ρ は便宜的に設定しただけでなく,その波の速度を表す(次元解析すればわかる). この運動方程式を解いて固有角振動数を求めるには,弦の横振動関数y(x, t)を y(x, t) = φ(x)ejωt (5.35) の単振動を考えればよい.ここで,φ(x)はxの関数であり,弦全長にわたる振 動の形状(振動モード)を表す.その形で角振動数ωで横振動することを表現 している.式(5.35)を式(5.34)に代入すれば −ω2φ(x)ejωt= c2d 2φ(x) dx2 e jωt ⇓ d2φ(x) dx2 + ³ ω c ´2 φ(x) = 0 (5.36) と変形できる.式(5.36)の形の微分方程式の一般解は φ(x) = A cos³ ω cx ´ + B sin³ ω cx ´ (5.37) である.AとBは2階微分方程式の解の積分定数(未定係数)であり,それぞ れcosineとsineの振動成分の振幅と解釈できる. 具体的に境界条件を設定して固有角振動数を求める.弦の両端は固定されて おり曲げ剛性は無視できるので,境界条件として
134 5. 分布定数系解析基礎 φ(0) = 0 φ(`) = 0 (5.38) が設定できる.これらの境界条件式を式(5.37)に代入すると A = 0 B sin µ ω` c ¶ = 0 (5.39) の2式が得られる.定数AとBの両者が共に零になる解は静止している状態 であり無意味なので,A = 0は認めるとして,式(5.39)が振動について意味 をなすためにBは零ではなく, sin µ ω` c ¶ = 0 (5.40) が成立しなければならない.これを満足するためには ω` c = π, 2π, 3π · · · (5.41) とならなければならない.これを満足する角振動数ωが固有角振動数であるので, 結局,1次から無限次までの任意の次数の固有角振動数Ωi (i = 1, 2, 3, · · · ) は Ωi= iπc ` = iπ ` s T ρ (i = 1, 2, 3 · · · ) (5.42) である.第i次固有モードは式(5.42)のΩi を式(5.37)のω に代入して, A = 0も代入することで φ(x) = B sin µ iπ ` x ¶ (i = 1, 2, 3 · · · ) (5.43) と得られる.たとえば,1次と2次の固有モードを描けば,図5.5に示すよう
} T D S • P ˘ Q ¯ L [ h ‘ 図 5.5 弦の 1 次と 2 次の固有モード形: (a) 1 次 (b) 2 次 な形状であることがわかる.1次は弦の全長がちょうど半波長,2次は1波長 分のなるモード形である. 定性的に,弦の固有振動数は,弦の長さと線密度の平方根に反比例し,張 力の平方根に比例し,2次,3次・・・の固有振動数は1次固有振動数のそ れぞれ2倍,3倍・・・ときれいに等間隔であることがわかる.固有角振動 数を式(5.37)に代入すれば弦の振動の形状が求まる.
136 5. 分布定数系解析基礎 5. 3 章 末 問 題 【1】図5.6に示す平均律音階の1点イ(a1)の振動数は440Hzと規定されて いる(ただし,演奏者の好み等により多少変化させる場合もある). さて,縦 弾性係数E = 206GPa,材料密度ρ = 7860kg/m3,有効長さ` = 1m,直径 φ = 1.175mmのピアノ線で,そのイ音を出すための張力T [N]を計算しなさ い∗1) .なお,計算式の導出は文字式で行い,与えられた数値は最後に代入し て答えの数値解を求めなさい. 【2】図5.7はオルゴールの音源である櫛とメロディー回転筒の例である.縦弾 性係数E = 206GPa,材料密度ρ = 7860kg/m3,厚さh = 0.6mmの金属板 でオルゴールの櫛を作ることを考える.各櫛の歯は幅一定の片持ち梁と仮定し て,440Hzの音を出すための櫛の歯の長さを求めよ. ∗1) 【楽器用ピアノ線について】 ミュージックワイヤに用いる素材は,JIS の SWRS82A,SWRS87A,SWRS92A という 0.80 ∼0.95 の炭素を含有し,きず,脱炭,不純物元素含有量を厳しく規定したピアノ線材が用いら ている.この線材は,ばねなどに用いられている一般のピアノ線材の仕様と大きな違いはない. しかし,ミュージックワイヤは,ばね用ピアノ線より厳格な規格内に,丁寧に手をかけてつくら れている. まず、その第1は真円度.弦は打弦されると振動するが,このときの振動は単なる打弦方向の 上下運動だけではなく,水平方向の運動も発生する.真円度が悪いとこれら運動に影響を及ぼ し,調律のばらつきや音質の低下につながる.真円度は検査項目では偏径差として数値化され, ミュージックワイヤの場合は一般のピアノ線の半分である(検査基準が厳しい). 機械的性質は一般のピアノ線とほぼ同じだが,ミュージックワイヤには一般のピアノ線にな い,平打ち性とペンチ曲げ性という特別な特性が要求されている.平打ち性は巻線加工を行うと き,巻線のゆるみ防止に両端を叩いて扁平にするが,その際に割れてはいけないので,ハンマー で線径の 1/2 まで叩いてつぶし,割れの出ないことを検査する.また、ミュージックワイヤは チューニングピンに巻きつけて張力を与えるが,このときワイヤは極めて鋭角に曲げられる.こ のような過酷な加工にも耐えられることを,エッジの半径が 0.2mm 以下である特殊なペンチを 用いて,90 度に曲げたのち,元の位置にもどすという検査で確認する.(鈴木金属工業(株)の ホームページから引用)
図 5.6 イ音(a1)の振動数計算の問題説明図