【論 文
1
.
UDC :624.
042.
7:620.
1 日本建 築 学会構 造系論文 報 告 集 第 365号・
昭 和 61 年 7 月非 定 常
ラ
ン
ダ
ム
振 動解析
に
対
す
る
位 相 傾 斜
の
確率特性
の
応 用
に
関
す
る
基 礎 的研 究
、
正 会 員曽
田
五月 也
*1.
序地 震 動は そ の振 幅
・
周波数特性の いずれも,
が 時 間 的に 変 動する非 定 常な不 規 則過程であ ること よ り,
構 造 物モ デル の ランダム振 動 解 析に当たっ て も外 乱を その よ うに モ デル 化する く ふ う が行わ れて いる。
その 中で は,
定 常 な白色 外 乱に時 間の関 数であ る振 幅 変調 関数や周 波 数 特 性を変調す る た めの関 数 を 乗じ ること に よっ て非
定 常 外 乱を模擬 す る手 法が多 用さ れ て い る。 これ らの 変 調 関 数 は既 往の地震デー
タの分 析 等に よっ て経 験 的に定め ら れ た り,
あ るい は数 学 的な処 理の要 易さ か ら便宜的に定め ら れ た りして い る が,
振 幅 変 調による周 波 数特性へ の 影 響, あるいは その 逆の影 響につ い て は余り考 慮さ れて い ない よ うであ る。
理論的な不 規 則 振 動 解 析の手 法には,
多くの場 合,
小 型の計 算機に よっ て も要 易に計算がで き ること や,
種々のパ ラメー
タの変化に対し て も安 定し た 解が得られ ること な どの長所が ある反 面,
外 乱の モ デル 化に関し て は前 述の よ うに 未 だ検 討を 必要と す る点が少 な く ない。
最近の研究4)
−
S)に よれ ば,
地 震 動の非定常 性は震 源と 考え ら れ る 断 層の特 性や地 震 動の伝 播 経 路の特性に よっ て大 略の 傾向が支配 され る こと が明らかに さ れて お り, 今 回の筆 者の研究は,
実 際の地 震 動 あるいは断 層モ デ ル による模 擬地震 波の 分析に よ り外 乱の周 波 数帯域の違い によっ て振 幅 特 性の時 間的 変化が異な り この 分 布は 外 乱 の位 相に関す る特 性の中で特に位 相 傾 斜に強く依存す る とし た,
大 崎ら9や 和 泉 ら4)・
1°)の 指 摘に注 目し た もので ある。 位 相 傾斜の特性を利 用する と,
外乱の 全 継 続 時 間 を周 期と し た時の パ ワー
スペ ク トル特 性を変え ること な く任意に振 幅 変 調で き る こ とを示す。
また,
文 献4)−
8) な どにおい て震 源の特 性と 地 震 動の周 波 数特 性,
振 幅 特 性,
位相特性など との関 係の定 式 化が試み ら れ てい る手 法 に 順 じて,
対 象と す る地震動の周波 数 特 性 と 位 相 特 性 の確率特 性と が推 定さ れ た 場合に,
同外 乱の平 均 値や自 己相 関々数がいか な る形で数式表現さ れ るか を導き,
さ 本 研 究の一
部は 昭 和 59, 60年 度の建 築 学 会 関東 支 部研 究報告 会お よび秋 季 年 次 講 演 会に おい て発 表し た1 )−
3)。
寧 佐 藤工業 (株) 中 央 技 術 研究 所・
工博 (昭和60年11月1日原 稿 受 理 〉 らに これ らの関数を線形 系の不規 則 振 動を 理論 的に解 析 することへ 応 用さ れることを示す。
一
般の外 乱 2(t)につ い て,
そ の継 続 時 間を周 期と し た場 合の パ ワー
ス ペ ク トル密 度 関 数 S。
〔ω)の概 形は,
例え ばFig.1
に実線で示す ところの nonwhite な分 布と な る。
本 研 究では その分布を同 図 中の破 線の よ うに区 分 的に一
様な パ ワー
を有す る制 限帯域白 色外乱の和と し て 近 似 表 現 し,
.
個々 の帯域でそ の位相傾斜の特 性に従っ て 振 幅 特 性が時 間 的に任 意に変 動す る と考え る。
以下の 2
〜
4章で はFig,
2
の ように帯 域の上限お よ び 下 限の振 動 数 を ωぴ,
ω L とする制 限 帯 域 白色外乱 x (t
) の非定 常な諸 確 率 特 性 (平 均,
2 乗平 均,
自己相 関々数 〉 と位相傾斜の特 性との関 係につ い て検 討 する。 個々 の制 限帯域外 乱の和 として一
般の外 乱を表す場 合に, 同 外 乱 の確 率特性, お よ び同 外 乱に対す る線 形振動系の 応 答の 求め方に関して は 5章にま と めて示す。 聾 口1囚
O oFig
.
1 Nonwhite poweT spectral density functlon and its appro.
ximation by rectangular functions
.
」
1 亞
ー
…
2Tda ! Sx 〔ω
) 0 0ω
Lω
UFig
,
2 Power spectral density functlon of barLd.
limited whitenolse
.
2.
非 定 常 制 限 帯 域 白色 外 乱の 平 均 値 り 外乱の 円 振 動 数 WiC に対 応する位 相 角をilit
とし て複 素フー
リエ 係 数を次式 X(ωD
=
a(cos φ、+ ‘sin φ、)……・
……一
(2,
1
) で表す と き,
外 乱x (t)は フー
リエ 級数 を 用い て一
48
一
n x(
t
)=
ΣX
(ω 陀)e‘ω κt…・
……・
・
…………・
・
(Z.
2
) k1−
n と なる。 た だ し,一
般の外 乱と して.
考慮 する振 動 数の正 帯 域が等間 隔A
ω で n 等 分さ れ て い る と して,
ωu=
U ・
A
ω,
ω、
=L ・
△ω,
蛛 = 舮△ω な ど とす る。
(2.
1)式 を (2.
2)式に代人 す る際に,X
(ω∂と その共 約な複 素 数X
* (ω κ)との間に はX
(一
ωre>=x
* (ωん)…一 ・
……・
・
……・
・
…・
…
(2.
3} の関 係が成 立し,
ま た,
外乱の継 続 時 間T, はT
・−7
/
・
……・
・
…・
・
・
・
…ttt
・
一 ……・
・
一
(・.
・) と表さ れ ること よ りx(・)
・
=
…漏
(・・s…、・c・s・“。t
−
sin φκsin tUtet)Aω……・
……・
・
…
(2.
5)と な る。 森 を確
.
率 変 数とし て (2.
5)式 両辺の期 待 値は・[・(・)]
一
・・拡
(・[・ ・s φ日・ ・s 婦
一
E[siniPiC
]sin ωht )Aω…・
…・
・
(2.
6)と なる
。
式 中の 記 号E [・
]は集 合 平 均を表す。
(2.
6)式 のE
[cos φ君,
E[sin φ司な どは以 下の とお りに して求 め る。互に隣り 合っ た 振 動 数 に対応 す る位 相 角の差を位相差 分9它称し次の よ うに定 義す る。 △φi
=
φご一
φ‘−
1・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
…
(2.
7) こ の位 相差 分 を微 分の 形 式で △φノムω の よ うに表し た ものを位相傾 斜11) (位 相の 傾ぎ り と 呼ぶ ことにす る。
位相傾斜を用いて位 相 角 姦 は次の よ うに表され る。
偏 ・
盞
鴿
……一 …・
………・
……
〔・.
・) た だ しφL はこ の帯域の下 限 振 動 数 ω〒軌 に対 応す る位 相 角で あ る。…
般の外乱を考え る場 合に振 動 数ゼロ に 対 応す る位 相 角を φ。 とし て,
これ を位 相 傾 斜とは独 立に [0,− 2
π]の一
様 乱 数で与え ることにす る.
こ の と き に φLは φL=
φo十 φ・
・
・
・
・
・
・
・
・
・
・
・
・
…
t・
・
・
・
・
・
・
・
・
・
・
・
…
一
・
・
・
・
…
(2.
9) と表すこ と がで き る。 た だ し,
φ は Wt.
よ り も小さい振 動 数 域に お け る位 相 差 分の総 和で ある。
φ。を一
様乱 数 と す れ ばE
[cos φ。
]=
E[sin φ,]一
・
Oと な る こ とよ り, φ がどの よ う な も ので あっ て もE
[COSeL
]=
E [COS φ 。]E [COS di]一.
E
[sin φo]E[sin Φ]=
O
E
[sin φ、]=E
[sin φ。]E
[COS ψ]十
E
[cos φD]E [sin Φ]‘
O
………・
・
・
・
・
…………・
(2.
ユ0) とな り,
さ らに ・[・ ・S φ圃 ・ ・S φ・]・[
・ ・S(
謝
・・)
]
一
E [… ¢L]・[
…(
盞
会
籌
A・)
]
一
・ ・[… φ冠一
・[・・ φ・]・[
・ ・s(
艦
・・)
]
・
E
[・ ・S φ・]・[
…(
皇
鴿
・・)
]
一
・・
・
・
・
・
……・
・
…・
(2.
11) とな る の で 〔2.
6)式に代入 し て,
結局,
外乱x 〈t
)の 平 均 値は位 相 傾 斜の特 性や帯 域の特 性とは無 関 係で常にE
[x(t
)]=O−………・
………・
………・
・
……
(2.
ユ2
) と な る。
3.
非 定常制限帯域 白色外乱の自己相 関々数 任 意の2
時 刻 をti,
t
!と して,
外乱 x(t)の 自己相 関々 数は (2.
ユ)一
(2.
4
)式の 関 係を用い てRx
エ(ti
,t2
>=E
[x(t1
)x(t2
)]一
(
T
. α2
π)
2 、熱
・[・(w、)・ ・ (・・t)]・
exp [i
(ωκ彦1一
ωitz)]△ω2…………
(3.
ユ)一
・(
α を.
憂)
2『
鹹
1
・[・ ・s(幅 }ユ
・
COS (ωret、一
ω、 t2)−
E [sin (iPit
一
φε)][J u
・
sin (blttl一
ωlt2)IA
ω 2十Σ Σ
it
;
L !f・
L
’
iE
[COS (φit十φε)]COS (tUhtl 十tOlt2
)一
E [… (φ・+φ・)]… (… tl+・・昭1
…・
………・
・
…・
・
…………・
・
(3,
2
} と表す こと がで き る。
上式に は 2個の位相角 φκお よ び φ‘の 和・
差,
す な わ ち φ辻 φ、に閧す る 正弦お よ び余 弦 の平 均 値が含ま れ る が,
その う ち和に関して は前章の (2.
10) 式の場 合と同 様に してE[cos (2φL)]
=
O, E [sin (2
φL)]=0………
(3.
3)の関 係が成 立する こと よ り
E[cos (φ,+φ、)]= 0
,
E
[sin (φ、+φ∂];O…
(3.
4)とな る
。
従っ て 自己相関々数はR・ ・(
t1
,t
・)一 ・(
・農
)
2軸
・[・・s(φ、一
φ、}]・
COS (・ ・、t
一 t・、t、
)− E
[sin (φ、一
φ、)]・
sin (tUκtl一
ω ‘置2>IA
ω2………
(3.
5)と な り
,E
[cos (φ厂dit
)],
E
[sin (φκ一
iltj
]のみ が 必要とな る。 位 相 傾 斜 Aφ/Aω の確 率 密 度 関数 を正規分布
,
も し く は正規分布に類 似し た関 数であると するな らば1ト3剛,
2ケの 位 相 角の差 φ厂 φ‘はll
−
hl個の位相傾 斜の和で ある から やは り 正規 確 率 変 数とし て近 似でき る。
す な わ ち,.
確 率 変 数 φ厂 φ‘の確 率 密 度 関 数はその 平 均 と 分 散 と が分か れ ば, 次の正 規 確率 密 度 関 数で表す ことが で き る]z ) e一
一
49
一
・(
d
…一
¢1)7m
。im
、、.et
]…
P
[
−
y
(姦一
禦
贈
lr
∵・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
…
(3.
6} た だ し,
上式中で σ[・
],
σ2[・
]の記号ば そ れ ぞ れ標準偏 差, 分散を表す。
位 相 角の差 森一
φ』の期 待 値は (2.
8)式 より・[・
一
・・1コー
砿
器
・・]
一
(・一
’・聞
・・・
t−・
…
t−・
・
・
・
・
・
…
一
一
・
・
・
・
・
・
・
・
・
・
・
…
(3『
7) と な る。
また, 分 散は位 相 傾 斜 Aφ,IAtU
,
[i−一
h 〜
1
]を 互に独 立な確 率 変 数で あ る と して・ ・ [φiC
−
iPt
]−
IH
卜
・・隴 ]
…一 ……
(… } と な る。 (3.
7), (3.
8)式 を (3.
6 )式に代入 し て φκ一
φ、 の正 弦お よび余弦に関す る平均 値 を求めれば次 式が得ら れ る。
Tdfi
・[… (φ厂 ・・1}]
一一
exp{
一
。,1
・− llA
・}
・
S・・1
昜
(・・1
)A・}
・[・ ・s(φ副
一
exp【
一
警
1
・一
・1
・・}
.
・
C・S{
η (ic− 1
)A
・}
・
・
…
一
一
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
…
(3.9
) た だ し,
位 根 傾 斜の平 均・
分散をそれぞれ・
[
△φ 面]
一
÷
・慌
]
一(
ぞ
)
’……・
賦 と し,
(2.
4 >式の関係を利用 し た。
(3.
9)式 を (3.
5
)式に代入整 理 して さ らに △ω が cav−
tOL に比 して十 分に小 さい もの と すれば (3.
5}式を 次の積 分に変換で き る。
Rxx
(・,,
・t2
)一
・(
a 2π)
∬
°
exp1 ・1
…一
・・11
・
COSI
〔b
,blL− b2to2
)}d
ω2d ω1・
………・
………・
……
(3.11
} ただし,
Tα
Tdπ,
T.
一
彦2…
(3.
12)− ti,
b
,=
α=一一
…一
,b
・=
m m s である。
上 式 を実 際に積 分す れ ばR
=x・・・・
…1
− ・(
α 2π)
2・
(81
+・・+R
・+R
・・・F
(
一
a一
α 。・+房
+ 。・+b
;)
纛
.
(b、−
b,)(ω 一 ω。)’
sln 2 (b
,− b
,)(ω。+ω∂’
COS 2−.
r
.
50 一
a2− b
,b2
[cosl
(b
,− b2
)a)di
R2
;一
(α2十bf
)(α2十bi
) 十cosl (b
,− b2
)ω,1
]一
α(〜冫1十bz
) expIa
(ω L广 ω L)} R3;
(α2+醐 (α2+ bl>
・
[sin 〔b
,tU,.
− b2
ωり)−
sin (bltOL
,
− b
,ω1.
)]R・
一
(
論 牆
碕
… S ・b
・a・・一
・・ftiu・ 十COS (b2
ωr.
−
bi
ωu)]…………・
・
……・
…・
…
∴…
〔3.
ユ3
> を得る.
特にb
,− b
,+墅 一
西 と す れば2乗 平 均 値 れ の時 刻 歴 が 次 式で与え られ る。
朏 ・]
一
・(
Tda2Ji
)
21講
・a・v−
di
・1
.
_
2〔α:− b2
) + 1 (al十b
! )2 (a! 十b2
)z
。
exp }α(ω v一
ω L)i
・
[4 absinlb
(cav一
ω L)} ・ ・〔・・一
・り・・s 臨一
ω1
]1
・
・
・
・
・
・
・
・
・
・
・
…
一
一
・
一・
・
・
…
−t…
(3.
14 ) 外 乱の振 幅 特 性と位 相 傾 斜の依存性を定性 的に実 証する こ と が すで に試み られて いる榊 謝 が,
(3.14
)式嫁両 者の関 係 を確 率 論 的な見 地よ り定量的に表し た もの であ ・洞 式・ ・,
・÷
こお・ てE
[・・(・}]・駄 値を・ る こ と, ま た位 相 傾 斜の特 性が同じであ る 場合に,
帯 域 の幅によっ て振 幅 特 性の 非 定 常 性が異な る が,
帯域の中 心 振 動 数の大・
小の影 響は受け ない こと などが分か る。
広帯 域white noise で は (3.
13),
(3.
14>両式 と も1項 目のみ が支 配 的になっ てそれ ぞ れR
・ ・・・・・
…)一 ・(
T
, α 2π)
2(
蒜
・ 。講
、)
論
,.
(b,−
b,)(ω u一
ω L)°
Sm 2・
c・s堕
〔彑
・ )1
幽 )・
…・
・
(・.
15).
.
・[・・(t
>]一
・(
Tda2
π)
2論
・t・u−
t・L・・
…・
(・・
16) の よ う な簡潔な表 現で近似で きる。Fig.
2の パ ク ス ペ ク トル密 度関 数を持つ定 常な外 乱 諷 の を 考え るとその平 均パ ワー
はE
[♂]=
2a2(ω t,
一
ω L}……・
…・
・
……・
…・
…・
(3.
17) と表さ れ, これを用いる と (3.
15),
(3.
16}の各 式は 92(ti)十92(t2) 2 Rxx(ti,
tz)=
=
E[万2] 2 (b
,− b2
)(COI.
,
一
ω L) (δ一 δ,)(ω 一 ωL)・
sin−
2… s (δ且
一
半 キ
ω……
(・・
18
) E [X2(t)]=
E [万2]・
92(t)・
……・
・
………
(3.
19)と書き直すこと がで き る
。
ただ し関 数 g(t)は周 波 数 特 性には関 係な く次 式 とな る。
・
・ω
籌
ゾ
……・
・
一
・3・
…従 来か ら広く用い ら れてい る手 法で は
,
定常な外乱1
{t
)と振 幅変調 関 数ψ(t)との積と し て非定常 外 乱x(t) をX(
t
)=di
(t
)°
ψ(t)……・
・
…・
…・
……・
…・
・
…・
(3.
21 ) の よ う に 表 す が,
こ の場 合の x(t}の 自己相 関々 数,
2 乗 平均はそ れ ぞ れ 脇 謝 一 ・鬮 ψ(t ・)e
{ti) (、1一
纛
一
ω.
(b
,− b
,)(ω 。一
ω、)’
Sln・
−
2 (b
一b
,)〔ω。+ω、)’
c°s2
’
』 ’
…
(3・
22 )E[xz(
t
)]=E
[ji2
]ψ2(t
)・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
…
《
3.
23
) と な る12’ 。 2乗 平 均に関 して は (3.
19)式と (3.
23 )式 と が全く同 じ形で表さ れ るの に対し,
自己相関々数に関 し て (3.
18 >式と (3.
22)式と は振 幅 変 調関数の2
乗に 関 する相 加 平 均と相 乗平 均との違い で あるこ と が分か る。
理 想white noise の場合に は自己相 関々数 が デル タ 関 数と な り, ψ(t
)= ・g(t)であれば (3.18
), (3.22
)の両 式はまっ た く同じ に な る。 理 想white noise と振 幅変調 関 数の積 として もモ デル化し た非 定 常white noise とい う特 別の場合に対して は,
振 幅 変 調関数の具 体 的な形で は無く そのintensity
moment に のみ依存して位 相傾 斜 の確 率 密 度 関 数の形が決まる と し たN .
C .
Nigam の 研 究があ る13j。 これに対 し, 今 回の筆 者の研 究で は,
位 相 傾 斜の確率密度 関 数の具 体 的な形で は な くそ の モー
メ ン ト(平均・
分 散 〉に の み依 存して振幅の時 間 的 変 化 を表 す関 数が決るの で, Nigam の結果と は丁 度 表 裏の関 係 にあ ることにな る。
4.
理 論 式の精 度の検証4
.
1 パ ワー
スペ ク トル密 度 関 数および位相 傾斜の特 性の分 類外 乱の継 続 時間 を
T
.と して,
全 継 続 時間に対す る フー
リエ 変 換よ り求ま るパ ワー
ス ペ ク トル密 度 関 数Sx
(ω)がFig.
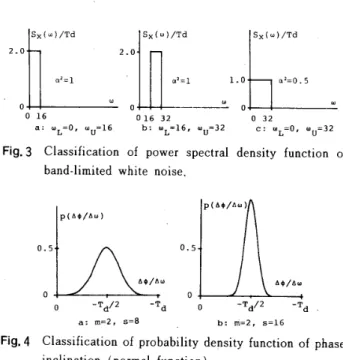
3の よ う な矩 形 関 数とな る制限帯 域 white noise につ い て計 算す る。
帯域の上限, 下 限を ωu,
ω L と して [ω‘,
ωv]=
[0
,16
], [16,
32],
[0,
32]の3
種と す る。 た だ し,
at(ωr ω∂
=16.
0 ……・
…一 ・
…・
…・
…・
・
…
(4.
1) と規 準 化して,
いずれの外 乱の平均パ ワー
も等しくし た。
位相 傾斜の確 率 特 性 を 規 定す る 量 は (3
.
10)式の平 均 お よび分 散で あるが,
同 式 中の m,
s の 値は [m,
s]=
[2,18], [2、
16]の組み 合 わせ 2種を 用い た。 2,
3章 で も記し た と お り,
非 定常外 乱の確 率 構 造を定める理 論 2.
O5x {Ul 1〆Tdα
1 2.
0Sx 〕/Td ♂軍
11.
o Sx〔mu匚/Td ゴ=
D.
5四
山
0 0 0 0 16 016 12 0 ]2 a:=
0・ω
U#
16 b:写
16・“
uny32 C・・
L−
°・・
U−
コ2Fig
.
3 C置asslfication of power spectraldensity
fu【LctiQn ofband
.
1imited white noise.
0
.
5 P〔Aφ/ム
国
凸中/APt o o”
Td/2−
Td a: m=
2尸
s=
8 o.
DO¶
Td/2−
Td b:
di.
2,
s=
15Fig
・
4
Classification of probabi】ity density function of phase inClinati。n (n・rmal fUnCti・n).
解で は位相 傾斜の平 均
・
分 散のみ重 要でその確率密 度関 数の 具 体 的な形を必 要とは し ない。Fig.
4の a,
b
は い ずれもシミュ レー
シ ョン にお け る サ ンプル波の作 成の た め に用い たAip
/A
ω の確 率 密 度 関 数と して正規関 数を表 し た もの で ある。
同じ平均 値と分散を持つ 矩 形 分 布の関 数 を 用い て も シミュ レー
ショ ンの結果に ほ と んど違い の 無い ことは文 献1)に示してあ る。 4.
2 シ ミュ レー
ショ ン の 方 法 サンプル 波はFFT
(高速フー
リエ 変 換 )14 )を 用い て 作 成する。
位 相 傾斜を も とに (2.
8)式か ら位 相 角を与え,
さ ら に (2.
1)よ りフー
リエ係 数 を求め て フー
リエ 逆変 換 を 行え ぱ非定 常外乱 x(t}を求 める ことがで き る。
本 解 析で は n= 128,
△ω=
1と し て外 乱の周期はT
.= 2π で ある。 シ ミュ レー
ション は 100ケのサンプ波を用い て 行つ た。
4.
3 平均お よ び 2乗 平 均の時 刻歴につ い て平均値と 2乗 平 均 平 方根 (
RMS
)の各時刻歴につ い て,
理 論 解と シ ミュ レー
ショ ン解との比較を し た もの がFig.
5,
6で ある。
Fig.
5は位相傾 斜の特 性を規 定する 量が m = 2 , s= 8の場 合で,上よ り順に Fig。
3の パ ワー
ス ペ ク トル密度関 数の 分 類a〜
c に対 応する。 各 図で太 い実 線はRMS
の理論解を表し て いる。
平 均 値の理 論 解 は常に ゼロと なっ て,
座 標の横 軸 (時 間軸 )と一
致 する ため省 略し て あ る。RMS
の理 論 解お よ び時 間 軸に沿っ て細かく変 動して いる点線は シ ミュ レー
ショ ン に よ る RMS お よび平 均を表す。 Fig.
6はFig.
5 と同 様の計 算 を位 相 傾 斜の特 性が m=
2,
s=
16の場 合に関して行っ た結果で あ る。
い ずれの 図におい て もシ ミュ レー
ショ ン によ る平 均 値は ほとん どゼロ と なっ てお り, 理論 解が ゼ ロ で あ ることに良 く対 応 し てい る。RMS
に関して も理 論 解と シ ミュ レー
ショ ン解との対 応は良 好で ある。
4.
4 自己 相 関々 数につ い て51
一
50
.
o.
e50.
0.
050.
0.
21 2rFig
.
5 Mean and RMS Qf non−
stationaryband−
limited randomexcitation 伽
一
2,
8=
8).
50.
o.
050,
「
2T 0.
D50.
∬
2t o.
0 1 2胃
Fig
.
6 Mean andRMS
of nQn.
stationary band.
limited randomexcitation (m
蕭
2,
s=
16).
外 乱の継 続 時 間 Td=
=
2
π 中で任 意の 2時 刻ti,
t2
を そ れぞれ tl=
=
t,
t
,=
t+τと表すことにす る。
置= π/4
,2
π/4,3
π/4,
4π/4の各 時 刻につ い て τ=一
π/4−
o (破 線 )お よ び τ=
0〜
π/4(実 線 )の範 囲に対する自己相 関々 数 をFig.
7,
8に示 す。 外乱の特 性は前節の時 刻 歴の計 算と同 様に分 類し てある。
E[xt(t
)]の精 度 をFig.
5, 6 で確 認 してある の で,Fig.
7,8
の縦 軸はRxx
(t,
t十τ)=
R瀛 君,
t+ r)/E[x’ (t
)]の よ うに無 次 元 化 し て あ る。
横 軸はi
τ1
と して,
τ の 正負につ い て重ね て図 示して あ る。 太線は (3.
13 )式による理 論 解 を表し,
細 線は シ ミュ レー
ショ ン に よ る解 を表 す。 た だ し,
亡=
4π/4の 場合の理論解はτ の 正負に関し完全に対 称で あ るの で 太い破 線は 省 略して ある。Fig.
7 は位相 傾斜の特 性が m=
2,
s=
8で表さ れ る場 合であり,
左 右の図の 区別は 帯 域 幅 [tU,.
,ω 配]を α :[0,
16],b
:[16,
32]と区 別し た ことに よる。Fig.
8は同 様に して,
m=
2, 8=
16の 場合で ある。 Fig.
7,
8 と も,
先に RMS 時 刻 歴の比 較一
52
一
を し た場合程で は無いが,.
理 論 解とシ ミュ レー
シ ョ ン解 との対応は概 して良 好である。Fig.
9に はt=
4π/4に お け る正負 対 称な 自己相 関々 数Rr
、c(t,
t
+ r)(1
τ1
≦π)とそ の フー
リエ 変 換か ら求め たパ ワー
スペ クトル 密 度 関 数Sx
(ω)とを表 し た図であ る。
上 よ り順に帯 域の違い 3種に対す る計 算 結 果を示す。 各 図に お い て.
太い 実 線は定 常な外 乱に対す る関 数であ り,
細い実 線・
破 線は位 相 傾 斜の特 性 を 表 すパ ラメー
ター
が m’
=
・
2,
s;
16 お よ び m = 2,
s・=8
である非 定 常 外 乱に対寸
る関 数で あ る。 (.
3.
13 )式が正解で あれば細 い実 線・
破 線の区 別は無く,
と も に定常な外 乱に対する 関 数と一
致 する筈で あ る が,
同 式の導入 過 程にお けるい くつ か の仮 定に よっ て生じ る誤差がこ の程度で ある こと を 示し た。
4,
5 振 幅 変 調に伴う 周 波 数特 性の 変 化に関 す る考 察 非 定 常な外 乱を模 擬す る た めに,
定常な外乱に振 幅 変 調 関 数 を乗 じ る手 法が従 来 より広く用い ら れ ていること は序およ び 3章に記し たと おり であ る。
本 節で は 振 幅変 1.
o.
11 o.
11一
o.
一
1.
L 0.
L o.
1一
1 0.
1一
1 o.
1一
1 D.
一
1.
−
1.
Fig
.
7 Comparison of theoretical a皿d.
simulated Auto
−
correlation functions of non
−
stationary band−
limitedrandom excitation by Phase Inclinaしion Method(m
・
・
2,
1
.
0.
ll一
o.
1一
↓ 0.
⊥ ↓一
o.
1.
o.
1 0.
11冒
0.
↓一
↓ O.
一
1.
−
LFig
.
8 Comparison Qf theoretical and simulated・
Auto.
correlation
functions
ef non.
statiDnary l〕and・
limitedrandom excitation by Phase lnclination Method (m
=
2,
s
・
=
16).
調さ れ ること事に よっ て元の定 常な外 乱の周 波 数 特 性が 如 何に変 化 する かを検 討 する。 前 節の Fig.
9と同 様に,
無 次 元 化 し た 自 己 相 関々数 とそ の フー
リエ 変 換に よ り得られ るパ ワー
スペ ク トル密 度 関 数 をFig.
10に示す。
元の定 常な外 乱の周 波 数 特 性 3種に対 応 して上よ り3組の図 を示して ある。
振 幅 変 調 関 数ψ(t)は (3.
22)式の g{t)と等し くψ(
晴
’
’
… ’
15
・
2) と し て, m =2
お よ び s=8,16
につ い て計 算 例を示す。 太い実 線は変 調 前の定 常 外 乱の 自己相関々数,
パ ワー
スペ ク トル密 度 関 数である の に対し, 細い実線は (5.
2) 式で m=
2,
s=
16 とし て振 幅 変 調 を 行っ た場 合の両関 数であ る。
同 様に,
細い破 線は m=
2,
s=
8の場 合で あ る。
定常 外乱 が振 幅 変 調さ れ る と,
元の制 限 帯 域 内の パ ワー
が減少し,
その 分が同 帯 域の外へ 広 が る傾 向を明 Sx〔”}/TdFig
.
g Auto・
correlation and power spectra 且density functions Qfstationary and non
.
stationaly random excitations.
瞭に認め ることができ る
。
この傾 向は帯 域 幅の 狭い程,
また,
振 幅 変 調関数の変 化が急 激な 程強く な り,
帯 域の 中心振 動 数の大小に も多少関係が有る よ う で あ る。Fig.
9,
loを比較す れば,
非 定 常外乱の モ デル化に 際して,
その 振 幅の非 定 常な特 性を与え る た めに は,
位 相 傾斜の確率 特性に基づい て モデル化 する手 法 (位 相 傾斜法 :
Phase
Inclination
Method )の方が振 幅 変 調 関 数を 用 い る手 法 (変 調 関 数 法 :Modulating
Function
Method
)よりも,
変 調 前 後に おける周 波 数 特 性の不 変 性という面で優れ て い るとい え よ う。
5,一
般の非 定 常 外 乱に対 する線 形 応 答の定 式 化 5.
1一
般の外 乱の平 均 値および自 己 相 関々数の定 式 化 前 章まで で個々 の制 限 帯 域 白色 外 乱の確 率 特 性の定 式 化に対して用い た手 法 を一
般の外 乱の場 合に応 用す る方 法 以 下に示す。
一
般の非 定 常 外 乱z(t)を N ケの制 限 帯 域 波の和とし て次式で表す。 z(t)=
ΣユXi〔t
)・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
…
一
一
・
・
・
・
・
…
(5.1
) ’=
1 2 章において示し た と お り, 帯域や位相傾斜の特性と は 無 関 係に個々 の帯 域 波の平 均 値は ゼロ と な るので一
般の一
53
一
Sx‘ul /Td
Fig
.
10 Auto・
correlation and power spectral density funchonsof stationary and non
−
stationary random excitations.
外乱の平 均値も ゼロと な る。 す な わ ち
,
E [z(t)]= 0・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
…
(5.
2) であ る。 z(t)の 自己相 関々数 }ま N rv Rza(t,,
ち)= Σ Σ E[XJ(ti)コcX t2)]…………
(5.
3) 「=
1J=
1 と表さ れ る が ∬=J
の 成分につ い ては (3.
13) 式で与え ら れ る。1
キJ
の成 分は以 下の と おり にな る。 Xi,
XJ の帯 域はFig,
11
の と お り と して,
各々 の帯域 内の 円振 動 数tOki ω 1 に対応
する位相角をdiit
,
φtで表せ ば,
Xl,
XJ の複 素フー
リ工 係 数はX
,(ω∂= α(COS φκ十 isi皿 φh)・
・
・
・
・
・
・
・
・
・
・
…
(5.
4 )XKtUr)
=
=
β(COS φε十 isindil
)と な り
,
これ よ りXi,
XJ の相互相関々数は・_ (
1
。t
,)一
・es
(
2
π)
2
菖嵩
・
1
}E
[COS (tlit
一
φ1)]COS ((b’
κt1−
to, t2)
−
E [sin (φκ一
φ‘)]
・
sin (φkti−
a,it2)}]△ω2
……・
(5.
5> とな る。 た だし,
φκ+φ、の正弦・
余 弦の平 均 値がい ず れ も ゼロ と な ることを利用 す る。
,
一 54 一
2Tdゴ 2Td巳’
oFig
.
11.
Power spectral density function of two band.
limitedwhite noises
,
:x、,
XJ の帯 域の 関 係 がFig.
1
ユのと お りで あ り,
‘≧h
と すれ ば正 規 確 率 変 数 φ厂 φどの平均・
分散は次 式と な る。
E[φκ一
φ【]=
kE[△φ]−
IE[△φ]十M I σ2[ilit
一
朔;
∫σ2[△ φ]− k
σ’[△φ]+Σ2・
・
・
・
・
…
t−・
tt・
tS・
・
・
・
・
・
・
・
・
・
・
…
tt・
・
(5.
.
6) ただしlM
,Σ]2 は そ れ ぞ れM =− U
}・
E
[△φ]十L
,E
[△φ]− E
[φ]x2
= σt[φ]…
(5.
7> で, Φは振 動 数が ωu,と ω 、」の間の位相差分の和に相当 す る。
φκ一
φ‘を 正規確率 変数と す れば, (5,
6
)の平均・
分散 を用い てE
[cos (φk−
ill
)],
E
[si皿(φk一
φ置)〕が表さ れ, さ らに (5。5
)式に代入 して整 理 す れ ば最 終 的に次 の積分 と な る。
娜 。t
、)一
・di
(
T
,2
π)
z・
exp(
一
弖
Σ・)
・
[
・・s蝋 蹴
ex晦
一
・Wl>
・
COS (blto1
− b
、tOt)dto
,d
ω i−
S
・・(M
>瓢
7exp
(aWt一
伽 )・
si・(b
・W・−
5
・w・)d
…d
・・]
”……
(・・
8) 上の2
重 積 分は ω 1,
ω2 に関す る独 立な1
重 積 分の積に 変 換さ れて容 易に行うこと ができ る。 結 果を下に記す。・_ (・1
,
瀚一
・di
(
£
)
2exp(
−
il2
コt)
・
}(CI・
C2 十 8t・
Sl)・
COS (M
) 十〔Sl・
Cz−
Cl・
82)・
sin (M
)1
,
(1
キJ
)・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
…
−t・
・
−t・
・
(5『
9
)c1一
論
1
[・xp (−
a・・)1
−
・’・ ・s (b
’・)+
b
,sin (b
、ω)}]芻
・・一
誡
窮 [exp (・・t・)laJ
・ ・s (b・ ・) +b
、sin (b
.ω)}耽.
Sl−
。鳶
[ ・・p(一
・・)1
−
.
a’… (・’・)− b
,COS (わ,ω}膿 ; Sz−
。i
・.li
−
El
,i
[exp (酬 ・’・・s 〔・・ω}.
一
b
、COS (b
、W}1
ユ臨P
,
・
P
・
,
・
.
・
.
■
.
.
■
■
Td
πtTd
πi α・;−
sf・
α 尸一一
言「
’
’
”・
・
一・
一・
・
・
…
(5,
10)T
¢b
’=万
一t
・b
・一
藷
一
t・,
E
[
瓠
一一
需
E[
嵳
i
]
一一
募
≡
『
>
a2
[
会
爰
i
]
一(
詈
テ
)
t ・・[
鴿]
一
(
?
)
2・
・
・
・
・
・
…
一
一
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
…
(5.
ll) 5.
2
一
般の外乱に対す る線形 1自 由 度 系の 2乗平均 応答の解法 非 定常 不規則外 乱 z(t)に対す る線形 1自 由 度 系の変 位応答を y(t)と してその 2乗 平均 はE
[y’ {t
)]一
∫
tlLth
(t−
.,)h
’
(tL
.,)R
。Z{・T・.・T・}d
・・dTt
一
齲 ∫
τ
ん(彦一
融 (t−
rt)●
Rx 、
X」
(Tl,
rt)drtdtt・
・
・
・
・
・
・
・
・
・
・
・
…
(5.
12 ) と表さ れ る。 た だ しh
(t
)は初 変位・
初速度を ゼロと し た時の単 位 衡 撃変位 応 答 関 数であ り減 衰 定 数を ζと す れ ばh
(t)一
二
exp ← ζ。,。t)。i
。(孤ε),
莇一
。。π
ω 0・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
…
(5.
13) で あ る。
∬=
」の場合の積分はy
.(t
)とし て次 式Y
・(t
)一
∫τ
んh
瞭一
丁・)・R・
、,i(rl,T・}
d
・・drt
・
・
・
・
・
…
4■
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
…
t−…
(5.
14) を次の よ うに整 理 する。
距
蝨
exp (一
・ζ… t)[・… s (・観 ・) 十1,sin (2砺 ε)−
1,]…
………・
・
S
(5」5) ただし, 1,−
1,は次の と おり であ る。・,
一
ズ∬
exp1 ζ岫(T・・+・T・)1
・・s臨 (Tl+・・)1
・
E[コじ,(τ、)Xl(τ,}]dT,dτ, ・z一
囂
置 expl ζ飾(Tl + Ts)1
… 属 〔祠・
E
[xK T,>x,(v,)]d
τ,晦 ・イ ∬
exp1 ζ岬
釧 ・ ・s 臨一
T2)}・
E [x,(r、)x,(Tt)]d
“dr2
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
…
−t…
t・
・
・
…
t−・
(5.
16) (5.
16)式に自己相 関々数を代入 し た と きにexpl9 ・・rl
−
(
_
−1
一
塁
π)
z+(
舞
一
・)
’…
(5・
17 ) ある い は 即1
ζ婦[
(
.
杯
(
約
τ
昇
(
務
一
T2)
’]
’
’
”…
tt”
15
・
18) な る項が有る た め に (5.16
)の各積分は陽な形で解くこ と がで き ない。そ こで,
応答の 全継 続 時 間を 適当な 時 間々 隔に分 割して そ の間では (5.
17),
(5.
18)の各 式を近似 的に一
定 値と扱 う手 法 を用いる。
自己 相 関々数 (3.
13
) の R,項 以 外の項を含む積 分は rl, τ2 に関 する 1重 積 分 の積と な り, 各 積 分は区 分さ れ た時 間 内に対し て陽な形 で表すこ とがで きる。一
方,R ,
項 を 含む積 分で は 2重 積分 が 必要と な り, τ1−
r2=
=
u, τ1十τz=
v・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
…
(5.
19
) の 積分変数の変 換の 後に,
最初に v に関す る積 分 を 行 え ば,
u に関す る 正弦積分, 余弦積分 14L151 含ん だ形で解 を得ること が で き る。
∬〈」の場合の積分 はY
,Kt
)と して,
次式蹴
イ ∬
ゐ(t−−
q)h
(t−
Tz)Rxpc
,(Tl,
・T!)d
・,d
・・・
t−・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
・
…
tt・
・
・
…
(5.
20) はRxnc、
(T、、
T、)が τ1と τ!の それ ぞれ の関数の積に分解 さ れ る た め 比較的容易で あ る。
た だ し,
ここで も (5.17
) 式の形 を し た 関 数 部 分に対 して は前 と 同様に 区 分的に一
定値と し て扱う 近似手法が 必要で あ る。
以上の よ う に し て求め たyl
,ω,
y
粛 〉を用いて求め る2
乗 平 均 変 位応答E
[y2(t)]が N N N E [@2(t)]ニ ΣY
,Kt
)十2 Σ ΣY
,Kt
)……
(5.
20 ) 「己
1 fFl J≡
J十
1 と して得ら れ る。
な お,1,
」2
つ の 帯域が離れ てい て (… )式中の exp(
一
去
Σ・)
が ゼ・ と近似・ れ ・駘 ・,
減 衰の小 さい振 動系で周 波 数 応 答 関 数の ピー
ク が帯域 幅 に比べ て細く鋭い場 合には 上式の 2項 目を簡 略 化して ゆ N−
] E[y2(t)]=
ΣY
.(t)十2Σ Y,,
,. ,{t)………
(5.
21} ’i
匸 1=
1 とでき る。
5.
3
解 析結果お よ び考察 震 源の特性,
波動の伝播特 性などとの関係に よっ て位 相 傾斜の確 率 特性 を どの よ う にモ デル化 す る か,
ま た, そのモデル化の相違によっ て構 造物の応答が どの よ うに 変化す る か な ど につ いて の議論は別の機 会に行う こ と に して,
本節では,
本章に示 し た線形 応 答解析法の精度の 検証例を示す。 外 乱は帯 域が連 続し た 2ケの制 限 帯 域 波の合 成と して 考え る。
こ れ らの 帯 域 をFig.
11の よ うに1,
J
と区 別 して, 同 図お よ び (5.
11) 式にある諸 変 数を mt=
2,
Sr=
8,
ω 1.
1=
0,
ω Uf=
16,
α=
1.
0−
55
一
0
.
1・
・
。・。
o 》 〜
π
3》? 2π
Fig
.
12Compariso
ロ of theoretical and simulat 巳d RMS dis.
placement response of a linear system wlth ωo
=
ユ.
Q,
ζ
≡
0.
05.
MJ=
4, 8,=8
, ωL」=16
, tOVJ=32
, β=1.0
と す る。
振 動 系の固 有 振 動 数 an は1,
J
両 帯域の 境 界 の振 動 数に等 しくω、=
16 と し て両帯域 波の 相互相 関々 数Rx,
x.
(ti
,t
,)の影 響が強 く表れ る よ う に し た。 減 衰 定 数は ζ ・O.
05で あ る。
Fig.
12は解析 解と シ ミュ レー
ショ ン解との比 較で あ る が, シ ミュ レー
ショ ンは修正線 形 加 速 度 法に より 100 波の サンプル法に対して行っ た (図 中 点 線 )。
解 析 解は,
前 節に述べ た考え方に従い, 応 答の全 継 続 時間を 区 分化 して図 中の黒 丸の点につ い て求めた の あるが,
便 宜 的に 破線で結んである。
解 析 解とシ ミュ レー
ショ ン解との対 応は非 常に良 好であり, 外 乱の自己相 関々数を陽な形で 求め た (5,
3),
(3.
13), (5.
9)の各 式,
お よびそ れ らの 関 数を用い た線 形 系の 2乗 平 均 応 答の近 似 解 法 が妥 当で ある こ とが確 認さ れ た。
こ こで は変位 応答のみ を示し た が,
(5.
13}式のh
{t)をh
(t)に代え れば 速 度 応 答が求 め られ る。
さ らに,
変位と速 度との積の応 答 も求めれ ばE
[(抄十2
)2]=4
ζ2(砧E
[シ2]十ω言E
[y2] 十4ζω港E [yg ]・
…
t−・
・
・
・
・
・
・
・
・
…
(5.
22) の関 係か ら加速度 応 答を求め る こともで き る。
5.4
線形 応 答 解 析 法に関 する補 足5.2
節で は外乱の 自己相 関々数を利 用し た時 間 領 域の 樌 分 に よ る 応答 解 析の手法 を示し たが,
応 答の フー
リエ 変 換y
〔ω)が外 乱の フー
リエ 変in
X(ω)と系の周 波 数 応 答 関 数H
(ω)とによっ てy
(ω)=H
(ω)・
X
(ω)……・
………・
・
…………
(5,
23 ) と表さ れ るこ と を利 用 すれ ば,
応 答 y(t
)がY
〔ω)の 逆 フー
リエ 変換とし てy(
t
)=
ΣH
(ωk)X
(ω κ)exp (icakt
)・
・
…・
…
(5.
24)陀
=
−
n に よ り与え ら れ ること よ り,
2乗 平 均 応 答を・[幽
一
∫
:
f
:
H
(紬 )・・(c・}・[・(妨 )・・(岫}]鹽
e“ω1一
ω 21 τd
ω Id ω 2…・
…………・
(5.
25} な る周波 数 領 域の積分によっ て得る こと も で きる。
た だ しこ の場 合に は,
周 波 数 領 域を適 当に区 分し た積分 を行 う 必要がある。
.
− 56 一
6.
結 び 以上の各 章の内 容を要約す る と以 下の とお りにな るe 1) 位 相 傾 斜 を 正 規 分 布も し くは正規 分 布に類 似し た 分 布を持つ 確 率 変 数と す れば,
位 相 角の 差に関す る確 率 密 度 関 数 を正 規 分 布で 近似す ること がで き る。2) 位 相 傾 斜の特 性を用い て非 定 常 外 乱の平 均, 2 乗 平 均
,
自己相関々数 な どの 定 式化を行う場 合に, 外乱の 振 動 数 がゼロの 成分に対応 する位 相 角 φ。の確 率分布の 影 響 を受け る。一
般の外 乱を複 数の制 限 帯 域 波の和 と し て表す 場 合に,
φ。
を 様 な乱 数とす れ ば, 個々 の帯 域 波の振 幅 特 性の時 間 的変化 の ピー
ク発 生 時 刻は位 相 傾 斜 の平 均に より決 まり,
ピー
ク の尖度は主に位 相 傾斜の分 散に よ り決る。
ま た,
個々 の 帯 域 波の平 均は ゼ ロで, し たがっ て外 乱 全体と して も その平 均 値はゼロ と な る。
3) 外 乱 振 幅の非 定常性を振 幅 変 調 関 数と定 常外 乱 と の積と して表尊
方 法に は,
制 限 帯 域 white noise の帯域 幅の狭く な る程,
ま た変 調 関 数の非 定常性の強い程,
変 調 前 後での周波数特性の変 化が大き く な る という欠点 が あ る。
これに対 し,
位 相 傾 斜の確 率特性に基づ い て外 乱 振幅の非 定 常 性 を決 める方 法で は,
外 乱の全 継 続 時 間を 周期と し た時の パ ワー
スペ ク トル密 度を変え ること無く 振 幅変 調を行え るとい う利 点が ある。
この利 点は,
理 論 式におい て もほ と ん ど保 持さ れ るこ と が認め ら れ た。
4) 近 年
,
位 相 傾 斜の特 性を利 用して非 定 常 外 乱 を模 擬す る手 法が注 目され ている が,
本論で示 した手 法によ り そ の よ う な模 擬 外 乱の確 率特性を理 論 的に得る ことが で き,
さ らに同外乱 に対 す る線 形 系の応 答 を理論 的に求 め る こと が で き る。 断 層モデル等により位 相 傾 斜の確 率 特 性 と震 源 過程と の関係も 明 らかにさ れつ つ あるの で,
本 手法 は 構 造 物モ デルの不 規 則 振 動 解析に対し て震 源 過 程の影響を考慮す る手 法の 1つ として有 効な手段に な り 得る。
謝 辞本研究を進めて行くに当た り
,
千 葉 大学教授尾崎昌凡 博 士よ り数々 の指導と助 言と を賜り ま し た。
厚く御 礼申 し上げ ま す。
参 考 文 献 ]) 曽 田五月也 ;非 定 常 不 規 則 外乱の平 均 お よ び2乗 平 均に対す る位 相 特 性の影 響 (そ の 1
,
Band limited whitenoise の場 合
1,
日本 建 築 学 会 関東支部 研 究 報 告,
昭 和59年 7月
,
pp,
245−
2482) 曽田五 月也:同上 (その 2