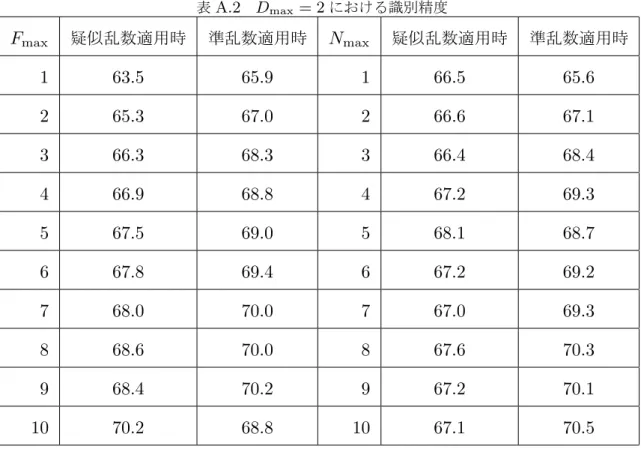
26 Feature Extraction with Randomness for an Application to Machine Learning from Text Data
60
0
0
全文
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(13)
(14)
(15)
(16)
(17)
(18)
(19)
(20)
(21)
(22)
図
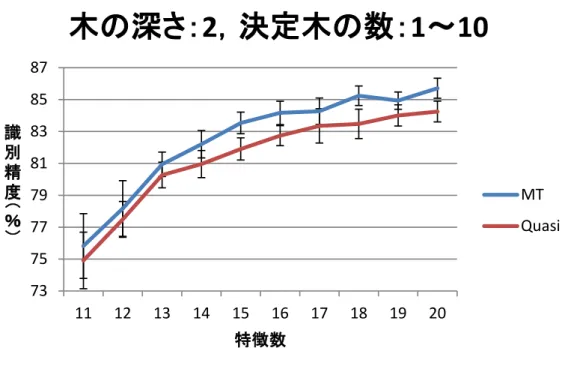
+2
Outline
関連したドキュメント
これはつまり十進法ではなく、一進法を用いて自然数を表記するということである。とは いえ数が大きくなると見にくくなるので、.. 0, 1,
(注)本報告書に掲載している数値は端数を四捨五入しているため、表中の数値の合計が表に示されている合計
、肩 かた 深 ふかさ を掛け合わせて、ある定数で 割り、積石数を算出する近似計算法が 使われるようになりました。この定数は船
巣造りから雛が生まれるころの大事な時 期は、深い雪に被われて人が入っていけ
2リットルのペットボトル には、0.2~2 ベクレルの トリチウムが含まれる ヒトの体内にも 数十 ベクレルの
られる。デブリ粒子径に係る係数は,ベースケースでは MAAP 推奨範囲( ~ )の うちおよそ中間となる
(注)本報告書に掲載している数値は端数を四捨五入しているため、表中の数値の合計が表に示されている合計
その太陽黒点の数が 2008 年〜 2009 年にかけて観察されな