あもんノート
ユークリッド幾何学、ニュートン力学から、相対論、量子論、素粒子 論、宇宙論、そして超ひも理論まで、理論物理学を簡潔にかつ幅広く網 羅したノートです。TOP へは下の URL をクリックして行けます。専用 の画像掲示板で、ご意見、ご質問等も受け付けております。 http://amonphys.web.fc2.com/目 次
第19章 素粒子論の計算 3 19.1 クリフォード代数とトレース公式 . . . . 3 19.2 μ粒子の対生成 . . . . 4 19.3 メラー散乱 . . . . 6 19.4 バーバー散乱 . . . . 8 19.5 コンプトン散乱 . . . 10 19.6 実験室系におけるコンプトン散乱 . . . 13 19.7 対消滅 . . . 14 19.8 荷電π粒子の寿命 . . . 16 19.9 レプトン対のヘリシティ . . . 17 19.10 μ粒子の寿命 . . . 19 19.11 中性子の寿命 . . . 21 19.12 中性π粒子の寿命 . . . 22 19.13 ファインマングラフの数値計算 . . . 24第
19
章 素粒子論の計算
ファインマングラフに基づく素粒子論の解析的計算は、特にフェルミオンが絡 む現実的な問題においては、ガンマ行列の存在のため複雑かつトリッキーで、間 違えやすいです。そこでここではいくつか代表的な計算例を紹介します。量子電 磁力学(QED)と素粒子論は既知とします。19.1
クリフォード代数とトレース公式
ガンマ行列のクリフォード代数は、 {γµ, γν} = 2gµν でした。これに注意すると、 {γµ, γµ} = 2δµµ = 8 ∴ γµγµ = 4. また、 γµγαγµ = (2gµα−γαγµ)γµ = 2γα− 4γα = −2γα. 同様にやって、 γµγαγβγµ = 4gαβ, γµγαγβγγγµ = −2γγγβγα を得るでしょう。 一方、ガンマ行列n個の積のトレース: tr(γµ1γµ2· · · γµn) については、ガンマ行 列の成分のあり方からn が奇数のときは 0 で、n = 2 のときは tr(AB) = tr(BA) に注意して、 tr(γµγν) = 1 2tr({γ µ, γν}) = gµνtr 1 = 4gµν. n = 4 のときは、 tr(γµγνγργσ) = (1/2) tr({γµ, γνγργσ}) = (1/2) tr({γµ, γν}γργσ − γν{γµ, γρ}γσ + γνγρ{γµ, γσ}) = gµνtr(γργσ) − gµρtr(γνγσ) + gµσtr(γνγρ) = 4gµνgρσ − 4gµρgνσ + 4gµσgνρと計算されます。これらをガンマ行列のトレース公式といいます。 トレースに γ5 が含まれる場合、すなわち tr(γ5γµ1γµ2· · · γµn) は、n が奇数のと きはやはり成分のあり方から 0 で、また、 trγ5 = 0, tr(γ5γµγν) = 0 も直接的に確かめられるでしょう。一方、tr(γ5γµγνγργσ) については、これが4つ の添字について完全反対称であることがわかるので、²µνρσ を4元レビ・チビタと して、 tr(γ5γµγνγργσ) = ²µνρσtr(γ5γ0γ1γ2γ3) = −i²µνρσtr(γ5γ5) = −4i²µνρσ となります。 これら公式はディラック場を含むファインマングラフの計算で頻繁に用いられ るので、少なくともここに示したものは全て暗記してしまった方がよいでしょう。 また、ディラック場の平面波振幅の性質、 (/p − m)us(p) = 0, (/p + m)vs(p) = 0, X s us(p)¯us(p) = /p + m, X s vs(p)¯vs(p) = /p − m も思い出しておくべきでしょう。ここで /p は γ ·p の略記です。
19.2
μ粒子の対生成
まずは、電子と陽電子の衝突によるμ粒子の対生成 : e¯e → µ¯µ の断面積を求めてみましょう。これは QED におけるもっともやさしい計算問題 といえます。 グラフは素電荷 e の最低次で図19.1だけであり、よって散乱振幅は、 M = −igµν (k1+k2)2 ¯ v2(ieγµ)u1u¯3(ieγν)v4 = ie 2 (k1+k2)2 (¯v2γµu1)(¯u3γµv4) となります。ui = usi(ki), vi = vsi(ki) という略記を用いました。よって、 X s1∼s4 |M|2 = e 4 (k1+k2)4 X s1∼s4 (¯v2γµu1)(¯u3γµv4)(¯u1γνv2)(¯v4γνu3) = e 4 (k1+k2)4 X s1∼s4 tr(γµu1u¯1γνv2v¯2) tr(γµv4v¯4γνu3u¯3) = e 4 (k1+k2)4 tr(γµ/k1γν/k2) tr ¡ γµ(/k4−m)γν(/k3+m) ¢ .図 19.1: μ粒子の対生成 m ∼ 106 MeV はµ粒子の質量で、電子の質量 (∼ 0.5 MeV) はこれと比べてずっ と小さいので無視しました。系のエネルギーが 2m より大きくないとこの反応は 生じず、反応が生じる場合、電子は重心系において常に超相対論的(エネルギーÀ 質量)であることに注意してください。よってこの近似は妥当なわけです。 トレース公式で展開すると、 X s1∼s4 |M|2 = e 4 (k1+k2)4 ¡ 4k1µk2ν + 4k1νk2µ − 4gµνk1·k2 ¢ ס4k3µkν4 + 4k3νkµ4 − 4gµνk3·k4 − 4gµνm2 ¢ = 32e 4 (k1+k2)4 ¡ k1·k3k2·k4 + k1·k4k2·k3 + m2k1·k2 ¢ . 重心系においては、エネルギーの保存に注意して、 k1µ = (|k|, k), k2µ = (|k|, −k), k3µ = (|k|, k0), k4µ = (|k|, −k0) とおけるので、散乱角(kとk0の成す角) を θ として、 X s1∼s4 |M|2 = 32e 4 (2|k|)4 ³ (|k|2−|k||k0| cos θ)2 + (|k|2+|k||k0| cos θ)2 + 2m2|k|2 ´ = 4e 4 |k|2 ¡ |k|2 + |k0|2cos2θ + m2¢ となります。 スピンを観測しないものとすると、始状態においては平均をとり、終状態にお いては和をとることになるので、微分断面積は、 dσ dΩ = 1 64π2(2|k|)2 |k0| |k| 1 4 X s1∼s4 |M|2 = e 4|k0| 256π2|k|5 ¡ |k|2 + m2 + |k0|2cos2θ¢
と評価され、またエネルギー保存から |k0| = p|k|2−m2 です。断面積は、 σ = 2π Z π 0 dθ sin θ dσ dΩ = e4p|k|2−m2¡2|k|2+m2¢ 96π|k|5 となります。
19.3
メラー散乱
電子の2体弾性散乱 : ee → ee をメラー散乱といいます。グラフは摂動の最低次で図19.2の2つです。 図 19.2: メラー散乱 これらを A, B とすると、 A = ie 2 (k1−k3)2 (¯u3γµu1)(¯u4γ µu 2), B = −ie 2 (k1−k4)2 (¯u4γµu1)(¯u3γ µu 2). B の式のマイナス因子はフェルミオンの統計符号因子です。 X s1∼s4 |M|2 = X s1∼s4 |A + B|2 = X s1∼s4 |A|2 + X s1∼s4 |B|2 + X s1∼s4 AB∗ + X s1∼s4 A∗B と展開し、各項を計算していきましょう。 X |A|2 = e4 (k1−k3)4 X (¯u3γµu1)(¯u4γµu2)(¯u1γνu3)(¯u2γνu4) = e 4 (k1−k3)4 tr ¡ γµ(/k1+m)γν(/k3+m) ¢ tr¡γµ(/k2+m)γν(/k4+m) ¢ = e 4 (k1−k3)4 ¡ 4k1µk3ν + 4k1νk3µ − 4gµνk1·k3 + 4m2gµν ¢ ס4kµ2k4ν + 4k2νk4µ− 4gµνk2·k4 + 4m2gµν ¢∴ X|A|2 = 32e 4 (k1−k3)4 ¡ k1·k2k3·k4 + k1·k4k2·k3 − m2k1·k3 − m2k2·k4+ 2m4 ¢ . m は電子の質量です。P|B|2 はこの式の kµ3 と kµ4 を入れ換えた式なので、 X |B|2 = 32e4 (k1−k4)4 ³ k1·k2k3·k4 + k1·k3k2·k4 − m2k1·k4 − m2k2·k3 + 2m4 ´ . また、 X AB∗ = −e 4 (k1−k3)2(k1−k4)2 X (¯u3γµu1)(¯u4γµu2)(¯u1γνu4)(¯u2γνu3) = −e 4 (k1−k3)2(k1−k4)2 tr¡γµ(/k1+m)γν(/k4+m)γµ(/k2+m)γν(/k3+m) ¢ ですが、この式のトレース部は、クリフォード代数の公式に注意して、 tr¡¡−2/k4γν/k1 + 4m(k1ν+k4ν) − 2m2γν ¢ (/k2+m)γν(/k3+m) ¢ と変形され、これを展開してできる3つのトレース部は、順に、 −32 k1·k2k3·k4 + 16m2k1·k4, 16m2(k1·k2 + k1·k3 + k2·k4 + k3·k4), 16m2k2·k3 − 32m4 を与えるので、 X AB∗ = 16e 4 (k1−k3)2(k1−k4)2 ³ 2k1·k2k3·k4 + 2m4 − m2¡k1·k2 + k1·k3 + k1·k4 + k2·k3 + k2·k4 + k3·k4 ¢´ . これは実数ですから、PA∗B も同じ式になります。 重心系をとり、入射運動量を k, 散乱角を θ とすれば、 k1·k2 = k3·k4 = 2|k|2 + m2, k1·k3 = k2·k4 = |k|2(1−cos θ) + m2, k1·k4 = k2·k3 = |k|2(1+cos θ) + m2 に注意して、 X |A|2 = 8e4 (2|k| 2+m2)2 + |k|4(1+cos θ)2 + 4m2|k|2cos θ + m4 |k|4(1−cos θ)2, X |B|2 = 8e4 (2|k|2+m2)2 + |k|4(1−cos θ)2 − 4m2|k|2cos θ + m4 |k|4(1+cos θ)2, X AB∗ = XA∗B = 8e4 4|k| 4 − m4 |k|4sin2θ
となります。これらを加えて整理すれば、 X |M|2 = 16e 4 |k|4sin4θ ³ 9|k|4 + 6|k|4cos2θ + |k|4cos4θ + 4m2|k|2 + 12m2|k|2cos2θ + m4 + 3m4cos2θ ´ = 16e 4 sin4θ µ (4−sin2θ)2 + m 2(m2+4|k|2) |k|4 (4−3 sin 2θ) ¶ . よって微分断面積は、 dσ dΩ = 1 64π2¡2p|k|2+m2¢2 1 4 X |M|2 = e 4 64π2(|k|2+m2) sin4θ µ (4−sin2θ)2 + m 2(m2+4|k|2) |k|4 (4−3 sin 2θ) ¶ となります。
19.4
バーバー散乱
電子と陽電子の弾性散乱 : e¯e → e¯e をバーバー散乱といいます。グラフは摂動の最低次で図19.3の2つです。 図 19.3: バーバー散乱 これらを A, B とすると、 A = ie 2 (k1−k3)2 (¯u3γµu1)(¯v2γ µv 4), B = −ie2 (k1+k2)2 (¯v2γµu1)(¯u3γ µv 4). B の式のマイナス因子はフェルミオンの統計符号因子です。ここでは簡単のため高エネルギー極限(|ki| À m)において考えましょう。この とき電子の質量 m を無視できて、 X spins |A|2 = e4 (k1−k3)4 tr¡γµ/k1γν/k3 ¢ tr¡γµ/k4γν/k2 ¢ = 32e 4 (k1−k3)4 ¡ k1·k2k3·k4 + k1·k4k2·k3 ¢ , X spins |B|2 = e 4 (k1+k2)4 tr¡γµ/k1γν/k2 ¢ tr¡γµ/k4γν/k3 ¢ = 32e4 (k1+k2)4 ¡ k1·k3k2·k4 + k1·k4k2·k3 ¢ , X spins AB∗ = −e 4 (k1−k3)2(k1+k2)2 tr ¡ γµ/k1γν/k2γµ/k4γν/k3 ¢ = 32e 4 (k1−k3)2(k1+k2)2 k1·k4k2·k3. 重心系をとり、入射運動量を k, 散乱角を θ とすれば、 k1·k2 = k3·k4 = 2|k|2, k1·k3 = k2·k4 = 2|k|2sin2(θ/2), k1·k4 = k2·k3 = 2|k|2cos2(θ/2) となることに注意して、 X |A|2 = 8e4 1 + cos4(θ/2) sin4(θ/2), X |B|2 = 4e4(1 + cos2θ), X
(AB∗ + A∗B) = 2XAB∗ = −16e4 cos
4(θ/2) sin2(θ/2). よって、高エネルギー極限での微分断面積は、 dσ dΩ = 1 64π2(2|k|)2 1 4 X ¡ |A|2 + |B|2 + AB∗ + A∗B¢ = e 4 128π2|k|2 µ 1 + cos4(θ/2) sin4(θ/2) − 2 cos4(θ/2) sin2(θ/2) + 1 + cos2θ 2 ¶ となります。
19.5
コンプトン散乱
電子と光子の弾性散乱 : eγ → eγ はコンプトン散乱と呼ばれます。ファインマングラフは摂動の最低次で図19.4の 2つです。 図 19.4: コンプトン散乱 まとめて式にすると、 M = −ie2εµλ0(q0)ενλ(q) ¯us0(p0) µ γµ 1 /p+/q−mγν + γν 1 /p−/q0−mγµ ¶ us(p) です。電子の4元運動量を始状態と終状態においてそれぞれ pµ, p0µ とし、光子の それらを qµ, q0µ としました。 光子が始状態や終状態にあると、スカラーモードと縦波モードについて少し考 えてやる必要があります。 εµ0(q) + εµ3(q) = qµ/|q| および、簡単に確かめられる等式 : 1 /p+/q−m /qus(p) = us(p), u¯s0(p 0)/q 1 /p0−/q−m = −¯us0(p 0) に注意すると、任意のスカラーモードを縦波モードに入れ換えたとき、散乱振幅 M は符号を変えるだけであることがわかるでしょう。すなわち、 M |λ=0 +M |λ=3 = 0, M |λ0=0 +M |λ0=3 = 0. このような等式はワード・高橋恒等式と総称されます。これにより、 X λ,λ0 dλdλ0|M|2 = X λ=1,2 X λ0=1,2 |M|2が成り立ちます。ここで dλ は λ = 0 のとき −1, 他のとき+1 を与える因子です。 そうすると、 X phys |M|2 := X s,s0 X λ=1,2 X λ0=1,2 |M|2 = X s,s0,λ,λ0 dλdλ0|M|2 = e4 X s,s0,λ,λ0 dλdλ0 εµ λ0(q0)ενλ(q) ερλ0(q0)εσλ(q) × ¯us0(p0) µ γµ 1 /p+/q−mγν + γν 1 /p−/q0−m γµ ¶ us(p) × ¯us(p) µ γσ 1 /p+/q−mγρ+ γρ 1 /p−/q0−m γσ ¶ us0(p0) ですが、 X λ dλεµλ(q)ενλ(q) = X λ,λ0 (−gλλ0)εµλ(q)ενλ0(q) = −gµν および 1 /p+/q−m = /p+/q+m 2p·q, 1 /p−/q0−m = − /p−/q0+m 2p·q0 に注意すると、 X phys |M|2 = e 4 4(p·q)2 tr ¡ (/p0+m)γµ(/p+/q+m)γν(/p+m)γν(/p+/q+m)γµ ¢ + e4 4(p·q0)2 tr ¡ (/p0+m)γν(/p−/q0+m)γµ(/p+m)γµ(/p−/q0+m)γν ¢ − e 4 4p·q p·q0 tr ¡ (/p0+m)γµ(/p+/q+m)γν(/p+m)γµ(/p−/q0+m)γν ¢ − e4 4p·q p·q0 tr ¡ (/p0+m)γν(/p−/q0+m)γµ(/p+m)γν(/p+/q+m)γµ ¢ と展開されるでしょう。最初のトレース部は、クリフォード代数の公式により、 4 tr¡(/p0−2m)(/p+/q+m)(/p−2m)(/p+/q+m)¢ となりますが、4元運動量保存則 p0µ = pµ + qµ − q0µ および p02 = m2 からわかる q·q0 = p·q − p·q0 という等式に注意すると、ガンマ行列4つの積から来る寄与、2 つの積から来る寄与、ガンマ行列を含まない項から来る寄与は、順に、 16m4+16m2p·q+16m2p·q0+32 p·q p·q0, −48m4+16m2p·q−16m2p·q0, 64m4 となるでしょう。よって、 最初のトレース部= 32m4 + 32m2p·q + 32 p·q p·q0. また、2番目のトレース部は、最初のトレース部を q → −q0, q0 → −q と置換した ものなので、 2番目のトレース部 = 32m4 − 32m2p·q0+ 32 p·q p·q0.
一方、3番目のトレース部は、やはりクリフォード代数の公式により、 tr¡(/p0+m)¡−2/pγν(/p+/q)+4m(2pν+qν)−2m2γν ¢ (/p−/q0+m)γν¢ となりますが、展開して得られる3つのトレース部は、順に、 −16m4−16m2p·q+32m2p·q0, 64m4+32m2p·q−32m2p·q0, −16m4−16m2p·q0 を与えるので、 3番目のトレース部 = 32m4 + 16m2p·q − 16m2p·q0. 再び置換 q → −q0, q0 → −q により、 4番目のトレース部 = 32m4 + 16m2p·q − 16m2p·q0. よって結局、 X phys |M|2 = 8e4 Ã p·q p·q0 + p·q0 p·q − 2m 2 µ 1 p·q0 − 1 p·q ¶ + m4 µ 1 p·q0 − 1 p·q ¶2! を得ます。 特に重心系においては、 pµ = (E, p), qµ = (|p|, −p), p0µ = (E, p0), q0µ = (|p|, −p0) とおけて、ここで E = p|p|2 + m2 です。散乱角を θ とすれば、 X phys |M|2 = 8e4 Ã E + |p| cos θ E + |p| + E + |p| E + |p| cos θ − µ m sin θ E + |p| cos θ ¶2! と整理されます。よって微分断面積は、 dσ dΩ = 1 64π2(E + |p|)2 1 4 X phys |M|2 = e 4 32π2(E + |p|)2 Ã E + |p| cos θ E + |p| + E + |p| E + |p| cos θ − µ m sin θ E + |p| cos θ ¶2! となり、これはクライン・仁科の公式(重心系版)と呼ばれます。断面積は、 σ = e 4 16π(E + |p|)2 µ 2E E + |p| + 4m2 |p|2 + µ 1 + E |p| − 2m2E |p|3 ¶ log E + |p| E − |p| ¶ と計算されます。
非相対論的極限 (m À |p|) におけるコンプトン散乱はトムソン散乱と呼ばれま すが、その微分断面積、および断面積は、 dσ dΩ = e4 32π2m2 (2 − sin 2θ), σ = e4 6πm2 となることがわかります。 (余談) コンプトン散乱の計算は、丁寧に導出が書かれている文献が見つからず、ほとんど独自 に行ったのですが、ワード・高橋恒等式や q·q0 = p·q − p·q0 の存在になかなか気付かず、1ヶ月ほ ど悩み苦しみました。ここでは読者が同じ苦しみを味合わなくて済むよう、計算の過程を比較的 丁寧に書きました。
19.6
実験室系におけるコンプトン散乱
コンプトン散乱において、始状態で電子が静止している系を実験室系といいま す。重心系に対する実験室系の速さは、重心系における電子の速さ v = |p|/E で あり、実験室系における始状態の光子の角振動数(=エネルギー)を ω, 終状態の それを ω0 とすると、光のドップラー効果に注意して(電磁気学の章参照)、 ω = √1 + v 1 − v2 |p| = |p| m (E + |p|), ω0 = 1 + v cos θ√ 1 − v2 |p| = |p| m (E + |p| cos θ) です(図19.5)。 図 19.5: 重心系と実験室系 また、実験室系における散乱角を Θ とすれば、光行差により、 cos Θ = cos θ + v 1 + v cos θ = E cos θ + |p| E + |p| cos θ であり、この式から、 sin Θ = m sin θ E + |p| cos θ, ∂ cos Θ ∂ cos θ = µ m E + |p| cos θ ¶2が得られるでしょう。 以上の式から、実験室系におけるコンプトン散乱の微分断面積は、 dσ d(cos Θ)dφ = µ ∂ cos Θ ∂ cos θ ¶−1 dσ dΩ = e4 32π2m2 µ ω0 ω ¶2µ ω0 ω + ω ω0 − sin 2Θ ¶ となることがわかり、これがクライン・仁科の公式の実験室系版です。コンプト ン散乱は素粒子論より物性論で扱われることが多いため、このような実験室系に おける式の方が広く知られているようです。 ω, cos Θ の式を逆に解くと、 |p| = p ω 1 + (2ω/m), E = m + ω p 1 + (2ω/m), cos θ = (m + ω) cos Θ − ω m + ω(1 − cos Θ) となることに注意して、散乱後の光子の角振動数 ω0 は、 ω0 = ω 1 + (ω/m)(1 − cos Θ) で与えられることがわかります(∗)。 (*注) これは実験室系におけるエネルギー運動量保存則からも簡単に導かれる関係式で、高校 物理でも扱われます。波長で表せば λ0 = λ + (2π/m)(1 − cos Θ) となります。
19.7
対消滅
次に電子と陽電子の対消滅 : e¯e → γγ を考えましょう。グラフは摂動の最低次で図19.6の2つです。 図 19.6: 対消滅 まとめて式にすると、 M = −ie2εµλ0(q0)ενλ(q) ¯vs0(p0) µ γµ 1 /p−/q−mγν + γν 1 /p−/q0−mγµ ¶ us(p).ここからコンプトン散乱と同様な計算により、 X phys |M|2 = e 4 4(p·q)2 tr ¡ (/p0−m)γµ(/p−/q+m)γν(/p+m)γν(/p−/q+m)γµ ¢ + e 4 4(p·q0)2 tr ¡ (/p0−m)γν(/p−/q0+m)γµ(/p+m)γµ(/p−/q0+m)γν ¢ + e 4 4p·q p·q0 tr ¡ (/p0−m)γµ(/p−/q+m)γν(/p+m)γµ(/p−/q0+m)γν ¢ + e 4 4p·q p·q0 tr ¡ (/p0−m)γν(/p−/q0+m)γµ(/p+m)γν(/p−/q+m)γµ ¢ を得るでしょう。トレース部は、1番目が、 −32m4 + 32m2p·q + 32 p·q p·q0. 2番目が、 −32m4 + 32m2p·q0 + 32 p·q p·q0. 3番目と4番目が、 −32m4 + 16m2p·q + 16m2p·q0 となります。よって、 X phys |M|2 = 8e4 Ã p·q0 p·q + p·q p·q0 + 2m 2 µ 1 p·q + 1 p·q0 ¶ − m4 µ 1 p·q + 1 p·q0 ¶2! と整理されます。重心系においては、
pµ = (E, p), qµ = (E, p0), q0µ = (E, −p0), E = |p0| = p|p|2 + m2
とおけて、散乱角を θ とすれば、 X phys |M|2 = 8e4 Ã E +|p| cos θ E −|p| cos θ + E −|p| cos θ E +|p| cos θ + 2m2 E µ 1 E −|p| cos θ + 1 E +|p| cos θ ¶ − m4 E2 µ 1 E −|p| cos θ + 1 E +|p| cos θ ¶2 ! = 16e4 E 4 − |p|4cos4θ + 2m2|p|2sin2θ (E2 − |p|2cos2θ)2. よって、微分断面積は、 dσ dΩ = 1 64π2(2E)2 E |p| 1 4 X phys |M|2 = e 4 64π2E|p| E4 − |p|4cos4θ + 2m2|p|2sin2θ (E2 − |p|2cos2θ)2.
また、断面積は、θ の積分範囲が 0 ∼ π/2 であることに注意して、 σ = e 4 32πE|p| µ −1 − m 2 E2 + µ E |p| + m2 E|p| − m4 2E3|p| ¶ logE + |p| E − |p| ¶ となります。
19.8
荷電π粒子の寿命
荷電π粒子は、4フェルミ型の弱い相互作用 : LI = − GF √ 2 fπ∂µπ ∗ ¯lγµ(1−γ 5)ν を通じてレプトン対に崩壊すると考えられます : π− → l¯ν. l は電子もしくはµ粒子で、ν はそれらと対を成すニュートリノです。τ 粒子への 崩壊は τ 粒子の質量が荷電 π 粒子のそれより大きいため有り得ません。GF は フェルミの結合定数、fπ はπ粒子の崩壊定数です。 図 19.7: 荷電π粒子の崩壊 崩壊のファインマングラフは最低次で図19.7であり、よって散乱振幅は、 M = −iG√Ffπ 2 (−ikµ) ¯us(p)γ µ(1−γ 5)vs0(p0) = −G√Ffπ 2 u¯s(p)(/p+/p 0)(1−γ 5)vs0(p0) = −GF√fπml 2 u¯s(p)(1−γ5)vs0(p 0).ここで ml は電子族のレプトンの質量です。ニュートリノ族の質量は0としまし た。よって、 X s,s0 |M|2 = (GFfπml)2 2 X s,s0 ¯ us(p)(1−γ5)vs0(p0) ¯vs0(p0)(1+γ5)us(p) = (GFfπml) 2 2 tr ¡ (/p+ml)(1−γ5)/p0(1+γ5) ¢ = (GFfπml)2 tr ¡ (/p+ml)/p0(1+γ5) ¢ = 4(GFfπml)2p·p0. 重心系においては pµ = (E, p), p0µ = (|p|, −p), E = p|p|2 + m2l であり、 X s,s0 |M|2 = 4(GFfπml)2 |p|(E + |p|) となります。よって崩壊幅は、 Γ T = |p| 32π2m2 π X s,s0 |M|2 · 4π = (GFfπml) 2 2πm2 π |p|2(E + |p|) ですが、エネルギー保存から mπ = E + |p| で、これを |p| について解くと、 |p| = (m2π − m2l)/(2mπ) を得るので、これらを代入して、 Γ T = ¡ GFfπml(m2π − m2l) ¢2 8πm3 π となります。
me ∼ 0.51100 MeV, mµ ∼ 105.66 MeV, mπ ∼ 139.6 MeV,
fπ ∼ 128 MeV, GF ∼ 1.166 × 10−11MeV−2 という近似値を用いると、崩壊先が µ 粒子の場合 Γ/T ∼ 2.52 × 10−14 MeV, 崩 壊先が電子の場合 Γ/T ∼ 3.23×10−18 MeV となり、µ 粒子への崩壊が圧倒的優 勢であることがわかります。すなわち主崩壊は π− → µ¯νµ であり、π− の寿命は τπ− ∼ (2.52×10−14 MeV)−1 ∼ 2.61×10−8 sec と計算されます。 寿命が実験値と合うのは崩壊定数 fπ をそのように決めたので当然ですが、電子 および µ 粒子への崩壊の分岐比が実験値とよく合うのは、荷電 π 粒子崩壊が弱い 相互作用によることの証拠と考えられます。
19.9
レプトン対のヘリシティ
上の計算では崩壊後のレプトン対のヘリシティ s, s0 について和を取っています が、実のところ重心系においては s = s0 = +1 以外の寄与は全て 0 になります。実際、重心系においては、 Mss0 = −GF√fπml 2 u¯ (l) s (p)(1−γ5)v(ν)s0 (−p) ですが、 vs(p) = iγ2u∗s(p), us(p) = µ R(θ, φ) 0 0 R(θ, φ) ¶ fs(|p|) および、 R(π − θ, φ ± π) = ±iR(θ, φ)σ1, R†(θ, φ)²R∗(θ, φ) = ² det R∗(θ, φ) = ² に注意すると、 Mss0 = ±i √ 2GFfπmlfs(l)†(|p|) µ σ3 0 0 0 ¶ fs(ν)∗0 (|p|) を得ます。よって、 f+(k) = √ k0 + k 0 √ k0 − k 0 , f−(k) = i 0 √ k0 − k 0 √ k0 + k に注意すると、s = s0 = +1 以外の成分は全て 0 で、 M++ = ±i 2GFfπml p |p|pE + |p|, E = q |p|2 + m2 l です。これは角運動量保存と反ニュートリノのヘリシティが必ずプラス(右巻きス ピン)であることからも当然成り立つべき事柄で、π− → l¯ν で生じるレプトン対 は必ずプラスのヘリシティを持ちます。 この現象を鏡に映すと、鏡の中の世界ではレプトン対のヘリシティは必ずマイ ナスになり、それは “こちらの世界” ではあり得ない現象で、パリティの破れのわ かりやすい検証例になっています(図19.8)。ニュートリノのヘリシティを直接的 に測定することは不可能ですが、電子族のレプトンは電荷を持っているので、そ のヘリシティを容易に測定できます。 ちなみに、もし鏡に映すことで粒子と反粒子が逆になると考えれば、鏡の中で の崩壊は π+ → ¯lν であり、このときレプトン対のヘリシティはマイナスでよく、 それは崩壊幅まで含めてこちらの世界と違いがありません。これは4フェルミ型 の弱い相互作用のモデルが CP 対称性を持っていることの帰結です。
図 19.8: 鏡の中の世界のヘリシティ
19.10
μ粒子の寿命
次はμ粒子の崩壊です。崩壊モードはエネルギー保存から弱い相互作用による µ → e¯νeνµ だけで、ファインマングラフは最低次で図19.9であり、散乱振幅は、 M = −iG√F 2 u¯1γ µ(1−γ 5)v2 u¯3γµ(1−γ5)us(k) です。 図 19.9: μ粒子の崩壊 µ粒子の質量を m とし、電子とニュートリノの質量を無視すると、 X s,s1∼s3 |M|2 = G2F 2 tr ¡ /p1γµ(1−γ5)/p2γν(1−γ5) ¢ tr¡/p3γµ(1−γ5)(/k+m)γν(1−γ5) ¢ = G 2 F 2 × 8 ¡ pµ1pν2 + pν1pµ2 − gµνp1·p2 − i²µνρσp1ρp2σ ¢ × 8¡p3µkν + p3νkµ − gµνp3·k − i²µνλτpλ3kτ ¢ = 128G2F p1·p3p2·k.²µνρσ² µνλτ = −2(δλρδστ − δτρδλσ) に注意。重心系においては、 X s,s1∼s3 |M|2 = 128G2Fm|p1||p2||p3|(1 − cos θ). ここで θ は p1 と p3 が成す角です。 終状態が3体ですから、ここからが少々難しいです。 dΓ = | < f |S|i > | 2 < i|i > d3p1 (2π)32p0 1 d3p2 (2π)32p0 2 d3p3 (2π)32p0 3, < i|i >= 2k0V, | < f |S|i > |2 = (2π)4T V δ4(p1+p2+p3−k)|M|2 に注意して、 dΓ T = δ4(p 1+p2+p3−k) 16(2π)5k0p0 1p02p03 1 2 X s,s1∼s3 |M|2 d3p1d3p2d3p3 = 4G 2 F (2π)5 δ 4(p 1+p2+p3−k)(1 − cos θ) d3p1d3p2d3p3 = G 2 F 8π5 δ(|p1|+|p3|+|p1+p3|−m)(1 − cos θ) d 3p 1d3p3 ですが、d3p1d3p3 = 8π2|p1|2|p3|2d|p1|d|p3| sin θdθ に注意し、さらに、 |p1| = m 2 s, |p3| = m 2 t, cos θ = x とおくと、 Γ T = G2Fm5I 32π3, I = Z dsdt s2t2 Z 1 −1 dx (1 − x) δ(ps2+t2+2stx + s + t − 2) を得ます。y = √s2 + t2 + 2stx で置換すれば、積分 I は、 I = 1 2 Z dsdt Z |s+t| |s−t| dy y¡(s + t)2 − y2¢δ(y + s + t − 2) = −2 Z Σ dsdt (s + t − 2)(s + t − 1) となり、ここで Σ は、 |s − t| < 2 − s − t < |s + t| ∴ s < 1 かつ t < 1 かつ s + t > 1 で与えられる三角形内部領域です。よって、 I = −2 Z 1 0 ds Z 1 1−s dt (s + t − 2)(s + t − 1) = 1 6
と計算され、崩壊幅は、 Γ T = G2 Fm5 192π3 ∼ 3.01 × 10 −16MeV となります。µ 粒子の寿命は T /Γ ∼ 2.19 × 10−6sec となりますが、これは実験値 とよく合っています。
19.11
中性子の寿命
次に中性子の崩壊 : n → pe¯νe を考えます。ファインマングラフは最低次で図19.10であり、散乱振幅は、 M = −iG√ F 2 u¯1γ µ(1−γ 5)v2 u¯3γµ(a−bγ5)us(k). ここで a, b は弱い相互作用におけるバリオンに関する構造定数です。 図 19.10: 中性子の崩壊 よって、 X s,s1∼s3 |M|2 = G2F 2 tr ¡ (/p1+me)γµ(1−γ5)/p2γν(1−γ5) ¢ × tr¡(/p3+mp)γµ(a−bγ5)(/k+mn)γν(a−bγ5) ¢ = G2F 2 × 8 ¡ pµ1pν2+pν1pµ2−gµνp1·p2−i²µνρσp1ρp2σ ¢ × 4 ³ (a2+b2)¡p3µkν+p3νkµ−gµνp3·k ¢ +mnmp(a2−b2)gµν − 2iab²µνλτpλ3kτ ´ = 32G2F ³ (a+b)2p1·p3p2·k+(a−b)2p1·k p2·p3−mnmp(a2−b2)p1·p2 ´ . me, mp, mn は、それぞれ、電子、陽子、中性子の質量です。重心系においては、p1 と p2 のなす角を θ とし、また、|p3| ¿ mp という近似 を用いれば、 X s,s1∼s3 |M|2 = 32G2Fmnmpp01p02(a2+3b2+C cos θ), C = (a2−b2) |p1||p2| p0 1p02 となります。よって、 dΓ T = δ4(p 1+p2+p3−k) 16(2π)5m nmpp01p02 1 2 X s,s1∼s3 |M|2 d3p1d3p2d3p3 = G2F (2π)5 δ 4(p 1+p2+p3−k)(a2+3b2+C cos θ) d3p1d3p2d3p3 = G 2 F (2π)5 δ ³p m2 e+|p1|2+|p2|+mp−mn ´ (a2+3b2+C cos θ) d3p1d3p2 であり、d3p1d3p2 = 8π2|p1|2|p2|2d|p1|d|p2| sin θdθ に注意すれば、 dΓ T = G2 F 2π3(a 2+3b2)|p 1|2 ³ mn−mp− p m2 e+|p1|2 ´2 d|p1|. すなわち崩壊幅は、 Γ T = G2Fm5e(a2+3b2) 2π3 J µ mn−mp me ¶ , J(k) = Z √ k2−1 0 ds s2 ³ k−p1+s2 ´2 となります。 a ∼ 0.98, b ∼ 1.25, GF ∼ 1.166 × 10−11MeV−2,
me ∼ 0.5110 MeV, mn ∼ 939.565 MeV, mp ∼ 938.272 MeV
および J(2.531) ∼ 1.636 を用いると、中性子の寿命は、T /Γ ∼ 1.42 × 1024MeV−1 ∼ 933 sec と計算されます。実験値は 9 × 102sec なので、おおよそ合っているこ とがわかります。 (余談) 中性子の寿命の計算は独自に行ったものですが、結果が実験値と合っているので、間違っ てはいないでしょう。
19.12
中性π粒子の寿命
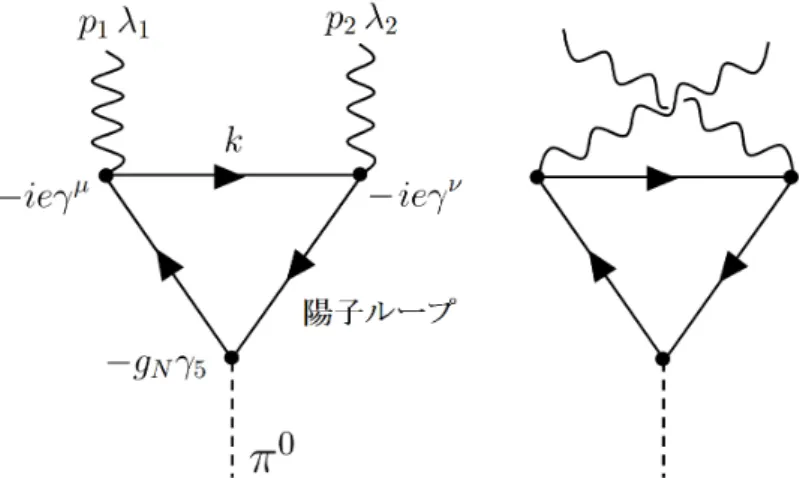
次に中性π粒子 π0 の崩壊 : π0 → γγ を考えてみましょう。図 19.11: 中性π粒子の崩壊 最低次におけるグラフは図19.11の2つで、順に A, B とします。A は、 A = εµλ1(p1)ενλ2(p2) Z d4k (2π)4 (−1) × tr µ (−gNγ5) i(/k − /p2 + m) (k−p2)2−m2+i² (−ieγν) i(/k + m) k2−m2+i²(−ieγµ) i(/k + /p1 + m) (k+p1)2−m2+i² ¶ = igNe2εµλ1(p1)ενλ2(p2) Z d4k (2π)4 × ¡ tr (γ5(/k − /p2 + m)γν(/k + m)γµ(/k + /p1 + m)) k2−m2+i²¢¡(k+p 1)2−m2+i² ¢¡ (k−p2)2−m2+i² ¢ . m は陽子の質量です。分子のトレース部分は 4im ²µνρσpρ1pσ2 と計算され、また、2 光子の4元運動量 pµ1, pµ2 は、陽子の質量 m に比べて十分小さいはずなので、分 母においては pµ1, pµ2 を 0 と近似して、 A = −4gNe2m ²µνρσεµλ1(p1)ενλ2(p2)p ρ 1pσ2 Z d4k (2π)4 1 (k2 − m2 + i²)3 となります。この式の積分部分は、 I := Z d4k (2π)4 1 (k2 − m2 + i²)3 = Z d4k (2π)4 1 ¡ (k0)2−|k|2−m2+i²¢3 = Z d3k (2π)4 Z ∞ −∞ dk0 (k0 + α)3(k0 − α)3, α = p |k|2 + m2 − i² 2p|k|2 + m2 と表せますが、k0 積分の部分は留数の評価により −3πi/(8α5) を与えることが確 かめられるでしょう。よって ² → +0 の極限をとって、 I = Z d3k (2π)4 −3πi 8¡|k|2 + m2¢5/2 = −i 32π2m2
となり、A の式は、 A = igNe2 8π2m ²µνρσε µ λ1(p1)ε ν λ2(p2)p ρ 1pσ2 となります。 一見、発散しそうなループグラフでしたが、γ5 の存在によりこのように収束し ます。(ループグラフの積分についてはくりこみ理論の章で一般的な公式を与え ます。) 一方、B の式は A の式で pµ1, pµ2 および λ1, λ2 を入れ替えたものであり、これ は A と一致することがわかるでしょう。よって散乱振幅は、 M = A + B = 2A = igNe2 4π2m ²µνρσε µ λ1(p1)ε ν λ2(p2)p ρ 1pσ2 となります。 ここで重心系をとって、p1 = −p2 = p とします。このとき散乱振幅は p の方 向には依存しないはずなので、p をある座標軸の方向(例えばz軸方向)に定めて 評価することが可能です。そうすると、M = Mλ1λ2 として、 M11 = M22 = 0, |M12| = |M21| = gNe 2|p|2 2π2m がわかるでしょう。よって崩壊幅は、 Γ T = 2π |p| 32π2M2 X λ1=1,2 X λ2=1,2 |Mλ1λ2| 2 = gN2 e4|p|5 32π5M2m2 = g2Ne4M3 210π5m2 となり、ここで M は π0 の質量です。また、|p| = M/2 を用いました。 gN ∼ 10, e ∼ 0.303, M ∼ 135 MeV, m ∼ 938 MeV という近似値を代入すると、π0 の寿命として T /Γ ∼ 9 × 10−17sec が得られ、こ れは実験値とよく合っています。 (余談) ここではいにしえ素粒子論 (前期素粒子論) を用いて π0 → γγ の幅を求めましたが、標 準模型もしくはクォークモデルにおいてある種の低エネルギー近似をし π0 → γγ の幅を求めよう とすると、素朴には 0 になってしまうことが知られています。しかしアノマリーの効果をきちん と取り入れると上と同様な結果になります。このため π0 → γγ はアノマリーに関する問題 (パズ ル) として非常に有名です。
19.13
ファインマングラフの数値計算
これまでは散乱の微分断面積や断面積を求めるにあたり、ヘリシティに関する 平均や和をとり、巧みに解析的な計算を行ってきましたが、特定のヘリシティに関する断面積を知りたい場合もあるでしょう。そうした場合、解析的計算は非常 に複雑になるので、数値計算に頼るのが普通です。ファインマングラフの数値計 算を行うには、ディラック粒子や光子の波動関数(平面波振幅)の成分を具体的に 書き下す必要があります。 ディラック粒子の波動関数は、運動量 k の方向の天頂角を θ, 方位角を φ = 0 として、 u+(k) = cos(θ/2)pk0 + |k| sin(θ/2)pk0 + |k| cos(θ/2)pk0 − |k| sin(θ/2)pk0 − |k| , u−(k) = i − sin(θ/2)pk0 − |k| cos(θ/2)pk0 − |k| − sin(θ/2)pk0 + |k| cos(θ/2)pk0 + |k| . ここで k0 = p|k|2 + m2 であり、m はディラック粒子の質量です。反粒子につい ては公式 : vs(k) = iγ2us(k)∗ があります(量子電磁力学の章参照)。 一方、光子については、運動量 k, ヘリシティ ±1 の光子の消滅演算子を a±(k) として、 a±(k) = √1 2(a1(k) ∓ ia2(k)) ∴ a1(k) = √1 2(a+(k) + a−(k)) a2(k) = √i 2(a+(k) − a−(k)) でしたから、 X λ=1,2 εµλ(k)aλ(k) = X λ=± εµλ(k)aλ(k) より、ヘリシティが対角化された 光子の波動関数として、 εµ±(k) = √1 2(ε µ 1(k) ± iεµ2(k)) を得ます。k の天頂角を θ, 方位角を 0 とすれば、 εµ1(k) = (0, cos θ, 0, − sin θ)µ, εµ2(k) = (0, 0, 1, 0)µ ですから、 εµ±(k) = √1
2(0, cos θ, ±i, − sin θ)µ.
ヘリシティを対角化した光子の波動関数は実でないことに注意。このため終状態 の光子について付与すべきは、εµλ(k) ではなく、その複素共役 εµλ(k)∗ = εµ−λ(k) と いうことになります。
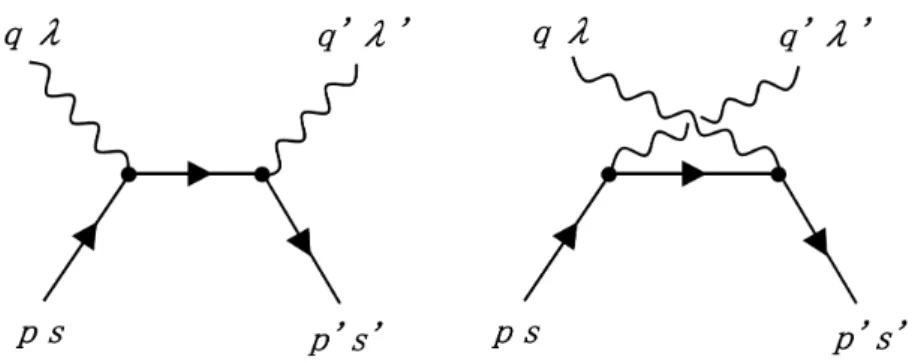
図 19.12: 電子陽電子対消滅 一例として、電子と陽電子の対消滅 : e¯e → γγ を考えてみましょう。グラフは最低次で図19.12でした。 左のグラフの式を A とすると、 A = εµλ(q)∗ενλ0(q0)∗v¯s0(p0)(ieγν) i /p − /q − m(ieγµ)us(p) = 2πiα p·q v¯s0(p 0)/ε −λ0(q0)(/p − /q + m)/ε−λ(q)us(p). ここで m は電子の質量、α = e2/(4π) は微細構造定数です。重心系で考えれば、 散乱角を θ, 散乱の方位角を 0 として、
pµ = (E, 0, 0, p)µ, qµ = (E, E sin θ, 0, E cos θ)µ,
E = pp2 + m2, p0 = −p, q0 = −q とおけます。軸対称性から散乱振幅の大きさは方位角に依存しないことに注意。 一方、交差グラフを B とすると、これは A の式において qµ ↔ q0µ, λ ↔ λ0 と置 換したものなので、数値計算においては簡単に処理できるでしょう。散乱振幅は、 M = A + B で与えられ、微分断面積および断面積は、 dσ dΩ = 1 64π2(2E)2 E p |M| 2 = |M|2 256π2Ep, σ = 2π Z dθ sin θ dσ dΩ で与えられます。θ の積分範囲ですが、λ = λ0 のときは 0 ∼ π/2, そうでないとき は 0 ∼ π ということになります。 特に断面積 σ = σλλss00(p) については、 σssλλ00(p) = σλ 0λ ss0 (p).
また、QED の C 対称性および P 対称性から、 σssλλ00(p) = σλλ 0 s0s(p), σλλ 0 ss0 (p) = σ−λ−λ 0 −s−s0 (p) が成り立つので、σ++++(p), σ++−−(p), σ+−++(p), σ+−++(p), σ+−+−(p) の5つを計算すれば十 分です。数値計算による結果を図19.13に記します(∗)。σ+−++(p) は恒等的に 0 にな るようなので、グラフには記していません。 図 19.13: 電子陽電子対消滅の断面積
(*注) 数値計算には Excel VBA を用いました。ソースを「あもんノート/数値計算 for VBA」 に置いておきます ( URL: http://amonphys.web.fc2.com/ )。