49
第
2
章 ネットワーク構造
—
つながりを見る
網目状に何かが互いに繋がっているものを,ネットワークといいます.道路網, 通信網などはが代表的なネットワークです.要素をつなぐものが目に見えなくて も,ネットワークを用いてその構造を記述できる場合があります.たとえば,工 程の前後関係とか,人やモノの組み合わせなどが挙げられます.ネットワークの 性質をうまく使うことで,問題を効率的に解いたり,モデルをわかりやすく表現 することが可能になります.2.1
再びクッキー屋
2.1.1 だれがどこでつくるか
模擬店で販売するクッキーをつくるのに,サークルの部員の部屋を使う予定です.部屋を提供 してくれる部員だけにつくらせるのは不公平なので,ほかの部員も手伝いに行くことになっていま す.あなたは責任者として,だれがどこへ手伝いに行くのか決めなくてはいけません. まず,クッキー作りに使える部屋は3 つあります.1 つは自宅住まいの学生のものなので広さ に余裕があり,6 人が同時に作業できます.ほかの二つは下宿生の部屋なので手伝いは 3 人までが 限度です. 部員が全部で15 人いて,そのうち部屋の提供者 3 名を除く 12 名を割り振るにあたっては次の ことを考慮しなければなりません. • 各製作場所に,必要な人数がいなければならない. • できるだけ,距離的に近い場所に割り振るようにしなければならない. 距離については,どのような基準をとるかが悩ましいところです.たとえば,もっとも移動距離が 長い人を評価の目安にするか,あるいは全員の平均的な距離を考えるかで,結果は変わってくるこ とでしょう.とりあえず,もっとも簡単でかつ部員に説明のしやすい「平均距離最小化」の基準で 割り振りを考えることにしました. 対象の部員に番号をつけて,3 つの製造場所 A,B,C までの距離を計算したところ,表 2.1 の ようになりました(部員の部屋と製造場所の位置関係は図表 2.2 参照).さて,だれをどこに割り振 るべきでしょうか?2.1.2 素朴な方法
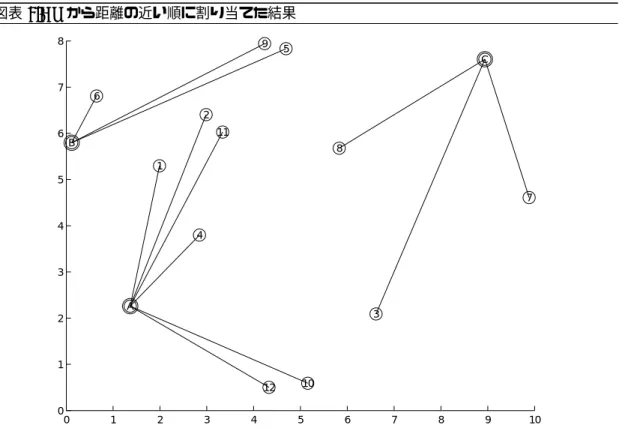
最初は素朴な方法で考えてみます.A の定員が多いので,まずここから埋めていくことにしま す.A から距離の近い部員を 6 人選びます.残った 6 人から,今度は B から近い部員を 3 名選び, 残りをC に回すことにしました.その結果が,表 2.3 です.製造場所 A には,1・2・4・10・11・12図表2.1 製造場所までの距離 (km) 部員 製造場所A 製造場所 B 製造場所 C 1 3.1 1.9 7.3 2 4.5 2.9 6.1 3 5.3 7.5 6.0 4 2.1 3.4 7.2 5 6.5 5.0 4.3 6 4.6 1.1 8.3 7 8.8 9.8 3.1 8 5.6 5.7 3.7 9 6.4 4.6 4.7 10 4.1 7.2 8.0 11 4.3 3.2 5.8 12 3.4 6.8 8.5 定員 6 名 3 名 3 名 図表2.2 製造場所と部員の位置関係 0 1 2 3 4 5 6 7 8 9 10 0 1 2 3 4 5 6 7 8 A B C 1 2 3 4 5 6 7 8 9 10 11 12
2.2. ネットワークの表現 51 の部員が,製造場所B には,5・6・9 の部員が,製造場所 C には,3・7・8 の部員が出かけること になります.この場合の総移動距離は,45.1km となりました.12 人の平均移動距離は,3.76km です.A への割り当てられた人の移動距離は少ないものの,B,C に割り当てられた 6 人中 5 人が 平均を超えています.不公平であると,文句が出るかもしれません. 図表2.3 A から距離の近い順に割り当てる.次に,B,C に割り当て 部員 製造場所A 製造場所 B 製造場所 C 4 2.1 3.4 7.2 1 3.1 1.9 7.3 12 3.4 6.8 8.5 10 4.1 7.2 8.0 11 4.3 3.2 5.8 2 4.5 2.9 6.1 A:小計 21.5 6 4.6 1.1 8.3 9 6.4 4.6 4.7 5 6.5 5.0 4.3 B:小計 10.8 8 5.6 5.7 3.7 3 5.3 7.5 6.0 7 8.8 9.8 3.1 C:小計 12.8 別の方法も考えてみましょう.今度は,近いところを最優先するという方法です.表を見ると, 部員6 から製造場所 B への距離が 1.1km で,ほかのすべての距離よりも小さいので,部員 6 を製 造場所B へわりあてます.次に近いのは,1–B 間の距離 1.9km なおで,部員 1 も製造場所 B へ わりあてます.次いで,4–A,2–B と近いところから順に割り当てをしていきます.この結果,表 2.5,図 2.6 を得ました.総距離は,42.7km(平均 3.56km) です. 2 つの図 2.4 と 2.6 を見比べてみると,前者の方が集合場所 A への割り当てが優先されている 分,C にしわ寄せが来ており,後者については人数の多い A に移動距離が長い人がいます.ほか に異なる割り振り方はたくさんありそうですが,部員に納得してもらうためにも「平均距離」の規 準で見たとき,これ以上は改善できないという案を示さないといけません.ここでは,ネットワー クという概念を用い,線形計画法を援用した手法によって最適解を導くことにします.いくつか準 備をしてから,2.6.1 節で再度この問題を取り上げることにしましょう.
2.2
ネットワークの表現
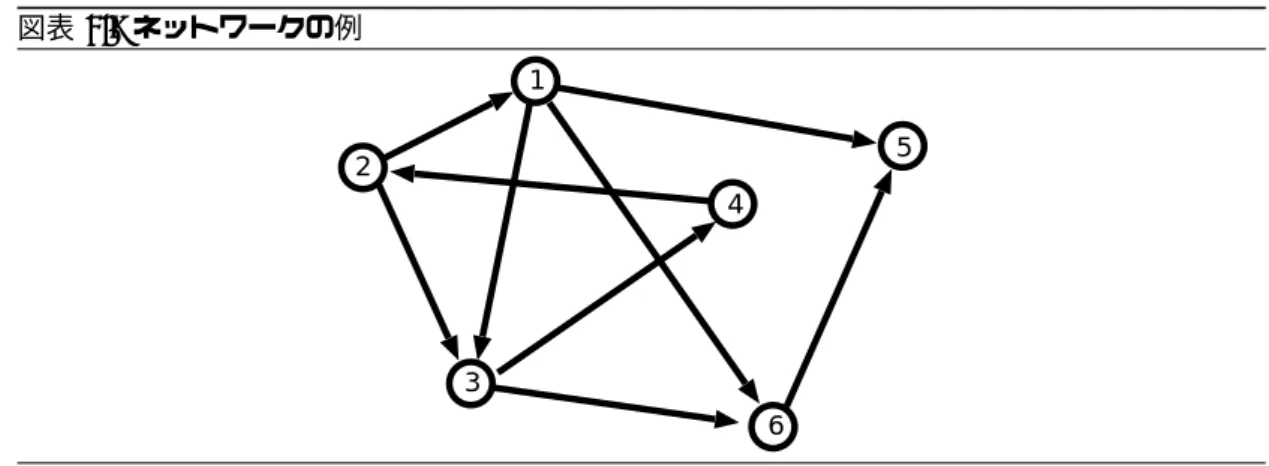
ネットワークは何かのつながりを表すものです.現実の様々なネットワークも結局は,何が何 とつながっているか,という関係に還元することができます.したがって,その構造を表現するに は,ネットワークの結び目と結び目同士のつながりについての情報が必要です. 結び目に相当する部分を,端点(vertex) あるいは頂点と呼びます.そのつながりを示すのに, 端点同士を結ぶ線を引き,これを枝(edge) あるいは辺 (arc) と呼ぶことにします. 例えば図表2.7 は 6 個の端点と 9 本の枝からなるネットワークです. ネットワークをモデル化するにあたって,いつも図に頼ることができるとは限らないので,記 号を使って表してみるにしましょう.図表2.4 A から距離の近い順に割り当てた結果 0 1 2 3 4 5 6 7 8 9 10 0 1 2 3 4 5 6 7 8 A B C 1 2 3 4 5 6 7 8 9 10 11 12 図表2.5 距離の近い順に割り当て 部員 製造場所 距離 6 B 1.1 1 B 1.9 4 A 2.1 2 B 2.9 7 C 3.1 12 A 3.4 8 C 3.7 10 A 4.1 5 C 4.3 11 A 4.3 3 A 5.3 9 A 6.4 総距離 42.7
2.2. ネットワークの表現 53 図表2.6 距離の近い順に割り当てた結果 0 1 2 3 4 5 6 7 8 9 10 0 1 2 3 4 5 6 7 8 A B C 1 2 3 4 5 6 7 8 9 10 11 12 A B C 1 2 3 4 5 6 7 8 9 10 11 12 A B C 1 2 3 4 5 6 7 8 9 10 11 12 まず,端点には名前をつけます.ここではすべての端点に番号をふって区別しました.場合に よっては,数字ではなく,a, b, c, . . . などを使ったりします. 枝は,どの端点から始まって,どの端点を至っているかに着目します.端点i から出て,端点 j へいたる枝を ij とします.この流儀にしたがって,図表 2.7 の例の 9 本の枝に名前をつけると, 13, 15, 16, 21, 23, 34, 36, 42, 65 となります. 枝が出発する端点を始点,枝が至る端点を終点と呼びます.端点i から端点 j へ至る枝 ij の始 点はi,終点は j です.枝 ij と枝 ji を区別して考えます. n 個の端点と m 本の枝からなるネットワークを考えます. 端点の集合:V = {1, 2, . . . , n} 枝の集合:E = {e1, e2, . . . , em} 端点集合V と枝集合 E の組 G = (V, E) をあわせて,グラフ (graph) といいます.グラフ上の枝 に向きがある場合(枝 ij と枝 ji を区別する場合) を有向グラフ,向きがない場合を無向グラフと呼 びます. グラフの端点や枝に重みの情報を付け加えて,ネットワークの表現とする場合もあります.重 みについては輸送問題の節で説明しましょう.
図表2.7 ネットワークの例 1 2 3 4 5 6 演習問題2.1 次のような端点の集合Vと枝の集合Eがあたえられたとき,そのネットワークを図示せよ. 端点の集合:V =f1; 2; 3; 4; 5; 6g 枝の集合:E =f12; 24; 26; 36; 41; 45; 52g
2.3
輸送問題
輸送問題(transshipment problem) とは,ネットワーク上で入口 (source) から出口 (sink) に向 かって,モノを流す際に,最適な経路とその経路上の流量を求める問題と考えることができます.
2.3.1 輸送問題の例
ある会社が製品を3 つの工場で生産しています.ここで作られた製品は 2ヶ所にある直営店で 販売されています.工場の生産量の合計と直営店の需要量の合計は一致しており,各工場の生産量 と各直営店の需要量はそれぞれ表2.8 のようになっています. 図表2.8 工場と直営店 工場A 工場 B 工場 C 直営店 P 直営店 Q 生産・需要量 12 7 9 15 13 対応する端点 1 4 5 3 8 この工場と直営店は図表2.9 ような道路網で結ばれています.図の端点は,工場,直営店,中 継点のいずれかを表しています.枝(道路) の横の [ ] の中の数値は,その道路を利用して,製品 を1 単位輸送する際にかかる費用 (消費する燃料の費用,通行料,渋滞による機会費用の損失額な ど) です.需要量は,直営店に対応する端点の横に□で囲って示しました.生産量は負の需要とし て解釈し,マイナス記号をつけて記入してあります. 基本的にこの道路網では,ほとんどの道が一方通行ですが,端点3,6 間では両方向に通行でき ます. 以上の条件のもとで,各工場から直営店に製品を輸送する際の費用を最小にするには,どのよ うな経路でどれくらいの量を送ればよいでしょうか.2.3. 輸送問題 55 図表2.9 工場・直営店間の道路網 1 2 3 4 5 6 7 8 [10] [8] [18] [15] [25] [6] [3] [5] [8] [4] [9] [5] [4] [11] -12 -9 -7 15 13 [3]
2.3.2 輸送問題の定式化
この問題を線形計画問題として定式化してみることにします. 端点i と端点 j が枝 ij を介して繋がっているとき,端点 i から端点 j に製品を送ることができ ると考えます(枝 ji が存在しない場合は,枝 ij が存在しても端点 j から端点 i にモノを送ることは できないことに注意).枝 ij を通るモノの量を変数 xijを用いて表します.xijの値が0 であれば, その枝を使ってはモノを流さないことを意味します. このネットワークにおける総輸送費用は,各枝に通すモノの量に1 単位当たりの輸送費用をか けて,それをすべての枝について合計すれば得られます.枝の集合E を E = {12, 14, 24, 25, 31, 36, 37, 43, 47, 56, 58, 63, 64, 78, 86} とします.また,枝ij の 1 単位当たりの輸送費用を cijで表します.この問題では,例えば,c12= 8, c58= 9 などとなります.以上の表記を用いると総輸送費用 z は, z = ∑ ij∈E cijxij = 8x12+ 18x14+ 15x24+ 4x25+ 6x31+ 5x36+ 5x37+ 3x43 + 10x47+ 25x56+ 9x58+ 4x63+ 11x64+ 3x78+ 8x86 と表せます. 次に,この問題の制約条件を考えることにしましょう.この問題において満たすべき条件は,流 量均衡条件と呼ばれるものです.これは,モノが流れる際に,消費されない限り途中で消えてなく なったりしない,という条件です.具体的には,各端点において,流入量の合計と流出量の合計が 一致する,という表現になります.例えば,端点2 に流入する量は端点 1 からの来る x12です.流 出する量は,端点4 へ流す x24と端点5 へ流す x25です.端点2 は中継点なのでこれ以外の流入出 量はありません.したがって, x12= x24+ x25でなくてはなりません. では,入口である工場の端点ではどうなるでしょうか.端点1 での流入量は x31で,流出量は x12とx14です.これに加えて12 単位の生産量が存在します.したがって,端点 1 では, x31+ 12 = x12+ x14 が成り立っていなくてはなりません.この式を書き直すと, x31− x12− x14= −12 となります.同様に出口である直営店(端点 8) は, x58+ x78= x86+ 13 です. 以上の条件をすべての端点について書くと x31− x12− x14 = −12 x12− x24− x25 = 0 −x31− x36− x37+ x43+ x63 = 15 x14+ x24− x43− x47+ x64 = −7 x25− x56− x58 = −9 x36+ x56− x63− x64+ x86 = 0 x37+ x47− x78 = 0 x58+ x78− x86 = 13 (2.1) となります. 輸送問題を線形計画問題として定式化すると, min 8x12+ 18x14+ 15x24+ 4x25+ 6x31+ 5x36+ 5x37+ 3x43 +10x47+ 25x56+ 9x58+ 4x63+ 11x64+ 3x78+ 8x86 s.t. x31− x12− x14= −12 x12− x24− x25= 0 −x31− x36− x37+ x43+ x63= 15 x14+ x24− x43− x47+ x64= −7 x25− x56− x58= −9 x36+ x56− x63− x64+ x86= 0 x37+ x47− x78= 0 x58+ x78− x86= 13 xij ≥ 0, ij ∈ E (2.2) となります.(2.2) を解くと,最適解は以下の通りです. x12= 4 x14= 8 x24= 0 x25= 4 x31= 0 x36= 0 x37= 0 x43= 15 x47= 0 x56= 0 x58= 13 x63= 0 x64= 0 x78= 0 x86= 0 演習問題2.2 1. 方程式系(2.1)においては端点の数だけ制約式が存在する.すべての制約式の右辺と左辺 を足しあわせるとどうなるか確かめなさい.
2.3. 輸送問題 57 2. 方程式系(2.1)を行列で表現する際の係数行列を書きなさい. 演習問題2.3 宮城県に拠点をおくメーカーが,県内の工場と配送センターを結ぶ配送計画の見直しをすること になった.工場は,利府,名取,古川にあり,配送センターは,仙台北部,仙台南部,石巻,古 川にある.各工場の生産可能量,および配送センターの需要が以下のように与えられている. 工場 生産可能量 配送センター 需要 利府 200 仙台北部 400 名取 400 仙台南部 300 古川 500 石巻 200 古川 200 また,各工場と配送センター間の製品1単位の輸送にかかる費用は以下のように与えられている. 配送センター 仙台北部 仙台南部 石巻 古川 工 場 利府 3 4 5 4 名取 3 2 4 3 古川 3 4 4 2 輸送費用を最小にするにはどうすればよいか. 1. ネットワークを図示せよ. 2. 輸送問題として定式化せよ.
2.3.3 参考:需給が一致しない場合
前節の問題では,工場の生産量の合計と直営店の需要量の合計が一致していました.供給量と 需要量を常に一致させるのは困難なため,一般には,需給のギャップを想定した方が自然です.し かし,流量均衡条件が成り立つためには,ネットワーク上の総供給量と総需要量が一致していなく てはなりません.生産量の合計が,需要を上回っているような場合は,どのように問題を表現すれ ばよいでしょうか. 現実に需給のギャップがある場合,たとえば供給量が過剰な場合,モノは在庫となります.輸 送問題に置いても同様です.仮想的な在庫を表す端点をもとのネットワークに導入すればよいので す.すなわち,図2.10 のように,倉庫を表す端点 9 をつくり,そこと各工場を表す端点間に枝を 張ります. 図2.10 では,端点 8 における直営店の需要量が 13 から 3 に減少したことをうけて,仮想的な 在庫の量を10 と設定しました.また,各工場と仮想的な在庫を結ぶ枝 19,49,59 の輸送費用は 0 としています.これは,この在庫が仮想的なもので,実際の製品の移動はないことに対応してい ます. この問題の最適解は,以下の通り. x12= 0 x14= 8 x19= 4 x24= 0 x25= 0 x31= 0 x36= 0 x37= 0 x43= 15 x47= 0 x49= 0 x56= 0 x58= 3 x59= 6 x63= 0 x64= 0 x78= 0 x86= 0図表2.10 仮想的な在庫の導入例 1 2 3 4 5 6 7 8 [10] [8] [18] [15] [25] [6] [3] [5] [8] [4] [9] [5] [4] [11] -12 -9 -7 15 3 [3] 9 10 [0] [0] [0] 演習問題2.4 端点の集合Vと枝の集合Eがつぎのように与えられているとする. V =f1; 2; 3; 4g E =f12; 13; 21; 23; 24; 34; 43g 1. グラフ(V; E)によって表されているネットワークを図示せよ. 2. このネットワークが生産拠点と販売拠点との間の配送網を表しているとする.端点1に生 産拠点があり毎日a単位の製造を行っている.一方,端点3と4に販売拠点があり,それ ぞれb単位,c単位の需要がある.また,各枝には以下のように単位あたりの輸送に掛る 費用が存在している. 枝 12 13 21 23 24 34 43 費用 2 5 4 1 4 2 7 生産量と販売量の間に以下の関係がある場合について,費用を最小にするような配送計画 を求める問題を定式化せよ. (1) a = b + cの場合 (2) a > b + cの場合 (3) a < b + cの場合 必要であれば,与えられたネットワークに端点と枝をつけ加えても構わない.
2.4
生産/在庫計画
前節の輸送問題は,空間上の位置関係(工場と直送店の場所)がネットワークを用いて表され ていました.ネットワークは必ずしも物理的な場所に関係するとは限りません.時間軸上のつなが りをネットワーク構造を用いて表すことができます.2.4.1 ガソリンの購入計画
ガソリンの卸売りをしている会社があります.ガソリンの値段と需要は毎期変動するので,月 毎に販売計画を調整しなければ,在庫が過剰になったり製品が供給できなくなったりします.この2.4. 生産/在庫計画 59 会社は,ガソリンの貯蔵施設を保有しているので,在庫をうまく使って価格や需要の変動に対処し ています. 今,4 期先まで,値段と需要についてある程度信頼のおける推計値が得られました. 期 単位当たりの値段 需要 1 期 90 140 単位 2 期 85 120 単位 3 期 92 150 単位 4 期 90 120 単位 販売と貯蔵については次のような条件があります. • ガソリンは期首に購入 • 第4 期の終りに,在庫として少なくとも 20 単位のガソリンが必要 • 販売価格は,4 期間にわたり一定 • 貯蔵施設のキャパシティーは十分大きい 需要を満たし,かつ収益を最大にするためには,各期にどれくらいガソリンを購入すればよいで しょうか. この問題は,実はとても単純な問題です.モデル化するまでもなく解けます.なぜなら,販売 価格が一定で,しかも在庫の容量に制限がないので,仕入れ価格が一番安いときにたくさん買えば いいからです.したがって,1 期目の期首に,その期に必要な分 (140 単位) だけを購入し,もっと も安い2 期目に以後必要な量をすべて (120 + 150 + 120 + 20 = 410 単位) 購入することが最適です. 結局,購入量と仕入れ価格の合計は 1 期目: 140 2 期目: 410 3 期目: 0 4 期目: 0 (2.3) 総仕入価格:90 ∗ 140 + 85 ∗ 410 = 47540 となります. 次に,あえてこの問題をネットワークを用いて表してみましょう.各期間ごとの購入量,販売 量,在庫量を,あたかもガソリンがネットワークを流れるものとして表現してみると,図2.11 を 得ます. 端点6,7,8,9 が需要を表しており,端点 0 がガソリンの仕入先を表します.端点 0(仕入先) から端点1,2,3,4 にガソリンが移動することが,購入に相当します.したがって,枝 01,02, 03,04 の費用をガソリンの単位当たりの仕入れ価格に設定しています.枝 12,23,34,45 を流れ る量が在庫量になります. このネットワークは輸送問題と全く同じ形式なので,同じようにLPに定式化してみます. min 90x01+ 85x02+ 92x03+ 90x04 s.t. −x01− x02− x03− x04= −550 x01− x12− x16= 0 x12+ x02− x23− x27= 0 x23+ x03− x34− x38= 0 x34+ x04− x45− x49= 0 x45= 20, x16= 140, x27= 120, x38= 150, x49= 120 xij ≥ 0, すべての ij (2.4)
図表2.11 ガソリンの販売・在庫を表すネットワーク 0 1 2 3 4 5 6 7 8 9 140 120 150 120 -550 20 [90] [85] [92] [90] (2.4) の最適解は, x01= 140, x02= 410, x03= 0, x04= 0, x12= 0, x16= 140, x23= 290, x27= 120, x34= 140, x38= 150, x45= 20, x49= 120, となり,(2.3) と同じ結果を得ました. 今の問題は,あえてネットワークを書いてわざわざLP に定式化しなくても解くことができま した.では,もう少し複雑な設定をしてみましょう.在庫として保有するガソリンに保管費用がか かるとします.1 単位当たり 3 とします. この場合はモデル化のステップが必要でしょう.ネットワークができていれば簡単に対応でき ます.在庫を表す枝に費用をつけるだけです.結果は,図2.12 のようになりました. 定式化するとつぎのようになります. min 90x01+ 85x02+ 92x03+ 90x04+ 3x12+ 3x23+ 3x34+ 3x45 s.t. −x01− x02− x03− x04= −550 x01− x12− x16= 0 x12+ x02− x23− x27= 0 x23+ x03− x34− x38= 0 x34+ x04− x45− x49= 0 x45= 20, x16= 140, x27= 120, x38= 150, x49= 120 xij ≥ 0, すべての ij (2.5) 計算結果は次の通りです. x01= 140, x02= 270, x03= 0, x04= 140, x12= 0, x16= 140, x23= 150, x27= 120, x34= 0, x38= 150, x45= 20, x49= 120
2.4. 生産/在庫計画 61 図表2.12 ガソリンの販売・在庫を表すネットワーク:保管費用あり 0 1 2 3 4 5 6 7 8 9 140 120 150 120 -550 20 [90] [85] [92] [90] [3] [3] [3] [3] 演習問題2.5 1. 上記の問題では,在庫の容量は考えていなかった.貯蔵するガソリンは最大100単位まで という制約がある場合の問題を線形計画問題として定式化せよ. 2. 上の問題をさらに発展させて.在庫の容量制約に,次の条件を付け加える.まず,各期の 販売価格をその期の仕入れ価格の1.1倍とする.また需要は必ずしも満たさなくてもいい が,満たせない分に関しては,仕入れ値の1.2倍のペナルティがかかるとする. [総売り上げ]−[総仕入れ価格]−[在庫費用]─[ペナルティの合計]を最大にするためには どのように定式化すべきか.
2.4.2 生産シフトの決定
ある工場では,生産量や在庫量を調整することで,製品需要の変動に対応しています.生産量 の調整は2 段階で行います.通常シフトでは 1 単位当たり 500 円で生産が可能です.ただし通常シ フトでは,最大80 単位までしか生産できません.通常シフトで生産が追い付かないときは,臨時 シフトをとって増産体制に入ります.臨時シフトではさらに20 単位まで増産可能ですが,生産費 用は高くなり,1 単位当たり 650 円です.在庫には上限はありませんが,1 期間毎に 1 単位当たり 100 円の保管費用がかかります. 4 期先までの需要が 期 1 2 3 4 需要量 85 60 90 105 と与えられている場合,費用を最小にするような各期の生産量と在庫の量をネットワークとして表 してみると,図2.13 のようになります. 枝ij を流れる量を xijとして最適解を求めると,次のようになります. x13= 80 x20= 15 x23= 5 x40= 5 x46= 75 x50= 20 x69= 15 x79= 80 x80= 20 x9,12= 5 x10,12= 80 x11,12= 20図表2.13 生産量と在庫量のネットワーク 1 2 3 4 5 6 7 8 9 10 12 11 13 [0] [0] [0] [0] [0] [0] [0] [0] [500] [650] [650] [650] [650] [100] [100] [100] [500] [500] [500] -80 -20 -20 -20 -20 -80 -80 -80 60 90 85 105 60 非負の流量を持つ枝のみ示しました.この結果を見ると,通常シフトは第2 期以外では最大限生産 を行う一方,臨時シフトの生産は第1 期に 5 単位,第 4 期に 20 単位のみとなっています.在庫は 第2 期末,第 3 期末にそれぞれ 15 単位,5 単位生じています. 演習問題2.6 図2.13で表現されたネットワークを用いて,費用を最小にする生産在庫計画を求める問題をLP として定式化せよ. 演習問題2.7 あるレンタカーショップの1週間(営業日は6日間)の運用問題を考えるこのレンタカーショッ プでは,全部で30台の車をレンタルしている.レンタルした車は必ずメンテナンスに出すので, 常に30台が営業可能というわけではない.もし店頭にある車の台数が十分でないならば,姉妹 店からお金を払って借りてくる必要がある.姉妹店との取り決めで,借りる期間は1週間となっ ている. メンテナンスには,通常では3日かかり,その費用は1台当たりp円である.しかし,q(> p) 円支払うことで,1日でメンテナンスを終えることができる.他の姉妹店から借りてくる場合は, 1日あたりr円かかる. 今から1週間について第j日目の需要がdjであるとわかっているとき(7日目は休業日なので d7= 0とする),このレンタカーショップの営業費用を最小にする計画を作るものとする. ただし,週始めにおいてはメンテナンスに出してある車はないものする.そのためには,5,6日 目にレンタルした車は,1日でメンテナンスを終えるようにしなければならない.また,このレ ンタカーショップの車種は1つだけで,しかも貸し出した当日に返却されるとする. 上記の設定を車の在庫管理の問題としてとらえ,ネットワークの図をつくれ.[ヒント:車がネッ トワークを流れると考えましょう.各営業日において車は,ショップにあるか,レンタルされて いるか,メンテナンスに出ているか,のいずれかです.]
2.5
整数性
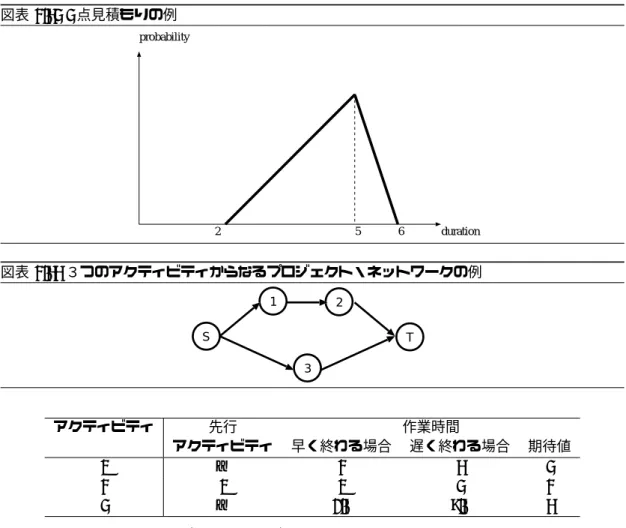
図2.14 のネットワークを例に使って,輸送問題の解の性質をみることにします.端点 1 に 10 単位の供給があり,端点5 と 7 に,それぞれ 6 単位と 4 単位の需要があるとします.枝の費用を2.5. 整数性 63 図表2.14 輸送のネットワーク 7 4 1 3 2 5 6 -10 6 4 cijとおいて,輸送問題を定式化すると, min +c12x12+ c13x13+ c14x14+ c23x23+ c25x25+ c26x26 +c34x34+ c35x35+ c36x36+ c37x37+ c46x46+ c47x47+ c65x65+ c76x76 s.t. −x12− x13− x14= −10 +x12− x23− x25− x26= 0 +x13+ x23− x34− x35− x36− x37= 0 +x14+ x34− x46− x47= 0 +x25+ x35+ x65= 6 +x26+ x36+ x46− x65+ x76= 0 +x37+ x47− x76= 4 xij≥ 0, すべての ij (2.6) となります.問題(2.6) の輸送費用をかえて,いくつか問題を解いてみました.その結果を表にし たのが,表2.15 です. 演習問題2.8 表2.15を参照して,最適解においてどのようなルートを通って配送しているか,図に記入せよ. この結果から以下のことがわかりました. • 最適解はすべて整数である. • 最適な配送ルートはつながっている • 最適は配送ルート上では,ある端点へいたる道はひとつしかない(並行する道がない) 以上は,ただ一つの問題についてパラメータをかえて数値実験を行っただけなので,もしかしたら 別のネットワークでは異なる結果になるだろうと思う人がいるかもしれません.実は,上記の結果 はネットワーク特有の構造から導かれています.一定の条件を満たす輸送問題すべてに当てはまる のです. 説明のために,新しい言葉を導入しておきます. • 端点u と端点 v の経路とは,端点 u と端点 v を結ぶ枝と端点からなるネットワークの一部を いう.経路をたどると,端点u から端点 v へ至ることができる (枝の向きはかんがえなくて もよい). • 閉路(cycle) とはある端点から出発して同じ端点に戻ってくる経路である.
図表2.15 輸送費用の変化と輸送量 枝ij 12 13 14 23 25 26 34 35 36 37 46 47 65 76 (1) cij 9.0 9.5 3.4 4.4 4.8 1.5 1.4 5.4 7.3 4.0 3.6 2.9 8.7 6.3 xij 6 0 4 0 6 0 0 0 0 0 0 4 0 0 (2) cij 2.5 9.8 6.5 2.3 6.9 6.7 1.4 0.3 2.7 1.2 0.7 8.6 1.9 0.4 xij 10 0 0 10 0 0 0 6 0 4 0 0 0 0 (3) cij 7.4 5.4 2.8 3.7 0.2 8.9 8.7 2.6 5.7 1.6 6.0 3.4 6.6 8.7 xij 6 0 4 0 6 0 0 0 0 0 0 4 0 0 (4) cij 9.0 3.3 7.4 4.2 4.0 5.1 1.7 5.3 6.5 0.2 8.4 8.1 7.0 4.7 xij 0 10 0 0 0 0 0 6 0 4 0 0 0 0 (5) cij 0.2 5.7 4.6 9.1 2.9 0.7 4.8 9.9 9.3 5.7 6.6 7.8 1.1 0.1 xij 6 4 0 0 0 6 0 0 0 4 0 0 6 0 (6) cij 5.5 0.1 4.6 2.0 7.9 6.2 0.2 9.0 7.7 9.1 7.6 3.9 3.4 5.1 xij 0 10 0 0 0 0 4 6 0 0 0 4 0 0 (7) cij 9.6 6.8 0.6 6.0 4.0 2.2 1.9 0.8 0.1 7.9 0.2 8.8 3.6 7.3 xij 0 0 10 0 0 0 0 0 0 0 6 4 6 0 (8) cij 6.0 1.6 3.2 2.4 0.1 4.0 6.5 0.9 7.7 9.7 7.2 7.9 2.4 2.0 xij 0 6 4 0 0 0 0 6 0 0 0 4 0 0 • ネットワークが連結であるとは,ネットワーク上の任意の2 つの端点間に必ず経路が存在す ることである. • 木(tree) とは,連結でかつ閉路の存在しないネットワークのことである. • 全域木(spanning tree) とは,もとのネットワークのすべての端点を含む木のことである. 輸送問題における実行可能基底解は,“木” に対応していることが知られています.直感的には 以下のように説明できます. 1. まず適当に実行可能な輸送案をつくってみてください.その案では当然,需要点と供給点の 間に経路があるはずです. 2. 次に,その案に閉路があるかどうか探してください.もし閉路があったなら,二つの可能性 があります.一つはその閉路が一方通行で元に戻ってくる場合,もう一つはある端点へ流す 経路が2 種類ある場合です.前者であれば,同じところに戻すような流し方は不合理なので, その閉路のどこかの枝を輸送案からはずしましょう.後者であれば,2 種類の経路のうち輸 送費用が安い方があれば十分なので,高い方をはずします(費用が同じ場合でも,どちらか 一方があれば十分です).この段階で,輸送案から閉路はなくなりました. 3. 最後に,輸送案では通らない端点を探します.その端点と輸送案が通る端点とを結ぶ枝をみ つけて,(輸送量 0 として) 輸送案に付け加えましょう. 4. 最終的に,ネットワークのすべての端点が連結されて,かつ閉路の存在しない輸送案になっ たはずです.すなわち全域木が構成されました. 例で確かめてみましょう.図表2.16(A) は,2.3.1 節の輸送問題の実行可能解です.実線で表現 された枝の費用の横,あるいは下に書かれた数値が輸送量であり,破線で書かれた枝の輸送量は0 です.すべての端点で流入量と流出量が等しいことを確認してください.
2.5. 整数性 65 図表2.16 実行可能解 (A) 1 2 3 4 5 6 7 8 [10] [8] 10 [18] 4 [15] [25] 5 [6] 2 [3] [5] [8] 1 [4] 10 [9] 14 [5] [4] 3 [11]3 -12 -9 -7 15 13 [3] 14 (B) 1 2 3 4 5 6 7 8 [10] [8] 10 [18] 2 [15] [25] [6] [3] [5] [8] 6 [4] 10 [9] 19 [5] [4] 6 [11] -12 -9 -7 15 13 [3] 9 (C) 1 2 3 4 5 6 7 8 [10] [8] 12 [18] 0 [15] [25] [6] [3] [5] 0 [8] 8 [4] 12 [9] 21 [5] [4] 8 [11] -12 -9 -7 15 13 [3] 7
この実行可能解には1→4→3→1という閉路が存在しています.この閉路にそって流入量を 増減させても端点1,3,4における流量のバランスは保たれています.現在の実行可能解では, 枝14:4 枝43:14 枝31:2 となっているのを,閉路に沿って流量を1 単位増やして, 枝14:5 枝43:15 枝31:3 としても,やはり実行可能解です.しかし,流量を1 単位増やしたことで,全体の輸送費用は 18 + 3 + 6 = 27 だけ増加してしまいました.だから,実行可能性を保ちつつ輸送費用を下げるに は,閉路に沿って流量をできる限り減らすべきです.ここでは,最大2 単位まで減らすことができ て,次のようにすることができます. 枝14:2 枝43:12 枝31:0 さらに,閉路6→4→3←6もみてみましょう.これは端点6から,端点3にむかって二つの 経路があると見ることができます.端点6への流入量6 単位のうち,3 単位を直接端点3に送り, 残りの3 単位を端点4を経由して端点3に送っています.前者であれば費用は 4 ∗ 3 = 12 で済むの に対し,後者の費用は(11 + 3) ∗ 4 = 56 かかります.したがって,端点6への流入量 6 単位を端点 3に送るのに後者の経路を使うのは効率がよくありません.したがって, 枝64:0 枝43:9 枝63:6 とすべきでしょう.同じように,閉路5→8→6←5も効率の悪い輸送をしているので, 枝58:19 枝86:6 枝56:0 としました.閉路上の流量を見直した実行可能解は図表2.16(B) となります.この段階でも閉路が 存在しているので,端点でのバランスを保ちつつ流量を減らすことが可能です.枝14 の流量を 2 単位減らして,他の枝の流量も調整します.さらに端点7をくみこむため枝37 を輸送案に加えて, 図表2.16(C) をえました.この輸送案が全域木になっていることに注意してください. 輸送問題の基底形式表現と全域木の対応関係を数学的に示すこともできますが,ここでは割愛 します.興味がある人は適当な専門書を参照してください. さて,実行可能解は木であることから最適解も木になっています.ここで,需要量と供給量が すべて整数である場合を考えましょう.木は,その名前の通り末端(葉,leaf とよばれます) から, だんだんと枝が合流していきます(大本は根,root とよばれます).需要が整数であるなら,末端 の需要点に流れる量も(0 もふくめて) 整数のはずです.それが合流して,上流の枝に流れる量と なっても整数です.つまり木の構造と需要(と供給) が整数であることから,実行可能解は必ず整 数になります. 定理2.1 (輸送問題の整数性) 輸送問題が,次のような線形計画問題として定式化されたとする. min [総輸送費用] s.t. [流入量] − [流出量] = [需要 or 供給], すべての端点 [非負条件] すべての枝 需要と供給がすべて整数で,輸送問題に最適解が存在すれば,最適解も整数である. 上記の定理は,輸送問題の“よい” 性質を保証するものです.この性質を利用して,組合わせや 割り当てを決める問題に応用することができます.
2.6. 割当や組合わせを決める問題 67
2.6
割当や組合わせを決める問題
2.6.1 クッキーの作成場所
2.1 節の続きです. 今考えているのは,部員の製造場所への割り当てです.部員が製造場所に移動していくので, 輸送の最適化問題として考えることもできそうです.部員の部屋から,部員が1 単位 (=1 人) 供 給されて,需要点である製造場所へ運ばれるイメージです.各需要点の需要を定員に設定してみ ましょう.さて,運ぶものは部員自身なので分割は不可能ですが,今は定式化の都合を優先させ て,部員の部屋から需要点へ運ばれる物(=部員) の量を連続変数を使って表してみましょう.部員 i (i = 1, . . . , 12) の部屋から,それぞれの需要点 j (j = A, B, C) へ物が運ばれる可能性があるので, その量をxij (i = 1, . . . , 12; j = A, B, C) と表しましょう.つまり,36 個の変数を用意することに なります. 必要な制約は,供給点と需要点それぞれに存在します.供給点においては,部員は1 単位まで しか供給できないので, xiA+ xiB+ xiC= 1, i = 1, . . . , 12 となっていなくてはなりません.また,需要点では定員があるので, x1A+ x2A+ · · · + x12A= 6 x1B+ x2B+ · · · + x12B= 3 x1C+ x2C+ · · · + x12C= 3 を満たしていなくてはなりません.非負制約も忘れてはいけません. xij≥ 0, i = 1, . . . , 12; j = A, B, C 平均移動距離の最小化は,総移動距離の最小化でもあるので,目的関数を 3.1x1A+ 4.5x2A+ · · · + 3.4x12A + 1.9x1B+ 2.9x2B+ · · · + 6.8x12B+ 7.3x1C+ 6.1x2C+ · · · + 8.5x12C (2.7) とおきます. 以上をまとめると, min 3.1x1A+ 4.5x2A+ · · · + 3.4x12A +1.9x1B+ 2.9x2B+ · · · + 6.8x12B +7.3x1C+ 6.1x2C+ · · · + 8.5x12C s.t. xiA+ xiB+ xiC= 1, i = 1, . . . , 12 x1A+ x2A+ · · · + x12A= 6 x1B+ x2B+ · · · + x12B= 3 x1C+ x2C+ · · · + x12C= 3 xij ≥ 0, i = 1, . . . , 12; j = A, B, C (2.8)となり,輸送問題が定式化されました.最適解は,
x1A= 1 x2B= 1 x3A= 1
x4A= 1 x5C= 1 x6B= 1
x7C= 1 x8C= 1 x9B= 1
x10A= 1 x11A= 1 x12A= 1
となりました.残りの変数の値は0 です.最適解が 1 または 0 であることは,輸送問題の整数性に よって保証されます.物の輸送と便宜的に考えて定式化してきたのを,再度人の移動に置き換えて 解釈しなおすと, 製造場所A へ行く部員 1,3,4,10,11,12 製造場所B へ行く部員 2,6,9 製造場所C へ行く部員 5,7,8 となります.この場合の最適値は,42.1(km) です.こうしてみると,最初の素朴な方法も値とし ては悪くない気がします.しかし,図2.4 と図 2.17 を比較すると,製造場所 C への割り当てのバ ランスが改善していることがわかります.また,図2.6 では,製造場所 A に極端に遠い人が割り当 てられていたのが,図2.17 では,比較的集合場所に近いところに割り当てられています. 図表2.17 最適化問題を解いた結果 0 1 2 3 4 5 6 7 8 9 10 0 1 2 3 4 5 6 7 8 A B C 1 2 3 4 5 6 7 8 9 10 11 12 演習問題2.9 問題(2.8)は,平均移動距離最小化に対応している.では,もっとも移動距離が長い部員の移動 距離を最小化にするような割り当て(最長移動距離最小化基準)を得るためには,どのような定 式化を行えばよいか.
2.6. 割当や組合わせを決める問題 69
2.6.2 2 部グラフ
部室の掃除 クッキーの袋づめを部室で行うと決めたものの,現在の汚れ具合いではとても食べ物を扱う作 業が許されるとは思えません.責任者であるあなたが音頭をとって部室の大掃除を行うことにしま した.毎度のことですが,わがままな部員が多くて,掃除の役割分担ではいつももめることになり ます.以前責任者が分担を一方的に決めたときはいやな仕事に割り振られた部員が怒り出したこと もありました.じゃんけんで決めたときは,最後に負けた部員が逃亡してしまい,結局責任者が泣 く泣くその仕事をする羽目になりました. 今年度大掃除の分担を決めるに当たって,あなたが部員の話を聞いてみたところ,みな仕事に たいして好き嫌いがあり,しかもそれは必ずしも全員一様でないことに気づきました.うまく皆の 意見を調整すれば,なんとか全員が不満を抱かずに済ませることができるかもしれません. 当日集まれる8 人の部員にアンケートを取ったところ,表 2.18 のような結果を得ました.各部 員が仕事についてどれが好ましいか順位をつけてもらったものです.あなたは,部員の割り当てに 応じて決まる数値の合計が小さいほど部員の不満は少ないだろうと考えました. 図表2.18 部員の仕事に対する好き嫌いの順序 部員 1 2 3 4 5 6 7 8 a 窓ガラス 6 8 5 1 1 1 4 7 b 照明 1 5 3 2 3 4 1 6 c 棚1 2 7 8 7 6 2 7 8 d 棚2 3 3 4 8 2 5 8 4 e 机1 7 1 6 4 8 8 2 2 f 机2 4 4 1 3 7 6 6 5 g ごみ 8 6 7 6 5 3 5 3 h 床 5 2 2 5 4 7 3 1 この割り当て問題を,ネットワークを使って解いてみることにします. 図2.19 のようなネット ワークを描きました.図2.19 のように,端点の集合を 2 つに分けたときに,すべての枝の始点が 一方の集合に属する端点となり,終点が他方の集合に属する端点となるネットワーク(グラフ) を 2 部グラフと呼びます. 図表2.19 部員と仕事のネットワーク 1 2 3 4 5 6 7 8 a b c d e f g h 6 1 1 部員の端点に供給が1 存在し,仕事の端点に需要が 1 あるというように考えると,これは輸送 問題となります.枝の費用を選好順序として,最小費用輸送問題をとくことで,不満の少ない割り当てを決めることができそうです. 2.5 節で示したように,輸送問題型の定式化では解は必ず整数になるので,部員の端点からで る8 本の枝のうち,かならず 1 本だけに 1 単位の流量があります.そして,そこが部員に割り当 てる仕事になります. 定式化は,次の通りです. min n ∑ i=1 ∑ j∈J cijxij s.t. ∑ j∈J xij = 1, i = 1, . . . , n n ∑ i=1 xij= 1, j ∈ J xij ≥ 0, i = 1, . . . , n; j ∈ J ただし,cijは部員i を仕事 j に割り当てたときの選好順序を表し,J = {a, b, , . . . , h} とおいてい ます. 結果は,図2.21 の通りです.最悪でも 3 番目までに割り当てられているので,おそらく部員に 不満はないことでしょう.ためしに,ジャンケンで勝った人からわりあてを決めた場合を見てみま しょう.部員8 が一番で,以下,部員 5,部員 6,部員 3,部員 7,部員 4,部員 2,部員 1 の順序 で仕事を選ぶことになりました.部員は残っている仕事の中から一番自分の選好順序が高いものを 選びます.結果は表2.20 の通りです.じゃんけんで負けてしまった人は,あまりいい仕事につけ なかったようです. 図表2.20 ジャンケンで決めた場合の分担 部員(選んだ順序) 8 5 6 3 7 4 2 1 選んだ仕事 h a c f b e d g 選んだ仕事の順位 1 1 2 1 1 4 3 8 図表2.21 仕事の分担 1 2 3 4 5 6 7 8 a b c d e f g h 1 3 2 1 1 1 1 2 演習問題2.10 ある会社の従業員にたいする仕事の割り振りを考える.従業員5人に対して,割り振る仕事も5 つある.従業員はそれぞれの仕事に対して,得手不得手があり,各々の仕事をこなす時間はそれ ぞれ以下の表のようになっている.従業員Bは仕事1を,従業員DとEは仕事4と5を行う ことはできない. 全体の仕事にかかる時間が最小になる仕事の割り振りを決める問題を定式化せよ.
2.6. 割当や組合わせを決める問題 71 図表2.22 従業員が仕事を終えるのに要する時間 (単位:時間) 仕事1 仕事 2 仕事 3 仕事 4 仕事 5 従業員A 5 4 8 7 3 従業員B — 4 9 11 5 従業員C 6 5 8 5 4 従業員D 7 9 11 — — 従業員E 6 8 10 — — 演習問題2.11 1. 10人の学生を,3つのゼミのいずれかに所属させることを考える.各ゼミは定員4人を 越えて学生を所属させることはできないが,少ない分には構わない.また,各学生jがゼ ミiに所属したときの満足度ujiは事前の調査でわかっているものとする.学生の満足度 の総計を最大にするようなゼミの所属を決める問題をあらわすネットワーク(2部グラフ) をつくれ. 2. 最低定員(最低でも所属しなければいけない人数)が2人と設定されているとする.上と同 様にネットワークであらわせ.
2.6.3 参考:最大マッチング問題
2.6.2 節では,あらかじめ組み合わせの数は与えられていました (掃除の分担でいえば,8 人を 8 種類の仕事にわりあてました).今度は視点を変えて,可能な組合わせの中でなるべくたくさん の組をつくることを考えてみます. プロジェクトの担当 ソフトウェア開発会社が,クライアント企業からの注文に応じてシステム開発を行っています. クライアント企業ごとにプロジェクト・チームを結成し,一人のマネージャーを責任者として配 置して開発を行います.この会社には,プロジェクト・マネージャーを勤めることができる従業員 が10 名いますが,それぞれ専門分野があり,専門の異なるプロジェクトを担当することはできま せん. 営業部門が11 件の注文を受注してきたので,それぞれにマネージャーを配置しようとしていま す.各プロジェクトの内容を検討したところ,従業員が担当可能なプロジェクトは,図表2.23 の 通りであることがわかりました.同時に担当できるプロジェクトは1 件だけなので,担当者がみつ からないプロジェクトはクライアントと交渉して納期を伸ばしてもらわないといけません.営業責 任者がしりたいのは,担当者がいますぐ見付からないプロジェクトがあるかどうか,です. 図表2.23 従業員が担当可能なプロジェクト 従業員 担当可能なプロジェクト 1 a, e, j, 2 c, f, 3 a, b, e, 4 d, f, 5 d, g, 従業員 担当可能なプロジェクト 6 a, h, i, k, 7 d, f, 8 g, h, 9 f, g, 10 d, k,この問題は最大マッチング問題と呼ばれるものです.マッチングとはグラフに属する枝の集合 で,マッチングに属する枝は互いに始点も終点も共有しません.従業員とプロジェクトを端点と見 なし,可能な組合わせを枝と見なして2 部グラフをつくると.プロジェクトの担当問題は,このグ ラフのマッチングの数を最大にする問題と考えることができます1. 図表2.24 担当可能な組合わせを表す 2 部グラフ 可能な組合わせを表す2 部グラフを作ってみましょう.これは,図表 2.24 となります.つぎに この2 部グラフを埋め込んだネットワークを作ります.あらたに端点 s と t を導入します.端点 1, 2, . . . , 10 へ s 枝を張り,端点 t から端点 a, b, . . . , k へ枝を張ります.最後に t から s へ枝を張り ます.端点1, 2, . . . , 10 に供給が 1 単位あり,端点 a, b, . . . , k に需要が 1 単位あるとします.また 端点s と t には,それぞれ 10 単位の需要と 11 単位の供給があるとします.枝にかかる輸送費用 は,枝ts 間のみ 1 をつけ,ほかはすべて 0 としましょう.これで輸送問題として定式化すること ができます(図 2.25). 図表2.25 担当可能な組合わせを表す 2 部グラフを埋め込んだグラフ 1参考までに,マッチングと被覆の関係を述べます.一般のグラフにおいて,被覆(cover) とはグラフの端点の集合で, グラフ上の任意の枝は,必ず被覆に属する端点が始点もしくは終点となっている, という性質を持ちます.同じグラフ上で,マッチング M に属する枝の数(jMj) と,被覆 C に属する端点の数 (jCj) のあい だにはjCj ≥ jMj が成り立ちます.2 部グラフにおいては,最大マッチング M∗と最小被覆 C∗にかんして,jC∗j = jM∗j が成り立ちます.
2.6. 割当や組合わせを決める問題 73 輸送問題として定式化し,解いた結果, x1j= 1 x2c= 1 x3e= 1 x4s= 1 x5g= 1 x6i= 1 x7d= 1 x8h= 1 x9f= 1 x10k= 1 xta= 1 xtb= 1 xts= 9 を得ました.これを図示したのが図2.26 です.今,同時進行できるプロジェクトの最大数は 9 で あることがわかりました.当面,担当者のいないプロジェクトa と b を発注した企業には,納期 の延長交渉をしなくてはなりません. 図表2.26 プロジェクトの担当者 ツアーと添乗員 旅行会社が,7 月に 8 つのツアーを計画しています.各ツアーのスケジュールは,2.27 の通り です. 図表2.27 ツアーのスケジュール ツアー名 1 2 3 4 5 6 7 8 出発日 7/2 7/2 7/6 7/9 7/12 7/12 7/15 7/20 帰着日 7/13 7/9 7/13 7/11 7/19 7/14 7/19 7/23 期間 12 8 7 3 8 3 5 4 各ツアーには添乗員が同行することになっています.ツアーi の帰着日がツアー j の出発日よ り前であれば,i と j に同じ添乗員を割り当てることができます.ただし,1 週間以上のツアーに 同行した場合,次のツアーまで少なくとも2 日以上の間隔を空けるというルールがあります.この 旅行会社の7月のツアーのためには,少なくとも何名の添乗員が必要でしょうか. この問題も添乗員とツアーの最大マッチング問題と考えることができます.まず,各ツアー間 の前後関係を2 部グラフで表してみましょう.端点 i から端点 j′に枝が存在しているのは,ツアー i に同行した添乗員がツアー j′に同行できることを意味しています.
図表2.28 ツアーの順序関係 (左) と 2 部グラフを埋め込んだネットワーク (右) 1 2 3 4 5 6 7 8 1’ 2’ 3’ 4’ 5’ 6’ 7’ 8’ 1 2 3 4 5 6 7 8 1’ 2’ 3’ 4’ 5’ 6’ 7’ 8’ 9 10 [-1] -1 1 8 -8 -1 -1 -1 -1 -1 -1 -1 1 1 1 1 1 1 1 2 部グラフにもとづいて,ツアーの順序関係を輸送問題型のネットワークとして表してみます. 8 の需要を持つダミーの端点 9,8 の供給を持つダミーの端点 10 を導入します.端点 i(i= 1, . . . , 8) は供給1 を持ち,端点 i’(i’= 1, . . . , 8) は需要 1 を持ちます.費用は,枝 109 のみに −1 かかるもの とします.これを輸送問題とみて,最小費用を求めると,添乗員の最小人数がわかります. ¯¯ ¯¯ ¯¯ ¯¯ ¯¯ ¯¯ ¯¯ ¯¯ ¯¯ ¯¯ ¯¯ ¯¯ ¯¯ ¯¯ ¯¯ ¯¯ ¯ min − x109 s.t. x18′+ x19= 1, x25′+ x26′+ x27′+ x28′+ x29= 1 x38′+ x39= 1, x45′+ x46′+ x47′+ x49′+ x49= 1 x59= 1, x67′+ x68′+ x69= 1, x78′+ x79= 1 x89= 1, x101′ = 1, x102′ = 1, x103′ = 1, x104′ = 1 x25′+ x45′ + x105′ = 1, x26′+ x46′ + x106′ = 1 x47′+ x67′ + x107′ = 1, x18′+ x28′ + x38′+ x68′+ x78′+ x108′ = 1 8 ∑ i=1 xi9+ x109= 8 8′ ∑ j=1′ x10j+ x109= 8 xij ≥ 0 すべての ij
2.7. 参考:最大流問題 75 これを解くと, x18′ = 0 x19= 1 x25′ = 1 x26′ = 0 x27′ = 0 x28′= 0 x29= 0 x38′ = 0 x39= 1 x45′ = 0 x46′ = 1 x47′= 0 x49′ = 0 x49= 0 x59= 1 x67′ = 1 x68′ = 0 x69= 0 x78′ = 1 x79= 0 x89= 1 x101′ = 1 x102′ = 1 x103′= 1 x104′ = 1 x105′ = 0 x106′ = 0 x107′ = 0 x108′ = 0 x109= 4 を得ました.xij′ = 1 となるツアーの組をみると,2–5,4–6,6–7,7–8 です.これは,4 のツ アーに同行した添乗員は,6 のツアーにも同行できることを意味するので,一人の添乗員によって 4–6–7–8 のツアーをカバーできることがわかりました.結局,掛け持ちができないツアー (1,3) の 数とあわせて4 人の添乗員がいれば,7 月のツアーをすべてまかなうことができるのです. 一般的に,n 個のツアーがあり,2 部グラフのマッチング M の個数が |M| だったならば,必要 な添乗員の数はn − |M| です.添乗員の数を最小にするには,マッチングを最大にすればよいとい うのは,この関係から導かれます.
2.7
参考:最大流問題
輸送問題においては需要と供給があらかじめ与えられており,ネットワークを動く量は総量にお いて決まっています.この節で扱う最大流問題は,枝ごとに流量の上限が決まっている場合,ネッ トワークに流せる最大の流量を求めるものです.2.7.1 パイプラインの例
図表2.29 パイプラインs
t
<12>
<10>
<3>
<2>
<5>
<8>
<4>
<9>
<11>
<7>
1
2
3
4
5
6
図2.29 のようなパイプラインがあります.パイプラインを表す各枝には,そのパイプに単位時 間当たりに流せる最大の流量が決まっていて,⟨·⟩ にその値が示してあります. 端点 s から端点 t へオイルを流すとして,最大どれくらいの量を流すことができるでしょうか. この問題もやはり線形計画問題として定式化することができます.端点t から端点 s へ仮想的 なパイプを導入して,ネットワークを修正します.この枝ts の流量に上限はなく,流量 1 単位当 たりの費用を1 とします (図表 2.30 参照).このネットワークにおいて,目的関数を xtsとおいて,最大化問題を解けば,最大流が得られる.通常の輸送問題と違って,需要と供給量がない変わりに, 枝に流量の上限が与えられています.定式化すると,枝の流量の上限は決定変数(枝の流量) の上 限制約として制約式に現れます. 図表2.30 パイプラインに仮想的なパイプを導入
s
t
<12>
<10>
<3>
<2>
<5>
<8>
<4>
<9>
<11>
<7>
[1]
1
2
3
4
5
6
max xts s.t. xts− xs1− xs2= 0 xs1− x13− x14= 0 xs2− x26= 0 x13− x35= 0 x14− x45− x46= 0 x35+ x45− x5t= 0 x46+ x26− x6t= 0 x5t+ x6t− xts= 0 xs1≤ 12, xs2≤ 8, x13≤ 5, x14≤ 2, x26≤ 7 x35≤ 3, x45≤ 4, x46≤ 11, x5t≤ 10, x6t≤ 9 xij ≥ 0, ij ∈ E (2.9) 最適解は xs1= 5 xs2= 7 x13= 3 x14= 2 x26= 7 x35= 3 x45= 2 x46= 0 x5t= 5 x6t= 7 xts= 12 となりました.2.7.2 生産キャパシティ
ある部品メーカーは,原材料を中間製品に加工し,A,B,C の 3 種類の最終製品を製造してい ます.6 種類の中間製品と加工の工程は,表 2.31 のようにまとめられます.加工の前後で,部品の 数量は変化しません.原材料,中間製品,最終製品の関係をネットワークで表すと図2.32 となり ます.端点が中間製品や最終製品を,枝が工程を表しています(原材料を S とおきました).これを2.7. 参考:最大流問題 77 みてもわかるように,最終製品C を生産するにあたって,S → 1 → 4 → 6 → C や S → 2 → 4 → C という異なる工程が存在します. 図表2.31 加工の工程 工程 加工前→加工後 a 原材料→中間製品1 b 原材料→中間製品2 c 中間製品1 →中間製品 3 d 中間製品1 →中間製品 4 e 中間製品2 →中間製品 4 f 中間製品3 →中間製品 5 工程 加工前→加工後 g 中間製品3 →中間製品 6 h 中間製品4 →中間製品 6 i 中間製品4 →最終製品 C j 中間製品5 →最終製品 A k 中間製品6 →最終製品 B l 中間製品6 →最終製品 C 図表2.32 加工の工程 それぞれの工程には,使用する機械や作業員の技量,人数などにより一日に処理できる量に上 限があります(図表 2.33).原料の供給が十分にある場合,この工場で最大限製造できる最終製品 A,B,C の量はいくらになるでしょうか. 図表2.33 各工程の 1 日の加工量の上限 工程 a b c d e f g h i j k l 上限 12 15 18 3 7 6 5 12 3 8 9 12 最大流量 12 7 9 3 7 6 3 7 3 6 9 1 この問題は,一日あたりの最大加工量を,工程に対応する枝の流量の上限とみなすことで,最 大流問題として定式化することができます.図2.32 のネットワークに端点 T を導入し,端点 A, B,C から T に枝をはります.さらに,T から S に枝を張ると,図 2.30 と同じ形式になるので,あ とは(2.9) と同様に定式化をしてください.得られた線型計画問題を解くと,最終製品の最大生産 量はA が 6 単位,B が 9 単位,C が 4 単位となります.また,その場合の各工程の加工量を表 2.31 の最大流量に示しました.生産量を最大化すると,どの工程がボトルネックになっているかが判断 できます.
2.7.3 最小カット
問題(2.9) は線形計画問題です.では,このその双対問題はどうなっているのでしょうか.問題(2.9) の双対問題: min 12ξs1+ 8ξs2+ 5ξ13+ 2ξ14+ 7ξ26+ 3ξ35 +4ξ45+ 11ξ46+ 10ξ56+ 10ξ5t+ 9ξ6t s.t. −λs+ λt≥ 1 λs− λ1+ ξs1≥ 0 λs− λ2+ ξs2≥ 0 λ1− λ3+ ξ13≥ 0 λ1− λ4+ ξ14≥ 0 λ2− λ6+ ξ26≥ 0 λ3− λ5+ ξ35≥ 0 λ4− λ5+ ξ45≥ 0 λ4− λ6+ ξ46≥ 0 λ5− λt+ ξ5t≥ 0 λ6− λt+ ξ6t≥ 0 ξij≥ 0, ij ∈ E (2.10) 双対問題(2.10) において,λi (i = s, 1, 2, . . . , 6, t) は自由変数であす.ここで次の事実に注意し ましょう.今,最適解がλ∗i (i = s, 1, 2, . . . , 6, t) と ξ∗ij (ij ∈ E) であったとして,任意の実数 δ に より新たに λ†i= λ∗ i+ δ, i = s, 1, 2, . . . , 6, t をつくります.そうすると,λ†i (i = s, 1, 2, . . . , 6, t) と ξ∗ ij (ij ∈ E) も制約を満たし,かつ目的関 数値が同じなので最適解です.このままでは無数に最適解が存在してしまうので,λs= 0 と固定 します. (2.10) の制約式はすべて不等式です.したがって,最適解 (λ∗ s, λ∗1, . . . , λ∗t, ξ∗s1, . . . , ξ∗6t) が厳密 な不等式を満たす場合,例えば λ∗ 1− λ∗4+ ξ∗14> 0 となる可能性があります.しかし目的関数の性質(ξijの値をなるべく小さくする) より,これが起 こり得ないことはすぐにわかります.したがって最適解を代入すると,制約式はすべて等号で成り 立つはずです.以上のことから,(2.10) は min 12ξs1+ 8ξs2+ 5ξ13+ 2ξ14+ 7ξ26+ 3ξ35 +4ξ45+ 11ξ46+ 10ξ56+ 10ξ5t+ 9ξ6t s.t. −λs+ λt= 1 λs− λ1+ ξs1= 0 λs− λ2+ ξs2= 0 λ1− λ3+ ξ13= 0 λ1− λ4+ ξ14= 0 λ2− λ6+ ξ26= 0 λ3− λ5+ ξ35= 0 λ4− λ5+ ξ45= 0 λ4− λ6+ ξ46= 0 λ5− λt+ ξ5t= 0 λ6− λt+ ξ6t= 0 λs= 0 ξij≥ 0, ij ∈ E (2.11)
2.7. 参考:最大流問題 79 と等価です. 次に,s から t へのすべての経路を考えましょう.経路をすべて列挙すると, 1 番目: s—1—3—5—t 2 番目: s—1—4—5—t 3 番目: s—1—4—6—t 4 番目: s—2—6—t でとなります.各径路に含まれる枝の集合を以下のように定義します. P1= {s1, 13, 35, 5t} P2= {s1, 14, 45, 5t} P3= {s1, 14, 46, 6t} P4= {s2, 26, 6t} 1 番目の経路を例にとりましょう.双対変数の制約式は主問題の変数に対応していることから,1 番目の経路に含まれる枝に関係する双対問題の制約は, λs− λ1+ ξs1= 0 λ1− λ3+ ξ13= 0 λ3− λ5+ ξ35= 0 λ5− λt+ ξ5t= 0 となります.すべての式の両辺を足し合わせると, −λs+ ∑ ij∈P1 ξij− λt= 0 を得ました.λs= 0 より λt= 1 なので,結局 ∑ ij∈P1 ξij= 1 でなければなりません.この関係を使うと,双対問題は以下のように書き換えることができます. min 12ξs1+ 8ξs2+ 5ξ13+ 2ξ14+ 7ξ26+ 3ξ35 +4ξ45+ 11ξ46+ 10ξ56+ 10ξ5t+ 9ξ6t s.t. ∑ ij∈Pk ξij= 1, k = 1, 2, 3, 4 ξij≥ 0, ij ∈ E (2.12) この問題は,すべての経路上で最も流量が制約される場所(ボトルネック) を探す問題と解釈でき ます.これは最小カット問題とよばれるものです. 双対問題(2.10) の最適解: λs= 1 λ1= 1 λ2= 1 λ3= 1 λ4= 0 λ5= 0 λ6= 0 λt= 0 ξ13= 0 ξ14= 1 ξ26= 1 ξ35= 1 ξ45= 0 ξ46= 0 ξ56= 0 ξ5t= 0 ξ6t= 0 ξs1= 0 ξs2= 0 最適値は12 です.
演習問題2.12 7種類のチョコレートをそれぞれ3個づつ作った.このチョコレートを5つの箱に詰めるとする. 箱に入れることのできるチョコレートの数はそれぞれ6,4,5,4,3個である(チョコレートの 大きさに差はない).なるべくバラエティに富んでいた方がよいので,ひとつの箱に同じ種類の チョコレートは入れたくない.そのような詰め方が可能かどうか,最大流問題として定式化する ことで判定せよ.
2.8
参考:最短経路問題
(Shortest Path Problem)
仕事や遊びで旅行をするとき,目的地までどのようなルートをとるかを考えなくてはなりませ ん.鉄道を使うのか,自動車で行くか,あるいは飛行機か.交通手段が決まったとして,鉄道であ れば路線と乗り換え駅を考えなくてはいけません.自動車であっても,高速道を使うかどうか,ど の道を通るか,などについて,様々な条件を考慮して選択することになります.実際の旅行などは, 予算や興味の対象を考慮してルートを選択することになるでしょう. この節では,ルート選択を“距離” が最短になるように選ぶ問題を考えます.すなわち,ネット ワークの枝に,何らかの意味で端点間の遠近の度合を表す“ 距離” が与えられているものとして, 2 つの相異なる端点間の距離を最短で結ぶような経路を求めるということです.“距離” として考え られるものには,例えば,地理上の距離,交通費,移動時間などが挙げられます. A 地点から B 地点まで移動することを考えます.両地点間の移動に利用できる交通網は図 2.34 のネットワークによって表現することができます.枝上に与えられた数字は,その枝で表される交 通を利用した際の時間を表すとします.最短時間の移動経路はどのような経路になるでしょうか? 図表2.34 A 地点と B 地点間の交通網 2 4 1 6 3 5 1 7 3 6 10 2 8 2 5 2 最初に,輸送問題として定式化してみましょう. この問題を輸送問題の枠組で解くには,A 地点に供給量として 1 を,B 地点に需要量として 1 を与えます.そして,枝上の時間を,1 単位の輸送にかかる費用とみなして,最小費用輸送問題と して定式化すればよいのです.最適解において1 単位の物流が存在する経路が最短時間で移動でき る経路です.2.5 節で示したように,この種の輸送問題は,最適解では輸送料がどの枝でも必ず整 数(この場合は 1) になることを思い出してください. 最短経路を求める問題は最小費用を目的関数とする輸送問題として考えることができることを 示しました.あとは線形計画問題を適当なソルバで解けばよいことになります.しかし最短経路問
2.8. 参考:最短経路問題 (Shortest Path Problem) 81 題の解法は,LP ばかりではありません.例えばダイクストラ (Dijkstra) 法などのより効率的な解 法が存在するのです. 端点の集合V = {s, 1, 2, . . . , n} と枝の集合 E,および枝 ij ∈ E の距離 dij> 0 が与えられたと とき,以下の手続きを用いて,端点s から他の端点 j への最短経路を求めることができます. [ダイクストラ法のアルゴリズム:] ステップ1 初期化: 以下のように初期値を設定する. vs= 0 vj= ∞, j ∈ V, j ̸= s M = {s} N = ∅ ステップ2 端点の選択: M の中から,最小のラベルを持つ端点 i を選び出す. vi= minj∈M{vj} ステップ3 M と N の更新: N ← N ∪ {i} M ← M/{i} ステップ4 ラベルvjの更新: すべてのj ∈ V/M について,ij ∈ E が存在し,vi+ dij< vjならば, vj← vi+ dij M ← M ∪ {j} とする. ステップ5 終了判定: M = ∅ なら終了する.そうでなければ,ステップ 2 へ. ダイクストラ法が終了したときのラベルdj が,s から j への最短距離を与えます.図 2.34 の ネットワークに対してダイクストラ法を適用した際の途中経過を表2.35 にまとめました. 次に, 一般的な動的計画法 (dynamic programming, DP) による解法を見ることにします2. 端点の集合をV = 1, 2, . . . , n, t とします.端点 t が目標とする端点です (図 2.34 では,端点 6). 端点i から t まで,n−k ステップで到達する場合の最短距離を Jk(i) で表します.k = 0, 1, . . . , n−1 です.そうすると,Jk(i) は以下の関係を満たすものとして定義することができます3. { Jk(i) = minj=1,...,n[dij+ Jk+1(j)], k = 0, 1, . . . , n − 2; i = 1, . . . , n Jn−1(i) = ait, i = 1, . . . , n (2.13) 2ダイクストラ法もDP の一種と考えることができます 3(2.13) の 1 本目の式は再帰方程式と呼ばれます.
図表2.35 ダイクストラ法の適用例
初期化 step 1 v1= 0, vj= ∞, j = 2, 3, 4, 5, 6 M = {1}, N = {∅}
反復1 step 2 minj∈M{vj} = v1= 0 端点1 を選択 step 3 M = {∅}, N = {1}
step 4 端点 2: min{v0+ d12, v2} = min{0 + 1, ∞} = 1 ラベルを更新 端点3: min{v0+ d13, v3} = min{0 + 7, ∞} = 7 ラベルを更新 M = {2, 3}
step 5 M ̸= ∅ なので step 2 へ
反復2 step 2 minj∈M{vj} = min{v2, v3} = min{1, 7} = 1 端点2 を選択 step 3 M = {3}, N = {1, 2}
step 4 端点 3: min{v2+ d23, v3} = min{1 + 3, 7} = 4 ラベルを更新 端点4: min{v2+ d24, v4} = min{1 + 6, ∞} = 7 ラベルを更新 端点5: min{v2+ d25, v5} = min{1 + 10, ∞} = 11 ラベルを更新 M = {3, 4, 5}
step 5 M ̸= ∅ なので step 2 へ
反復3 step 2 minj∈M{vj} = min{v3, v4, v5} = min{4, 7, 11}=4 端点3 を選択 step 3 M = {4, 5}, N = {1, 2, 3}
step 4 端点 4: min{v3+ d34, v4} = min{4 + 2, 7} = 6 ラベルを更新
端点5: min{v3+ d35, v5} = min{4 + 8, 11} = 11 ラベルを更新しない M = {4, 5}
step 5 M ̸= ∅ なので step 2 へ
反復4 step 2 minj∈M{vj} = min{v4, v5} = min{6, 11}=6 端点4 を選択 step 3 M = {5}, N = {1, 2, 3, 4}
step 4 端点 5: min{v4+ d45, v5} = min{6 + 2, 11} = 8 ラベルを更新 端点6: min{v4+ d46, v6} = min{6 + 5, ∞} = 11 ラベルを更新 M = {5}
step 5 M ̸= ∅ なので step 2 へ
反復5 step 2 minj∈M{vj} = min{v5, v6} = min{8, 11}=8 端点5 を選択 step 3 M = {6}, N = {1, 2, 3, 4, 5}
step 4 端点 6: min{v5+ d56, v6} = min{8 + 2, 11} = 10 ラベルを更新 M = {6}
step 5 M ̸= ∅ なので step 2 へ
反復6 step 2 minj∈M{vj} = min{v6} = 10 端点6 を選択 step 3 M = {∅}, N = {1, 2, 3, 4, 5, 6}
step 4 M = {∅}
step 5 M = ∅ なので終了
結果 v1= 0, v2= 1, v3= 4, v4= 6, v5= 8, v6= 10 最短径路: 1—2—3—4—5—6
2.8. 参考:最短経路問題 (Shortest Path Problem) 83 ここで,dijは,枝ij の距離を表します.また dii= 0 とおきます. k = n − 1 から 0 にむかって,(2.13) を後ろ向きに計算 (後退計算) することで,DP を解くこ とができます.実際に,図2.34 に適用してみましょう. k = 4 (1 ステップで t に到達する場合): J4(4) = 5 J4(5) = 2 k = 3 (2 ステップで t に到達する場合): J3(5) = minj=1,...,n{d5j+ J4(j)} = d55+ J4(5) = 0 + 2 = 2 J3(4) = min{d44+ J4(4), d45+ J4(5)} = {0 + 5, 2 + 2} = 4 J3(3) = min{d34+ J4(4), d35+ J4(5)} = {2 + 5, 8 + 2} = 7 J3(2) = min{d24+ J4(4), d25+ J4(5)} = {6 + 5, 10 + 2} = 11 k = 2 (3 ステップで t に到達する場合): J2(5) = min{d55+ J3(5)} = 0 + 2 = 2 J2(4) = min{d44+ J3(4), d45+ J3(5)} = {0 + 4, 2 + 2} = 4 J2(3) = min{d33+ J3(3), d34+ J3(4), d35+ J3(5)} = {0 + 7, 2 + 4, 8 + 2} = 6 J2(2) = min{d22+ J3(2), d23+ J3(3), d24+ J3(4), d25+ J3(5)} = {0 + 11, 3 + 7, 6 + 4, 10 + 2} = 10 J2(1) = min{d12+ J3(2), d13+ J3(3)} = min{1 + 11, 7 + 7} = 12 k = 1 (4 ステップで t に到達する場合): J1(5) = min{d55+ J2(5)} = 0 + 2 = 2 J1(4) = min{d44+ J2(4), d45+ J2(5)} = {0 + 4, 2 + 2} = 4 J1(3) = min{d33+ J2(3), d34+ J2(4), d35+ J2(5)} = {0 + 6, 2 + 4, 8 + 2} = 6 J1(2) = min{d22+ J2(2), d23+ J2(3), d24+ J2(4), d25+ J2(5)} = {0 + 10, 3 + 6, 6 + 4, 10 + 2} = 9 J1(1) = min{d11+ J2(1), d12+ J2(2), d13+ J2(3)} = min{0 + 12, 1 + 10, 7 + 6} = 11 k = 0 (5 ステップで t に到達する場合): J0(5) = min{d55+ J1(5)} = 0 + 2 = 2 J0(4) = min{d44+ J1(4), d45+ J1(5)} = {0 + 4, 2 + 2} = 4 J0(3) = min{d33+ J1(3), d34+ J1(4), d35+ J1(5)} = {0 + 6, 2 + 4, 8 + 2} = 6 J0(2) = min{d22+ J1(2), d23+ J1(3), d24+ J1(4), d25+ J1(5)} = {0 + 9, 3 + 6, 6 + 4, 10 + 2} = 9 J0(1) = min{d11+ J1(1), d12+ J1(2), d13+ J1(3)} = min{0 + 11, 1 + 9, 7 + 6} = 10
計算結果をまとめると図2.36 となります.横軸にステップ数,縦軸に端点を取りました.図の 黒い丸の上にある数字はJk(i) の値です.端点 2 からの最短径路を知るには,k = 0 で i = 2 の場 所を見ます.この矢印をたどっていくと,2(—2)—3—4—5—6 が最短のルートであることがわか ります.端点1 から 6 までの最短距離が,ダイクストラ法で求めた値 (10) と等しいことを確認し てください. 図表2.36 DP によって解いた結果 k i 1 2 3 4 1 2 3 4 5 6 2 2 2 2 4 4 4 5 7 6 6 9 11 0 4 6 9 10 2 10 11 10 例題2.13 図書館で蔵書を収容するために新しい棚を設置することになりました.この蔵書の内訳は,4 イン チの高さが200 冊,8 インチが 100 冊,12 インチが 80 冊です.本棚は,棚の高さに応じた種類が あり,4 インチ,8 インチ,12 インチの 3 種類を選択できます.当然ながら 8 インチの棚には 4 イ ンチの本も収納できるし,12 インチであれば,全ての本を収納することが可能です.全ての本の 厚さは0.5 インチで一定であると仮定します.本一冊あたりの保管費用はその本が占める面積 (棚 の高さ× 本の厚み) に比例し,単位面積当り 5 ドルかかります.また,本棚はどの種類も 1 つの価 格は同じで,2300 ドルです.設置費用と保管費用の合計が最小になるような棚の高さの組合わせ はどのようになるでしょうか. [解答例] 図2.37 で表される最短経路問題を解くと最適な棚の高さの組合わせが得られます.ただし,枝 の距離を設置コストと保管費用の和としています.すなわち, 枝0 4 のコスト = 2300 + 4 × 0.5 ∗ 200 枝0 8 のコスト = 2300 + 8 × 0.5 ∗ (200 + 100) 枝0 12 のコスト = 2300 + 12 × 0.5 ∗ (200 + 100 + 80) 枝4 8 のコスト = 2300 + 8 × 0.5 ∗ 100 枝4 12 のコスト = 2300 + 12 × 0.5 ∗ (100 + 80) 枝8 12 のコスト = 2300 + 12 × 0.5 ∗ 80

![図表 2.10 仮想的な在庫の導入例 1 2 34 5 6 78[8][10][18][15][25][6] [3][5][8][4][9][5][4][11]-12 -9 -7 15 3[3]910[0][0][0] 演習問題 2.4 端点の集合 V と枝の集合 E がつぎのように与えられているとする. V = f1; 2; 3; 4g E = f12; 13; 21; 23; 24; 34; 43g 1](https://thumb-ap.123doks.com/thumbv2/123deta/7041044.788295/10.892.165.784.176.502/図表演習問題端点集合集合がつぎよう与えられいるする==.webp)
![図表 2.11 ガソリンの販売・在庫を表すネットワーク 0 1 2 3 4 5 6 7 8 9 140 120 150 120-550 20[90][85][92][90] (2.4) の最適解は, x 01 = 140, x 02 = 410, x 03 = 0, x 04 = 0, x 12 = 0, x 16 = 140, x 23 = 290, x 27 = 120, x 34 = 140, x 38 = 150, x 45 = 20, x 49 = 120, となり,(2.3) と同じ結果を得まし](https://thumb-ap.123doks.com/thumbv2/123deta/7041044.788295/12.892.158.794.188.767/ガソリンネットワーク=======となり得まし.webp)
![図表 2.13 生産量と在庫量のネットワーク 1 2 3 4 5 6 7 89 10 12 1113[0][0][0][0][0][0][0][0][500][650][650][650][650] [100] [100] [100][500][500] [500]-80-20-20-20 -20-80-80-80 60 9085 10560 非負の流量を持つ枝のみ示しました.この結果を見ると,通常シフトは第 2 期以外では最大限生産 を行う一方,臨時シフトの生産は第 1 期に 5 単位,第 4 期に 20](https://thumb-ap.123doks.com/thumbv2/123deta/7041044.788295/14.892.179.788.198.459/図表ネットワーク持つ枝この結果見るシフト期以外最大限生シフト.webp)

![図表 2.28 ツアーの順序関係 (左) と 2 部グラフを埋め込んだネットワーク (右) 1 2 3 4 5 6 7 8 1’2’3’4’5’ 6’7’8’ 12345678 1’2’3’4’5’ 6’7’8’9 10[-1]-118 -8-1-1-1-1-1-1-11111111 2 部グラフにもとづいて,ツアーの順序関係を輸送問題型のネットワークとして表してみます. 8 の需要を持つダミーの端点 9,8 の供給を持つダミーの端点 10 を導入します.端点 i(i= 1,](https://thumb-ap.123doks.com/thumbv2/123deta/7041044.788295/26.892.182.790.186.591/ツアー埋め込んネットワークグラフネットワークとしてダミー.webp)