心理学者は反応時間をどう分析するか

DOI: http://doi.org/10.14947/psychono.38.31

心理学者は反応時間をどう分析するか

井 関 龍 太

大正大学

How have psychologists treated response times?

Ryuta Iseki

Taisho University

Psychologists have analyzed response time data by their rules of thumb. Modern advances of statistical methods promote to create a new practice. Traditionally, outliers were discarded prior to statistical test and skewed data were converted by logarithms. Fitting approach reminds that analyzers intend to estimate parameters for RT distributions. In statistical tests, psychologists often conducted ANOVA by aggregating data across different trials in the same con-dition. This practice loss precision information of measurement. Linear mixed models is changing the situation. While practical issues are remain for several aspects of applying linear mixed model, consensus among psychologists would be increasingly required.

Keywords: response times, outliers, logarithmic conversion, ex-Gaussian, linear mixed models

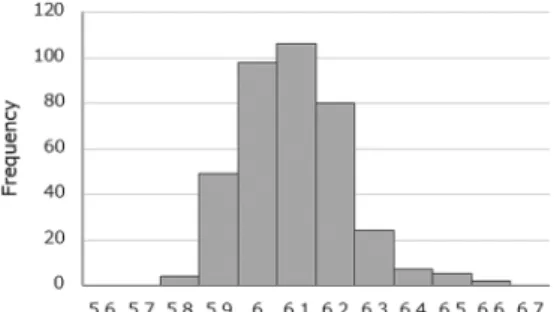
は じ め に 反応時間は，心理学実験において最も一般的な従属変 数のひとつだろう。その一方で，これほど広く用いられ ていながら反応時間データを分析するための理論的，形 式的なアプローチが確立されているとは言いがたい（数 理的なアプローチの試みとして，Luce, 1986）。本稿で は，現状広く用いられている分析方法をふり返り，そこ に含まれる前提と問題点を確認し，現代的な観点からの 改善策を図りたい。前半では個人ごとのデータの分析， 後半では代表値の分析について述べる。 個人ごとの分析 まず，具体的な反応時間データの例として，一名の実 験参加者（著者）が視覚探索課題を376試行行ったデー タの散布図をFigure 1に示した。大半のデータは400 ms 前後をばらついていることがわかる。一方，少数ではあ るが，600から800 ms前後にわたる他とは離れた値の データもあることが見てとれる。さて，こうしたデータ は一般的にどのように分析されているのだろうか。ま た，どのように分析することが適切なのだろうか。反応 時間データの分布をどのように見るかによって異なるア プローチが採られる傾向がある。 外れ値の除外 個人ごとの分析の終着点として設定さ れることが多いのが代表値の算出である。よく用いられ るのは平均値と中央値である。Figure 1のデータの平均 値は425.39 ms, 中央値は416.23 msであった。また，標準 偏差は64.12 msであった。反応の分布を反応時間帯ごと に見てとりやすくするために，同じデータについて作成 したヒストグラムをFigure 2に示した。このデータは， よく指摘される，右に裾野の長い分布となっていること

Copyright 2020. The Japanese Psychonomic Society. All rights reserved. Corresponding address: Department of Human Sciences,

Taisho University, Nishi-Sugamo, Toshima-ku, Tokyo 170–

8470, Japan. E-mail: r_iseki@mail.tais.ac.jp Figure 1. Scatterplot for sample data. J-STAGE First published online: March 11, 2020

がわかる。この図と平均値または中央値を照らし合わせ てみると，どちらの代表値を使ったとしても分布の中心 は400 msの帯にくることになる。そうすると，反応時 間の長いほうの反応は中心からは離れたものであるよう に見える。また，850 msの帯にある反応などは，他の棒 から連続していないこともあり，代表的な反応からかな り遠いものであるような印象を受ける。そこで，これら の反応は，研究者が調べようとしている反応分布を反映 しない，外れ値であると判断して，のちの分析から除外 することがよく行われる。外れ値の除外にはさまざまな 方法があるが（綾部・井関・熊田，2019を参照），最も 広く紹介されているのは正規（ガウス）分布に基づく方 法である。すなわち，反応時間課題における反応は正規 分布にしたがうと仮定して，正規分布から大きく外れた 反応は，調べたいものとは別の過程（注意のラプスな ど）によると考えるのである。平均値±3×標準偏差よ りも離れた値を外れ値とみなすなどの基準が用いられ る。外れ値の除外後に改めて平均値や標準偏差が計算さ れる。 変数変換アプローチ 外れ値を除外するのとは別のア プローチとして，数学的な変換を用いて反応時間データ を分析しやすい分布に変換するというアプローチもあ る。よく用いられるのが対数変換である（ほかの方法に ついては，綾部他，2019）。反応時間が対数正規分布に したがうとすれば，対数変換を行うことで反応時間デー タは正規分布に近づくはずである。一般線形モデルに属 する多くの統計手法（t検定や分散分析など）は分析の 対象となるデータが正規分布にしたがうことを仮定する ので，（物事の順序は逆転するようではあるが）反応時 間データも正規分布に従っているほうが都合がよい。 Figure 1のデータに対数変換を行ったものから作成した ヒストグラムをFigure 3に示した。分布は全体的に中央 寄りになり，期待されているように正規分布に近づい た。この変換後のデータの平均値は 6.04, 標準偏差は 0.14となり，単位は元の意味を失う。解釈しやすくする ために平均値を指数変換すると421.07 msとなり，ロー データの平均値よりもやや小さい値となる（幾何平均に 一致する）。変数変換を行った場合，変換後の値をその まま検定に用いることがふつうである。ここで注意する 必要があるのは，検定の結果は，変換後の値に対する推 論になるということである。すなわち，直接的に反応時 間に対する分析を行ったのではなく，反応時間を変換し た値に分析を行ったことになる。変換を行う根拠が妥当 であれば変換後の値に検定を行ったとしても何も問題は ない。しかし，検定に都合がよいからといった消極的な 理由しかないのであれば，このアプローチの採用を正当 化することは難しくなる。このためか，最近では変換ア プローチはあまり使用されなくなってきているように思 える。 特定の分布へのフィッティング 反応時間データの分 布を正規分布や対数正規分布ではなく，異なる2つの分 布を合成した形になると見るアプローチもある。データ の例でも見た通り，経験的には，反応時間では大部分の データは分布の中心に集まるが，ときどき長い反応が生 じる。これら2つの反応の傾向がそれぞれ別の心的過程 を反映すると考えることは不自然ではないだろう。後者 の，長い反応を生じる過程の働きについては，外れ値除 外のアプローチでも暗に仮定されていた。それを独立の 心的過程として明示的，積極的に評価しようというので ある。このフィッティング・アプローチでよく用いられ るのが，指数付き正規分布（ex-Gaussian）である。指数 付き正規分布は，正規分布と指数分布を足し合わせたよ うな形になる。指数付き正規分布は，μ （平均），σ （標準 偏差），τ （尾部）の3つのパラメータで形状が決まる理 論分布である。正規分布に相当する部分が大部分の平均 的な反応を生み出す過程を反映し（μとσ），指数分布に 相当する部分が散発的に生じる長い反応を生み出す過程

を反映する（τ）と考えるのである。この形は，実際に 観測される反応時間データに比較的似ている。ただし， 分布の形状が経験的に似ているという以上に，この分布 が人間の心的過程を適切に捉えていることを保証する理 由はない（正規分布などの他の分布を仮定する場合と同 様に）。 具体的な分析は，コンピュータを用いてデータに最も 当てはまるパラメータを探索することになる。Figure 4 にこれまでと同じデータに対して，Rのretimesパッケー ジを用いて指数付き正規分布へのフィッティングを行っ た結果を示した。実線が実際のデータ，点線が推定に よって得られた分布関数を表している。分布の頂点付近 に少しずれが見られるが，データのかなりの部分が推定 後の関数で表現されていることがわかる。また，推定に よって得られたμは371.77, σは31.86, τは53.61であった。 μは通常の平均と同じように解釈でき，この値に統計的 検定を適用することも多い。同様に，τに対しても統計 的検定を用いて分析が行われることがある。このように することで，平均的な反応を生み出す過程と長い反応を 生み出す過程の働きを独立に評価することができる。 フィッティング・アプローチはコンピュータによるパ ラメータ推定を行うことに注目するとこれまでとは異な る新奇な方法であるように見えるかもしれない。しか し，指数付き正規分布へのフィッティングという観点か らこれまでのアプローチを捉え返してみると，そもそも 平均値を計算するということは正規分布を仮定してその パラメータを推定することに等しい。つまり，指数付き 正規分布ではなく，正規分布へのフィッティングを行っ て，μとσを推定していたのである。このことが手計算で も可能であったのは，中心極限定理により，標本平均が 母平均の推定値として利用できたからである。また，標 準偏差については不偏性のための修正を採用することで 母標準偏差のパラメータとすることができた。このよう に見ると，個人ごとのデータの分析とは，それぞれの仮 定にしたがったパラメータ推定のアプローチであったと 考えることもできるだろう。正規分布に基づく外れ値の 除外は，正規分布を仮定し，そこから外れた（正規分布 の適用外である）値を除いてから改めて代表値を計算す るという点でパラメータの段階的推定であると見ること ができる。また，対数変換は，変換後の分布のパラメー タを推定していることになる。フィッティングの場合に は，他のアプローチとは異なり，正規分布以外の分布を 基準とすることになる。いずれにしても，分布とパラ メータ推定という観点から捉えることで，いずれのアプ ローチが自身の研究に適しているのかをより適切に判断 できるようになるのではないだろうか。 代表値の分析 典型的な反応時間の分析は，個人ごとの代表値を算出 したのちに，それらの代表値を使った統計的検定に向か うことが多い。しかし，反応時間データの場合には，こ こで考慮すべき事柄がある。それは，典型的な反応時間 の実験では，個人ごとに同一の条件について複数の試行 のデータが存在することである。このように実験を設計 することの理由としては，反応時間という指標の不安定 さがある。ひとつには個人ごとの変動が大きいこと，さ らには，要求する課題によっては誤答が発生することで ある。誤答試行の反応時間は，通常，代表値の分析から は除外される。正答の場合とは異なる心的過程を反映す るデータであると考えられるためである。では，ひとり につき，条件ごとに複数の反応時間データがある（しか も，誤答が存在する場合にはその個数も異なる）といっ た状況からどのように分析を行うのだろうか。反応時間 の実験を行ったことのない人であれば戸惑うのは無理も ないだろう。こんなとき，多くの心理学者は先輩あるい は教師として，これら“同じ”条件の試行を平均して代 表値を計算すればよいのだと教示しているのではないだ ろうか。確かに，一般的にはそのような分析方法が用い られている。しかし，そのような方法には疑問の余地が ある。 集計の問題 個人ごとに複数の試行のデータを平均す るといったやり方は，集計（aggregation）と呼ばれるこ とがある（Baayen & Milin, 2010）。反応時間を個人内で 条件ごとに集計してから分析するやり方は適切なのだろ うか。最初にこの方法を知ったときに違和感を抱いた人 もいるだろう。統計学の授業で分散について学んだと き，2つのグループの間で平均値は同じあっても分散は 異なる場合がある，これらを同じデータとみなすべきで Figure 4. Result of ex-Gaussian fitting for sample data.

はないと教わったはずである。複数の試行のデータを集 計してから検定にかけるということは，個人内のばらつ き（条件内の分散）を無視することになる。また，この ことは，平均というパラメータを推定するうえでの精度 に関する情報を捨てることを意味する。具体的には，試 行数が1試行であろうと100試行であろうと違いはない と仮定して分析することに等しい。実際には，“同じ” 条件の試行をくり返し実施しないと安定したデータを取 れないというのが心理学者の間で交わされる“秘伝”と なっているはずである（綾部他，2019を参照）。 一方で，集計しないと分析ができないという指摘にも 理はある。集計しないとすると，個人内での複数の試行 の違いを分析に組み込むことになる。この違いを独立変 数の効果と同様の固定効果として分析しようとすると， 運用上で多くの問題が生じる。ひとつには，外れ値や誤 答試行が存在することによって，参加者ごとに試行数が 異なると分析ができなくなる。また，固定効果として組 み込むということは，教条的には，水準の違いに研究関 心上の（つまりは，操作するということの）意味を見い だせなければならない。しかし，多くの場合は第一試行 と第二試行，第一試行と第三試行，……（以下，同様） の違いに逐一意味を見いだすことは難しい。つまりは， 概念的にもこの試行の違いを固定効果とみなすことには 無理があるのではないだろうか。 これらの問題は技術的に解決できる。固定効果ではな く，変量効果として分析に組み込むことでいずれの問題 も解決できる。変量効果であれば，各水準はランダムに 発生したものであるからそれぞれを無理に意味づける必 要はない。また，論点を先取りする形になるが，一般線 形混合モデルによる変量効果の推定はデータの欠測にも 比較的頑健である。 一般線形混合モデルによる分析 複数の試行の違いを 実際に変量効果として扱うには，一般線形混合モデルを 用いる。古典的な分散分析では，変量効果はひとつしか 扱うことができなかった。すなわち，参加者による誤差 の効果である。参加者内の分散分析のときには，球面性 の仮定という厳しい制約を課すことによって，実際には ひとつしかない変量効果を参加者内の効果（主効果と交 互作用）ごとに分割することによって対応していた。し かし，現実的には，球面性の仮定が成立しない場合も少 なくない。さらには，球面性の仮定が成立しない場合に は，タイプIエラー率が既定の有意水準を超えるという 問題が発生する。そして，刺激の違いや試行の違いなど の参加者以外の変量効果を扱うこともできなかった。 これに対して，一般線形混合モデルでは，複数の変量 効果を同時に推定できる。これにより，参加者による変 量効果に加え，刺激や試行の違いによる変量効果も加え た分析が行える。さらには，変量効果について，変量切 片だけでなく，変量傾きを区別して推定できる。変量切 片は，反応時間の分析の文脈で言えば，個人ごとのベー スラインの違いに対応する。すなわち，条件によらず， もともと反応時間が短い人と長い人の違いを表すことが できる。一方，変量傾きは，個人ごとの要因操作の影響 の違いを表す。つまり，研究者が操作した要因は人に よって効き具合（効果の大きさ）が異なることが考えら れるが，このような“効果の個人差”を反映するのが変 量傾きである。これらの特徴に加えて，球面性の仮定な どの現実的には成立することの難しい制約を課さずに参 加者内の効果ごとの変量効果を推定することもできる。 このような混合モデルによる分析は新奇なものに思える かもしれないが，理論的には，古典的な分散分析は一般 線形混合モデルの下位モデルと見なせる（分散分析は一 般線形モデルに包含され，一般線形モデルは一般線形混 合モデルに包含される）。したがって，試行ごとにデー タを集計したうえで混合モデルを使った分析を行うこと も可能である。 一般線形混合モデルでは，複数の試行のデータを集計 せずに，個々の反応のデータを直接入力して分析するこ とができる。しかし，平均をまったく使わないわけでは ない。分析者があらかじめ平均した値を入力する代わり に，線形モデルによって切片と傾きを推定する。これら のパラメータを推定することは，概念的には平均を計算 することと似ている（計算としては必ずしも同じはでな い）。通常の平均の計算と大きく異なるのは，それぞれ ばらばらに平均を計算するのではなく，個人ごとの切片 は母集団を表現する関数（線形モデル）の中で母集団の 切片と誤差によって表現され，個人ごとの傾きについて も同様であるというところである。したがって，データ 全体の構造をより反映した推定を行っていることにな る。 実際の研究で用いられるデータ構造には，研究者が操 作した要因の効果が加わるのでさらに複雑になる。要因 の効果は，古典的な分散分析の場合と同様に，固定効果 として扱う。固定効果は，変量効果に対してwithinの関 係になる場合もbetweenの関係になる場合もある。そし て，参加者の違いだけでなく，刺激の種類なども変量効 果になることがある。集計を行わず，試行ごとに得られ たデータを入力として分析する場合，古典的な分析では 平均することによって隠されてきた，刺激の違いの効果 を検討することもできる。研究テーマによっては，刺激

によって結果が異なる可能性について敏感にならざるを 得ない。一般線形モデルを用いれば，刺激の特性につい ての共変量を同時に投入した分析も可能である。ところ で，固定効果と変量効果が組み合わさると，ある要因は within participantかつbetween itemといった場合が起こり うる。たとえば，多義語と非多義語の語彙判断に関する 実験を行うことを考えてみよう。この場合，要因は語彙 の種類（多義語か否か）である。この要因を参加者内で 操作することにする。一方で，多義語である単語を多義 語でなくすることはできず，逆も言えるので，この同じ 語彙の種類の要因は，刺激項目に関してはbetweenの関 係になっている。より正確には，ネスト関係，クロス関 係といった用語を使ってこうした構造を記述する必要が ある（綾部他，2019を参照）。分析がややこしくなった ように思えるかもしれないが，このような状況は最近突 然に生まれてきたわけではない。これまでもまったく同 じ問題は潜在していたのだが，このような複雑な関係性 はすべて集計することで，すなわち，平均することに よって“なかったこと”にして済ませてきてしまったと いうのが実情である。 混合モデルの適用における問題 理論的には，参加者 内で同一条件に属する複数の試行のデータがある場合に は，一般線形混合モデルを用いて分析することが適切で ある。実際のデータの中に存在する構造，特に，データ の非独立性を無視して分析することは適切ではない。参 加者間要因と参加者内要因を区別して分析することも， この非独立性の考慮の一環といえる。つまり，これまで は技術的に困難であったために（しかたなく）平均する ことで済ませてきたが，現在ではそれらを考慮した分析 が可能になり，また，そうした考慮を行うことの必要性 が強く求められるようになってきている。 その一方で，一般線形混合モデルを使った分析につい ては，反応時間課題を中心とした実験室実験の状況のみ を想定したとしても，分析法にバリエーションがあり， いずれが妥当な方法であるか決着がついていないのが現 状である。ここでは，そのうちの3つのみを論じること にする（これらの論点を含む，より広い議論について は，Brauer & Curtin, 2018; McNeish & Kelley, 2019を参照）。

第一に，推定法の問題がある。現在広く使われている 混合モデルの推定法には，最尤法と制約付き最尤法 （REstricted Maximum Likelihood estimation, REML） が あ る。最尤法はさまざまな場面で広く用いられている方法 であるが，サンプルサイズが小さい場合にはバイアスが 生じることが知られている。一方，REMLは，サンプル サイズが小さいときでも不偏性を備えた推定値を生じる 方法である。古典的な分散分析と同じモデルを立てた場 合，REMLであれば，分散分析と同じ結果が得られる。 その意味で，古典的な手法との連続性という観点からは REMLが優れると言える。また，実験室実験はサンプル サイズが小さい場合が多いこともREMLを勧める理由に なるかもしれない。 混合モデルを使って分析する場合，サンプルサイズの 概念も複雑になる。レベル1のサンプルサイズ（典型的 な反応時間データを集計しないで分析する場合，試行 数）とレベル2のサンプルサイズ（参加者数）を区別す る必要がある。レベル2のサンプルサイズが分析結果に 及ぼす影響を調べた研究（McNeish, 2017）によれば，一 般には50名未満では固定効果のタイプIエラー率が既定 の有意水準を超えることが明らかになった。ただし， REMLとKenward–Rogerによる自由度修正法を用いた場 合，ベイズMCMC推定を用いた場合，モンテカルロ再 抽出法を用いた場合には10名程度の参加者でも適切な 推定量が得られた。このように，推定法の選択はサンプ ルサイズや検出力に大きく関わる。 一方で，最尤法による推定を行った場合にはモデル比 較を行えるが，REMLではモデル比較ができない。古典 的な分散分析ではモデル比較を用いないので，このよう な特徴はあまり重要でないと思う人もいるかもしれな い。しかし，後の論点とも関係するが，混合モデルを 使った分析ではモデル比較が重要になる可能性がある。 多数の固定効果と変量効果を含むモデルの場合（多くの 実験研究は古典的な分析では考慮されていないだけで多 数の要因を含んでいる），それらの変数の関係を適切に 記述したモデルを構成して分析を行う必要があるからで ある。最尤法と REMLのいずれを好むかは研究分野に よっても偏りがあるようで，現時点ではいずれがよいと も決めがたいというのが実情である。 第二に，有意性の判定方法の問題がある。混合モデル では，古典的な分散分析と同じような形では誤差の自由 度を計算できない。そこで，有意性を判定する方法には 大きく分けて2つがある。ひとつは，モデル比較に基づ く尤度比検定である。この方法は最尤法による推定を前 提とする。尤度比検定を用いず，AIC （Akaike Informa-tion Criteria）による比較を行うということも考えられる が，この方法ではサンプルサイズが小さいときにタイプ Iエラー率が増大しやすいという指摘がある（Matuschek, Kliegel, Vasishth, Baayen, & Bates, 2017）。もうひとつは，

データから自由度を推定することによってF検定を行う

方法である。複数の推定方法が提案されているが，Ken-ward–Roger法をREMLと併用するという方法が一定の評

価を得ているようである。有意性検定という手法にこだ わらないのであれば，ベイズファクターや再抽出法に基 づく評価を行うこともできる。 第三に，変量効果構造の決定法の問題がある。混合モ デルでは，すべての変量効果をモデルに含め，それらを 適切に指定しなければ推定値にバイアスが生じる。つま りは，本当は存在する変量効果を無視したり，それらの モデル上での指定が誤っていれば妥当な結果は得られな い。しかし，理論的にはそのような要請がなされるもの の，現実的には，特定の研究対象がどのような変量効果 構造を持っているのかは未知である。そこで，変量効果 構造を実践的に決めるためにはよく次のようなヒューリ スティックスが用いられる。まずは，最大の変量効果構 造を持つモデルで推定する。このような最大変量効果構 造を作るときの規則として，以下の 3つが挙げられる （Brauer & Curtin, 2018）。

1. あるユニットが非独立性を生じるならそのユニッ トによる変量切片を設定する 2. ユニット内予測変数にはユニットによる変量傾き を設定し，ユニット間予測変数には設定しない 3. 交互作用を構成するすべての要因がユニット内で あるときには，交互作用についてユニットによる 変量傾きを含める 大まかに言えば，独立変数以外にwithinの関係がある変 数があればすべて変量効果を考えることになる。このよ うな複雑なモデルは計算が収束しないことも多い。そこ で，収束しなかった場合には少しずつモデルを単純化し ていく。単純化のしかたについてもヒューリスティック スが提案されている（Matuschek et al., 2017）。 いったんモデルが収束した後にどうするかについて は，2つのアプローチがありうる。ひとつは最大維持ア プローチである。これは，収束に達した最初のモデルを 採用してその結果を解釈するというものである。このア プローチの欠点としては，モデルの選択がデータ依存に なることである。たとえばまったく同じ手続きでくり返 した完全な追試を行った場合でも，追試ごとに異なる変 量効果構造を持ったモデルを採用することになる可能性 がある。変量効果構造が偶然的でないデータの構造を記 述するものと考えるのであれば，このことは問題にな る。もうひとつのアプローチとして，モデル選択アプ ローチがある。このアプローチでは，収束に達した後も 分散が0に近い分散成分を除いてモデルをさらに単純化 していく。このことの根拠としては，0に近い分散成分 は適合度に寄与しないことと分散がほぼ0の変量傾きは 検出力を下げるということがある。もちろん，モデル選 択アプローチの場合も，得られる構造が恣意的にならな いとは限らない。 まとめると，理論的には，分析に使用するモデルは測 定の構造を反映したもののほうがよい。同一条件の複数 の試行があるのであれば，そのことが組み込まれている ほうがよい。参加者や刺激などがランダムにサンプリン グされているのであれば，いずれも変量効果にしたほう がよい。また，固定効果と変量効果のwithin/between関 係についても同様である。一般線形混合モデルによる分 析は，これらの要請に応えうるものである。一方で，分 析方法の性能の判断は，実用による評価を待たねばなら ない。混合モデルにおける具体的な実験デザインと分析 の検出力，タイプIエラーとの関係や刺激の多様性の影 響，外れ値の対処法との関係がどのようなものであるか は，これから検討していかねばならないだろう（混合モ デルでの検出力を高めるために反応時間を逆数変換する というアプローチについて，Brysbaert & Stevens, 2018）。 現実的な分析の選択肢として考えると，古典的な分散 分析は今後も併用されていくだろう。モデルとして適切 な場合には何の問題もないし，混合モデルのつもりでモ デルを組んでみたら分散分析だったということもありう るだろう。たとえば，参加者間の釣り合い型デザインの ときなどである。ただし，デザインの中に何らかの非独 立性を含んでいる実験は少なくない。参加者間のデザイ ンでも，同一の刺激が複数の条件にわたって用いられて いる場合もあるだろう（within item）。したがって，デー タの構造をよく吟味することは必要である。また，混合 モデルが収束しないために古典的な分散分析を使わざる を得ないということもしばらくの間は考えられる。しか し，今後は次第に混合モデルを使った分析に移行してい くものと予測される。現在，混合モデルをどのように適 用するのが適切であるのかといった議論に関する論文が 次々に出版されている（Brauer & Curtin, 2018; McNeish & Kelley, 2019）。これに伴って，研究者間でのコンセンサ スが形成されていくことが期待される。あるいは，混合 モデルはベイズとの親和性が高く，その応用がモデリン グの発想に近づいていることもあり，ベイズ統計学と融 合したりそれに置き換わったりすることも考えられる。 引用文献 綾部早穂・井関龍太・熊田孝恒（編） （2019）．心理学， 認知・行動科学のための反応時間ハンドブック 勁草 書房

Baayen, R. H., & Milin, P. (2010). Analyzing reaction times.

International Journal of Psychological Research, 3, 12–28.

and the analysis of nonindependent data: A unified frame-work to analyze categorical and continuous independent variables that vary within-subjects and/or within-items.

Psychological Methods, 23, 389–411.

Brysbaert, M., & Stevens, M. (2018). Power analysis and effect size in mixed effects models: A tutorial. Journal of

Cogni-tion, 1, Article 9.

Luce, R. D. (1986). Response times: Their role in inferring

ele-mentary mental organization. New York: Oxford Science

Publications.

Matuschek, H., Kliegl, R., Vasishth, S., Baayen, H., & Bates, D.

(2017). Balancing Type I error and power in linear mixed models. Journal of Memory and Language, 94, 305–315. McNeish, D. (2017). Small sample methods for multilevel

modeling: A colloquial elucidation of REML and the Ken-ward-Roger correction. Multivariate Behavioral Research,

52, 661–670.

McNeish, D., & Kelley, K. (2019). Fixed effects models versus mixed effects models for clustered data: Reviewing the ap-proaches, disentangling the differences, and making recom-mendations. Psychological Methods, 24, 20–35.