RSK対応を用いた箱玉系の組合せ論

RSK

対応を用いた箱玉系の組合せ論

福田香保理

*

神戸大学大学院自然科学研究科野海プロジェクト D3

2002 年 11 月 12 日

@

富士ハイツ

概要 箱玉系をワードとタブロウの組合せ論の観点から議論する

.

箱玉系 の各時刻の状態はロビンソン・シェンステッド・クヌース対応( $RSK$対 応) を用いてタブロウの組$(P, Q)$ に変換する事が出来る. タブロウの言 葉で言うと, $P$ シンボルは頭骨系の保存量であり, $Q$ シンボルは$P$ シン ボルに依存せずに発展する. また$Q$ シンボルの発展則は箱ラベルを用い て明示的に記述する事が可能である.

1

はじめに

1990

年に高橋・薩摩

([10], [8])

によって提案された箱と玉の系は, ある種の ソリ トンセルオートマトン

(

超離散可積分系

)

であり, 可積分系の分野におい て近年, 非線型可積分系の離散化 $([9],[11])$や量子代数における結晶基底の理 論$\langle$$[2],[4])$

などに関連して様々な研究がなされている

1.

本講演では, 箱玉系

をワードとタブロウの組合せ論の立場から解説する

.

箱玉系の各時刻の状態

が

_RSK

対応によりタブロウの組$(P, Q)$

と同

=視できるという事実に基づい

て, 主結果は以下のようにまとめられる

.

$\bullet$ 箱玉系の時間発展において $P$ シンボルは保存する. $\bullet$ $Q$ シンボルは$P$ シンボルに依存せずに発展し, その発展則は箱ラベル に着目することで明示的に記述される

.

本講演では考え易いスタンダードな場合のみを扱う

.

詳しい内容は改訂済 みの論文[1] に記述しているので, そちらを参照して頂きたい. 尚, 数$X$所, 数値の欠けた図や例があるが, 誤植ではなく (超初心者向けの) 演習問題

2

で す.

興味のある方はご自分で数字を埋めて完成させて頂くと雰囲気をつかん

で頂けるかと思います

.

$*E$_{-mail: jukuda@math} kobe-u.$ac$.jp

1 箱玉系に関する概説は例えば $[13],[14]$ を参照.

2 論文 [1] を見れば答えがわかる仕組みになっています.

表現論シンポジウム講演集, 2002 pp.14-29

2

準備

ここでは念の為にタブロウの組合せ論に関する基本事項,

即ち以下の議論で 断り無く用いる用語を簡単にまとめておく

.

詳しい定義などは文献 $([3],.[5],[7]$

など)

を参照して頂きたい.

2.1

タブロウワード

ヤング図形 $(a)$ とは, 有限個の箱を左上に詰めて, 各段の箱の数が下に向 かって非減少になるように並べた図形を言う

.

通常, 自然数の分割$\lambda=(\lambda_{1}\geq$ $\lambda_{2}\geq\cdots\geq\lambda\iota>0)$ と同=視されるものである. ヤングタブロウ $(b)$, または 単にタブロウ3 とは, 右に非減少, 下に増大となるように, ヤング図形の各箱 に1つずつ整数を記入したものを言う

(

マクドナルドの言葉では column-strict

tableau

のこと

[6]

$)$

.

$\lambda$ をタブロウの台と言う. 下図において, 各々の台は次

のようになる. $(a)$

:

$\lambda=(4,3,1)$

,

$(b)$

:

$\lambda=(4,3,2)$

,

$(c)$

:

$\lambda=(3,2,1)$

.

ス

タンダードタブロウ $(c)$ とは, 1か年 $n$

まで

1 個ずつ含んだタブロウのこと

を言う. 下図参照.

$(a)$ $(b)$ $(c)$

ここで,

あるタブロウに

1

つ整数を挿入して新たなタブロウを作る際のバ

ンピングアルゴリズム

(row-bumping,

or

$row- inserf$

ion)

を思い出しておく.

パンピング $Tarrow i$

(タブロウ

$T$ に整数 $i$ を挿入する

)

のルール : -番上の段に $i$ より大きな整数が無い場合は, その右端に新たな空箱を付 け加えて, そこに $i$ を挿入する. その他の場合, $i$ より大きな整数の中で, 最 も左に存在する整数$j$ を見つけて, $j$ を追い出した後に $i$を挿入し, 追い出さ れた$j$

を次の段に同様にして挿入する.

この操作を, 追い出された数字が段

の右端の新たな箱に収まるまで繰り返す.

与えられたワード

(数字の列)w

$=w_{1}w_{2}\cdots w_{n}$ に対して, $w$の数字を左から 右へ読んで, 空のタブロウ$\emptyset$

に順にパンピングして得られるタブロウを「ワー

ド$w$ のタブロウ

Tab

$(w)$」 と定義する.

Tab

$(w)=(\cdots((\emptysetarrow w_{1})arrow w_{2})arrow\cdots)arrow w_{n}$.

同様に, 与えられたタブロウ $T$に対して, $T$の数字を左から右, 下から上へ

(

図

1

参照

)

と読み上げたものを「タブロウ$T$ のワード_$W(T)$」 と定義する.

3 文献により異なるので注意が必要. セミスタンダードタブロウという表現の方がはっきりす

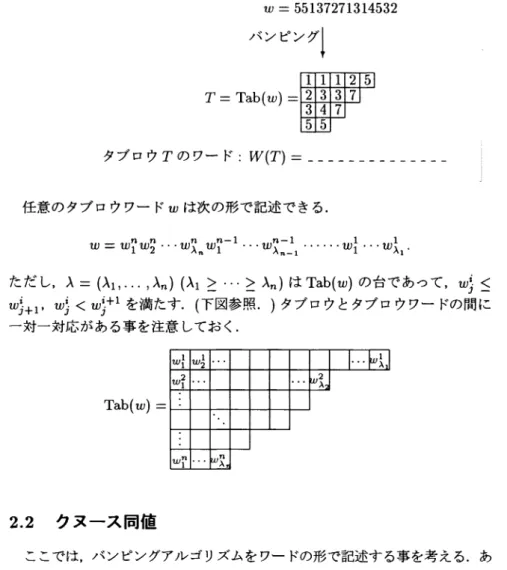
図1: タブロウワード $W(T)$ の読み方 この時,

_{Tab $(W(T))=T$}

となっている事に注意する. 与えられたワード $w$ が, あるタブロウのワードとなっている時, そのワードをタブロウワードと 呼ぶ. $w=55137271314532$ $\text{バンピング}\downarrow$ $T=Tab(w)=23\ovalbox{\ttREJECT} 135547371125$ タブロウ $T$のワード:

$W(T)=---$

任意のタブロウワード$w$ は次の形で記述できる.

$w=w_{1}^{n}w_{2}^{n}\cdots w_{\lambda_{n}}^{n}w_{1}^{n-1}\cdots w_{\lambda_{\mathfrak{n}-1}}^{n-1}\cdots\cdots w_{1}^{1}\cdots w_{\lambda_{1}}^{1}$

.

ただし, $\lambda=(\lambda_{1}, \ldots, \lambda_{n})(\lambda_{1}\geq\cdots\geq\lambda_{n})$は

Tab

$(w)$ の台であって, $w_{j}^{i}\leq$

$w_{j+1}^{i},$ $w_{j}^{i}<w_{j}^{i+1}$ を満たす.

(

下図参照

.

) タブロウとタブロウワードの間に ー対ー対応がある事を注意しておく.

2.2

クヌース同値

ここでは, パンピングアルゴリズムをワードの形で記述する事を考える. あ る段に1つ数字を挿入する法則4は次の形で記述できる. 4 自分より偉い人達を見て, その中で–番偉くない人を押し退けて, そこに自分が居座る.

$(ux’v)xarrow x’uxv$ $(u\leq x<x’\leq v)$

.

(1)

ここで, $x$ と $x’$ は数字を表し, $u$ と $v$ は非減少列を表す. 不等式$u\leq v$ は, $u$

の最大値が $v$ の最小値以下という意味である

.

この記述において, $x$ はワー

ド $(ux’v)$に挿入される数字である事を意味し, $x’$ はそのワードから追い出さ

れる数字である事を意味する. このパンピングの法則は

3

つの数字の並び変

えに分解する事が出来て, 以下の2 通りが基本法則となる.

$yzxarrow yxz$ $(x<y\leq z)$, (2)

$xzyarrow zxy$ $(x\leq y<z)$

.

(3)

これら2 つの変換, 及びその逆変換を, クヌース基本変換と呼ぶ. 定義1. 2つのワード$w$ と $w’$ が互いにクヌース基本変換で移り合う時, そ れらはクヌース同値であるといい, $w\approx w’$ と書く. 補題1. 互いにクヌース同値なワード$w$ と $w’$ から最大の数$p$を全て抜き取っ て出来るワードを $w_{0}$ と $w_{0}’$ とすると, それらはまた互いにクヌース同値な ワードになっている. 証明は例えば

[3]

を参照. 例1.

5152431245

$\approx$

5415213245.

これらクヌース同値なワードのクヌース基本変換は以下のように与えられる

.

5152431245

$\approx$

5

–431245

$(1 \leq 2<5)$ $=$

5512431245

551 –1245

$(2\leq 3<4)$ $*1$ $=$

5514231245

$\approx$

55

–31245

$(1\leq 2<4)$ _$*2$ $=$

5541231245

$\approx$

–1231245

$(4<5\leq 5)$ $=$

5451231245

$\approx$

5451

–

245

$(1<2\leq 3)$ $*3$ $=$

5451213245

$\approx$

5

–213245

$(1 <4\leq 5)$ 上記2 つのワード

5152431245

と

5415213245

から各々

5

を取り除いて出来る 2 つのワード 1243124と4121324はまたクヌース同値となっている.

1243124

4121324.

1243124

$\approx$

1

–124

$=$

1423124

$\approx$

–3124

$=$

4123124

$\approx$

41

–24

$(2\leq 3<4)$

. . .

$*_{1}$ $(1\leq 2<4)$

.

.

.

$*_{2}$ $(1<2\leq 3)$

. .

$.*_{3}$

2.3

バイワード

2 段の配列 (two-line array)

$w=$

において, 縦に並んだ の組が以下のような辞書式順序に並んでいる時, その配列をバイワード

(biword)

と言う. $\{$

$i_{1}\leq i_{2}\leq.$. . $\leq i_{n}$

,

$j_{k}\leq j_{k+1}$

if

$i_{k}=i_{k+1}$ $(k=1, \ldots , n-1)$.

更に上下の数字を入れ替えて改めて辞書式順序に並べ替えた配列を元のバイ ワード$w$ に対して, デュアルバイワード$\tau v^{*}$ と言う.

$w^{*}=$

.

ここで$\sigma\in S_{n}$ は, _{$j\sigma(1)\leq j\sigma(2)\leq\cdots\leq j\sigma(n)$} 及び, _{$j\sigma(k)=j\sigma(k+1)$} (7)0寺

$i_{\sigma(k)}\leq i_{\sigma(k+1)}$ を満足するような $n$次の置換である. 例2. バイワード

$w=$

のデュアルバイワードは $w^{*}=(1$

1

2

2 3

$5)$ である.

2.4

$RSK$

対応

バイワード$w$ と, 同じ台のタブロウの組$\{(P, Q)\}$の間にはー対ー対応$(R$ $SK$対応

)

がある. $P$ シンボル$P$ は下の段$(j_{1}, j_{2}, \ldots , j_{n})$ をパンピングして 得られるタブロウである. 一方, $Q$ シンボル$Q$ は, そのパンピングの過程に 従って数字を記入して作られる同じ台のタブロウであり, $P$ シンボルを作る

操作で九を挿入した際に出来る新たな箱と同じ位置の箱に

$i_{k}$ を書き込む事 で得られる. 例3. バイワード

$w=$

に対応するタブロウの組 $(P, Q)$ は, 図2のようにして得られる.

$P_{0}=$ $\emptyset$ $Q_{0}=$ $\emptyset$ $\downarrow$ $P_{1}=$ $\downarrow$ $\ovalbox{\ttREJECT}=$ $E3$ $\downarrow$ 馬 $\ovalbox{\ttREJECT}$ $\downarrow$ 政 $\ovalbox{\ttREJECT}$ $\downarrow$ $P_{5}=$ $\downarrow$ $P=P_{6}=$ $\downarrow$ $Q_{1}=$ _$E$ $\downarrow$ $Q_{2}=$ $H_{2}^{1}$ $\downarrow$ $Q_{3}=$ $H_{Z}^{I\sum}$ $\downarrow$ $Q_{4}=$ $\ovalbox{\ttREJECT}$ $\downarrow$ $Q_{5}=$ $\downarrow$ $Q=Q_{6}=$ 図2: パンピング過程

注意1. バイワードの上の段に $($

1

2.

.

.

$n)$ のように1から $n$ までの自然数

が1 個ずつ順に並んでいる場合は $RSK$対応ではな$\langle$ $RS$対応である. 更に

下の段が1 から $n$ までの自然数1 個ずつの時は, 単に $n$ 次の順列 (または

置換) と思う事が出来る. つまり, バイワード

$w=$

は, 順列

$\sigma=$ $(\sigma_{1}\sigma_{2}$

.

. .

$\sigma_{n})\in S_{n}$ と同ー視すれば良いので, 文献

[12]

などでR $S$対

応を知っていれば馴染みが深いと思う. 注意 $2$

.

=般にバイワードは, 含まれる の個数を $a_{ij}$ とする事で, 非負整 数からなる行列$A=(a_{ij})$ と=対= に対応させる事が出来る. $RSK$対応は, 非負整数を要素に持つ行列 $A$ と, 台の等しいタブロウの組$(P, Q)$ とのー対一 対応であるとも見なせる. 例4. 行列

$A=$

に対応するバイワードは

$w=(1$

1

1 2

2 2 2 3

$3)$ である. また, バイワードの上下の段を入れ換えると $P$ シンボルと $Q$ シンボルが 入れ替わる事は良く知られている.

(

例えば

[3]

を参照. ) 命題2.1. バイワード$w$がタブロウの組$(P, Q)$ に対応する時, デュアルバイ ワード$w^{*}$ は_{$(Q, P)$} に対応する.

3

箱玉系

ここから本題に入る.

本講演ではスタンダードな場合の箱玉系のみを用

$Aa$ て主結果を述べる. ここでスタンダードという用語は,

$RSK$

対応によって $P$

シンボルがスタンダードタブロウに対応するという意味で用いている

.

箱玉系とは$n$

色の有限個の玉が整数で番号付けられた無限個の箱の中を移

動して時間発展する=種の力学系である.

スタンダード箱膳系と言う時は, 全 部で$n$

個の相異なる色の玉が無限個用意された箱に散在していて

,

全ての箱の 容量が

1

であるという条件が付く

.

ここでは玉の色を表すのに数字

1,

2,

$\ldots,$$n$ を用い, 空箱を表すのに記号 $e(=n+1)$ を用いる

5.

3.1

スタンダード箱玉系

: オリジナルアルゴリズム

スタンダード箱玉系における時間発展則は次で定義される

.

1.

まず, 時刻$t$ から$t+1$ において, 全ての玉を一度だけ移動させる

.

2.

「$1$」 の玉を, その右にある

=番近くの空箱へ移動させる.

3.

同じ要領で他の玉も 「$2,3,$$\ldots,$$n$」 の順に移動させる.

これをオリジナルアルゴリズムと呼ぶ

.

例5. $n=5$ の場合の例を以下に示す. 時間発展した後の状態を右側に記入 してみて下さい.

3.2

バイワード表示

スタンダード箱玉系の各時刻の状態をバイワードで表示する事を考える

.

スタンダード箱玉系において, ラベル$i$

の箱に入っている玉の色を

$a_{i}$ で表し, 空箱の場合は$a_{i}=e$ と表示することにすると, 各時刻の状態は1,

.

.

. ,

$n$及び

$e=n+1$

の値をとる無限列

.

. .

$a_{-1}a_{0}a_{1}\cdots$ として表す事が出来る.

図

3 は時間発展の例を示したものである.

但し, 時間は下へ向かって進む ものとし, 空箱は$e$ の代わりにアンダーパ

–

で表示されている. 更に次の要領で,

空箱を無視した形のバイワード表示が可能である

.

即ち, 左から右へ順に見て, 玉の入った箱のラベノ垣1,$i_{2},$ $\ldots,$$i_{n}$ に対応する玉の色 5箱玉系に関する他の文献を参照される場合は特に空箱を表す記号に注意されたい.

—2457– 138—69

$---^{2457_{----}138_{--}69_{--}}$

———–2457—138

69

—————2457–18-369—

$---^{245_{-}178_{-}369_{--}}$

24–157-3689

24—157–3689

————————–24—-157—3689-$---24-$

157—-3689—

$---^{24_{---}157_{---}3689_{----}}$

$---24-157-3689$

図3: 時間発展の例

$a_{i_{1}},$$a_{i_{2}},$_$\ldots,$$a_{i_{\mathfrak{n}}}$ を記録することで下記のバイワードを得る.

$w=$

逆に勝手なバイワード$w$が与えられた時, 各 に対して 「ラベル$i$の箱に $j$ の玉が入っている」 と解釈することで, スタンダード箱玉系の時間発展に おける各時刻の状態とバイワードは–対ーに対応させることが出来る. スタ ンダード箱玉系での玉の色は, 1,2,.

. .

,$n$ が各々1個ずつなので, デュアルバ イワードは以下のようになる. $w^{*}$ _$=$ $b_{k}k$ $b_{n}n)$

.

このデュアルバイワード$w^{*}$ の下の段$b=(b_{1}, b_{2}, \ldots, b_{k}, \ldots, b_{n})$は箱ラベル $i_{1},$$i_{2},$ $\ldots,$ $i_{n}$ を並べ替えたもので

(箱ワードと呼ぶ),

左から $b_{1},$$b_{2},$ $\ldots,$$b_{n}$ の 順に, そのラベルの箱に入っている玉を移動させるというのが, オリジナル アルゴリズムになっている事を注意しておく. (元のバイワード$w$ の下の段 は, 玉の色1,2,.

.

. ,$n$ を並べ替えたワードで, これを玉$\text{ワ}-$ $\vdash$と呼ぶことに する. ) 例6. 例5において, 時刻$t$及び$t+1$の状態を各々バイワ一 \vdash ‘表示すると以 下のようになる. 数字を記入して完成させて下さい.

$w=(1$

2

3 5

$6$

)

$\Rightarrow$

$w’=(2$

3

1

4

$5)$ . また対応するデュアルバイワードは次のようになる. $w^{*}=(1$

2

3

4

$5$

)

$\Rightarrow$ $(w’)^{*}=(1$

2 3

4

$5)$ .

更に箱ワード表示を用いると, これと同じ時間発展を次のような形で記述す ることも可能である. (玉の色と総数は明らかに保存するので, 箱ラベルの変 化にのみ着目しようという考え方.) $b=(5,1,2,3,6)$ $\Rightarrow$ $b’=(7,4,5,8,9)$.

$RSK$

対応で知られているように, バイワードは同じ台のタブロウの組 $(P, Q)$ とー対– に対応させる事が出来る. 具体的には, 玉ワードをパンピン グして得られるのが $P$ シンボル, 箱ワードをパンピングして得られるのが $Q$ シンボルである6. そこでスタンダード箱玉系において, 与えられた状態 . . .$a_{-1}a0a_{1}\cdots$ に対して $(P, Q)$ を対応させて, これをスタンダード箱玉系の 状態と見なす事にする. 定理3.1. スタンダード箱玉系を $(P, Q)$ の時間発展と見なした時,

1.

$P$ シンボルは時間発展において保存する

.

2.

$Q$ シンボルは$P$ シンボルに依存せずに発展する. $Q$ シンボルの発展則の記述には,

次に述べる運搬車アルゴリズムが重要な

役割を果たす.

3.3

運搬車アルゴリズム

あるワード$w=(w_{1}, w_{2}, \ldots w_{n})$ から別のワード$w’=(w_{1}’, w_{2}’, \ldots, w_{n}’)$ へ の変換に運搬車と呼ばれる非減少数列$C=$ $(c_{1} , , c_{m})$

を用いるアルゴリズ

ムを導入する. 運搬車が元のワード$w$

に沿って左から右へと数字の積み下ろ

しをしながら通り過ぎた結果, 新しいワード $w’$ が得られると考える. 下図の ように運搬車は$w_{k}$ の横を通り過ぎる時, $w_{k}$ を積み込んで$w_{k}’$ を下ろす.

$\{$ $C=C_{0}$ $arrow$$w_{1}w_{1}.\cdot..\cdot.$ $C_{1}$ $arrow$ $C_{2}$ $arrow$ $C_{3}$

, $w_{2}w_{2}’....\cdot$

.

$w_{3}w_{3}’....\cdot$

.

$c_{n-1}$ $arrow w_{n}w_{n}’.\cdot...\cdot$ $C_{n}=C’\}$ 数字の積み下ろし規則は以下のように定義される. 数字の積み下ろし規則: $C_{k-1}=$ $(c_{1}^{(k-1)},, c_{2}^{(k-1)}, \ldots, c_{m}^{(k-1)})$ $(c_{1}^{(k-1)}\leq c_{2}^{(k-1)}$ $\leq\cdots\leq c_{m}^{(k-1)})$

を運搬車に既に積み込まれている数字の列とする

.

$w_{k}$ を今 から積み込む数字とする

.

$w_{k}$ と, $C_{k-1}$ に含まれている数字とを比べて, $w_{k}$ より大きい数字が $C_{k-1}$ に存在する時は, その中の最小値が下ろされて, 代 わりに$w_{k}$ が積み込まれる. そのような数字が存在しない時は, 単に$C_{k-1}$ の 中の最小値が下ろされて, 代わりに$w_{k}$ が積み込まれる. $(\text{下図参照}. )$ 6$P$ シンボルには玉の色という情報が詰まっていて, $Q$ シンボルには箱のラベルという情報 が詰まっている.

$w_{k}$ .

.

.

$\dot{v}$ $w_{k}’$ $w_{k}’$ $=$ $\{$ $min\{c_{i}^{(k-1)}\in C_{k-1}|c_{i}^{(k-1)}>w_{k}\}$

if

$\{c_{i}^{(k-1)}\in C_{k-1}|c_{i}^{(k-1)}>w_{k}\}\neq\emptyset$, $min\{c_{i}^{(k-1)}\in C_{k-1}\}$

otherwise.

$C_{k}$ $=$ $C_{k-1}$から $w_{k}^{j}$ を除き $w_{k}$ を加えて得られる非減少列.

与えられた2つの有限列 $C=(c_{1}, c_{2}, \ldots, c_{m})(c_{1}\leq c_{2}\leq\cdots\leq c_{m})$ と $w=(w_{1}, w_{2}, \ldots, w_{n})$ に対して, $C_{0}=C$ として, 上記の積み下ろし規則を 繰り返す事により新たに $C’=C_{n}$ と $w’$ を得る. この変換_{$(C, w)arrow(C’, w’)$}

を運搬車アルゴリズムと呼ぶ.

注意3. 運搬車アルゴリズムはクヌース変換の繰り返しであると理解できる

.

既述の積み下ろし規則において $k$番目の操作に対して, サブセクション

22

の法則(1) を適用することが出来る. $C_{k-1}$ が $w_{k}$ より大きな数字を持ってい る時は,

$C_{k-1}w_{k}=(ux’v)x$ $arrow$ $x’(uxv)=w_{k}^{j}C_{k}$ $(u\leq x<x’\leq v)$,

と考えられる. ただし$x’=w_{k}$ かつ$x=w_{k}’$ である. その他の時は,

$C_{k-1}w_{k}=\{x’v)x$ $arrow$ $x’(vx)=w_{k}’C_{k}$ $(x’\leq v\leq x)$

を自明な変換と考えれば良い. それゆえに $k=1,$$\ldots,$$n$ に対して$C_{k-1}w_{k}\approx$ $w_{k}’C_{k}$ が成り立つ. $Cw$ $=$ $C_{0}w_{1}w_{2}w_{3}\cdots w_{n}$ $\approx$ $\approx$ $w_{1}’C_{1}w_{2}w_{3}\cdots w_{n}$ $w_{1}’w_{2}’C_{2}w_{3}\cdots w_{n}$ $\approx$ $w_{1}’w_{2}’w_{3}’\cdots w_{n}’C_{n}$ $=$ $w’C’$

.

3.4

運搬車を用いた時間発展

以下では, 定理3.1 の証明に必要な命題を 2 つ準備する. スタンダード箱 玉系の時間発展は, オリジナルアルゴリズムと, 箱ワードの変換という2 種類の方法で記述することが出来る. まず, これら2つのアルゴリズムを既

に導入した運搬車アルゴリズムを用いて記述することを考える.

無限列で

は考えにくい為,

区間「

$p,$$q$

]

を定めておく. オリジナルアルゴリズムのー段

階の時間発展操作で最低限必要な区間は例えば

$p= \min\{i\in Z|a_{i}\neq e\}$,

$q= \max\{i\in Z|a_{i}\neq e\}+n$のように決めれば良い.

命題32. スタンダード毛玉系の与えられた状態に対して, 両側に続く $e$ の

無限列を取り除いて残った有限列を $A=(a_{p}, a_{p+1}, \ldots, a_{q-1}, a_{q})$ とする. こ

こで$p,$$q$ は上で定めたものとする. この時, オリジナルアルゴリズム $Aarrow A’$

は, $n$個の$e$ からなる $C=(e, e, \ldots, e)$

を初期状態とした運搬車アルゴリズ

ムで記述することが出来る.

例7. 例

5

と同じ例を考える

.

$n=5$で,

区間「

$p,$$q$] $=[1,11]$ を取り,

$C=(e, e, e, e, e)$, $A=(2,3,4, e, 1,5, e, e, e, e, e)$

に対して数字の積み下ろしを11 回行うことで,

$A’=(e, e, e, 2,3, e, 1,4,5, e, e)$, $C’=(e, e, e, e, e)$

を得る. 以下の図に数字を記入して下さい.

$e,$ $e,$ $e,$ $e,$

$e+^{2}$ $+^{3}$ $+^{4}$ $+^{6}$ $+^{1}$ $+^{5}$

$arrow$

$+^{e}$ $+^{e}$ $+^{e}$ $+^{e}$ $+^{e}$

次に, 箱ワー $\text{ト^{}\backslash }b=(b_{1}, \ldots, b_{k}, \ldots, b_{n})$

に対して運搬車アルゴリズムを適

用する. 上で与えた$p,$$q$ に対して, $b_{k}\in[p, q]$ が, 全ての $k=1,2,$$\ldots,$$n$ に 対して成り立っている事を注意しておく. 命題33. 与えられたスタンダード箱玉系に対して, 時刻$t$から$t+1$までの, 箱 ワードの時間発展$barrow b’$は, $C=(l_{1}, l_{2}, \ldots, l_{m})$ を初期状態とする運搬車アル ゴリズムで記述できる. ここで運搬車の初期状態$C$は, $l_{k}\in\{i\in[p, q]|i\not\in b\}$ と

$m=q-p+1-n$

で定義されるものとする

.

例8. 例

5

と同じ例を考える

.

$n=5$で,

区間「

$p,$$q$

]

$=[1,11]$ を取り, $C=(4,7,8,9,10,11)$

,

$b=(5,1,2,3,6)$ に対して数字の積み下ろしを5回行った結果, $b’=(7,4,5,8,9)$

,

$C’=(1,2,3,6,10,11)$ を得る. 以下の図に数字を記入して下さい. $4,7,8,9,10,11+^{5}$ $+^{1}$ $+^{2}$ $+^{3}$ $+^{\theta}$

(a) (b) (c) (d) (e) (f) (g) (h) 図4: 例5の2次元図

4

主結果の証明

4.1

命題の証明

ここでは前節で与えた2っの命題の証明の概略を述べる. その為に図4の ような2次元図を導入する.

まず=番上の段に時刻$t$ の状態$a$ を書$\text{く}(a)$

.

次に各々の$a_{i}$ の値を再度, 色

ごとに段を変えて書$\text{く}(b)-(g)$

.

ここでは例5 と同じ例を用いている. オリジ ナルアルゴリズムに従い,「$1$」 とその相棒, つまり右にある最も近くの $r_{e\rfloor}$ を線で結ぶ

(i).

次に 「$2$」 を見て同じ事をする

(j).

この例では,「$3J$ が移動 する先は, 最初に 「$1$」 があった場所なので, この場合,「$3$」 の相棒は「$1$」 と 思うことにする _(k). 全ての$a_{i}(\neq e)$ に対して同様の操作を行う. 線の引き方 としては=般に次のような法則がある事が分かる. $(*)$ ある数字に着目した時, その数字より右側かつ下側にある数字で最 も左に存在する数字へ線を引く. 但し. 同じ数字が並んでいる場合は. 右に ある方が大きい(少し上に位置している) と理解する. さてオリジナルアルゴリズムに従って図を作成していくと, 下から上へ向 かって各々の数字に着目することになる. この時, 玉の色ではなくて箱の番 号に着目して, その変換を記述したものが箱ワードの運搬車アルゴリズムに 相当する (命題52). 逆に左から右へ向かって各々の数字に着目したのが玉 を乗せた運搬車アルゴリズムに相当する (命題5.1). 絵を見て明らかなので, ここでは敢えて詳細は省くことにする

7.

7改訂版の論文[1] には詳細を記述しました.

4.2

定理

3.1 の証明

ここからは定理

31

の証明を簡単に説明する

.

命題5.1により, スタンダー

ド箱庶系の時間発展は玉を運搬する運搬車アルゴリズムで記述することが出

来る. これはクヌース変換の繰り返しであると理解できるので, 以下のよう

な変換によって $CA\approx A’C$

(クヌース同値)

を得る.

$CA$ $=$ $C_{p-1}(a_{p)}a_{p+1}, \ldots, a_{q-1}, a_{q})$

a$p^{\prime c_{p}(a_{p+1},a_{p+2}}’\cdots,$ $a_{q-1}$,a$q$)

$(a_{p^{J}}, a_{p+1^{J}})C_{p+1}$($a_{p+2},$ $a_{p+3},$$\ldots$ , a$q-1,$$aq$)

$\approx$ $(a_{p’}, a_{p+1’}, \ldots, a_{q-1^{J})}a_{q^{J}})C_{q}$ $=$ $A’C$

これより $CA$ と $A’C$ は同じタブロウに対応する事が分かる

.

$e$ は最大の数と

考えているので, $CA$及び$A’C$から各々$e$ を全て除いたワードを$A_{e}$ 及び$A_{e}’$

とすると, 補題1より, これらは再びクヌース同値になっていて $(A_{e}\approx A_{e}’)$, 対応するタブロウ $P$ を,

この時間発展における保存量と見なすことが出来る.

ここで, $A_{e}$ 及び$A_{e}’$ はバイワードに対応させた時の下の段のワード(玉ワー ド) に他ならない.

定理

3.1

の一つ目の主張はこれで証明できたことになる

.

次に定理3.1 の二つ目の主張を証明する為に, 箱ワードの運搬車アルゴ リズムを考える.

箱ワードの時間発展を表すのに

$T^{*}$ という記号を用いる $(T^{*}(b)=b’)$

.

ここで天下り的に以下に

2 つの補題を与える.

補題2. $a$ と $b$がクヌース同値なワードなら, 時間発展の結果$T^{*}(a)$ と $T^{*}(b)$ もクヌース同値である. 補題3. $b$ がタブロウワードなら, _$T^{*}(b)$ もタブロウワードである. 図5において, $b\approx W(Q_{1})$ なので, 補題2より次を得る. $T^{*}(b)\approx T^{*}(W(Q_{1}))$. $T^{*}(b)=b’$ かつ $b’\approx W(Q_{2})$ であるから, $W(Q_{2})\approx T^{*}(W(Q_{1}))$

.

更に補題3から, $T^{*}(W(Q_{1}))$ はタブロウワードである. 故に, $W(Q_{2})=T^{*}(W(Q_{1}))$

.

これは即ち$Q$ シンボル $Q_{2}$ が $Q_{1}$ のみから決まり $P$ シンボル $P_{1}$ には依存し ない事を示している. これで定理3.1 の二つ目の主張が証明できた.

$P_{1}$ $T^{*}(Q_{1})$ 図5: デュアルの時間発展$T^{*}$ また, タブロウワードとタブロウを同ー視することで, $Q$ シンボル$Q$ の時 間発展を以下のように定義し直す. $T^{*}(Q)=Tab(T^{*}(W(Q)))$

.

最後に, 以上を考慮に入れて,

区間「

$p,$$q$] $\subset Z$ を再度用いて, 次の命題を与 える. 命題41. スタンダード箱玉系において, $Q$シンボル $Q$の時間発展は箱ワード の運搬車アルゴリズムとして定義される. 運搬車の初期状態$C=(l_{1}, \ldots, \iota_{m})$ は区間$[p, q]$ に含まれる全ての空箱のラベルからなる非減少列として与えられ る. この時, 運搬車はタブロウ $Q$の左から右, 下から上へと走る.

参考文献

[1]

K. Fukuda, Box-ball systems and

Robinson-Schensted-Knuth

correspon-dence, (math $CO/0105226v3$).

[2]

K.

Fukuda, M.

Okado and Y.

Yamada, Energy

functions in box ball

systems,

Internat.

J. Modern

Phys.

A 15 (2000), no.

9,

1379-1392.

[3]

W.

Fulton,

Y

$o$

ung Tableaux,

London

Mathematical

Society

Student

Texts

35,

Cambridge University Press (1997).

[4]

G.

$H$

atayama,

A. Kuniba and T. Takagi,

Soliton

cellular

automata

as-sociated with finite

crystals,

Nulclear

Phys. $B$

577(2000),

619-645.

[5]

$D.E$

_{. Knuth,}

The art

of

computer

programming,

Volume 3, Sorting and

searching, Addison-Wesley

Series in

Computer

Science and Information

Processing. Addison-Wesley Publishing

Co.,

Reading, Mass.-London-Don

Mills, Ont.,

1973.

[6]

$I.G$

. Macdonald, Symmetric

functions

and Hall

polynomials,Second

Edi-tion,

Oxford

University

Press,

1995.

[7]

$B.E$

.

Sagan, The symmetric group. Representations, combinatorial

al-gorithms, and symmetric

functions,

Second

edition,

Graduate

Texts

in

Mathematics,

203.

Springer-Verlag, New

York,

2001.

[8] D. Takahashi,

On some soliton systems defined

by

using boxes and

balls,

Proceedings of the

International

Symposium on NonlinearTheoryandIts

Applications

(NOLTA ’93),

1993,

pp.555-558.

[9]

D.

Takahashi and J.

Matsukidaira,

Box and ball system with a carrier

and ultradiscrete

modified

$KdV$

_{equation, J. Phys. A 30 (1997)}

L733-L739.

[10]

D. Takahashi and J.

$S$atsuma,

A soliton cellular

automaton,

J.

Phys.

Soc.

Jpn.

59

(1990)

3514-3519.

[11] T. Tokihiro,

A. Nagai, and J.

Satsuma,

Proof of solitonical nature of

box and ball systems by

means

of inverse

ultra-discretization, Inverse

Problems 15 (1999),

no

6,

1639-1662.

[12]

堀田良之

,

「加群十話

-

代数学入門

-

」

sugaku books

3

朝倉書店,

1988.

[13]

数理科学

NO

435,

SEPTEMBER

1999.

[14] 時弘哲治

,

「箱玉系の数理

-

超離散ソリ トンの世界」 2002 年度日本数学