資産格差の数値解析（計算経済学の研究その16）

(1)

資産格差の数値解析

（計算経済学の研究その16）

Numerical Analysis of Asset Inequality

釜　　国男*

Kunio KAMA

　ピケティ『21 世紀の資本』の出版を機に、世界的に経済格差の問題が関心を集めている。とくに米国では格差の拡大が顕著である。2007年の調査によると、全米上位1%の富裕層が全資産の 33.8%を占め、2－10%の層は 37.7%、11－50%層は 26.0%、下位50%はわずか 2.5%を占めるにすぎない（FRB「Survey of Consumer Finances」による）。リーマン・ショックによる景気後退の影響で格差は一段と拡大している。資産だけでなく所得の格差も大きい。2013 年のデータによると、全所得に占める上位3%の割合は 30.5%で、下位90%は 52.7%にすぎない。米国ほどではないが、バブル崩壊後の日本でも格差は拡大している。格差問題は教育や税制、人口構成などさまざまな視点から論じられるが、ここではマクロ経済学の立場から検討したい。マクロ経済学では国民所得、失業率、インフレーションなどについて研究する。戦後しばらくの間はケインズ経済学が支持されたが、1970年代以降さまざまな批判を受けるようになった。一つはミクロ的基礎が欠落していることである。理論的な根拠に乏しいモデルで経済政策の効果を予測することは難しい。このためケインズ理論に代わって動学的一般均衡モデルが用いられるようになった。DSGE モデルの出現によってマクロ経済学が大きく進歩したことは間違いないが、残された問題も少なくない。その一つは上述した格差問題である。従来の同質的主体のモデルで格差問題を論じることは難しい。格差を論じるには異質的主体のモデルが必要である。格差問題と直接関係ないが、

Bewley(1986)、Huggett(1993)、Aiyagari(1994) は異質的主体のモデルを提案した。これらは重要な貢献であるが、離散時間のモデルであり分析手法の点で限界がある。景気変動を分析するには問題ないが、格差問題には連続時間のモデルを用いるべきである。ここでは Lasry=Lions(2007) の平均場ゲーム理論を用いて、Aiyagari のモデルを再定式化する。

1. 資産格差のモデル

　事前的に同質的な多数の消費者からなる経済を想定する。消費者は将来効用の割引現在価値を最大化する¹⁾。

* 創価大学名誉教授

(2)

maxc E e ^tu(c_t)dt

0



^ ⁻^ ⁽¹⁾

E₀は条件付き期待値、ct^は消費、ρ＞0 は主観的割引率であり、消費者は区間[0,1]に一様に分布している。予算制約は

dk_t =(w_tz_t +r_tk_t −c_t)dt ₍₂₎ である。ここでwt^{は実質賃金、}ztは効率単位で表した労働供給、rtは利子率である。消費と資本はつぎの条件を満たさなければならない。

c_t 0^, k_t b (3) b ≤ 0は外生的に与えられた借入限度である。

　期間の長さはDで割引率をe^－^ρ^Δとしよう。動的計画法を適用すると、ベルマン方程式は

t c

t z

k

V( , )=max{u(c)+e⁻^^EV(k_t₊_,z_t₊_)}

t t t t t t

t wz rk c k

k₊_ =( + − )+

と表される。Dが微小であればが微小であれば e⁻^^ =1− となり^となり

t c

t z

k

V( , )=max{u(c)+(1−)EV(k_t+,z_t+)}

と書ける。両辺から

と書ける。両辺から(1−)V(kt,zt) を差引くと^{を差引くと}

t c

t z

k

V( , )=max

 {u(c)+(1−)E[V(k_t₊_,z_t₊_)−V(k_t,z_t)]}

となり、Δで割ると

t c

t z

k

V( , )=max

 







 −

−

+(1 ) [ ( ⁺^, ⁺^) ( , )]

)

(c EV k^t z^t V k^t z^t

u 

となる。Δ→0 とすると

t c

t z

k

V( , )=max

 



 ( )+ 1 E[dV(k_t,z_t)]

c dt

u ₍₄₎ を得る。

　効率労働はつぎの拡散過程に従う。

dz_t =(−z_t)dt+dW_t^,z_t [z₁,z₂] ⁽⁵⁾

z₁ ≥ 0, z₂>z₁であり、Wtは標準ブラウン運動を表す。z_t>μであればdzt < 0、zt <μならば

dzt > 0 となり、z_t はμへ回帰する性質がある。定常状態では



 







  ,2

~ N ²

z_t

となる。V(k_t,z_t)に伊藤の公式を適用すると、

(3)

39

_t _t _t _t _t _t dW_t

z dt V z

z V z c V rk k wz

z V k

dV    

 +



 





 + 

 −

−

−

 +

=  ²₂ ²

2 )) 1 (

( ) (

) ,

(

両辺の期待値をとると

dt

z z V

z c V rk k wz

z V k dV

E _t _t _t _t _t _t 



 





 + 

 −

−

−

 +

=  ²₂ ²

2 )) 1 ( ( )

( )]

, (

[   

となり、(4) に代入すると

t c

t z

k

V( , )=max

 





 + 

 −

−

−

 +

+ ²₂ ²

2 )) 1 (

( ) (

)

(   

z z V

z c V rk k wz

c V

u _t _t _t _t (6)

が得られる。消費に関する１階の条件は

) , ( )

('c V k z

u = _k ₍₇₎

である。消費は資本と全要素生産性の関数であり、c(k,z)と表す。貯蓄は

) , (k z c rk wz s= + −

で与えられる。k = bでは

u('wz+rb)V_k(b,z) (8) が成り立つ。z₁≤z≤z₂ であり、境界条件

0 ) , (k z₁ = V_z

V_z(k,z₂)=0 (9)

を満たさなければならない。

　資本と労働供給は長期的に一定の分布に収束する。定常分布はつぎの偏微分方程式の解である。

] ) , ( 2 [

)] 1 ( ) , ( [ )]

, ( ) , ( [

0  ²₂ _g _k _z ²

z z z k z g z k s z k

k g 

+ 



− 



− 

= (10)

この式はコルモゴロフ方程式と呼ばれている。ただし

 



=

0

1 )

, (

b

dkdz z k

g (11)

と正規化する。

　企業は資本と労働を用いて財の生産を行う。利潤は

K r wN N K

F( , )− −( +)

=



で与えられる。ここで 0 ≤δ≤ 1 は資本減耗率である。利潤最大の条件は

N N K w F



=  ( , )

(12)

−



=  K

N K

r F( , )

である。生産関数をである。生産関数をF(K,N)=K^N¹⁻^^とすると, N = 1 とすると w=(1−)K^

r =K^⁻¹−

(4)

となる。均衡状態では



 

=

0

) , (

b

dkdz z k kg

K (13)

が成り立つ。

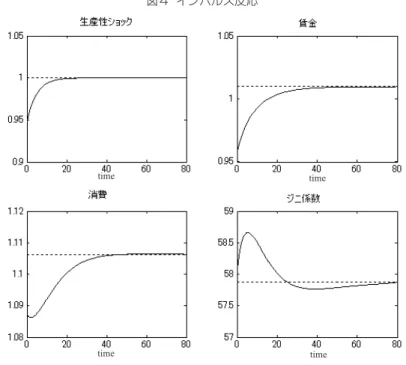
　競争均衡は (6),(10),(12),(13) 式を満たすV(k,z), g(k,z), K, w, rによって定義される。貯蓄によって資産の分布は変化し、資産分布は資本を通じて貯蓄に影響する。つまり (6) と (10) 式は同時に成立する。一般的な条件のもとでモデルは唯一の解をもつが、解析的な方法で解を求めることは難しい。そこで数値的な方法を用いることにした。最初に HJB 方程式の解法について説明しよう。

2. HJB 方程式

　HJB 方程式は資本と生産性に関する偏微分を含んでいる。このため偏微分方程式の代表的な解法である差分法を適用した²⁾。計算の必要上、資本の区間を[b,k_max]とする。差分法では [b,k_max]× [z₁,z₂] の領域を多数の小領域に分割して、分点 (k_i, z_j) における近似解を求める。つまり資本の区間を Dk = (k_max－ b)/N の間隔でN個の小区間に分割し、[z₁,z₂] を Dz = (z₂－z₁)/M の間隔でM個の区間に分ける。V(k_i,z_j)の解をV_{i, j}と表す。微分係数をつぎの前進または後退差分で近似する。

前進差分：

前進差分:

k V V_i _j Vⁱ ^j ⁱ ^j

kF 

= −

 _, ⁺¹^, ^,

後退差分：

後退差分:

k V V_i _j Vⁱ ^j ⁱ ^j

kB 

= −

 _, ^, ⁻¹^, (14)

貯蓄の符号でどちらの方法を用いるか決める。つまり貯蓄が正であれば資本は増加するので前進差分を用い、貯蓄が負であれば資本は減少するので後退差分を使う。状態変数の符号によって近似法を使い分けるこの方法は、風上差分と呼ばれている。風上差分を用いると計算速度は格段に速くなることがわかっている。労働については

z V V_i_j Vⁱ ^j ⁱ ^j

z 

= −

 _, ^, ⁺¹ ^,

_, ^, ¹ ^,₂ ^, ¹

) (

2 z

V V

V_i _j Vⁱ ^j ⁱ^j ⁱ ^j

zz 

+

= −

 ⁺ ⁻ ₍₁₅₎

で近似する。

　反復計算が収束するには、いくつかの条件を満たす必要がある。収束条件に関して、

Barles=Souganidis の定理がある。例えば常微分方程式

F(a,V(a),V ('a),V"(a))=0 をつぎの式で近似したとする。

S(a,a_i,V_i [,V_i])=0 (16)

(5)

41 ここで[V_i]はa_i以外の点における近似値である。つぎの三つの条件を課す。

(1) 単調性

　p≤ q であればS(Da,a_i,V_i,p) ≥≥ S(Da,a_i,V_i,q) となる。つまりSは[V_i]に関して非増加関数である。

(2) 一致性

　滑らかな関数Φ(a)に対して、

)) (

"

), (' ), ( , ( ])

[, , ,

( a a 0F a a a a

S  i i i →a   

→

 ₍₁₇₎

　となる。つまり稠密な近似を行うと打切り誤差は無視できる。

(3) 安定性

　すべての Da> 0 に対して誤差は一様有界である。

Barles=Souganidis(1991) の定理によると、近似式がこれらの条件を満たすとV_iはV(a)に局所一様収束する。この定理は多変数のケースでも成り立つ。またVが時間tを含んでいても構わない。実際の計算では一致性と安定性の条件を満たすことは難しくないが、単調性の条件を満たすスキームを考案することは簡単ではない。

　HJB 方程式の数値解法には陽解法と陰解法の二つの方法がある。つぎにこれらの方法について説明しよう。

2.1 陽解法

　価値関数の初期値を価値関数の初期値をV⁰ =[Vi⁰_,j],i=1,..,N,j=1,..,Mとして、つぎの漸化式を繰り返し計算すとして、つぎの漸化式を繰り返しる。

^, _, ( _, ) _, ( _, )

, 1 n

j i i n j

j i n k

j n i

j i nj n i

j

i V V u c V wz rk c

V + = + + −



+ −



_zV_iⁿ_,_j _j ² _zzV_iⁿ_,_j 2  +



+   (18)

ここでここで _j =(−z_j)_であり、であり、^であり、u('c_iⁿ_,_j)=_kV_iⁿ_,_jとする。とする。^とする。V_i_,ⁿ_j⁺¹^は^ははV_iⁿ_,_j^や^や^やciⁿ_,j^{の陽関数となる}^{の陽関数となる}

ので陽解法と呼ばれる。DとDk、Dzが CFL 条件を満たすと、はV_i_,ⁿ_j^は^や^V(k_i^{, z}_j⁾^{に収束する。先}

に述べたように、貯蓄の符合に基づいて前進または後退差分を用いる。つまり s_F =wz_j+rk_i −c_Fi_,_j^,u('c_Fi_,_j)=_kFV_i_,_j

s_B =wz_j +rk_i −c_Bi_,_j^,u ('c_Bi_,_j)=_kBV_i_,_j

(6)









 +









=



B F

i j

B j i kB

F j i kF j

i k

s s

rk wz u

s V

s V V

0 : ) ('

0 :

, ,

, ₍₁₉₎

とする。さらに (9) を考慮してつぎの条件を課す。

u('wz_j +rk₁)=_kBV₁_,_j

　以下のアルゴリズムを実行する。

[ ステップ 1]　資本の初期値を設定し、賃金と利子率をK₀を設定し、賃金と利子率を _w₀ =₍₁−₎_K₀^,, ,_r₀ =_K₀^⁻¹^ととする。そして価値関数を



)

( ₀ ₀

0, j i

j i

k r z w

V u +

=

とする。

[ ステップ 2]　消費の初期値消費の初期値c_i⁰_,_j =(u)'⁻¹(_kV_i⁰_,_j)_{を求める。}を求める。

[ ステップ 3]　(18) からからV_i¹_,_j を求める。^を

[ ステップ 4]　4] V¹ V⁰ であれば計算を終了し、そうでなければ資本を調整してステップ 2 へ戻であれば計算を終了し、そうでなければ資本る。

Dを十分小さくとると、先に示した三つの条件は満たされる。陽解法は簡単に実行できるが、収束するまで多数回反復する必要がある。このためつぎに説明する陰解法を用いた。

2.2 陰解法

　陰解法では HJB 方程式を次式で近似する。

Vⁱ^,ⁿ^j¹ Vⁱ^,ⁿ^j V_i_,ⁿ_j¹ u(c_iⁿ_,_j) _kV_i_,ⁿ_j¹(wz_j rk_i c_iⁿ_,_j)

− +

 +

=

 +

− ₊ ₊

+



_, ¹

1 2

, 2

+

+ + 



+ _zV_iⁿ_j _j  _zzV_iⁿ_j (20) 右辺は右辺はVを含んでおり、_i_,ⁿ_j⁺¹^{を含んでおり、}^{を含んでおり、}V_i_,_j をリカーシブに解くことはできない。そこで (20) ををリカーシブに解くことはできない。そこで

⁺ ⁺ ⁺ ⁺ ⁻

+

 +

=

 +

− ^, _, ¹ ( _, ) _, ¹( _, ) _, ¹( _, )

, 1 n

j n Bi

j i n kB

j n Fi

j i n kF

j n i

j i nj n i

j

i V V u c V s V s

V 

_, ¹ ² _, ¹

2

+

+ + 



+ _zV_iⁿ_j _j  _zzV_iⁿ_j (21) と書き換える。ここで(x)^＋と(x)^－は

(x)⁺ =max{x,0}^,(x)⁻ =min{x,0}

(7)

43 を意味する。(21) ははV_i_,ⁿ_j⁺¹ に関する連立1次方程式である。(14) と (15) を代入すると^{に関する連立}

+ = +



− ₊

+

) ( _,

, 1 1 ,

, n

j n i

j i nj n i

j

i V V u c

V  ⁺⁺ ⁺ ⁺ ⁺ ⁻⁺ ⁻

 + −



− ( ) ( _, )

,1 1 1 , ,

, 1 ,1

1 n

j Bi n j n i

j n i

j Fi nj n i

j

i s

k V s V

k V V

₂

11 1 ,

1 , 1 2 , , 1

11 ,

) ( 2

2 z

V V V

z V

V _iⁿ_j _iⁿ_j _iⁿ_j

j nj n i

j i

 + + −

 + −

+

− +

+ + +

+

+  

となる。右辺を

となる。右辺をV_i₋ⁿ₁⁺_,¹_j^、V_i_,ⁿ_j⁺¹^、 +n₁⁺_,¹ j

Vi ^、 _,n⁺−¹₁ j

Vi ^、 _,n⁺+¹₁ j

Vi について整理すると^{について整理すると}

n j j n i

j i j n i

j i j j n i

j i j n i

j n i

j i nj n i

j

i V V u c V A V B V C V V

V + = + + + + + + 



− ₊

+ +

− +

+ +

+

− +

+

11 1 ,

1 , 1 ,

, 1 1 ,

, 1 ,

, 1 1 ,

, 1 ,

,  ( ) ( ) (22)

となる。ここで

k

A s

n j Bi j

i =− 

)−

( _,

,

k s k

B s

n j n Bi

j Fi j

i + 

− 

=

−

+ ( )

)

( _, _,

,

k

C s

n j Fi j

i = 

)+

( _,

,

₂

2

) ( z z

j

j − 

−

=

  

2 2

) ( 2 z

=

 

₂

2

) (

2 z

z

j

j + 

= 

  

である。(9) の境界条件を考慮して

11 1 , 0

,+ = _iⁿ+

in V

V

, 1 11

,+ +

+ = _iⁿ_M

nM

i V

V

とする。したがってzの上限と下限では

^,¹ _,₁¹ _,₁ ₁_,¹₁ _,₁ _,₁¹ _,₁ ₁ ₁_,¹₁ _,₁ _,₂¹ ₁

11

, + = ( )+ + ( + +)+ + 



− ₊ ₊

+ +

−+ +

+

in n i

i n i

n i n i

i in

in V V u c V A V B V C V

V 

 +

+

 +

 + +

+

=

 +

− ₊

+ − + +

−+ +

+

11 , 1 ,

, 1 1 ,

, 1 ,

, 1 1 ,

, ,

, 1 ⁱⁿ^M _iⁿ_M ( _iⁿ_M) _iⁿ _M _i_M _iⁿ_M ( _i_M _M _M) _iⁿ _M _i_M _iⁿ_M

nM

i V V u c V A V B V C V

V 

となる。となる。Vⁿ =[V₁_,ⁿ₁...V_Nⁿ_,₁V₁_,ⁿ₂_.....V_Nⁿ_,₂...V₁_,ⁿ_M...V_Nⁿ_,_M]^,,

)]

( ),..., (

),..., (

), ( ),..., (

[ ₁ⁿ_,₁ ⁿⁿ_N_,₁ ₁ⁿ_,₂ ⁿ_N_,₂ ₁ⁿ_,_M _Nⁿ_,_M

n u c u c u c u c u c u c

u = ^{とおいて、}とおいて、(22) を行列で

(8)

表示すると

1( +¹ − )+ +¹ = + +¹

 Vⁿ Vⁿ Vⁿ uⁿ PⁿVⁿ ₍₂₃₎ となる。この式は

SⁿVⁿ⁺¹ =qⁿ (24) Sⁿ I−Pⁿ



 

 +

= ¹  , qⁿ uⁿ Vⁿ +

= 1

R Q Pⁿ = ⁿ +

と書ける。ここで

B_1,1 C_1,1 A1,2 B1,2 C1,2

0 ・ 0

0

0 ・ 0 0 A_1,NB_1,N

0 ・ 0

Qⁿ = ⁰ ^・ ⁰

0

⁰ ^B^1,M^C^1,M

A2.MB2.M C2.M

0 ・ 0 0 ・ 0

0 A_N,M B_NM

Φ₁+Ψ 0 ・・ Ω₁ 0 Φ₁+Ψ 0 ・・ Ω₁

・ 0 ・ 0 ・・・

0

・・ 0 ・ 0 ・・・

Ψ ・・ 0 Φ₁+Ψ 0 ・・ Ω₁

R = ・・・ 0 ・ 0 ・・・

・・・ 0 ・ 0 ・・・

Ψ ・・ 0 Φ_M+Ω_M 0 ・・ Ω_M Ψ ・・ 0 Φ_M+Ω_M 0 ・・

0

^・ ^・ ^・ ⁰ ^・ ⁰ ^・

・・・ 0 ・ 0

Ψ ・・ 0 Φ_M+Ω_M

である。Vⁿ⁺¹は

Vⁿ⁺¹=(Sⁿ)⁻¹qⁿ ⁽²⁵⁾

から求める。陰解法の利点は有限回の反復計算で解が得られることである。このため計算時間を大幅に短縮することができる。

(9)

45

3. コルモゴロフ方程式

　資本と労働供給の分布はつぎのコルモゴロフ方程式を満たす。

[ ( , )] 0

)] 2 ( ) , ( [ )]

, ( ) , (

[ ² ²₂ =

 + 



− 



−  g k z

z z z k z g z k s z k k g

 

この方程式を次式で近似した。

0 )"

2 ( )' (

)'

( _, _, − _, + ² _, =

− g_i_js_i _j g_i_j_j  g_i _j

これはg_{i, j}に関する連立1次方程式であり、HJB 方程式のように反復計算する必要はない。風上差分を用いて

)' (g_i_,_js_i_,_j

k s g s

g k

s g s

g_i _j _Fi_j _i _j _Fi _j _i _j _Bi _j _i _j _Bi_j

 + −



= −

−

− + + +

−

+ ( ) ( ) ( )

)

( _, ₁_, ₁_, ₁_, ₁_, _, _,

,

とする。zについては

z g g_i _j _j gⁱ ^j ^j ⁱ ^j ^j



= ⁺ ⁺ − 

 ^, ¹ ¹ ^,

, )'

(

で近似する。最後の項は

_, ^, ¹ ^,₂ ^, ¹

) ( )" 2

( z

g g

g_i _j gⁱ ^j ⁱ ^j ⁱ ^j

 +

= ⁺ − ⁻

とする。上の近似式に代入して整理すると

P'g =0 ₍₂₆₎ となる。これはg_{i ,j}を未知数とする連立 1 次方程式である。自明の解であるg= 0 は経済的に意味がない。代わりに

g=U⁻¹q

を計算した。q= [0,1,0,...,0]' であり、UはP' の第1列を 1,0,...,0 で置き換えた行列である。

4. 定常均衡

　最初に定常状態の解を求めよう。数値計算のポイントは (13) 式が成り立つようにすることである。つぎのアルゴリズムを実行した。

[ ステップ 1] 資本の初期値K₀を設定してw₀とr₀ を求める。

[ ステップ 2] 前節で説明した方法でg₀(k,z) を求める。

[ ステップ 3] 総資本



= =



= ^N

i M

j kigi j k z K

1 1 ,

0*

を計算する。。|K₀^*−K₀|^{ならば終了し、} ならば終了し、そうでなければ

資産格差の数値解析 （計算経済学の研究その16）