Transactions of JSCES, Paper No Development of Shell Element with Thickness Stretch Takeki YAMAMOTO, Takahiro YAMADA, and Kazumi MATSUI

Transactions of JSCES, Paper No.20150004

板厚変化を考慮したシェル要素の開発

∗

Development of Shell Element with Thickness Stretch

山本剛大

1

_{，山田貴博}

2

_{，松井和己}

2

Takeki YAMAMOTO, Takahiro YAMADA, and Kazumi MATSUI

1

_{横 浜 国 立 大学 大 学院 環 境情報 学 府 (〒240-8501 横浜市保土ヶ谷区常盤台 79-7)}

2

_{横 浜国 立大 学大 学院 環境 情報 研究 院 (〒240-8501 横浜市保土ヶ谷区常盤台 79-7)}

The finite element method is commonly used to simulate the behavior of sheet forming pro-cesses, in order to realize high precision machining. In the conventional shell elements, the plane stress condition which ignores the transverse normal stress is assumed. Thus, the conventional shell elements are not sufficient to simulate the complex behaviors, such as, the deformation of the sheet and the contact force at the sheet-die interface. In this paper, we present a formulation for considering the thickness change and the stress distribution by the surface traction in the shell element. We introduce a displacement variation along the transverse direction to MITC shell element, which is widely used for avoiding the transverse shear locking. Then, we can evaluate the equilibrium equation for the transverse direction by using the introduced variation. Further, we verify the proposed approach to compare the results of the proposed shell with that of the continuum elements.

Key Words: Finite Element Method, Shell Element, Thick Sheet, Total Lagrangian Method

1. はじめに

金 型 を 用 い た 板 曲 げ 加 工 は も の づ く り に お い て 広 く 用 い ら れ て い る ．近 年 ，製 造 プ ロ セ ス の 金 型 設 計 に 要す る時間や費用を大幅に削減したいという要望が非 常 に 強 く な り，設 計 段 階 に お け る 数 値 解 析 技 術 に 対 す る 要 求 精 度 が 高 く なって い る ．板 成 形 に 適 用 さ れ る 数 値 解 析 技 術 と し て ，有 限 要 素 法 を 用 い た 板 成 形 シ ミュ レーションが挙げられる．板成形シミュレーションに用 い ら れ る シェル 要 素 な ど の 構 造 要 素 に は ，曲 げ 部 分 で の 板 厚 変 化 や 金 型 か ら の 反 力 の 予 測 に 問 題 が あ る ．構 造 要 素 は 解 析 対 象 と し て 薄 板 を 想 定 し て お り，板 厚 方 向 に 平 面 応 力 状 態 を 仮 定 し て い る ．通 常 ，板 厚 が 異 な る 部 材 に 同 程 度 の ひ ず み が 生 じ る 場 合 ，板 厚 が 厚 い ほ ど 変 形 量 が 大 き く な る の で ，厚 板 に 対 す る 解 析 は 重 要 で あ る ．厚 板 の 挙 動 を よ り 正 確 に 把 握 す る に は 連 続 体 要 素 の 使 用 が 推 奨 さ れ て い る が ，メッシュ分 割 な ど の プ リ プ ロ セ ス や 計 算 時 間 を 含 む ，数 値 解 析 全 体 の 計 算 コ ス ト が 高 く な る こ と か ら ，厚 板 の 数 値 解 析 に 適 用 で き る 構 造 要 素 の 開 発 に 対 す る 需 要 が 高 まって い る ． ∗ _{原 稿 受 付 2015 年 01 月 09 日, 改 訂 年 月 日 2015 年 03 月 26} 日, 発行年月日 2015 年 04 月 16 日, c_{⃝2015 年 日本計算工学会.} Manuscript received, January 09, 2015; final revision, March 26, 2015; published, April 16, 2015. Copyright c⃝2015 by the Japan Society for Computational Engineering and Science.

板 厚 方 向 の 挙 動 を 扱 う シェル 要 素 の 開 発・研 究 は 広 く行われており，様々な手法が提案されている．一般的 に ，面 内 節 点 に お い て 並 進3自 由 度 ，回 転2自 由 度 を 有するシェル要素は，5パラメータシェル要素と呼ばれ る ．シェル要素 で 板 厚 方 向 を 扱う た め に は ，最低 限 ，3 次 元 構 成 則 を 利 用 で き る 定 式 化 が 必 要 が あ り，最 も 簡 単なアプローチとして，6パラメータシェル要素(1)，(2) が挙げられる．6パラメータシェル要素は，面内節点の 自 由 度 に 板 厚 変 化 の パ ラ メ ー タ を 導 入 し て い る ．し か し，6パラメータシェル要素の欠点は，面外垂直ひずみ が 定 数 で 評 価 さ れ て し ま う こ と で あ る ．つ ま り，曲 げ が 支 配 的 と な る 場 合 に 対 し て ，6パ ラ メ ー タ シェル 要 素 で は 面 外 垂 直 ひ ず み の 線 形 分 布 を 表 現 で き な い ．6 パ ラ メ ー タ シェル 要 素 の よ う に ，板 厚 方 向 の 変 形 を 考 慮 す る た め の 修 正 で 生 じ る ，曲 げ が 表 現 で き な い 現 象 は ，thickness locking(3)，(4)と 呼 ば れ て い る ．thickness

lockingは面外垂直ひずみが定数で表現される場合に生 じ る こ と が 明 ら か と なって お り，い く つ か の 回 避 手 法 が 提 案 さ れ て い る ． Braun et al.(1)は ，6パ ラ メ ー タ シェル 要 素 の 面 内 節 点 あ た り の 自 由 度 に さ ら に1つ 自 由 度 を 追 加 し た ，7 パ ラ メ ー タ シェル 要 素 を 提 案 し て い る ．7パ ラ メ ー タ シェル 要 素(1)，(2)は ，Andelfinger and Ramm(5)に よっ て 提 案 さ れ た 拡 張 ひ ず み 仮 定 法（ 以 下 ，EAS法 ）を 適 用 し た シェル 要 素 に 修 正 を 加 え た 要 素 で あ る ．追 加 し

た自 由度は面 外垂直ひずみの線形変化を表現する役割 を 担って お り，thickness lockingを 回 避 し て い る ．し か し ，EAS法 を 用 い た シェル 要 素 は 計 算 が 不 安 定 と な る た め ，安 定 化 の た め に 人 工 的 な パ ラ メ ー タ の 導 入 が 必 須 と な る ．さ ら に ，EAS法 で 面 外 垂 直 ひ ず み を 直 接 仮 定 す る た め ，面 外 方 向 に 生 じ る 応 力 分 布 に も 仮 定 が 含 ま れ ，板 成 形 で の 表 面 力 に よ る 応 力 分 布 に 仮 定 が 含 ま れ な い と は 保 証 で き な い ．シェル 要 素 を3次 元 的 に 扱 う た め に ，通 常 の シェル 要 素 が 中 央 面 上 に 配 置 し て い る 面 内 節 点 を ，上 面 と 下 面 に 設 け た ソ リッド シェル 要 素(6)や3Dシェル要素(7)∼(9)が開発されている．しか し ，こ れ ら の 要 素 も 面 外 方 向 に 線 形 な 変 位 場 を 設 け る とthickness lockingが 生 じ る た め ，EAS法 を 用 い て 面

外ひ ずみの分布を仮定する(6)_{，もしくは，面外方向に}

対する変位場を2次以上で近似する(7)，(8)必要がある． ま た ，Sussman and Bathe(9)は ，通 常 の シェル 要 素 が 持 つ 面 内 節 点 に お い て 新 た に2つ の ベ ク ト ル を 導 入 す る こ と で ，面 外 方 向 に 対 し て2次 の 変 位 場 を 設 け て い る．これらの手法ではthickness lockingを回避するため に ，面 の 法 線 に 対 応 す る ディレ ク タ ー あ た り の 自 由 度 が 増 加 す る た め ，モ デ ル 全 体 の 自 由 度 増 加 が 避 け ら れ な い ．Braun et al.(1)は ，multidirector理 論(10)を 用 い たモデル化も行っている．multidirector理論では，シェ ル 要 素 を 多 層 構 造 で モ デ ル 化 し ，各 層 で 定 義 さ れ る 法 線 ベ ク ト ル の 伸 縮 を 許 容 し て い る ．そ の た め ，各 層 で 面 外 方 向 にC0連 続 な 変 位 場 を 定 義 し て も ，各 層 で 定 数 と な る 面 外 垂 直 ひ ず み を 区 分 的 な 関 数 と 見 な せ ば ， 面 外 方 向 に 変 化 す る ひ ず み 場 を 構 築 で き る ．さ ら に ， multidirector理論に用いられる層状構造のlayer-wiseモ デルをもとに，multilayerシェル要素(11)∼(13)_が開発さ れ た ．Carrera(14)は ，変 位 場 と 応 力 場 の 両 方 を 変 数 と し て 導 入 す る ，す な わ ち ，層 界 面 で 変 位・面 外 せ ん 断 応 力・面 外 垂 直 応 力 が 連 続 と な る よ う に 自 由 度 を 追 加 したmultilayerシェル要素を開発した．これらの多層構 造 シェル 要 素 は ，層 数 が 増 加 す る に つ れ て 表 現 性 能 が 向 上 す る 一 方 ，当 然 ，自 由 度 の 増 加 を 伴 う． より具体的に，板成形シミュレーションを想定して開 発 さ れ た シェル 要 素 が い く つ か 存 在 す る ．風 間 ら(15) は ，シェル 要 素 の 上 面・下 面 にPseudo節 点 を 導 入 す る こ と で 表 面 力 に お け る 境 界 条 件 を 定 義 し ，さ ら に ，面 外 方 向 に2次 の 変 位 場 を 仮 定 し て い る ．表 面 に 境 界 条 件を 設定する ことで板成形での表面力の影響を評価し ようと試みている．また，岩田ら(16)，(17)_{は，厳しい曲} げ 変 形 の 場 合 に 実 験 ，お よ び ，ソ リッド 要 素 の 数 値 計 算結 果におい て塑性変形に対して無視できない応力値 と な る こ と を 指 摘 し て お り，従 来 の 平 面 応 力 状 態 に も と づ く シェル 要 素 を ベ ー ス に ，実 験 に よ る ひ ず み の 測 定 結 果 と ソ リッド 要 素 を 用 い て 算 出 し た ひ ず み と 応 力 の結果を反映する定式化を行っている．この手法でも， EAS法 と 同 様 の 欠 点 を 持 つ 一 方 ，実 験 結 果 や ソ リッド 要 素 の 数 値 計 算 結 果 を 反 映 で き る こ と で ，板 成 形 で の 表 面 力 を 考 慮 し て い る ．さ ら に ，一 条 ら(18)_{は ，岩 田}

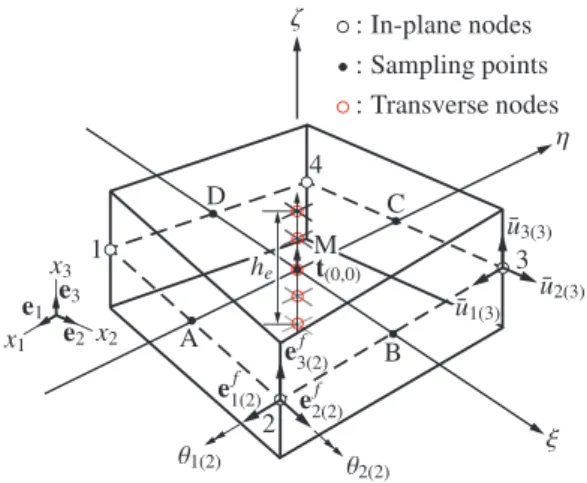
Fig. 1

4-node shell element with 5 transverse nodes

らの手法(16)，(17)を用いた面ひずみ予測を行うと共に， 実 試 験 と の 検 証 事 例 を 示 し て い る ． こ れ ま で 述 べ た よ う に ，板 厚 方 向 の 挙 動 を 把 握 す る た め の 様々な シェル 要 素 が 提 案 さ れ て い る が ，板 成 形 シ ミュレ ー ション に お い て 構 造 要 素 の 計 算 コ ス ト が 抑 え ら れ る と い う 利 点 を 損 な う こ と な く，構 造 要 素 の み で 完 結 す る 数 値 解 析 手 法 の 提 案 は 見 当 た ら な い ．そ こ で 本 研 究 で は ，構 造 解 析 に 広 く 用 い ら れ る ，双 一 次 補 間 と ひ ず み 仮 定 法 に も と づ く4節 点 シェル 要 素 で あ る MITC4シェル要素(19)に板厚方向の変形を表す変動量 を 導 入 す る こ と で ，板 成 形 で 生 じ る 表 面 力 を 外 力 と し て 扱 う こ と が で き ，そ の 外 力 に よ り 面 外 方 向 に 分 布 す る 応 力 状 態 を 表 現 で き る シェル 要 素 を 開 発 す る ．本 研 究 で 提 案 す る シェル 要 素 で は ，板 厚 変 化 を 表 現 す る 自 由 度 を 要 素 ご と に 独 立 と し て 定 義 し て い る た め ，剛 性 行 列 を 組 み 立 て る 際 に 縮 約 操 作 が 行 え る ．そ の た め ， 解くべき連立方程式の未知数の数は，MITC4シェル要 素 な ど の 一 般 的 な シェル 要 素 と 同 等 で あ る ．

2. 板厚変化を伴うシェル要素の定式化

本 研 究 で は ，板 厚 方 向 の 変 形 を 表 現 す る た め に 面 外 節 点 を 導 入 す る ．面 外 節 点 の 導 入 過 程 を 明 確 に し ，提 案 す る シェル 要 素 が 表 現 す る 変 位 場 の 定 式 化 を 以 下 に 示す．本定式化は，Total Lagrange法にもとづいて行う． は じ め に ，面 外 節 点 の 特 徴 を 示 し た 後 ，提 案 す る シェ ル要素を構成する面内節点と面外節点の 自由度による 変位場の定式化を行い，変位場からGreen-Lagrangeひ ず み で 表 現 さ れ る ひ ず み 場 を 算 出 す る ． 2.1 面 外 節 点 の 導 入 本 研 究 で 基 本 と な る4節 点 シェル 要 素 の 例 をFig. 1に 示 す．Fig. 1の よ う に ， 提 案 す る シェル 要 素 は4点 の 面 内 節 点 に 加 え て ，板 厚 変 化 を 表 現 す る 役 割 を 担 う 面 外 節 点（Fig. 1は ，例 と し て5点 の 場 合 ）を 用 い て 構 成 さ れ る ． 一 般 的 な シェル 要 素 で は 面 内 節 点 に お い て 板 厚 が 定 義 さ れ て い る が ，本 研 究 で は 要 素 内 で 板 厚 を 一 定 と 仮 定する．したがって，提案するシェル要素は板厚を要素 で 定 義 す る ．さ ら に ，提 案 す る シェル 要 素 は 要 素 ご と

に 板 厚 変 化 を 許 容 す る た め ，隣 り 合 う 要 素 で 板 厚 の 連 続 性 が 失 わ れ る ．こ の た め ，本 研 究 で 提 案 す る シェル 要 素 の 適 用 限 界 は ，板 厚 変 化 が 要 素 内 で 一 定 と み な せ る 範 囲 に 限 ら れ る ． Fig. 1に 示 す よ う に ，局 所 座 標 系 の 原 点(ξ, η, ζ) = (0, 0, 0)を 要 素 内 で 板 厚 を 評 価 す る サ ン プ リ ン グ 点M と す る ．提 案 す る シェル 要 素 で は 要 素 内 で 板 厚 を 一 定 と す る た め ，板 厚 方 向 を 代 表 す る 向 き を 要 素 内 で 定 義 す る必 要があ り，サンプリング点Mにおいて板厚方向 ベ ク ト ル を 定 義 す る ．し た がって ，あ る 時 刻 に お け る 板 厚 方 向 ベ ク ト ルt(0,0)は ，面 内 節 点aで 定 義 さ れ る ディレ ク タ ー ベ ク ト ルef_3(a)を サ ン プ リ ン グ 点Mに お い て 形 状 関 数Naで 補 間 し た ベ ク ト ル と し て ， t(0,0)= 4 ∑ a=1 Na(0, 0)ef3(a)    4 ∑ a=1 Na(0, 0)ef_3(a)    (1) と定義する．板厚方向の変形も要素内で一定と仮定し， 板 厚 方 向 ベ ク ト ルt(0,0)に 沿って 面 外 節 点 を 導 入 す る ． こ こ で ，面 外 節 点 は 板 厚 方 向 の 変 位 成 分 の み を 持 つ 節 点 と し て ，面 内 節 点 と は 独 立 に 定 義 す る ． 2.2 変 位 場 の 定 式 化 初 期 配 置 に お い て ，要 素 内 の 任 意 点 の 位 置 ベ ク ト ルXは ， X(ξ, η, ζ) = ¯X(ξ, η) + ˆX(ξ, η, ζ) (2) と 表 せ る ．こ こ で ，_X¯ は 初 期 配 置 で の 任 意 点 を 中 央 面 上 に 投 影 し た 点（ 以 下 ，初 期 配 置 で の 投 影 点 ）の 位 置 ベ ク ト ル ，_Xˆ は 初 期 配 置 で の 投 影 点 か ら 任 意 点 ま で の 位 置 ベ ク ト ル で あ る ．同 様 に ，現 配 置 に お け る 要 素 内 の 任 意 点 の 位 置 ベ ク ト ルxは ， x(ξ, η, ζ) = ¯x(ξ, η) + ˆx(ξ, η, ζ) (3) と 表 せ る ．こ こ で ，x¯は 現 配 置 で の 任 意 点 をζ = 0の 面 に 投 影 し た 点（ 以 下 ，現 配 置 で の 投 影 点 ）の 位 置 ベ ク ト ル ，xˆは 現 配 置 で の 投 影 点 か ら 任 意 点 ま で の 位 置 ベ ク ト ル で あ る ． 任 意 点 の 位 置 ベ ク ト ルX，xを 形 状 関 数Na（a = 1 ∼4）を 用 い て 離 散 化 す る と ，そ れ ぞ れ ， X(ξ, η, ζ) = 4 ∑ a=1 Na(ξ, η)Xa+Z(ζ) 4 ∑ a=1 Na(ξ, η)Ef_3(a) (4) x(ξ, η, ζ) = 4 ∑ a=1 Na(ξ, η)xa+ z(ζ) 4 ∑ a=1 Na(ξ, η)ef_3(a) (5) と な る ．ここ で ，Xa，xaはそ れぞ れ ，初期 配 置，現配 置における面内節点の位置ベクトル，Ef_3(a)，ef_3(a)は初 期 配 置 ，現 配 置 に お い て 面 内 節 点 で 定 義 さ れ る ディレ クターベクトル，Z，zは初期配置，現配置における厚 さ 関 数 を 意 味 す る ．こ の と き ，初 期 配 置 に お け る 厚 さ 関 数Zは 要 素 内 で 定 義 さ れ る 板 厚heを 用 い て ， Z(ζ) =ζ 2he (6) と 表 せ る ．通 常 の シェル 要 素 で あ れ ば ，Z = zと 表 現 さ れ る ．し か し ，本 研 究 で 提 案 す る シェル 要 素 は 板 厚 の 変 化 を 許 容 す る の で ，現 配 置 に お け る 厚 さ 関 数zを z(ζ) = ζ 2he+ w(ζ) = Z(ζ) + w(ζ) (7) と 定 義 す る ．こ こ で ，wは 面 外 節 点 の 変 動 量 を 意 味 し ，符 号 は 板 厚 方 向 ベ ク ト ル を 正 の 向 き と す る ．式 (7)か ら 現 配 置 に お け るζ = 0の 面 は 必 ず し も 面 内 節 点 の 存 在 す る 面 と は 一 致 せ ず，ま た ，中 央 面 に 一 致 す る と は 限 ら な い ．面 外 節 点 の 変 動 量wは 局 所 座 標 −1 ≤ ζi≤ ζ ≤ ζi+1≤ 1において，面外節点 間を一次 近 似 し ， w(ζ) = ζi+1− ζ ζi+1− ζi w(ζi) + ζ− ζi ζi+1− ζi w(ζi+1) = ζi+1− ζ ζi+1− ζi wi+ ζ− ζi ζi+1− ζi wi+1 (8) と表す．ここで ，wiは初期配 置におい て局所座標ζiに 配 置 し た 面 外 節 点 の 変 動 量 を 意 味 す る ． 以 上 よ り，要 素 内 の 任 意 点 の 変 位 ベ ク ト ルuは ， u = x− X = 4 ∑ a=1 Na(ξ, η)(xa− Xa) + z(ζ) 4 ∑ a=1 Na(ξ, η)ef_3(a)− Z(ζ) 4 ∑ a=1 Na(ξ, η)Ef_3(a) = 4 ∑ a=1 Na(ξ, η)ua+ Z(ζ) 4 ∑ a=1

Na(ξ, η)(ef_3(a)− Ef_3(a))

+ w(ζ) 4 ∑ a=1 Na(ξ, η)ef_3(a) (9) と 表 せ る ．こ こ で ，uaは 面 内 節 点 の 変 位 ベ ク ト ル で あ る ．こ の と き ，面 外 節 点 の 変 動 量wは 要 素 内 で 一 定 で あ る た め ，要 素 ご と に 定 義 さ れ る 板 厚 方 向 ベ ク ト ル t(0,0)の 方 向 に 沿って 変 動 す る ．式(9)の 最 右 辺 第3項 に お い て ，サ ン プ リ ン グ 点Mで 補 間 さ れ た ベ ク ト ル は 必 ず し も 単 位 ベ ク ト ル で は な い た め ，変 動 量 を 評 価 す る 際 に 補 正 が 必 要 と な る ．そ の 補 正 を 回 避 す る た め に ，式(9)の 最 右 辺 第3項 に 含 ま れ る ベ ク ト ル に つ い て ，単 位 ベ ク ト ル で あ る 板 厚 方 向 ベ ク ト ルt(0,0)を 用 い る ．す な わ ち ，変 位 ベ ク ト ルuを u = 4 ∑ a=1 Na(ξ, η)ua+ Z(ζ) 4 ∑ a=1

Na(ξ, η)(ef_3(a)− Ef_3(a))

+ w(ζ)t(0,0) (10) と 定 義 す る ．式(10)の 右 辺 に お け る 第1項 ，第2項 は 通常の4節点シェル要素の定式化と同様であり，第3項 が通常の定式化では現れな い板厚変化を表現する 項で あ る ． 2.3 ひ ず み 場 の 定 式 化 通 常 の ア イ ソ パ ラ メ ト リック 要 素 で は ，式(10)の 変 位 ベ ク ト ル の 微 分 を と る こ と で 要 素 内 で の 任 意 点 の ひ ず み を 直 接 算 出 で き る

が ，一 般 に 面 外 せ ん 断 ロッキ ン グ が 発 生 す る ．そ こ で ，

Dvorkin and Bathe(19)は ，Green-Lagrangeひ ず み の 面 外 せ ん 断 成 分 に つ い て の み ，サ ン プ リ ン グ 点 で 求 ま る 面外 せん断成分と再定義した内挿関数を用いるひずみ 仮 定 場 を 設 け る こ と で ，面 外 せ ん 断 ロッキ ン グ が 回 避 できるMITC4シェル要素を開発した．Fig. 1に示すサ ン プ リ ン グ 点A，B，C，Dに お い て 算 出 さ れ る Green-Lagrangeひずみの面外せん断成分_E˜B 23，E˜D23，E˜C31，E˜31A を 用 い て ，      ˜ E23= 1 2(1 + ξ) ˜E B 23+ 1 2(1− ξ) ˜E D 23 ˜ E31= 1 2(1 + η) ˜E C 31+ 1 2(1− η) ˜E A 31 (11) と 補 間 す る ．こ こ で ，_∼はξ，η，ζ方 向 を 基 底 と す る 曲線座標系で定義された物理量を意味し，_E˜₂₃，_E˜₃₁は 要素内の任意点におけるGreen-Lagrangeひずみの共変 成 分 で あ る ．本 研 究 で 提 案 す る シェル 要 素 は 式(11)に 示す補間方法を採用し，MITC4シェル要素と同様に面 外 せ ん 断 ロッキ ン グ を 回 避 す る ． 式(10)に含ま れる面 外節点 の 変 動量の 寄与項 は，面 外 垂 直 ひ ず み の み に 影 響 す る ．す な わ ち ，本 研 究 で 提 案 す る シェル 要 素 は ，通 常 の シェル 要 素 に 課 さ れ る 平 面 応 力 の 仮 定 を 用 い る こ と な く，面 外 節 点 の 変 動 量 か ら 面 外 垂 直 ひ ず み を 算 出 す る ． 板 厚 が 厚 く な る ほ ど ，面 外 せ ん 断 ひ ず み の 評 価 が 重 要となる．本研究で提案するシェル要素では面外せん断 ひずみの評価に関して，式(11)に示すように Reissner-Mindlin型 の 定 式 化(20)_{に 基 づ く} MITC4シェル 要 素 と 同 様 で あ る た め ，提 案 す る シェル 要 素 の 板 厚 に 対 す る 適 用 範 囲 はMITC4シェル 要 素 の 適 用 範 囲 と 同 程 度 で あ る ． 2.4 面 外 方 向 に 対 す る 拘 束 条 件 要 素 内 の 任 意 点 に お け る 板 厚方 向の移 動量uTDを，次のよう に平均 量_U¯_TDと 変 動 量u¯TDの 和 で 定 義 す る ． uTD= ¯UTD+ ¯uTD (12) ここで式(12)は，式(10)で定義される任意点の変位ベ ク ト ルuと 板 厚 方 向 ベ ク ト ルt(0,0)と の 内 積 と 同 義 で ある．そのため，式(12)の平均量_U¯_TDは面内節点の変 位 で 表 現 さ れ る 量 で あ り，変 動 量u¯TDは 面 外 節 点 の 変 動 量 が 表 す 相 対 量 で あ る ．こ の と き ，要 素 全 体 に お け る移動量uTDの平均値は平均量U¯TDと等しくなり，面 外節 点が面内節点とは独立に定義されることを利用す る と ， ¯ UTD= ∫ he 2 −he 2 uTDdz = ∫ he 2 −he 2 (_¯ UTD+ ¯uTD ) dz = ¯UTD+ ∫ he 2 −he 2 ¯ uTDdz (13) と な る の で ，変 動 量u¯TDに つ い て ， ∫ he 2 −he 2 ¯ uTDdz = 0 (14) が 得 ら れ る ．上 述 の よ う に ，式(14)は 面 外 節 点 の 変 動 量 に 対 す る 拘 束 条 件 と な る ．面 外 方 向 に 対 す る 拘 束 条 件を課す面外節点は表面から最も離れた面，すなわち， 初 期 配 置 の 中 央 面 上 に 導 入 し た 面 外 節 点 と す る ．そ の た め ，初 期 配 置 の 中 央 面 上 に 面 外 節 点 を 配 置 す る 必 要 が あ り，導 入 す る 面 外 節 点 の 個 数 は 必 ず 奇 数 と な る ． 2.5 面 外 方 向 の 仮 想 仕 事 式 面 外 節 点 をn個 導 入 し た 要 素eの 上 面 に 表 面 力feTDが 作 用 す る 場 合 を 想 定 す る ．上 面 に 配 置 さ れ た 面 外 節 点 番 号 をn，上 面 の表面積をAtopとすると，上面で定義される仮想仕事 δWextは ， δWext= ∫ Atop

feTD· δu(n)eTDdA (15)

と 表 せ る ．こ こ で ，δu(n)_eTDは 上 面 で の 変 位 の 変 分 で あ り，要 素eで 定 義 さ れ る 板 厚 方 向 ベ ク ト ルte(0,0)を 用

い て ，

δu(n)_eTD= δ ¯UeTD+ δ ¯u

(n) eTD = 4 ∑ a=1

Na(ξ, η)δ ¯UaTD+ δ ¯u(n)eTDte(0,0) (16)

と 定 義 さ れ る ．こ こ で ，δ ¯UaTDは 面 内 節 点aで 定 義 さ れ る 仮 想 変 位 ベ ク ト ル を 表 し ，δ ¯u(n)eTDは 面 外 節 点nの 仮 想 変 動 量 で あ る ．し た がって ，式(15)で 示 さ れ る 上 面 で の 仮 想 仕 事δWextは ， δWext= ∫ Atop ( feTD· 4 ∑ a=1 Na(ξ, η)δ ¯UaTD ) dA + feTD(n)Atopδ ¯u(n)eTD (17)

となる．ここで，feTD(n) は要素内 での表 面力の平均値 を 表 す．本 研 究 で 提 案 す る シェル 要 素 は 板 厚 方 向 の 変 形 が 要 素 内 で 一 定 な の で ，上 面 に お け る 板 厚 方 向 の 変 動 量wnも要素内で一定として扱える．したがって，表面 力feTDは 要 素 内 で の 表 面 力 の 平 均 値f (n) eTDを 用 い て ， ∫ Atop feTDdA = ∫ Atop f_eTD(n)te(0,0)dA = f (n)

eTDAtopte(0,0)

(18) と 表 せ る ．式(17)は 表 面 力feTDが 面 内 節 点 だ け で な く，面 外 節 点 に も 付 加 さ れ る こ と を 意 味 し ，提 案 す る シェル 要 素 で は 外 力 を 表 面 上 で 評 価 で き る ． 2.6 要 素 剛 性 方 程 式 の 縮 約 操 作 本 研 究 で 提 案 す る シェル 要 素 の 要 素 剛 性 方 程 式 は ，面 内 節 点 の 自 由 度uIPと 面 外 節 点 の 自 由 度uTDを 用 い て ， [ k11 k12 kt12 k22 ] { uIP uTD } = { fIP fTD } (19) と 表 現 さ れ る ．こ こ で ，kij(i, j = 1, 2)は 面 外 節 点 の 自 由度に応じて 拡張された要素剛性 行列を構成する行列

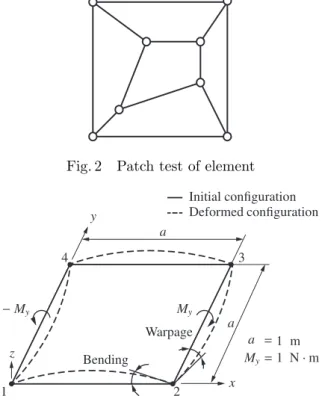
Fig. 2

Patch test of element

Fig. 3

Simulation model of pure-bending

を表し，k21= kt12となり，上付き文字tは転置を意味す る．式(19)のfIP，fTDはそれぞれ，面内節点と面外節 点 に 作 用 す る 外 力 ベ ク ト ル を 表 す．追 加 し た 面 外 節 点 の 自 由 度 が 要素 ご と に独 立 で ある こ と から ，式(19)に 対して縮約操作を行うことができ，要素剛性方程式は， kuIP= f (20) と な る ．式(20)の 要 素 剛 性 行 列k，要 素 外 力 ベ ク ト ル fは そ れ ぞ れ ， k = k11− k12k−122k t 12 (21) f = fIP− k12k−122fTD (22) で あ る ，式(20)に 示 す よ う に ，縮 約 操 作 を 行 う こ と で 面 内 節 点 の 自 由 度 数 に 対 応 す る要 素 剛 性 行 列kが得 ら れる．したがって，本研究で提案するシェル要素は，全 体剛性方程式の未知数の数がMITC4シェル要素などの 通 常 の シェル 要 素 と 同 じ と な る ．

3. 要素の基本性能に関する検証例題

3.1 パッチテスト はじめに，本研究で提案する シェル要素に対するパッチテスト(20)_{を行う．提案する} シェル 要 素 は ，Fig. 2に 示 す 要 素 形 状 に 対 し て 一 様 引 張・圧縮ひずみ状態を表現できる．また，提案するシェ ル 要 素 に よ る 一 様 曲 げ 状 態 の 表 現 に 関 し て は ，次 項 に て 述 べ る ． 3.2 thickness lockingに 対 す る 検 証 次 に ，純 曲 げ モ デ ル に 対 す る 微 小 変 形 領 域 の 数 値 計 算 に よ り， 本研究で提案するシェル要素のthickness lockingに関す る 検 証 を 行 う．解 析 対 象 は ，Fig. 3に 示 す よ う な 単 純

Table 1

Boundary condition of each vertex

Point

x

y

z

θ

1

θ

2

1

fixed

fixed

fixed

free

free

2

free

fixed

fixed

free

free

3

free

free

fixed

free

free

4

fixed

free

fixed

free

free

Table 2

Model parameters of pure-bending

Young’s modulus E [GPa]

100

Poisson’s ratio ν

0.30

Thickness h [m]

0.10

Transverse nodes

3, 5, 7, 9, 11, 13, 15

な 平 板 モ デ ル で あ る ．拘 束 条 件 と モ デ ル パ ラ メ ー タ は そ れ ぞ れTable 1，Table 2に 示 す と お り と し ，対 と な る2辺 に 曲 げ モ ー メ ン ト を 作 用 さ せ ，モ デ ル 全 体 を 1要 素 で モ デ ル 化 す る ．こ こ で は ，面 外 節 点 の 数 を 変 化 さ せ て 数 値 計 算 を 行 い ，得 ら れ た 数 値 解 に つ い て 検 討 す る ． 計 算 結 果 と し て ，頂 点 で の 角 度（ 曲 げ と 反 り ）に つ い て ，解 析 解 と の 相 対 誤 差 を 面 外 節 点 の 数 と 対 応 さ せ て 示 し た グ ラ フ がFig. 4で あ る ．図 中 の 横 軸 は 面 外 節 点 の 数 ，縦 軸 は 解 析 解 と の 相 対 誤 差 を 表 し て い る ． Fig. 4に は 提 案 す る シェル 要 素 の ほ か に ，MITC4シェ ル 要 素 を 用 い て 得 ら れ た 数 値 結 果 を 示 す． MITC4シェル 要 素 な ど の 一 般 的 な シェル 要 素 は 面 外 方 向 に 対 し て 平 面 応 力 を 仮 定 し ，さ ら に ，板 厚 の 変 化 を 考 慮 し な い ．そ れ に 対 し ，提 案 す る シェル 要 素 で は 面 外 方 向 に 平 面 応 力 を 仮 定 せ ず，3次 元 構 成 則 を 用 い る た め ，Fig. 3の モ デ ル で は 平 面 応 力 状 態 と し て ，表 面力がゼロという力学的境界条件を与え ていることに な る ．面 外 方 向 の 扱 い に 対 す る 相 違 に よ り，Fig. 4に おいて本研究で提案するシェル要素とMITC4シェル要 素 と の 結 果 に 相 違 が 生 じ る ． 提案するシェル要素に関して，面外節点の数が少ない 場 合 に 解 析 解 と の 相 対 誤 差 が 大 き く な る 傾 向 は ，Fig. 5に 示 す 面 外 垂 直 ひ ず み の 分 布 か ら 説 明 で き る ．Fig. 5の 面 外 垂 直 ひ ず み 分 布 は ，本 研 究 で 提 案 す る シェル 要素に関して面外節点の変動量を用いて 算出される積 分 点 で の 値 を プ ロット し た も の で あ る ．一 般 に ，面 外 垂直ひずみが定数となる場合に曲げ変形 が表現できな い現象はthickness lockingと呼ばれている(3)，(4)_．提案 するシェル要素では式(8)の定義にもとづき，面外節点 間 の 変 動 量 を 一 次 近 似 し て い る た め ，面 外 垂 直 ひ ず み はFig. 5に示すように面外節点間で定数となる．Fig. 5(a)，(b)を比較すると，面外節点の数を増加させるこ

Fig. 4

Relative error versus the number of

trans-verse nodes

Fig. 5

Transverse normal strain distributions

とで解析解の線形分布に近づき，thickness lockingを回

避できるため，Fig. 4に示すように面外節点の数が増

加 す る ほ ど ，解 析 解 と の 相 対 誤 差 が 小 さ く な る ． 本 研 究 で は ，相 対 誤 差 が1.0[%]未 満 で あ る こ と を

thickness locking回 避 の 判 定 基 準 と す る ．よって ，Fig.

5から面外節点の数を9点以上設けることにより， thick-ness lockingを 回 避 し た 数 値 計 算 を 実 現 で き る ． ま た ，提 案 す る シェル 要 素 は ，Fig. 2に 示 し た 要 素 分 割 を 用 い てFig. 3と 同 様 の 純 曲 げ 試 験 を 行 う と ，1 要 素 の 計 算 結 果 と 一 致 す る ．し た がって ，本 研 究 で 提 案 す る シェル 要 素 は 一 様 曲 げ 状 態 を 表 現 で き る ．以 上 よ り，提 案 す る シェル 要 素 で は 一 様 ひ ず み 状 態 を 表 現

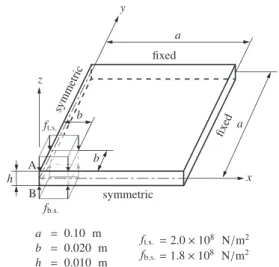
Fig. 6

Simulation model with surface tractions

で き る こ と が 保 証 さ れ る ． 3.3 表 面 力 に 伴 う 板 厚 変 化 と 応 力 分 布 解 析 対 象 と し て ，表 面 力 が 作 用 す る モ デ ル に お い て 板 厚 変 化 や 応 力 分 布 を 評 価 す る 場 合 ，構 造 要 素 で は な く 連 続 体 要 素 の 使 用 が 推 奨 さ れ る ．こ こ で は ，表 面 力 が 作 用 す る モ デ ル に 対 し て ，提 案 す る シェル 要 素 ，六 面 体 要 素 （ADINA），MITC4シェル 要 素 の 各 要 素 を 用 い て 微 小 変 形 領 域 の 数 値 計 算 を 行 い ，表 面 力 の 影 響 に つ い て 検 討 す る ． 解 析 対 象 はFig. 6に 示 す よ う に ，0 ≤ x ≤ 0.020， 0≤ y ≤ 0.020の上面と下面に表面力が作用するモデル と し ，物 性 値 は ヤ ン グ 率E = 1.0× 1011 [N/m2]，ポ ア ソン比ν = 0.3とする．荷重条件はFig.6に示すとおり で あ り，MITC4シェル 要 素 で は 外 力 の 合 成 に よ り，中 央面に対してz方向負の向きに0.2× 108[N/m2]の表面 力 を 作 用 さ せ る ．提 案 す る シェル 要 素 とMITC4シェル 要素は，面内 に対して10× 10の100要素とする．面外 方 向 に 関 し て ，提 案 す る シェル 要 素 で は 面 外 節 点 を9 点 配 置 し ，MITC4シェル 要 素 と 提 案 す る シェル 要 素 の 積 分 点 数 を 一 致 さ せ る ．一 方 ，六 面 体 要 素 で は 面 外 方 向の分割数をシェル要素と同じにするため，80× 80 × 8 の51, 200要 素 と す る ． Fig. 6に示したモデルの原点での面外方向の応力分

布 をFig. 7に 示 す．Fig. 7(a)に 示 す 面 外 垂 直 応 力 の 分 布 か ら ，提 案 す る シェル 要 素 で は 六 面 体 要 素 と 同 様 に ，表 面 力 を 考 慮 し た 応 力 分 布 が 表 現 さ れ て い る ．一 方，Fig. 7(b)に示す面外せん断応力はシェル要素と六 面 体 要 素 で 明 ら か に 分 布 が 異 な る ．こ れ は シェル 要 素 の面外せん断ひずみが，Reissner-Mindlinの仮定にもと づ い て 表 現 さ れ る た め で あ る ．面 外 せ ん 断 応 力 の 分 布 はシェル要素と六面体 要素で異なる が，Fig. 7(c)に示 すvon-Mises応 力 の 分 布 を 確 認 す る こ と で ，面 外 せ ん 断 の 差 異 に よ る 影 響 が 小 さ い と 判 断 で き る ． 提 案 す る シェル 要 素 は 面 外 せ ん 断 ひ ず み の 表 現 が Reissner-Mindlinの仮定にもとづいているため，六面体 要 素 の 面 外 せ ん 断 ひ ず み と 分 布 が 異 な る ．そ の た め ，

Fig. 7

Stress distributions in the simulation model

under surface tractions

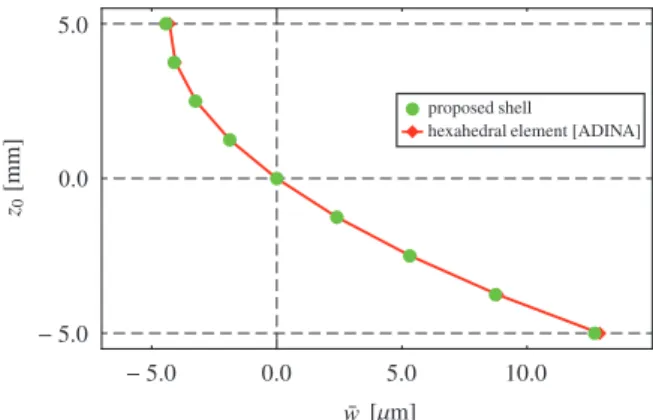
提 案 す る シェル 要 素 と 六 面 体 要 素 の 板 厚 変 化 を 比 較 す る 際 ，表 面 力 が 作 用 す る 領 域 に お い て 面 外 せ ん 断 ひ ず み の 影 響 が 最 も 小 さ い 場 所 を 検 討 す る 必 要 が あ る ．そ こで，本例題では板厚変化を比較する場所をFig. 6の 原点とする．Fig. 8は，Fig. 6に示したモデルの原点 に お け る 断面A-Bにつ いて，板厚方 向の変形 を示した 結 果 で あ る ．図 中 の 横 軸 は 面 外 節 点 の 相 対 変 動 量 ，縦 軸 はz方 向 に 配 置 し た 節 点 の 初 期 位 置z0を 表 し て い る．ここで，面外節点の相対変動量w¯iは，初期配置に お い て 中 央 面 上 に 配 置 し た 面 外 節 点 の 変 動 量wmidを 基 準 と し て ， ¯ wi= wi− wmid (23) と 表 現 す る ．Fig. 8か ら ，提 案 す る シェル 要 素 が 六 面

Fig. 8

Displacement variation in transverse

direc-tion with surface tracdirec-tions

Fig. 9

Plane strain bending: geometry and loading

体要素と同様の板厚変化を 表現していることが確 認で き る ． また，全体剛性方程式に要する総自由度は，提案する シェル要素，MITC4シェル要素では，605自由度（面内 節点数：121，節点自由度：5），六面体要素では，177,147 自由度（節点数：59,049，節点自由度：3）である．ただ し ，提 案 す る シェル 要 素 に お い て ，要 素 剛 性 方 程 式 に 要 す る 縮 約 操 作 で の 追 加 の 自 由 度 は900自 由 度（ 面 外 節 点 数：9，要 素 数：100）で あ る ．し た がって ，提 案 す る シェル 要 素 は ，従 来 の シェル 要 素 の 自 由 度 数 に 対 し て 極 端 な 増 加 を 伴 わ ず，六 面 体 要 素 に 近 い 精 度 の 計 算 結 果 を 示 せ る も の と な る ．

4. 有限変形領域の数値計算

4.1 Rolling up解析 Fig. 9に示すように ，片 端を固定支持した部材の他端に，強制回転角2πを作用 さ せ る モ デ ル を 用 い て ，rolling up解 析(9)_{を 行 う．ま} た ，St. Venant-Kirchhoff弾 性 体 モ デ ル を 用 い ，物 性 値 はヤング率E = 100 [N/mm2]，ポアソン比ν = 0.4とす る．さらに，境界条件として奥行き方向（y方向）に対 し て 平 面 ひ ず み 状 態 と す る ． 大変位を伴うモデルに対して，提案するシェル要素， 奥 行 き 平 面 ひ ず み の 仮 定 を 用 い た2次 元（x− z平 面 ） 四辺形要素（ADINA），MITC4シェル要素（ADINA）を 用い，数値計算結果を比較し検討する．ここで，使用す る す べ て の 要 素 に 対 し て ，更 新 方 法 をTotal Lagrange

法 に 統 一 す る ．さ ら に ，提 案 す る シェル 要 素 で は 仮 定 を 含 ま な い3次 元 構 成 則 を 用 い ，四 辺 形 要 素 で は 平 面

Fig. 10

Displacement variation for plane strain

bending

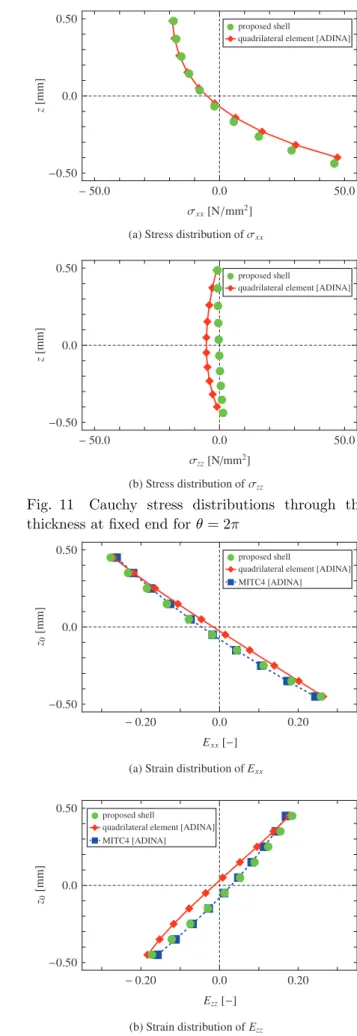
で は 平 面 応 力（z方 向 ）仮 定 に よ り 縮 退 し た 構 成 則 を を使用する．シェル要素はx− y平面において20× 1の 20要素とし，面外方向に対してレイヤー数を10（提案 す る シェル 要 素 で の 面 外 節 点 を11点 ）と す る ． 一方，四辺形要素による要素分割では，面外方向（z 方 向 ）に 対 す る 分 割 数 を シェル 要 素 と 一 致 さ せ ，x− z 平 面 に お い て100× 10の1, 000要 素 と す る ．ま た ，数 値 解 析 に 用 い る ス テップ 数 は ，シェル 要 素 で80ス テッ プ，四 辺 形 要 素 で40,000ス テップ と す る ． ま ず，固 定 端 に お け る 板 厚 方 向 の 変 形 をFig. 10に 示 す．図 中 の 横 軸 は 面 外 節 点 の 相 対 変 動 量 ，縦 軸 はz 方向に配置した節点の初期位置z0を表している．ここ

Fig. 11

Cauchy stress distributions through the

thickness at fixed end for θ = 2π

Fig. 12

Green-Lagrange strain distributions

thr-ough the thickness at fixed end for θ = 2π

Fig.13

Comparison of mid surface with neutral

sur-face in shell element

で，面外節点の相対変動量は式(23)を用いて評価する． こ れ ら の 結 果 か ら 提 案 す る シェル 要 素 と 四 辺 形 要 素 を 比 較 す る と ，端 部 の 回 転 量 が 大 き く な る ほ ど ，板 厚 方 向 に 配 置 し た 節 点 の 移 動 量 が 一 致 し な い ． 次 に ，固 定 端 に お け るCauchy応 力 のx方 向 垂 直 成 分σxxとz方 向 垂 直 成 分σzzの 分 布 をFig. 11に 示 す． 図 中 の 横 軸 はCauchy応 力 の 各 成 分 の 値 ，縦 軸 は 固 定 した 節点の位置を原点とする板厚 方向の座標を表して おり，現配置における四辺形要素の中心位置，または， 面外節点間の中央での値を示す．Cauchy応力のx方向 垂 直 成 分σxxの 分 布 に つ い て ，開 発 し た シェル 要 素 と 四辺 形要素の分布がほぼ一致して いることが確認でき る ．一 方 ，z方 向 に 対 す るCauchy応 力 の 分 布 は ，純 曲 げ 変 形 に よ り 平 面 応 力 が 成 り 立 つ は ず だ が ，四 辺 形 要 素 で は 断 面 内 で 負 の 応 力 が 生 じ る ． 同 様 に ，固 定 端 に お け るGreen-Lagrangeひ ず み のx 方 向 垂 直 成 分Exxとz方 向 垂 直 成 分Ezzの 分 布 をFig. 12に 示 す．図 中 の 横 軸 はGreen-Lagrangeひ ず み の 各 成 分 の 値 ，縦 軸 は 初 期 の 中 央 面 を 原 点 と し た 板 厚 方 向 の 座 標 を 表 し て お り，初 期 配 置 に お け る 四 辺 形 要 素 の 中 心 位 置 に お い て ，そ れ ぞ れ の 要 素 か ら 算 出 さ れ る 値 を 示 す．Green-Lagrangeひ ず み のx方 向 垂 直 成 分Exx とz方 向 垂 直 成 分Ezzの 分 布 傾 向 が ，開 発 し た シェル 要 素 と 四 辺 形 要 素 で ほ ぼ 一 致 し て い る が ，分 布 が 厳 密 に は 一 致 し な い ．一 方 ，開 発 し た シェル 要 素 ，お よ び ， MITC4シェル要素を用いて得られるGreen-Lagrangeひ ず み のx方 向 垂 直 成 分Exxとz方 向 垂 直 成 分Ezzの 分 布 は ，ほ ぼ 一 致 す る ．こ れ は ，開 発 し た シェル 要 素 に お い て ，式(10)に 示 す変 位 場uに 含 ま れ る 面外 節 点 の 変 動 量wが面 外 方 向 の 関 数ζのみ で 表 現 さ れ て い る こ と か ら 説明 で き る ．式(10)の 変 位場uを面 内 方 向 の 関 数ξ，ηにより微分することで得られるGreen-Lagrange ひ ず み の 面内 成 分 に は ，面外 節 点 の 変動 量wに よ る 板 厚変化の影響が含まれないため，MITC4シェル要素を

Fig. 14

Plane strain bending with surface tractions:

geometry and loading

用いて得られるGreen-Lagrangeひずみの面内成分と一 致 し ，Fig. 12の 分 布 傾 向 を 示 す． さ ら に ，Fig. 12で は ，四 辺 形 要 素 と シェル 要 素 で ひ ず み が ゼ ロ と な る 位 置 に ず れ が 見 ら れ る ．こ れ は ， シェル 要 素 で 定 義 さ れ る 変 形 の 幾 何 学 的 な 仮 定 に 起 因 す る も の で あ る ．通 常 ，シェル 要 素 は 板 厚 が 一 定 で あ る と 仮 定 す る ．そ の た め ，Fig. 13(a)に 示 す よ う に 初 期 配 置 で は ，面 内 節 点 が 存 在 す る 面 と 上 面 で 囲 わ れ る 領 域 の 面 積Sinと ，面 内 節 点 が 存 在 す る 面 と 下 面 で 囲 わ れ る 領 域 の 面 積Soutが 等 し く，面 内 節 点 が 存 在 す る 面 を 中 立 面 と み な せ る ．し か し ，純 曲 げ 変 形 を 受 け る とFig. 13(b)に示すように，面内節点が存在する面を 境 界 と す る 領 域 の 面 積sin，soutに 差 が 生 じ る ．こ れ に 対 し て ，上 面 ま で の 面 積s′inと 下 面 ま で の 面 積s′outが 等 し く な る よ う な 基 準 面 が 存 在 し ，こ の 基 準 面 は 中 立 面 で あ る ．シェル 要 素 の 中 立 面 に 関 し て ，上 述 の 幾 何 学 的 制 約 か ら 算 出 さ れ る 位 置 はFig. 12の 数 値 計 算 結 果が示す位置と一致する．したがって，シェル要素の幾 何 学 的 制 約 は 変 形 に 影 響 す る た め ，Fig. 11に 示 す よ う に 開 発 し た シェル 要 素 と 四 辺 形 要 素 の 変 形 状 態 が 一 致 し な い ． 4.2 有 限 回 転 と 表 面 力 を 伴 う モ デ ル Fig. 14 に 示 す よ う な 有 限 回 転 と 表 面 力 を 伴 う モ デ ル に 対 し て，提案するシェル要素の性能について検証する．Fig. 14の モ デ ル に 関 し て ，表 面 力 が 部 材 の 上 面 と 下 面 に 作 用 す る 側 の 端 面 はz方 向 の 並 進 変 位 の み を 許 容 し ， 他 端 で は 断 面 の 回 転 と 中 央 面 のz方 向 に 対 す る 変 位 を 拘 束 す る 境 界 条 件 を 設 定 し て い る ．さ ら に ，単 位 長 さ （1 [m]）の 奥 行 き 方 向（y方 向 ）に 対 し て ，平 面 ひ ず み 状態とする．St. Venant-Kirchhoff弾性体モデルを用い， 物 性 値 は ヤ ン グ 率E = 1.0× 106 [N/m2]，ポ ア ソ ン 比 ν = 0.3とする．荷重条件はFig. 14に示すとおりであ り，MITC4シェル 要 素 で は 外 力 の 合 成 に よ り，中 央 面 に 対 し てz方 向 負 の 向 き に0.05× 103 [N/m2]の 表 面 力 を 作 用 さ せ る ． 有 限 回 転 と 表 面 力 を 伴 う モ デ ル に 対 し て ，提 案 す る シェル 要 素 ，奥 行 き 平 面 ひ ず み の 仮 定 を 用 い た2次 元 （x− z平 面 ）四 辺 形 要 素（ADINA），MITC4シェル 要 素（ADINA）を用い，数値計算結果を比較し検討する． こ こ で ，使 用 す る す べ て の 要 素 に 対 し て ，更 新 方 法 を Total Lagrange法に統一する．さらに，提案するシェル 要素では仮定を含まない3次元構成則を用い，四辺形要 素では平面ひずみ（y方向）を考慮した構成則，MITC4

Fig. 15

Displacement variation for plane strain

bending with surface tractions

シェル要素では平面応力（z方向）仮定により縮退した 構 成 則 を 使 用 す る ．シェル 要 素 はx− y平 面 に お い て 50× 1の50要素とし，面外方向に対してレイヤー数を 10（提案するシェル要素での面外節点を11点）とする． 一方，四辺形要素による要素分割では，面外方向（z方 向 ）に 対 す る 分 割 数 を シェル 要 素 と 一 致 さ せ ，x− z平 面 に お い て500× 10の5, 000要 素 と す る ．ま た ，数 値 解 析 に 用 い る ス テップ 数 は10ス テップ と す る ． ま ず，表 面 力 が 作 用 す る 側 の 端 面 に お け る 板 厚 方 向 の 変 形 をFig. 15に 示 す．図 中 の 横 軸 は 面 外 節 点 の 相 対 変 動 量 ，縦 軸 はz方 向 に 配 置 し た 節 点 の 初 期 位 置z0 を表している．ここで，面外節点の相対変動量は式(23) を 用い て評価する．Fig. 15(a)，(b)について提案する シェル 要 素 と 四 辺 形 要 素 を 比 較 す る と ，変 形 が 線 形 に 近 い 範 囲 に お い て 板 厚 方 向 の 変 形 が 一 致 し ，非 線 形 に な る に つ れ 変 形 量 に ず れ が 生 じ る ． 次 に ，Fig. 15の モ デ ル に お い て 面 外 せ ん 断 変 形 が 最 も 小 さ い と み な せ る ，表 面 力 が 作 用 す る 側 の 端 面 で の 応 力 と ひ ず み に つ い て 評 価 す る ．Fig. 16，Fig. 17 に1ステップ後のCauchy応力，Green-Lagrangeひずみ の 各x方 向 垂 直 成 分 ，z方 向 垂 直 成 分 に 関 す る 板 厚 方 向の分布，Fig. 18，Fig. 19に10ステップ後のCauchy

応力，Green-Lagrangeひずみの各x方向垂直成分，z方

向 垂 直 成 分 に 関 す る 板 厚 方 向 の 分 布 を 示 す．Fig. 16，

Fig. 18の横軸はCauchy応力の各成分の値，縦軸は中

Fig. 16

Cauchy stress distributions (f

top

: 5.00

×

10

2

N/m

2

/ f

btm

: 4.95

× 10

2

N/m

2

)

Fig. 17

Green-Lagrange strain distributions (f

top

:

央 面 に 配 置 し た 節 点 の 現 配 置 で の 位 置 を 原 点 と す る 板 厚 方 向 の 座 標 を 表 し て お り，現 配 置 に お け る 四 辺 形 要 素 の 中 心 位 置 ，ま た は ，面 外 節 点 間 の 中 央 で の 値 を 示 す．Fig. 17，Fig. 19の 横 軸 はGreen-Lagrangeひ ず み の 各 成 分 の 値 ，縦 軸 は 初 期 の 中 央 面 を 原 点 と し た 板 厚 方 向 の 座 標 を 表 し て お り，初 期 配 置 に お け る 四 辺 形 要 素 の 中 心 位 置 に お い て ，そ れ ぞ れ の 要 素 か ら 算 出 さ れ る 値 を 示 す．Fig. 16のCauchy応 力 のx方 向 垂 直 成 分σxxとz方 向 垂 直 成 分σzzの 分 布 と ，Fig. 17の Green-Lagrangeひ ず み のx方 向 垂 直 成 分Exxとz方 向 垂 直 成 分Ezzの 分 布 を 確 認 す る と ，提 案 す る シェル 要 素を 用いて得 られる計算結果が四辺形要素の結果と一 致 す る こ と が 確 認 で き る ．こ れ は ，Fig. 15(a)に 示 し た 板 厚 方 向 の 変 形 に 対 す る 傾 向 と 一 致 す る ．

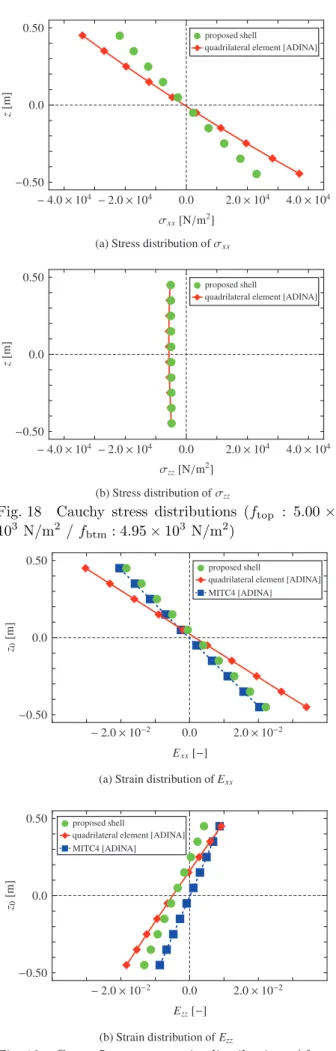
Fig. 18(a)に 示 し たCauchy応 力 のx方 向 垂 直 成 分 σxxで は ，提 案 す る シェル 要 素 と 四 辺 形 要 素 の 分 布 に つ い て ，分 布 の 傾 き が 明 ら か に 異 な る ．同 様 に ，Fig. 19(a)に 示 し たGreen-Lagrangeひ ず み のx方 向 垂 直 成 分Exxの 結 果 に お い て も ，傾 き の 相 違 が 確 認 で き る ． こ の 傾 向 は ひ ず み が 大 き く な る ほ ど 顕 著 と な り，変 形 量が増加するにつれて分布のずれも大きくなる．また， Fig. 19(b)に示したGreen-Lagrangeひずみのz方向成 分Ezzも ，シェル 要 素 と 四 辺 形 要 素 で 分 布 の 傾 き に ず れ が 生 じ る ．た だ し ，Green-Lagrangeひ ず み のz方 向 成 分Ezzに 関 し て ，提 案 す る シェル 要 素 と 四 辺 形 要 素 の 分 布 に ず れ が 生 じ る 一 方 ，提 案 す る シェル 要 素 で は 表 面 力 の 影 響 を 考 慮 し た 分 布 を 表 現 で き る た め ，Fig. 18(b)に 示 すCauchy応 力 のz方 向 垂 直 成 分σzzが ゼ ロ に な ら な い ．そ の た め ，提 案 す る シェル 要 素 は 有 限 回 転と表面力を伴うモデルに対して，適用が有効である． た だ し ，本 研 究 で 提 案 す る シェル 要 素 に 関 し て ，大 ひ ず み を 伴 う 部 分 で の 適 用 は 難 し い と い え る ．

5. おわりに

本 論 文 で は ，板 厚 変 化 を 表 現 す る た め の 面 外 節 点 を 導 入 し ，板 厚 方 向 の 変 形 を 考 慮 す る シェル 要 素 を 開 発 し た ．本 シェル 要 素 で は 面 外 方 向 の つ り あ い 方 程 式 を 評 価 す る た め に ，要 素 内 で 面 内 節 点 と は 独 立 に 面 外 節 点 を 導 入 し た ．板 厚 が 厚 く な る ほ ど ，表 面 力 を 中 央 面 で 評 価 す る 従 来 の シェル 要 素 に 対 す る 適 用 限 界 が 顕 著 と な る 一 方 ，本 シェル 要 素 で は 連 続 体 要 素 と 同 等 の 数 値 計 算 結 果 が 得 ら れ る こ と を 示 し た ．ま た ，有 限 変 形 に対する検証を通して，本シェル要素が従来のシェル要 素 の 定 式 化 と 共 通 す る 部 分 で ，ソ リッド 要 素 と の 結 果 に ず れ が 生 じ る こ と を 確 認 し た ．シェル 要 素 に 特 有 な 変 形 に 対 す る 幾 何 学 的 な 仮 定 を 考 慮 し た 上 で ，本 シェ ル 要 素 の 適 用 範 囲 を 設 定 す る 必 要 が あ る ． 板 成 形 を 対 象 と す る 数 値 解 析 に お い て ，有 限 変 形 領 域 で の 弾 塑 性 変 形 を 考 慮 す る 必 要 が あ る ．弾 性 領 域 か ら塑 性領域への移行判定と使用する構成則を検討しな が ら ，有 限 変 形 弾 塑 性 解 析 の 実 現 に 向 け て 進 め て い く 予 定 で あ る ．

Fig. 18

Cauchy stress distributions (f

top

: 5.00

×

10

3

N/m

2

/ f

btm

: 4.95

× 10

3

N/m

2

)

Fig. 19

Green-Lagrange strain distributions (f

top

:

謝 辞

本 研 究 は ，横 浜 国 立 大 学 環 境 情 報 研 究 院 共 同 研 究 プ ロ ジェク ト の 援 助 を 受 け て お り，こ こ に 謝 意 を 示 す．

参考文献

(1) M. Braun, M. Bischoff, and E. Ramm, Nonlin-ear shell formulations for complete three-dimensional constitutive laws including composites and lami-nates, Computational M echanics, 15, 1994, pp. 1–18.

(2) N. B¨uchter, E. Ramm, and D. Roehl, Three-dimensional extension of non-linear shell formulation based on the enhanced assumed strain concept, Int. J. N umer. M eth. Engng. , 37, 1994, pp. 2551–2568. (3) E. Carrera and S. Brischetto, Analysis of thickness locking in classical, refined and mixed multilayered plate theories, Composite Structures, 82, 2008, pp. 549–562.

(4) E. Carrera and S. Brischetto, Analysis of thickness locking in classical, refined and mixed theories for layered shells, Composite Structures, 85, 2008, pp. 83–90.

(5) U. Andelfinger and E. Ramm, EAS-elements for two-dimensional, three-dimensional, plate and shell structures and their equivalence to HR-elements, Int. J. N umer. M eth. Engng. , 36, 1993, pp. 1311– 1337.

(6) R. Hauptmann and K. Schweizerhof, A systematic development of ’solid-shell’ element formulations for linear and non-linear analyses employing only dis-placement degrees of freedom, Int. J. N umer. M eth. Engng. , 42, 1998, pp. 49–69.

(7) D. Chapelle, A. Ferent, and K. J. Bathe, 3D-shell elements and their underlying mathematical model, M ath. M odels M ethods Appl. Sci. , 14, 2004, pp. 105–142.

(8) D. N. Kim and K. J. Bathe, A 4-node 3D-shell el-ement to model shell surface tractions and incom-pressible behavior, Computers and Structures, 86, 2008, pp. 2027–2041.

(9) T. Sussman and K. J. Bathe, 3D-shell elements for structures in large strains, Computers and Structures, 122, 2013, pp. 2–12.

(10) P. M. Pinsky and K. O. Kim, A multi-director for-mulation for elastic-viscoelastic layered shells, Int. J. N umer. M eth. Engng. , 24, 1986, pp. 901–913. (11) M. Epatein and H. P. Huttelmaier, A finite

ele-ment formulation for multilayered and thick plates, Computers and Structures, 16, 1983, pp. 645–650. (12) H. P. Huttelmaier and M. Epstein, A finite ele-ment formulation for multilayered and thick shells, Computers and Structures, 21, 1985, pp. 1181–

1185.

(13) D. R. J. Owen and Z. H. Li, A refined analy-sis of laminated plates by finite element displace-ment methods – I. Fundadisplace-mentals and static analysis, Computers and Structures, 26, 1987, pp. 907–914. (14) E. Carrera, Multilayered Shell Theories Accounting for Layerwise Mixed Description, Part 1: Governing Equations, Am Inst. Aeronaut Astronaut J. , 37, 1999, pp. 1107–1116. (15) 風間宏一,伊藤耿一,陸宏,永井康友,板材成形FEM シ ミュレ ー ション に お け る 板 厚 方 向 応 力 を 考 慮 し たシェル要素–スプリングバック予測精度向上に関 す る 研 究   第1報–,日 本 塑 性 加 工 学 会 誌 塑 性 と 加 工, 45, 2004, pp. 832–836. (16) 岩 田 徳 利,蔦 森 秀 夫,石 倉 洋,梅 津 康 義,村 田 篤 信, 与 語 康 宏,諏 訪 高 典, 高 精 度 ス プ リ ン グ バック 予 測 の た め の シェル 要 素 開 発（ 第1報 ∼ 第3報 ）, 塑 性 加工 連 合 講 演 会 講 演 論 文集, 55, 2004, pp. 197–202. (17) N. Iwata, H. Tsutamori, M. Niihira, H. Ishikura, Y. Umezu, A. Murata, Y. Yogo, Numerical Prediction of Springback Shape of Severely Bent Sheet Metal, N U M IF ORM , 39, 2007, pp. 799–804.

(18) 一 条 尚 樹,岩 田 徳 利, 岩 田 隆 道,三 田 太 一, 蔦 森 秀

夫,プレス成形に伴う面ひずみ評価技術および予測

技 術 の 開 発, 日 本 塑 性 加 工 学 会 誌 塑 性 と 加 工, 54, 2013, pp. 35–39.

(19) E. N. Dvorkin and K. J. Bathe, A continuum mechanics based four-node shell element for general non-linear analysis, Engineering Computations, 1, 1984, pp. 77–88.

(20) K. J. Bathe, F inite Element P rocedure, Prentical-Hall, Inc. , 1996