搭載モデルベースの誘導制御則と統計的ロバスト飛 行制御設計

九州大学学術情報リポジトリ

Kyushu University Institutional Repository

搭載モデルベースの誘導制御則と統計的ロバスト飛 行制御設計

塚本, 太郎

https://doi.org/10.15017/1807032

出版情報：Kyushu University, 2016, 博士（工学）, 課程博士 バージョン：

権利関係：Fulltext available.

再使用宇宙輸送システムの誘導制御則設計に関する研究

―搭載モデルベースの誘導制御則と統計的ロバスト飛行制御設計―

2016 年 12月

塚本 太郎

概要

将来の再使用宇宙輸送システムはその繰返し運用の中で遭遇する多様な条件に対応して 飛行する能力が必要である．また，安全性，信頼性，柔軟な運用性の観点から，物理的に 帰還可能であればいかなる状況からでも帰還できる能力を持つことが望ましい．このため，

誘導制御則は飛行中の大きな特性変化に対応可能であると同時に，広い飛行領域に対して 効率的に設計ができ，種々の異なるミッションに対して容易に再設計のできる設計方法が 求められる．これらの要求を実現するために，搭載モデルベース制御，すなわち，オンボ ードの機体運動モデルを積極的に利用する誘導制御則は有望な技術である．本論文の前半 において，ダイナミックインバージョン，制御アロケーションといった搭載モデルベース 制御アプローチを小規模飛行実験および有翼ロケット実験機からなる実証システムの飛行 制御へ適用し，そこで識別されたロバスト性等の実際的な課題の解決方法を提案する．一 方，宇宙往還機等の誘導制御系は空力特性をはじめとする様々な不確定性に対する耐性が 必要であり，モンテカルロシミュレーションを用いた統計的評価が設計結果の標準的な確 認手段となっている．さらに，このモンテカルロ評価結果を評価関数として制御パラメタ を最適化する統計的最適化は，信頼性の高い飛行制御系を設計する実用的な方法であり，

前半で提案した誘導制御則のパラメタ調整への適用が期待されている．しかし，統計的最 適化の課題の一つはその重い計算負荷である．本論文の後半では計算負荷を低減する効果 的なアプローチの一つとしてベイズ推定に基づく確率推定手法を統計的ロバスト制御系の 設計問題に適用することを提案する.

Abstract

Future reusable space transportation systems should have ability to fly in various flight conditions encountered in their repetitive operations. Ability to return from any physically returnable situation will be also desired for safety, reliability, and flexible operability. Therefore, guidance and control algorithms capable to manage large characteristics change during flight are desired, and so are design methods capable to effectively design controllers for broad flight envelope and to easily re-design them for various different operations. On-board model based control (OMBC) approach, which positively uses the information of mathematical dynamics model installed into an on-board flight control computer, is a promising candidate technology to achieve these requirements.

In the first half of this thesis, OMBC approaches, such as dynamic inversion, control allocation, are applied to flight control of experimental vehicles: a small unmanned aerial vehicle and an experimental winged rocket. Practical issues such as robustness are extracted and solutions are proposed.

On the other hand, guidance and control system should be tolerant against various uncertainties,

such as errors in aerodynamic characteristics. Stochastic evaluation using Monte Carlo simulation

(MCS) is a standard method to verify overall performance of guidance and control against such

uncertainties. Stochastic optimization technique, where control parameters are optimized using the

result of MCS as a performance index, is considered as a practical approach to design a reliable

flight controller. However, heavy computational burden is an issue of stochastic optimization. In the

latter half of the paper, probability estimation techniques based on Bayesian inference are proposed

to be applied to stochastic robust flight control design problems as an effective approach to reduce

computational load.

1

目次

第

1

章 緒論

9

1.1

本研究の背景と概要

9

1.2

本論文の構成

11

第

2

章 搭載モデルベースの誘導制御

12

2.1

ダイナミックインバージョン誘導制御

12

2.1.1

基本的考え方，定式化

12

2.1.2

階層構造化ダイナミックインバージョン

13

2.1.3

ダイナミックインバージョン制御のロバスト性

16

2.2

外乱オブザーバによる誤差補償

17

2.3

制御アロケーション

22

2.3.1

定式化

23

2.3.2

擬似デバイス

25

第

3

章 搭載モデルベースの誘導制御の適用例

26

3.1

小規模飛行実験への適用

26

3.1.1

小規模飛行実験の概要

26

3.1.2

小規模飛行実験の誘導制御

27

3.1.3

ダイナミックインバージョン制御

28

3.1.4

外乱オブザーバ補償

29

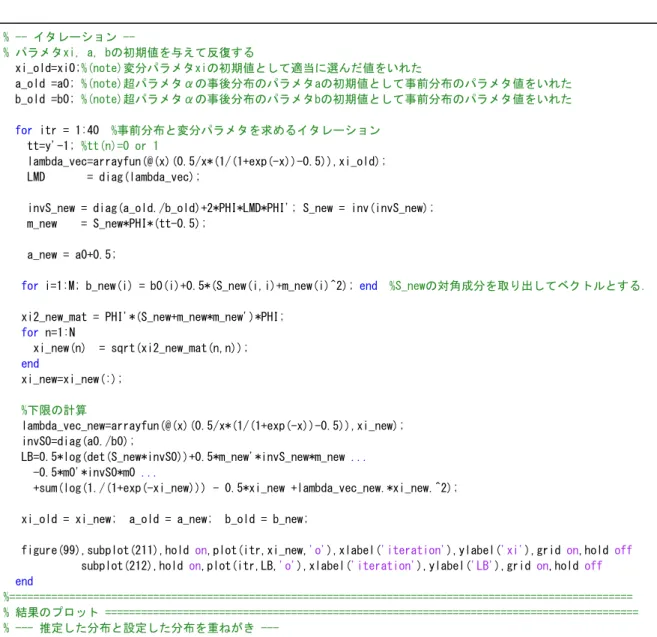
3.1.5

誤差を陽に考慮したパラメータ調整

30

3.1.6

風成分推定

34

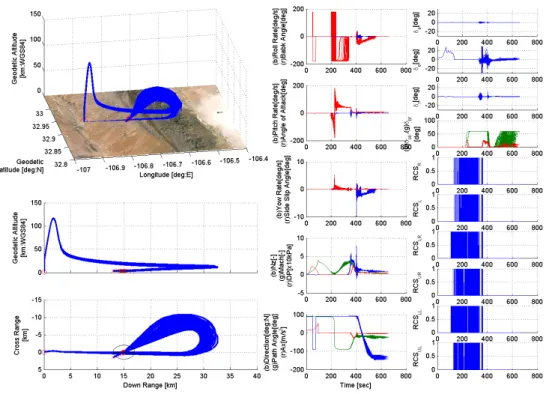
3.1.7

飛行実験

38

3.1.8

まとめ―小規模飛行実験で得られた成果

49

3.2

有翼ロケット実験機への適用

50

3.2.1

誘導制御の概要

51

3.2.2

階層構造ダイナミックインバージョンを用いた初期検討

51

3.2.3

動圧制御による縦面内誘導

53

3.2.4

姿勢制御

(

迎角制御

) 55

3.2.6

シミュレーション評価

65

2

第

4

章 統計的設計手法

67

4.1

統計的設計問題

67

4.1.1

統計的ロバスト性解析

67

4.1.2

統計的ロバスト設計

68

4.1.3

確率推定手法を用いた最適化

68

4.2

確率推定手法

69

4.2.1

確率的分類問題とロジスティック回帰

70

4.2.2

関連ベクトルマシン

71

4.2.3

確率密度比推定に基づく手法

74

4.3

サンプリング手法

75

4.3.1

一様乱数の発生

75

4.3.2

変換法

(

逆関数サンプリング

) 75

4.3.3

伝承サンプリング

77

4.3.4

棄却サンプリング

79

4.3.5

マルコフ連鎖に基づくサンプリング

81

4.4

確率推定手法の飛行制御系設計への適用例

86

4.4.1

確率密度比推定の縦制御系の設計への適用

86

4.4.2

確率的分類とハイブリッドモンテカルロアニーリングを用いた設計例

91

第

5

章 結論

98

参考文献

100

3

記号表

(

第

2

章・第

3

章

)

Z

：

Z

方向位置

Y

：

Y

方向位置

V

： 速度

γ

： 経路角

χ

： 方位角

V

T： 対気速度

γ

a： 経路角

(

対気

) χ

a： 方位角

(

対気

)

α

： 迎角

β

： 横滑り角

A

y： 横方向加速度

A

z： 上下方向加速度

u

： 機体

x

軸方向速度，

w

： 機体

z

軸方向速度，

φ

： ロール角

θ

： ピッチ角

ψ

^{： ヨー角}

p

： ロール角速度

q

： ピッチ角速度

r

： ヨー角速度

δ

e： エレベータ舵角

δ

a： エルロン舵角

δ

r： ラダー舵角

δ

th： スロットル開度

n

z： 荷重倍数

g

： 重力加速度

ρ

^{： 大気密度}

h

： 高度

h

s： スケール高度

q

： 動圧

S

： 基準面積

c

： 縦基準長

b

： 横基準長

D

： 抗力

L

： 揚力

Y

W： 横力

(

風軸

)

Y

B： 横力

(

機体軸

) F

T： 推力

I

yy： ピッチ軸回りの慣性モーメント

M

： ピッチ軸回りの空力モーメント

, ,

q

M M M

δ α ： 有次元微係数

(

ピッチングモーメント

) C

mα： 安定微係数

(

迎角静安定

)

C

lβ： 安定微係数

(

上半角効果

)

4 C

nβ： 安定微係数

(

方向静安定

)

x

： 状態ベクトル

u

： 制御入力ベクトル

ν

： 仮想的な入力変数ベクトル

f ( )

： 状態方程式右辺の関数

K

： ゲイン

τ

： 時定数

T( )

： 状態量の変数変換を表す関数

ξ

： 変数変換後の状態ベクトル

F( )

： 変数変換後の状態方程式の右辺の関数

x

i^：

i

番目の階層の状態ベクトル

f

i^：

i

番目の階層の状態方程式右辺の関数

K

i：

i

番目の階層のフィードバックゲイン

T

i

( )

：

i

番目の階層の状態量の変数変換を表す関数

ξ

i： 変数変換後の

i

番目の階層の状態ベクトル

F

i

( )

： 変数変換後の

i

番目の階層の状態方程式の右辺の関数

i0

ξ

^：

ξ

i^の基準値

ξ

i

∆

：

ξ

_iの微小変化

P(s)

： 制御対象の伝達関数

P

n

(s)

： 制御対象のノミナルモデルの伝達関数

R(s)

： 外乱オブザーバ補償で用いる理想応答モデルの伝達関数

Q(s)

：

外乱オブザーバ補償で用いるローパスフィルタの伝達関数

x

： 最適化する変数

(

制御アロケーション

) J

： 評価関数

(

制御アロケーション

) C

： 重み行列

(

制御アロケーション

) A

1

,A

2

,A

3： 等式・不等式制約条件の係数行列

b

1

,b

2

,b

3： 等式・不等式制約条件の定数項ベクトル

LMNc

δ

^： 擬似デバイス操舵コマンド

1^c

, ,

_n^c

δ δ

∆  ∆

： 実デバイス操舵コマンド増分値

w

*： 重み係数

, ,

c c c

L M N

∆ ∆ ∆

^： モーメントコマンド増分値

min

,

max

δ δ

∆ ∆

： 操舵量増分の上下限値

δ

₊

, δ

₋

∆ ∆

^： 正方向，負方向の操舵量増分値

*

,

*

,

*

L M N

_{δ δ δ} ： 舵効き係数

, ,

ref ref ref

L M N

： モーメント基準値

δ

_*ref ： 操舵量基準値

δ

RCSi：

i

番目のガスジェット開度

[0-1]

r

_CG^{： 重心の位置ベクトル}

f

_RCSi^：

ⁱ

番目のガスジェット推力ベクトル

r

RCSi^：

i

番目のガスジェットの取付位置の位置ベクトル

f

RCSi^：

ⁱ

番目のガスジェットの発生する推力の大きさ

5

θ

RCSi：

i

番目のガスジェットの取付角

(

ピッチ方向

) ψ

RCSi：

i

番目のガスジェットの取付角

(

ヨー方向

)

δ

θ： 推力偏向舵角

(

ジンバル角

)(

ピッチ方向

) δ

ψ： 推力偏向舵角

(

ジンバル角

)(

ヨー方向

) r

NZL^{： 推力作用点}

⁽

^{ジンバル支点}

⁾

^位置

F

T^{： 推力ベクトル}

∆r

NZL^{： 推力作用点}

(

ジンバル支点

)

の重心に対する相対位置

J

i^：

i

番目の評価項目の評価関数

(i=1,2...,N)

w

i^：

i

番目の評価関数の重み

(i=1,2...,N) T

sim： シミュレーション評価時間

t

final： 飛行終了時間

p

, ,

q r

K K K

： 姿勢制御ゲイン

(

角速度

)

ay

,

az

K K

： 姿勢制御ゲイン

(

加速度

) K

_φ： 姿勢制御ゲイン

(

ロール角

) K

q

, K

_q： 動圧制御の制御ゲイン

K

α： 姿勢制御ゲイン

(

迎角

) k

M角： 安定性改善用の調整ゲイン

q

REF^{： 動圧制御の基準値}

q

∆

： 動圧の基準値からの偏差

b

T： 推力のバイアス

U

W:E

, V

W:E

, W

W:E： 風速成分

(

地面固定系

)

η

：

白色ガウス雑音

(

プロセスノイズ

)

U

, ,

V W

η η η

： プロセスノイズ

(

風速成分の変動に対応

) , ,

CD CY CL

η η η

： プロセスノイズ

(

空力係数の変動に対応

) η

bT： プロセスノイズ

(

推力バイアスの変動に対応

)

ζ

： 白色ガウス雑音

(

観測ノイズ

) , ,

AX AY AZ

ζ ζ ζ

： 観測ノイズ

(

加速度

)

U

, ,

V W

ζ ζ ζ

^{： 観測ノイズ}

(

対地速度

) ζ

VT： 観測ノイズ

(

対気速度

) x

^{KF： 状態量}

z

^{KF： 観測量}

, w

ζ： 観測ノイズ

u

d^{： 決定論的入力}

v

η： プロセスノイズ

h ( )

^： 観測方程式の右辺の関数

KF

,

KF

∆ x ∆ z

^：

^{x z ,}

^{の微小変化}

F G H , ,

： 線形化した状態・観測方程式の係数

Φ , H

： 離散化した状態方程式の係数行列

x

k^{： 離散化した状態量}

6 v

k^{： 離散化した擬似入力}

y

k^{： 離散化した出力}

w

k^{： 離散化した外乱}

z

k^{： 離散化した観測値}

K

k^{： カルマンゲイン}

R

k^{： 観測雑音の共分散}

ˆ

_k

x

^{： 状態量推定値}

ˆ

_k⁻

x

： 更新前の状態量推定値

P

k^{： 誤差共分散推定値}

P

k⁻： 更新前の誤差共分散推定値

Q

_k^： プロセスノイズの共分散

(

添字

)

( )

STS ：

STS(Slow Time Scale)

システム

( )

FTS ：

FTS(Fast Time Scale)

システム

( )

TRIM ： トリム状態

( )

ｃ ： コマンド

( )

ｍ ： 計測値

( )

RCSi ：

i

番目のガスジェット

( )

NZL ： 推力偏向

(

第

4

章

) p(x)

： 確率密度分布

x

： 制御パラメータ

(

確率変数

) r(x)

： 確率密度比

p

success

(x)

： 成功サンプルの確率密度

p

all

(x)

： サンプル全体の確率密度

( | , ) x µ Σ



： 正規分布の確率密度

π

k： 混合ガウス分布の第

k

要素の混合係数

(k=1,2,...,K) μ

k： 混合ガウス分布の第

k

要素の平均値

(k=1,2,...,K)

∑_k： 混合ガウス分布の第

k

要素の共分散行列

(k=1,2,...,K) x

： 航空機運動モデルの状態量

u

： 制御入力

y

： 出力

K

α： 迎角フィードバックゲイン

(

制御パラメータ

)

K

q： ピッチ角速度フィードバックゲイン

(

制御パラメータ

) K

Iα： 迎角積分フィードバックゲイン

(

制御パラメータ

) K

δe： エレベータループゲイン

(

不確定パラメータ

)

T

D： 遅れ時間

(

不確定パラメータ

)

σ

： 標準偏差

1 2

[ , , , ] ε ε ε

^k

ε = 

： システムに含まれる不確かなパラメータ

1

, , ,

2 _N

ε ε  ε

^：

N

個の乱数ベクトル

P

： 確率

N

： サンプル数

N

U： 設計要求を満足しないサンプルの数

7

P

empirical： 実験的確率

x

： 制御系が含む調整可能な設計パラメータからなるベクトル

x

： 連続値の入力

t ∊{0,1}

：

2

値の離散出力

{ } x

_{n n}^N=1

X =

： 入力の集合

{ } t

_{n n}^N=1

T t = =

： 出力

(

観測値

)

の集合

P(T|X)

： 入力

X

の下での出力

T

の条件付き確率

( | , , )

P t x X T

：

x

に対する

t

の条件付事後確率

w

： 重みパラメータベクトル

σ(

・

)

： ロジスティックシグモイド関数

m

( ) x

φ

： 基底関数

K(x, x

m

)

： カーネル関数

w

m： パラメータベクトル

w

の各成分

α

： 超パラメータベクトル

iNEW

α

： 超パラメータの更新値

U(0,1)

： 一様分布

q(x)

：

棄却サンプリングでの提案分布

P(x'|x)

： 状態

x

から

x'

への遷移確率

S(x*|x

⁽ⁿ⁾

)

：

Metropolis

法で用いる提案分布

x*

： 候補となる状態

π(x)

： 平衡状態の分布

H(p,x)

： ハミルトニアン

(

運動量

p,

位置

x) K(p)

： 運動量

p

での運動エネルギー

(=p

²

/2m) V(x)

： 位置

x

でのポテンシャルエネルギー

r(i, j)

：

i

番目と

j

番目のレプリカ間での交換の確率

E(x)

： エネルギー

κ： ボルツマン定数

T

： 絶対温度

, , ,

A B C D

： 線形状態方程式の係数行列

(

添字

)

( )

MP ： 最大点

(Maximum Point)

8

略語表

ADS

：

Air Data Sensor

ALFLEX

：

Automatic Landing Flight Experiment ARD

：

Automatic Relevance Determination

CRV

：

Clue Return Vehicle DI

：

Dynamic Inversion DOB

：

Disturbance Observer ECO

：

Engine Cut Off

EM

：

Expectation Maximization EP

：

Expectation Propagation FTS

：

Fast Time-scale System

GM-KLIEP

：

Gaussian Mixture Kullback-Leibler Importance Estimation Procedure GP

：

Gaussian Process

HIMES

：

Highly Maneuverable Experimental Space Vehicle HMC

：

Hybrid Monte Carlo

HSDI

：

Hierarchy Structured Dynamic Inversion JAXA

：

Japan Aerospace Exploration Agency

MC

：

Monte Carlo

MCMC

：

Markov Chain Monte Carlo MCS

：

Monte Carlo Simulation

NDI

：

Nonllinear Dynamic Inversion OMBC

：

Onboard Model Based Control

RCS

：

Reaction Control System RMS

：

Root Mean Square

RVM

：

Relevance Vector Machine SSRV

：

Small Scale Research Vehicle

STS

：

Slow Time-scale System

TAEM

：

Terminal Area Energy Management

TVC

：

Thrust Vectoring Control

9

第 1 章 緒論

1.1

本研究の背景と概要

現在の宇宙輸送技術は多段ロケットによる使い捨て型の打上げシステムが主流であり，

1950

年代のスプートニク衛星の打ち上げから始まり，アポロ，ソユーズなど米ソの宇宙開 発時代，その後の打上げ事業の商業化の時代を経て技術の蓄積がなされてきた．

一方，有翼

/

再使用型の輸送システムの研究開発の起源も古く，

1960

年代の

X-15, X-24

と いった

NASA

の

X-

シリーズの実験機に始まり

1980

年代にはスペースシャトルとして結実 した．しかし，再使用型の宇宙輸送システムとして過去に実用化された唯一の例であるス ペースシャトルは，再使用するための整備などの運用コストが当初の想定を大きく上回り，

また安全性の面でも二度の重大事故を引き起こして

2010

年代に入って退役することになる．

その後，従来型の使い捨て型ロケットが打ち上げシステムの主流に戻り，技術的にも成熟 度を高めているが，その分，将来的に劇的に打上げコストを低減する見込みはほとんどな いといってよい．

こうしたなかで，米国ではスペース

X

社によるロケットの部分再使用への試みが急ピッ チで進んでおり，再び再使用化の流れが起きようとしている．また，スペースシップワン やブルーオリジンに代表される再使用可能なシステムによる商業的なサブオービタル飛行 の事業化の動きや，小型の衛星システムの普及，ベンチャー企業による小型の打上げシス テム開発の動向をみると，今後の宇宙輸送システムは需要に応じ使い捨て，再使用を使い 分けバリエーションを増やしていくのではないかと想像される．また，環境や地上の安全 への影響をも考慮すると，最終的には輸送システムは回収

/

再使用化の方向をたどっていか ざるをえないのではないかと思われる．

将来的な再使用宇宙輸送システムを考えるとき，経常的な往還運用で遭遇する多様な条 件に確実に対応し，かつ，緊急時には物理的に帰還可能ないかなる状況からでも機体を生 還させる能力を持たせることで安全性

/

信頼性

/

運用性の向上を図ることが課題となる．

この際，誘導制御則およびその設計手法には以下のような事項が要求される．

広範囲な飛行領域への対応

離陸

/

上昇・再突入・遷音速域・進入

/

着陸と広範囲にわたる飛行条件

(

速度・高度

)

に対応 可能であること，特に再突入時や遷音速域での大きな特性の変化に対応できることが必要 となる．これについては従来の飛行制御では飛行条件の変化による特性変化に対し，想定 される飛行条件を代表する多数の設計モデルに対して設計したゲインを切り替えるゲイン スケジュールの手法で対応してきた．しかしながら，この方法では多数の誘導制御ゲイン

10

を設計して組み合わせる必要があり，システムの設計

/

修正ループのスケジュールに無視で きない影響を与えてきた．特に，開発においては設計条件や機体のコンフィギュレーショ ンが，開発の進捗によって変更することはしばしばであり，修正した形態での飛行能力の 検証のために誘導制御則の設計がこれに迅速に対応することが求められる．

(2)

異なる状況に対する柔軟性

将来的に再使用宇宙輸送システムが経常的に運用される状況を考えると，ペイロード，

投入軌道などの異なるミッションに柔軟に対応できることや，故障・アボートによる着陸 地点変更など飛行中の変更に柔軟に対応できることが必要になると考えられる．再使用宇 宙輸送システムは元来軽量化を極限まで追求する必要から，余裕を切り詰めた設計となっ ているため，ミッションやコンフィギュレーションの変更に対して誘導制御則を柔軟・迅 速に変更して最適化して機体能力を有効に使うことが望ましい．

(3)

誤差に対するロバスト性

実際の飛行においては，空力特性，アクチュエータ性能，センサ特性など設計モデルに 対する様々な誤差が存在する．特に，高層，高速での空力特性については飛行データが少 なく，また，風洞試験で全ての飛行条件や舵角設定を網羅することも難しいので，

CFD

に 頼らざるを得ない部分も多く，信頼性の高いモデルを構築することが難しい．このため，

大きな不確定性を想定して誘導制御系を設計する必要がある．

(1),(2)

のような要求に対して，詳細な機体運動モデルを誘導制御則に組み込むことにより，

飛行条件の変化をオンボードの機体運動モデルを用いて補償し，特性の変動に対応すると ともに設計を効率化することが効果的である．ここでは，このようなアプローチを搭載モ デルベース制御

(On-board Model Based Control, OMBC)

と呼ぶことにする．ダイナミックイン バージョンはそのような手法の代表的なものであり，これを航空機，宇宙往還機に適用す る試みはこれまでも行われてきており，その基本的な有効性が示されている

[1][2][3]

．この 手法は機体ダイナミクスの逆モデルを用いることにより特性の変化をキャンセルして所望 の応答特性を実現するものである．

(3)

の誤差に対するロバスト性に関しては，誤差に対する必要十分なロバスト性を確保す る手法として，モンテカルロシミュレーションをベースとした統計的手法に基づく評価や 制御パラメータの最適化が研究され，有効なツールであることが示されている

[4][5][6]

．し かしながら，この手法は膨大な計算量を伴うため，適用に当たっては調整パラメータの個 数を少なくする，効率のよい最適化アルゴリズムを選択する，分散処理システムを利用す る，など種々の工夫を要する．

ダイナミックインバージョン制御に代表される，搭載モデルを用いる制御は，機体の運

11

動特性に対する既知の情報を活用して性能の向上や設計の効率化を図るものである．搭載 モデル情報を利用することで，細かいゲインスケジュールをせずに済み，調整すべきパラ メータの個数を減らすことができるため統計的最適化と組み合わせることで課題の一部を 解決することができると考えられる．

その一方で，モデルを積極的に使用するがゆえに想定したモデルに誤差があった場合に その影響がストレートに性能に現れやすい．実際，ダイナミックインバージョンを適用し た制御で空力誤差を考慮した場合に著しく応答性能や安定性が劣化してしまうことがしば しば起こる．このため，なんらかの誤差を保証する構造とあわせて使用することが望まし い．誤差の影響を補償する方法としてニューラルネットワークや適応制御を利用する方法 もあるが，比較的シンプルな構造で効果のある手法として外乱オブザーバにより誤差項を 推定して入力にフィードバックする方法が知られている．これはロボットなどの分野で適 用されて有効性が報告されているものであるが，ここで扱う搭載モデルベースの飛行制御 にも適用することができると考えられる．

1.2

本論文の構成

本研究では搭載モデルベースの制御，特にダイナミックインバージョンの実機開発への 適用における課題の解決を図ることを目的とした研究を行う．

第

1

章では研究の背景と概要を記述してきた．次章以降の構成は以下のようである．

第

2

章では本論文で提案する搭載モデルベースの誘導制御について具体的な内容を記述 する．まず，広い飛行領域における誘導制御則を容易に構成することのできるダイナミッ クインバージョン制御手法，特に設計の見通しをよくするための制御構造の階層化につい て記述する．更にダイナミックインバージョンと組み合わせて使用する技術として，複数 の制御デバイスを有効に組み合わせることのできる制御アロケーション，モデル誤差の影 響を低減する外乱オブザーバによる誤差補償を取り上げ，定式化等について説明する．

第

3

章では飛行実証システムへの適用例について記述する．ここでは小型の無人実験機 である小規模飛行実験機と，サブオービタルの飛行を行う有翼ロケット機を取り上げる．

第

2

章で記述した手法の具体的な制御対象への適用方法の実際と，飛行実験やシミュレー ション評価を通して識別された課題や解決方法について記述する．

第

4

章では統計的手法によるロバスト性の評価および設計の方法について記述する．統 計的設計を改良するための新しいアプローチとして，近年，機械学習等の分野で開発され ている確率推定に基づく手法の適用を提案し，例題に適用して有効性を確認する．

第

5

章では全体のまとめを行う．

12

第 2 章 搭載モデルベースの誘導制御

本章では搭載モデルに基づく誘導制御について記述する．最初に搭載した機体運動の逆 ダイナミクスを用いて飛行条件による特性の変動をキャンセルして，広い飛行領域で所望 の応答を得ようとするダイナミックインバージョン制御について，その基本的考え方，定 式化，課題とその解決方法について述べる．次に，所望の運動に必要な制御力を使用可能 なデバイスで実現するための制御アロケーション手法について記述する．

2.1

ダイナミックインバージョン誘導制御

ダイナミックインバージョン制御は誘導制御則に組み込んだ機体運動の逆ダイナミクス を用いて飛行条件による特性の変動をキャンセルして所望の応答を得ようとするものであ る．モデルの使用により，ゲインスケジュールを排除することができるため，飛行経路の 変更等に対しても飛行領域全体にわたる多数のゲインの再設計

/

解析

/

調整作業を要せずに 対応することができ，設計作業の効率化を図ることができる．

2.1.1

節ではその基本的な考 え方，定式化を示す．

2.1.2

節では階層構造化を用いた手法について，

2.1.3

節ではオンボー ドで誤差を補償するための手法について記述する．搭載機体モデルを用いるため，誤差の 影響の補償が重要となるが，ここでは外乱オブザーバをもちいた誤差補償を検討している．

2.1.1

基本的考え方，定式化

最も単純な場合として状態方程式が

( , )

x f x u  = (2.1.1-1)

で表される系を考える．ここで，

x

は状態量，

u

は制御入力である．

このとき，右辺を

( , ) f x u

ν ≡ _(2.1.1-2)

と置くと

x v  = (2.1.1-3)

となり，仮想的な入力変数

ν

に対する線形の状態方程式

(

この場合は一次の積分系

)

とみなす ことができる．これに対して線形の設計法を適用することにより所望の特性をもった閉ル ープ系を構成することができる．例えば，

x

cを状態量

x

に対するコマンドとして，

(

_c

)

v = − K x x −

，

K = 1/ τ _(2.1.1-4)

というフィードバック則を適用すれば，結果として得られる系は

(

_c

)

x  = − K x x − (2.1.1-5)

となる．ここに

K

はフィードバックゲイン，τは対応する時定数である．ラプラス変換し て整理すると，この伝達関数は

13 1

c

1

c

x K x x

s K τ s

= =

+ + ^(2.1.1-6)

となり，時定数

τ

の一次遅れ特性が得られる．

この時，実際の制御入力

u

は

(2.1.1-2)

を

u

について解くことにより得られる．これを

1

( , )

u f x =

⁻

ν _(2.1.1-7)

のように表すことにする．

状態量

x

がベクトルの場合でも制御入力ベクトル

u

が状態と同数の独立な成分をもち，

(2.1.1-2)

を

u

について解くことができる場合には全く同様に考えることができる．

2.1.2

階層構造化ダイナミックインバージョン

ここでは，宮沢ら

[7][8][9]

によって提案された階層構造化ダイナミックインバージョン制 御について記述する．これは運動方程式の状態量を時間スケールで分割し

(

階層構造化），階 層ごとの低次元のシステムについてダイナミックインバージョンの手法を適用して制御則 を導くものである．

ダイナミックインバージョン制御の課題の一つとして零ダイナミクスの取扱いの問題が ある

[10]

．これはシステムが入力で直接制御できない内部ダイナミクスを持つ場合に所望の 応答を持つ制御則を構成することが困難になる問題であるが，状態変数を分割して各々が １階の微分方程式¹となるように変数を選択することで，この難点を回避することができる．

また，時間スケール分割することでロバスト性を改善する効果があるという報告もある

[11]

．

2.1.2.1

階層構造化

一般に剛体航空機の運動は次のような部分（階層）に分解することができる．

(1)

回転運動のダイナミクス：操舵によりモーメントが発生，そのモーメントが積分され

て回転角速度が生成される．

(2)

姿勢のキネマティクス：回転角速度が積分されて姿勢角が生成される．姿勢角は空気

の流れに対する相対的な機体の姿勢となることから，姿勢角によって機体に働く力が 発生する．また，推力の調節により機体に働く力を調整する．

(3)

並進運動のダイナミクス：力に比例した加速度が積分されて速度が生成される

. (4)

位置のキネマティクス： 速度が積分されて位置が生成される．

このように制御変数である操舵角や推力から機体の位置までは

4

つの段階に分解するこ とができる．そのそれぞれを一次の状態方程式

1 従って相対次数

0

でありゼロダイナミクスを持たない．

14

1 1

( , , )

1 2

x  = f x x 

2 2

( , , )

2 3

x  = f x x  (2.1.2-1)

3 3

( , , )

3 4

x  = f x x 

4 4

( , , )

4

x  = f x u 

で表現することができる．省略した部分は各階層で対象とする運動とは時間スケールの異 なる状態量や入力であり各階層の定式化においては一定値として扱う．例として第一階層 を取り上げて説明する．この場合は状態変数のうち

x

1が被制御量，

x

2を制御入力として取 り扱う．このとき，

1

( , , )

1 2

v f x x ≡  (2.1.2-2)

によって仮想的な入力を定義すれば運動方程式は

x v 

1

= (2.1.2-3)

と，一次の積分系となる．これに対しフィードバック則

1

(

1 1_c

)

v = − K x x − (2.1.2-4)

を適用すれば閉ループの応答は

1 1

(

1 1_c

)

x  = − K x x − (2.1.2-5)

となりゲイン

K

1を適当に選ぶことによって所望の時定数をもった応答を実現できる．逆ダ イナミクス

2_c 1 1

( , , )

1

x = f v x

⁻

 (2.1.2-6)

をもちいて

v

を変換すればこの階層での実際の制御入力が得られ，これを次の階層でのコマ ンドとすることにより階層的な制御を実現することができる．

図

2.1.2-1

階層構造的ダイナミックインバージョンの制御構造の例

e a r δ δ δ

 

 

 

 

 

φ θ b

  

  

 

T a a

V γ ψ

 

 

 

 

 

∫

F4 ∫

F4

F4 FFF333 ∫∫ FFF222 ∫∫ FFF111 ∫∫

F3-1

K₃(s) F3-1

F3-1

K₃(s)

K₃(s) FFF222-1-1-1 KKK₂₂₂(s)(s)(s) F1-1

K₁(s) F1-1

F1-1

K₁(s) K₁(s) F4-1 K₄(s)

F4-1

F4-1 KK₄₄(s)(s)

h y

s e e

  

  

 

ξ

1

ξ

2 p

q r

  

  

 

ξ

3

ξ

4

ξ

4c

ξ 

4c

ξ 

_3c

ξ

_3c

ξ 

_2c

ξ

_2c

ξ 

_1c

ξ

_1c

－+

－+

－+ －

+

ξ ^

4

ξ ^

₃

ξ ^

₂

ξ ^

₁

5

u

ξ =

5c

u

c

ξ =

ec ac rc δ δ δ

 

 

 

 

 

c c c

p q r

  

  

 

c c c φ θ b

 

 

 

 

 

c hc yc

s e e

 

 

 

 

 

Tc ac ac

V γ ψ

 

 

 

 

 

[

機体ダイナミクス

]

[

誘導制御則

]

回転ダイナミクス

舵角

(

→トルク

)

→角速度

姿勢キネマティクス 角速度→姿勢角

並進ダイナミクス 姿勢

(

→力

)

→速度

位置キネマティクス 速度→位置

15

2.1.2.2

変数変換による制御状態量の変更

状態量の選択によっては解析的に逆ダイナミクスを表現することが容易でない場合があ る．このような場合，変数変換に基づく手法が便利である．

状態方程式

(

変換前

)

が以下のように与えられているとする．

1 1

( , )

1

x  = f x 

2 2

( , )

2

x  = f x  (2.1.2-7)

3 3

( , )

3

x  = f x 

4 4

( , )

4

x  = f x 

ここで，状態量の変換が次のように関数

T

により与えられるとする．

1 1 2 3 4

1

2 1 2 3 4

2

3 1 2 3 4

3

4 1 2 3 4

4

( , , , ) ( , , , ) ( , , , ) ( ) ( , , , ) T x x x x T x x x x T x x x x T x T x x x x ξ

ξ ξ ξ ξ

 

   

   

=     =   =

 

     

(2.1.2-8)

この変換により状態方程式が以下のように変換されるとする．

1

F

1

( ,

1 2

) ξ  = ξ ξ 

2

F

2

( ,

2 3

)

ξ  = ξ ξ  (2.1.2-9)

3

F

3

( ,

3 4

) ξ  = ξ ξ 

4

F

4

( ,

4 5

u ) ξ  = ξ ξ ≡ 

変換後の状態微分を計算する関数

F

を変数変換

T

と変換前の状態微分を計算する関数

f

を用 いて表すことができる．

( , )

^{i i}

( , )

i

F

i i

T x T f x

x x

ξ ξ ∂ ∂

= = =

∂ ∂

    (2.1.2-10)

この関係を用いれば，変換後の方程式が陽な関数としてあらわされていなくても変換前の 方程式を用いて変換後の逆ダイナミクスモデルを計算することができる．変数変換の手法 は制御状態量を容易に変換することができるため，設計初期の被制御量の選択の検討など にも便利な手法と思われる．なお，適用する運動方程式や状態量については，時間スケー ルの異なる階層や縦

/

横の干渉が悪影響を及ぼさない様に物理的な考察に基づいて変数や近 似を選択する必要がある．

2.1.2.3

逐次線形近似による逆ダイナミクスの計算

さらに，非線形の逆ダイナミクスは一般に解析的に解くことができないが，状態が与え られれば，逆ダイナミクスを以下のように逐次線形近似によって計算することができる．

まず，変換後の状態方程式をテーラー展開して一次の項までとると，

0

0 0 0 0 0

1 1 1 1

1

1 1

1

( , ) ( , ) ( , ) ,

( , )

i

i i i i i i i i i i i i i

i

i i i i i

i

F F F

F

ξ

ξ ξ ξ ξ ξ ξ ξ ξ ξ ξ

ξ

ξ ξ ξ ξ

ξ

+ + + +

= +

+ +

+

= ≈ + ∆ = + ∂ ∆

∂

∆ = ∂ ∆

∂



    ((((   

 

(2.1.2-11)

16

これから，

1

1 1

1

( , )

i i i i i

i

ξ F ξ ξ ξ

ξ

−

+ +

+

 ∂ 

∆ =   ∂    ∆  (2.1.2-12)

なので，

10

1

1 0 1 0 0 0 0

1 1 1

1

( , ) ( , ) ( , ) ,

i

i i i i i i i i i i i i i

i

F F F

ξ

ξ ξ ξ ξ ξ ξ ξ ξ ξ ξ

ξ

+

−

− −

+ + +

= +

 ∂ 

=   ≈ + ∆ = ((((   +   ∂     ∆  (2.1.2-13)

により逆ダイナミクスを計算することができる．また線形化された方程式は安定性を議論 する場合などにも便利である．

2.1.3

ダイナミックインバージョン制御のロバスト性

ダイナミックインバージョンによる制御は構造のわかりやすさ，また異なる飛行条件で の設計を容易に行えることなどから大変便利なものであるが，搭載プログラムにインスト ールされている数学モデルに強く依存するため，モデル誤差に対する感度が強くロバスト 性の観点から問題がある場合がある．ここでは，ダイナミックインバージョン制御のロバ スト性の評価方法について記述し，ロバスト性を改善するための方策について述べる．

2.1.3.1

ロバスト性評価の方法

(1)

線形解析による安定余裕解析

制御対象，制御則をそれぞれ線形近似することにより，通常の線形システムと同様の安 定解析を行うことができる．特に，非線形性があまり強くないシステムにおいては，必要 条件として線形での安定性を評価しておくことが重要である．

(2)

誤差シミュレーション解析による評価

非線形の制御システムの安定性，性能を評価する最も直接的で信頼できる方法は想定さ れる不確定性を考慮した非線形シミュレーション解析であろう．しかしながら，シミュレ ーションでモデル化されていない高周波の領域における振動や，逆にゆっくりとした発散 傾向は非線形シミュレーションで必ずしもとらえきれない場合があり，線形の安定解析，

あるいは飛行条件を固定した短時間の応答シミュレーションによる評価と併用するのがよ いと考えられる．また線形の安定解析についても，誤差を考慮したモンテカルロ評価をと りいれることができる．また，

Bothworth

らの文献

[12]

では逐次フーリエ変換による実時間 安定余裕計算手法を飛行実験に適用しており，これをモンテカルロシミュレーションに適 用する可能性について言及している．

17

2.1.3.2

ロバスト性向上の方策

(1)

不確定性を考慮したパラメータ調整

第一に考慮すべきは制御パラメータの調整により種々の不確定性に対し十分な余裕を 確保することである．第

4

章で取り扱う統計的ロバスト制御設計手法では種々の誤差の 影響を考慮したうえでパラメータを最適化することができる．モンテカルロ評価には非 線形シミュレーションによる所望の飛行の達成度，線形解析による応答性評価など，種々 の評価基準をとることができる．姿勢制御系の設計の観点からは機体特性のほか飛行条 件や環境条件の不確定性によるばらつきを考慮することができる．

(2)

搭載モデルの調整

搭載した数学モデルにより，飛行条件の違いをキャンセルして吸収することがダイナ ミックインバージョンの長所であるが，機体固有の安定性が強い場合などに逆モデルに よりこれをキャンセルしてしまうことは，時として制御パラメータの調整による安定余 裕の確保を困難にしてしまう場合がある．また，選択した

”

ノミナル

”

モデルがロバスト 性の観点から必ずしも最も望ましいというわけではない．一方，見方を変えると搭載モ デル自体も制御システムの一部ととらえることができ，必要であれば調整可能なもので あることに気付く．そこで，搭載モデル自体に調整可能なパラメータを導入し，ロバス ト性の回復に使用することができる．

Wacker

らの文献

[13]

では

X-38CRV

に適用されたダ イナミックインバージョン制御について紹介しているが，搭載モデルとしてノミナルモ デルをそのまま用いるのではなく，モデルパラメータの想定される不確定性の範囲でで きるだけ安定性のよいモデルを選択することで制御則の安定余裕を確保する方法につい て記述している．また，ダイナミックインバージョンを適用する際の横滑り角の値とし て，オブザーバや横加速度からの推定値を用いるよりも固定値

0

を用いるほうがロバス ト性がよいと言及している．

(3)

誤差補償器の追加

通常の線形の制御と同様に付加的な補償器を追加することによって，誤差の影響を軽 減することが可能である．適応制御を利用する方法や外乱推定器を用いる方法がある．

誤差補償は応答性能に対する誤差の影響を低減するが，遅れの影響などを受けやすいの でこれらについても留意する必要がある．また，適当な前置補償器等を使用することに よって応答性能を落とすことなくロバスト性を改善することが可能である．

後の章の適用例では誤差を補償する手段として外乱オブザーバを適用する

.

そのため，

次節では

,

これについてやや詳しく記述する．

2.2

外乱オブザーバによる誤差補償

ダイナミックインバージョン制御の誤差に対する耐性を向上するための手法の一つとし て外乱オブザーバによる誤差補償について記述する．

18

外乱オブザーバによる外乱・誤差補償は外乱やモデル誤差が存在する場合に入力

u

をシ ステムに対して行ったとき，その応答と入力により，モデル誤差と外乱からなる誤差項を 推定し，その項を新たな入力

u

にフィードバック補償することで，モデル誤差，外乱の影 響を抑えようとするものである．外乱オブザーバを使った誤差補償はロボット等のモーシ ョンコントロールの分野で研究されており，良好な結果が報告されている．

外乱オブザーバによる誤差補償構造について，ここでは直観的にわかりやすい説明を試

みる．図

2.2-1

のように外乱，誤差を含む制御対象

P(s)

からの出力に対しノミナルモデルの

逆

P

n-1

(s)

を通したものと，入力

u

の差をとり，ローパスフィルタ

Q _(s)

を通すことにより，誤 差項の推定を行うことができる．図

2.2-2

は図

2.2-1

と等価な書き換えを行ったものである．

特別な場合として，逆ダイナミクスを利用した制御で制御対象と逆ダイナミクスをあわ せたものが近似的に単純な積分系とみなすことができる場合を考えると

,

図

2.2-3

のように なるが，さらに実装を考慮して純粋微分を含まないように図

2.2-4

のように書き換えること ができる．

図

2.2-1

外乱オブザーバによる補償

図

2.2-2

外乱オブザーバによる補償

(

図

2.2-1

と等価

)

19

図

2.2-3

逆ダイナミクス

+

プラントに対し外乱オブザーバを適用

図

2.2-4

逆ダイナミクス

+

プラントに対し外乱オブザーバを適用

(

図

2.2-3

と等価で純粋微分を含まない形

)

(

例

)

小型自動着陸実験機

(ALFLEX)[14]

の平衡滑空飛行時の姿勢・回転運動

小型自動着陸実験機

(ALFLEX)

の平衡滑空飛行時の姿勢・回転運動に対する簡易モデル

(

付 録

A)

に対して非線形ダイナミックインバージョン

(Nonlinear Dynamic Inversion, NDI)

を適用 した例で外乱オブザーバ補償の効果を調べる．

[制御則①] 単純な比例フィードバックによる NDI

制御を適用したもの

(NDI)

．

(

図

2.2-5a) [制御則②] ①のノミナル応答を理想応答としてフィードフォワードし，外乱オブザーバ

による誤差補償をした制御系

(NDI-DOB(

その

1))

．

(

図

2.2-5b)

[制御則③] 外乱オブザーバによる誤差補償をした制御系．②の構造に (

角速度

)

コマンドへ のフィードバックループを付加し，定常誤差の抑制を図ったもの

(NDI-DOB(

その

2))

．理想 応答としてはノミナルの一次系の応答を考え，閉ループの応答が理想応答に一致するよう に前置補償器を設定した

(

結果として①と同じ定数ゲインとなる

)

．

(

図

2.2-5c)

の三種類の制御系を構成し，舵効き誤差のケースでこれらを比較した．図

2.2-6

は迎角に

0

→

8deg,

バンク角に

0

→

10deg

のステップ入力を入れた場合の応答

(

破線はコマンド

)

を示し

ている．これによると，ノミナルではいずれもほぼ同じ応答を示しているが，舵効き誤差 をいれて舵の効きを減らしてゆくと，

NDI

のみの制御は応答が極端に悪化し，舵効きが

50%

では発散してしまうのに対し，

NDI-DOB

制御

(

②

)

では舵効きが減っても応答の極端な劣化

20

はなく，

50%

になっても安定な応答を示している．さらに

NID-DOB

制御

(

③

)

では応答もほ とんど劣化しない．この結果は外乱オブザーバによる誤差補償が有効に効いていることを 示している．

図

2.2-5a NDI

制御 ブロック図

図

2.2-5b NDI-DOB

制御

(

外乱オブザーバ補償つき

NDI

・その

1)

ブロック図

図

2.2-5c NDI-DOB

制御

(

外乱オブザーバ補償つき

NDI

・その

2)

ブロック図

σ α β σc αc βc

pc qc rc

Lc Mc Nc

δec δac δrc

K

Φ

Kω

p q r

往還機 ダイナミクス 姿勢運動の

逆システム

回転運動の 逆システム

制御 アロケーション 姿勢角コマンド

姿勢角

角速度コマンド

角速度

制御ゲイン 制御ゲイン

モーメントコマンド

舵角コマンド

21

図

2.2-6a

ノミナルでの応答の比較

(

実線：姿勢角応答，破線：コマンド

)

図

2.2-6b

舵効き誤差あり

(0.7

倍

)

での応答の比較

(

実線：姿勢角応答，破線：コマンド

)

0 10 20

-5 0 5 10 15

バンク角[deg]

NDI ErrFact=1

0 10 20

-5 0 5 10

迎角[deg]

0 10 20

-5 0 5

横滑角[deg]

0 10 20

-5 0 5 10 15

バンク角[deg]

NDI-DOB(その１) ErrFact=1

0 10 20

-5 0 5 10

迎角[deg]

0 10 20

-5 0 5

横滑角[deg]

0 10 20

-5 0 5 10 15

バンク角[deg]

NDI-DOB(その２) ErrFact=1

0 10 20

-5 0 5 10

迎角[deg]

0 10 20

-5 0 5

横滑角[deg]

0 10 20

-5 0 5 10 15

バンク角[deg]

NDI ErrFact=0.7

0 10 20

-5 0 5 10 15 20

迎角[deg]

0 10 20

-5 0 5

横滑角[deg]

0 10 20

-5 0 5 10 15

バンク角[deg]

NDI-DOB(その１) ErrFact=0.7

0 10 20

-5 0 5 10

迎角[deg]

0 10 20

-5 0 5

横滑角[deg]

0 10 20

-5 0 5 10 15

バンク角[deg]

NDI-DOB(その２) ErrFact=0.7

0 10 20

-5 0 5 10

迎角[deg]

0 10 20

-5 0 5

横滑角[deg]

22

図

2.2-6c

舵効き誤差あり

(0.5

倍

)

での応答の比較

(

実線：姿勢角応答，破線：コマンド

)

2.3

制御アロケーション

制御アロケーション

[15]

は機体の回転運動を制御するために必要なモーメントを効果的 に発生するために冗長なデバイスに対し操舵量を配分する技術である．とくに再使用宇宙 輸送システムでは打上げ時や大気上層での飛行においてガスジェットや推力偏向と空力舵 面を組みあわせて機体姿勢を制御する必要があり，また動圧やマッハ数による舵効きの変 化に合わせて柔軟に操舵の組合せを変更できることが好ましい．

制御アロケーションはダイナミックインバージョンに代表される非線形制御と組み合わ せて使用されることが多く，種々の手法が検討されている．その中でも線形計画法を用い た方法は舵角範囲などの拘束を考慮した解を比較的少ない計算量で確実に得られる手法で ある

.

制御デバイスの設計においては全ての飛行領域に対して十分な操舵力が確保できるよう にすることが必須ではあるが，搭載アルゴリズムへの実装においては仮に一時的な操舵力 の不足があったとしても，求解が破綻することがないように処置する必要がある．また，

設計段階におけるシミュレーション検討などでは不足モーメントがどの程度かを知ること は舵面設計へのフィードバックの観点から有用であると考えられる．

0 10 20

-5 0 5 10 15

バンク角[deg]

NDI ErrFact=0.5

0 10 20

-5 0 5 10

迎角[deg]

0 10 20

-5 0 5

横滑角[deg]

0 10 20

-5 0 5 10 15

バンク角[deg]

NDI-DOB(その１) ErrFact=0.5

0 10 20

-5 0 5 10

迎角[deg]

0 10 20

-5 0 5

横滑角[deg]

0 10 20

-5 0 5 10 15

バンク角[deg]

NDI-DOB(その２) ErrFact=0.5

0 10 20

-5 0 5 10

迎角[deg]

0 10 20

-5 0 5

横滑角[deg]

23

ここでは標準的な線形計画法による制御アロケーションの枠組みにおいて，実際の操舵 デバイスに加え三軸方向のモーメントを発生する仮想的な擬似デバイス入力を付け加える ことで，線形計画法の解の存在を保証し，かつ，最適な操舵配分をしても必要なモーメン トを発生できない場合に，不足するモーメントをリアルタイムで計算することができるア ルゴリズムを提案する．類似の定式化はモーメント残差と操舵量を同時に最小化する

mixed-optimization problem

の枠組みで

Bodson

ら

[16]

などによって提案されており，本質的な 差異はないが，ここで提案する構成方法は，付加的に導入する変数の数が少なくよりシン プルである．また，付加的な変数を仮想的な操舵デバイスと解釈することは直感的に分か りやすいので重みや上下限値等の調整パラメータの設定において見通しがよくなる効果も 期待できる．なお，

Bodson

らは操舵量の評価関数に

|ℓ

1

|

ノルム

(

各操舵の絶対値の和

)

でなく

|ℓ

∞

|

ノルム

(

各操舵の絶対値の最大値

)

を用いた線形計画法により各舵面の負荷を分散する手法 について提案しているが，ここでの構成においても同様なことを行うことができる．

本節では，線形計画法による制御アロケーションの定式化について記述する．また，第

4

章では数値例として，有翼ロケット機のサブオービタル飛行に適用することでその有効性 を確認する．

2.3.1

定式化

線形計画問題は一般的に以下のような線形の等式

/

不等式拘束条件のもとで，線形の評価 関数

J

を最小化する非負の実ベクトル

x

を見つける問題として扱うことができる．線形計画 法の解法については，文献

[17]

を参照していただきたい．

(1)

評価関数

J Cx = (2.3.1-1)

(2)

不等式制約条件①

A x b

₁

≤

₁

(2.3.1-2) (3)

不等式制約条件②

A x b

₂

≥

₂

(2.3.1-3) (4)

等式制約条件

A x b

₃

=

₃

(2.3.1-4)

線形計画法を制御アロケーション問題に適用するために以下のような定式化を行う．

最適化する変数として基準となる状態からの操舵量の増分からなるベクトルを考える．

1

c c c T

LMN n

x =   δ ∆ δ  ∆ δ   (2.3.1-5)

ここで

δ

_LMN^{c はモーメント}

[ L M N , , ]

の不足を補う仮想的な入力

(

擬似デバイス

)

であり，

0

～

1

の間の値をとる．これらは後述のように最適化時の重みを大きくとることで可能な限り

0

に近づけるようにする．一方，

∆ δ

₁^c

, ,  ∆ δ

_n^cは

1

サンプリング時間での実デバイス操舵量の 増分に相当するもので全て非負である必要がある．実際には空力舵面の多くや推力偏向操 舵は増分が正負の値をとりうるので次のように分解して非負の値を持つ二つの変数として 扱う．

min max

max min

: , 0 ,0

δ δ δ

δ δ

₊

δ

₋

δ

₊

δ δ

₋

δ

−∆ ≤ ∆ ≤ ∆

⇒ ∆ = ∆ − ∆ ≤ ∆ ≤ ∆ ≤ ∆ ≤ ∆ ^(2.3.1-6)