en 最近の更新履歴 yyasuda's website

(1)

Introduction to Market Design and

its Applications to School Choice

Yosuke YASUDA

Osaka University, Faculty of Economics Email: yosuke.yasuda@gmail.com

Web: https://sites.google.com/site/yosukeyasuda/

(2)

Outline of My Talk

- Introduction + Basic Theory + My Research

 

Market Design

  Applications in Real Life

  Theory (1) --- Matching Problem

 

School Choice Problems

  Background

  My Research

  Theory (2) --- Exchange Problem (if time remains…)

(3)

MARKET DESIGN FOR

ECONOMIC “ENGINEERING”

Putting Game Theory to Work

(4)

Nobel Prize in Economic Science 2012

- Roth and Shapley for Market Design!

(5)

Market Design

- From Theory to Practice

 

Applying new insights in microeconomic

theory, market design tries to (re-)design

actual markets and to fix market failures.

 

Experiments and simulations are used to

check the performance. Engineering

 

New mechanisms proposed by economists

are implemented in real world. Practical

⇒

Let’s look at real life examples!

(6)

[1] Spectrum Auctions

- The Greatest Auction Ever

  The first spectrum auction was operated in New Zealand in 1990, which was not so successful.

  How can we appropriately sell spectrum licenses with potentially highly interdependent values?

  In 1994, on the advice of economists, the U.S.

Federal Communications Commission (FCC) started the simultaneous multi-rounds ascending-bid

(SMRA) auctions:

  “The Greatest Auction Ever” (NY Times, 1995)

  The British spectrum auction of 2000 designed by economists raised about 22.5billion pounds!

(7)

[2] Markets for New Doctors

- Economics Changes Labor Markets

  In each year, around 20000 new American doctors are assigned to their hospitals via a centralized

clearinghouse: National Resident Matching Program.

  Both students and hospitals submit their ranking

orders, and assignments are made based on these reported preferences.

  This matching program was re-designed in 1998: (student-proposing) deferred acceptance algorithm.

  Japan (2003-) and some regions in UK adapted the same resident matching program.

(8)

[3] Kidney Exchange

- Economics Saves Lives

  The shortage of transplantable kidneys is a serious problem: 11000 transplants / 70000+ waiting list.

  A live-donor may want to donate her kidney to a

particular patient, say to her husband, but often it is biologically incompatible.

  Economists provided a way to resolve this mismatch problem in 2004: pooling incompatible patient-donor pairs and appropriately exchange their partners.

  This kidney exchange mechanism is implemented in New England, and started to save patients’ life!

(9)

[4] School Choice Program

- Economics Improves Education

  School choice, which enables students to choose public schools beyond their residence area, is

implemented in many countries.

  Its idea has broad public support, but how to operate school choice remains actively debated.

  Based on economists’ advise, NYC and Boston redesigned their mechanisms in 2003 and 2005.

  Both practically and theoretically important issues remain to be solved: frontier of market design!

(10)

Real Life Applications

- There are Many Success Stories!

  Auction Design

  Radio spectrum

  Treasury bills

  AdWords (Google)

  Matching Mechanisms

  Medical residency

  Kidney exchange

  Public school choice

(11)

Real Life Applications

- There are Many Success Stories!

  Use “Money”

  No “Money”

(12)

Real Life Applications

- There are Many Success Stories!

  Auction design

Paul Milgrom (Stanford)

  Matching mechanisms

Alvin Roth (Harvard)

(13)

Real Life Applications

- There are Many Success Stories!

  Auction design

Paul Milgrom (Stanford)

  Matching mechanisms

Alvin Roth (Stanford)

(14)

Lessons from Practices

- An Expert Says (in Roth, 2008)…

 

Prof. Alvin Roth lists three key factors for

successful market design:

  Marketplaces need to

1. Provide thickness, that is, they need to attract a sufficient proportion of market participants.

2. Overcome congestion that thickness brings, by making it possible to consider enough alternative transactions to arrive.

3. Make it safe and sufficiently simple to participate in the market.

(15)

Traditional Econ. vs. Market Design

- What’s New for Market Design?

Traditional Economics

  Markets/institutions are exogenously given.

  Mainly focuses on ideal markets, i.e., perfectly competitive market.

  Supply & demand analysis.

  Rely on market mechanism.

⇒ Importance of laws, custom, and the role of government are often under evaluated.

Market Design

  Markets/institutions can be constructed.

  Analyze other markets and institutions than perfectly competitive market.

  Game theoretical analysis.

  Try to fix market failure.

⇒ Institutional (re-)design that makes markets well-

functioned is crucial.

(16)

MATCHING PROBLEM AND

ITS SOLUTION

Market Design in Practice (1)

(17)

What is “Matching Problem”?

- Matching over Individuals between 2 Groups

 

Each member in one

group is matched

with a member in

the other group.

 

How can we achieve

desirable matching

outcomes?

(18)

Variety of Matching Problems

- From the Simplest to the Most Complicated

 

One-to-One

  Marriage Market Men and Women

 

One-to-Many

  Labor Market Workers and Firms

  School Choice Students and Schools

 

Many-to-Many

  Business Upstream and Downstream Firms

(19)

A Simple Matching Problem

- 3 Boys and 3 Girls

 

Boys’ Preferences

 

Girls’ Preferences

 

How can/should we make partners in order to

achieve efficient or fair outcomes?

David John Mark 1st Susan Susan Helen 2nd Linda Helen Susan

3rd Helen Linda Linda

Susan Linda Helen 1st Mark Mark John 2nd David David Mark 3rd John John David

(20)

Inefficient Matching

- Suppose Make Couples in Alphabetical Order…

 

Boys’ Preferences

 

Girls’ Preferences

 

David-Helen, John-Linda => worst partners

 

Switching partners makes them better off!

(21)

Pareto Improvement is Possible

- Clearly Superior to the Original Matching

 

Boys’ Preferences

 

Girls’ Preferences

 

Make all 4 better off while the other 2 same.

 

The original matching was Pareto inefficient.

(22)

Unstable Matching

- Suppose Boys Can Choose Girls in Order…

 

Boys’ Preferences

 

Girls’ Preferences

 

The outcome is always Pareto efficient!

 

But Mark-Susan has “justified-envy”…

(23)

Pair Can “Block” the Outcome

- Mutually Preferable Pair Failed to be Matched

 

Boys’ Preferences

 

Girls’ Preferences

 

Mark-Susan can improve their situation.

 

The original outcome was unstable...

(24)

Theory of Stable Matching

- What is so Surprising?

 

Stable Matching ^： No pair (or individual)

cannot become better off if they deviate.

  Everyone is matched with the best partner available to him/her! (given other pairs)

  Unstable mechanisms tend to be abandoned.

 

Properties of Stable Matching:

  Exists for ANY one-to-one matching problems.

  Every stable matching is Pareto efficient.

  Can be found by Gale-Shapley(GS) mechanism.

(25)

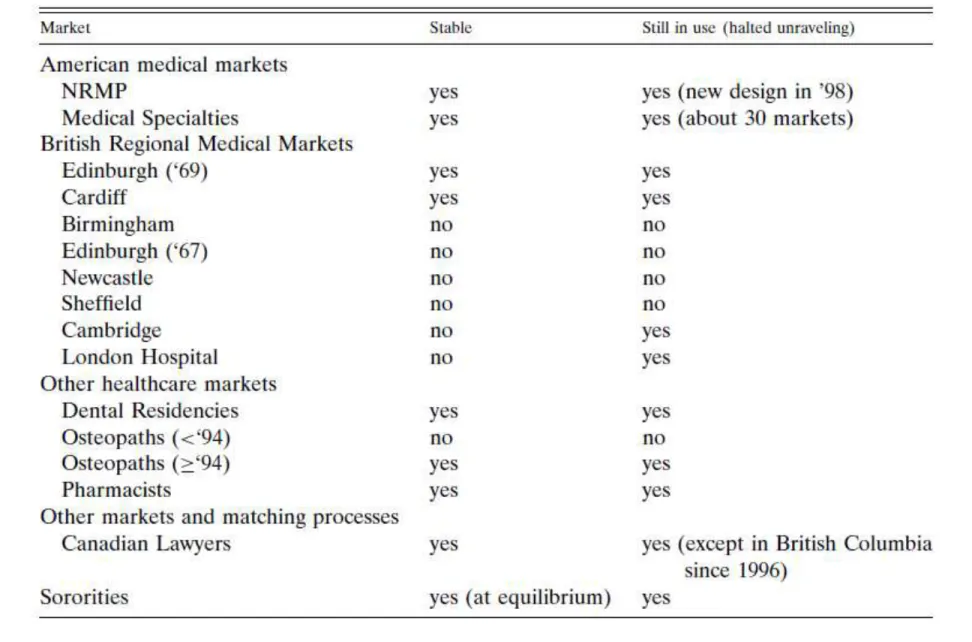
Table made by Al Roth (2002, Econometrica)

(26)

How to Find Stable Matching

- (Boys-Proposing) GS Mechanism

1.

Everyone submits preference (ranking).

2.

Clearing house operates as follows:

1. Every boy proposes to his top ranked girls.

2. Each girl keeps the favorite boy among those who propose to her and reject all other boys.

3. Boy whenever gets rejected proposes to the girl who is ranked one below (on his ranking).

4. Girl switches tentative partner whenever more favorite boy proposes to her (and reject others).

Outcome finalizes when no boy is rejected!

(27)

Remarks on GS Mechanism

- Which Side Makes Proposal Does Matter.

 

In general there are many stable matchings.

  Our example happens to have exactly one.

 

Two procedures produce different outcomes.

  Boys prop.^⇒Best stable matching for ALL boys

  Girls prop.^⇒Best stable matching for ALL girls

  This time, both derive the same (stable) outcome.

 

What is boys/girls best or optimal Stability?

  Every boy/girls is matched with the most favorite partner among the girls/boys who will become a

(28)

PRACTICE OF GS

MECHANISM

An Easy Way to Find Stable Matching

(29)

How to Use GS Mechanism

- 1

^st

Round: Boys’ Proposal

 

Boys’ Preferences

 

Girls’ Preferences

 

David and John propose to Susan.

 

Mark proposes to Helen.

(30)

How to Use GS Mechanism

- 1

^st

Round: Girls’ Rejection

 

Boys’ Preferences

 

Girls’ Preferences

 

Susan keeps David and rejects John.

 

Helen keeps Mark.

(31)

How to Use GS Mechanism

- 2

^nd

Round: Boys’ Proposal

 

Boys’ Preferences

 

Girls’ Preferences

 

John rejected in the 1

^st

round (by Susan)

proposes to Helen.

(32)

How to Use GS Mechanism

- 2

^nd

Round: Girls’ Rejection

 

Boys’ Preferences

 

Girls’ Preferences

 

Helen switches her tentative partner to John

and reject Mark.

(33)

How to Use GS Mechanism

- 3

^rd

Round: Boys’ Proposal

 

Boys’ Preferences

 

Girls’ Preferences

 

Mark rejected in the 2

^nd

round (by Helen)

proposes to Susan.

(34)

How to Use GS Mechanism

- 3

^rd

Round: Girls’ Rejection

 

Boys’ Preferences

 

Girls’ Preferences

 

Susan switches her tentative partner to Mark

and reject David.

(35)

How to Use GS Mechanism

- 4

^th

Round: Boys’ Proposal

 

Boys’ Preferences

 

Girls’ Preferences

 

David rejected by Susan proposes to Linda.

 

No further rejection => Mechanism finishes!

(36)

Properties of GS Mechanism

- Simple yet Powerful System of Matching

 

Incentive Problem

  No proposer has incentive to manipulate.

  Receiver may have such incentive…

  There exist NO incentive compatible (strategy-proof) mechanism that implements stable matching.

 

Extension of GS Mechanism

  Allowing “unacceptable” is straightforward.

  Need to break “ties” if preferences are weak. Naturally extends to one-to-many problems.

(37)

Applications of GS Mechanism

- Let’s Make Use of GS Mechanism in Real Life!

 

Actual Examples in Practice

  Medical Residency Matching (Japan, US, UK)

  Attorney Training (Canada)

  Public School Choice (NYC, Boston)

  College Admission (Hong Kong)

 

Potential Applications

  Matching over students and research laboratories.

  Assignment of new employees (to division)

(38)

INSTITUTIONAL

BACKGROUND

Choosing Public Schools

(39)

Public School Choice

- Institutional Background

  Traditionally, students are assigned to public schools according to where they live.

  Starting with school districts in the U.S. during 1980’s, several countries have adopted school choice programs.

  In Japan, it was officially introduced in 1998.

  Around 20% of the cities employ the system.

(40)

Redesign in Boston

- Huge Social Experiment

  Old method, “Boston” mechanism (BOS), has been used until 2004.

  Boston city consulted economists

(Prof. Atila Abdulkadiroğlu and others) alternative methods, and decided in 2005 to replace BOS with new one.

  Student-proposing “deferred acceptance” mechanism (DA).

  Proposed by Gale-Shapley (1962).

  The switch has received some academic support.

  Boston mechanism is still most widely used.

⇒ Which mechanism is better?

(41)

Before: Boston Mechanism (BOS)

- Intuitive and most Popular

 

Students submit ordinal rankings.

 

Schools assign seats to those who listed

them as a first choice, according to their

intrinsic priorities, e.g., walk-zone, siblings.

  If not enough seats, use a lottery to break ties.

  Enough seats, assign the remaining seats to those who listed them as a second choice, …

 

Process ends when no student is rejected.

(42)

After: Deferred Acceptance (DA)

- Similar to BOS Except for One Thing

 

Ties among students are initially broken.

  Tie-breaking is necessary to run DA mechanism.

 

Schools assign seats to those who listed

them as a first choice, according to their

intrinsic priorities, only tentatively.

  In each round, new applicants and those previously held are equally considered.

 

Process ends when no student is rejected.

(43)

Boston Mechanism vs. DA

- BOS is Manipulable While DA is Not

  Simplicity

  BOS is a very intuitive mechanism.

  DA is slightly complicated because of its tentative way to assign students.

  Incentive for manipulation

  BOS has a room for strategic manipulation.

  Risk, regret, thinking cost, …

  In DA, it is optimal for each student to report truthfully.

  No regret, leveling playing field, ...

⇒ But, is manipulation really a bad thing?

(44)

Parents Sentiments

- Interview from BPS Public Hearing

  I’m troubled that you’re

considering a system that takes away the little power that parents have to prioritize…

  … what you call this strategizing as if strategizing is a dirty word…

(Recording by the Committee, 05-11-04)

  The lack of “choice” with DA was indeed met with resistance from some parents.

  Some parents seem to prefer the old system to DA.

⇒ How about performance, i.e., efficiency or equity?

(45)

Standard View in the Literature

- DA Performs ALWAYS better than BOS

  DA achieves equitable (stable matching) and efficient assignment, while BOS does not.

  DA is always more efficient than BOS: In DA, every student is (weakly) better-off than in BOS.

  Naïve students, who always submit their ranking truthfully, suffer in BOS.

⇒ These combined with non-manipulability are the reasons why economists supported DA over BOS.

(46)

Is DA Really Better than BOS?

- Some Remaining Issues

  However, ALL the above results are derived by

simple models that impose unrealistic assumptions:

  Strict school priorities: Each school has strict priority ranking over students.

  Complete information: Students know all the relevant information such as other students’ true preferences.

  Evidences from experimental studies are also mixed.

  In reality, BOS is still most widely used.

  Public school choice in the US, Japan, Korea, Spain, college admissions in Germany and China.

(47)

MY RESEARCH

New Insights into School Choice

(48)

Two Main Papers

- with Atila Abdulkadiroglu and Yeon-koo Che

 

Resolving Conflicting Preferences in School

Choice: The Boston Mechanism Reconsidered

  American Economics Review, Vol.101: 399-410, 2011.

 

Expanding “Choice” in School Choice

  American Economic Journal: Microeconomics, Forthcoming.

(49)

Our Discovery Changing the View

- BOS Can be Better than DA

  Unlike these existing models, in reality

  schools have at best coarse priorities,

  students know neither schools’ actual (after tie-breaking) priorities nor other students’ preferences, and

  families tend to have similar preferences about schools.

  Considering such a realistic environment, we show that BOS can perform better than DA.

⇒ Dramatically changing school choice debate.

⇒ Let’s look at the next simple example.

(50)

Our New Findings

- Simple Illustration

  3 students: {1,2,3} are assigned to 3 schools: {A,B,C}, each with one seat.

  The schools are indifferent to all three students, who have the same rankings: A>B>C but with different vNM utility numbers.

  Each student maximizes expected utility numbers.

1 2 3

A 8 8 6

B 2 2 4

C 0 0 0

  Every assignment is ex post Pareto efficient, so no difference between DA and BOS, but...

(51)

Our New Findings

- DA Results in a Random Assignment

  All students submit true rankings, and they will be randomly assigned to the schools with equal

probabilities:

  Calculating expected utilities, we obtain

  EU1 = EU2 = EU3 = 10/3

  The following assignment is more efficient:

  Assign student 3 to school B, and students 1 and 2 randomly between schools A and C.

  EU’1 = EU’2 = EU’3 = 4 > 10/3

  DA is NOT ex ante Pareto efficient.

(52)

Our New Findings

- BOS Achieves ex ante Efficient Assignment

 

Students 1 and 2 rank schools truthfully

(which are their optimal strategies), and 3

strategically ranks B as her first choice.

  This unique Nash equilibrium coincides with the previous efficient assignment.

  BOS is more efficient than DA in this example.

  The result holds in more general environment:

  with more than 3 schools/students, more than one seat for each school, and incomplete information.

(53)

Why Can BOS Work better than DA?

- Strategic Manipulability Increases Efficiency

  DA elicits truthful revelation of preference rankings.

  Insensitive to underlying utility numbers.

⇒ Impossible to reveal the intensities of preferences.

  BOS induces participants to (indirectly) reveal their utility numbers through strategic manipulation.

  Potential to resolve conflicts based on their utilities.

⇒ Strategic manipulability or “strategizing” may be useful for efficient resolution of conflicting interests.

(54)

Policy Implication

- Careful Investigation is Needed ^…

 

Our results contrast with the standard

view, and cautions against a hasty rejection

of the Boston mechanism in favor of DA.

  BOS may NOT be such a bad mechanism.

 

We clearly show the tradeoff between

incentives and ex ante expected welfare.

  Informing the school choice debate of this new tradeoff is novel and of great importance.

(55)

ACY (forthcoming, AEJ)

Expanding “Choice” in School Choice

 

Based on ex ante welfare, our other project

“Expanding ‘Choice’ in School Choice”

  Propose a simple and practical mechanism: variant of the DA which allows students to influence how they are treated in ties.

  Show that our new proposal maintains truthful revelation of ordinal preferences and supports a greater scope of efficiency.

  Better way to balance the tradeoff between

incentives and ex ante efficiency: best of both!?

(56)

EXCHANGE PROBLEM AND

ITS SOLUTION

Market Design in Practice (2)

(57)

What is “Exchange Problem”?

- Exchange among Objects

 

Agents in a group try

to exchange their

items among them.

 

How can we achieve

desirable exchange

(assignment)?

(58)

A Simple Exchange Problem

- 5 Members Exchanging Their Items

 

Members’ Preferences

 

How can/should we make transfers in order

to achieve efficient or fair allocation?

A B C D E 1^st B B E C D 2^nd C E D D A 3^rd A A C E E 4^th E D B A C 5^th D C A B B

(59)

Inefficient Allocation

- Suppose Receive Item from the Next Person…

 

Members’ Preferences

 

B receives C (5

^th

) and D receives E (3

^rd

).

 

Exchanging the items makes them better off!

(60)

Pareto Improvement is Possible

- Clearly Superior to the Original Allocation

 

Members’ Preferences

 

Make B&D better off while other 3 the same.

 

The original allocation was Pareto inefficient.

(61)

Receiving Worse Item than His/Hers

- Suppose Members can Select Items in Order…

 

Members’ Preferences

 

The outcome is always Pareto efficient.

 

B receives a worse item than his endowment.

(62)

Individual Can “Block” the Outcome

- B is not Willing to Exchange his Item…

 

Members’ Preferences

 

B prefers NOT to follow his assignment (E).

 

The allocation was not individually rational.

(63)

Theory of (Strict) Core

- What is so Surprising?

 

Strict Core: No group (or individual) cannot

become better off if they jointly deviate.

  Exchange within sub-group is not profitable.

  Everyone obtains the best item available to him/ her! (given other members’ preferences)

 

Properties of (Strict) Core Allocation

  Exist exactly one for ANY exchange problem.

  Always Pareto efficient and individually rational.

  Top Trading Cycles(TTC) mechanism finds it!

(64)

PRACTICE OF TTC

MECHANISM

An Easy Way to Find Core Allocation

(65)

How to Find Core Allocation

- TTC Mechanism

1.

Everyone submits preference (ranking).

2.

Clearing house operates as follows:

1. Everyone points to his/her best ranked item.

2. If cycle is formed, its members transfer their

items accordingly and exit (from the procedure).

3. Remaining members points to their best ranked item (among remaining items)

4. Continue this process until everyone exits.

3.

Exit members receive their assignment.

(66)

How to Use TTC Mechanism

- Everyone Points to his/her Best Item

A

C B

D

E

(67)

How to Use TTC Mechanism

- Transfer Realizes within Each Cycle!

A

C B

D

E

(68)

How to Use TTC Mechanism

- A Pointing to Himself Finalizes Mechanism

 

Members’ Preferences

 

It is Pareto efficient and Individually rational!

 

No one has incentive to manipulate!!

(69)

Applications of TTC Mechanism

- Let’s Make Use of TTC Mechanism in Real Life!

 

Closely Related Examples in Practice

  Kidney exchange (US)

  Public school choice (San Francisco)

 

Potential Applications

  Office room re-allocation

  Exchange of used items (books, clothes, DVD…)

  Re-allocation of relief supplies

(70)

References

- The Papers Referred in Slides

  Abdulkadiroglu, Che and Yasuda (2011), “Resolving Conflicting Preferences in School Choice: The Boston Mechanism

Reconsidered” American Economics Review, Vol.101: 399-410.

  Abdulkadiroglu, Che and Yasuda (forthcoming), “Expanding ‘Choice’ in School Choice” American Economic Journal: Microeconomics.

  Gale and Shapley (1962), “College Admissions and the Stability of Marriage” American Mathematical Monthly, Vol.69: 9-15.

  Roth (2002), “The Economist as Engineer: Game Theory,

Experimentation, and Computation as Tools for Design Economics” Econometrica, Vol.70: 1341-1378.

  Roth (2008), “What Have We Learned from Market Design?” Economic Journal, Vol.118: 285-310.

  Shapley and Scarf (1974), “On Cores and Indivisibility” Journal of

(71)

SLIDES NOT IN USE

(72)

Trend of School Choice in Japan

- Number of Adapting Cities is Increasing!

(73)

Why does Game Theory Matter?

- Choose Schools Wisely!

  Seats are limited!

  It is impossible to assign each student to his/her best school.

  Need to (strategically) think which schools to apply / avoid.

  Mechanism matters, because

  Students’ assignments and incentives will vary.

  General idea of school choice gaining political support, but the exact method is debated.