講義ノート3:多期間モデル(直接の解法)
稲葉 大
初稿 2008 年 10 月 27 日
updated 2010 年 5 月 26 日
目 次
I 有限期間 4
I.1 有限期間の中央計画者問題 . . . 4
I.2 共役変数と投資財価格 . . . 6
II 無限期間 7 II.1 無限期間の中央計画者問題 . . . 7
II.2 定常状態 (steady state) . . . 7
II.3 ダイナミクス . . . 9
(i) 位相図(phase diagram) . . . 9
(ii) 動学的な経路の導出 . . . 11
II.4 ダイナミクスの具体的な分析 . . . 13
(i) 具体例 . . . 13
II.5 数値計算による解法:狙い撃ち法 (shooting algorithm) . . . 14
(i) アルゴリズム . . . 14
(ii) Matlab Code . . . 15
II.6 線形近似 . . . 20
(i) 数学の準備 . . . 20
(ii) 線形近似の例 . . . 22
III 競争均衡 25 III.1 経済環境 . . . 25
(i) 家計の効用 . . . 26
(ii) 生産技術 . . . 26
III.2 家計と企業の行動 . . . 26
(i) 家計の効用最大化問題(Consumer Problem (CP)) . . . 26
III.3 企業の利潤最大化問題 (Firm Problem (FP)) . . . 28
III.4 競争均衡 (Competitive Equilibrium) . . . 29
IV 補論1:最大値原理 31 IV.1 最大値原理の十分性 . . . 32 IV.2 連続時間の最大値原理 . . . 32
第2回の講義ノートでは二期間のモデルについて,動学的一般均衡モデルを取り扱った.二 期間から多期間(有限期間)への拡張は容易であり,本質は全く変わらない.数式による見た 目もまったく変わらないため,理解も用意であると思われる.そのため,多期間になることで 難しいと感じる場合には,二期間のモデルをしっかりと復習しておくこと.期間が無限にある 無限期間の場合は,若干取り扱いに注意が必要だが,やはり本質は同じである.
以下では,まず中央計画者問題について有限期間期間および無限期間のケースについて考察する が,分権経済の場合は家計の最適化問題について同じ手法を利用可能である.二期間モデルで見 たとおり,いまのモデルにおいて中央計画者問題と分権経済とでは,達成される配分(allocation) は同じである.そこでまずは簡単な中央計画者問題から考察することにする.繰り返しだが,中 央計画者問題とは、資源制約と生産関数の下で、計画当局が経済の全ての主体に消費計画を提 示して、それを実行させることができる問題のことである.問題の解(均衡経路)を求める方法 はいくつかあるが,この講義では代表的な二つを紹介する.ひとつはラグランジュ乗数法を用 いた巨大な非線形計画問題を解くといった「直接の解法」.もう一つは,動的計画法(dynamic programming) を用いた方法である.ここで紹介するベーシックな最適成長モデルにおいては, どちらの方法を用いても良い.しかし実際にはどちらの方法を用いるかは,モデルの性質によっ て異なり,動的計画法しか利用できないケース(例えばサーチモデル,離散選択のモデルなど) のための準備として動的計画法を学んでおく必要がある1.
まずは直接の解法を用いて,中央計画者問題の解を求めよう.そのまま定常状態とダイナミク スの分析を行う.その後,動的計画法へと戻ることにする.
1
講義では時間があれば触れるが,recursive competitive equilibrium との関係でも動的計画法を理解しておく ことに意味がある.
I 有限期間
I.1 有限期間の中央計画者問題
中央計画者が代表的家計と同じ効用を持っているとする(あるいは代表的家計の効用を最大 にするように行動している)ときの,中央計画者問題は次のようになる.
(SP) max
ct,it,kt+1
T
∑
t=0
βtu(ct) subject to
ct+ it = f (kt)
kt+1− kt= it− δkt, t= 0, · · · , T, k0 = k0
kT+1 ≥ 0.
ここで0 < β < 1 は,割引因子 (discount factor) である.効用関数 u(·) と生産関数 f(·) は, u(0) = 0, u′(·) > 0, u′′(·) < 0, u′(0) = ∞, u′(∞) = 0
f(0) = 0, f′(·) > 0, f′′(·) < 0, f′(0) = ∞, f′(∞) = 0
という性質をもつと仮定する.ctは一人当たり消費,itは一人当たり投資,t 期初(あるいは t− 1 期末)の ktは一人当たり資本ストックである.kT+1はT 期末に残した一人当たり資本ス トックである.
中央計画者が経済の配分を決定する問題なので,ここには市場は存在しない.よって当然な がら,市場価格というものも,ここでは登場しない.中央計画者は,代表的家計の効用を最大 にするように,その経済の生産技術に基づいて生産を行い,生産物を配分していくという問題 を解いているのである.
(SP) からあらかじめ itを消去しておくと,
(SP) max
ct,kt+1
T
∑
t=0
βtu(ct) subject to
kt+1− kt= f (kt) − ct− δkt t= 0, · · · , T, (遷移式 (transition equation)) k0 = k0
kT+1 ≥ 0.
直接にこの問題を解く方法は,巨大な非線形制約問題として,ラグランジュ乗数法を用いて 解く方法である.ラグランジアンは次のように定義される.
L =
T
∑βtu(ct) +
T
∑βtλt
{f(kt) − ct− kt+1+ (1 − δ)kt
}+ λ−1(k0− k0) + µkT+1. (1)
ここで,経済の状態を表すktを状態変数(state variable),経済で選択可能な変数 ctを制御変
数(control variable) と呼ぶことがある2.βtλtはラグランジュ乗数であり,共役変数(costate variable) と呼ばれる3.それぞれについて一階条件を求めてみると,
∂L
∂ct
= βtu′(ct) − βtλt= 0 (for t = 0, 1, 2, · · · , T )
∂L
∂kt+1 = −β
tλ
t+ βt+1λt+1
{
f′(kt+1) + (1 − δ)}= 0 (for t = 0, 1, 2, · · · , T − 1)
∂L
∂kT+1 = −β Tλ
T + µ = 0
∂L
∂λt
= βt{f(kt) − ct− kt+1+ (1 − δ)kt
}
= 0 (for t = 0, 1, 2, · · · , T )
∂L
∂λ−1 = k0− k0 = 0. と,クーン・タッカー条件
kT+1 ≥ 0, µ ≥ 0, µkT+1 = 0. 以上を整理すると,
u′(ct) = λt (for t = 0, 1, 2, · · · , T ) (2) λt = βλt+1{f′(kt+1) + (1 − δ)} (for t = 0, 1, 2, · · · , T − 1) (3)
βTλT = µ (4)
kt+1− kt= f (kt) − ct− δkt (for t = 0, 1, 2, · · · , T ) (5)
k0 = k0 (初期条件) (6)
kT+1 ≥ 0, µ ≥ 0, µkT+1 = 0 (クーン・タッカー条件). (7)
(2),(3) より,Euler 方程式
u′(ct) = βu′(ct+1){f′(kt+1) + (1 − δ)} (8) を導くことができる.これはちょうど,二期間のモデルでt=0 のときに相当していることがわ かる.
クーン・タッカー条件(7) 式より,
βTλTkT+1 = 0 (9)
という横断性条件を導出することができる.βTλT >0 であるから,横断性条件より kT+1 = 0.
であることがわかる.つまり経済が終了するT 期末には,資本は残らず使い果たされている.
2
どの変数が状態変数や制御変数になるかは,モデルによって異なる.
3
計算の利便性およびλtを定常にする目的から,ラグランジュ乗数にβtをつけてβtλtとしている.ラグラン ジュ乗数を単にλtとしても結果は同じものになるが,λtが異なっていることには注意が必要である.
I.2 共役変数と投資財価格
いまktを資本と考えると,遷移式kt+1− kt= f (kt) − ct− δktは,投資を表している.λtはこ の遷移式のラグランジュ乗数であるから,投資が限界的に1 単位増加したときに,どれだけ効 用が増加するかを表す値である.つまり効用で測った投資財の「潜在価格(shadow price)」と 考えることができる(潜在価格 (shadow price) とは,仮に市場が存在して,価格が付けられたと すれば,成立する価格のことである.ここでは消費者が資本ストックを保有し,自分で持って いる財で投資を行うため,投資財の市場が無い.そのため,潜在価格として投資財価格があら わされる.).
投資財価格のダイナミクスは(3) 式より, λt = βλt+1
{
f′(kt+1) + (1 − δ)} (for t = 0, 1, 2, · · · , T − 1) (10)
と表されている.投資財の価格は将来によって規定された前向きの変数(forward-looking variable) となっている.
横断面条件は次のように書きなおすことができる. βTλTkT+1 = 0
⇐⇒βTu′(cT)kT+1 = 0 ((2) より.)
この式は,「投資財価格λT × 残す資本kT+1の割引現在価値」であり,最後の期末に資本ストッ クkT+1を残すことの割引現在価値はゼロであることをあらわしている.
問題が二期間のときには0 期,1 期の関係だけであったものが,多期間のときには t 期と t+1 期 の関係として同じ形になっていることを確認したい.(この問題と最大値原理(maximum principle) との関係は,補論を参照.)
II 無限期間
II.1 無限期間の中央計画者問題
無限期間の問題も基本的には同じである. (SP) max
ct,kt+1
∞
∑
t=0
βtu(ct)
s.t. kt+1− kt = f (kt) − ct− δkt
k0 = k0.
効用関数,生産関数に関する仮定は今までと同じとする. L =
∞
∑
t=0
βtu(ct) +
∞
∑
t=0
βtλt
{f(kt) − ct− kt+1+ (1 − δ)kt
}+ λ−1(k0− k0) (11)
kt+1,ct,λ について一階条件を求めてみると,
∂L
∂ct
= βtu′(ct) − βtλt= 0
∂L
∂kt+1 = −β
tλ
t+ βt+1λt+1{f′(kt+1) + (1 − δ)}= 0
∂L
∂λt
= βt{f(kt) − ct− kt+1+ (1 − δ)kt
}= 0
∂L
∂λ−1
= k0− k0 = 0.
となり,整理すると,
u′(ct) = βu′(ct+1){f′(kt+1) + (1 − δ)} (12) kt+1− kt= f (kt) − ct− δkt (13)
k0 = k0 (14)
と横断性条件は有限期間から,T → ∞ とした,
t→∞lim β
tu′
(ct)kt+1= 0. (15)
II.2 定常状態 (steady state)
最適なパス(optimal path) は,以下の必要条件
u′(ct) = βu′(ct+1){f′(kt+1) + (1 − δ)} (16) kt+1− kt= f (kt) − ct− δkt (17) k0 = k0
と横断面条件を満たす経路である.(16) 式は,一人当たり消費 ctの動きを表す差分方程式であ る.一方(17) 式は,一人当たり資本ストック ktの動きを表す差分方程式である.この二つの式 から連立差分方程式という形でシステムが表されている.差分方程式を解くにあたって,まず は定常状態の分析から行ってみよう.定常状態とは,一人当たり資本,一人当たり消費が一定 であるようなところである.つまり,定常状態の値をc
∗
,k
∗
,λ
∗
とおくとき, u′(c∗) = βu′(c∗){f′(k∗) + (1 − δ)}
k∗− k∗ = f (k∗) − c∗− δk∗ を満たす.少し操作すれば,
1 = β{f′(k∗) + (1 − δ)} (18) c∗+ δk∗ = f (k∗) (19) (18) は,消費についての差分方程式において,ct= ct+1 = c∗とおいたものである.つまり消費が一 定である所をあらわしている.一方,(19) は資本についての差分方程式において,kt = kt+1 = k∗ とおいたものである.つまり資本が一定である所をあらわしている.両方を同時に満たす定常 状態は,これら二本の交点であり,連立方程式の解となる.いま生産関数f(k) の関数形は,具 体的には特定化していないため,以下ではグラフを用いてみることにする4.縦軸に消費c,横 軸に資本ストックk をおくとき,(18),(19) は以下のグラフとして描くことができる.
c
k∗ k
ct+1 = ct
kt+1 = kt
E
kg
c∗
図 1: Steady state
(18) 式は,グラフにおいて垂直な直線で描かれる.この直線上では ct+1 = ct,つまり消費が
一定である.(19) 式は,グラフにおいて山形の曲線で描かれる.この直線上では kt+1 = kt,つ 4
生産関数を例えばコブ=ダグラス型などに特定化した場合には,解析的に解くことができる.後に例として紹
まり資本が一定である.よって,c と k ともに一定となる線の交点E 点が定常状態となる. 修正された黄金律(modified golden rule)
定 常 状 態 の 消 費 を 最 大 に す る と い う 意 味 で の 黄 金 律 水 準 の 資 本 ス トックkg は ,(19) 式より f′(kg) = δ である.これ以上資本が大きくなりすぎれば,定常状態において消費はむしろ小 さくなってしまい,動学的に非効率(dynamic inefficiency) であると言われる.一方この黄金律 水準よりも左側であるところは,動学的に効率的(dynamic efficiency) であるという.この問題 では,消費者の異時点間の効用最大化問題を考慮した場合に,定常状態はk
∗
がであり(18) 式 より,f
′(k∗) = 1β − 1 + δ を満たす.f′(·) は減少関数であるため,k∗ < kgであることがわかり, 定常状態において動学的に効率であることがわかる.
II.3 ダイナミクス
(i) 位相図(phase diagram)
繰り返しだが,最適な経路(optimal path) は,以下の必要条件
u′(ct) = βu′(ct+1){f′(kt+1) + (1 − δ)} (20) kt+1− kt= f (kt) − ct− δkt (21) k0 = k0
と横断面条件を満たす経路である.以下ではモデルのダイナミクスまたは動学的な経路を考察 していくことにする.定常状態を基準として考える.
(ct+1 = ct線)
「ct+1 = ct線」について考察をしてみる.いま資本がk
∗
のにいるとすると
ct+1
ct = 1,つまり
1 = β{f′(k) + (1 − δ)}を満たしている.「ct+1 = ct線」の左側はk だけを減らした領域である. f′(k) は減少関数であるから,
1 < β{f′(k) + (1 − δ)} とわかる,よって,左側の領域では,(20) 式より,
u′(ct) u′(ct+1) = β
{
f′(kt+1) + (1 − δ)}>1
⇐⇒u′(ct) > u′(ct+1)
⇐⇒ct+1 > ct
である.最後の不等式は,効用関数の仮定よりu
′(· · · ) が減少関数であることからわかる.以上 の考察から,「ct+1 = ct線」の左側では
ct+1 > ct
⇐⇒ct+1c
t
>1
であり,消費は増加する傾向があることがわかる.つまり図2 に矢印で示したように「ct+1 = ct
線」の左側では消費は上昇する方向に増えていく.まったく同じ考察から,「ct+1= ct線」の右 側では,消費は減少する.
経済学的な理由は以下の通りである,資本ストックが小さい領域では,生産関数の過程より資 本から得られるリターンであるf
′(k) + (1 − δ) が大きい.つまりいま消費をすることをやめて投 資に回し,将来消費をすることのリターンが大きいということである.よって,消費はct+1 > ct という関係を満たすことになる.逆に資本ストックが大きい領域では,生産関数の過程より資 本から得られるリターンであるf
′(k) + (1 − δ) が小さい.つまりいま消費をすることをやめて投 資に回し,将来消費をすることのリターンが小さいということである.よって,消費はct+1 < ct という関係を満たすことになる.
c
k∗ k
ct+1 = ct
kg
図 2: ct+1 = ct線
(kt+1 = kt線)
「kt+1 = kt線」について考察をしてみる.「kt+1 = kt線」上にいるとするとkt+1 = kt,つまり c+ δk = f (k) という関係を満たしている.この曲線の上側はここから k を一定として,c だけ を減らした領域である.
c+ δk > f (k) とわかる,よって,上側の領域では,(21) 式は,
kt+1− kt = f (kt) − ct− δkt <0
⇐⇒kt+1 < kt
であり,資本は減少する傾向があることがわかる.つまり3 図に矢印で示したように「kt+1 = kt
線」の上側では資本は減少する.まったく同じ考察から,「kt+1= kt線」の下側では,逆に資本 は増加する.
c
k kt+1 = kt
kg
図 3: kt+1 = kt線
(ii) 動学的な経路の導出
図2 と図 3 を重ねて表示することで,k と c の位相図 (phase diagram) を作成することができ る.この図を作成することで,資本と消費がある水準のときに,どういった動学的経路をたどっ ていくかを,領域によって分析できる.たとえば領域I にいるとき,領域 I にいる場合,資本も 消費も時間とともに増えていく.領域II の場合には,資本は増え,消費は減っていく.領域 III では,資本も消費も減っていく.領域IV では,消費は増え,資本は減っていく.
c
k∗ k
ct+1= ct
kt+1 = kt
E
kg
c∗
IV
I
II III
図 4: 位相図I
ここで,資本ストックの初期値がk0(以下の図の点線の位置)であったときの,最適な経路 を見つけてみよう.最適な経路は繰り返しだが,(20),(21) 式と横断面条件を満たす経路であ る.すなわち,定常状態に到達する経路である5.図5 では,c
∗
0という消費の初期値からスター トすることで,最適な経路に到達できる.
c
k∗ k
ct+1 = ct
kt+1 = kt
E
kg
k0 cl0 c∗0 cu0
O E′
図 5: 位相図 II
それでは,c
∗
0以外の経路を選んではいけないのだろうか?例えば,cu0を選んだ場合.領域I に いる間は,消費も資本も増え続けるが,kt+1 = ktの線と交わり,領域IV に入ってしまったあと は,消費は資本を食いつぶすことで増え続け,資本は減っていく.いずれ資本を食べつくせば, 生産も消費もできず,原点に飛んでしまう.つまり資本も所得も消費もゼロになってしまう.終 わりがゼロになってしまうことが分かっていると,終わりの限界効用がlimc→0u
′(c) = ∞ であ るため,今消費をしないで投資に回し,将来投資をしたほうが望ましくなる.とすれば,cu0 と いう消費水準は高すぎるため,投資に回す分を増やし,消費は抑えられてくる.
逆にcl0を選んだ場合.領域I にいる間は,消費も資本も増え続けるが,ct+1 = ctの線と交わ
り,領域II に入ってしまったあとは,消費を減らして,資本を貯え続けていく.最終的に一切 消費をせず,資本だけを蓄積し続け,E
′
点へと収束してしまう.消費額はゼロに収束するため, 最後の限界効用はlimc→0u
′(c) = ∞ である.一方資本ストックは,E′の水準で一定である.こ のとき横断性条件を考えてみよう.E
′
はkgよりも明らかに動学的に非効率な領域にある.つま りf
′(k) < δ となっている.このとき,(20) 式より, u′(ct+1)
u′(ct) =
1
β{f′(kt+1) + (1 − δ)} > 1 β となっている.つまりu
′(ct) が1β より早く増加することがわかる.よって,横断性条件の左辺
t→∞lim β
tu′
(ct)kt+1 5
を考えると,u
′(ct) が β1 より早く変化するため,limt→∞βtu
′(ct) = ∞ となる.一方 limt→∞kt = kE′と有限の値であるため,
t→∞lim β
tu′(c
t)kt+1 = ∞
となり横断性条件を満たさないことになる.よって,cl0という消費の初期値は低すぎるため,消 費を増やすことになる.
結果として,合理的な経済主体のもとではc
∗
0へと消費額は決まることになる.図5 の cl0から始 まる経路を,
あんてん
鞍点経路(saddle path) と呼ぶ.これは図を 3 次元的に理解し,矢印の進む方向は 低いところと考えれば,馬の鞍の形に似ていることからついた名前である.
II.4 ダイナミクスの具体的な分析
生産関数や効用関数を具体的な関数に特定化すれば,連立差分方程式を解くことで解を得る ことができる.しかし,一般に非線形の差分方程式は解析的に解くことができない.そのため, ダイナミクスの分析は,先の分析のようにグラフを用いて一般的なことしか言えないことが多 い.その場合,通常の二つの方法でダイナミクスを分析する.一つは,コンピューターを用い た数値計算を行うことで,非線形のダイナミクスを求める分析である.ここでは狙い撃ち法に ついて紹介する.もう一つは,定常状態のまわり(近傍)だけで,関数を線形に近似してその ダイナミクスを分析である.ここではまず,線形近似の問題を考えることにする.
(i) 具体例
効用関数と生産関数に具体的な関数形を決めて例を紹介する.最適な経路は,
u′(ct) = βu′(ct+1){f′(kt+1) + (1 − δ)} (22) kt+1− kt= f (kt) − ct− δkt (23) と初期条件と横断面条件を満たす経路である.以下効用関数と生産関数に具体的な関数形を仮 定して考察してくことにする.効用関数は,
u(c) = c
1−σ
1 − σ とする6.一方,生産関数は,
f(k) = Akα とする7.よって,均衡条件は次のようになる
c−tσ = βc−t+1σ{αAkt+1α−1+ (1 − δ)} (24) kt+1− kt= Aktα− ct− δkt (25)
6
このような効用関数を相対的危険回避度一定(constant relative risk aversion, CRRA) 型効用関数という.さ らにσ → 1 のとき,u(c) = log c となる性質をもつ.
7
コブ=ダグラス型生産関数Y = AKαL1−αを一人当たりに直すと,y= Akαとかくことができる.
II.5 数値計算による解法:狙い撃ち法 (shooting algorithm)
コンピューターを用いた数値計算を行うことで,非線形ダイナミクスを求める分析方法は多 数あるが,ここでは最も簡単な狙い撃ち法を紹介する.この方法は,通常モデルに不確実性が 無い問題について解を得るために用いられる.最適なパスは,初期値k0から初めて,(24) 式と, (25) 式を満たし,定常状態に到達するような経路である.このような経路は,位相図で分析し たとおり,最適なc0を選ぶことで達成される.そこで,いろいろな初期値c0を試して,差分方 程式をシミュレーションし,定常状態に到達するような調度良いc0を見つける.これを狙い撃 ち法(shooting algorithm) という8.
準備として定常状態を求めておく.(24) 式と (25) 式からなるシステムの定常状態を求める. 1 = β{αAk∗α−1+ (1 − δ)} (26)
c∗+ δk∗ = Ak∗α (27)
より,
k∗ = {1
β − (1 − δ)
αA
}α−11
(28)
c∗ = Ak∗α− δk∗ (29)
と計算できる.
(i) アルゴリズム
位相図による最適パスからわかるように,c0よりも少しでも大きい消費の初期値を選んでし まうと,発散してしまう.逆に,c0よりも少しでも小さい消費の初期値を選んでしまうと,E
′
へと飛んで行ってしまう.先に分析したように,これらは両方ともに,経済学的に最適な経路 から排除される.ちょうど定常状態に向かう鞍点経路に乗るc0を見つけるために,次のような 操作を行う.
8
狙い撃ち法は,最近では日本経済の失われた10年を考察したHayashi and Prescott (2002),Kobayashi and Inaba (2006) などで使われている.
狙い撃ち法(shooting algorithm) 1. 定常状態を求める.
2. 消費の初期値の候補の下限 clと上限cuを決める. 3. c0 = cl+c2 u にする.
4. 所与の初期値 k0と,今選んだc0に基づいて,(24),(25) 式を t = 1, 2, 3, · · · , 逐次に 解いていく.
5. 十分に大きいの t を計算したとき
(a) もし kt> k∗なら,cl = c0と置き換えて,step 3 に戻る. (b) もし kt< k∗なら,cu = c0と置き換えて,step 3 に戻る.
(c) もし k∗− kt < ϵ なら,次に進む.
6. 得られた c0を最適な初期値として,ct, ktを最適経路とする.
(ii) Matlab Code
shooting のための Matlab コードを以下に示す.Matlab の使い方については,上坂 (2000) が 一番分かりやすい.頭に%がついている文は,コメントであり,計算には影響しないプログラム のメモとして書いている.
% determinisitic model
% shooting algorithm for simple optimal growth model
% u(c)=c^(1-sigma)/(1-sigma)
% y=Ak^alpha
% 2008/11/22
% Masaru Inaba at YNU
% 以下の 6 行は,Matlab を正常に機能させるのに必要なだけで,
% shooting と関係ない. clear all;
close all;
set(0,’defaultAxesFontSize’,12);
set(0,’defaultAxesFontName’,’century’); set(0,’defaultTextFontSize’,12);
set(0,’defaultTextFontName’,’century’);
%================
% parameters
%================
alpha=0.3; % capital share beta=0.98; % discount factor delta=0.08; % depreciation rate sigma=2; % relative risk aversion T=100; % maximum time for simulation
A=1*ones(T,1); % productivity (which is constant for all t)
%====================
% steady state values
%====================
A_ss=1; %productivity in ss
% ss capital, equation (28)
k_ss=((1/beta-(1-delta))/(alpha*A_ss))^(1/(alpha-1));
% ss consumption, equation(29) c_ss=A_ss*k_ss^alpha-delta*k_ss;
%=====================
% initialization
%=====================
k_0=0.1; % initial value of capital
% lower bound of initial value of consumption c_under=0.000000001;
% upper bound of initial value of consumption c_upper=A_ss*k_0^alpha-delta*k_0;
% initialize path vector of capital as zero vector k=zeros(T,1);
% initialize path vector of consumption as zero vector c=zeros(T,1);
%======================
% shooting algorithm
%======================
while (abs(k(T)-k_ss)>1e-8)&(abs(c(T)-c_ss)>1e-8); % start while iteration
% initialize path vector of capital as zero vector k=zeros(T,1);
% initialize path vector of consumption as zero vector c=zeros(T,1);
c0temp=(c_upper+c_under)/2; % initialization of c_0
%---
% at t=1
%---
t=1; % note that Matlab can not apply the number of index 0 k(t)=k_0;
c(t)=c0temp;
% equation (25)
k(t+1)=A(t)*k(t)^alpha-c(t)-delta*k(t)+k(t);
% equation (24)
c(t+1)=(c(t)^(-sigma)...
/(beta*(alpha*A(t+1)*k(t+1)^(alpha-1)+(1-delta))))^(-1/sigma);
%---
% for t=2 to T-1
%--- for t=2:T-1;
% equation (25)
k(t+1)=A(t)*k(t)^alpha-c(t)-delta*k(t)+k(t);
% flag 1 means k(t) is too big
if k(t+1)>2*k_ss; flag=1; break; end;
% flag 2 means k(t) is too small if k(t+1)<0; flag=2; break; end;
% equation (24)
c(t+1)=(c(t)^(-sigma)...
/(beta*(alpha*A(t+1)*k(t+1)^(alpha-1)+(1-delta))))^(-1/sigma); end
%---
% diagnosis
%--- if t==T-1;
if k(T)>k_ss;
flag=1 % flag 1 means k(T) is too big else
flag=2 % flag 2 means k(T) is too small end
end
if flag==1;
c_under=c0temp elseif flag==2;
c_upper=c0temp end
clear flag
end % end of while iteration loop
disp(’We found!’); % the end of shooting algorithm.
%=============================
% code for the graph plottings
%=============================
% data for equation (27);
k_Eprime=(delta/A_ss)^(1/(alpha-1)); % position of E’
% data for plotting equation (27)
k_27=linspace(0,k_Eprime,1000); % vector of k in (27) c_27=A_ss.*k_27.^alpha-delta.*k_27; % vector of c in (27)
% data for plotting equation (26) c_26=linspace(0,2*c_ss,100); k_26=k_ss*ones(100,1);
% data for initial value plotting k_initial=k_0*ones(100);
c_kinitial=linspace(0,(A_ss*k_0^alpha-delta*k_0),100);
% data for optimal initial consumption coptini=c(1,1)*ones(100);
koptini=linspace(0,k_0,100); figure(1);
% plot equation(27)
plot(k_27,c_27);axis([0,1.05*k_Eprime,0,1.3*c_ss]);hold on;
% plot equation(26) plot(k_26,c_26);
plot(k,c,’m’,’LineWidth’,2);% plot for optimal path plot(k_initial,c_kinitial,’:’); % plot for k_0 plot(koptini,coptini,’:’); % plot for optimal c_0 text(k_0,-0.15,’k_{0}’);
text(-0.8,c(1,1),’c_0’); text(k_ss,-0.15,’k_{ss}’); text(k_ss,1.03*c_ss,’E’);
text(k_Eprime,-0.15,’E^\prime’); hold off;
figure(2);
% plot equation(27)
plot(k_27,c_27);axis([0,1.3*k_ss,0,1.3*c_ss]);hold on;
% plot equation(26) plot(k_26,c_26);
plot(k,c,’m’,’LineWidth’,2);% plot for optimal path plot(k_initial,c_kinitial,’:’); % plot for k_0 plot(koptini,coptini,’:’); % plot for optimal c_0 text(k_0,-0.15,’k_{0}’);
text(-0.2,c(1,1),’c_0’); text(k_ss,-0.15,’k_{ss}’); text(k_ss,1.03*c_ss,’E’);
text(k_Eprime,-0.15,’E^\prime’); hold off;
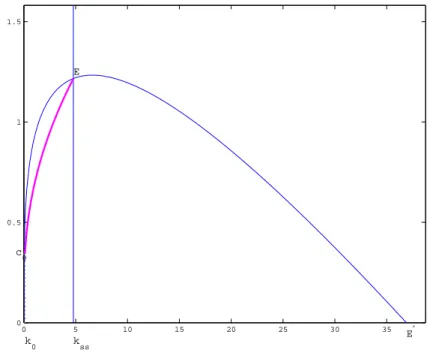
=========================================================== Matlab コードはここまで.以下に,このコードで作成したグラフを表示すると,
0 5 10 15 20 25 30 35
0 0.5 1 1.5
k0 c0
kss E
E′
図 6: Phase diagram for shooting 1
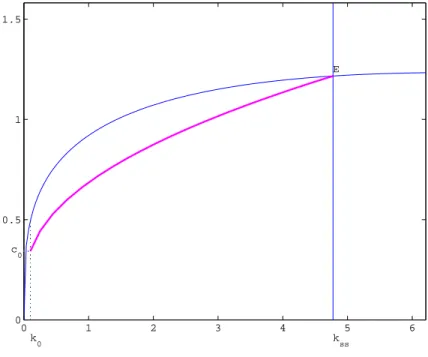
左側を拡大すると,
0 1 2 3 4 5 6 0
0.5 1 1.5
k0 c
0
kss E
図 7: Phase diagram for shooting 2
II.6 線形近似
(i) 数学の準備
非線形な関数を線形(1次関数)に近似することを線形近似という.線形近似はテイラー展 開の特殊なケースといえる.テイラー展開とは,微分可能な関数f(x) を,ある点 a のまわりで 次のように展開できることをいう9.
f(x) = f (a) + f′(a)(x − a) + 1 2!f
′′(a)(x − a)2+ 1 3!f
′′′(x − a)2+ · · ·
⇐⇒ =
∞
∑
n=0
1 n!f
n(a)(x − a)n
この式では,1次だけでなくそれ以上に無限先まで展開している.これを1次まで近似したも のが,
f(x) ≈ f(a) + f′(a)(x − a) (30) テイラー展開による一次近似(線形近似)である.この近似は,次のグラフを見ると分かりや すい.関数f(x) を x = a というまわりで線形に表現したものである.
2変数の関数の場合には,
f(x, y) = f (a, b) + fx(a, b)(x − a) + fy(a, b)(y − b) + 1
2!{fxx(a, b)(x − a)2+ 2fxy(x − a)(y − b) + fyy(a, b)(y − b)2} + · · ·
9 (1996) を参照
a f(x)
x f(x)
f(a) + f′(a)(x − a)
図 8: 線形近似のイメージ
ただし,fx =
∂f(x,y)
∂x これも1次までの線形近似では,
f(x, y) ≈ f(a, b) + fx(a, b)(x − a) + fy(a, b)(y − b) (31) と書くことができる.
また,経済学ではしばしば対数線形近似(log-linearization) が行われる.これは,ある変数 x を次のように変換して,ln x について ln a のまわりで線形近似を行うものである10.
x= eln x とする11と,f(x) = f(eln x
)
である.これをln x について線形近似をすると,(30) 式より, f(x) ≈ f(eln a) + ∂f(e
ln x)
∂ln x (ln x − ln a)
⇐⇒f(x) ≈ f(a) + af′(a)(ln x − ln a)
2行目の第2項の微分については脚注を参照12.これを対数線形近似と呼ぶ.この式にはある
10ln は自然対数であり ln x = logex.
11e はネイピア数である.dedxx = exという特徴を持っている.
12
2行目の第2項の微分については,
x= elnx に注意して,f(x) = f(e
lnx)
をln x で微分すれば良い.
∂f(elnx)
∂ln x
= ∂f(x)
∂x
∂elnx
∂ln x
= f′(x)x
特徴がある.実は対数の差分は,変化率の近似になっている.つまり ln(x) − ln(a) = ln(xa)= ln( x − aa + 1
)
≈ x− aa (32)
x−a
a は,x が a から何パーセント離れているかを表しているため,a からのパーセントかい離
(persentage deviation)と呼ばれる.a を,モデルの定常状態だと解釈すれば,定常状態から何 パーセント離れているかでモデルを記述することができる.以下では,線形近似を用いるが,後 に対数線形近似も利用することがあるので,きちんと理解しておくこと.
(ii) 線形近似の例
以下の記述は,Dirk Kruger の講義ノートを一部参照している.(24) 式と (25) 式からなるシ ステムを定常状態のまわりで線形近似することで,定常状態のまわりでの振る舞いを見ること ができる.定常状態のまわりで近似をするため,横断面条件は満たされていることが仮定され ていると考えて良い.まず定常状態は,(26) 式と (27) 式より,
k∗ = {1
β − (1 − δ) αA
}α−11
c∗ = Ak∗α− δk∗ と計算できる.
まずは,(25) 式を線形近似してみよう.各項線形近似すると, kt+1 ≈ k
∗ + 1 × (kt+1− k∗) kt ≈ k
∗ + 1 × (kt− k∗) Aktα ≈ Ak∗α+ αAk∗α−1(kt− k
∗) ct ≈ c
∗+ 1 × (ct− c∗) δkt ≈ δk
∗+ δ × (kt− k∗)
よって,(25) 式は
kt+1− kt = Akαt − ct− δkt
⇐⇒(k∗+ kt+1− k∗) − (k∗+ kt− k∗) = Ak∗α+ αAk∗α−1(kt− k∗)
− (c∗+ ct− c∗) − {δk∗+ δ(kt− k∗)}
⇐⇒(kt+1− k∗) − (kt− k∗) = αAk∗α−1(kt− k∗) − (ct− c∗) − δ(kt− k∗) ((27) 式を利用)
ここでxˆt≡ xt− x
∗
と定義すると13,
ˆkt+1− ˆkt= αAk∗α−1kˆt− ˆct− δˆkt
⇐⇒ˆkt+1 =(αAk∗α−1+ 1 − δ)ˆkt− ˆct
⇐⇒ˆkt+1 = β1ˆkt− ˆct ((26) 式を利用)
⇐⇒ˆkt+1 = θ1kˆt− ˆct (33) ここで,θ1 = 1
β >0 と置いている.
一方,(24) を線形近似する.各項ごとに線形近似すると,第一項目は, c−tσ ≈ c∗−σ− σc∗−σ−1(ct− c
∗) 第二項目は,
βc−t+1σ{αAkα−1t+1 + (1 − δ)}≈ βc∗−σ{αAk∗α−1+ (1 − δ)}
− σβc∗−σ−1{αAk∗α−1+ (1 − δ)}(ct+1− c∗) + βc∗−σ{α(α − 1)Ak∗α−2}(kt+1− k∗) よって,(24) 式は,定常状態の式も利用して,
−σc∗−σ−1(ct− c∗) = −σc∗−σ−1(ct+1− c∗) + βc∗−σ{α(α − 1)Ak∗α−2}(kt+1− k∗) と書くことができる.xˆt≡ xt− x
∗
と定義すると,
− σc∗−1ˆct = −σc∗−1cˆt+1+ β{α(α − 1)Ak∗α−2}ˆkt+1
⇔ ˆct= ˆct+1+ θ2ˆkt+1
⇔ ˆct+1− ˆct= −θ2kˆt+1 (34)
それぞれの係数をθ2 =
β
{
α(α−1)Ak∗α−2
}
−σc∗−1 >0 で置き換えている. 線形近似した式(33),(34) をまとめると,
kˆt+1 = θ1ˆkt− ˆct
ˆ
ct+1− ˆct= −θ2kˆt+1
これらの式からctを消去して,
kˆt+2− (1 + θ1+ θ2)ˆkt+1+ θ1ˆkt= 0
⇔ ˆkt+2− θ3kˆt+1+ θ1ˆkt= 0
という二階の差分方程式が得られる.ここでθ3 = 1 + θ1+ θ2と置く.この差分方程式の特性方 程式を分析することで,ダイナミクスの特性を分析できる.この二階差分方程式の特性方程式
13ˆx は定常状態からのかい離(定常状態からどれだけ離れているか)を表している.
は次のような二次式で表されるµ2− θ3µ+ θ1 = 0 の解は,µ1,2 =
θ3±√θ32−4θ1
2 である.解のひと
つはµ1 >1,もう一つ µ2 <1 は負である14.この事実は,システムが「鞍点」を持っているこ とを示している.この差分方程式の解の候補は,
kt− k
∗ = b1µt1+ b2µt2
である.第一項はµ1 >1 であるため,発散していってしまう.一方,第二項は µ2 <1 であるた め0 へと収束していく.定常状態に収束していく経路が求めたい解であるから,選ぶべき解は, 定常状態kt = k
∗
へと収束してく第二項のみということになる.よってb1 = 0.
==
14
ここでいくつかの得られる情報を用いて,解の値を分析する. まず,
θ3> θ1+ 1 であるため,判別式
θ32− 4θ1>(θ1+ 1)2− 4θ1= θ12− 2θ1+ 1 = (θ1− 1)2>0
である.判別式が正であるということは,二次式の解は二つとも実数であることがわかる.さらに µ1× µ2=θ
2 3
4 ±
θ32− 4θ1
4 = θ1= 1 β >0
である.θ3>0 であるため,µ1=
θ3+√θ32−4θ1
2 >0 である.よって µ2>0 であり,二つの解は正の実数であるこ とがわかる.
さらに大きい方の解は, µ1=θ3+√θ
2 3− 4θ1 2 >
θ3+√(θ1+ 1)2− 4θ1
2 =
θ3+ θ1− 1
2 > 2θ1
2 = θ1= 1 β
⇒µ1>β1
µ1× µ2= β1 より,
µ2<1 µ >1,もう一つ µ <1 は負である
c
k∗ k
ct+1 = ct
kt+1 = kt
E
kg
c∗
図 9: Linearized dynamics
III 競争均衡
これまでの問題は,中央計画問題であった.以下では,家計と企業がそれぞれに効用および 利潤の最大化を行っている競争的な経済での市場均衡を分析していくことにする.以下の記述 は,二期間のモデルと全く同じといってよい.当然,厚生経済学の基本定理も成立する.
III.1 経済環境
• 経済の期間は無限期間であるとする.
• 家計(消費者 consumer)は代表的家計 (one representative household) として表されると する.
• 家計は,資本と労働を所有している.家計は企業を所有しており,企業の利潤は配当とし て家計に支払われる.(ただし競争的企業を仮定しているため配当はゼロである.以下で は配当を明記しない.)
• 家計は,各期得られる所得を,消費と貯蓄に振り分ける.貯蓄を原資として,投資を行い, 資本ストックを増やす.
• 代表的な企業は,資本と労働を生産要素として,家計から雇い生産を行う.家計も企業も 競争的に行動すると仮定する.つまり,両者とも,価格決定に影響力を持たず,市場の価 格を所与としてプライス・テイカーとして行動する.
• この経済の財 (goods) は,消費ができ,また投資として資本蓄積にも使えるとする.
(i) 家計の効用
家計は現在から将来効用の現在価値を最大にするように各期の消費を決定する.家計の効用 関数は,次のようにあらわされる.
∞
∑
t=0
βtu(ct). (35)
u(·) は効用関数であり,
u(0) = 0, u′(·) > 0, u′′(·) < 0, u′(0) = ∞, u′(∞) = 0 という性質をもつと仮定する.
(ii) 生産技術
企業の生産技術は,以前と同様である.ここでは代表的家計は,一人であり,労働供給も1 であることから,一人当たりの生産関数を
yt = f (kt) (36)
と書くことにする.この関数f(kt) の形は,次のようになる. M P K = f′(k) > 0 f′′(k) < 0
k→0limf
′(k) = ∞
k→∞lim f
′(k) = 0
III.2 家計と企業の行動
(i) 家計の効用最大化問題 (Consumer Problem (CP))
代表的家計は,予算の制約のもとで,効用を最大にするように消費と投資を決定する. (CP) max
ct,it,at+1
∞
∑
t=0
βtu(ct).
s.t. ct+ it= wt+ rtat (37) at+1− at= it− δat (38) a0 = a0
(37) 式は,t 期における家計の予算制約である.a は家計が保有している資本ストックであり, 初期の保有量a0は与えられている.w は実質賃金(real wage) である.この家計の労働力は 1 単 位と仮定しているため,労働所得はw∗ 1 となる.資本の r は実質レンタル料 (real rental price) である.家計が持る資本を企業にレンタルするときの価格である15.
15 w と r は家計にとって所与である.