問8.2 解答 運動方程式

機械力学１講義 第８回

2006.12.11

ラプラス変換

実f(t) → 複素F(s)

∫^{∞ −}

= 0 ( ) )

(s f t e dt

F ^st

∫ −⁺∞^∞

= ⁱ

i

stds e s i F

t

f ^σ

π σ ^{( )}

2 ) 1 (

積分の収束条件

o σ

t

( )

虚

実

^と

^の変数域

ラプラス逆変換

ラプラス変換による強制振動の解析

（前回の復習）

t

：時間，

：複素数

複素

→ 実f(t)

微分方程式を機械的に解く方法

ラプラス変換表

at cosh a sinh at 1

at cos a sinat 1

t (t) u

(t) δ

2

2 a

s s

−

2 2

1 a s −

2

2 a

s s +

2 2

1 a s +

2

1 s

s 1

1 (t)

f F(s)

at a e

bt sinh

1 (s−b¹)² −a²

(s b)² a² b s

−

−

at −

e^bt cosh

at a e

bt sin

1 (s−b¹)² +a²

at tcos

a at t sin 2

at e^bt cos

( ^{2 2})²

2 2

a s

a s

+

−

(^{s2 +sa2})²

(^s−sb−)^2b+a2 (t)

f F(s)

∫^{∞ −}

= 0 ( ) )

(s f t e dt

F ^st = ∫ −⁺∞^i∞

i

stds e s i F

t

f ^σ

π σ ^{( )}

2 ) 1 (

機械振動では 無数の関数が 現れるが，

これだけあれ ば，ほとんどの 場合が解ける．

表があれば，

無限積分，複

素積分不要．

ラプラス変換の公式

) (t f

e ^at F (s − a)

dt

df sF (s) − f (0)

2 2

dt f

d s ² F (s) − sf (0) − f ′(0)

) 0 ( )

0 (

) 0 ( )

(

) 1 ( 2

1

−

−

−

−

′ −

−

−

n n

n n

f f

s

f s

s F s

n L

n

dt f d

指数関数の積 微分

２階微分

n

階微分

) (t

f F (s)

ラプラス変換表と公式を組合わせれば，ほとんどの問題が解ける．

x

k c

m f ( )t

6.4

ラプラス変換による任意外力の応答計算

x = & =

① ②

⑥

⑦

ラプラス変換

( )^s

X x →

③

④

⑤

⑧

(t) f kx x

c x

m &&+ & + =

( )^s

F f →

( ) ( )^{0 0}

2X sx x

s

x&&→ − − &

( )⁰

x sX

x& → −

{^{s X sx v} } ^{c{sX x } kX F}

m ² − _o − _o + − _o + =

（未知）

（表の値を代入）

初期値を代入

k cs ms

v m k cs ms

c x ms

k cs ms

X F

+ + +

+ + + +

+

= ₂ + _{0 2 0 2}

o o

o cx mv

msx F

kX csX

X

ms² + + = + + + X

で整理

ラプラス逆変換

⑧





+ + +





+ + + +





+

= ⁻ + ^{− −}

k cs ms

L m k v

cs ms

c L ms

k x cs ms

L F

x ¹ _{2 0} ¹ _{2 0} ¹ ₂

⑩

k cs ms

v m k cs ms

c x ms

k cs ms

X F

+ + +

+ + + +

+

= ₂ + _{0 2 0 2}

⑨

m

n = k /

ω ω_d =ω_n ¹−ζ ² 簡単な分数に分解

= x

0 0

0 =v =

x の解（特解） f = v₀ = 0 の解（基本解）

0 = 0

= x

f の解（基本解）

t e

v ^t _d

d

n ω

ω ^{ζω sin} 1

0 −



 



 +

− t t

e

x _d

d d n

nt ω

ω ω ζω

ζω cos sin

 0



 





+ +

−

k cs ms

L F

2

1 +

+

減衰振動系のステップ応答（前回の復習）

部分分数に分解

(t) Fu kx

x c x

m &&+ & + = ^{x(0) = x}&^{(0) = 0}

[ ]u s L = 1

2 2

2 1 1

n ns

s s m F

ω ζω +

⋅ +

⋅

=













+ +

− +

 =













+ +

− +

⋅

= 2 2 2 2 2

2 1 2

2 1 2

1

n n

n n

n n

n s s

s s

k F s

s s s

m X F

ω ζω

ζω ω

ζω ζω ω

c

m x

k

) (t Fu

u

0 1

t 2

1

2 k

mω_n = m

k

n =

ω ^c_mk

2 ζ =

F s kX

csX X

ms₂ + + = ⋅ 1

s F k cs X ms

+

= ₂ +1

u(0)

は何でもよい 両辺ラプラス変換

( ) ( )^{x s X}

sx X

s

x&&→ ² − 0 − & 0 = ^{2 x}& ^{→ sX − x}( )^{0 = sX}

分母：sの2次式，分子：1次式

( )^{12 2}

1 sin

a b

at s a e

L ^bt

+

= −





[ ^cos ] _{( )2 2}

a b

s

b at s

e L ^bt

+

−

= −

( ) ( )

( )

( ) ( )

( ) ( ) 









 ⋅

+

− + +

+

− +

=













+

− + +

+

− +

=













+ +

− +

=













+

− +

− +

=

n d

n d

n n

d n

n d

n n

d n

n

n n

n

n

s s

s s

k F

s s

s s

k F

s s s

k F

s

s s

k X F

ω ζω ζω

ω ζω

ζω

ω ζω

ζω ω

ζω ζω

ω ζω

ζω

ω ζω

ζω

ζω

2 2

2 2

2 2

2 2

2 2

2 2

2

1 1

1 1 2 1 2











 +

+ +

− +

= s s s

s k

X F

n n

n 1

2 2

2 ζω ω 2

ζω

1 ζ 2

ω

ω_d = _n −

a →ωd

b → −ζωn

[ ]u s L = 1



 



 − −

= u t e⁻ t e⁻ t

k t F

x ^nt _d

d n t d

n ω

ζω ω

ω ^ζω

ζω 1 sin

cos )

( )

(













− −

−

= e⁻ t e⁻ t

k F

t d d n

nt ω

ζ

ω ζ ^ζω

ζω sin

1 cos

1 2

a →ωd

b → −ζωn

( ) ( ) 









 ⋅

+

− + +

+

− +

= _n

d n

d n

n

s s

s s

k

X F ζω

ω ζω

ω ζω

ζω

2 2

2 2

1 1

( )^{12 2}

1 sin

a b

at s a e

L ^bt

+

= −





[ ^cos ] _{( )2 2}

a b

s

b at s

e L ^bt

+

−

= −

[ ]u s L = 1

不連続関数が あっても問題なし

（











 −

−

− +

= ⁻ cos( )

1 1 1

2

2 ω φ

ζ

ζ _ζω

t k e

F

d nt

1 2

tan ζ

φ ζ

= −

1 ζ 2

ω

ω_d = _n −

x

k F

o t

ステップ応答













−

± + e^{− nt} k

F _ζω

ζ ζ

2 2

1 1 1

0 )

0 ( )

0

( = x =

x &











 −

−

− +

= ⁻ cos( )

1 1 1

2

2 ω φ

ζ

ζ _ζω

t k e

x F ^nt _d

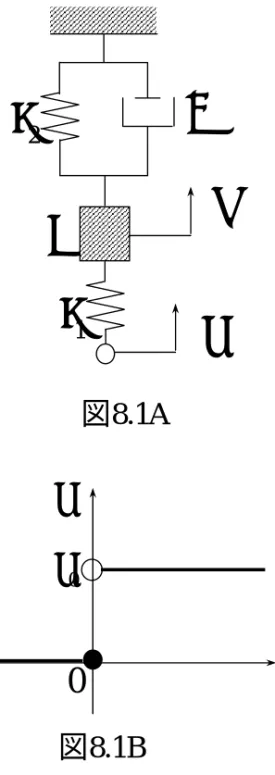
図

k2

k1

m

c

x y

図

x

0 x0

t

xがx=x

u(t)とステップ状に移動．

x

は定数，uは単位ステップ関数．

m k k_{1 2}

1

= +

ω ₂ ¹

1

<

= ω

ζ m

c

◎問8.2 前問をラプラス変換により解 け．また，t→∞におけるyは，x=x

に対 するmの静的釣合位置hに一致するこ とを確かめよ．

0 2 1

1 x

k k

h k

= +

( ) ( )^{0 = y 0 = 0}

y &

kr r

c kx

x c x

m &&+ & + = & +

0 )

0 ( )

0

( = x =

x &

) ( )

(t X s

x → [ ]

s Au A

L s

R t

r( ) → ( ) = =

{^{sR r} } ^kR

c kX

csX X

ms² + + = − (0) +

6.3.4 ステップ関数の初期値が問題になる場合

ステップ関数uの初期値は１か0か

) (

)

(r x k r x c

x

m &&= &− & + −

1 )

( lim )

0

( = 0 =

+

→ u t

u t

0 )

( lim )

0 (

0 =

= →− u t

u t

0 )

0

( =

u

1 u, w

u

w

0 t

t

k

m

c

( )^t

x

( )^{t Au(t)}

r =

[ ]

L ^st 1

) ( )

( =

∫

[ ]

L ^st 1

) ( )

( =

∫

1 u v

0 t

ラプラス変換が同じで，初期値

の関数がある．

t>0

では

．よって，

u

と

のラプラス変換 は同じ

1

1

s k A Au

A c kX

csX X

ms² + + = ( − _o)+

) 1

( 2

2 ^{2 2}

2 n n n nA uo

s X A

sX X

s + ζω +ω =ω + ζω −











 + −

+

= + 2 (1 )

2

2

2 2 n n o

n n

s u s

s

X A ω ζω

ω ζω













+ +

+ − +

+

− +

= ₂

2 2

2 ( )

) 2 1 ( )

( 1

d n

o n

d n

n

s

u s

s A s

X ζω ω

ζω ω

ζω ζω

{^{sR r} } ^kR

c kX

csX X

ms² + + = − (0) + s

s A

R( ) = ^{r(0) = Au(0) = Au}_o( )^{= 0}

m

n = k ω

u

の初期値を

とおく

両辺

で割る

X

で整理

部分分数分解

mk c 2

ζ =

























−

− −

−

= ⁻ u t

t e

t u A

x ^t _d ^o ω_d

ζ ω ζ

ζω sin

1

) 2 1 cos (

)

( 2

u → 1s

2 2 1

1

) (

cos

1

d t d

s t s

e ζω ω

ω ζω

ζω

+ +

→ +

−

2 1)2

( sin

1

d d d

t

t s

e ζω ω

ω ω

ζω

+

→ +

−













+ +

+ − +

+

− +

= ₂

2 2

2 ( )

) 2 1 ( )

( 1

d n

o n

d n

n

s

u s

s A s

X ζω ω

ζω ω

ζω ζω

ラプラス変換公式

ラプラス逆変換

m u u Ac

m A c u

A

x _{n o} ^o

n o

n

) 1

) ( 1

2 ( 2 )

1 ( 2

) 0

(+ = − = ω − = −

ζω ω

&

0 /

) 0

( = Ac m ≠ x&

























−

− −

−

= ⁻ u t

t e

t u A

x ^nt _d ^o ω_d

ζ ω ζ

ζω sin

1

) 2 1 cos (

)

( 2

u_o=0

のとき（ｒ＝

u_o=1

のとき（ｒ＝













−

− + +

−

= ⁻ u t

t u

e A

x _n ^nt _{o d} ^o ω_d

ζ ω ζ

ζ

ω ^ζω sin

1

) 1 (

2 cos 1

) 1

(

2 2

2

&

0 )

0 (+ = x

初期条件は

?

のはず

t>0

t>0

（

からの極限）

1 1 0

1 1 0

m n

c ζ ω

= 2

1

u(0)=0 v(0)=1

0 t

























−

− −

−

= ⁻ u t

t e

t u A

x ^nt _d ^o ω_d

ζ ω ζ

ζω sin

1

) 2 1 cos (

)

( 2

0 )

0 ( = x&

r=Au，u_o=0 A

m Ac

x&(0) = /

r=Av

，

質点は無限大の加速度で移動 速度が不連続に変化

t=0でrが無限大の速度

ダンパーは無限大の力を発生

m

c

( )^t

x

( )^{t Au(t)}

r = 1

t>0

t=0

で

は不連続

も不連続

0 ) 0 ( )

0

( = x =

x &

撃力

kr r

c kx

x c x

m &&+ & + = & +

) ( )

(t kAu t

cA +

= δ

o t

) ( t u

) ( t

∞ δ

1

δ dt =

Au du

r =

ラプラス変換後に微分公式使用 微分後にラプラス変換

kA s cA

kX csX

X

ms 1

2 + + = ⋅1+

[ ]^{(t) =1}

L δ [ ]

t s u

L 1

)

( =

u(0)=0

と置いたものと同じ．

u(0)

を使わない解法

微分公式で初期値発生

) 0 ( )

( )

(t sR s r

r& → −

t=0近傍の力積（力×時間）

∫

∫

= ^ε

ε ε

ε cr kr dt cAu kAu dt

I ( & ) ( & )

t=0の運動量変化＝力積＝

m cA m

I =

初速度に一致 t=0の速度変化

[ ] [ ]

[

]

= ^ε_−ε ^{0 ε}₀ (ε ) ( ε)⁰

=1

初期値に関する考察

c kx

x c x

m &&+ & + = & +

) ( )

(t kAu t

cA +

= δ

o t

) ( t u

) ( t

∞ δ

1

ε

−

ε

δ関数（∞）の影響は初速 度に現れる．

関数（有限）

は初期値に影響しない．

以下の方程式は等価

) ( )

(t cA t kAu

kx x

c x

m &&+ & + = + δ

0 )

0

( =

x ^x_&^{(0) = 0} t ≥ 0

0 )

0 ( =

x m

x&(0) = cA t > 0

x x&

(t) cAδ

o t

∞

kA kx

x c x

m &&+ & + =

①

②

撃力

k

m

c

( )^t

x

( )^{t A}

r =

δ関数は 初期値に 置き換えら れる．

撃力が過ぎた後

特解 基本解 一般解

運動方程式 初期条件

デルタ関数を除けば，時間領域解法も可能

0 )

0 ( =

x ^x_&^{(0) = cA m}

kA kx

x c x

m &&+ & + =

(^{C t D t})

e

x = ^−ζωnt cosω_d + sinω_d A

x =

(^{C t D t})

e A

x ^{= + −ζωnt cos}ω_d ^{+ sin}ω_d 0

) 0

( = A+C = x

m cA D

C

x&(0) = −ζω_n +ω_d =

初期条件に代入

1 ζ 2

ζ −

= A D

A C = −













+ −

− +

= ⁻ A t

t A

e A

x ^nt _d ω_d

ζ ω ζ

ζω sin

1

cos 2

未定係数の決定 解

(t>0)

δ cA

δ cA

kAu u

cA kx

x c x

m &&+ & + = & +

0 )

0 ( )

0

( = x =

x & k

m

c

( )^t

x

( )^{t Au(t)}

r =

ステップ応答のまとめ

kA s s u

s cA kX

csX X

ms 1

) 0 1 (

2 +







 ⋅ −

= +

+

①直接ラプラス変換，

を使用．

) ( )

(t kAu t cA

kx x

c x

m _&&+ _& + = δ +

kA s cA

kX csX

X

ms 1

2 + + = ⋅1+

②

を微分した後にラプラス変換

du

を使用