再直交化付きブロック逆反復法による
固有ベクトルの並列計算
石上 裕之
1,2,a)木村 欣司
1,b)中村 佳正
1,c) 概要:本論文では,並列計算機向けの実対称3重対角行列の固有ベクトル計算アルゴリズムとして再直交 化付きブロック逆反復法を提案する.逆反復法による固有ベクトル計算における再直交化計算では,従来, ベクトル演算や行列-ベクトル乗算といった並列化粒度の比較的小さい演算を用いたアルゴリズムが中心であった.また,逆反復法の改良アルゴリズムとしてMultiple Relatively Robust Representation(MRRR)法 が提案されているが,計算対象の行列の固有値分布によっては,固有ベクトルの直交性が失われてしまう ことが知られている.本論文で提案する再直交化付きブロック逆反復法は,行列乗算中心の実装が可能な 同時逆反復法を基にした,大粒度の並列性を持つアルゴリズムである.更に,提案アルゴリズムにより, MRRR法で計算が破綻してしまうような固有ベクトルを,行列乗算を用いて再計算することも可能になる. 共有メモリマルチコアプロセッサシステム上での数値実験において,提案アルゴリズムにより,逆反復法 や同時逆反復法と同等の計算精度が達成され,より高速な並列計算が実現されることを示す. キーワード:固有ベクトル計算,逆反復法,同時逆反復法,再直交化,マルチコア計算
Reorthogonalized Block Inverse Iteration Algorithm
for Parallel Computation of Eigenvectors
Hiroyuki Ishigami
1,2,a)Kinji Kimura
1,b)Yoshimasa Nakamura
1,c)Abstract: A reorthogonalized block inverse iteration algorithm is proposed for parallel computation of eigenvectors
for symmetric tridiagonal matrices. The reorthogonalization process in the inverse iteration algorithm for computing eigenvectors is mainly based on the vector operations or the matrix-vector multiplications, whose parallel granularity is relatively small. Multiple Relatively Robust Representations (MRRR) algorithm is also proposed for computing eigenvectors, but the MRRR algorithm occasionally loses orthogonality. The proposed algorithm is derived from the simultaneous inverse iteration algorithm, which enables us to implement matrix-matrix multiplications and then has large parallel granularity. The proposed algorithm helps us to modify eigenvectors of the matrix, which the MRRR algorithm fails to compute with good orthogonality. Numerical experiments on shared memory multi-core processors show that the proposed algorithm achieves high accuracy as and is faster than both the inverse iteration algorithm and the simultaneous inverse iteration algorithm.
Keywords: Eigenvector computation, Inverse iteration, Simultaneous inverse iteration, Reorhtogonalization,
Multi-core processing
1 京都大学大学院情報学研究科
Graduate School of Informatics, Kyoto University, Kyoto 606–8501, Japan
2 日本学術振興会特別研究員(DC)
Research Fellow of Japan Society for the Promotion of Science (DC)
a) hishigami@amp.i.kyoto-u.ac.jp b) kkimur@amp.i.kyoto-u.ac.jp c) ynaka@i.kyoto-u.ac.jp
1.
はじめに
n× n実対称密行列Aに対する標準固有対問題 Avi= λivi, i = 1, . . . , n を考える.ここで,λi ∈ RはAの固有値(λ1< · · · < λn),vi ∈ Rnはλiに対応する固有ベクトルである.実対称密行 列の固有対計算は多くの科学技術計算で現れる基本的な線 形計算である.振動解析における固有モード計算や蛋白質 などの構造解析で用いられる分子軌道計算では,全固有対 ではなく,一部の固有対のみが必要とされる.以下では, このような問題を部分固有対問題と呼ぶ.近年,これらの シミュレーションは大規模かつ複雑なものになり,部分固 有対問題の対象となる行列も大規模化している.このよう な大規模な問題を高速に解くため,近年では並列計算機の 利用が一般的となっており,並列計算機向きの部分固有対 計算法の需要が高まっている. 一般に,実対称行列の固有対計算は,前処理として直交 変換によって3重対角化した後,3重対角行列の固有対を 計算する.元の行列の固有ベクトルは,3重対角化の逆変 換を施すことによって得られる.3重対角化や逆変換の手 法については,高い並列化効率を達成する様々なアルゴリ ズムが提案されている[4], [11], [14], [21]. 実対称3重対角行列の一部の固有対のみを計算する手法 としては,二分法と逆反復法を組み合わせる方法(BI法)
[16]やMRRR (Multiple Relatively Robust Representations)
法[7], [9]がある.どちらの手法も,数値計算ライブラリ
LAPACK (Linear Algebra PACKage [2])に採用されており,
STEVX,STEGRとしてルーチンが提供されている. BI法では,二分法で求めたい固有値を計算し,得られた 固有値を基に,対応する固有ベクトルを逆反復法によって 計算する.二分法による固有値計算は,大粒度の並列計算 が可能である一方,従来の逆反復法はマルチコアCPU上 においても並列化しにくいことが知られている.これは, クラスター固有値に対応する固有ベクトル計算において, ベクトル演算中心の再直交化計算を行っており,並列化に よる高速化のボトルネックとなっているからである.この 問題に対して,行列-ベクトル乗算を用いた再直交化アルゴ リズムを適用することで,固有ベクトルの並列計算を高速 化ができることが示されている[13], [15].しかし,キャッ シュヒット率や並列化効率の点で,行列-ベクトル乗算は行 列乗算に及ばない.行列乗算を用いた逆反復アルゴリズム があれば,更に高い並列化効率を達成できると期待される. 一方,MRRR法もまた逆反復計算に基づくアルゴリズム であるが,逆反復法とは異なり再直交化計算を回避するた め,逆反復法に比べて計算量を抑えることができる.また, [18]では,並列計算機向けのMRRR法の実装法も提案され ており,高い並列化効率を達成することが示されている. しかし,Glued-Wilkinson行列[6], [8]のような非常に密集 した固有値を持つ行列に対しては,MRRR法の計算時間は 増大してしまうことが報告されている[6].また,行列の 固有値分布によっては,MRRR法による固有ベクトル計算 では直交性を失ってしまう例があることも知られている. 実際,下位ルーチンとして3重対角行列向けのMRRR法 を実装したLAPACKのSYEVRルーチンに対して,特定の 行列に対するバグ報告がなされており,未だ解決がなされ ていない[1].このように,計算量の意味で有利なMRRR 法でも対応できない行列があることから,二分法と逆反復 法の組み合わせによる固有対計算法の並列実装についても 研究を進める必要がある.また,MRRR法による固有ベク トル計算が破綻してしまうケースについて,逆反復法で再 計算することで固有ベクトルの直交性を改善する方法も考 えられる.勿論その際にも,行列乗算での実装が可能なア ルゴリズムが求められる. 本研究では,行列乗算を用いた並列化効率の高い固有ベ クトル計算法として,再直交化つきブロック逆反復法を提 案する.このアルゴリズムは,行列乗算を中心とした実装 が可能な同時逆反復法を基にした,大粒度の並列性を持つ アルゴリズムである.提案アルゴリズムを導入することに より,MRRR法で計算が破綻してしまうような固有ベクト ルを,行列乗算中心のアルゴリズムで再計算することも可 能になる.本論文の構成は以下の通りである.2章では, 固有ベクトル計算法の従来アルゴリズムとして逆反復法お よび同時逆反復法について述べる.3章では,提案アルゴ リズムである再直交化付きブロック逆反復法について述べ る.4章では,本研究の性能評価で用いる実装コードにつ いて述べる.実装コードはマルチコアプロセッサ向けのも ので,スレッド並列化の方法についても述べる.5章では, 共有メモリマルチコアプロセッサシステム上での性能評価 の結果を示す.6章はまとめである.
2.
従来アルゴリズム
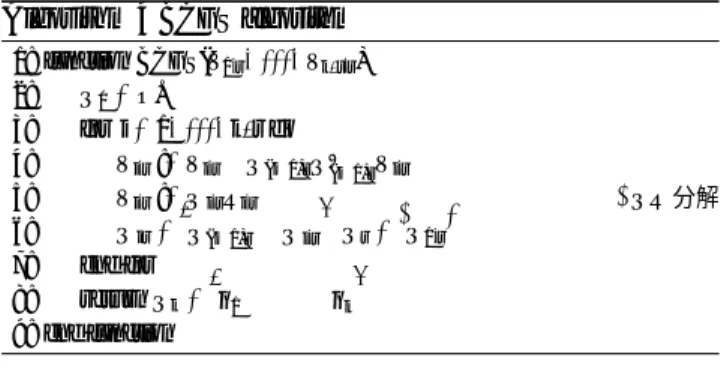
本章では,従来アルゴリズムとして,逆反復法および同 時逆反復法について述べる.また,本研究では,倍精度演 算による数値計算について論じる. 2.1 逆反復法 n次元実対称3重対角行列Tの固有ベクトル計算につい て考える.Tの固有値をλj∈ R(λ1< λ2< · · · < λn)とし, qj ∈ Rnをλjに対応するT の固有ベクトルとする.逆反 復法による固有ベクトル計算では,まず,λjの近似固有値 ˜ λj,一様乱数により生成したn次元ベクトルv(0)j を用意す る.このとき,以下の連立方程式を反復して解くことによ りベクトルv(i)j が得られる. ( T− ˜λjI ) v(i)j = v(i−1)j , i = 1, 2, . . . . (1) ここで,Iはn次元単位行列である.i→ ∞において,v(i)j は固有ベクトルqjに収束する.m(≤ n)本の固有ベクト ルを逆反復法で計算する場合,計算量はO(mn)となる.実 装上では,反復計算の過程におけるオーバーフローの回避 のため,反復毎にv(i)j を正規化しなければならない. T の固有値が互いに十分離れている場合,上記の逆反復Algorithm 1逆反復法(Inv)
1: function Inv(T, ˜λ1, . . . , ˜λmc) 2: Q0:= 0
3: for j= 1, . . . , mcdo
4: i := 0
5: Generate v(0)j from random numbers
6: T− ˜λjI := PjLjUj ▷部分ピボット選択付きLU分解 7: repeat 8: i := i + 1 9: Solve PjLjUjv(i)j = v (i−1) j ▷連立方程式の求解 10: v(i)j ⊥ Qj−1となるようv(i)j を再直交化 ただし,Qj−1:= [ q1 · · · qj−1 ] 11: untilconverge 12: Normalize qj:= v(i)j/∥v (i) j∥ 13: end for 14: return Qmc:= [ q1 · · · qmc ] 15: end function 計算により直交性を保ったまま固有ベクトルを得ること ができる.しかし,固有値どうしが近接している場合に は,逆反復計算のみでは直交性が失われてしまうことが知 られており,この場合それらの固有ベクトルについて再 直交化計算を行う手法が提案されている[12].以下では, 近接している固有値をクラスターと呼ぶ.隣り合う固有 値どうしが同じクラスターに属するかどうかについては, Peters-Wilkinsonの判定基準[17]が広く使われている.こ の判定基準では,|˜λj−1− ˜λj| ≤ 10−3∥T∥(2≤ j ≤ m)を満たす とき,λj−1とλjは同じクラスターに属するとみなす.ここ で,行列ノルム∥T∥としてはどのノルムをとっても良いと されているが,実装上は,1-ノルムを用いる.以下の議論に おいても,クラスターの判定基準として,Peters-Wilkinson の判定基準を用いるものとする. Algorithm 1はクラスター固有値に対して再直交化計算を 施す逆反復法の擬似コードを表している.Algorithm 1は LAPACKに提供されている実対称3重対角行列向け逆反復 法の倍精度実装コードDSTEINに基づいている.DSTEIN では,式(1)を数値安定に解くため,T− ˜λjIを部分ピボッ ト選択付きLU分解し,得られたPj,Lj,Ujを用いて連立 方程式の求解を行うという方法を採用している.ここで, LU分解の結果は,ある固有ベクトルの計算過程において は不変であることから,6行目に一度だけ行い,結果をメ モリに保存しておくことで計算量を削減できる.連立方程 式の求解は,反復ループ内部に当たる9行目において行う. また,10行目は再直交化プロセスに当たり,DSTEINで は修正グラム・シュミット(MGS)法が採用されている. mc個のクラスター固有値に対応する固有ベクトルを再直 交化する場合,計算量はO(m2 cn ) となる.このため,クラ スター固有値の数が多くなれば,固有ベクトル計算にかか る計算時間の大半が再直交化に費やされることになる. Peters-Wilkinsonの判定基準を用いた場合,数千以上のサ イズの行列の固有値の大半が一つの固有値クラスターに属 してしまうことが知られている[7].このため,逆反復法 による固有値計算を行う場合には,固有値クラスターに着 目した並列化をするのではなく,反復内の各演算における 並列化をしなくてはならない.MGS法は,AXPY演算や 内積計算といった演算内での並列化には不向きな演算のみ で実装されているため,MGS法を再直交化プロセスに採 用しているDSTEINを並列計算で上手く高速化することは 難しい. 逆反復法を並列計算において高速化するため,再直交化 プロセスにおいて行列-ベクトル乗算中心のアルゴリズム を用いる方法が提案されている[13], [15].一つは,行列 -ベクトル乗算が利用可能な古典グラム・シュミット(CGS) 法を用いる方法である.CGS法はMGS法と代数的に等価 であるため,計算量は同じである.行列-ベクトル乗算で実 装可能であるため,MGS法よりも演算性能を向上させる ことができる一方,CGS法による再直交化計算では直交性 が悪化する可能性があることが知られている.これを回避 するため,CGS法を2回繰り返すCGS2法[10]が提案さ れているが,計算量はMGS法の2倍必要となる.もう一 つは,Householder変換による再直交化計算にcompact WY 表現[19]を導入する方法である[22].この方法について, [13]では計算量を削減した実装が提案されているが,最小 でもMGS法の1.5倍の計算量が必要となる.このように, 行列-ベクトル乗算を利用できる再直交化アルゴリズムは, いずれもMGS法よりも多くの計算量を必要とする.この ため,計算機環境や使用するライブラリによっては,MGS 法を用いた逆反復法よりも高速な並列計算ができるとは限 らない. 2.2 同時逆反復法 同時逆反復法[5]は,クラスター固有値に対応する固有 ベクトルの計算に行列乗算を利用できるアルゴリズムであ る.[5]では,行列T の重複固有値σに対する定式化が示 されている.本論文では,行列Tのあるクラスター固有値 λ1, . . . , λmcに対して,それぞれの近似値λ˜1, . . . , ˜λmc を用 いて定式化したアルゴリズムを同時逆反復法とする. 同時逆反復法では,まず,n× mc行列V(0)を乱数により 生成し,QR分解V(0):= Q(0)R(0)により正規直交行列Q(0) を計算する.Q(0)を初期行列とした以下の2式で表される 計算を反復することで,λ1, . . . , λmcに対応する固有ベクト ルq1, . . . , qmcを計算することができる. ( T− ˜λkI ) v(i−1)k = q(i−1)k , k = 1, . . . , mc, (2)
V(i) := Q(i)R(i). (3)
ここで,v(i)k とq(i)k はそれぞれV(i)とQ(i)の第k列ベクトル
である.同時逆反復法は,式(2)において,式(1)で表され
る連立方程式の求解をmc本同時に行い,再直交化計算の
Algorithm 2同時逆反復法(SInv) 1: function SInv(T, ˜λ1, . . . , ˜λmc) 2: Generate V(0):=[v(0) 1 · · · v (0) mc ] 3: V(0):= Q(0)R(0) ▷ QR分解 4: for k= 1, . . . , mcdo 5: T− ˜λkI := PkLkUk ▷部分ピボット選択付きLU分解 6: end for 7: i := 0 8: repeat 9: i := i + 1 10: for k= 1, . . . , mcdo 11: Solve PkLkUkv(i)k = q (i−1) k ▷連立方程式の求解 12: end for
13: V(i):= Q(i)R(i) ▷ QR分解
14: untilconverge 15: return Q:=[Q(i)] 16: end function 計算を行う. Algorithm 2は,同時逆反復法を表す擬似コードである. 同時逆反復法においても,連立方程式(2)の求解は,部分 ピボット選択付きLU分解(5行目)の結果をメモリに保 存し,それらを用いて連立方程式の求解(11行目)を行 う.ここで,5行目および11行目の演算は,kについて同 期なしで並列化が可能である一方,保存しなければいけな いPk,Lk,Ukの要素数は,逆反復法のmc倍必要になる. 13行目におけるn× mc行列V(i) のQR分解は行列乗算中 心の実装が可能で,逆反復法における再直交化計算と同程 度の計算量で行える. 以上のように,同時逆反復法では,大半の計算を行列乗 算中心の実装を行えるだけでなく,行列乗算で実装できな い計算についても,同期コストの少ない並列化を施すこと が可能である.したがって,同時逆反復法は逆反復法より も高速な並列計算が期待できる.
3.
提案アルゴリズム
本章では,同時逆反復法にブロックサイズパラメータ r(≤ mc)を導入した,再直交化付きブロック逆反復法を提 案する.以下では簡単のため,rをmcの約数とする. 3.1 再直交化付きブロック逆反復法 再直交化付きブロック逆反復法では,あるmc本の固有ベ クトルをr本ごとのブロックとみなし,ブロック内の全ての 固有ベクトルを計算した後,次のブロックについての固有 ベクトル計算を行う.固有ベクトルのうち,q1, . . . , q( j−1)r の計算が終了し,q( j−1)r+1, . . . , qjrのr本の計算を行う場 合について示す.ここで,j= 1, 2, . . . , mc/rとする. 再直交化付きブロック逆反復法では,任意のn×r行列V(0)j,r を乱数により生成し,QR分解V(0)j,r := Q(0)j,rR(0)j,r により正規 直交行列Q(0)を得る.Q(0)を初期行列として次の3ステッ プから成る反復計算を行うことにより,λ( j−1)r+1, . . . , λjrに Algorithm 3再直交化付きブロック逆反復法(RBInv) 1: function RBInv(T, r, ˜λ1, . . . , ˜λmc) 2: Q0:= O 3: for j= 1, . . . , mc/r do 4: i := 0 5: Generate V(0)j,r :=[v(0)( j−1)r+1 · · · v(0)jr] 6: V(0)j,r := Q(0)j,rR(0)j,r ▷ QR分解 7: for k= ( j − 1)r + 1, . . . , jr do 8: T− ˜λkI := PkLkUk ▷部分ピボット選択付きLU分解 9: end for 10: repeat 11: i := i + 1 12: for k= ( j − 1)r + 1, . . . , jr do13: Solve PkLkUkv(i)k = q(i−1)k ▷連立方程式の求解
14: end for
15: V(i)j,r:= V(i)j,r− Q( j−1)rQ⊤( j−1)rVj,r
16: V(i)j,r:= Q(i)j,rR(i)j,r ▷ QR分解
17: Q(i)j,r:= Q(i)j,r− Q( j−1)rQ⊤( j−1)rQ(i)j,r
18: Q(i)j,r:= Q(i)j,rR(i)j,r ▷ QR分解 19: untilconverge 20: Qjr:= [ Q( j−1)r Q(i)j,r] (Qr:= [ Q(i)1,r]) 21: end for 22: return Qmc= [ q1 · · · qmc ] 23: end function 対応する固有ベクトルq( j−1)r+1, . . . , qjrが得られる.ここ で,V(i)j,r =[v(i)( j−1)r+1 · · · v(i)jr],Q(i)j,r =[q(i)( j−1)r+1 · · · q(i)jr]
とする. (i) 以下のr本の連立方程式を解く. ( T− ˜λkI ) v(i)k = q(i−1)k , k = ( j − 1)r + 1, . . . , jr. (4) (ii) q1, . . . , q( j−1)rと直交するようにV(i)j,r を再直交化する (iii) (ii)で得られたベクトルを並べたn× r行列をQR分解 し,Q(i)j,rとする 同時逆反復法と異なる点は,まず,(i)において解くべき 連立方程式がr本になることである.この計算も同期なし の並列化が可能で,メモリ使用量は逆反復法のr倍必要で ある.しかしながら,r≪ mcである場合,同時逆反復法に 比べてメモリ使用量は非常に少なくなる. また,同時逆反復法におけるQR分解の代わりに,(ii)の 再直交化計算と(iii)のQR分解を行う.(ii)は,jステップ 目においてO(( j− 1)r2n)の計算量を要するが,行列乗算に よって実装が可能である.(iii)はn× r行列のQR分解で あることから,計算量はO(r2n)で,やはり行列乗算を中 心としたアルゴリズムで計算可能である.したがって,同 時逆反復法におけるQR分解や逆反復法における再直交化 計算と同程度の計算量を行列乗算中心の実装で計算するこ とができる.これら2段階の再直交化計算はブロック再直 交化計算とも呼ばれ,CGS法やCGS2法のブロック版アル ゴリズムであるブロックCGS(BCGS)法[20]やBCGS2 法[3]を適用することができる.
ルを計算するのが再直交化付きブロック逆反復法である. このアルゴリズムは,r= mcの時は同時逆反復法,r= 1 の時は逆反復法と等価なアルゴリズムとなる. Algorithm 3は,BCGS2法を適用した再直交化付きブロッ ク逆反復法の擬似コードである.15行目から18行目が BCGS2法を適用した部分で,15行目と17行目が(ii)に, 16行目と18行目が(iii)に対応する計算となる. 3.2 提案アルゴリズムの収束性 同時逆反復法の収束性から,提案アルゴリズムである再 直交化付きブロック逆反復法の収束性を示す. 同時逆反復法において,最も収束しにくい悪条件な場合 は,T の近接固有値全てが重複してしまう場合である.し たがって,この場合に収束性が保証されるのであれば,本 研究で用いた同時逆反復法により得られるベクトル列が固 有ベクトルに収束することは明らかである.一方,[5]で 定義された同時逆反復法は,行列Tの代数的重複度l (< n) の固有値σに対して,V(i), Q(i)∈ Rn×lとすると以下の2式 の反復となる.
(T− σI) V(i)= Q(i−1),
V(i):= Q(i)R(i).
以上の計算によりQ(i)が重複固有値σに対応する固有ベク トルが張る空間に収束することは,[5]のLemma 5.9.2に おいて証明されている.したがって,Tの近接固有値に対 する同時逆反復法の収束性は保証される. 提案アルゴリズムでは,以上の演算に加えて,計算済み の固有ベクトルに関する再直交化計算を反復の過程で行っ ている.この操作は,V(i)に含まれている計算済みの固有 ベクトルの成分を抜き取ることに過ぎないため,固有ベク トルの収束に悪影響を及ぼすことはない. 以上の議論により,提案アルゴリズムにより得られるベ クトル列は固有ベクトルに収束する.
4.
マルチコア CPU 向け実装コード
本章では,5章の性能評価に用いる,逆反復法,同時逆 反復法,提案アルゴリズムである再直交化付きブロック逆 反復法の実装コードについて説明する.それぞれのコード はマルチコアCPU向けに実装され,その並列化方法につ いても説明する. 本研究では,実装の多くに既存のLAPACKルーチンやBLAS(Basic Linear Algebra Subprograms)を利用できる.
これらは,Intel Math Kernel Library(MKL)において並列 実装が提供されており,各ルーチンの内部でスレッド並列 化できる.ただし,一部のLAPACKルーチンや,BLASの ベクトル演算にあたるものは並列化されていないが,CPU 向けに高度にチューニングされたルーチンとして提供され ている.しかしながら,これらの中でも,実装コードにお いて並列化可能なものについては,OpenMPの指示文を使 用したスレッド並列化を施した. 4.1 逆反復法 逆反復法の実装コードは,Algorithm 1の10行目の再直 交化計算を除き,LAPACKのDSTEINルーチンを基に作成 した.連立方程式(1)の求解においては,LAPACKルーチ ンを用いることができる.6行目における部分ピボット選 択付きLU分解はDLAGTF,9行目の計算ではDLAGTS を用いることができる.これらのルーチンは,内部演算の 並列化が難しく,Intel MKLにおいても並列実装は提供さ れていない. 10行目の再直交化計算には,MGS法とCGS2法を適用し た.これらの実装コードをそれぞれ,Inv-MGS,Inv-CGS2 とする.MGS法の内部演算は全てベクトル演算であるた め,Inv-MGSは並列計算を行わない実装コードとなる.一 方,CGS2法は行列-ベクトル乗算ルーチンDGEMVによっ て実装できるため,Inv-CGS2はDGEMVについてスレッ ド並列計算を行う実装コードとなる. 4.2 同時逆反復法 同時逆反復法は,各固有値クラスターにAlgorithm 2を 適用するような実装を行った.このため,同時逆反復法に よる固有ベクトル計算の前に,固有値を各クラスターに分 けるルーチンが必要となる.このルーチンは並列化を施さ ないが,m個の固有値に対してO(m)程度の計算量で済む. 逆反復法と同様に,連立方程式の求解では5行目の計算 にDLAGTF,11行目の計算にDLAGTSを使用できる.同 時逆反復法では,1回の反復において連立方程式をmc本解 くことになるが,これらの連立方程式は独立に計算できる ため,OpenMPにより4行目と10行目のforループについ てスレッド並列化した. 以下では,本研究において3行目と13行目のQR分解 に適用したアルゴリズムについて述べる. 4.2.1 CGS2法の再帰的実装に基づくQR分解 再直交化計算におけるCGS法は,行列-ベクトル乗算に よる実装であった.しかし,QR分解にCGS法を適用す る場合,計算順序を入れ替えることで,行列-ベクトル乗 算で表現されていた計算を行列乗算に置き換えることが でき,行列乗算の割合を高めることができる.この考えに 則り,横澤らは[23]において再帰的分割法に基づくCGS 法の実装を提案している.本研究では,この再帰的実装 のCGS法を,rCGS法とする.rCGS法は行列乗算ルーチ ンDGEMMを中心としたBLASを用いて実装できるため, Intel MKLを利用することでBLAS内でのスレッド並列化 がなされる. CGS法同様,rCGS法も計算対象の行列によっては,ベ クトルの直交性が悪化してしまう場合がある.したがっ
表1:各コードにおいて使用した主なルーチンとその並列化方法
Table 1 Main routines and parallelism in each code.
Inv-MGS Inv-CGS2 SInv-rCGS2 SInv-BCGS2 RBInv
初期行列のQR分解 rCGS2法 BCGS2法 rCGS2法
連立方程式の求解 DLAGTF DLAGTF DLAGTF DLAGTF DLAGTF
DLAGTS DLAGTS DLAGTS DLAGTS DLAGTS
再直交化計算 MGS法 CGS2法 QR分解 rCGS2法 BCGS2法 ブロック再直交化 BCGS2法 BCGS2法内部のQR分解 rCGS法 rCGS法 黒字:並列化なし 青字:OpenMPによるforループのスレッド並列化
赤字:Intel Math Kernel Libraryによる,演算内部の各BLASにおけるスレッド並列化
Algorithm 4BCGS algorithm 1: function BCGS(V1,r, . . . , Vk/r,r) 2: Q0= O. 3: for j= 1, . . . , k/r do 4: Vj,r:= Vj,r− Q( j−1)rQ⊤( j−1)rVj,r 5: Vj,r:= Qj,rRj,r ▷ QR分解 6: Qjr= [ Q( j−1)r Qj,r] (Qr=[Q1,r]) 7: end for 8: return Qk= [ q1 · · · qk ] 9: end function て,同時逆反復法の実装には,rCGS法を2回繰り返した rCGS2法によるQR分解を適用した.この実装コードを SInv-rCGS2とする. 4.2.2 BCGS2法によるQR分解 [20]では,QR分解におけるCGS法の行列乗算の割合を 増やす方法として,BCGS法が提案されている.BCGS法 はCGS法にブロックサイズパラメータrを導入したもの である.Algorithm 4は,n× k行列のQR分解を行う場合 のBCGS法を表す擬似コードである.4行目は,既に計算 済みのベクトルと直交するように,ブロック内部のベクト ルの計算を行っており,行列乗算を用いることができる. 5行目は,ブロック内部でのQR分解を行っており,rCGS 法を用いることで大半の計算を行列乗算による演算で実装 することが可能である. CGS法と同様に,BCGS法も計算対象の行列によって は,ベクトルの直交性が悪化してしまう場合がある.この ため,BCGS法を2回繰り返すBCGS2法[3]が提案されて いる.BCGS2法も,行列乗算ルーチンDGEMMを用いた 実装ができるため,Intel MKLを利用することで演算内の スレッド並列化が可能になる.ここで,BCGS2法の計算 量はrCGS2法と同程度である. BCGS2法によりQR分解を行う同時逆反復法の実装コー ドをSInv-BCGS2とする. 4.3 再直交化付きブロック逆反復法 再直交化付きブロック逆反復法についても,同時逆反復 法と同様の実装を施すことができる.まず,固有ベクトル 計算の前に,固有値を各クラスターに分けるルーチンを加 える.次に,Algorithm 3の8行目の計算にDLAGTF,13 行目の計算にDLAGTS,それぞれのLAPACKルーチンが 適用できる.ここで,再直交化付きブロック逆反復法で は,1回の反復でr本の連立方程式を解くため、OpenMP によって7行目と12行目のfor文をスレッド並列化した. 以上の実装は同時逆反復法にも共通する計算である. 再直交化付きブロック逆反復法では,15行目と17行目 の計算があるため,それぞれ,行列乗算ルーチンDGEMM を2回用いる.また,RBInvのQR分解は,全てn× r長方 行列のQR分解であるため,BCGS2法ではなく,CGS法 の再帰的実装を基としたアルゴリズムを適用する.具体的 には,6行目にはrCGS2法,16行目および18行目のQR 分解にはrCGS法を実装した.これら行列乗算およびQR 分解の計算部分については,Intel MKLを利用することで, 演算内でのスレッド並列化することができる. 以上のように実装した再直交化付きブロック逆反復法の コードをRBInvとする. 表1は本章で述べた,逆反復法,同時逆反復法および再 直交化付きブロック逆反復法の実装コードについて,実装 したルーチンやアルゴリズム,それらの並列化方法をまと めたものである.
5.
数値実験
数値実験では,表2に示される共有メモリマルチコアプ ロセッサシステム1ノードを使用し,スレッド並列計算を 行った.実対称3重対角行列T1およびT2の全固有ベクト ルを計算することにより,提案アルゴリズムの性能を評価 する.評価においては,4章において説明した実装コードである,Inv-MGS,Inv-CGS2,SInv-rCGS2,,SInv-BCGS2,
1.E-01 1.E+00 1.E+01 1.E+02 1.E+03 0 5250 10500 15750 21000 26250 31500 E lap sed T im e [s ] Matrix Dimension Inv-MGS Inv-CGS2 Sinv-rCGS2 Sinv-BCGS2 RBInv
(a) Elapsed time of all code
0 100 200 300 0 5250 10500 15750 21000 26250 31500 E lap sed T im e [s ] Matrix Dimension Sinv-rCGS2 Sinv-BCGS2 RBInv
(b) Elapsed time of SInv-rCGS2, SInv-BCGS2, and RBInv
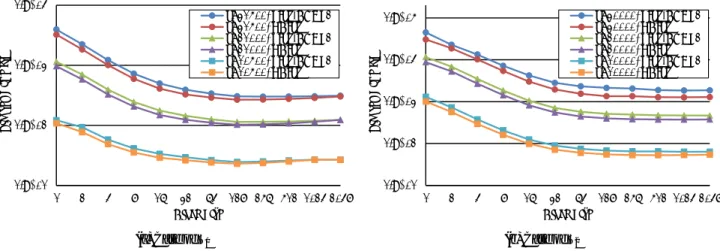
1.E-17 1.E-15 1.E-13 1.E-11 1.E-09 0 5250 10500 15750 21000 26250 31500 Or th og on ality Matrix Dimension Inv-MGS Inv-CGS2 Sinv-rCGS2 Sinv-BCGS2 RBInv (c) Orthogonality∥QQ⊤− I∥∞/n 1.E-17 1.E-15 1.E-13 1.E-11 1.E-09 0 5250 10500 15750 21000 26250 31500 R esid ual Matrix Dimension Inv-MGS Inv-CGS2 Sinv-rCGS2 Sinv-BCGS2 RBInv (d) Residual∥T Q − QD∥∞/n 図1:固有ベクトル計算における逆反復法,同時逆反復法,再直交化付きブロック逆反復法の比較(r= 256,テスト行列T1)
Fig. 1 Comparison of Inv, SInv, and RBInv code in computing eingenvectors of T1. Note that r= 256.
表2:実験環境(Appro Green Blade 8000)
Table 2 Specifications of Appro Green Blade 8000
CPU Intel Xeon E5-2670 ( 2.6GHz, 8 cores× 2 ) RAM DDR3-1600 64GB
Compiler Intel Fortran Compiler 13.1.3
Options -O3 -xHOST -ipo -no-prec-div -static -openmp Libraries LAPACK 3.4.2
Intel Math Kernel Library 11.0 update 1
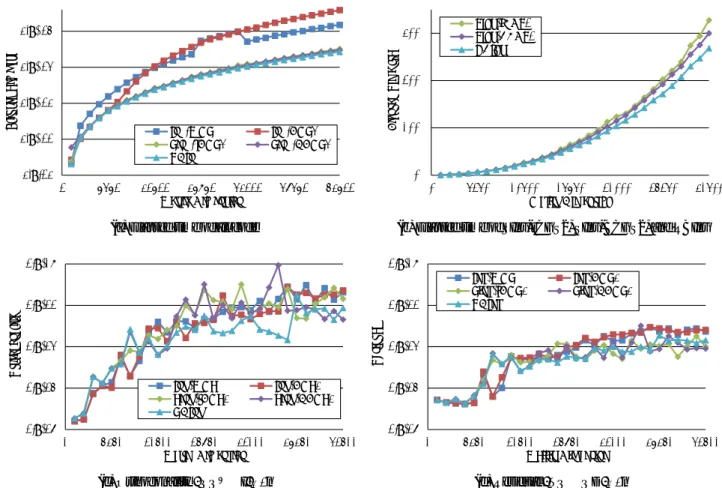
ルーチンそのものであるが,本実験においては,Intel Fortran Compilerで改めてコンパイルしたものを使用した. 性能評価のテスト行列には,固有値分布の異なる二つの 実対称3重対角行列T1,T2を用いた.テスト行列T1は Glued-Wilkinson行列[6], [8]である.この行列の固有値は, Peters-Wilkinsonの判定基準において,大きさがn/21とな るクラスターと2n/21となるクラスターがそれぞれ7つ, 計14のクラスターに分かれることが知られている.更に, それぞれのクラスターに属する固有値が非常に密集してお り,条件数の悪い問題として知られている.テスト行列T2 は,全要素を(0, 1)の範囲の一様乱数により生成した実対 称3重対角行列を用いた.この行列の固有値は,小次元行 列ではある程度の数のクラスターに分かれる一方,大次元 行列ではほとんどが一つのクラスターに含まれる.数値実 験において実際に用いた行列でも,nが10000以上の場合 においては,9割以上の固有値が一つのクラスターを成す 行列となった. また,各テスト行列の固有値は,Intel MKLに実装され たLAPACKのDSTEBZルーチンを利用することにより計 算した.DSTEBZは,実対称3重対角行列の固有値を二分 法によって計算する倍精度演算ルーチンである. 最後に,各コードにおいて,許容する反復回数は5回で ある.しかし,全ての実験において,いかなる入力行列の 場合でも3回の反復回数で収束することが確認できている. 5.1 各コードの性能比較 図1および図2は,それぞれテスト行列T1およびT2に 対する16スレッド並列計算での数値実験を行った結果を 示すものである.この比較においては,SInv-BCGS2およ びRBInvのブロックサイズパラメータはr= 256とした. 図1aと図2aでは,全固有ベクトル計算に要した計算時間 の比較を行っている.これらの図から,特に大次元の行列 に対して,行列乗算を中心とした固有ベクトル計算法で ある同時逆反復法および再直交化付きブロック逆反復法 の実装コードが,逆反復法の実装コードであるInv-MGS,
1.E-01 1.E+00 1.E+01 1.E+02 1.E+03 1.E+04 1.E+05 0 5000 10000 15000 20000 25000 30000 E lap sed T im e [s ] Matrix Dimension Inv-MGS Inv-CGS2 Sinv-rCGS2 Sinv-BCGS2 RBInv
(a) Elapsed time of all code
0 500 1000 1500 0 5000 10000 15000 20000 25000 30000 E lap sed T im e [s ] Matrix Dimension Sinv-rCGS2 Sinv-BCGS2 RBInv
(b) Elapsed time of SInv-rCGS2, SInv-BCGS2, and RBInv
1.E-20 1.E-18 1.E-16 1.E-14 0 5000 10000 15000 20000 25000 30000 Or th og on ality Matrix Dimension Inv-MGS Inv-CGS2 Sinv-rCGS2 Sinv-BCGS2 RBInv (c) Orthogonality∥QQ⊤− I∥∞/n 1.E-20 1.E-18 1.E-16 1.E-14 0 5000 10000 15000 20000 25000 30000 R esid ual Matrix Dimension Inv-MGS Inv-CGS2 Sinv-rCGS2 Sinv-BCGS2 RBInv (d) Residual∥T Q − QD∥∞/n 図2:固有ベクトル計算における逆反復法,同時逆反復法,再直交化付きブロック逆反復法の比較(r= 256,テスト行列T2)
Fig. 2 Comparison of Inv, SInv, and RBInv code in computing eingenvectors of T2. Note that r= 256.
Inv-CGS2よりも高速な並列計算を実現していることが分
かる.また,図1bおよび図2bでは,図1aと図2aで示し
た結果のうち,SInv-rCGS2,,SInv-BCGS2,RBInvの計算 時間のみを比較したものである.これらの図から,特に 大次元の行列に対しては,提案アルゴリズムの実装コー ドであるRBInvが最も高速であることが分かる.実際, RBInvは,n= 31500のT1の全固有ベクトル計算につい て,Inv-MGSに対して約6倍,Inv-CGS2に対して約15倍, n= 30000のT2の全固有ベクトル計算でも,Inv-MGSに対 して約12倍,Inv-CGS2に対して約31倍高速であった.ま た,RBI-BCGSは,同時逆反復法の実装コードSInv-rCGS2 やSInv-BCGS2に比べて,T1の全固有ベクトル計算では 10%,T2の全固有ベクトル計算では20%近い性能向上が確 認できている.同じくCGS法をQR分解に実装した同時 逆反復法コードSInv-rCGS2およびSInv-BCGS2と比べる と,RBInvで使用されるメモリ空間は少ないため,より高 い演算性能が得られたと考えられる. 図1cおよび図2cでは各コードによって得られた固有ベ クトルの直交性∥QQ⊤− I∥∞/n,図1dおよび図2dでは各 コードによって得られた固有ベクトルの残差∥T Q−QD∥∞/n を表している.ここで,Dは対角要素に固有値が並ぶ対 角行列である.これら固有ベクトルの計算精度を表すグ ラフから,同じ反復回数の固有ベクトル計算において,
SInv-rCGS2,SInv-BCGS2,RBInvは,従来アルゴリズムで
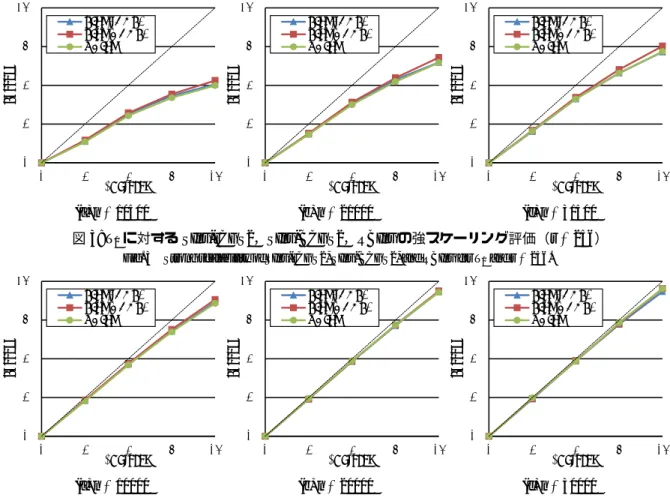
あるInv-MGSやInv-CGS2と同等の計算精度を得られるこ とが分かる.しかしながら,T1の直交性を表すグラフにお いて,SInv-rCGS2のn= 19550,SInv-BCGS2のn= 24150 など所々精度の劣化が見られる以上,同時逆反復法は再直 交化付きブロック逆反復法よりも精度面での信頼性に欠 ける. 5.2 強スケーリングの評価 図3および図4は,行列T1およびT2の問題サイズを固 定した時の,SInv-rCGS2,SInv-BCGS2,RBInvの並列化効 率を評価した結果である.全てのグラフにおいて,各手法 を1スレッドで計算したときに要した計算時間を基準に, スレッド数を変化させた時どの程度の高速化が見られるか を示している.この比較においても,SInv-BCGS2および RBInvのブロックサイズパラメータはr= 256とした. 16スレッドを使用することで,RBInvは,テスト行列T1 のn= 10500において約4倍,n= 21000において約6倍, n= 31500において約7倍の並列化効率を達成した.また, テスト行列T2のn= 10000において約11倍,n= 20000に おいて約13倍,n= 30000において約14倍の並列化効率
1 2 4 8 16 1 2 4 8 16 Sp ee du p #Threads SInv-rCGS2 SInv-BCGS2 RBInv (a) n= 10500 1 2 4 8 16 1 2 4 8 16 Sp ee du p #Threads SInv-rCGS2 SInv-BCGS2 RBInv (b) n= 21000 1 2 4 8 16 1 2 4 8 16 Sp ee du p #Threads SInv-rCGS2 SInv-BCGS2 RBInv (c) n= 31500
図3: T1に対するSInv-rCGS2,SInv-BCGS2,RBInvの強スケーリング評価(r= 256)
Fig. 3 Strong scalability of SInv-rCGS2, SInv-BCGS2, and RBInv for T1and r= 256.
1 2 4 8 16 1 2 4 8 16 Sp ee du p #Threads SInv-rCGS2 SInv-BCGS2 RBInv (a) n= 10000 1 2 4 8 16 1 2 4 8 16 Sp ee du p #Threads SInv-rCGS2 SInv-BCGS2 RBInv (b) n= 20000 1 2 4 8 16 1 2 4 8 16 Sp ee du p #Threads SInv-rCGS2 SInv-BCGS2 RBInv (c) n= 30000
図4: T2に対するSInv-rCGS2,SInv-BCGS2,RBInvの強スケーリング評価(r= 256)
Fig. 4 Strong scalability of SInv-rCGS2, SInv-BCGS2, and RBInv for T2and r= 256.
を達成し,T1に対する結果よりも良い結果が得られた.こ れは,固有値が大規模なクラスターを成すテスト行列T2の 方が,全体の計算量に対する再直交化計算やQR分解を行 う割合が大きくなるからであると考えられる.これらの計 算は行列乗算中心のキャッシュヒット率の高い計算であり, このことによる演算性能の向上が起因して,T2に対して高 い並列化効率が得られたと考えられる.どちらのテスト行 列に対しても,問題サイズが小さい時よりも大きい時の方 が高い並列化効率を得られた.また,RBInvはSInv-rCGS2 と比較するとほとんど同程度の並列化効率を達成している が,SInv-BCGS2には少し劣るという結果が得られた. 5.3 異なるブロックサイズパラメータにおける性能 図5は,行列T1およびT2の問題サイズを固定し,異な るブロックサイズrを与えた場合のSInv-BCGS2,RBInv の計算時間を比較している.強スケーリングによる性能評 価と同様に,問題サイズには,行列T1に対しては10500, 21000,31500,行列T2に対しては10000,20000,30000 を選んだ. 図5からは,SInv-BCGS2とRBInvの両方について,同 様の傾向が観察される.まず,行列の種類やサイズに係わ らず,ある程度の大きさまでは,ブロックサイズrに反比 例するように計算時間が削減される.これは,rの値を大 きくすることにより,QR分解や再直交化計算における行 列乗算の割合が増えるからである.その一方で,どの行列 サイズにおいてもr= 2048のときに計算時間が最も短くな るわけではないことが分かる.したがって,再直交化付き ブロック逆反復法のブロックサイズパラメータrは,大き い値を設定すれば必ず高速されるというわけではない. 以上の性能評価により,ブロックサイズrを上手く設定 することで計算時間の削減が計られることは明らかであ る.しかし,rの値が大きい場合の計算時間の変化幅は徐々 に小さくなっているため,他の性能評価において設定した r= 256のような値であれば,最適に近い性能での並列計 算ができていると見なせる.
6.
まとめと今後の課題
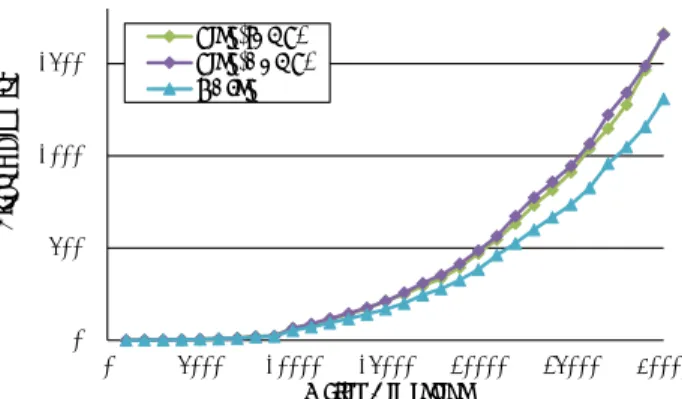
本論文では,並列計算機向けの実対称3重対角行列の固 有ベクトル計算アルゴリズムとして再直交化付きブロック 逆反復法を提案した.提案アルゴリズムは,行列乗算を中 心とした固有ベクトル計算法である同時逆反復法にブロッ クパラメータを導入したもので,大粒度の並列性を持つ. 共有メモリマルチコアプロセッサシステム上での性能評価 では,提案アルゴリズムが,速度と精度両面において優れ た並列計算を達成することを示した.また,異なるブロッ1.E+01 1.E+02 1.E+03 1.E+04 1 2 4 8 16 32 64 128 256 512 1024 2048 E lap sed T im e [s ] Block Size n=31500, SInv-BCGS2 n=31500, RBInv n=21000, SInv-BCGS2 n=21000, RBInv n=10500, SInv-BCGS2 n=10500, RBInv (a) Case of T1 1.E+01 1.E+02 1.E+03 1.E+04 1.E+05 1 2 4 8 16 32 64 128 256 512 1024 2048 E lap sed T im e [s ] Block Size n=30000, SInv-BCGS2 n=30000, RBInv n=20000, SInv-BCGS2 n=20000, RBInv n=10000, SInv-BCGS2 n=10000, RBInv (b) Case of T2 図5:異なるブロックサイズrに対するSInv-BCGS2およびRBInvの計算時間
Fig. 5 Elapsed time of SInv-BCGS2 and RBInv for each block size parameter r.
クサイズパラメータの値を選択した場合の性能評価では, ある程度のサイズまで大きくすることで最適に近い性能が 得られることを示した. 今後の課題としては,1章において述べた,MRRR法と 提案アルゴリズムを組み合わせた新しいアルゴリズムの実 装が考えられる.このアルゴリズムにより,MRRR法で計 算が破綻してしまうような行列に対しても,高速高精度な 固有ベクトル計算が可能になると期待できる.また,より 大規模な問題への適用のため,提案アルゴリズムの分散並 列環境での実装および性能評価も重要な課題である. 謝辞 有益なコメントをいただいたHPCS14の査読者の 方々に感謝いたします.本研究は,科学研究費補助金特別 研究員奨励費(課題番号:25・2820),および基盤研究(B) (課題番号:24360038)による助成を受けた.また,本研 究の結果の一部は,京都大学学術情報メディアセンターの スーパーコンピュータAppro Green Blade 8000を利用して 得られたものである.
参考文献
[1] : See the past records in LAPACK BUG LIST Homepage, http://www.netlib.org/lapack/bug list.html.
[2] Anderson, E., Bai, Z., Bischof, C., Blackford, L. S., Demmel, J. W., Dongarra, J., Du Croz, J., Hammarling, S., Greenbaum, A., McKenney, A. and Sorensen, D.: LAPACK Users’ Guide
(Third ed.), SIAM, Philadelphia, PA, USA (1999).
[3] Barlow, J. L. and Smoktunowicz, A.: Reorthogonalized block classical Gram-Schmidt, Numer. Math., Vol. 123, No. 3, pp. 1–29 (2012).
[4] Bischof, C. H., Marques, M. and Sun, X.: Parallel ban-dreduction and tridiagonalization, Proc. Sixth SIAM
Confer-ence on Parallel Processing for Scientific Computing, pp. 22–
24 (1993).
[5] Chatelin, F. C. and Ahu´es, M.: Eigenvalues of Matrices, SIAM, Philadelphia, PA, USA (2012).
[6] Demmel, J. W., Marques, O. A., Parlett, B. N. and V¨omel, C.: Performance and accuracy of LAPACK’s symmetric tridiag-onal eigensolvers, SIAM J. Sci. Comput., Vol. 30, No. 3, pp. 1508–1526 (2008).
[7] Dhillon, I. S.: A new O(n2) algorithm for the symmetric tridi-agonal eigenvalue/eigenvector problem, PhD Thesis, EECS Department, University of California, Berkeley (1997). [8] Dhillon, I. S., Parlett, B. N. and V¨omel, C.: Glued
matri-ces and the MRRR algorithm, SIAM J. Sci. Comput., Vol. 27, No. 2, pp. 496–510 (2005).
[9] Dhillon, I. S., Parlett, B. N. and V¨omel, C.: The design and implementation of the MRRR algorithm, ACM Trans. Math.
Softw., Vol. 32, No. 4, pp. 533–560 (2006).
[10] Giraud, L., Langou, J., Rozloˆzn`ık, M. and van den Eshof, J.: Rounding error analysis of the classical Gram-Schmidt or-thogonalization process, Numer. Math., Vol. 101, No. 1, pp. 87–100 (2005).
[11] Imamura, T., Yamada, S. and Machida, M.: Development of a high performance eigensolver on the peta-scale next genera-tion supercomputer system, Prog. Nuclear Science and
Tech-nology, Vol. 2, pp. 643–650 (2011).
[12] Ipsen, I. C. F.: Computing an Eigenvector with Inverse Itera-tion, SIAM Review, Vol. 39, No. 2, pp. 254–291 (1997). [13] Ishigami, H., Kimura, K. and Nakamura, Y.: On
implemen-tation and evaluation of inverse iteration algorithm with com-pact WY orthogonalization, IPSJ Transactions on
Mathemat-ical Modeling and Its Applications, Vol. 6, No. 2, pp. 25–35
(2013).
[14] Katagiri, T. and Itoh, S.: A massively parallel dense sym-metric eigensolver with communication splitting multicasting algorithm, High Performance Computing for Computational
Science - VECPAR 2010, Lecture Notes in Computer Science,
Vol. 6449, Springer Berlin Heidelberg, pp. 139–150 (2011). [15] Katagiri, T.: Performance Evaluation of Parallel
Gram-Schmidt Re-orthogonalization Methods, High Performance
Computing for Computational Science - VECPAR 2002,
Lec-ture Notes in Computer Science, Vol. 2565, Springer Berlin Heidelberg, pp. 302–314 (2003).
[16] Parlett, B. N.: The Symmetric Eigenvalue Problem, SIAM, Philadelphia, PA, USA (1998).
[17] Peters, G. and Wilkinson, J.: The calculation of specified
eigenvectors by inverse iteration, Handbook for Automatic
Computation, pp. 418–439, Springer-Verlag, Berlin (1971). [18] Petschow, M. and Bientinesi, P.: MR3-SMP: A symmetric
tridiagonal eigensolver for multi-core architectures, Parallel
Computing, Vol. 37, No. 12 (2011).
[19] Schreiber, R. and van Loan, C.: A storage-efficient WY repre-sentation for products of Householder transformations, SIAM
[20] Stewart, G.: Block Gram-Schmidt orthogonalization, SIAM
Journal on Scientific Computing, Vol. 31, No. 1, pp. 761–775
(2008).
[21] Wu, Y.-J. J., Alpatov, P. A., Bischof, C. H. and van de Geijn, R. A.: A parallel implementation of symmetric band reduc-tion using PLAPACK, Proc. Scalable Parallel Libraries
Con-ference, Mississippi State University (1996).
[22] Yamamoto, Y. and Hirota, Y.: A parallel algorithm for incre-mental orthogonalization based on the compact WY repre-sentation, JSIAM Letters, Vol. 3, pp. 89–92 (2011).
[23] 横澤拓弥,高橋大介, 朴泰祐,佐藤三久:行列積を用い
た古典Gram-Schmidt直交化法の並列化,情報処理学会論 文誌コンピューティングシステム(ACS),Vol. 1, No. 1, pp. 61–72 (2008).