Title
Effectiveness of Hierarchical Connection for the Parallel and
Distributed Genetic Algorithm
Author(s)
Matsumura, Takashi; Nakamura, Morikazu
Citation
沖縄大学マルチメディア教育研究センター紀要 = The
Bulletin of Multimedia Education and Research Center,
University of Okinawa(1): 49-58
Issue Date
2001-03-31
URL
http://hdl.handle.net/20.500.12001/6323
Ef
r
e
c
t
i
v
e
ne
s
so
fHi
e
r
ar
c
hi
c
alCo
nne
c
t
i
o
n
f
ort
hePar
a
ll
e
la
ndDi
s
t
ibut
r
e
dGe
ne
t
i
cAl
g
or
i
t
hm
ThkashiMatsumura,MorikazuNakamura Dept.ofhfom ationEng.,UniversityoftheRyukyus
I
nt
hi
spa
pe
r
,
wepr
opos
eapa
ra
ll
e
la
nddi
s
t
ibut
r
e
dge
ne
t
i
ca
lgor
it
hm (
PDGA)a
nd e
va
lua
t
ei
t
s
e
f
fe
c
t
i
ve
ne
s
sc
ompa
re
dCo
newi
t
h l
a
t
t
i
c
et
opol
ogy
. Wef
i
nd
tha
tourpr
opos
e
dhi
e
r
a
rc
hi
c
a
lPDGA
obt
a
insa
lmos
ts
a
m eorbe
t
t
e
rs
ol
ut
i
on
tha
n Cone
. Mo
r
e
ove
r
,
wepr
o
pos
ea
ndi
nve
s
t
i
ga
t
et
he
pr
oc
e
s
s
l
●
ngt
i
mebyt
hehi
e
r
rc
a
hi
c
lPDGAo
a
nbusc
or
me
c
t
i
on.
Ef
f
e
c
t
iv
e
ne
s
so
fHi
e
r
ar
c
hi
c
a
lConne
c
t
i
o
n
f
ort
hePar
a
l
l
e
la
ndDi
s
t
r
i
but
e
dGe
ne
t
icAl
g
or
i
t
hm
松村 隆,名嘉村 盛和 琉球大学 工学部 情報工学科 本論文は並列分散遺伝 アル ゴ リズム (PDGA)を提案す る。PDGAの特徴 の一つ として、トポ ロジーの階 層構造があげ られ る。本研究では、既存 の疎結合マルチプ ロセ ッサシステムな どで使用 され るネ ッ トワー ク トポロジーを階層化す ることを考 え、従来法の トポロジー と比較す ることで PDGAの性能 評価 を行 う。 また、バス型のネ ッ トワー クでの PDGAの実現方法や評価実験 も行 う。
1
Introduction
One of the aim of operations research (OR) is to obtain the optimum solution by a.pplying scientific meth-ods to a planning and management of systems. Many methmeth-ods used in operations research were developed during World War IIto reduce the guesswork out of missions such as deploying radar, searching for enemy submarines, and getting supplies where they were most needed. Following the war, numerous .peacetime applications emerged, leading to the use of OR and management science (MS) in many industries and occu-pations. Recently, OR relates to the decision support system (DSS) and computer integrated manufacturing (CIM), and applies to other fields. An application of OR to concrete problems needs to be constructed a mathematical model formulated theprobl~mat first, then we solve the optimum solution of the model.
However, most of practical combinatorial optimization problems are known as NP-hard problems. That is, no polynomial algorithms have been developed and their non-existence is generally believed. Consequently, the approximated optimum solving methods attract a great deal attention of scholars. They are to find the approximated optimum solution for polynonlial time instead of the optimum solution.
The research of combinatorial optimization based on approximation approach is hot. Specially, the emergence of meta-heuristics such as genetic algorithms (GAs), simulated annealing (SA), and tabu search (TS) activates this field. They can be regarded as problem independent approaches in a sense that they are not for specific optimization problem but just give general frameworks to design optimization programs. This is the reason why they are called "Meta-heuristics." One of the most desirable characteristics of the approximation algorithm is robustness for problem instances, that is, the solution quality does not depend heavily on problem instances.
The recent advancement of parallel processing allows us to execute efficiently with low cost optimization algorithms on parallel processing platforms (multiprocessor systems). Parallel optimization based on Meta-heuristics not only reduces the computation time but also may improve the solution quality and robustness of the approximation algorithm.
GAs are focused as one of meta-heuristics to solve combinatorial optimization problenls. Many papers report its effectiveness and usefulness [7,20,30-32,36,46]. However, GAs generally take expensive com-putation cost. Thus, there are some proposals on parallel execution of GAs to reduce the computation cost [2,23,26,35,39,40]. On the other hand, the distributed computation of GAs cont.ributes to keeping variety of chromosomes to avoid immature convergence in which the chroDl0some set was divided into the number of processors and the processors operated on the assigned chromosome set in parallel. We call this method "parallel and distributed computation of GAs" which contributes to keeping the va.riety of the chro-mosomes to avoid convergence at the local optimum points by distributing and to saving the computation cost byparallelizing. In the experimental results, we observed that the distributed co~putationof GAs can obtain better quality solutions that the centralized one. The reason is that the distributed computation can keep variety of chromosomes while the other can easily get immature convergence [26].
We consider a parallel and distributed computation of genetic algorithms on loosely-coupled multiproces-sor systems. We name the parallel and distributed genetic algorithm: PDGA. Loosely-coupled ones are more suitable for massively parallel executions and also more easily VLSI implementation than tightly-coupled ones. However, communication cost problem on parallel processing is more serious for loosely-coupled mul-tiprocessor systems. We propose a parallel and distributed execution method of GAs on loosely-coupled multiprocessor systems of fixed network topologies where each processor element (PE) ca.rries out genetic operations on its own chromosome set and communicates ,vith only the neighbors in order to reduce commu-nication cost. From the previous work [26], we can guess that the quantity and frequelicy of cODlmucommu-nication among PEs affect the solution quality of the parallel and distributed GAs. Therefore, the solution quality generated by our neighbor communication way seems to depend on the network topology of the multipro-cessor system.
In Sect. 2, the explanation of genetic algorithms and combinatorial optimization problems (0/1 multiple knapsack problem as an instance problem) is given for preliminaries of this research. In Sect. 3, we describe the detail of the parallel and distributed genetic algorithm: PDGA. In Sect. 4 we investigate the effectiveness of the PDGA by comparing Cone and lattice topology. Moreover we show the implelnentation of the PDGA on bus connection in Sect.4. Finally, We conclude this paper in Sect.5.
2
PreliIIlinaries
2.1
Genetic Algorithms
Genetic algorithms (GAs) are stochastic algorithms whose .search methods model some natural phenomena, genetic inheritance and Darwinian strife for survival [21,25,27,32,46,49]. GAs use a vocabulary borrowed from natural genetics, chromosome, crossover, mutation, and so on.
Each chromosome represents a potential solution to a problem, and evolution process runs on a population of chromosomes corresponds to a search through a space of potential solutions. Such a search requires balancing two objectives, exploiting the best solutions and exploring the search space. GAs are a class of general purpose search methods which strike a remarkable balance between exploration and exploitation of the search space.
Genetic algorithms have been quite successfully applied to optimization problems like scheduling, adaptive control, game playing, cognitive modeling, transportation problems, traveling salesman problems, optimal control problems, database query optimization, and so on [6,7, 28,47].
A simple version of GA, say simple GA, can be described as follows:
procedure simple GA; begin
Initialize a population; repeat
Evaluate all the chromosomes;
Select the chromosomes for the next generation; Create new chromosomes by applying crossover and mutation according to the crossover and mutation rate;
untilthe termination condition holds; end;
A population is a set of chromosomes (individuals). Initializing a population is to generate the first chromosomes. A chromosome consists of a genes sequence which should be designed according to the problem domain knowledge. The genetic algorithm repeats the evaluation and genetic operations until the termination condition holds. We need to design also a fitness function which is used to calculate the fitness value of each chromosome in the evaluation. Selection is performed based on the fitness value to choose surviving chromosomes, that is, the fitter chromosomes have higher probability to survive in the next generation. The crossover operation is to generate new offsprings from the parent chromosomes by exchanging a part of parent genes. The .mutation is to change a gene independently. Both of the crossover and mutation operation are performed according to the crossover rate and the mutat.ion rate. There are lots' of styles of crossover and mutation.
2.2
Combinatorial Optimization Problems
Computational complexity theory plays an important role in combinatorial optimization, separating the easy problems that can be solved in polynomial time from the NP-hard problems for \vhich no polynomial time algorithms are known [4,34].
The first combinatorial optimization problems to be extensively studied were problenls on graphs, in-cluding the shortest path problem, max flow problems, and mat.ching [8,14,18,38]. Many conlbinatorial optimization problems can be formulated as integer programming problems. In formulating an integer pro-gramming problem, there are many tricks that cal?- be used to make the problem' easier to solve [1,24,41].
Branch and bound algorithms are commonly used to solve integer progranlming problems. Branch and bound algorithms are discussed in nearly all of the textbooks described above, including[3,19,22,37]. Branch and bound and dynamic programming algorithms for the knapsack problenl are discussed in [44].
Heuristics for combinatorial optimization problems are algorithms that find "good" solutions without any guarantee that. the solution. are optimum. In recent years, there has been a lot of interest in heuristics, including genetic algorithms[7,31,32], simulated annealing [5,11,12,31], and tabu search [5,15-17].
Approximation schemes are algorithms that are guaranteed to produce a solution that is within f of optimality. Of particular interest are polynomial time approximation schemes algorithms that given f find an answer within a factor f of optimality while running in polynomial time [3,13,37]. Very recently, work on
transparent proofs has resulted in a large number of theorems about the non existence of polynomial time approximation schemes for various problems [10,29].
0/1 Multiple Knapsack Problem
In this section, we explain the 0/1 multiple knapsack problem. This problem is employed as an instance problem of the experimental evaluation in Sect. 4.
The 0/1 knapsack problem is a well-known NP-hard problem [44,45]. We are given a knapsack of capacity C and nobjects. Each object has its weightWi, and profitPi. We are interested in filling the knapsack with the objects so that the total profit in the sack can be maximized. In other ,vords, we wa.nt to find a vector
i= (Xl,X2,·· .,Xn ), Xi E {a,I},such that
E?=l
WiXi ~C andP(i)=
E7:IPiXi is lnaximunl. Each object is either placed in all m knapsacks, or in none at all. This problem is also known as the single-line integer programming problem [3], and has been studied in the context of genetic algorithnls (see e.g. [42]).The 0/1 multiple knapsack problem consists of m knapsacks of capacitiesCl, C2,· •. ,Crn andn objects, each of which has a profitPi. Unlike the simple version in which the weights of the objects are fixed, the weight of the i-th object is denoted byWij when it is considered for possible inclusion in the j-th knapsack of capacity
Cj. Once more, we are interested in finding a vector i
=
(Xl,X2, . . .,xn ) that guarantees that no knapsack is overfilled:E7=1
WijXi ~ Cj for j=
1,2"·,,n and that yields the maximum profit P(i)=
E?:l
XiPi.This problem is also known as the zero-one integer programming problem [34], and also as the 0-1 linear programming problem [44].
We note that it can also be thought as a resource allocation problem, where we have m resources (the knapsacks) and n objects. Each resource has its own budget (knapsack ca.pacity), and 'U'ij represents the consumption of resource j by object i. Once more, we are interested in maximizing the profit, while \vorking within a certain budget.
The only two algorithms that deliver optimum solutions are based 011 the dynamic programming and
the branch and bound approaches. While the latter can be used with any kind of knapsack, dynamic programming is impractical for solving multiple knapsack problems. Nevertheless, Inany approaches embed either one of the two techniques into specialized algorithms to solve large instances of kna.psack problems.
The following is a formal definition of the 0/1 multiple knapsack problem in which we make use of Stinson's terminology for combinatorial optimization problems [9].
Problem instance:
knapsacks: 1 2 m capacities: Cl C2 Cm
The capacities and profits of the objects are positive numbers, while the weights of the objects are nonnegative.
objects: 1 2 n profits: PI P2 Pn weights: Wlj W2j Wnj of objects w.r.t j-th knapsack, 1~ j ~m.
Feasible solution: A vector i = (Xl,X2,···,xn ) where Xi E{O,I}, such that:
E7=1
WijXi ~ Cj for j==
1, 2, .. " mObjective function: A function P(i)
=
E~=lPiXi, where i=
(Xl,X2, .. " xn ) is a feasible vector.Optimum solution: A feasible vector that gives the maximum profit; i.e., a vector that maximizes .the objective fUllction.
3
A Parallel and Distribut'ed Genetic Algorithlll
This section considers a parallel and distributed genetic algorithm, say PDGA, on loosely-coupled multipro-cessor systems. Loosely-coupled ones are more suitable for massively parallel executions and also more easily VLSI implementation than tightly-coupled ones. However, communication cost problem on parallel process-ing is more serious for loosely-coupled multiprocessor systems. We propose in here a parallel and distributed execution method of GAs on loosely-coupled multiprocessor systems of hierarchical network topology where each processor element (PE)' carries out genetic ope.rations on its own chromosome set and communicates with only the neighbors in order to reduce communication cost.
3.1
Procedure PDGA
At the beginning of an execution, each PE generates its own chromosome set according to the GA parameters sent from the host processor. Then each PE carries out genetic operations, crossover, mutation, and selection, on its population at each generation like in ordinary GAs. Before the next generation, the chromosome migration takes place through the associated communication processor if its condition holds. That condition is called migration condition.
The ,procedure for each PE is shown as follows: procedurePDGA;
begin
Initialize a population according to given parameters; repeat
Evaluate all the chromosomes;
ifthe migration condition holds then Take place the chromosome migration; end if;
Select the chromosomes for the next generation by the roulette wheel way with the elite strategy;
Create new chromosomes by applying crossover an.d mutation according to the crossover and mutation rate; until the termination condition holds;
end;
In the previous work [48], we can. guess that the quantity and frequency of communication among PEs affect the solution quality. of the parallel and distributed GAs. Therefore, the solutjon quality generated by our neighbor' communication way seems to depend on the network topology of the multiprocessor system. We also proposed Cone topology (See. Fig. 1) for interconnection networks of a parallellnachine. The solution obtained from cone topology was better than that from ordinary topologies, ring, torus, a.nd hypercube.
A feature of cone topology is hierarchical connection of ring topology. Consequently, its hierarchical topology brings out the effectiveness of migrant chromosome among PEs. We propose the PDGA not to take account of the particular (cone) topology. The PDGA has to be organized by two PEs at least. Each layer has several PEs as a group and they are connected to specific neighboring PEs since many connections of other PEs occur the immature convergence in a chromosome set. Some PEs in the layer have a connection
,
.
n
- 2
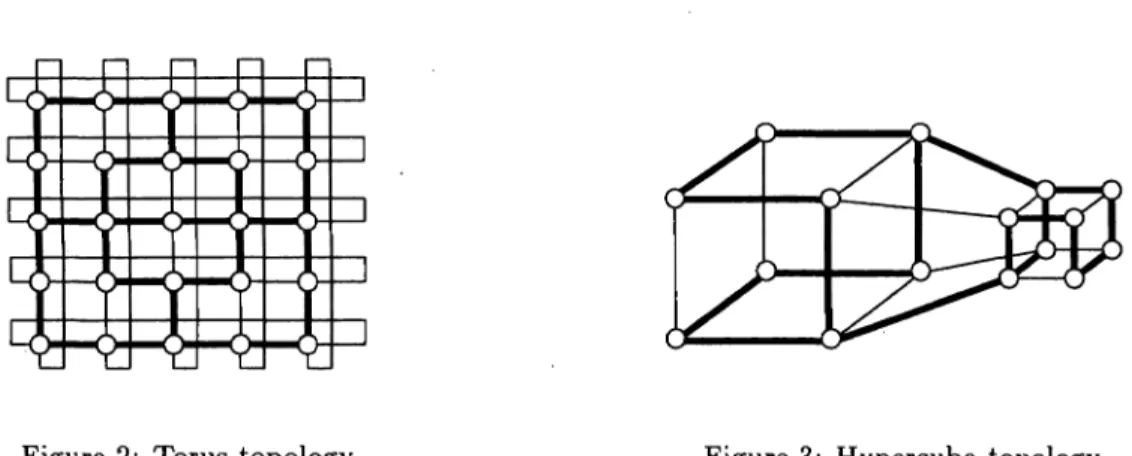
Figure 2: Torus topology. Figure 3: Hypercube topology.
network to an immediate upper layer PE except for the lowest layer one. That is, migrant emigrates froin another PE located in the same,or upper layer. The migration from upper to lower layer does not admit on the PDGA.
4
ExperiDlental Evaluation
4.1
PDGA on Ordinary Topology
Figures 2 and 3 show a torus and hypercube topology, respectively (four edges are omitted for being easy to see in Fig. 3). They are ordinary topology for the multiprocessor systems and each PE has several direct connection links. Many direct links affect the evolution by PDGA as immature convergence. We propose not to use all connection links of PE for avoiding the immature convergence, moreover to control active (migration) connections. We generate the hierarchical topology virtually in the previous two ordinary ones. Thick line means the active link and those lines compose the hierarchical topology in Fig. 2 and 3. That is, in Fig. 2 there are three layers in which the outside and small square show the lowest and middle layer, respectively. The center PE represents by itself the top layer. Each layer connects by active links. Figure 3 has two layers, the big and small cube show the lowest and top layer, respectively. Two active links connects with two layers.
We evaluate the solution quality generated by the proposed method to investiga.te the influence of Inod:.. ified ordinary topology to the hierarchical one. In this experiment, we solve by the PDGAeight benchmark instances of multiple knapsack problem [43]. Our PDGA is run on a virtual multiprocessor system imple-mented on a Linux machine with Java. Throughout the experiment, the following parameters are used in each PE:
• generation span
=
100• population size
=
3 • crossover rate=
1.0• mutation rate = 0.0 (no mutation)
In the experiment, we execute thePDGAon the virtual multiprocessor systems to COlnpare two topologies, cone and lattice in which our proposed PDGA runs. Figure 4 shows 6 x 6 lattice network a.nd it is regarded as hierarchical topology of three layers.
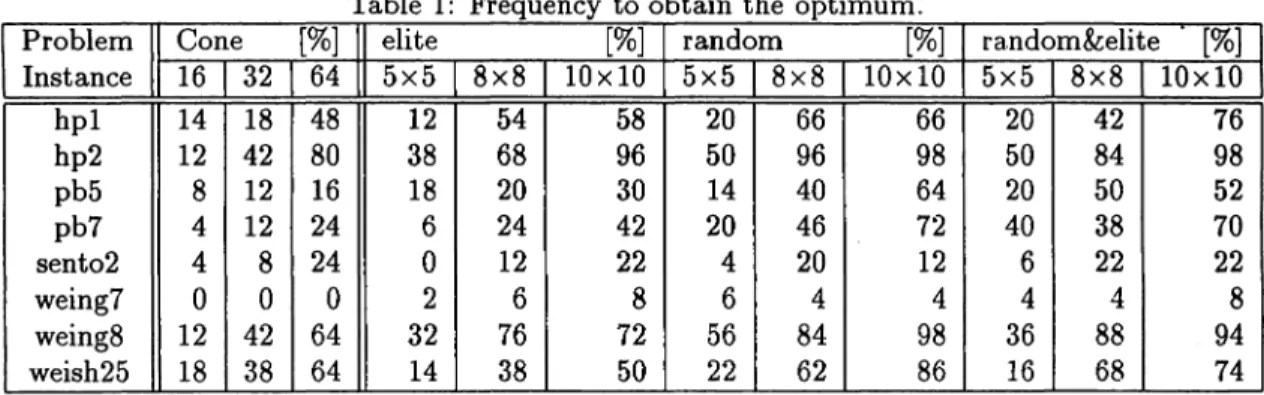
Table 1 shows experimental results comparing cone and lattice topology. Three columns, namely 16, 32, and 64 in cone, represent bypercentage how often among fifty executions of the previousPDGAobtains the optimum solution for eight problem instances in cone topology and three cases of the number of processors, say 16, 32, and 64. The value of remaining nine columns has the same substance and they are obtained from lattice- topology by the hierarchical PDGA. Names of columns, elite, -random, and random&elite, in Table 1 mean the type of migrants. The column of elite indicates that migrant is an elite chromosome which has the best fitness value in the population, random a randomly-selected chromoson1e, random&elite a randomly-selected chromosome in the same layer and an elite one for upper layer. These columns are divided into three inner columns according' t.o the size of lattice topology (the number of processors).
Figure 4: 6 x 6 lattice topology.
Table 1: Frequency to obtain the optimum.
Problem Cone [%] elite [%] random [%] random&elite [%]
Instance 16 32 64 5x5 8x8 10x10 5x5 8x8 10x10 5x5 8x8 10x10 hp1 14 18 48 12 54 58 20 66 66 20 42 76 hp2 12 42 80 38 68 96 50 96 98 50 84 98 pb5 8 12 16 18 20 30 14 40 64 20 50 52 pb7 4 12 24 6 24 42 20 46 72 40 38 70 sent02 4 8 24 0 12 22 4 20 12 6 22 22 weing7 0 0 0 2 6 8 6 4 4 4 4 8 weing8 12 42 64 32 76 72 56 84 98 36 88 94 weish25 18 38 64 14 38 50 22 62 86 16 68 74
From these tables, we find that the results obtained from lattice topology is almost saIne or better than cone. That is, we obtained better solution quality than torus from lattice topology by the PDGA, since the solution quality obtained from cone is better than that of torus from the previous experiment [48].
4.2
PDGA
on Bus Connection
We propose and evaluate the implementation of the PDGA on multiple PCs connected by bus-based network (e.g., Ethernet) in this section.
The hierarchical PDGA on bus is implemented by C++ with MPI [33]. Processes generated by MPICH have to be divided into several groups, that is, a process group corresponds to one layer and the leader of group communicates to the upper. Figure 5 shows a process group and its message passing on twenty-five processes. Each process group has the same number of processes and each process sends a migrant to neighbor in the group, that is, each process communicates with another process in the sanle layer as the PDGA with a ring topology. A leader of each process group sends the migrant to its upper layer.
We investigate the solution quality and processing time of the hierarchical PDGA on Ethernet. The problem instances and GA parameters are the same as in the previous experiment. An elite chromosome is selected as a migrant transfered within the same group, and also one chromosome is chosen randomly in leader's population as a migrant to upper layer. We use 4 PCs (SMP Linux RedHat) connected with 100Base-TX switching HUB. Each process carries out its own operation for 0.5 seconds.
Table 2 shows the experimental results comparing two problem instances, hpI and weish25. The column, namely "groupxlayer" represents the size of process group and the number of layers. The values in column "GO time" and "Comm time" mean the average processing tilne for genetic operation and for communication at all process, respectively. The last colum'n shows the average of fitness value of the final solution. From these results, we find out that communication time increases as the number of processes goes on increasing,
group4 group3 group2 group! ,~
-
- - -- - --
---
-
-- -- - - ---
--- ---', : groupO , , I "..
--
-
- ---
- --
-
- - --
-
----
-
--
- - ---
--,'o
:process • :Ieader processFigure 5: PDGA using MPI.
Table 2: Processing time and fitn.ess average of hierarchical PDGA on bus connection. hpi (chromosome length=28) weish25 (chromosome length=80) group x layer GO time
[%]
Comm time[%]
fitness ave GO time[%]
COlnm time[%]
fitness ave4x4 20.67 79.33 3378.28 44.65 55.35 9767.60 5x5 16.89 83.11 3393.14 42.64 57.36 9824.60 6x6 13.46 86.54 3395.26 36.85 63.15 9827.78 7x7 11.54 88.46 3396.94 35.99 64.01 9832.56 8x8 10.64 89.36 3399.20 31.94 68.06 9833.90
that is, many processing delays which are the collision of packets, the blocking from another process are occurred on Ethernet network. Moreover, since the optimum values are 3418 (hpI) and 9939 (weish25), the lower improvement of obtained fitness values (see "fitness ave" columns in Table 2) is cased by much communication among processors. We find out that many delays of message passing and less migration are an important factor for the solution quality using the Ethernet.
5
Concluding Relllarks
This paper considered the influence of the PDGA on hierarchical topology. In the experiment, we compared cone with lattice topology according to the fitness value. We found that our proposed PDGA obtained almost same or better solution than cone. Moreover, we investigated the processing tilne by the PDGA on bus connection. From the experiment using Ethernet, the solution quality of the PDGA did not improve very much. This was caused by the comm~nicationdelays among processes. As future works, we analyze more detail issues about the delays among processors on bus connection, and develop the PDGA on Ethernet using MPI. We also consider to apply the PDGA to a dynamical interconnection networks.
References
[1] C.Barnhart, E.L.Johnson, G.L.Nemhauser, G.Sigismondi, and P.Vance, "Formulating a mixed integer programming problem to improve solvability," Operations Research, vo1.41, pp.l013-1019, 1993. [2] C.C.Pettey and M.R.Leuze, "A.theoretical investigation of a parallel genetic algorithln," Proceedings
[3] C.D.papadimtriou and K.Steiglitz, Combinatorial Optimization: Algorithms and Complexity, Prentice Hall, NJ, 1982.
[4] C.D.Papdimtriou, Computational Complexity, Addison Wesley, MA, 1994.
[5] C.R.Reeves, Modern Heuristic Techniques for Combinatorial Proplems, Halsted Press, New York, 1993. [6] D.B.Fogel, Evolutionary Computation: Toward a New Philosophy of Machine Intelligence, IEEE Press,
1995.
[7] D.E.Goldberg, Genetic Algorithms in Search, Optimization, and Machine Learning, Addison Wesley, MA,1989.
[8] D.P.Bertsekas, Linear Network Optimization: Algorithms and Codes, MPI Press, MA, 1991.
[9] D.R.Stinson, An Introduction to the Design and Analysis of Algorithms, The Charles Babbage Research Center, Winnipeg, Canada, 1987.
[10] D.S.Johnson, "The np-completeness column: An ongoing guide," Journal of Algorithms, vol. 13, pp.502-524, 1992.
[11] E.H.L.Aarts and J.Korst, Simulated Annealing and Boltzmann Machines: A Stochastic Approach to Combinatorial Optimization and Neural Computing, John Wiley and Sons, Chichester, 1989.
[12] E.H.L.Aarts and P.J .M.V .Laarhoven, Simulated Annealing: Theory and Applications, I(luwre Academic Publishers, 1987.
[13] E.Horowitz and S.Sahni, Fundamentals of Computer Algorithms, Computer Science Press, MD, 1984. [14] E.Lawler, Combinatorial Optimization: Networks and Matroids, Saunders College Publishing, Fort
Worth, 1976.
[15] F.Glover, "Tabu search: Part I," ORSA Journal on Computing, vol. 1, pp.190-206, 1989. [16] F.Glover, Tabu Search: A Tutorial, 1990.
[17] F.Glover, "Tabu search: Part II," ORSA Journal on Computing, vol.2, pp.4-32, 1990.
[18] F.Glover, D.Klingman, and N.Phillips, Network Models in Optimization and their Applicat.ions in Practice, John Wiley and Sons, New York, 1992.
[19] G.L.Nemhauser and L.A.Wolsey, Integer and Combinatorial Optimization, John Wiley and Sons, New York, 1985.
[20] H.I{itano, Designing Neural networks using Genetic Algorithms with Graph Generation System, Com-plex Systems, 1990.
[21] H.Kitano, Genetic Algorithms, Sangyou Tosho, 1993. in Japanese.
[22] H.M.Salkin and K.Mathur, Foundations of Integer Programming, North-Holland, Ne\v York, 1989. [23] H.Miihelenbein, M.Schomisch, and J .Born, "The parallel genetic algorithm as function optimizer,"
Proceedings of the Fourth International Conference on Genetic Algorithms, pp.271-278, 1991.
[24] H.P.Williams, Model Building in Mathematical Programming, John Wiley and Sons, New York, 1985. [25] J .Holland, Adaptation in Natural and Artificial Systems, University of Michigan Press, 1975.
[26] J.Okech, M.Nakamura, S.Kyan, and K.Onaga, "A distributed genetic algorithm for the multiple knap-sack problem using pvm," Proceedings of ITC-CSCC'96, pp.899-902, 1996.
[27] K.A.D.Jong, "Genetic algorithms: A 10 year perspective," Proc. of the First International Conference on Genetic Algorithms, pp.169-177, 1985.
[28] K.Bennet, M.C.Ferris, and Y.E.Ioannidis, "A genetic algorithm for database query optimization," Proc. of the Fourth International Conference on. Genetic Algorithms, pp.520-526, 1991.
[29] L.Babai, "Combinatorial optimization is hard," Focus, vol.12, pp.3-18, 1992.
(301 L.Booker, Representing Attributed-Based Concepts in a Classifier System, Morgan Kaufmann, 1991. [31] L.Davis, Genetic Algorithms and Simulated Annealing, Morgan Kaufmann, CA, 1987.
[32] L.Davis, .Handbook of Genetic Algorithm, Van Nostrand Reinhold, New York, 1991.
[33] MPI forum, "MPI: A message-passing interface standard," 1995. http://www.mpi-forum.org/.
[34] M.R.Gareyand D.S.Johson, Computers and Intractability: A Guide to the Theory of NP-Completeness, W.H.Freeman and Company, New York, 1979.
[35] P.Spiessens and B.Manderick, "A massively parallel genetic algorithm implementation and first analy-sis," Proceedings of the Fourth International Conference on Genetic Algorithms, pp.279-286, 1991. [36] R.A.Caruana and J.D.Schaffer, Represen~ationand Hidden Bias: Gray vs. Binary Coding for Genetic
Algorithms, Proc. of 5th International Workshop on Machine Learning, 1988. [37] R.G.Parker and R.L.Rardin, Discrete Optimization, Academic Press, Boston, 1988.
[38] R.K.Ahuja, T.L.Magnanti, and J.B.Orlin, Network Flows: Theory, Algorithms, and Applications, Pren-tice Hall, NJ, 1993.
[39] R.Sterritt et al., "P-caega: Aparallel genetic algorithm for cause and effect net.works," Proceedings of the lASTED International Conference, Artificial Intelligence and Soft C~omput.ing,pp.105-108, 1997. [40] R.Tanese, "Distributed genetic algorithms," Proceedings of the Third International Conference on
Ge-netic Algorithms, pp.433-439, 1989.
[41] R.W.Ashford and R.C.Daniel, "Some lessons in solving practical integerprogranls," Journal of the Op-erational Research Society, vo1.43, pp.425-433, 1992.
[42] S.Khuri and A.Batarekh, "Heuristics for the integer knapsack problem," Proceedings of the Xth Inter-national Computer Science Conference, pp.161-172, 1990.
[43] S.Khuri, T.Back, and J.Heitkotter, "The zer%ne multiple knapsack problem and genetic algorithms," Proceedings of the 1994 ACM Symposium of Applied Computing, pp.188-193, 1994.
[44] S.Martello and P.Toth, Knapsack Problems: Algorithms and CODlbinatorial Optilnization, John Wiley ans Sons, New York, 1990.
.,
[45] S.Sahni, "Approximate algorithms for the 0/1 kna.psack problem," J. ACM,vol.23, pp.115-124, 1975. [46] S.S.Patnaik, "Genetic algorithms: A survey," IEEE Computer Society, COlnputer, vo1.27, no.6,
pp.17-26, 1994.
[47] T.Back, Evolutionary Algorithms in Theory and Practice, Oxford University Press, 1995.
[48] T.Matsumura, M.Nakamura, J.Okech, and K.Onaga, "A parallel and distributed genetic algorithm on loosely-coupled multiprocessor systems," IEICE Trans. Fundamentals, vol.81-A, no.4, pp.540-546, 1998. [49] Z.Michalewicz, Genetic Algorithms