有限変形場におけるポテンシャル流体と回転シェル容器の相互作用問題の解析

Architectural Institute of Japan

NII-Electronic Library Service

Arohiteotural エnstitute 　of 　Japan

、【論 文】 　　　日本．建築 学 会 構 造 系 論 文 報 告 集 第 435 号・1992_年5月

Joumal　of　Struct，　Constr．　Epgng，　AIJ，　No．435，　May，1992 1

rNONLINEAR 　

OSCILLATION

　

ANALYSES

　

OF

　

INTER

−

ACTIVE

　

BEHAVIORS

　

BETWEEN

．　

THE

　

POTENTIAL

FLUID

　

AND

_．

，

TANKS

　

OF

　

SHELL

　

OF

　

REVOLUTIQN

．

　

　

　

　

　

　

　

　

　

　

　

　

　

　

　

IN

　

FINITE

　

DEFORMATIONS

　有限変形場にお ける_ポ．テン シャ ル流体と回転シェ ル容器の 相互作用 問題の解析

Youichi

　

MI

〈

rAKAWA

＊

皆 川 洋一 ₁

　ALagrangian　function　which 　governs 　illteractive　beh4Viors　between　the　potential　fluid　and 　elas −

tic　tanks　under 　ground　e’xcitatio 皿s　is　shown ．　Then ，　the　variation 　of　the　Lagrangian　function　is』de−

rived ．　Applying　combination 　of　the　finite　element 　method 　and 　the　Galerkin’s　method 　to　the　varia ，

tion　_yields　to　ordinary 　differential　equations 　of　motion 　with 　arbitrary　degrees　of　fFeedom．　Adopt．

ing　t｝1e　

Galerkin

’s　prqced_りre　enab 且es　to　obtain 　sta恒onary 　solutions 　of　a．cylindric _尹l　sheU 　tank　con −

taining　water 　under 　periodic　force

，　which 　simu 且aしe　nonlinear 　vibratien 　responses 　of　a　tank　on

shaking 　table．’．．．．．

　Key 盟ortlS _：のylindn’cal ∫hell

，　tank，　nonlinear 　m

’_bration

，　Potential　

fluid

，　subharmonic ，　higher−ham　onic

　　　　　　　　　円筒シェ ル，タン ク，非線形 振 動，ポテンシャ ル流 体，分数 調 波振 動，高 調 波振動

lntroduction

　There ．were 　many 　reports 　to　investigate　responses 　of　cylindrical 　shell　tanks　contaiping 　fluid　

in

vibration 　tests．　

Clough

　et　als｝_showed

　that　responses 　of　vibrations 　on 　a　shaking 　table　included　vibration modes 　where ．the　sections 　of　cylindrical 　shells 　took　out −of−round 　shapes _，　which ．were 　to　be　related ．　_to

initial　imperfections　of 出e．　tank　geometry ． ・ ．

　Assuming 　an　inviscid　and 　incompressible　

fluid

　in　infinitesimal　

deformations

、yields　to　a　

linear

　theory

of　the　

interactive

　

behavior

　

between

　the　potential　

fluid

　and　elastic　tanks　which 　enablesus 　to　obtainuseful

engineering 　knowledges5）・8  But，　this　theory　offers 　no 　e弄planations　to　response

’ s

，

observed in_vibration

tests　which 　_are　sure　to　nOnlinear 　vibrations5 〕_．’

　　　　　　　ト 　Luke ’，

　showed 　that　the　_pressure ．expression 　of　the　_potential　

fluid

　gave　a．precise．Lagrahgian　fμnction ．

for

．the　classical 　water 　wave 　problems　in　

finite

　wave 　

height

．　The　Lagrangian　is　

defined

　in　the　region 　of deformed　configurations ，　Applying　la　step ・

by

・step 　integration　method 　to　the　

function

　

derived

　from　the

functional

，　

Nakayama

　and ，　

Washizulgl

　analyzed 　transient　sloshing 　responses _，　

Applying

　the　Maclaurin ’s series　to．　the　functional，　_We　can 　get　a　Lagrangian　

defihed

　in　the　region 　of　undefor 焼ed　configurations ． Adoptirig　the　procε

dure

，　Kimura　et　a13）・and 　

Ohmori

　et　alio 　analyzed 　the　nonlinear 　periodic　sloshing ．

responses 　and 　showed 　some 　

higher

−

harmonic

　sloshing 　vibrations ．　 The　main 　sloshing response corresponding 　tothe_lowest　natural 　frequency　is　few　affected with thb　elastic ・deformations　of

containers7 ，_．

　But ，　vibration 　tests　show 　that　

breathi

ロg　vibrations 　of　elastiq 　containers 　under 　some

external 　

frequency

　regions 　stimulate 　sloshing 　vibratlons 　wi ヒ

h

　

large

　amplitUdeslsJ ．

　Minakawa ［o ）・i2 ］_showed

．

　a　Lagrangian　

function

　of　interactive　

behaviors

　

between

　the　potential　

fluid

　and elastic　tanks

．

in　finite　

deformations

，　where 　the　iptegral　6f　pressure　expression 　of　the　fluid　was 　

dealt

　as

本 論 文の一部は文 献 11 〕，13 ｝，16 ｝に報告し た。

＊ Prof．．　Faculty　of　Engineering　Kagoshima 　Univ、，Dr．Eng． _鹿児島 大学 教 授・工博

一

₉₁

一

Architectural Institute of Japan

ArchitecturalInstitute of Japan

negative external work.

Herewe

derive

basic

differential

equations of theinteractiyebehaviorsbetween the_potentialfluidand elastic tanks in

finite

deformations

when subjected base rnotions and establish ordinary differential

equations of motion of the _problems. Inorder toobtain

differential

equations that allow us to study

every nonlinear vibration _{phenomenon taking place}inthe interactivesystem, we consider nonlinear effects with respect tothe

free

surface and theinteractivesurface

between

the_potential

fluid

and elastic

containers. Then, numerical analyses of theequations

let

us understand some of nonlinear responses observed invibration testsisLiG).

1.

A Pressure Expression of the PotentialFluidinMotion

Inorder todescribeatank containing the _potential

fluid

inrnotion, we take a Cartesiancoordinates in

inertiaspace,say origin O and

OX,

OY,

OZ.

Local

Cartesian

coordinates

fixed

toatankinmotion are

set ox, oy, oz, where unit vector corresponding to ox, oy, oz and

denoted

i,

j

and k.

The

unit

vector k ismeasured _positive along the outward directednormal tothe undisturbed freesurface of the

fluid

_(Fig.1),

Considering shells of revolution, we employ a cylindrical coordinates

(o-r,

e,

z)

instead

of the

local

coordinates

(o-x,

_y, 2).

Suppose

thattanks move with velocity v,observed

by

an ebserver ina inertiaspace, and an obseryer

fixed

tothe tank observes fluidvelocity v at a _point,an observer inthe inertiaspace observes fluidvelecity _q at the same _point.

q=vo+v････････'･･--･-････-'-･･----･-･-･---･･-･･-･･-･･-････････-･･-･---････････---･-･･-･･---･-･-･･(1) Introducinga velocity potential_¢ intothe velocity v observed

by

an obseryer

fixed

tothe tank _yieldsto

v=grad

ip

-･--･････--･---･--･･･--･･-･･---･･･-･-･････-････-･･･-････--･---･･--･･･････････････-

(

₂

)

Setting2 coordinate ttndisturbed free surface 2,, the acceteration of gravityg, we obtain a _pressure expression of the _potential

fluid

at a

_position

r

pL[Sgrad

ip

grad

ip+

di+

bor+g(x-zo)i

== _p( t)-･･･-････････････････-･-･･････-･-････････-･････-

(

3

)

where dotsdenote

derivatives

with respect to time and _p, is mass

density

of the

ftuid,

Setting

wave height_n on the

free

surface

Sf

of the

fluid,

elastic

deformations

vector u on an

inter'activesurface

between

the

fluid

and theshell

S,,

The

strain energy

density

function

of the elastic

tank A ancl mass

density

of the tank _pE, we

have

a

Lagrangian

functien

k(ip,

_n, u) thatgoverns the interactive

behavior

of elastic tanks containing the _potentialfluidin finitedeformationsiO'･i!'

1}t(

_ip,

_v, u)= _.]:t'

[fflC,.,.,

pL

(i;

grad

op

grad

ip+

di+

ber+g(z'zo)]dV

-fflLl

Ik

(S

_bab

_{+avo)-A<u)jdv]dt} ･--･･--･---････-･･････-･--･･･････････-･･-･-

₍

₄

₎

where 14iand VL are volumes of theelastic tank and thepotential

fluid,

respectively,

The

fluid

volume

is

a

function

with respect tothe wave

height

_o, and elastic detormationsu. Applying a step-by-$tep

integration

rnethod to the

function,

we may _gettimetransient response ef a contalner with _potential

_z k fluid,But,itisnotasuitable way tounderstand globalperiodic

response

features

of the container under _periodicexcitation.

..--lt ""'Ks S L --- --..sS ,n1;i z _t..-' o e x,r i Y x Cylindrical

92

-' Nst)x ltx2yj

Fig.1 Tank inMotion

Then,

adepting themethod of

Maclaurin's

series tothe

function,

we tryto

derive

a nonlinear

differential

equation with respect to

each component of

deformations

defined

in the regien Qf

undefermed configurations,

Then, a variation of a functiondefined in _the volume is evaluated

by

sfflC,...,Fdv=fllllC,.,.,aFdv+flCFaoknL

...,..ds'

Architectural Institute of Japan

NII-Electronic Library Service

ArchitecturalInstitute ofJapan

(see

Appendix 1),where _nL isan outward directednormal vector of the.fluid,and

S'

isthe area after

deformations,

Considering

Eq.

₍

5

),

we can obtain the variation of Eq.

(

4

)

6zlh:=

J[`'

[fl)C,

[aL

(e

grad

ip

grad

ip

+

di

+

bor

+g(z L _Zo)16

rpknL].; .,..

dS'

+flC

[pL

(Sgrad

gbgrad ge+ gb+

bbr+g(z

`L _zo)]].

auntds'

'

+fflLl,.,.,pL

(g

rad grad 6ip+sdi)dV-fflC

[pEaab(u+

v,)- ou oA1ou]dv]dt-- ･･･-

(

6

)

The

3rd term of

Eq.

(

6

)

is

_partially

integrated

with the aid of

Appendix

1

the Third Term=L'i

[fk...,pLgrad

_{ipnLacaS'-fl4)pLijknL5todS'-fL}

_pLanL6vdS'

]

,

-ffl.,.,

bL

_div

_(grad

_¢

_)esipdv

_dt

--･r･････-･--･･････--･･-･････-･･----･･-L

₍

₇

₎

where

S,

and

Sb

are the interactivesurface and undeformed surfaces of･the

fluid,

respectively. The a'rea elements on the

free

surface Sf and the interactivesurface S,are expressed as

follows:

nLdS'=(-n,.i-n,.j+k)dxdy on

S.･-･-･･---･･-･･････････-･-･････:･････-･---･･(8)

nLdS'I( zv,sti+t zv,et2-(1+u,s+-l)

b,e)n]

rdeds on'

Si--:････････r･--･･-･･････-･---

(

_g

)

'

where the expressions shown

in

Appefidix3are

used, . _. '

Applying the methocl of Maclaurin'sseries with respect to_,eachcomponen,t of

deformations

tothese･

'

functions we obtain '

'

[t

grad ¢ grad

ip

+

di

+

bor+g(2-2o)].iS

grad

ip

grad

ip+

di+

bor+g(2-zo)

tt

+ zvl

(}

grad

ip

grad

di),.+

di,.-

D.

cos a cos

e-

b,

cos aSin

e+(b2+g)

sin a+S w2

di,..

.H."".HH."-"HH-"""""".HH."""""."H-H.HHHH.H..-H""---(10)

where

be;b.i+b.j+bzk.

[{grad

ip-ti)a

¢

].#(grad

ip-b)0ip+wl(grad

ip),.crip+(grad

di-u>fith,.l

････--･-t･････････-･･

(11)

where _quadratic and cubic terihs with to respect each component of

deformations

are employed. Introdgcing combination of Eqs,(8

),

(9

),

(11),

and

<12)

intoEq,(6

),

we can finallyobtain the variation

alh=y:ti

[fL

_p,

[S

_grad

¢ grad

di

+

di

+

bor+

rp

I

(S

grad

di

grad ¢

),2+

th,z+

b-+gl

+Sth,..ep2]arprdedr

+fl41_pL

[(

_¢,z- rp,rip,r-l, o,eip,e-

ij)6ip+

rp

I(ip,2-nirip,r-",

rp,e¢ ,e-

ij)6ip),z

+S _rp21(ip,.-

_ij)6cbL..]

rdedr+fk _pL

grad

di'nLcripdS

'

+flC pL

[

cru zv,s

(e

_grad

ip

_･grad

ip

_+.

di

₊ tv

di,.+

b.(ep-

_{w cos} a cos e)

+D.{g-zvcosasine)+D.(z+tosina)+gCz-2o+wsin'a)'1

+tiv-;-zv,elS _{grad ¢} 'grad

ip+

di+

_wdi,n+

Dx(x-

_{zvcos a} cos e)

'

+

b.(y-wcos

asin e)+e.(z+wsin a)+ g(z-zo+ tvsin a)1

-fiw

(Sgrad

ipgrad

ip+b+w

(S

grad

di･grad

op,.+

wdi,.+S zv2di,nn

+

b.(x-

tvcos orcos

e)+

b,(y-

zvcos a sin e)+

b.(z+

wsin a)

Architectural Institute of Japan

ArchitecturalInstitute ofJapan

+g(z-zo+wsina)l]rdeds

+fl41 _pL

[

sipIw,sdi,s+Lil7, zv,edi,e-

iptn+

ab+(dau,s-tv,sto+"

(ile)v,e-

zv,eb)]

+ tv

[(w,sip,s+"t

ZV,eip,e'e,n),.

a

_¢ +(-

_ip,n+

W,sdi,s+"t IV,eip,e+ th)6ip,n]

+li w2(-

di,n+

de)6w,..]

rdeds

-fflLl _pL

_div

_(grad

_{sb)sipdv+fflC1}

_6v

_{AE

_(u+bo)+

_oAlaaFdv]

_dt

･･---･-･･･--･-････-･

_a2)

which _governs the

interactive

behavior

between

the potential

fluid

ancl elastic tanks

in

finite

deformations.

Since

the variation isdefinedin the initialundeformed configurations, we can _get fionlinear ordinary

differential

equations with constant coefficients when applying some discretizing proceduressuch as the Galerkin'smethod,

2.

Derivation

ot Nonlinear

Ordinary

'DifferentialEquations of Motion

There may

be

several ways to analyze

Eq,

(12}.

Here,

we appty combination of the

finite

element

method and theGalerkin'smethod totheequation, and obtain nonlinear ordinary

differential

eq.uations of motien.

Applying

the

finite

element method tethe

linear

homogeneous

termsof

Eq.

(12),

we

have

eigenvalue _problems that enable us toobtain natural frequenciesand corresponding eigenvectors.

Then

substituting the eigenvectors to Eq.

(12),

and adopting the Galerkin'smethod, we obtain nonlinear

ordinary

differential

equations of motion with arbitrary

degrees

of

freedom.

2.1 Analysis of NaturalFrequencies and Eigenyectors

'

A functional

Ik(

di,

o,es

)

corresponding tothe linearhomogeneous terrnsof Eq.

(12)

isexpressed as

follows

Ik(gb,

o,u)==

J[t'

[fk

_pL

(

_{gbo+S gn2)}rdedr+fl4 pL

(-

di

w-e gzv2sin a) rdeds

+ffzai _pL

_grad

_ipsrad

di

dV-ffL

(i

_{pEaa-AL<u)]dv]dt} ････-･････--

"3)

where

integrals

are _performed inregions of initialundefermed configurations and AL(u)

is

_quadratic

term with respect to displacementcomponents of the strain energy densityfunction.

Adopting circular strip elements forthe wave height_n, triangular ring elements forthe velocity

potential

ip,

and conical

frusta

for

theshells of revolution, and expanding them inthe Fourierseries in

circumferential

direction,

we

have

the expressions

u=Z][en][N]1d.L o=Zcosne[N.]ln.l,

ip=Zcosne[IVw]1ge,l''"''-''''''････(14-],2,3)

n=o n!o ntie

where

ld.L

lny.I

and

lgb+g

are _generalizedcoordinates, nodal vectors corresponding to the shells of

revolution, the wave

height,

and the _potential

fluid,

respectively.

The

expressions

lead

gradgb==EI][e"][L]lgehl,

w=Zcosne[N.]Id.l-･･････`･----･-･･････････････J･･i･･-･･･-(14-4,5)

n=O n=O .

Substituting

Eq.

₍₁₄₎

into

Eq.

_(13>,

we obtai,n the

following

variation

alk'::J:t][Olgehi'[lgh]lgbhl+01n,,l'[G.]ln.l'filgeAi'[S.]lh.l+cri,laI'[S.]'lsbll

- - tt

-Dlgbn'[R.]Id.lrOid.I'[R.]'lsbAl+crIdnl'([llf;2]Iddi+[Kn]Idnt)]dt'''''''''''''-"'''''''-''(15)

where

[lvh];p,ffXl[L]'[e"]'[e"][L]dv,

[G.]=pLfltg,g[N.]'costne[N.]rdedr,

[Sn]

r= _sb.

flC

[Ne]

'cos2 _nO

[Nn]

_{rded r,}

[Rn]

== -pL

flC[Ne]T

_{cos2 ne}

[N.]

_rdeds,

-94-Architectural Institute of Japan

NII-Electronic Library Service

ArchitecturalInstitute of Japan

'[M.]-fflLliig[iy]'[e"]T[e"][N]dv,

ld.F[K.]ld.I-2ffllQAL(u)dv

_.

' '

and the superscripts

f

and iof _generalizedcoordinates mean thatthey are corresponding tothe surfaces

Sr

and

S,,

respectively.

t t ./

If

generalizedcoordinates corresponding to nodal velocity _potentials

Ggbhl

ale resolved intoeach regipns

lgb(},

lcbAI

apd

lgb#l

corresponding to

S.,

S,

and

VL,

we

have

the

following

equations

zmt.vtfVv!PlriIP:tL

Vtt

ViL

VL, .!Pl,,

l31l

ip:gbAdik-[S,n

Re.]l?nldn1O･---･---･-･---

(16-1)

.

[

+[

2.

]l

d'7h.l

RO.

]

'

l

tz'il

=O

(16"2)

The

above _yield to

'

[M

'] _+[K']

l,drp".I

_:=O

"""'""""'"H'HH'"v"H'-'-"'""L-"'･--･--･-･--･---(17-1)

[:i,i

[Son

RO.]i3･ll,

lipkl=-[W:LL]L'[VL.VLi]I:ll'''''''"'''''''

-'''(17-2,3)

'

where

[M']=([:

_1[l.]'t'[So"

_RO.]

'[ipff]-i[So"

RO.])･

[K*],=[Go"

£

.]

[Vel]-'=([

Y,;

:,l]-[

_{vWl,':][v.]-i[v,.v,,])}

-i

' '

The expression Eq.

(17-1

)

allows us toobtain natural

frequencies

a).,and corresponding eigenvectors'

y.i

(.i=1,

2,･･･), where generalized coordinates with

different

Fourier

number cann'o,t coupled because of the orthogonality of the Fourier expansion, and natural f.requenciesare 'num'beredto satisfy

-t. t.

Wnl<Wn2<tuns<'''

2.2

Nonlinear･

Ordinary

Differential

Equations

of

Motion

Selecting suitable modes of vibrations

leads

toa moclal matrix

[Y].

The normal mode corresponding t6 the naturat

frequency

cv. and

the

eigenvector y.,isexpressecl aS

ein,..

,Asstirhing.thatall unknown

i

generalized coordinates'are expressed

by

a superpositi6n of the selected modes of vibrations, we

have

' '

idl=[Ya]leL

lnl=![Y"]le}･････････:･･････････-････････････-:･--･--･････--･-･･････-･-･･･i････････(18-1,2)

'

where

l6I

isthe normal coordinate v.ector. '

SubstitutingEqs.

(18-1,

2)into

Eqs,

_(17-2,

3), we obtain an expression

forgeneralized

coordinate

for

t t

'

the velocity ･potential

' ', '

1'

- . t

l

¢

I-[Y"]lel･････････-･････----･･-･･--･--･･-････-･-･-･････････････････････---･･･-･･････････-･-････････(18-3･)

'

Substituting,Eqs.(I8)ipto

Eq,(14)

and usin.g the summation conventiori,,we obtain

'

- t t

ua = Y:k, _o= Y7e,

¢ == Y."･

6j

(a=1,

2,3_o'=1, ･-)-`････--･-･･････`･･･-･･"-･･--･･･i･･i

('19)

' where ui, u2, and u3 mean u, v, and w, respectiveli. ' '･

'

Substituting

Eq.

(19)

into

Eq.

₍₁₂₎

and applVing the

Galeikin's

method, we obtain '

olh=y:t![cr&

(M.g,+lilr,ye,+lilr,,,ee,+Iilr..e&s+I2;,og,e,+I:;ke,4,

_. ' ', _,

+I2S,ile,e,g,-.f}+Ii5,.e.+IP,,.eb.)+0e,(lllZe,e,+IISO,lee,&)]dt

fo==1,2･,3),

-.,...,.,."".,.,.,.,.HH...,h..."-."H".H".,.,,･-･-････-･･･････--･-･･･-(20)

'

where

b,,

b,

and

D3

mean

b.,

b.

and _b., respectively. '

t t

The

expression

leads

thefbllewing equations of motiofi

tt t t ' -H rrm. - t.

M,,6,+K,,e+lil.,efi+K.,,Sene+(lr･,!-:-Il･j2)e,G+(I:Jk-IIJ-2)g,e,

･ "- - -.

-Il,OO,le,e,g,+(I:e･kl-Il,O,Ol)E,e,e,-ll,OO,IE,eL,e,+P,.D.+P..gb.=.fl････:;･･･-･･--i･･:･･t････-･･･(21) ' ' '

-95-Architectural Institute of Japan

ArchitecturalInstitute of Japan

This

nonlinear ordinary

differential

equations letus obtain bothtransient and stationary

dynamic

solutions of the

interactive

behavior

between

the_potentialfluid and elastic tanks

in

finite

deformations.

3.

VibrationTests and

Numerical

Analyses

Tanks

employed in vibration tests may

have

some _geometricalimperfections.

Though

shaking tables areintendedtoexcite inadirectionwith sinuSoidal wave, _periodicvibrations observed on thetablemay

have

noise components of vibrations such as

higher-

and sub- harmonic components.

On

theothe/r

hand,

the nonlinear ordinary

differential

equations of motion may show various complex

dynamic

behaviors

depending

upon some _pararneters of the specimen and the external

force.

Here,

in

order tounderstand

global featuresof responses of a cylindrical shell tank observecl invibration tests,we analyze a model tank on a shaking tableexited with a _periodic

harmonic

wave. Analyzed responses are examiiLed and compared with these obtained by the vibration test.

3.1

Cylindrical

Shell

Tank Model

An

analyzecl cylindrical shell

is

made with vinyl-chloride

film

of thicknessO,51mm, and

have

diameter

83.

68

mm, height200 mm, and a

lid

with acrylic resin ef thickness 8 mm at the top ofthe shell,

Adopted

material properties of the

film

and thelidare shown in

Table

1.Settingwater

height

of the tank

170mm, and acceleration of the shaking table3_g

(

=2 940cmlsecZ :root-mean-square value), we made

a test model.

We

have

a mesh model

for

the

fin'ite

elernent idealizationof thesystem as shown inFig.2, where the

cylindrical shell and the

lid

are

divided

in

20elements, and the water volume and the

free

surface are

clivided

in48 and 4 elements, respectively.

3.2

Response

Curves

obtained

by

VibrationTests

a)

Typical

Responses of

Shell

Displacement

obtained

by

Vibration

Tests

Here, inorder toset up objectives of numerical analyses, we summarize typical responses obtained

by

vibration tests.Adopting amplitudes of responses of relative displacements

from

theshaking table, we measured shell

displacement

at three_points.

Two

of themwere locatedon excitation axis

e=oe

at lgo

mm and 100mm above the tank

bottom,

another was locatedat angle

e==

900

from

theexcitation axis at

100

mm above thebottom, Amplitudes-frequency responses of thefundamentalharmonic oscillation at the three _pointsare shown in

Figs.3-1,

3-2, and Fig.3-3.

Main

resonance regions of the normal

coordinate

e,

and

6,

are observed

in

neighborhood of the external

frequencies

124Hz and 4osHz, respectively. The amplitudes-frequency responses of 112-and lf3-subharmonic oscillations

for

the

three _pointsare shown

in

Figs.4

and

Fig.5,

respectively.

It

was one of the most remarkable nonlinear responses that in

neighborhood of the resonance region of

62,

112- and

1!3-subharmonic oscillatiens branched out and showed significant vibrations.

The

response amplitude of the l12-subharmonic

oscillation

in

the region is

larger

than the response of the

fundamental oscillation.

And

the response of the

113-subharmonic oscillation

is

as much as that of

fundamental

oscillation.

However,

except the neighborheod of the reso-nance region of

e2,

we could harldyobserve responses of the

subharmonic oscillations. Itisnot

known

the reason why the Tablel MaterialProperties

MeterialYeung'skodiluGPaPoisso"'sRatio"assbensitykglm3

Viny]-chLoride

F[ln 3.3S o.ss 1.,37xlos

herv}ieplete3.34 o.se '1.22xlO`

k

coas

s

83,ee" Lid ,unit:"

wt51

Fig.2 Sectionef Model Cylindrical Tank and Mesh forAnalysis

-96-Architectural Institute of Japan

NII-Electronic Library Service

ArchrtecturalInstrtute ofJapan ( Fig 3-1 1( Fig.3-2 ( Fig.3-3 ( Fig.4-1 ( Fig.4-2 d( Fig.4-3 mm) ,6 ,5 ,4 3 ,2 ,1 o 30 60 90 !20 150 IBO 210 240 ?70 300 330 360 390 420 450 ' CHz)

ShellDisplacement-Frequency Curveof Fundamental Oscillationat _e=Oe at 190mm above TankBottom rnm) ,6 ' . .s ,4 ,3 ,2 .1 e 0 (Hz)

ShellDisplacement-FrequencyCurve of Fundamental Oscillationat 0==e"at 100mm above Tank Bottorn

mm) .6 .5 ,4 ,3 / ,2 1 o O <Hz) ShellDisplacement-FrequencyCurveof Fundamental Oscillationat e 90eat 100mm above TankBottom

mm) .2 .15 .1 ,05 o 0 (Hz)

SheLI Displacement-Errequency Curveof 112-subharmonic Osci]latronat e=OO at 190mm above Tank

' Bettommm) .2 .15 ,1 ,05 o

OcH,)

Shell Displacement-Frequency Curveof 112-subharmonlc Oscillationat e=OO at 100mm above Tank

Bottommm) .2 15 .l ,05 o ' 0 (Hr)

Shell･Displacement-Frequency Curveof 112-subharmonic Oscrllattonat e=900 at 100mm above Tank

Bottom

--

97

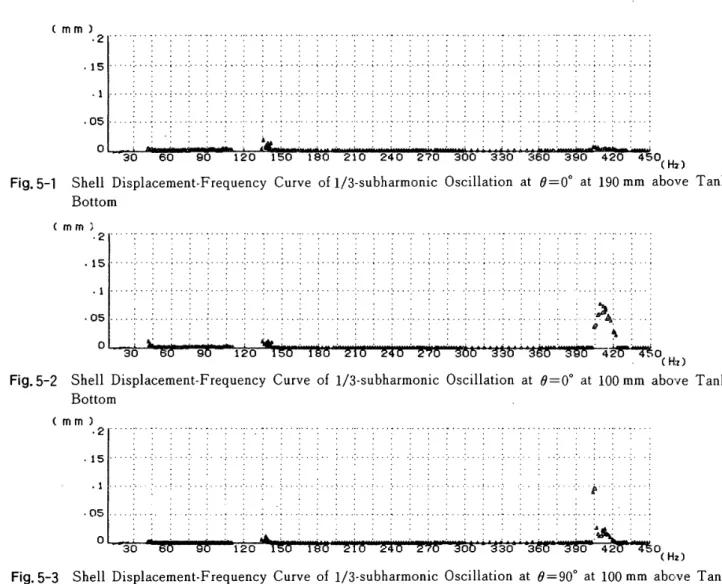
Architectural Institute of Japan ArchitecturalInstitute ofJapan {mm} ,2 .15 .1 .05 o Fig.5-1 Shell i.. :- -:

1

I ; -/- ,/. t :, .i. i, -:. ./ tttt t t t ttt t t t / t t t t t t tttt cm 30 60 90 t20 Displacement-Frequency Bottomm) ,2'''':''･1･･･ tt tt tt tt lt tt tt '''''1' '' '1''' tt ,1 t/_.05 ttttttttttttt tt tt tt tt o-tttttt ttttttttt tttttt tttttt tttttt tttttt tttttt ....I. _{.. ,..../ ., .1. .. .1 .} ttttt ttttt tttttt ttttt/ i--･1-･--1---.･-1--･-1･ tttttt ttttt tttttt_tttttt t...,.t,..t.,.._tttttt .,t, tttttt tttttt .ttttt ' 114 Curve of113-subharmonic ;. 1 1 tttt 330 Oscillation

i'

-I･ -,-360 3O 42 4O CH7i) at e=oO at 190mm above Tank

Fig.5-2 ( 30 9 120 ShellDisplacement-Frequency Bottommm) .2'････1･･･/'･･1'･'1'-･/･･･:'･･/･･=･ tttttttt tttttttt tt tttttt .ts･････I･･･!･･･1･･'1'_ttt/ttl '''''''1'''''' tttttttt tttt ttt -1 . /,,., 1..,..,/.,..1.,.,/. .t t t.. t tt ttt t tt tt t 05 tttt ttt tt tt ttttt ttt tt tt tttttttt tttttttt tt tttt/t .t.. ... o- -･ ･･ Curveof 113-subharmonic ttt_t ttt_t ttt ttt ttt It/t /t.tltt Oscillation

oK 4mgo . CH,t) at e=OO at 100mm above tttlt 1 _'e'1 la Fig.5-3 Tank 30 i20

Shell

Displacement-Freqttency Bottom o

Curveof _{113-subharmonic} Osci

3011ation3 042 O

(Hi) at e=90e at 100mm above Tank

subharmonic vibration responses take place,

b)

Expressions

of Response of the Strainof CircumferentiaiDistributien

Adopting

sampling timeinterval12rr!to

(w

:

frequency

of the extemal periodic

force)

and sampling

number 64

fer

every _point,we obtain responses of strains of circumferential

distribution

at 16_points at the mid-height

85

mm

from

the

bottom

of cylindrical shell tank, They were evaluatecl to coeffic:ients of

Fourier

series

for

the circumferential

direction.

The

responses of thestrains were also resolved to

harmonic,

higer-harmonic,

and sub-harmonic oscillation components as follows

e(e, t)#

tY.,

[I

Qolt+tl,

(Q..

eos ye+R,,sin ve)l cos

kgt

+( Soh+

tl,(S.hcos

ve+ Tvksin ve)] sin

hlitt]

･･･-i-"････-･･･････---････････-･･,,..

(22)

In

order to compare the strain responses with analyzed responses we introduce root-mean-square

values of strain with respect tecircumferential

distribution

for each

harmonic

oscillation of component

as follows

its1,=[Q:,+

Sg,+S

tT.,(QZ..+R:,+

Si,+ Ti,)i12]

(h=

1,2,--, 31)--･-････.,..,..,,,.,,.

(23)

Setting

acceleration of the shaking table 3

g

<root-mean-square

value), we had the strain-frequency response curves at the mid-height line.The strain-frequency responses of

fundamental

harmonic

oscillation are

depicted

in

Fig.6, where

h=6

in

Eq.(23).

The

1/2-subharmonic and the lf3-subharmonic are shown in

Figs.

7-1

and

7-2,

respectively. Responses of the subharmonic oscillations are observed inthe region ef the externai

frequency

[404,

422].

The

instable region of the subharmonic

-98-Architectural Institute of Japan

NII-Electronic Library Service

ArchitecturalInstitute of Japan , xi6G 4oo 350 300 zso 200 150 1OO 50 e

lell..,..

1:1 lh･･･ /t :t .tt rms '

･-･--･ ･-･･

1/1･

-"",･11

･.OtiSui･.･E;.ti-pti'IYb.+htsGS

3o so go i?o tso IBO 210 240 27e 3DO 330 360 390 420 450(H,) 'Fig.6Strain

(Fms)-Frequency

Curveof the FundamentalOscillationobtained byVibrationTest

'

'

-6

xio soo '''':;'';･'''v'''7'''i''r'v''/''''i'.'/'''.''''l'''1'''i'''i''''1''''i'''1'''i'''T''''

f'ti''''"'i'''1

4oo･･･-･/･･./･･･/････/･･･+･･･/･･i････/･･･-i･･･/･･-E---/--- /-'.' l''/' '/''']･''/'･･･/･'''/''. ,'''r',/ ttttttttttttttt tttt tttt

;::1:lll:il111il:i-･･･'i'''ll･1111･11:i:l:i･1･111111Illl:I/11.･l･;il･i:i･111;1･ll･1;11i･1:Il"S,il:l:l･

1.00･･-･･1････1････1,･･･.･-1. --1---S-･･1-･･1････1････'i ･i･･-I･･-･'1-･･1････1･･-'1･''''1''''1'4''1,,'''i e' ''' ''''' ' ' ' 3o 13 41 OcH,)

Fig.7-1 Strain

(rms)-Frequency

Curveef 112-subharmonlc Oscillationobtained by VibiationTest -6

xio soo '''''i''i'',,,'/'''i'''/'''.''''I''i''i'''/''''1''''i/'･''I'''/''''i''''i'''1''''1''''1''''''Fm'si'"'I''_/

400'''''r"r'''v'.I'''i'''/' /,''''l''''i'''i'''{''''/' 't''1'/'''r':'''/''''/''''/''_{, .} ','''r''':

'

ttttt... ttttt tttt

300-････1･-･･;･･･:････1-･･1････:･･･.'-･･･1････i･･･:･-･･/････.･-/････,････.･･/････1････l･.･-1･･,･1･-･･1.･.-･･･1,.･,1.･.,i

t /tttttttttttttttt.tt t. .ttt

200 .---1---

l-

--,1-

[--･-,i---i,･･･-1--･

1･-･･i,･･-i･･･-1-･･･i････'lv･･1････1i････1i････l'･･'/1''''1i''''1''''1''''l'!'''1''''1'

''i

ioo--･･･i-･･･I････1････I････I････/････'････i････1･･･-l････1････1･-･･1････1････1･･･E････1････,････.･-1････,･･･l-･K･･･1-･･･, 111111･11/11//1////1// lsl1 o . 30 13 .. . 41 O(va) ' t . '

Fig.7-?.Strain

(rms.)-FIequency

Curveof 1!3-subharmonic Oscillationo,bt7ined by VibrationTeE,t

'oscillations

may

be

clividedin

two region,

One

is

th'eregion

[404,･

406]_, another isther'egion

[407,

4Z2] , where responses of strains in

Fig.7

and these of the displacementof thg cylindrical shell shDwn in

Figs.4 and5may indicate

differnet

vibration' modes. .

The subharmonic oscillation

Fesponsgs

happened

tg

branch

ou't in a regien of external

frequency

(Hz)

[404,

422],' which did.n'tobserved under-the acceleration

_gf

the shaking ,ta.ble'1

g.

The

strain corresponding to

Eq.

(23)

is

also used as the strain for each harmonic oscillation in

following'theoretical afialyses.

3.2 Natural Frequencies of a

Cylindrical

Shell

witb PartiallyFilled

Water

,

Computed

natural

frequencies

of

bulging･

vibrations are shown in

Table2,

_where resonated

frequencies

observed

in'vibration

tests are also depicted. , ' ･

3.4 Nonlinear VibrationAnalysesZ) , ,

The

vibration modes corresporiding

to

the normal･ coordinates

g,,and

e,

are employed forthe

Galerkin's

method, These normal modes takenon-zero values under _ground excitations, _generallyL

And

modes corresponding to,e,

(i=4,5,6)

which can take

identical

zero values are employed to

derive

model nonlinear ordinary differentialequations of motion. /

3,5

Response-Curves

of the Fundamental

Harmonic

Oscillation

of

Each

Norpaal

Coordinate

a)

Response-Curves

of the Fundamental

Harmonic

Oscillation

,The

fundarnental

harmonic oscillation of the'normal coordinates are examined

by

assuming the

following

steady-state solutioqs .. , ,. . ･,

Si=CH,iCOSa,t,

62=Cn,iCOswt

････-･--･･･････.･･(24-1,2),

Computed

strain. response-curve･at the

mid-height

circular

line

(85

mm

from

the

bottom

of the

･sheli'_{tank) isshown inFig.8} with

O,

where

another curve with v cerresponds to _strain

response curves obtained by the

linear,theory.

Table2 Natural･FrequencieSof EachCiicumferential Number N(Hz) No1234567 124 2ee'408 No.1(eMp.)(theery)205.tttt.218.3.1.2.2t5;-124.4161''tttttt163.0....tt123,9126tttttt131.1186tttt186.1283.6･420.'4' co5 22g40.36380tttttt354.04T3t-tttt4T8.5 Ho.2(exp,),(lheery)7as,7co3.9429.3se3ttt31S.6272,4ttt283.4tt-t-t He.3texp,i{theery)8se.9701.7T66,7605.5510,Ot..47S.75e8.7.'oo'hl'o' -99-NI･I-Elect'ronic Library

Architectural Institute of Japan ArchitecturalInstitute of Japan xtoLe soo 400 300 2eo 1OO o ttt tt. .tt .. ttt tt ttt tt/_{ttt. .t} ttt]ttt/ t .L rms 1;t i･P.. -t 'e'.''i' 'i 30 -65 100 135 170 205 240 275 345 3BO 415 45U(H.) Fig.8 Strain

(rms)"Frequency

Re]ationsforFunclamentalHarmonicOscillation

×lde soo 400 300 200 1OO o 0cH,) Fig9 Strain

(rms)-Frequency

RelationsforFundamentalHarmomc Oscillation xi66 4oo 350 300 250

?:8

100 50 O oeooo 0(H2) Fig.10-1 Strain

(rms)-Frequency

Curvesof the Fundamental Oscillation obtained byApalyses and Test '_-s

xio

l

,

i

,

i

, too

sg b'("H'z'" Fig.10--2Strain

_{(rms)-Frequency}

Curvesof the Fundamental Osillationexcept Vibration Modes with N=1

There

isfew

difference

between

them inthe

figure.

b) Branching Response-Curves of the

Fundamental

Harmonic

Osciliation"'

Harmonic responses of the normal coordinates

e,

(

i=4,

5,6)may branchout fromsome _pointson the response-curve of the normal coordinates

having

a Fourier expansion number

for

circumferential

direction

N=1.

In

ordeT toanalyze the branchingresponse-curves, we assume

Gi=C",iCostot,

ei==:C",icoswt

(i=4,5,6)t･t--･･････---･--･･-･-･･･t････-･(2s-1,2)

Computed

branchingstrain response-curves at the mid-height circular

line

corresponding to

e,

₍

i--4,5,6)are shown in

Fig.9

with

Q,

where the responses with

O

are the sarne with

Fig.8.

Response

curves of

e,

branch

out

from

thepointofthe external

frequency

thatcorresponds tothenatural

frequency

e,

(i=4,5,6)

on the response curves of

a,,

where

&,

(i=4,5,6,)

have

identicalnaught 'values. The fundamentalharmonic oscillation component C,,,itakes non-zero value when C",iand C6,,,are

identical

zero.

However,

both

C.,,

and

C,,n

take non-zero values er identical zero, c)

Comparison

of the Fundamental Harmonic

Oscillation

Responses

Strainresponses ef the

fundamental

harmonic

oscillation obtained

by

the vibration testsare shown in Figs.10-1and _10-2with

D,

where analyzed response curves obtained in

b)

are shown with

O

and

O.

Strain

responses

(root-rnean-square

value with respect tocircumferential

distribution)

with and without the modes of vibrations which

have

the Fourierexpansion number IV=1 are depictedinFig.10-1and Fig.

_10-2,

respectively. Analyzed response curves of the fundamentalharmonic oscillation simulate the responses obtained

in

experimental tests,_globally. And, response curves inFig.9 shows that the

-100-Architectural Institute of Japan

NII-Electronic Library Service

ArchitecturalInstitute ofJapan xid6 ioooi soo･ 600･ 4oe･ 200. o

--

11

1'1....[1----･ _, . t"t./ ･･i･/･ _,･-i-･

･･･-i･

[' ,,..,. '

7(,

/1;

iill.i'

Il

...,

'}'dsv' . ' _t/-tttttttt}1 _ttt1/ _.t 'at/'le.sl/･i i _/ttt t .. tttt ' x166 30 Fig.11 1000 ･･･-･1･ ･ / eoo 1 ' 6DO････-1-･･ 400 .････1･･･ 2eo. ･･ o 65 100 135'170 205

Branching Strain

(rrT}s)-Frequency

i 240 275 Curvesof 310 345 380 415 450(H.) 112-subharmonic Oscillation

l'?Q'

S-Lt//;4"-1･il

' ...,.. ..IN, ttt t ttt t ]tt t/tttlt[. t ttt. ...t 1. ,--1..I. {. ./ ttt tt ttttt lttt ./. .1. ttt t/tt ' rms ttt

g51;C12,'1<O

_./ .t x16e 37 Fig.'12 600 ･--･･:･ 500 ' 400 tt..t ' 300 -････1･ -･ 1 200 ..t .t.. 1eD...1... o' 373 376 Branching tttttttttt ttttttt tt.. ttttt_.lttt/ttt tlttttlt tttt t..t 379 3S2 3S5 3Se 39: Strain

_{(rms)-Frequency}

tt_t1.tt tlttttl.ttt1.ttt1ttttlttttlttt ttttttt_t/...t t/tt..1....1. .t.1..t .1t...I..t t tt tttttt t t t t t t t t t ttt t t t i t t t t t t t - t t t ttt t t 1･ 1/1/I1 t t t t . t . t t ttt t t tt t t t t t t t tt t t t.t t . t/ttttt ttt.t.t 394 397 Cgrvesof ':'i'.t,1, ..,l,.tt tt.ttttttt.tttt ttttt tttttttt tttt ' 'i'' 400 4e3 406

4og 4i2 415cHi) 112-subharmonic Oscillation ' / 'I' t/t ' 360 -365 370 375 380 3e5 390 395 400 405 410 4t 420(H,)

Fig.13 BranchingStrain

_{(rms)-Frequency}

Curvesof 113-subbarmonicOscilt'ation

normal mocles.･

having

the

FourieT

expansion number N :l 1

(out-of-round

_modes) includethe _{response of}

fundamental

harmonic

oscillation components inthe responses of cylindrical shell tanks on a shaking table.3.6

Response

Curves

of

Subharmonic

Oscillations

･

Normal coordinates corresponding tovibration modes with IV>･1 may take non-zero response under some magnitude of the_ground excitations. Here, we examine

branching

responses of

e,

(

i=4,

5), and

instable

pointgon theresponse curves of the normal coordinates with IV=1, where the 112-subharmonic

oscillation component of

k,

and the 113-subharmonicoscillation component of

&,

may

branch

out,

a),

Simple

Branching _,Responses of the lf2-subharmonic Oscillation

Taking intoaccount coupling of thenormal coordinate

6,

and one of

e,

(i=4,

5),･we

assume the

followingsteady-state solutions . ,

' '

Si=C",i

cos blt,

e,=Ciuf!cos

w12 t･･････････････-･･････････････t････････--･-･････-･-･･･-(26-1,2)_,

Branching

response _gurves at the mid-height circular

line

where the 112-subharmonic,oscillation

component

have

non-zero value are shown in

Fig,

11with

Q.

There

appear response curves inthe

neighborhood of the external frequency 262Hz and 372Hz, where the 112-subharrnonicoscillation component corresponding to

a,

and

gl,

respectively, takes non-zero value.

b)

Branching

Responses

of the 1!2-subharmonic

Oscillations

in

a

'Resonance

Region

In order to examine effects of a resonance region of

S,

on responses of the _{1/2-subharrhonic}

oscillation, we consider theequations ef motion where normal rnodes

6i,

eL2,

and

ai

are adopted, and

assume '

Si=CnnCOS

tut,

G2=C",iCOS

tot,

ai=

Csinf2COS

to/2t"''''''''''''""'''''''''(27Tl,2,3)

Branching

strain response curves at the mid-height circular

line

where the 112-subharmonic oscillation component havenon-zero value are shown inFig.12with

Q.

Since

the

harmonic

oscillation

component

C,2,,

increaseinthe region of external

frequency

(Hz)

[403,

407], the'112-subharmonic

oscillation component

C,,,,!,

decreases

and takes identicalzero value

in

a small region ofthefrequency '

[407.25,

407.33]. ･ ･ .

-Architectural Institute of Japan ArchitecturalInstitute of Japan x16e looo soo 6ee 4oo 200 o 0cHt)

Fig.14-1 BranchingStrain

(rms)-Frequency

Cuivesof 1!2-subharmonic Oscillation -e xlo 6oo

::g

;gg

100 o (H.)

Fig14-2 Branching Strain

{rms)-Freqtiency

Curves of 113-subharmonic Oscillation

c)

Branching

Responses

of the 113-subharmonic

Oscillation

Taking into account coupling of the normal coordinate

6,,

G,

and

ai,

we assurne the

following

solutions

6i=Cn,icoswt,

a2=C,2,icoswt,

ei=C",,13cosw/3t････-･･-･----･-･-･･･---･(28-1,,2,3)

There are two response curves, where the113-subharrnonicoscillation component

C,i,v:

takes non-zero

values.

They

are shown

in

Fig.13

with t)s.

d)

Branching

Responses

of

Coupling

of the 112-and the 113-subharmonic

Oscillati.ons

Inorder toexamine coupling of the

112-

and the

113-subharmonic

oscillations inaresonance region of

G,,

we consider the equations of motion where normal modes

Gi,

62,

&i

and

",

are adopted, and assume the

following

solutions

en=Ctu

cos tut,

G2=Ciz,i

cos a)t---･-･･-･･--･---････-･･･-･････---･--･････--･･-････

(2g･-1,

2)

et=C",vscos

cv13 t,

fti=Csi,v2cos

cv12 t･････--･･････-･･-････-････--･--･･･----･-･･-･･･

(29･-3,4)

Branching

strain response curves atthe mid-height circular

line

of the 1!2- and the 113-subharmonic

oscillations are shown inFig.14-1 with

O

and Fig.14-2with A, respectively. Inthe region of external

frequency

_(Hz)

_[372,

402], the112-subharmonic oscillati,on component

Cst,iit

takes non-zero value under the 113-subharmonic oscillation component C,,,,!,=O, which isdealtinb). Inthe neighborhood of the

frequency

402Hz,

C,,,,!,

branches

out, and C,,,,f,decreasestozero at thefrequency402,7

Hz.

Similarly,

in

the region where the external

frequency

is

larger

than 406.7Hz, the component

C,,,v2

takes non-zero value under

C.,,13=O.

The

113-subharmonicoscillation component

has

non-zero value

inthe region of the external

frequency

[405.

3,406.7].

In

the region of the

frequency

_[402.

7,405.3],

response curves are coincide with theseshown inc), where

C"a!3

takesnon-zero values and

Csui,

take

identical

zero.

Though

responses of the l12-and the 113-subharmonicoscillations occur insmall region of external

frequency

under some magnitude of _ground acceleration, they

become

significant vibrations.

e)

Comparison

of the

Analyzed

Responses

with

These

in

Vibration

Tests

Strain

responses of the 1/2- and the 1/3-subharmonic oscillations at the micl-height circular line observed in vibration testsunder the external acceleration

3

_g are already shown inFigs.7-1and 7-2

with

[],respectively.

These subharrnonic oscillations appeared ina srnall

frequency

regions

[4o4,

422].When the acceleration of the shaking table2g, they appeared inthe

frequency

region

[409,

413].

According

tothe responses observed

in

vibration tests,the responses of the subharmonic oscillation in

the

frequency

regions

[4o4,

406]might take

different

vibration modes with these

in

[407,

422],

Then,

responses invibration testsrnay

have

connection with other vibration modes.

But,

itseems that the

branching

responses of the subharmonic oscillation inthe resonance region of the normal coordinate

fi,

-102-Architectural Institute of Japan

NII-Electronic Library Service

ArchitecturalInstitute of Japan

are

_{qualitatively}

the nonlinear vibration phenornenon caused by coupling of the 112- and the

113-subharmonic oscillations taking place in

different

normal cbordinate with

different

Fourier

expansion numbers･in circumferential

directions

of cylindrical shell tanks.

''

.

Inorder to_,determinestable responses interms of analyses of stationaFy solutions of the interactive

systems, we hav.etosolve the equations of motion with more

degree

of freedom and more numbers of

harmonic

oscillation components, and examine the stability of obtained steady-state solutions, which

needs more elaborate studys.

4.

Conclusions

1. A basicdifferentiqlequations which _governthe dynamic interactivebehaviorsbetween the _potential

fluid

and elastic tanks in

finite

defQrmations

are

derived.

The equations and th'e

boundary

conditions are

defined

ininitialundeformed configurations:

' _{2. A}

procedureof combination of the

finite

element method and the Galerkin'smethod.allows'us to

obtain nonlinear ordinary

differential

equations of mQtion with arbitrary numbers of unknowns.'

3.

In

Qrder toobtain steady-state solutions of the ordinary

differential

equations under _{periodicground'} excitations, we･apply _the

Galerkin's

_proceduretotheequations. Analyzing a cylindrical shell tank

without

initial

_geometrical

imperfections,

we can obtain responses where'subharmonic oscillations

branch

out and _grow significant yibrations with _,largeamplitudes. _.

4. Typicalresponses curves of a cylindrical shell tank with _partiallyfilledwater observ,ed in'vibration testsare shown,

In

a sm.all region of theexternal

frequency

responses _pf 113-and

112-subharmonic

oscillations

happened

to

branch

out and

become

remarkable vibrations with targe

displacements

and '

t t

st-ralns. '

'

'

5.

Comparing

the responses obtained

by

analyses and thgseobserved invibration tests,we may

eonclude that responses analyzed here simulate the subharmonic responses observed in _{the tests,} Appendix 1

Increment ExpresFions of a Functionatof- which IntegralRegions _contain Unknown Variables

The fluidvo]ume isafunctionofnot only initialconfigurations butalso the wave height _oandi elastic deformatlonsof shells u.

Thlen, the increment of a iunctiondefipedin the fluidvolume i"givenby

A.XllllLl,.,.,FdV==ffl(1,.,.,AFdti+LCFAoknt･

...,..dS'+ntFAun .dS'-'-''-'-'"''""-'-･-･-･･----･-(a)

where

ihe

vector n, isthe outward no[mal directionof thefluid,and S'isthe area after deforrnations. Appepdix2

PartialIntegralof

h

Functlonalof which IntegratRegionscontairf Unknown Variables The expression (a}in Appepdix 1 leadsto

gtY]lll(l..,Fdv=ffXl,.,.,iidv+.XIC)F:hk.nL

...dsf+./](1Fabni- .ds''--"-'--'-'','-'-'h-"---･-･･--(b)

'

Sinceeach terms take naught values at arbitrary time, we have

,Ct].[]tlXI,.,.,SdVdt=Xlt'['YIC.FbhnJ ...,,dS'-Y](IFani. .dS'ldt''''-'''''-''-'-'-'''-'-v･--･--･---(c)

Appendix 3

Strain and Curvature,and Area ElemeAtof a ConicalFrustum

ExpTessing an initialrnid-plane of the shelt rO LnFig.1,we have

rO=( ro+ssin a)cos ei+(re+ssin a)sin oj+scos ak "H-''"-"""-HH-H'r'H"""""""""""H---'h:H"" {d'l}

A?={r,.r,.)ii'=], A;=(r,er,e}V'== ro+rsina'"--'"-''-'--"'-H'H"Hhh'HHHH''H''''''''''''''''''-'"'-''"--'(d-2,3)

Througholitthis_paperthenotation (),.denotesdlfferentiationwith respect s, narnely. ( )..±a( )la2and ( ),e=a( }fee. Assumingthatdeforrnationsofaconical frustumsatisfy theKirchnoff-Loveassumption, we haveunit tangentialvectors _t,and _t,, and the norrnal vector n

ti=r:.IAr=sin acos di--sinasin di+cosak ･---･--･･･---･---･---･---･--･---･--･･･････････----:;(e-])

t,=rl:elA:= L-sin ei+cos bj,n=-cos ecos ai-sin ecos of+sinak '-'--"-'-r---''''"---･(e-2,3)

A

Architectural Institute of Japan

Arohiteotural エnstitute 　of 　Japan

The　axes　directed　to_山e　unit　vectors 　ti　and 　n　are 　set 　s・and 　n−axes ．　Using　the　unit　vectors ，　we 　express 　the　deformation　vector

　 　　配＝ut 」十v‘診十 wn 　7，7・鹽・7・r・7・一・一・・鹽・鹽・鹽・P・P・・7・7・7…　，・…　r・P・・r・r7r鹽，鹽・鹽，7・・…　

一・・P・P・p’，・・・・・・・・・・・…

　『・『・・鹽，・・・・…　『・『…　『…　鹽…　鹽・鹽・鹽・鹽，・一・』・7…　7・’｛f）

The　_position　vector 　after　deformations　is　given　by 　 　 　紀o呂_rO

十ロ・・・・・・・・・・・・…7・・・・…　7・77r7・・凾・・・・・・・・・・…　鹽・鹽一・・・・・…　P・…　7…　一・・・・…匸・・・・・…　P7P7P・・…一・・・・・・・・・・・・・・・・…　一鹽一一・一一一・・・・・・・・・・・・…　（9）

Adopting　the　expressiQn 　derived　from　Novozhllovi7），_wehave_thenorma 亘vector 　af ヒer　deformations

　　　n’＝

1

−∂13t］一含z3t ：十〔1十εu 十ezDnV1（1十2∂｝，｝〔1十2｛｝

92

）｝

1 ／2・・一・・・・・・・・・…一・・・・・・・・・・・・・…一…一・・・・…一・・・・・・・・・・・…一・・・・・・・・・…∴・ （h）

where

　 　　e，1＝u，s，　 em＝＝（u．e−vsin 　cr）／r，∂12＝v，，，　 e、、置似θ＋ usin α一ωcosa ｝／r 　 　　e、，＝ω，。，a，、＝〔ω．，＋VCOS 　a）／r，　 e：、　＝・　a．＋（el，＋ei，＋ ek）／2

　 　　∂

1

_尸 en十（蝕 ＋∂1，＋錫 ）／2

　Taking　lnto　account 　u，　v，ω《 r、　and　using　the　unlt　vectors 　before　defQrmatbns，　 we 　express 　an　area　element 　on　the　interactive sUrfaCe 　 after 　defOrmationS．

　　

　

n、Cls

’

≒

｛

w，。t、＋

÷

贓 一（1＋u，S＋

÷

v，e）・

1

・ded・

　　　　　　　

・…一 ・・・・・・・・・……・…・…・・……・…_ω

Reterences

1）Luke，　J．C．：Avariational　principle　for　a　fluid　with 　a　free　surface ，　J．　Fluid　Mech，　Vol、27，　part．2，　PP．395−397，1967

2＞Minakawa，　Y．　and　Hangai，　Y．_：NQn 且iロear 　Lateral　Vibrations　of　SheLls　of　Revolution，　Proc．　of　25th　Japan　National 　　 Congress　for　Applied　Mechanics，　pp．59〜73，1975

3） 木村憲 明，大 橋 弘 隆 ：軸 対 称 容 器におけるス ロ ッシング の非 線 形応答，日本機 械学 会論文集，第

一_{部，第385号，pp．3024}〜_3033，

　 　 19784

；Minakawa，　Y．：The　Periodic　Solutien　PrQblems　of　RonhneaτEquations　Qf　Motion　under 　Periodic　FoTce，　Proc、　of　27th 　　

Japan

　Nationat　Congress　for　Applied　Meehanics，　pp．429−45e，1977

5＞C且ough ，　R．　W．，Niwa，　A．，and　Clough、　D．P．：Experimental　Seismic　Study　ef　Cylindrical　Tapks，Proc．ASCE ，VoL．105，

　 　 no．ST　l2，　 pp．2565〜2597，1979

6＞堀　直人，谷　資信， 田中 弥 寿 雄 ；液 体の入っ た円筒シェ ル の動 的 解 析，日本 建 築 学 会 諭 文 報 告 集，第282号，pp．83−94，

　 　 昭 和54年8月

7） 池 田 駿 介、秋 山成興，中村 広昭，白井 伸一：円筒タン ク の液 体 動揺に関 する研 究，土木 学 会 論 文 報 告 集，第 290号，pp．53〜65_，

　 　 1979年10月

8）Haroun，　M ．　A．　and 　Housner，　G．　W．：Dynamic　Characteristics　of 　Liquid　Storage　Tanks ：Complications　in　Free　Vibrat｛on 　　 Analysis　of　Tanks，　Proc．　ASCE ，　Vol．_ユe8，　No．　EM 　5，　_pp．783〜818，1982

9＞ 皆 川 洋一；液 体の 入っ た 円筒シェ ル の非 線形 振動解析，日本 建 築 学 会 大会 学 術 講 演 梗 概 集，pp．2565〜2566，昭 和59 年10月

10） 皆川 洋一：有限変 形 場で のポテ ン シ ャ ル流 体と弾 性 体 容 器の相互作 用を支配 す る 汎 閧 数，日 本 建 築 学 会 構 造 系論 文 報 告 集，第 　 　 362号，pp．105〜115_．昭 和6ユ年4月

］1） 皆川 洋一：加 速 度を受け るポテンシャ ル流 体と弾性 体 容 器の相 互 作 用の汎 関 数 と 第一変 分，日本 建 築 学 会 大 会 学 術 講 演 梗 概 集， 　　 構造1，pp．243−244， 昭 和61年8月

12｝Minakawa，　Y．_：Lagrangian　FunctiQns　of 　the　lnteractive　Behavior　Between　Petential　Fluid　and　Elastic　Container．s　in　Fields 　　 of　Finite　Deformations：PTe¢．　IASS 　Symposium，　Osaka，　Vol．1，　pp．73−80，1986

131 皆 川 洋一：加 速 度 を 受 け る 有 限 変 形 場に おけ る ポ テンシャ ル流体と弾 性 体の相 互 作 用 問 題の解 析，日本 建 築 学 会 中国 ・九 州 支 　　 部 研究 報 告，第 7号 ・1，pp．125〜128_，昭 和62年3月 14） 大 森 博 司，松 井 徹 哉，日 比 野浩：液体貯槽の有限 振幅液面動 揺に_関す る研 究，日本 建 築 学 会 構 造 系 論 文 報 告 集，第375号， 　　 PP．65−72，1987年5_月 15） 皆 川 洋一：水の入っ た円 筒シェ ル の水 平振動にお け る非 線形 振 動応答 の 影 響の評 価，平 成元年 度 科学 研究 費 補助 金 〔一般研 究 　　 C）研 究成 果報 告 書 16）　皆 川 洋一：円筒シヱ ル の水 平 振 動 実 験にお ける高次 振動モードお よ び非線 形 振 動の生起，日本 建 築 学 会 大 会 学 術講演梗 概 集， 　　構 造1，pp．1233−1234，1990年10月

17）　Novezhilov：Foundations　ol　the　Nonlinear　Theory　ef　Elasticity，　GraylDck　Press，1953

18）Kyuichiro　Washizu ：Variational　Methods　in　Elastic　and　Plasticity，　Pergamen　Press，　PP．522−528

（Manuscript　received 　September　10，1991；Paper　Accepted　February　28，1992_）

Architectural Institute of Japan

NII-Electronic Library Service

Arohiteotural エnstitute 　of 　Japan

和 文要 約 序 　 水の入 っ た円筒シi ル を水 平 振 動 台に設置 して応 答を 測 定した実 験 結 果はい くつ か報 告され_， 微 小 変 形 を仮 定 し た線 形 振 動 理 論か らは予 測できない 振 動が観 測さ れ た と報告され て い る。Cloughら5） は円 筒 断 面が 正 円で は な くなる振 動モ ードが生起する ことを報 告し，シi ル の 初 期 不 整がこ の振 動モードの発生に関 与して い る も の と 指 摘 し て い る。皆 川15〕．16 ）_は 周 期 的地 動 を受け る 円 筒 シェ ル の周 方 向フーリエ_{級 数 展 開 次 数} N ＝7まで の振動モー ドと外 力 振 動 数と同一の振 動 数を有す る基 本 振 動 数の ほ か，外 力 振 動 数の 2，3倍の振動 数を持つ 高 調 波 振 動， および1／3，ユ／2，3／2 倍の_振動数を持つ分 数 調 波 振 動の 応 答と を組み合わ せ た応答曲線を示 している。 　容 器に 入っ た 液体と容器の相 互 作 用 問 題は液 体を ポテ ンシャ ル流 体と_塚定し た定式 化が な さ れて_{， 多}く の線 形 解 析が報告fi〕_{さ れ 工学 的に有用な知 見が得ら れ ている。} し か し なが ら，この線 形理論は実験で観 測 され てい る非 線 形 振 動と判 断さ れ る応 答の生 起を解明 する基 礎 式 を も た ら さ ない。L叫ke1；はポテン シャ ル流 体の圧 力 積 分が 有限 波高の境界条 件を含む厳 密なス ロ ッシング振 動の汎 関 数と なる こ とを示し た。こ の汎 関 数か ら得られる運 動 方 程 式へ _{逐 次 積 分 法 を適 用}し て，中 山，鷲 津1e ｝は有 限 波 高の ス ロ ッ シ ン グ振 勤の 過 渡 応 答を解析し て い る。 Luke の示した汎 関 数は変形後の 形 状で定 義 され て いる の で，周 期 的 外 力の も のでの振 動の定性的な振 動 特性 を 把握す るの には適切では ない。こ の 汎 関 数，あるい はこ の_関数に基づ い て得ら れ る基 礎 式を変 形 前の領 域に お い て波 高に関 するマ クロ ーリン展 開し て得ら れ る基 礎 式 を 利用し て，_木村ら3い 大森ら14） は非線形 振 動と しての ス ロ ッ シ ン グ振 動を解 析してい る。皆川10 ）・12 ］_は この流 体の 圧力表現を容器変形， お よび液体自由 表 面での波 高の変 ． 化に伴う流体場の変 化 を 考 慮し た流 体 場で積 分すると有 限変形 場，す なわち流 体の有限波 高お よ び弾 性 体 容 器の 変 形に伴う流 体 場の変 化 を考 慮に入れ た変 形 場，で のポ テンシャ ル流 体と容 器の相互作 用 問題 の 汎関数と な るこ と を示し，_有限変形 場での 基 礎 式 を 誘 導し た。本 論 文は， ま ず 三方 向の_加速度 外力 を受け る有限変形 場で のポ テン シャル流体と 回転シェ ル容器の相互 作 用 問 題の基 礎 式 を 誘 導し，この基 礎 式ヘ モ ーダル アナ リシ ス法 （Galerkin 法）を適 用2， し て非線形常微分方 程 式へ _導びく方 法 を示 す。つ ぎ に 周期 外 力 を 受け るこ の常 微 分 方 程 式へ _{調 和}バ ラン ス_法を適 用して，_{実験 結}果が報告さ れ てい るモ デル に_{生 起}す る振 動 応 答を解析 し， 解 析され た応 答と実 験か ら得ら れ る応 答の対 応 を検 討 し，実 験において観 測され る非 線 形 振 動 応 答15 〕・16 〕が理 論 解 析か ら裏 付け ら れ ること を示す。 1．ポテ ン シャ ル 流体の圧 力 表 現 式 　慣性系に_{右手 系}デカ ル ト全体座標系 （0−xjy ， Z） を定め る。容器に右 手 形 デカ ル ト座 標で表された局 部 座 標 系 （o−x，y，　z）を定 義す る。 こ の局 部 座 標 系の x， y， z 方 向の 単 位 方 向ベ ク トル をそ れぞれ i，　

j

， ’_k と表 す。 局 部 座 標 系は回 転シ〕・ル で構 成さ れ た容 器 を扱 うの で適 宜 円 筒座標系 （rt θ，’z_）を も利用す る。 容 器は回 転しない で速度 v。で運 動 す る もの と 仮 定 す る。容器 と ともに運 動 する観 測者が観 測す る容器内の_{流 速}を v と する。この と き慣性 系に有る観測者の_観測す る容器の流 速 q は （1）式の よ うに表 さ れ る川 。 式 （1）・で表 現 さ れ る容 器と と もに運動す る観 測 者が観 測す る容 器 内の 流 速に （2＞式で_表さ れ る速 度ポテン シャ ル ψ を導 入 する。 局 部座標 系に お け る 流体自 由 表 面の静 水時の z 座 標g。，重 力 加速度 g と し， 式 （2 ）の速度ポ テン シャ ル を利用 す る と，座 標 r に お け るポテンシャル 流体の 圧 力 は （3）式の よ うに表現 され る6 　流体自由表面 （S∫）の Z 方 向 波 高 η， ． 容器 と の_相互 作用面 （S，）での弾 性 体 容 器の変 位ベ ク トル h， 弾 性 体 容器 の ひずみエ _ネルギー密 度 関 数 をA，流 体 場 VL，弾 性体の体 積 睦， 流 体お よ び弾 性 体の質量密 度をそ れ ぞ れ _ρt，およびρE と す れ ば，こ の相互作・用 問 題を支 配 す る汎

ma

数　1_，（_ψ，_ワ，　u ）は （4）』式の よ うに表さ れ る。 　 式 （4）の流 体 場は波 高 η，相互作 用 面で の弾 性 体 容 器の変 位ベ ク トル u との関 数と して定 義さ れ る。式 （5） を考 慮し て，（4＞式の第一変 分 δ1， を算 定 し て （6） 式 を得る。 　流 体 自 由表 面 Sノ，相 互 作 用 面 S‘で の変形 後の面 積 分 要 素は （8），（9｝式の よ うに表現さ れ る （付録 3参 照 ）。 変形後．の位 置での 関 数の 評 価 は （10｝，（ll）式の表 現 を 採 用 す る。 　 （8），（9 ）式 を （7）式へ _{代 入し} ， （10）， （11） 式， お よび付 録2 を考 慮す る、と，（6｝式は （12）式の よ う に表 現され る。 2．・非 線 形 常微 分 方 程 式の誘 導 　 　 　、 　こ こ で は，（12） 式へ Galerkin_{法を適 用 し}て，非 線 形 常 微 分 方 程 式を誘 導4Pす る。 こ の方 法は 二つ の手 順 を踏 む。1．（12）式の線 形 問題 め 固 有 振 動 数お よ び振 動モ ー ドを 解 析 する。 2．得 られた固 有 振 動モードを 用い’t Galerkin法 （モ ーダル ・リダク ショ ン法 ）を （12）式 一 105一 N工 工一Eleotronio _Library