SHELXL入門講座(5)
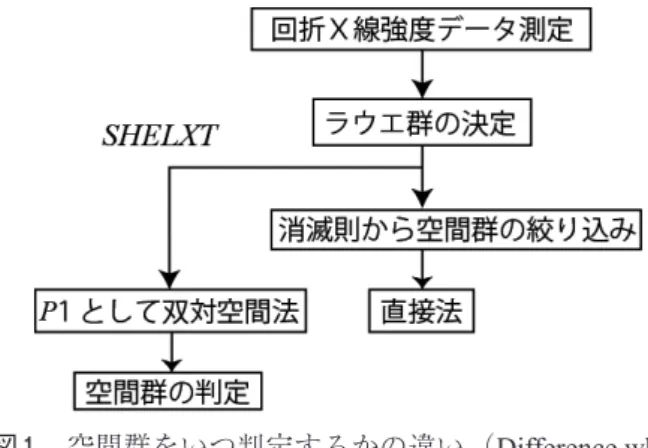
1.はじめに 構造決定のプログラムSHELXTは2014年に正式にリ リースされた.実はそれに先立ち3年にわたって200人 を超える協力者により試運転が行われ改良がなされた.1) SHELXTは低分子用の双対空間法プログラムであり,本 来の空間群を仮定せずにP1として構造を解き,その後 に空間群を導出するという画期的なものである(図1). 従来は反射の消滅則から可能な空間群を絞り,順に直 接法で試す方法をとっていた.このとき,空間群P21/cや P212121などのように,消滅則から一義的に空間群が決ま る場合はよいが,2∼3種類の可能性がある場合や,反射 が規則的に消えているか曖昧なときに,多少とも試行錯 誤が必要であった. SHELXTの出現により,そのような手間をかける必要 がなくな っ たのは喜ばしいことであるが,プログラム が何でもやってくれるおかげでブラックボックス化し, ユーザーにとって逆に不安だという声も聞こえる.作者 G. M. Sheldrickがその原理を論文1)や学会で解説し,そ の資料もSHELXのホームページで公開している.2)しか し,それらの情報が日本ではまだ浸透していないのが実 状である.そこで,今回はその理論的な背景ならびに計 算過程の概略を述べ,プログラム使用上の注意を解説す ることにした. 2.位相問題 2.1 構造を解く方法 結晶構造解析の基本式を次に示す. 結晶構造因子 F( )k =F( )k exp(
iϕ( )k)
(1) 回折X線強度 I( )k = F( )k 2 K (2) 電子密度 ρ r( )=1∑
k ( )k ( ) V F exp −2πik⋅r (3) ここで,反射指数hklがベクトルkに,そして分率座標xyz がベクトルrに対応する.つまり,式(3)を書き直すと, ρ xyz V hklF hkl hx+ky+lz( )
=1∑
( )exp{
−2πi(
)
}
(4) となる.式(1)からわかるように構造因子F(k)は一般 に複素数であり,X線強度測定からはその振幅|F(k)|だ けが得られ,位相ϕ(k)の情報は失われる.したがって, どうにかして位相を推定しないと,式(3)から電子密度 が計算できず,結晶構造がわからない.これを位相問題 という. この位相問題つまり構造を解くための代表的な方法 は,パターソン関数法と直接法である. (1)パターソン関数 P nvw V hklF hkl hu+kv+lw ( )=1∑
( )2exp{
−2πi( )}
(5) これは構造因子の位相がわからなくても計算でき,そし てそれは原子間ベクトルの集合に相当する.重原子を含SHELXT による構造および空間群の決定
慶應義塾大学自然科学研究教育センター大場 茂
Shigeru OHBA: Determination of the Structure and Space Group
by SHELXT
SHELXT is a revolutionary program which solves the structure
assuming space group P1, and determines the space group type based on the assigned Laue group and calculated P1 phase angles. The background and procedures of the computation will be summarized, and important points to check the results will be noted.
図 1 空間群をいつ判定するかの違い.(Difference when the space group is determined.)
む構造では,重原子間のベクトルが強く現れるため,パ ターソン関数から重原子の位置を求めるのは比較的容 易である.その後は,重原子の位置を手掛かりにフーリ エ合成をくり返すことで構造を解くことができる.軽原 子だけからなる構造でも,パターソン関数は役に立つ. SHELXTではパターソン関数を加工し,それを初期構造 モデルとして利用する(後述参照). (2)直接法 構造因子の振幅|F|に基づいて,位相ϕを理論的に推 定する方法を直接法という.これは推定した位相がおお むね正しければ,それを基に計算した電子密度分布に正 のピークが離散的に現れ,深い谷は生じないはずだとい うことが根拠となっている.電子密度を計算する際に各 反射のフーリエ成分が重なり合って,単位胞中のどこか に正のピークが形成される.また,強い反射ほどその寄 与が大きい.そのような考えから,次の3反射位相関係 式が導かれた. ϕ
( )
h ≈ϕ( )
k +ϕ(
h k−)
(6) すなわち,exp
{
iϕ( )h}
≈exp{
iϕ( )k}
exp{
iϕ(h−k)}
(7) ここで,≈は等しいと推定されることを表す.また,例え ば反射hとkがそれぞれ311と101とすると,h−kは210 である.このように指数が特別な関係にある3つの反射 の組について,それらの強度が大きいほど上記の位相関 係式(6)が成り立つ確率が高くなる.構造に対称心があ ると,(原子座標の原点を対称心にとることで)構造因子 Fが実数となり, exp iϕ h{
( )}
= ±1 (8) となる.つまり,Fの符号s(h)が正か負かという問題に 単純化され,式(7)は次のようになる. s( )h ≈s( )k s(h k− ) (9) なお,直接法の計算では構造因子F(h)そのものでは なく,規格化構造因子E(h)を用いる.これは原子の電 子雲が広がりをもたず,静止した点であるような結晶の 構造因子に相当し,|E(h)|2の平均値が1になるように定 義されている. E F F h h h ( )2 ( )2 ( ) 2 = o o ε εθ (10) ここで,ε(h)は平均強度係数であり,一般反射について はほぼ1であるが,結晶の点群に依存してh0lなどの特別 な型の反射に対して2や4などの値となる.3)式(10)の 右辺の分母は反射hの強度の期待値に相当し,実際には sinθ/λの測定範囲を細かく分割してそれぞれの区画に含 まれる反射についての平均値を計算する.従来の直接法 では,単位胞中の各元素の個数が既知であるものとし, ウイルソンプロットを基に平均の等方性変位変数ならび に式(2)のスケール因子Kを求めていた.このため,入 力した化学式が不正確な場合,直接法の計算結果が影 響を受けるという問題があった.SHELXTでは,sinθ/λの 区画の強度の平均値をそのまま使って規格化構造因子 を計算する. 2.2 古典的な直接法と双対空間法 古典的な直接法では,選んだ少数の反射に対して位相 セットを何十通りも,あるいは数多くの反射に対して位 相セットを何百通りも発生させる.そして各位相セット について,位相関係式を使って全体ができるだけつじつ まが合うように位相を調整しながら拡張していく.一通 り計算が終わったら,各種の指標を基に,一番有望そう な位相セットを用いてフーリエ合成を行う.基本的に, 逆空間から実空間へのフーリエ変換は1回だけである. これに対して最近よく使われる双対空間法(dual-space methods)は,実空間と逆空間の双方で得られる情報に 修正を加えながら,フーリエ変換および逆フーリエ変換 を数多く(SHELXTではデフォルトで100回)くり返す方 法である(図2).計算の出発点は逆空間でも実空間でも よい.つまり,逆空間において反射にランダムな位相を 割り当てる代わりに,実空間において単位胞中にランダ ムに原子をまき散らしてもよい.ただし,逆空間では推 定される位相関係式が成り立つはずであること,そして 実空間では負の深い谷が生じないはずであることから, 位相や電子密度に修正を加えながら収束させていく.な お,双対空間法のアルゴリズムの詳細については,ほか の解説を参照されたい.4) SHELXTでの双対空間法の出発点は,実空間における パターソン重ね合わせ最小関数である.これはパターソ ン関数の強いピークの中で原点からある程度離れている ものを1つ選び,そのベクトルvにそって原点をずらし てパターソン関数を重ね合わせ,値の小さいほうを選ん だものである(図3).ただし,実際には式(5)において |F|2の代わりに E F3 を用いることで,先鋭化したパター ソン関数を計算する.そして,原点を+v/2あるいは−v/2 図 2 双対空間法.(Dual-space methods.)だけずらした先鋭化パターソン関数を各グリッド点につ いて計算し,値の小さいほうをとることでパターソン重 ね合わせ最小関数Ps(u)が得られる.5) Ps( )u =min
{
P(
u v+ 2)
,P(
u v− 2)
}
(11) 単位胞中の原子数をNとし,それぞれの原子間ベクトル が重ならないと仮定すると,パターソン関数のピークが N2−N個であるのに対して,その重ね合わせ最小関数の ピークは2N−2個となる.これは,元の構造とそれを反 転したものとが重なった像に相当する.5)選んだパター ソン関数のピークがもし2つの異なる原子間ベクトルが 重なったものであるときは,重ね合わせ最小関数は2つ の部分構造にそれらを反転したものとが加わった像とな る.いずれにしても初期構造モデルとしては不完全であ り余分なピークもかなり残っているが,それでもランダ ムな構造モデルよりは数段ましである.なぜなら空間群 P1を仮定するので,単位胞中の原子の相対的な位置さ え正しければ,構造モデルとして申し分ないからである. 2.3 P1 で構造を解く背景 古典的な直接法が盛んに行われていた頃に,構造が解 けないときの解決策として,対称性を下げて空間群P1 を仮定すると比較的小さいタンパク質も含めて構造が 効率良く解けることがわかった.6)なお,どのような単純 格子の空間群であっても,P1はその部分群であるため, 形式上解析が可能となる.また,複合格子の場合は軸変 換して単純格子にすることはせず,例えばC底心格子の ときは空間群C1(つまり単位胞内にC底心以外に対称性 が存在しない構造)として取り扱う.このような場合も 含めて便宜上P1と呼んでいる. 対称心の有無をはじめとして,本来の正しい空間群を 仮定したほうが位相がある程度制約されるため,理論的 に位相問題のハ ー ドルが低いはずである.それならば なぜ,P1を仮定すると解が得やすくなるのであろうか. それは,位相が柔軟に変化することで,偽の解に陥りに くくなるためと推定される.ただし,P1で構造が解けて も,本来の空間群の標準的な原点のとり方(場合によっ ては結晶軸のとり方も)合わせる必要がある.例えばP1 であれば,対称心の位置を見出して原子座標をずらさな ければならない(図4).P1の場合,対称心であれば,そ のどの位置を原点に選んでもよい.しかし,対称性が高 くなってくると,単位胞中に非等価な対称心が存在する 場合も出てきて,その判別もしなければならない.この ような原点シフトの作業は手間がかかるので,どのよう な空間群に対しても自動化するアルゴリズムが考案され た.6,7)ただし,対称要素を探し出してからそれらを組み 合わせて空間群を割り出す7)のではなく,各空間群に対 してP1の位相が適合するか検査する方法6)をSHELXT では採用している. 2.4 分解能の改善 分解能とは分離して認識できる2点間の最小距離のこ とであるが,便宜的にX線回折法では測定した反射デー タの面間隔の最小値dminをさす.dmin=1 2
(
sinθ λ)
max (12)回折強度測定で高角側の反射がほとんど得られないと 電子密度の分解能が不十分で,構造モデルが得にくくな る.これは特にタンパク質結晶の構造決定において問題 となる.この困った状況を手軽に改善する方法が考え出 された.それはある分解能の範囲内で,測定されていな い反射の振幅と位相を(推定される電子密度を基に)計 算して双対空間法に導入するという方法である.8)これに より,(次に計算する)電子密度が改善され,それに伴っ てほかの反射の位相も改善されるという仕組みである. 測定していない反射データを外挿するというこの方法は 俗にfree lunch法と呼ばれ,SHELXTでも採用している. そのデフォルトの分解能はdmin=0.8 Åであり,これは 2θmax(Mo Kα)=52.7 に相当する.ただし,反射データ の分解能があまりにも低くて外挿の範囲が広くなると, 反射の振幅と位相を正しく推定することが難しくなる.8) 図 3 パターソン重ね合わせ最小関数.(Patterson super-position minimum function.)
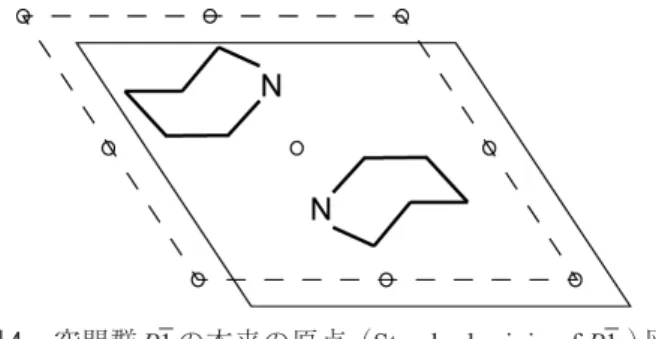
図 4 空間群P1の本来の原点.(Standard origin of P1.)図 中の小さい○は対称心を表し,破線はP1としての 単位胞の取り方の例を示す.
3.構造の対称性 空間群P1を仮定して構造を解いたとき,結晶構造の 対称性がどのように現れるか,実空間と逆空間に分けて 考えてみよう. 3.1 実空間での対称性 空間群の対称性により,実空間において位置rとその 等価位置Rr+tで電子密度が同じになる.すなわち, ρ(Rr t+ )=ρ( )r (13) ここで,Rは対称操作の回転部分,そしてtは並進部分 を表す.9)構造解析の最終段階では精度の高い構造モ デルが得られているので,想定されていない対称性を PLATON/ADDSYMのようなプログラムで見出し,本来の 空間群を推定することが可能である.しかし,直接法で 解いたばかりの構造では,元素の割り付けすら不完全で あることもあり,ましてや原子座標の精度も高くないた め,実空間における対称性の判定は比較的困難である. 3.2 逆空間での対称性 SHELXTで空間群の対称性を判定する決め手は,逆空 間における等価反射間の位相の関係である.実空間にお いて(その空間群の標準的な原点のとり方をしていると き)Rr+tが等価位置ならば,反射hに対してRhが等価 反射となり,そして構造因子に次のような関係が成り 立つ.9) F Rh( )=F h( )exp(−2πih⋅t) (14) すなわち,ϕ( )Rh =ϕ( )h −2πih⋅t (15) ただし,原点がΔxだけシフトしているときの原子座標 をx ,位相をϕ(h)と表すと次のようになる. x’ x= − ∆x (16) ϕ’( )Rh=ϕ’( )h −2πh⋅t 2π− (Rh−h)⋅∆x (17) また,原点がΔxだけシフトしているときの構造因子を F(h),シフトしていない(つまり本来の原点を選んだ) ときの構造因子をF(h)とすると, F’( )h =F( )h exp(−2πih⋅∆x) (18) F’( )Rh =F( )Rh exp(−2πiRh⋅∆x) (19) となる.このことから,式(15)を基に式(17)が導出さ れることが理解できるであろう. SHELXTでは指定されたラウエ群を前提とする.そし て,各ラウエ群について,可能な空間群およびその対称 要素はわかっているので,その適合性を順に調べる.そ の際に原点シフトΔxの可能性について,単位胞中の特 定の領域内でのグリッド点について試して,式(17)の 関係がすべての等価反射に対してほぼ成り立つ(つまり 後述する指標αがある値よりも小さい)ときに,適応す る空間群の候補と判断する.また,計算で求めた原点シ フトに基づいて,原子座標の初期値を修正する. 3.3 空間群選出の指標 前節の式(17)より,正しい原点シフトのときに反射 hとその等価反射Rhとについて,次の量ηは非常に小さ くなるはずである. η ϕ’= ( )Rh −ϕ’( )h +2π
{
h⋅t+(Rh−h)⋅∆x}
(20) ただし,反射の位相は2πの整数倍を足しても引いても 同じものを意味する.このため,式(20)の計算に際し てはmodulo 2πであることを考慮して,|η|≦πとする. SHELXTで空間群を判定する指標αは,すべての反射 のすべての(それぞれRとtで関係づけられる)等価反射 の対について,F2の重みを付けたη2の和として定義され る.ただし,ランダムな位相に対してαが1になるよう に規格化する.すなわち,αは規格化した平均二乗の位 相誤差(mean square phase error)を意味する.この値が小 さいほど,空間群と原点シフトが正しいと推定される. 3.4 可能な空間群の数 単斜晶系(ラウエ群2/m)で単純格子Pの場合,(主軸 をb軸と仮定し)結晶軸のとり方の違いも考慮すると, 可能な空間群は全部で14である(表1).しかし,直方P (ラウエ群mmm)では,全部で120にもなる(表2).9)対 称心の有無をまず判別するとしても,対称心がないと わかった場合に空間群の数は56となる.もし,キラルな 分子で一方の対掌体しか含まれていない結晶であれば, ゾーンケ群に限られる.つまり,直方晶系では点群222 に限定されるので,可能性のある空間群の数は56から8 に減少する. 表 1 単斜Pで主軸bのときの可能な空間群.(Possible space groups for monoclinic P with unique axis b.)対称心 なし あり
点群 m 2 2/m
可能な
空間群 Pm, Pa, Pc, Pn P2, P21 P2/m, P2P2/c, P21/m, P2/a, P21/a, 1/c, P2/n, P21/n
表 2 直方Pで異なる軸設定も考慮したときの可能な 空間群の数.(Number of possible space groups for orthorhombic P considering different settings.)
対称心 なし あり
点群 222 mm2, m2m, 2mm mmm
可能な空間群の数 8 56 48 64 120
4.SHELXT の計算手順 (1)計算パラメータの設定 SHELXTでは各計算処理段階において,デフォルトの 設定がいくつもなされている.通常はそのまま使っても 何も問題はない.ただし,プログラムに柔軟性をもたせ るために,それらのパラメータが変更できるようになっ ている.それがコマンド行オプションである.図5に示 すようにSHELXシステム用のinsファイルとhklファイ ルがあれば,SHELXTを走らせることができる.そのファ イル名を○○.insとすると,SHELXTを実行するコマン ドは「shelxt ○○」であるが,必要があればそれに続けて 例えば「-m1000 -c」のように指定する.この「-m」や「-c」 がそれぞれのオプションの指定であり,文字に続いて数 字が入っていれば,それをデフォルト値と置き換えるこ とを意味する.すべてのオプションの記号やその意味に ついては,印字出力ファイルlxtの最初にリストが示さ れているので,それを参照されたい.
なお,BrukerのAPEX 310)の構造決定(Find Structure)
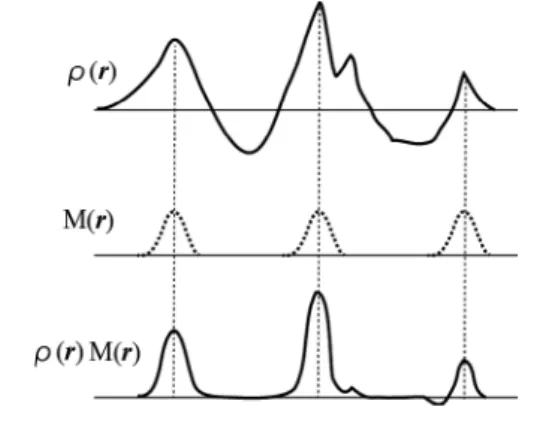
画面で,構造を解く方法の選択肢として SHELXT は Intrinsic Phasingと表示される.またそれを実行する際に コマンド行オプションを直接指定することはできない. その制御画面中の「Chirality」欄の初期設定はAnyであ り,特別なことがない限りそのままにしておくのが無 難である.ただし,その他の選択肢としてChiralとNon-centrosymmetricとがある.このうちChiralを選択すると 「-c」オプションが設定されてゾーンケ群だけが空間群探 索の対象となる.Non-centrosymmetricを選択したときは 「-n」オプションが設定され,対称心のない空間群に限定 される.以下の手順については,これらのオプションが 設定されていない場合を念頭において説明する. (2)データの読み込み SHELXTは○○.insファイルから格子定数などのデー タを読み込む.まず,その中のLATTから空間格子の型 を,そしてSYMMコマンド行の情報を基にラウエ群を 割り出す.また,SFACコマンド行から元素の情報を得 る.11)ただし,それぞれの原子の個数の情報は無視する. UNITからHKLFまでの間のすべてのコマンド行も無視 する.そして,○○.hklファイルから反射データを読み 込む. 上記の(insファイルから割り出した)ラウエ群を前 提として等価反射の強度を平均し,規格化構造因子を 計算する.そして逆空間におけるそのすべての等価反射 の指数を発生させ,その構造因子の振幅を共通の値に する. (3)双対空間位相改善ループ パターソン重ね合わせ最小関数からP1として双対空 間ループを開始する.ただし,パターソン関数のずらし 方を変えて,位相決定を何回か試す.この双対空間ルー プにおいては,実空間で電子密度に修正を加え,逆空間 では位相関係式ができるだけ成り立つように位相を精密 化する.4)ただし,SHELXTでは次のように修正した構造 因子を用いる. Go( )h =Eo( ) ( )hqFoh1−q (21) ここで,E(h)は規格化構造因子であり,デフォルトで o q=0.5である.そして,フ ー リエ合成の係数として, mG(h)−(m−1)Go (h),および位相ϕc (h)を用いて電子c 密度を計算する.ただしmのデフォルト値は3であり, G(h)とϕc (h)は電子密度のフ ー リエ変換から求めたc (G(h)に対応する)構造因子の振幅と位相である.すなo わち, ρ( )r=1
∑
h{
3G( )h −2G( )h}
{
ϕ( )h−2πh⋅r}
V o c expi c (22) なお,構造モデルによるバイアスを避けるために,電子 密度のピークを一定の割合でランダムに削除する.そし て残りの各ピーク位置の周りで大体同じ形の正規分布 になるようにマスクM(r)を電子密度ρ(r)に掛けて修 正する(図6).このような摂動および修正をデフォルト で3サイクルごとに1回行う.ただし,負の電子密度の除 去は毎回行う. (4)最善の位相セットの選択 各位相セットに対して,次のような指標を計算する.図 5 ファイルの入出力.(Input and output files.)
図 6 マスクM(r)による電子密度の修正.(Correction of the electron density with the mask.)
①CC:G(h)とGo (h)の間の相関係数.大きいほどよい.c
②R(weak):(消滅反射も含めて)|E(h)|o 2の小さいほう
から10%の反射の|E(h)|c 2の平均値.小さいほどよい.
③CHEM:分子として解釈可能な(距離1.1∼1.8 Å,角 度95∼135 で配列している)電子密度ピークの割合. ④CFOM:総合良度指数(combined figure of merit)CFOM= 0.01CC−XR(weak)(ただし,係数Xはデフォルトで1). 結晶構造が分子からなるとは限らないため,CHEMは デフォルトではCFOMに組み込まれていない. CFOMが大きいほど,良い位相セットと推定される. 例を表3に示す.これは有機セレン化合物12)の計算結果 である.1) 4つの位相セットが試され,それらのR(weak) はあまり差がないが,一番目の位相セ ッ トの相関係数 CCが大きいことからCFOMも最大となり,これが最善と 判定された.分子としての電子密度の解釈の指標CHEM も良好であり,期待がもてる.このようにP1としての位 相を求めてから,次にそれを基に空間群を決定する. (5)原点シフト Δxと空間群の候補の選出 SHELXTは,まずP1としての位相誤差の指標αを計算 する(これをα0と呼ぶ).α0が0.3よりも小さいときは, おそらく対称心のある構造と推定される.ただし,21Sc よりも重い原子を含む構造のときは疑似対称心という可 能性もあることから,SHELXTでは対称心のない空間群 も検査する. 表 3 で引用した有機セレン化合物の結晶は,単斜Pで ある.α0が0.175と小さいが,重原子を含むことからこ の場合,次のような計算過程をたどる.①標準の軸設定 以外のときも含めて,全部で14の空間群(表1)につい て,原点シフトと等価反射の位相の適合を検査する.② αが閾値(デフォルト0.3)よりも小さい空間群を候補と する.そして(次に述べるように)電子密度を解釈し,構 造を等方性で精密化する.これで,表4のような計算結 果が得られる. (6)実空間精密化ループと電子密度のスケーリング 候補として選び出された各空間群について,その空間 群が正しいものと仮定して等価反射の位相を平均し,さ らにフーリエ変換と逆フーリエ変換を10回くり返して, よりよい電子密度を求める.その際に行う修正は,実空 間において負の電子密度をゼロに置き換えることだけ である.その後,各ピーク位置の周りで球内(半径のデ フォルト0.7 Å)の電子密度を積算し,絶対尺度に直す ために,次の検査(a)∼(d)を順番に試みる(失敗した ら,その次を試す). (a) 指定された元素の中に炭素が含まれているときは, 電子密度が似た値で,C−C距離(1.25∼1.65 Å)に あるピークを探す.十分な数だけ見付かれば,それ らが平均で原子番号6になるようにスケ ー ルを定 める. (b) もしホウ素の含有が予期されているときは,1.65∼ 1.8 Åの結合距離をもつホウ素のカゴ構造を探す. (c) 酸化物陰イオンについてサーチする.酸素原子は互 いに似たような積分電子密度をもつはずで,また, それらと中心原子との距離も似た値になるはずで ある. (d) もし,上記の検査がいずれもうまくいかないときは, 予期されている元素のうち一番重いものが,積分電 子密度の最大ピークと対応するとみなす. (7)電子密度ピークへの元素の割り振り 電子密度のスケール因子が定まったら,各ピークの 電子数に応じて元素を割り振る.もし,軽原子のみが (SFACで)予期されているのにもかかわらず,異常に高 いピークがあるときは,ハロゲン化物イオンが入ってい るものとみなし,Cl,BrあるいはIとして追加する. (8)等方性の精密化 得られたモデル構造を等方性で精密化し,R1すなわ ち残差因子R(F)を計算する.対称心のない構造のとき は,パーソンズの商の方法13)でフラック変数を求め,も しそれが0.5よりも大きいときは構造モデルを反転する. この段階で求まった構造モデルのままでは,原子や分 子の一部が等価位置に分散している可能性がある.そこ で,原子をできるだけ寄せ集め,またそれらの中心が単 位胞内に納まるように原子座標を調整する. (9)空間群の判定 三斜晶系のときは基本的にα0の値で空間群を判定す る.ただし,重原子が(SFACに)予期されている場合は α0が小さくても疑似対称心という可能性もあることか ら,P1とP1の両方を候補とする.三斜晶系以外のとき は,指標αが小さい空間群をすべて候補とする.そして, 等方性で精密化した後のR1などを基に,その中から最 表 3 有機セレン化合物の位相決定例.(Example of phase
determination for organoselenium compound.)[出典: Sheldrick,1)Fig.2を改変]
Try* N(iter) CC R(weak) CHEM CFOM
1 100 95.3 0.118 0.974 0.835 2 100 85.0 0.146 0.460 0.704 3 100 82.7 0.126 0.567 0.701 4 100 82.6 0.109 0.689 0.717 *異なるパターソン重ね合わせベクトルを使用. 表 4 有機セレン化合物の空間群決定例 .(Example of space group determination for organoselenium compound.)[出典:Sheldrick,1)Fig.3を改変]
R1 Rweak α 空間群 Flack File Formula 0.21 0.10 0.12 P21/m − _a C28 O4 Se
0.10 0.05 0.04 P21 −0.01 _b C22 O2 Se
も有望な空間群を選ぶ. 表 4 に示した例では3つの候補(P21/m,P21,Pm)の うち,ほかに比べてR1が明らかに小さいことから,空 間群はP21と判定された.なお,最終的に選ばれなかっ た空間群についても,必要に応じてユーザーがさらに精 密化を行って検討できるようにするために,候補となっ た空間群それぞれに対応させて,ファイル名を_a,_b, _cなどで区別して,resおよびhklファイルが出力される (図5).このように反射データのファイルも個々に出力 するのは,軸変換ならびに指数変換を行う場合もあるか らである(後述参照). 5.lxt ファイルの見方 SHELXTに空間群の決定を任せるとしても,ユーザー は少なくとも印字出力ファイルlxtで大事なところを確 認しておく必要がある.lxtファイルには最初に定型部 分(各種オプションの説明およびデフォルト値)のリス トが示され,その後に,「Command line parameters(入力 された変数)」として,○○.insや○○.hklの○○にあた るファイル名が示され,指定されたオプションがあれば その後に続く.ちなみに「-t3」というようなオプション が入っていたとしても,構造の決定には直接かかわらな い.これはthread(スレッド),つまり計算機の並列処理 の流れを何本にするか(この場合3)という指定であり, その本数はプログラムが自動的に判断している. そして,パターソン関数のピーク座標のリストの次 に,双対空間ループの結果が続き,CFOMが最も大きい 解についてのP1としての位相誤差α0が示されている.
lxtファイルの最後の部分「Space group determination (空間群決定)」をよく見てほしい.候補として選ばれた 空間群が1つだけのときはもうそれで決定である.もし 候補が複数ある場合,その中に正しい空間群があるのは まず間違いないが,最終的にプログラムが判定した空間 群が正しいとは限らない.特にFormula(これは水素を除 く非対称単位中の化学式)が予想通りであるかどうかに 注目する.また,そこに予期せぬ元素(Cl,BrまたはI) が仮定されていたら,電子密度を解釈するためにプログ ラムが便宜上これらの元素を仮に割り当てたことがわか る.実際,このように想定外の重原子が結晶中に含まれ ている可能性もあるであろう.しかし,構造モデルが正 しくないため,電子密度が異常な結果になったというサ インともみなせる. 6.SHELXT での計算例 著者が保有している反射データで計算をいくつか行っ てみた.その例などを以下に紹介する. 6.1 三斜晶系 P1 合成して得られた有機化合物C16H20O2はラセミ体で あり,結晶は三斜晶系で,結晶の密度からZ=2である. SHELXTでP1として位相が計算された後,α0が0.057と (0.3よりも)小さいことから対称心のある構造と判定さ れた. SHELXTが空間群をどのように判定するのかさらに明 らかにする目的で,上記と同じデータを用いて動作試験 を行った.すなわち,insファイル中のSFACにわざとBr を追加してSHELXTを走らせてみた.これにより,α0が 小さいけれどもP1とP1の両方が空間群の候補とされる. そして,どちらを仮定しても化学式は(Brを含まず)正 しく求まり,等方性での精密化後のR1はそれぞれ0.178 と0.182となった.P1のほうがR1がわずかに低いが,構 造モデルとしてモニタ ー 画面に現れたのは独立 1分子 (つまりP1のほう)であった.このようにR1にあまり差 がない場合,対称性のより高い空間群のほうを選ぶとい う判断が働くことがわかる. 6.2 単斜晶系 P21 重原子を含まない有機化合物(I)C12H13FN2O3Sはキ ラルであり,その合成方法から一方の対掌体だけに限ら れていたが,念のために空間群はゾーンケ群に限定しな いで解析する.結晶は単斜PでZ=4である.SHELXTで P1として構造が解かれ,α0は0.697であった.この値が 0.3よりも大きいので対称心なしと判定され,対称心のな い空間群6個が検査された(表1).その結果,αが0.3よ りも小さい空間群としてP21だけが候補として選出され た(表5).電子密度から推定された化学式(Formula)は, 独立な2分子に対応して分子式のほぼ2倍である.ただ し,NやOの一部がCとして間違って割り振られた.プ ログラムのユーザーは初期構造モデルの画像を疑いの目 で見て,化学的知識を基に元素の修正を加える必要が あることは言うまでもない. 6.3 直方晶系 P212121 キラルな有機化合物(Ⅱ)C13H15ClN2O3と(Ⅲ)C13H15BrN2O3 は一方の対掌体だけに限られており,どちらの結晶も直 方Pである.SHELXTでP1として構造が解かれ,α0はそ れぞれ,0.701と0.320であった.この値が0.3よりも大き いことから対称心なしと判断され,どちらも対称心のな い空間群56個について検査が行われた.その結果,αが 0.3よりも小さい空間群としていずれもP212121だけが候 補として選出された(表5).なお,結晶中に21Scよりも 重い元素を含む(すなわちSFACで指定された)場合,α0 表 5 キラルな有機化合物(Ⅰ)∼(Ⅲ)の空間群決定. (Space group determination of chiral organic compounds.) 結晶 R1 Rweak α 空間群 Flack Formula (Ⅰ) 0.12 0.030 0.002 P21 0.13 C27 F2 N2 O5 S2
(Ⅱ) 0.10 0.026 0.001 P212121 0.03 C13 N3 O2 Cl
が小さくてもSHELXTはデフォルトとしてそのラウエ群 に可能なすべての空間群を試す.ただし,それはあくま でも疑似対称心への対策である.重原子が入っているた め,見掛け上対称心のない構造になるということはあり 得ない.このため,α0が0.3より大きければ対称心のあ る空間群の検査は行われない. 6.4 直方晶系 Pba2 ラセミ体の有機化合物(Ⅳ)C22H28Br2O2の結晶は直方 PでZ=2である.SHELXTでP1としての位相が計算さ れ,α0は0.118であった.0.3以下なので通常ならば対称 心ありと判定するところであるが,重元素Brが予期され ているため,プログラムは対称心のある空間群64個だけ でなく,対称心のない空間群56個も含めて検査する.そ の結果,5つの候補が選び出された(表6).R1がほかよ りも明らかに小さいことから,Pba2が最終的に選ばれ, そしてそれが本当に正しい空間群であった. なお,表6を見ると同じ空間群Pmc21(No.26)でも軸 設定が違う場合が見られる.この空間群 Pmc21の場合, 結晶軸a,b,cのとり方を変えると,空間群の記号も変 わってくる(表7).これらを非標準設定という.構造解 析にあたっては特別な理由がない限り,空間群の標準設 定に直すことが義務づけられている.このため,SHELXT ではこのような場合に軸変換を行う.実際に _c.resや _d.resファイルには軸変換後の格子定数が出力され,ま た_c.hklや_d.hklファイルにはそれに応じて指数変換さ れた反射データが出力される. 6.5 六方晶系 P63/mmc SHELXTによ っ て決定された空間群が常に正しいと は限らない.プログラムの作者Sheldrick自身が,論文1) に注意喚起のために示した例を次に紹介する. それ は,六方晶系でラウエ群6/mmmの無機化合物であり, SHELXS97で構造が解かれ,対称心のない空間群P62cと して論文発表された.14)しかし,注目すべき危険信号と してcheckCIFで対称心が検出されていた( 警告B).デ ポジ ッ トされた反射デ ー タをもとに,SHELXTで検討 すると,次のようになった.結晶中に21Scよりも重い元 素Mnを含むため,SHELXTはこの場合に対称心のある 4つの空間群だけでなく,対称心のない12の空間群も検 査する.その結果,5つの空間群が候補として選ばれた (表8).R1がほかよりも下がっていることから,対称心の ない空間群P6m2が最終的に選び出された.実はこの結 晶の真の空間群は,対称心のあるP63/mmcであった.論 文で発表されたP62cもSHELXTが選んだP6m2も誤りで ある.表8のP6m2やその他の空間群はP63/mmcの部分 群であり,得られた構造モデルは本質的にすべて同じ解 であった.電子密度を解釈する際に,たまたまP6m2の ときだけCaとMnを正しく判別できたため,それがR1の 低下に反映したのであった.これは比較的希なケースで はあろうが,SHELXTが選んだ空間群が常に正しいとは 限らない.おおまかに見積もって,空間群の正解率は約 97%とのことである.1)つまり,100%ではない.Sheldrick 曰く,「経験の浅い人がプログラムの計算結果をすべて 正しいと思い込むことが一番危険である」. 7.プログラムの限界 SHELXTは単結晶X線回折用であり,中性子回折には 適用できない.また,結晶構造が(乱れのない)原子から なることを前提としている.このため,ひどく乱れてい る構造あるいは双晶には対応しきれない.もし,SHELXT でうまく初期構造が出ない場合は,消滅則に基づく空間 群の決定に立ち戻る必要があろう.そして,通常はあり 得ないような消滅則から双晶であることがわかるかもし れない.9)いずれにしても構造が解けて精密化がほぼ収 束したら,できるだけ早く仮にCIFを出力してcheckCIF で検査し,空間群間違いの警告が出ないか,また解析上 の不備がないかを確認するとよい. 表 6 ラセミ有機化合物(Ⅳ)の空間群決定.(Space group determination of an organic racemate.)
R1 Rweak α 配向*) 空間群 Flack Formula
0.237 0.049 0.069 as input Pbam − C16 O3 Br 0.156 0.031 0.040 as input Pba2 0.15 C11 O Br 0.220 0.044 0.060 c, a, b Pmc21 0.49 C27 O9 Br2 0.224 0.045 0.066 c, b, −a Pmc21 0.49 C16 O3 Br 0.242 0.047 0.079 as input P21212 0.49 C12 O5 Br *)標準設定への軸変換を示す(表7参照). 表 7 Pmc21の非標準設定および標準設定への軸変換.
(Non-standard setting of Pmc21 and transformation of
the axes to the standard setting.)
空間群 非標準の軸設定 標準設定への軸変換*) P21ma c, a, b b, c, a P21am −c, b, a c, b, −a Pm21b a, −c, b a, c, −b Pb21m b, c, a c, a, b Pcm21 b, a, −c b, a, −c *) SHELXTの出力ファイルlxtではOrientation(配向)として表 示される. 表 8 空間群決定に際して注意を要する例.(Example of space group determination where caution is needed.) [出典:Sheldrick,1) Fig.6を改変]
R1 Rweak α 空間群 Flack Formula 0.073 0.005 0.018 P63/mmc − Ca4 O17 S2
0.074 0.004 0.016 P63mc No Fp Ca O17 S5
0.039 0.004 0.017 P6m2 No Fp Ca3 Mn O17 S2 0.069 0.005 0.017 P62c 0.49 Ca4 O17 S2 0.069 0.004 0.019 P6322 0.42 Ca4 O17 S2
謝 辞 SHELXTによる計算がブラックボックスを通り越し, ユ ー ザ ー に不安を与えているとの高谷 光先生( 京大 化研 )からの指摘が,この解説記事を書くき っ かけと なった. 文 献
1) G. M. Sheldrick: Acta Cryst. A71, 3 (2015). 2) http://shelx.uni-goettingen.de/
3) 日本化学会編:5版実験化学講座11 物質の構造Ⅲ 回折, p.111, 丸善(2006).
4) G. M. Sheldrick, et al.: International Tables for Crystallography, Vol.F, 2nd ed., pp.413-432, Chichester, Wiley (2012).
5) G. M. Sheldrick: Methods Enzymol. 276, 628 (1997).
6) M. C. Burla, B. Carrozzini, G. L. Cascarano, C. Giacovazzo and G. Polidori: J. Appl. Cryst. 33, 307 (2000).
7) L. Palatinus and A. van der Lee: J. Appl. Cryst. 41, 975 (2008). 8) R. Caliandro, B. Carrozzini, G. L. Cascarano, L. De Caro, C.
Giacovazzo and D. Siliqi: Acta Cryst. D61, 556 (2005).
9) 大場 茂 , 植草秀裕:X 線結晶構造解析入門, 化学同人(2014). 10) Bruker AXS Inc.: APEX 3 ver. 2016.1-0 (2016).
11) 大場 茂, 植草秀裕:結晶構造精密化SHELXLの使い方, 三 共出版 (2016).
12) W. Clegg, K. Harms, G. M. Sheldrick, G. von Kiedrowski and L. -F. Tietze: Acta Cryst. B36, 3159 (1980).
13) S. Parsons, H. D. Flack and T. Wagner: Acta Cryst. B69, 249 (2013).
14) M. C. Barkley, H. Yang, S. H. Evans, R. T. Downs and M. J. Origlieri: Acta Cryst. E67, i47 (2011).
プロフィール
大場 茂 Shigeru OHBA
慶應義塾大学自然科学研究教育センター Research and Education Center for Natural Sciences, Keio University
〒223-8521 横浜市港北区日吉4-1-1
4-1-1 Hiyoshi, Kohoku-ku, Yokohama, Kanagawa 223-8521, Japan
e-mail: ohba@a3.keio.jp