ファジイ理論を利用した高等学校数学教育の教材構造分析
Structure Analysis of Instruction Items in High School Mathematics Education
Applying Fuzzy Theory
○松崎 佑己
1,瀧澤 武信
2○Yuki MATSUZAKI
1, Takenobu TAKIZAWA
2 1早稲田大学大学院教育学研究科
1
Graduate School of Education, Waseda University
2早稲田大学政治経済学術院
2
Faculty of Political Science and Economics, Waseda University
Abstract: In this paper, the authors discuss structure analysis of instruction items. We describe how to get the similarity structure graph, the partition tree, the connectivity structure graph, the approximate structure graph, and the cognition structure graph after scoring the quizzes in the classroom.
We also discuss the case study concerning exponent and logarithm in high school mathematics education.
1. はじめに
高校数学教育で使用されている教科書は, それぞ れの筆者が考える教授順序に従って記載されている が, 実際授業を行う際は,教科書通りの順序で教え ることが適切であるとは必ずしも言えない.本研究 では, 項目間の類似構造分析, 関連構造分析から得 られる認知構造グラフから, より適した教授順序を 分析し, 実際の授業に役立てる方法を提案する.2. 分析方法
教材構造分析は, 図 1 のような分析方法で行われ る. 図1 教材構造分析の分析方法 教材項目から作られる教材構造グラフ I と, テス ト実施により得られる認知構造グラフ Φz から適切 な教授順序を判断する. 0 とする. 得点行列 X から, 各項目ごとの学習者の得点パタ ーンを集計すると, Pi ,Pj の項目間にクロス集計表 Cij が得られる. (図 2) 図 2 クロス集計表 Cij クロス集計表 Cij のa, b, c, d は次のように定義され る. 定義 1 a = ∑ xkixkj 𝑛 𝑘=1 b = ∑ xki(1 − xkj) 𝑛 𝑘=1 c = ∑ (1 − xki)xkj 𝑛 𝑘=1 d = ∑ (1 − xki)(1 − xkj) 𝑛定義 2 より, クロス集計表 Cij から, 類似係数 sij と関連係数 tij が得られる. 定義 2 sij= a + d 𝑛 ∈ [0,1] tij= a + d (a + c) + (c + d)∈ [0,1] ただし, a = c = d = 0 のときは, tij= 1 とする. 次の定理を用いることにより, クロス集計表 Cij を考えなくても類似係数 sij と関連係数 tij が得られ る. 定理 sij= sji= 1 − (∑𝑛 | 𝑘=1 xki− xkj| ) 𝑛 ∈ [0,1] tij= 𝑛sij 𝑛 + ∑𝑛𝑘=1xkj− ∑𝑛𝑘=1xki ∈ [0,1] また, 類似係数 sij と関連係数 tij から, 類似構造 行列(グラフ) S = (sij)と関連構造行列(グラフ) T = (tij)が得られる. 類似構造行列(グラフ) S をクラス ター分析すると, 分割樹形図 P を得る. これにより, 各項目間の類似性がわかる. 関連構造行列(グラフ) を近似三値分析すると, 近似三値グラフ T∗ を得る. これにより, 各項目間の順序性がわかる. 最後に, 分割樹形図 P と近似三値グラフ T∗ から, 類似構造グラフ Φz(𝑧 = 𝑧 0)が得られる.
3. 事例研究
教材構造分析の応用事例として, 「指数」「対数」 に関して, 高校 1 年生 75 名を対象に実施したテス トの結果に基づく分析について説明する. 指数のテスト問題は (1) 432× 2−5 (2) 9−5 2÷ (3−1)3 (3) 432× 16− 5 4÷ (2−1)3 (4) y = 2x− 1 (グラフをかけ) (5) y = (1 3) x+1 (グラフをかけ) (6) 4x=1 8 (7) 9x+ 3x− 12 = 0 (8) 22x+1− 2x− 1 < 0 である. また, 対数のテスト問題は (1) log2 4 5+ log210 (2) log2 14 3− 1 2log2 49 9 (3) log3√12 + log3 3 2− 3 2log3√3 3 (4) log48 (5) 3log35 (6) y = log2(x − 1) (グラフをかけ) (7) y = log1 3(x + 1) (グラフをかけ) (8) 2x= 3 (9) 2 log3(x + 2) = log3(4 − x) (10) log2(x − 3) + log2(x − 5) < 3 である. 教材構造グラフ I を考える上で, 指数の問題につ いては, (A)指数の性質を利用する基本問題(1, 2, 3, 6 が該当), (B)グラフ(4, 5 が該当), (C)方程式, 不等式 (7, 8 が該当)で構成されている. 対数の問題については, (A)底の変換(4, 5, 8 が該 当), (B)対数の性質を利用する基本問題(1, 2, 3 が該 当), (C)グラフ(6, 7 が該当), (D)方程式, 不等式(9, 10 が該当)で構成されている. 以上より, 教材構造グラフ I は図 3, 図 4 のように 考えられる.図3 指数の教材構造グラフ I 図4 対数の教材構造グラフ I 指数, 対数のテスト結果から得た得点行列 X から, クロス集計表 Cij を計算することにより,指数につい ては図 5, 対数については図 6 のような類似構造行 列 S が得られる. 図5 指数の類似構造行列 S また, 類似構造行列 S をクラスター分析すると, 指数については図 7, 対数については図 8 のような 分割樹形図 P が得られる. 図7 指数の分割樹形図 P 図8 対数の分割樹形図 P 得点行列 X から, クロス集計表 Cij を計算するこ とにより, 指数については図 9, 対数については図 10 のような関連構造行列 T が得られる.
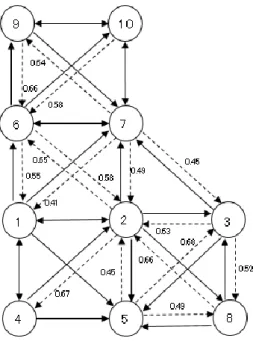
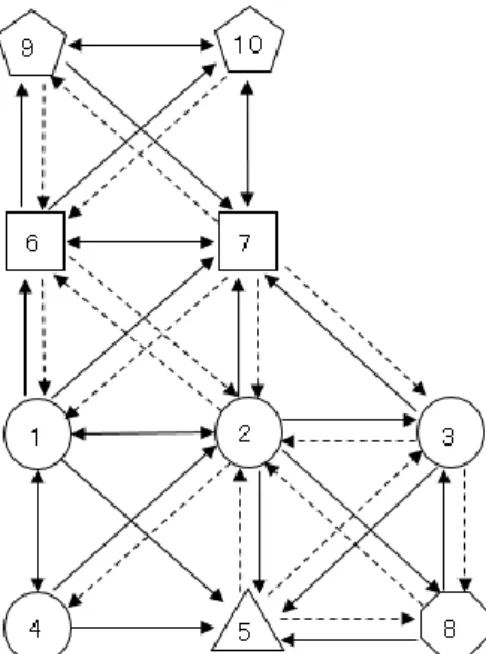
図9 指数の関連構造行列 T 図10 対数の関連構造行列 T 関連構造行列 T を近似三値分析すると, 指数につ い て は 図 11 の よ う な 近 似 三 値 グ ラ フ T∗ (p∗= 0.19, 𝜀 = 0.2) が, 対数については 図 12 のような近 似三値グラフT∗(p∗= 0.18, 𝜀 = 0.2) が得られる. 図11 指数の近似三値グラフ T∗ 図12 対数の近似三値グラフ T∗ 分割樹形図 P と近似三値グラフ T∗ より, 指数に ついては 図 13 のような認知構造グラフ Φz(𝑧 = 0.68) , 対数については図 14 のような認知構造グラ フ Φz(𝑧 = 0.77) が得られる. 図13 指数の認知構造グラフΦz(𝑧 = 0.68)
図14 対数の認知構造グラフΦz(𝑧 = 0.77) 認知構造グラフ Φz から, 指数の 8 項目, 対数の 10 項目について, 次のようなことがわかる. 1. 指数の 8 項目については 4 つのクラスター {1, 2, 3, 6}, {7, 8}, {4}, {5} に分類することができる. 2. 対数の 10 項目については 5 つのクラスター {1, 2, 3, 4}, {6, 7}, {9, 10}, {5}, {8} に分類することがで きる. 3. 指数について, 同じグラフの問題であるが, 項 目 4 と項目 5 をつなぐ実線が存在しないことから, 項目 4 の底が 1 以上のときと, 項目 5 の底が 1 以下 のときのグラフの問題は, 関係性が薄いという認識 を持っていることがわかる. 4. 指数について, おおまかではあるが 1→5→8 や 2→5→8 や 3→5→8 という流れがあることから, 教 材構造グラフで提唱した(A)→(B)→(C)の流れが正 しいことが確認できる. 5. 対数について, 項目 5 への実線は多くあるが, 項目 5 から他の項目への実線が存在しないことから, 生徒にとっては基礎的な問題であるという認識では 造グラフで提唱した(A)→(B)→(C)→(D)の流れが正 しいことが確認できる.
4. まとめ
項目間の類似構造分析, 関連構造分析から得られ る認知構造グラフにより適切な教授順序を分析し, 事例研究を行った. 現行の教科書通りに進めると, 指数については 6→1,2,3→4,5→7,8 という順序になるが, 本手法 による分析では多少違いはあったものの, 大部分は 一致しているため, 本手法の妥当性が示された. 対数については 8,5→4→1,2,3→6,7→9,10 とい う順序になる. こちらも, 指数同様, 多少違いがあ ったものの妥当性は示された. また, 指数と対数の認知構造グラフから, 指数に ついてはグラフの指導, 対数については導入部分の 指導が適切でなかったことが今回の研究でわかった. 特に, 対数の項目 5 と項目 8 の問題については対 数の定義そのものであり, 教科書ではセットで教え るよう記載がされている. しかし, 本研究の結果か ら, 生徒は項目 5 と項目 8 の問題を類似したものと して捉えていないことがわかった. 今後, 指数と対数を指導する際は, 以上の点に気 を付けて指導をしていきたい. また, 指数と対数の単元だけではなく, 他の単元 の事例研究も今後は行っていきたい.参考文献
[1] 山下元,須田宏:ファジィ数学入門‐ソフトサイ エンスの基礎と応用‐,森北出版,1997 [2] 山下元,瀧澤武信,他:ファジィ理論 基礎と応 用,共立出版,2010 [3] 永島謙一:ファジィ理論の教材構造分析への応 用,修士論文(早稲田大学),2010Tel:080-5645-8336