超特異多項式，保型微分方程式および超幾何級数に関する研究

(1)

九州大学学術情報リポジトリ

Kyushu University Institutional Repository

超特異多項式，保型微分方程式および超幾何級数に関する研究

中屋, 智瑛

https://doi.org/10.15017/1931729

出版情報：Kyushu University, 2017, 博士（数理学）, 課程博士バージョン：

権利関係：

(2)

A Study on Supersingular Polynomials, Modular Diﬀerential Equations,

and Hypergeometric Series

Tomoaki Nakaya

Graduate School of Mathematics Kyushu University

January 2018

(3)

(4)

Acknowledgments

Firstly, the author would like to express sincere thanks to his supervisor Professor Masanobu Kaneko for warm encouragement and valuable comments, and for introducing him to the study of the connection between modular forms and supersingular polynomials. He would also like to thank Professor Hiroyuki Tsutsumi and Dr. Yuichi Sakai, who introduced him to the study of supersingular polynomials with certain levels. Finally, he would like to thank his parents and brother for their continuous support.

(5)

(6)

Introduction

This thesis consists of three chapters. In Chapter 1, we extend results of Kaneko-Zagier and Baba-Granath on relations of supersingular polynomials and solutions of certain second order modular diﬀerential equations. This extended result gives an infinite series of modular diﬀerential equations related to supersingular polynomials. In Chapter 2, we focus on the following facts:

the set of prime numbers p such that the supersingular j-invariants in characteristic p are all contained in the prime field is finite. And surprisingly, it is well known that this set of primes coincides with the set of prime divisors of the order of the Monster simple group. In this chapter, we present analogous coincidence of supersingular invariants in level 2 and 3 and the orders of the Baby monster group and the Fischer group. The proof uses a connection between the number of supersingular invariants and class numbers of imaginary quadratic fields. In Chapter 3, we introduce Ochiai’s findings for the solutions of certain modular differential equations studied by Kaneko-Koike and discuss its further implications. Moreover, we use the Ramanujan-Serre differential operator to show that three differential equations related to extremal quasimodular forms, which appeared in the study by Kaneko-Koike, are essentially same. As an application, we simplifies the result on the solutions of certain modular differential equations by Sakai.

(9)

(10)

Chapter 1

On modular solutions of certain modular diﬀerential equation and supersingular polynomials

An elliptic curve E over a field K of characteristic p > 0 is called supersingular if it has no p-torsion over K. This condition depends only on the j-invariant of E, and it is known that there are only finitely many supersingular j-invariants, all being contained in Fp² . We define the supersingular polynomial ss_p(X) as the monic polynomial whose roots are exactly all the supersingular j-invariants:

ssp(X) = ∏

E/F^p E:supersingular

(X−j(E)) .

Because the set of supersingular j-invariants in characteristic p is stable under the conjugation overFp, we have ss_p(X)∈Fp[X].

Various lifts of ssp(X) to characteristic 0 are reviewed and studied in Kaneko and Zagier [1].

In particular, they constructed a lift by using a certain diﬀerential operator on the space of modular forms. Baba and Granath [2] extended this construction by introducing new diﬀerential operators.

In this chapter, we unify and generalize these results, by considering a diﬀerential operator arising from a product of Eisenstein series E₄, E₆, and the discriminant function ∆. With this operator we construct a second-order diﬀerential operator which gives rise to an endomorphism of M_k. We write an eigenform of this operator explicitly in terms of hypergeometric series. For k=p−1, we show that the associated polynomial Fe of this eigenform F satisfies

ssp(X) =X^δ(X−1728)^εFe(X) mod p, with suitableδ, ε∈ {0,1}.

1.1 Modular forms and supersingular polynomials

For positive even integerk, we denote byM_kthe space of holomorphic modular forms of weightk on Γ = PSL₂(Z). LetE_k(τ) be the Eisenstein series of weight kon Γ defined by

E_k(τ) = 1− 2k Bk

∑∞ n=1

(∑

d|n

d^k⁻¹ )

qⁿ (q=e^2πiτ),

(11)

where τ is a variable in the Poincar´e upper half-plane H and Bk thekth Bernoulli number. For evenk≥4, we haveE_k(τ)∈M_k. We also define the discriminant function ∆(τ)∈M₁₂ and the elliptic modular function j(τ) respectively by

∆(τ) = E4(τ)³−E6(τ)²

1728 =q

∏∞ n=1

(1−qⁿ)²⁴=q−24q²+ 252q³−1472q⁴+· · · and

j(τ) = E₄(τ)³

∆(τ) = 1

q + 744 + 196884q+ 21493760q²+· · · . The Gauss hypergeometric series is defined by

2F₁(α, β;γ;x) =

∑∞ n=0

(α)_n(β)_n (γ)n

xⁿ

n! (|x|<1)

where (α)0 = 1 and (α)n=α(α+ 1)· · ·(α+n−1) (n≥1). We note that the series2F1(α, β;γ;x) becomes a polynomial whenα orβ is a negative integer andγ is not a negative integer.

For even k≥4, we can writek uniquely in the form

k= 12m+ 4δ+ 6ε with m∈Z_≥0, δ ∈ {0,1,2}, ε∈ {0,1}. (1.1) Under this notation, any modular formf(τ)∈M_k can be written uniquely as

f(τ) =E4(τ)^δE6(τ)^ε∆(τ)^mfe( j(τ))

, (1.2)

where feis a polynomial of degree less than or equal to m. We call fethe associated polynomial of f.

The following representation of ss_p(X) is essentially due to Deuring [3]. To be more precise, he proved that the polynomialH_p₋₁(X) of [1, Proposition 5] is equal toss_p(X).

Lemma 1. Let p ≥ 5 be a prime number and write p−1 in the form 12m+ 4δ+ 6ε (m ∈ Z_≥0, δ∈ {0,1,2}, ε∈ {0,1}). Then

ssp(X) =X^m+δ(X−1728)^ε2F1

(

−m, 5

12− 2δ−3ε

6 ; 1;1728 X

)

mod p. (1.3) Proof. We define the monic polynomial U_n^ε(X) of degree n≥0 by

Xⁿ₂F₁( ₁

12,₁₂⁵ ; 1;¹⁷²⁸_X )

=U_n⁰(X) +O(₁

X

), Xⁿ⁻¹(X−1728)2F1

( ₇

12,¹¹₁₂; 1;¹⁷²⁸_X )

=U_n¹(X) +O(₁

X

).

By [1, Proposition 5], we have ss_p(X) = U_m+δ+ε^ε (X) modp. The first two parameters of the hypergeometric series in (2.1) reduce modulo pto

(

−m, 5

12 −2δ−3ε 6

)

≡











(₁₂¹,₁₂⁵) (modp) ifp≡1 (mod 12), (₁₂⁵,₁₂¹) (modp) ifp≡5 (mod 12), (₁₂⁷,¹¹₁₂) (modp) ifp≡7 (mod 12), (¹¹₁₂,₁₂⁷) (modp) ifp≡11 (mod 12).

Since ₂F₁(a, b;c;x) =₂F₁(b, a;c;x), we see thatU_m+δ+ε^ε (X) is congruent to the left-hand side of (2.1) modulo p.

(12)

1.2 Construction of the endomorphism

In this section, we construct an endomorphism ϕ_g,k of M_k. Let r, s, t be integers, not all zero, and k be an even integer greater than or equal to 4. Then, for the meromorphic modular form g(τ) =E4(τ)^rE6(τ)^s∆(τ)^t̸≡0 of weightu:= 4r+ 6s+ 12tandf ∈M_k, we define the diﬀerential operator∂_g by

∂_g(f)(τ) =∂_g,k(f)(τ) =f^′(τ)−k u

g^′(τ) g(τ)f(τ)

(

′= 1 2πi

d

dτ =q d dq

) ,

and form∈Z_≥0, δ ∈ {0,1,2} andε∈ {0,1}withk= 12m+ 4δ+ 6ε, define the operatorϕ_g,kby ϕ_g,k(f) = 1

E4

{

(∂_g,k+2◦∂_g,k)(f)−t²k(k+ 2) u² E₄f

−432

u² (sk−uε)(sk−uε+ 4(r+ 2s+ 3t))E₄∆

E₆² f (1.4)

+192

u² (rk−uδ)(

rk−uδ+ 6(r+s+ 2t))∆ E₄²f

} .

Note that the function g(τ) is not always a holomorphic modular form. Except for the case of (r, s, t) = (0,0,1), the image off ∈M_k under∂_g,k is not holomorphic in general.

Theorem 1. The diﬀerential operator ϕ_g,k is an endomorphism of M_k. To prove the theorem, we need two lemmas.

Lemma 2. The operator∂_g is written as

∂g(f) = 4r

u ∂_E₄(f) +6s

u ∂_E₆(f) +12t

u ∂_∆(f) =∂_∆(f) + k 6u

( 2rE6

E₄ + 3sE₄² E₆

)

f. (1.5) Proof. This is easily computed by using the well-known relation (due to Ramanujan)

E₂^′ = E₂²−E₄

12 , E₄^′ = E₂E₄−E₆

3 , E₆^′ = E₂E₆−E₄²

2 . (1.6)

Lemma 3. Putv= (sk−uε)/2 andw= (rk−ua)/3. Then

u ∂g,k(E₄âE₆^ε∆^c) =vE₄â+2E₆^ε⁻¹∆^c+wE₄â⁻¹E₆^ε+1∆^c,

u²(∂_g,k+2◦∂_g,k)(E₄^aE₆^ε∆^c) = 1728v(v+ 2(r+ 2s+ 3t))E^a+1₄ E₆^ε⁻²∆^c+1

+ (v+w)(v+w−2t)E₄^a+1E^ε₆∆^c (1.7)

−1728w(w+ 2(r+s+ 2t))E₄^a⁻²E₆^ε∆^c+1. Proof. One can easily see that the operator ∂∆satisfies the Leibniz rule:

∂_∆,k+l(F G) =∂_∆,k(F)G+F ∂_∆,l(G)

for F ∈ M_k and G∈ M_l. Hence we can prove the lemma by direct calculation using (1.5) and the following relations:

∂∆(E4) =−1

3E6, ∂∆(E6) =−1

2E₄², ∂∆(∆) = 0, E₄³−E²₆ = 1728∆.

(13)

Proof of Theorem 1 For even k ≥ 4, write k in the form k = 12m+ 4δ+ 6ε as before and assume the numbersa, csatisfya≡δ mod 3 (0≤a≤3m+δ),0≤c≤m, andk= 4a+6ε+12c, so that the forms E₄^aE₆^ε∆^cconstitute basis elements of M_k. We now compute ϕ_g,k(E₄^aE₆^ε∆^c).

Since (v+w)(v+w−2t) = t²k(k+ 2)−2t(k+ 1)uc+u²c², we can obtain from (1.7) the following equation:

u²(∂_g,k+2◦∂_g,k)(E₄^aE₆^ε∆^c)−t²k(k+ 2)E4·E₄^aE₆^ε∆^c

= 1728v(v+ 2(r+ 2s+ 3t))E^a+1₄ E₆^ε⁻²∆^c+1+u²c{c−2t(k+ 1)/u}E₄^a+1E₆^ε∆^c

−1728w(w+ 2(r+s+ 2t))E₄^a⁻²E₆^ε∆^c+1.

Furthermore, by using 1728v(v+ 2(r+ 2s+ 3t)) = 432(sk−uε)(sk−uε+ 4(r+ 2s+ 3t)), we have u²(∂g,k+2◦∂g,k)(E₄^aE₆^ε∆^c)−t²k(k+ 2)E4·E₄^aE₆^ε∆^c

−432(sk−uε)(sk−uε+ 4(r+ 2s+ 3t))E4∆

E₆² E^a₄E₆^ε∆^c

=u²c {

c−2t(k+ 1) u

}

E₄^a+1E₆^ε∆^c−1728w(w+ 2(r+s+ 2t))E₄^a⁻²E₆^ε∆^c+1.

We defineλ(x) = ¹⁹²_u2 (rk−ux)(rk−ux+ 6(r+s+ 2t)), then 1728w(w+ 2(r+s+ 2t)) =u²λ(a).

Adding u²λ(δ)E₄^a⁻²E₆^ε∆^c+1 to both sides of the above equation and dividing them by u²E4, we get

ϕ_g,k(E₄^aE₆^ε∆^c) = 1 E₄

{

(∂_g,k+2◦∂_g,k)(E₄^aE₆^ε∆^c)−t²k(k+ 2)

u² E4·E₄^aE₆^ε∆^c

−432

u² (sk−uε)(sk−uε+ 4(r+ 2s+ 3t))E4∆

E₆² E₄^aE₆^ε∆^c +48

u²(rk−uδ)(rk−uδ+ 6(r+s+ 2t))∆

E₄²E₄^aE₆^ε∆^c }

=c {

c−2t(k+ 1) u

}

E₄âE₆^ε∆^c−(λ(a)−λ(δ))E₄â⁻³E₆^ε∆^c+1. (1.8) The right-hand side is an element of M_k if a ≥ 3. If a < 3, we have a = δ (because a ≡ δ (mod 3)) and the coefficientλ(a)−λ(δ) ofE₄â⁻³E₆^ε∆^c+1 vanishes, hence the right-hand side is in M_k. Thusϕ_g,k is an endomorphism of M_k.

1.3 Modular solutions of ϕ

_g,k

(f ) = 0 and supersingular polynomi- als

Throughout this section, we assume 2t(k + 1) ̸= cu(1 ≤ c ≤ m) for given r, s, t and k = 12m+ 4δ+ 6ε. By equation (1.8), we see that the matrix representation of ϕ_g,k in the ordered base{E₄^3m+δE₆^ε, . . . , E₄^δE₆^ε∆^m}is triangular matrix and obtain the eigenvaluesc(c−^2t(k+1)_u ), 0≤ c≤mofϕ_g,kas diagonal elements. Hence, under the assumption, all eigenvalues of endomorphism ϕ_g,k are diﬀerent.

Theorem 2. (i) The following modular form F_g,k(τ) = 1 +O(q) is the unique eigenvector of ϕ_g,k with eigenvalue 0:

F_g,k(τ) =E₄(τ)^3m+δE₆(τ)^ε×

2F1

(

−m, 5

12 +(2r−3s−6t)(k+ 1)

6u −2δ−3ε

6 ; 1−2t(k+ 1) u ;1728

j(τ) )

. (1.9)

(14)

(ii) Let k=p−1 wherep ≥5 is prime and assume that u ̸≡0 (modp). Then the associated polynomialFe_g,p−1(X) ofF_g,p−1(τ) hasp-integral coeﬃcients and

ssp(X) =X^δ(X−1728)^εFeg,p−1(X) mod p.

Proof. (i) By using (1.5) and (1.6) to expand the diﬀerential equationϕg,k(f) = 0, we obtain f^′′(τ) +A(τ)f^′(τ) +B(τ)f(τ) = 0, (1.10) A(τ) =−k+ 1

6 E₂+k+ 1 3u

( 3sE₄²

E6

+ 2rE₆ E4

) , B(τ) = k(k+ 1)

12 E₂^′ −k(k+ 1)

36u ·9sE₄^′E₄²+ 4rE₆^′E6

E4E6

+E₄³−E₆² E₄²E₆²

{sε(k+ 1)

2u E₄³−2rδ(k+ 1)−uδ(δ−1)

9u E₆²

} .

This is a special case of modular diﬀerential equations with regular singularities at elliptic points for SL₂(Z) treated in [4]. More explicitly, the diﬀerential equation (1.10) is expressed as follows using the symbol in [4, Theorem B]:

Dk

(s(k+ 1)

u , 2r(k+ 1)

3u , sε(k+ 1)

2u , 2rδ(k+ 1)−uδ(δ−1) 9u

) .

Applying [4, Theorem C] to this parameters, we get the hypergeometric representation of F_g,k(τ). We note that the exponent of E₆(τ) is a solution of the following quadratic equation:

x²−

(2s(k+ 1) u + 1

)

x+2sε(k+ 1) u = 0.

Since ε∈ {0,1}, we have ε(ε−1) = 0 and thus the left hand side of the above equation factor into (x−ε)(x−2s(k+ 1)/u+ε−1). As pointed out in [4, Remark 4], we can choose εas exponent ofE₆(τ).

(ii) For k = p−1, by (1.2) and the hypergeometric formula (1.9), the associated polynomial Feg,p−1(X) ofFg,p−1(τ) is as follows:

Fe_g,p₋₁(X) =X^m₂F₁ (

−m, 5

12 +(2r−3s−6t)p

6u −2δ−3ε

6 ; 1−2tp u ;1728

X )

≡X^m₂F₁ (

−m, 5

12 −2δ−3ε

6 ; 1;1728 X

)

mod p.

Hence X^δ(X−1728)^εFe_g,p−1(X) is congruent toss_p(X) modulo pby Lemma 1.

Remark 1. The case of (r, s, t) = (0,0,1) was studied in the paper [1] by Kaneko and Zagier.

The corresponding operator

∂∆,k(f)(τ) =f^′(τ)− k

12E2(τ)f(τ) :Mk→Mk+2 (1.11) is called the Ramanujan-Serre derivative. We note that the logarithmic derivative of ∆(τ) is equal to E2(τ). If k ̸≡ 2 (mod 3), the function F∆,k(τ) coincides with Fk(τ) in [1, Section 8.]

up to a constant multiple. Moreover, Baba and Granath studied the cases of (r, s, t) = (1,0,0) and (0,1,0) in [2]. The corresponding operators are given respectively by

∂_E₄_,k(f)(τ) =f^′(τ)−k 4

E₄^′(τ)

E₄(τ)f(τ), ∂_E₆_,k(f)(τ) =f^′(τ)−k 6

E₆^′(τ) E₆(τ)f(τ).

Hence, the diﬀerential equationsϕE4,k(f) = 0 andϕE6,k(f) = 0 coincides with [2, Eq.(5)] and [2, Eq.(8)] respectively. Consequently, the symbols F_E₄_,k(τ) andF_E₆_,k(τ) we use are same as theirs, but the definition of our operator ϕ_g,k and their operator ϕare slightly diﬀerent.

(15)

Chapter 2

The number of linear factors of supersingular polynomials

2.1 Introduction

For any prime p ≥5, we define the numbers ν, δ, ε ∈ {0,1}, which will be used throughout this chapter, by

ν = 1 2

( 1−

(−2 p

))

, δ = 1 2

( 1−

(−3 p

))

, ε= 1 2

( 1−

(−1 p

)) ,

where (_p^·) is the Legendre symbol. We recall Lemma 1 in Chapter 1 : Letp≥5 be a prime and m= [p/12]. Then

ssp(X) =X^m+δ(X−1728)^ε2F1

(

−m, 5

12− 2δ−3ε

6 ; 1;1728 X

)

mod p. (2.1) For p = 2 and 3, we have ss₂(X) = X mod 2 and ss₃(X) = X mod 3 (see [3, p.201]). From this expression we easily see that

degssp(X) =m+δ+ε= p−1 12 +1

4 (

1− (−1

p ))

+1 3

( 1−

(−3 p

)) .

The polynomial ssp(X) factors into linear and quadratic polynomials in Fp[X] by the result of Deuring [3] that all supersingular j-invariants lie in Fp².

Leth(√

−d) denote the class number of the imaginary quadratic fieldQ(√

−d). The following theorem is essentially due to Deuring ([3, §10] and [5, Eq.(9)]), but is expressed in somewhat diﬀerent form (see also [6, Lemma 2.6]).

Theorem 3. Ifp≥5, the number L(p) of supersingularj-invariants that lie in Fp is L(p) = 1

4 {

2 + (

1− (−1

p )) (

2 + (−2

p ))}

h(√

−p)

=







1 2h(√

−p) ifp≡1 (mod 4), 2h(√

−p) ifp≡3 (mod 8), h(√−p) ifp≡7 (mod 8).

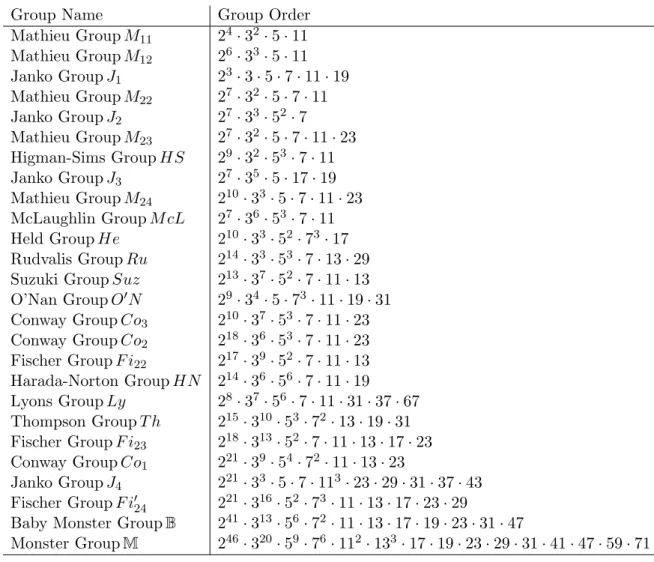
Let M be the monster group. It is the largest sporadic finite simple group and has order

#M= 808017424794512875886459904961710757005754368000000000

= 2⁴⁶·3²⁰·5⁹·7⁶·11²·13³·17·19·23·29·31·41·47·59·71.

(16)

In 1975, A. Ogg noticed that the prime divisors p of #M agree with those p such that all characteristic p supersingular j-invariants that lie in Fp (see [7, p.7]). By the definition of the polynomial ss_p(X) and the number L(p), Ogg’s observation is paraphrased as the following theorem.

Theorem 4. For a prime numberp,

degssp(X) =L(p) ⇐⇒ p|#M.

This theorem can be proved by using class number estimate, but it does not explain why such a relationship exists.

In this chapter, we consider analogues of these theorems in the case of higher levels. The supersingular polynomialss^(Np ^∗⁾(X) for the Fricke group Γ^∗₀(N) (N = 2,3) was defined by Sakai [8].

It is derived from the invariant diﬀerential for Γ^∗₀(N) (N = 2,3) and has hypergeometric series representation.

Definition 1. For primesp≥5, let m₂ = [p/8] andm₃= [p/6], and set ss⁽²_p ^∗⁾(X) =X^m²^+ε(X−256)^ν₂F₁

(

−m₂,3

8 −ε−2ν

4 ; 1;256 X

)

mod p, ss⁽³_p ^∗⁾(X) =X^m³^+δ(X−108)^δ₂F₁

(

−m₃,1 3+ δ

3; 1;108 X

)

mod p.

For p ∈ {2,3} and N ∈ {2,3}, we have ssp^(N^∗⁾(X) = X modp. The degrees of these polynomials are given as follows.

degss⁽²_p^∗⁾(X) =m₂+ε+ν= p−1 8 +3

8 (

1− (−1

p ))

+1 4

( 1−

(−2 p

)) , degss⁽³_p^∗⁾(X) =m3+ 2δ = p−1

6 + 2 3

( 1−

(−3 p

)) . We shall prove:

Theorem 5. Ifp≥5 is a prime, then the number of linear factorsL^(N^∗⁾(p) ofss^(Np ^∗⁾(X) (mod p) is

L⁽²^∗⁾(p) = 1 8

{ 2 +

( 1−

(−1 p

)) ( 4 +

(−2 p

))}

h(√

−p) +1 4h(√

−2p), L⁽³^∗⁾(p) = 1

2 (

1− (−3

p ))

L(p) +1 8

{ 2 +

( 1 +

(−1 p

)) ( 2 +

(−2 p

))}

h(√

−3p).

Let Bbe the Baby monster group andF i^′₂₄be the largest of Fischer’s groups. The orders of these groups are given by

#B= 4154781481226426191177580544000000

= 2⁴¹·3¹³·5⁶·7²·11·13·17·19·23·31·47,

#F i^′₂₄= 1255205709190661721292800

= 2²¹·3¹⁶·5²·7³·11·13·17·23·29.

An exact analogue of Theorem 4 for the sporadic groups Band F i^′₂₄ holds true.

Theorem 6. For a prime numberp,

degss⁽²_p^∗⁾(X) =L⁽²^∗⁾(p) ⇐⇒ p|#B, degss⁽³_p^∗⁾(X) =L⁽³^∗⁾(p) ⇐⇒ p|#F i^′₂₄. In Section 2.4, we give some conjectures for higher levels N.

(17)

2.2 Preliminaries

2.2.1 Factorization of the Legendre polynomials

Using the theory of elliptic curves, Brillhart and Morton determined the number of linear factors of the following polynomials W_m(x) modp:

Wm(X) :=

∑m r=0

(m r

)2

X^r=2F1(−m,−m; 1;X). (2.2) It is well known that the Hasse invariant for elliptic curves in Legendre form

E_λ :y² =x(x−1)(x−λ)

isW_(p₋_1)/2(λ) and the elliptic curveE_λ is supersingular if and only if W_(p₋_1)/2(λ)≡0 mod p.

Theorem 7 (Brillhart, Morton [9]). Letp≥5 be a prime andN1(p, m) be the number of linear factors of Wm(X) modp. Then

N₁ (

p, [p

4 ])

= 1 4

{ 2 +

( 1−

(−1 p

)) ( 4 +

(−2 p

))}

h(√

−p)−ε, N₁

( p,

[p 3

])

=δ(2L(p)−1), N₁ (

p, [p

2 ])

= 3δ h(√

−p).

We note that the polynomial W_m(X) and the Legendre polynomial P_n(x) := 1

2ⁿn!

dⁿ

dxⁿ(x²−1)ⁿ=

(x−1 2

)n∑n r=0

(n r

)2( x+ 1 x−1

)r

satisfy the following relation:

W_m(X) = (1−X)^mP_m

(1 +X 1−X

)

. (2.3)

Moreover, Morton determined the number of a certain quadratic factors of the Legendre polynomials.

Theorem 8 (Morton [10, 11]). Let p≥5 be a prime and B(p, m) be the number of irreducible quadratic factors of the formX²+C of the Legendre polynomial Pm(X) modp. Then

B (

p, [p

4 ])

= 1 4

{ h(√

−2p)−2(ε+ν) }

, B (

p, [p

3 ])

= 1 4

{ aph(√

−3p)−4δ }

, where

a_p = 1 2

{ 2 +

( 1 +

(−1 p

)) ( 2 +

(−2 p

))}

. 2.2.2 Supersingular polynomials for Γ₀(N) (N = 2,3,4)

Tsutsumi introduced the supersingular polynomials for congruence subgroups of low levels in [12]

and obtained hypergeometric representations for them. There exist algebraic relations between the elliptic modular invariant j(τ) and modular functionsj_N(τ) for Γ0(N) (N = 2,3,4):

(j₂(τ) + 192)³−j(τ) (j₂(τ)−64)² = 0,

j3(τ) (j3(τ) + 216)³−j(τ) (j3(τ)−27)³ = 0, (2.4) (j₄(τ)²+ 224j₄(τ) + 256)³−j(τ)j₄(τ) (j₄(τ)−16)⁴ = 0.

(18)

We prepare the set

S_N :={j_N ∈Fp|thej-invariant determined by (2.4) is supersingular}. We then define

ss^(N)_p (X) = ∏

jN∈SN

(X−jN)∈Fp[X]

for the prime p ≥ 5. Note that we ignore the duplication of elements of the set S_N. Because the set S_N is stable under the conjugation over Fp, we have ss^(Np ⁾(X) ∈ Fp[X]. The following proposition are stated in [12, Proof of Theorem 4] as a congruence relations of ss^(Np ⁾(X) and certain polynomial likeU_n^ε(X) appearing in the proof of Lemma 1.

Proposition 1 (Tsutsumi). (i) Let p≥5 be a prime andm= [p/4]. Then ss⁽²⁾_p (X) =X^m+ε2F1

(

−m,3 4− ε

2; 1;64 X

)

mod p. (2.5)

(ii) Letp≥5 be a prime and m= [p/3]. Then ss⁽³⁾_p (X) =X^m+δ₂F₁

(

−m,2 3− δ

3; 1;27 X

)

mod p. (2.6)

(iii) Let p≥5 be a prime and m= [p/2]. Then ss⁽⁴⁾_p (X) =X^m₂F₁

(

−m,−m; 1;16 X

)

mod p. (2.7)

The degrees of these polynomials are given as follows.

degss⁽²⁾_p (X) = p−1 4 +1

4 (

1− (−1

p ))

, degss⁽³⁾_p (X) = p−1 3 +1

3 (

1− (−3

p ))

, degss⁽⁴⁾_p (X) = p−1

2 .

Proposition 2. If p ≥ 5, the number L^(N⁾(p) (N = 2,3,4) of characteristic p supersingular jN-invariants that lie in Fp is

L⁽²⁾(p) =N₁ (

p, [p

4 ])

+ε, L⁽³⁾(p) =N₁ (

p, [p

3 ])

+δ, L⁽⁴⁾(p) =N₁ (

p, [p

2 ])

.

Therefore, by Theorems 3 and 7, the numbersL^(N)(p) (N = 2,3,4) are constant multiples of the class number h(√−p).

Proof. We only prove the first equality, the other cases being similar. For m= [p/4], W_m(X) =₂F₁(−m,−m; 1;X) = (1−X)^m₂F₁

(

−m, m+ 1; 1; X X−1

)

and since ³₄− ^ε₂ ≡m+ 1 (modp), ss⁽²⁾_p (Y)≡Y^m+ε₂F₁

(

−m,3 4 −ε

2; 1;64 Y

)

≡Y^ε(Y −64)^mW_m ( 64

64−Y )

mod p (2.8) Because the number of linear factors is unaﬀected under the linear fractional transformation of variable, we have L⁽²⁾(p) =ε+N₁(p,[p/4]) by Theorem 7.

(19)

We can regard the polynomial ss⁽²⁾p (X) modp as the polynomial part of X^[p/4]+ε₂F₁

(1 4,3

4; 1;64 X

) ,

and hence easy calculation of binomial coeﬃcients gives the following explicit formula ofss⁽²⁾p (X).

The case of ss⁽³⁾p (X) can be shown similarly.

Theorem 9. For a primep≥5, ss⁽²⁾_p (X) =

(p−1+2ε)/4∑

n=0

(2n n

)(4n 2n )

X^(p⁻^1+2ε)/4⁻ⁿ mod p,

ss⁽³⁾_p (X) =

(p−1+2δ)/3∑

n=0

(2n n

)(3n n

)

X^(p⁻^1+2δ)/3⁻ⁿ modp.

Similarly, we obtain the following theorem concerning the square of supersingular polynomials by applying Clausen’s formula

2F1(α, β;α+β+ 1/2;x)²=3F2(2α,2β, α+β; 2α+ 2β, α+β+ 1/2;x). (2.9) Theorem 10. For a prime p≥5,

ss_p(X)² = (X−1728)^ε

(p−1+8δ)/6∑

n=0

(2n n

)(3n n

)(6n 3n )

X^(p⁻^1+8δ)/6⁻ⁿ mod p,

ss⁽²_p^∗⁾(X)² = (X−256)^ν

(p−1+6ε)/4∑

n=0

(2n n

)2( 4n 2n )

X^(p⁻^1+6ε)/4⁻ⁿ modp,

ss⁽³_p^∗⁾(X)² =X^δ(X−108)^δ

(p−1+2δ)/3∑

n=0

(2n n

)₂( 3n

n )

X^(p⁻^1+2δ)/3⁻ⁿ mod p.

Here, we would like to point out the similarity between Theorem 10 and the expansions of certain Eisenstein series in terms of 1/j(τ) and similar local parameters described below. By Lemma 1, we have

ss_p(X) =X^m+δ(X−1728)^ε₂F₁ (

−m, 5

12 −2δ−3ε

6 ; 1;1728 X

)

mod p

≡









X^m+δ2F1

( 1 12, 5

12; 1;1728 X

)

mod p ifp≡1 (mod 4),

X^m+δ(X−1728)2F1

( 7 12,11

12; 1;1728 X

)

mod p ifp≡3 (mod 4).

We note the following hypergeometric transformation

2F1(α, β;γ;z) = (1−z)^γ⁻^α⁻^β2F1(γ −α, γ−β;γ;z) and hence have

2F₁ ( 1

12, 5

12; 1;1728 X

)

= (

1−1728 X

)1/2 2F₁

( 7 12,11

12; 1;1728 X

) .

It is well known that the Eisenstein series of weight 4 onSL₂(Z) has the following hypergeometric representation for suﬃciently largeℑ(τ):

E₄(τ) =₂F₁ (1

12, 5

12; 1;1728 j(τ)

)4

∈M₄(SL₂(Z)).

(20)

In [8], it is shown that the Eisenstein series of weight 4 on the Fricke group Γ^∗₀(N) (N = 2,3) has the following hypergeometric series expression:

(2E2(2τ)−E2(τ))²=2F1

(1 8,3

8; 1; 256 j₂^∗(τ)

)4

∈M4(Γ^∗₀(2)), (3E₂(3τ)−E₂(τ)

2

)₂

=₂F₁ (1

6,1

3; 1; 108 j₃^∗(τ)

)₄

∈M₄(Γ^∗₀(3)).

The calculation of the binomial coeﬃcients using Clausen’s formula (2.9) gives the following:

E4(τ)^1/2 =

∑∞ n=0

(2n n

)(3n n

)(6n 3n )

j(τ)⁻ⁿ, 2E₂(2τ)−E₂(τ) =

∑∞ n=0

(2n n

)2( 4n 2n )

j₂^∗(τ)⁻ⁿ, 3E₂(3τ)−E₂(τ)

2 =

∑∞ n=0

(2n n

)2( 3n

n )

j₃^∗(τ)⁻ⁿ.

These expressions are very similar to the polynomial of Theorem 10. Based on these similarities, we propose conjectural expressions of squares of the supersingular polynomials ss⁽⁵p^∗⁾(X) and ss⁽⁷p ^∗⁾(X) in Section 2.4.

2.3 Proof of main theorems

In order to prove Theorems 5 and 6, we start with the next proposition on the algebraic relation between the polynomial ss^(Np ^∗⁾(X) andss^(N)p (X) for N = 2,3.

Proposition 3. (i) Let p≥5 be a prime and m= [p/8]. Then we have (X−64)^m+ε+νss⁽²_p^∗⁾

( X² X−64

)

=X^ε(X−128)^νss⁽²⁾_p (X) mod p.

(ii) Letp≥5 be a prime and m= [p/6]. Then we have (X−27)^m+2δss⁽³_p ^∗⁾

( X² X−27

)

=X^δ(X−54)^δss⁽³⁾_p (X) mod p.

Proof. We only prove the case of level 2, the other case being similar. Now m = [p/8] and so p−1 = 4(2m+ν) + 2ε, the polynomial (2.5) is

ss⁽²⁾_p (X) =X^2m+ε+ν₂F₁ (

−2m−ν,3 4 −ε

2; 1;64 X

)

mod p. (2.10)

Forα=−m−ν/2, β= 3/8−ε/4, we haveα+β+ 1/2≡1 mod p. Based on this, we apply the formula (Kummer’s relation)

2F₁ (

2α,2β;α+β+ 1 2;z

)

=₂F₁ (

α, β;α+β+1

2; 4z(1−z) )

to the right-hand side of (2.10) and get ss⁽²⁾_p (X) =X^2m+ε+ν2F1

(

−m−ν 2,3

8 −ε

4; 1;256(X−64) X²

)

mod p. (2.11)

(21)

Ifν = 0, there is nothing to do:

ss⁽²⁾_p (X) =X^2m+ε₂F₁ (

−m,3 8 −ε

4; 1;256(X−64) X²

)

mod p.

Ifν = 1, we apply Gauss’s relation

2F₁(α, β;γ;z) = (1−z)^γ⁻^α⁻^β₂F₁(γ −α, γ−β;γ;z)

to the left-hand side of (2.11). Then the first two parameters of the hypergeometric series of (2.11) reduces modulop to

1−α≡m+3 2 ≡ 3

8 −ε−2

4 , 1−β ≡ 5 8 +ε

4 ≡ −m mod p.

Since the exponent is 1−α−β≡1/2 mod p, (

1−256(X−64) X²

)1/2

= X−128 X . Therefore when ν = 1, we have

ss⁽²⁾_p (X) =X^2m+ε(X−128)2F1

(

−m,5 8+ ε

4; 1;256(X−64) X²

)

mod p.

Summarizing these cases, we finally obtain ss⁽²⁾_p (X) =X^2m+ε(X−128)^ν 2F1

(

−m,3

8−ε−2

4 ; 1;256(X−64) X²

)

mod p. (2.12) By multiplying both sides of the above equation by X^ε(X−128)^ν, we get the assertion:

X^ε(X−128)^νss⁽²⁾_p (X)

= (X−64)^m+ε+ν

( X² X−64

)m+ε( X²

X−64 −256 )ν

2F₁ (

−m,3

8 −ε−2ν

4 ; 1;256(X−64) X²

)

= (X−64)^m+ε+νss⁽²_p^∗⁾

( X² X−64

)

mod p.

Lemma 4. The roots of W_(p₋₁₋_2ε)/4(X) over Fp are distinct and all lie in Fp².

Proof. Firstly, we prove that if λis a root of W_(p₋_1)/2(X), then 1−λis also a root of it. The polynomial W_m(X) = ₂F₁(−m,−m; 1;X) can be regarded as a polynomial solution of certain hypergeometric diﬀerential equation at X= 0 (exponent zero), so this polynomial coincide with the polynomial solution of the same equation atX= 1 (exponent zero) up to a constant multiple.