電子図書館用高速データベース管理システム[稲田]

情報処理技術演習問題の分類

1. 分類実験

情報処理技術者資格試験問題には何章の問題であるかの区別はない．概ね同じ章の問題が連続して出題される が，100%正しいわけでない．したがって，過去問題を章別に分類管理するには，人手による分類作業が必要と なる．本研究では自動分類を試みる． 情報処理技術者資格試験の過去問題 1,140 問を教師データ，320 問をテストデータとして分類実験を行った． データは問題文および選択肢をchasen で形態素解析して，そのデータから計算した tfidf 値を用いた．２乗和が 1（ベクトルの長さが 1）になるようにノーマライズした実験も行った．元の単語数は 5,563 語であるが，一つの 問題にしか現れない単語を除いたため，3,109 語となった． 三つの手法（Neuro，SVM，類似度）で分類を行った．精度はそれぞれ 93.7%，90.8%，90.5%となった． 計算時間は類似度手法が圧倒的に高速である．SVM はまだ十分にマスターしていないことから，現在のプロ グラムは遅い．また，Neuro もここでは最も基本的なモデルを用いているので，遅い．拡張 BP 法の採用などに より，数倍の高速化が実現できるかもしれない． 形態素解析から名詞，動詞，形容詞を取り出した．動詞，形容詞を無視した結果も求めたいところである．か えって，いい結果が得られるかもしれない． 類似度手法は数学的にはどのような最適化問題を解いていることになるのであろうか？ Linear Kernel に当 るのか？ データフォーマットは以下の通り（教師データ1,2 および 1140 を示した）．印刷の都合で，一つのレコードが複 数行になっているが，データでは１レコードが１行となっている．各レコードの最初の数値が章番号で，その後 にターム番号とそのtfidf 値のペアが続く．ペアはターム番号が小さい順に並んでいる． 1.1. 今後の課題（修論，卒論として）  類似度算出（および分類）では TfIdf ファイルの全てのタームを用いている．類似度算出では誤差を生むタ ー ム も存 在す る． この よう な ター ム

_i

に つい て は ニ ュー ラル ネッ トワ ー ク入 力-中 間層 の 結合 荷重



ij M ( M

N

j



1 

,

2

,

,

)はほぼ 0（もしくは負の値）となっているのではなかろうか？もしそうならばこのよ うなタームを除去すれば類似度の精度が改善される可能性がある．  Neuro など他の手法に頼らず，類似度計算で直接，誤差を生むタームを除去できないか？  主成分分析によって特徴ベクトルの次数を低減することも考えられる．ただし，何となくだが，精度は上が らない気がする．  ニューラルネットについては拡張 BP 法についても調べる．ただし，収束は速くなるが，精度は変わらない と思われる．  今回は 1,460 問について調べたが，さらに追加して，現在 1,940 問のデータを持っている．データ数を増や しても大きな改善は見込めないが，次のフェーズでは，1,940 問のデータを使用する．  ニューロでは 94%の分類精度が得られた．しかし，類似度手法で，類似度最大のものに分類するときの精度 は85%程度である．類似度そのものの改善ではこの値を向上させる必要がある． [tfidf1.data]…1,140 レコード sparse 7 1 61 1.09 79 3.91 208 3.29 249 4.65 659 0.12 690 1.65 740 0.01 1279 2.87 1287 1.84 1411 2.84 1981 2.07 2151 1.82 2481 2.67 2643 2.27 2722 6.77 2743 1.56 2980 3.27 1 3 15.8 145 1.24 531 9.16 535 9.95 593 1.18 613 1.34 659 0.12 681 0.37 740 0.01 1717 2.87 1731 2.51 1981 2.07 2324 1.3 2579 2.74 2599 2.87 2744 1.5 2867 3.97 ・・・ 7 288 2.39 436 3.52 497 3.17 591 0.93 613 1.34 626 0.26 631 3.8 649 1.06 665 1.66 681 0.37 687 1.43 740 0.01 1287 2.92 1473 2.9 1506 2.13 1664 6.77 1766 1.61 1811 3.6 1846 3.0 2057 3.7 2076 5.38 2212 2.74 2221 2.62 2559 4.38 2734 1.18 2890 4.56

1.2. ニューラルネットワーク 付録には拡張BP 法の解説を載せているが，今回の実験では基本 BP 法を用いた．即ち，



_k



1

.

0

としている． 学習パラメータは





0

.

8

,

　





0

.

2

とした．ノーマライズした場合にも，まれに（数回）局所解に陥り，収束 しないことがあったが，初期値を乱数で決めていることから，再実行では収束した． 入力データをノーマライズしたとき，中間層の数と認識率の関係を次表に示す．実行時間は 3,４分である．（い ずれ正確に測定すべきである） なお，ノーマライズしないときは学習が容易に収束しそうになかったので実験 を中止した． 中間層数 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 正解率(%) 83.7 87.5 90.9 92.5 91.2 90.3 93.1 91.8 91.8 90.6 90.9 91.2 92.1 91.5 90.6 89.6 92.1 91.8 中間層数 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 正解率(%) 91.5 92.1 92.5 93.7 93.7 92.1 91.5 90.9 27:91.5 最高値は93.7％であるが，中間層数による変動が比較的大きい．中間層数=7～19 では正解率にムラがある． 中間層数=22～26 付近では安定しており，最高値は 93.7％である． 1.3. SVM * K(w, x): カーネル関数(Kernel Function) * linear(default) (w * x) innerproduct(w, x) * polynomial (a w * x + b)^d

* gaussian(radial basis function) exp(-1/(2a) ||w - x||^2) a: sigma_squared * neural tanh(a w * x + b) 1.3.1. Linear ノーマライズなしのとき，Linear Kernel に対する結果を下表に示す． C 0.001 0.002 0.003 0.004 0.005 0.006 0.007 0.008 0.009 0.010 0.011 0.012 正解率(%) 88.1 89.7 89.7 90.6 90.6 90.3 90.9 90.6 90.6 90.3 91.3 90.9 C 0.02 0.03 0.04 0.05 正解率(%) 89.7 89.7 89.7 89.7 比較的安定した結果が得られている．C=0.007～0.012 での平均正解率は 90.8％である． 他のカーネル関数についても実験中であるが，今のところ，いい結果が得られていない．この最適化問題自身 がおおよそ線形問題に近いということかもしれない．しかし，線形問題ならば，ニューラルネットワークでの中 間層の数は1 でもいいのではなかろうか？中間層の数として 24，25 が最良ということはリニア問題ではないこ とを意味しているはずだが． ノーマライズしたときのLinear Kernel に対する結果を下表に示す．実行時間は c=0.001 など値が小さいとき はニューラルネットよりかなり速い． C 0.001 0.002 0.003 0.004 0.005 0.006 0.007 0.008 0.009 0.010 0.011 0.012 正解率(%) 84.4 83.8

C 1E-04 2E-04 3E-04 4E-04 5E-04 6E-04 7E-04 8E-04 9E-04 0.001 0.001 正解率(%) 67.8 76.9 81.6 82.8 81.9 84.7 84.7 85.0 84.4 84.4 84.4

1.3.2. Polynomial

java -Xmx500MB SVM -m 1140P10.model -f tfidf1140.data -p –d 1.1 c=0.010 100% → precision=89.37% (Error Rate=34/320)

c=0.009 100% → precision=89.06% (Error Rate=35/320)

java -Xmx500MB SVM -m 1140P10.model -f tfidf1140.data -p -d 0.9 -c 0.09 precision=88.75% (Error Rate=36/320)

C:¥EL¥SVM>java -Xmx500MB SVM -m 1140P10.model -f tfidf320.data -p -d 0.9 -c 0.09 -b 0 –z precision=88.43% (Error Rate=37/320)

Gausian

java -Xmx500MB SVM -m 1140G1.model -f tfidf1140.data -g -c 1 -z c=1.0

1.4. 類似度による分類

1.4.1. 複数レコードの判定結果からの判定

各教師データとの類似度

sim

を求めて，類似度の高い順に

n

件のレコードについて，

sim

degreeを章別に和を求 め，その値が最大となる章を解とする． 旧データ ノーマライズなし(n=20) degree 1.2 1.3 1.35 1.4 1.45 1.5 1.55 1.6 1.65 1.7 1.8 1.9 正解率 90 90.9 91.2 91.2 91.2 90.9 90.6 90.6 90.6 90.3 90 89.6 ノーマライズあり(n=20) degree 1.2 1.3 1.35 1.4 1.45 1.5 1.55 1.6 1.65 1.7 1.8 1.9 正解率 90 90.3 90.3 90.3 90.6 90.6 90.9 91.2 91.2 91.2 90.9 90.3 ノーマライズなし(degree=1.4) データ数(n) 13 14 15 16 17 18 19 20 21 22 23 24 25 26 正解率 89 89.3 89 89.6 90 89.6 89.3 91.2 90.6 90.6 90.3 90.3 90.3 90 ノーマライズあり(degree=1.65) データ数(n) 13 14 15 16 17 18 19 20 21 22 23 24 25 26 正解率 89.3 89.6 90.9 90.3 91.2 90.6 91.2 91.2 90.9 90.9 90.9 90.9 90.9 90.6 ノーマライズなし(n=20) degree 1 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2 2.1 正解率 89.3 89.6 90 90.9 91.2 90.9 90.6 90.3 90 89.6 89.6 89.6 ノーマライズあり(n=20) degree 1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2 2.1 2.2 正解率 88.4 89 89 89.3 89.3 89.3 89.6 90 89.3 90 89.6 89.6 ノーマライズなし(degree=1.4) データ数(n) 13 14 15 16 17 18 19 20 21 22 23 24 25 26 正解率 89.0 89.3 89.0 89.6 90.0 89.6 89.3 91.2 90.6 90.6 90.3 90.3 90.3 90.0 ノーマライズあり(degree=2.0) データ数(n) 13 14 15 16 17 18 19 20 21 22 23 24 25 26 正解率 90.3 90.0 90.0 89.3 90.3 90.0 90.6 90.0 89.6 90.0 90.0 89.6 89.6 89.3 tfidf 値は小数点以下 2 桁としている．旧データでは tfidf 値が 0.1 未満のものは無視していた．新データでは 無視していない．ニューラルネットおよびSVM では新データの方が若干いい結果となっているが，類似度法で はわずかであるが，悪くなっている． ノーマライズなしのとき，degree=1.4，n=20～25 の平均正解率は 90.5%である． java CbS 20 1.4（正解率 91.2%）での誤りの発生を次表に示す． 正 誤 1 3 2 3x2 3 2, 5x2, 7x2 4 1, 2, 6, 7 5 2, 3 6 2x2, 3, 4x2, 7x3 7 1x2, 2x2, 3x3

6 章，7 章において正しく認識されていない比率が高い．また，誤って 2 章，3 章，7 章とするケースが多い． 1.4.2. 類似度最高レコードによる判定 前項で

n



1

とすれば，分類先を類似度最高のレコードと同じ章と判定することになる． ノーマライズなしのとき85.0%，ノーマライズありのとき 84.0%である．

2. 付録

2.1. 階層型ニューラルネットワーク 2.1.1. バックプロパーゲーション法 ニューラルネットワークの代表的なアルゴリズムの一つとしてバックプロパゲーション（BP）法がある1),3)_。 BP法は、図 1 に示すような階層型ニューラルネットワークを対象として、二乗誤差和を評価関数として誤差を 逆伝搬させながら結合荷重を修正することにより学習を進める。学習の高速化とネットワークの構造化を図るも のとして、これを発展させた拡張BP法が知られている2)_。 ユニットの出力関数としては、通常、シグモイド関数

1 1

/ (



exp(





x

))

が用いられ、BP法では、傾き



は 定数（特に1が多い）である。拡張BP法では、傾き



はユニット毎に異なる値を取れるものとして、結合荷重と 同様に誤差を逆伝搬させながら傾きを修正し学習を進める。 ①中間層出力計算 ②出力層出力計算 教 ③ 教 師 誤 師 入 ｜ ｜ ｜ 差 出 力 ｜ ｜ ｜ 計 力 ｜ ｜ ｜ 算 ⑤中間層 ④出力層 結合荷重,傾き修正 結合荷重,傾き修正 図 1 階層型ニューラルネットワーク 拡張BP法の概略は次の通りである。

i

番目の入力ユニットの出力信号を

x

_i、

j

番目の中間ユニットの入力および出力信号をそれぞれ

u

_jおよび

y

_j、

k

番目の出力ユニットの入力および出力信号をそれぞれ

v

_kおよび

z

_kとすると、ニューラルネットワークの状態 は

u

_{j ij}M

x

i N i I









0 (1)

v

_k O_jk

y

j N j M









0 (2)

y

u

j j M j







1

1 exp(



)

(3)

z

v

k k O k







1

1 exp(



)

(4) で記述される。ここで、

N

I、

N

Mおよび

N

Oはそれぞれ入力層、中間層および出力層のユニット数である。



_ijM

および



jk O_{はそれぞれ、入力-中間層および中間-出力層の各ユニット間の結合荷重である。入力層、中間層の}

₀

番目のユニットは、しきい値を結合荷重に含めて統一的に扱うための仮想的なユニットである。

_x

0



1

、

y

0



1

であり、





0 j M_および





0k O _{は、それぞれ}

_j

_{番目の中間ユニットおよび}

_k

_{番目の出力ユニットのしきい値にあたる。} このネットワークに関する評価関数

E

を

E

T

_k

z

_k k NO









1

2

2 1

(

)

(5) で定義する。ここで、

T

_kは

k

番目の出力ユニットへの教師信号を表わす。 拡張BP法は、式(8)の評価関数をもとに、出力誤差を逆伝搬させながら結合荷重、出力関数傾きを修正するこ とにより学習を行う。結合荷重、出力関数傾きの修正量はそれぞれ





 



ij ij

E

 

(6)





 



k k

E

 

(7) によって計算する。ここで、



_ijは



_ijM_、



jk O_を、



kは



j M_、



k O_{を代表する。} 出力層では、結合荷重および出力関数のパラメータの修正量は





O_jk

 

k O k O j

y



₍₈₎





_kO



k O k

v



₍₉₎ となる。ここで



_kO k k k k

T

z z

z



(



) (

1



)

₍₁₀₎ である。 中間層に対しては、





_ijM

 

j M j O i

x



₍₁₁₎





_jM



j M j

u



₍₁₂₎ となる。ここで









O N k O jk O k O k j j M j

y

y

1

)

1

(









(13) である。 実際のプログラムでは、振動を減らし、学習の収束を早めるために、(8)式の代わりに





O_jk

 

 



k O k O j jk O

t

y

t

(

 

1

)



( )

₍₁₄₎ を用いる3)_{。ここで、}



_{は1 より小さい正の定数、}

_t

_{は修正の回数を表わす。(9)式、(11)式および(12)式につい} ても同様である。 学習アルゴリズム [ステップ 1] 学習サンプルを読み込み、配列に格納する。（配列への格納は必須ではない） [ステップ 2] 階層型ニューラルネットワークの入力-中間層間の結合荷重を



0 5

.

～

0 5

.

の乱数で、中間-出力層間の結合荷重 を



01

.

～

0 1

.

の乱数で初期化する。また、出力関数の傾きを全て

1

で初期化する。 [ステップ 3] 学習サンプルに対して、拡張 BP 法を用いて結合荷重と出力関数の傾きを修正する。このとき、出力ユニット の誤差の最大値

max{|

|}

k

T

k



z

k を行単位の誤差配列に格納する。また、全体を通じての最大誤差も求める。 [ステップ 4] ステップ 3 全体での最大誤差が

0 05

.

未満のとき、学習を完了する。また、この最大誤差が

0 1

.

未満であり、 かつ前回の学習サイクルにおける最大誤差との差が

0 01

.

未満の状態が10 回連続したときも学習を完了する。 学習を継続するときは、ステップ 3 に戻る。 認識アルゴリズム [ステップ 1]

認識を行うデータを読み込み、属性ベクトルを算出して、属性配列に格納する。 [ステップ 2] 学習によって得た結合荷重、出力関数の傾きデータを用いて、中間層の計算を経て、出力ユニットの出力の値 を求める。ニューラルネットワーク自体での認識では、出力の値が

0 5

.

未満のとき論理値

1

、そうでなければ論 理値

0

とする。 2.2. SVM 2.2.1. SVM とは

SVM(Support Vector Machine)は，Vapnik によって提案された二値分類のための教師ありアルゴリズムであ る[1]．その概念図を図 2に示す． 学習データセットを次のベクトルで表す．

),

,

(

,

),

,

(

x

₁

y

₁



x

_u

y

_u

x

_j



R

n

,

y

_j



{



1

,



1

}

ここで，

x

_jは事例j を表す特徴ベクトル，

y

_jは事例j の教師信号（正例を＋1，負例を－1 とする）である． SVM は，

x

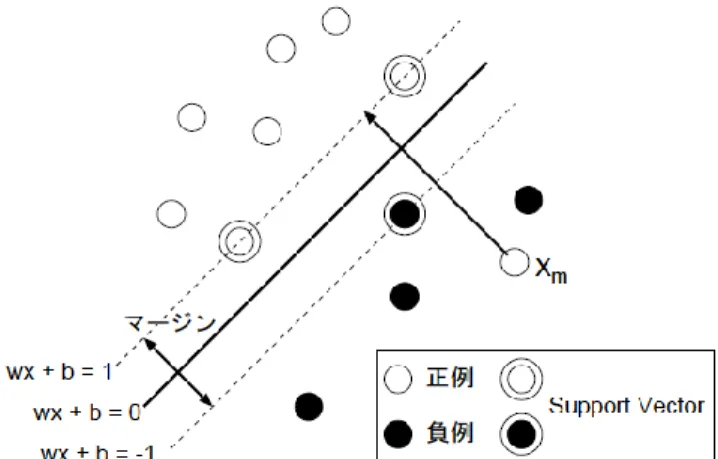
_jを次の分離平面で正例，負例に分離する．

図 2 SVM の概念図（Support Vector Machines）

R

R

w

x

w

・



b



0

,



n

,

b



まず，学習セットが線形分離可能な場合を考える．SVM ではマージン最大となる分離平面を求める．マージ ンは

2

/

||

w

||

であり，これを最大化するには以下の2 次計画問題を考えればよい． b ,

Minimize

w

0

1

)

(

y

subject to

||

||

2

1

)

(



2 _j



_b





J

w

w

w

・

x

_j 学習事例が線形分離不可能な場合には，各学習事例に関して非負の



_jを導入して，以下の最小化問題とする． C は正しく分離できなかった学習事例（図 2の

x

_m）に対するペナルティ項の重み係数である．  , ,

Minimize

b w

₂

||

||

C

subject to

y

(

)

(

1

)

0

1

)

,

(

_{j j} u 1 j j 2























b

J

w

w

w

・

x

_j この 2 次計画問題をラグランジュの未定乗数法を用いて解くことによって判別関数

f

(

x

)



sgn(

g

(

x

))

が求ま る．

g

(x

)

は以下の式となる．ここで，



_jは正のラグランジュ乗数である．









u j j j j

y

b

g

1

)

(

)

(

x



x

・

x

0



j



となる

x

_jはsupport vector と呼ばれ，判別関数は support vector のみによって記述される．

さらに，ベクトルの内積によって定義される Kernel 関数を用いることによって，線形 SVM のアルゴリズム を容易に非線形に拡張することができる．これによって複雑な分離平面を記述することができる．

g

(x

)

は内積 をカーネル関数

K

(

x・

_j

x

)

で置き換え，以下の式で表される．









u j j j j

y

K

b

g

1

)

,

(

)

(

x



x

x

代表的なカーネル関数として次のpolynomial 関数が知られている． d

K

(

x

,

y

)



(

x

・

y



1

)

別の文献[3]では判別関数







i i i i

y

K

b

f

(

x

)



(

x

,

x

)

で表されている．ここで，



_iは各学習事例に対して与えられる係数であり，次の2 次計画問題を解くことによっ て得られる．















i i i i i i j i j i j i j i

y

C

K

y

y

0

,

0

subject to

,

)

,

(

2

1

minimize

,











　　

x

x

（これは双対問題に当る）

0

,

0

subject to

,

2

1

)

W(

minimize











α

y

e

α

α

e

Qα

α

α

T T T

C 　　

)

,

(

_{i j} j i ij

y

y

K

Q



x

x

2.2.2. SVM に対する最適化手法

SMO(Sequential Minimal Optimization)法では，二つの係数



_s，



_tのみを変数，他の



_iを定数として，部分 問題の最適化を行う（解析的な方法で簡単に解が得られる）ことを繰り返して，全体問題の最適化を行う． 二つの変数の選び方がポイントとなる．今，アルゴリズムの

k

回目の繰り返しにおいて，実行可能解（制約条 件を満たす解）

α

kが得られていると仮定する．

}.

1

,

0

,

1

,

|

{

)

(

},

1

,

,

1

,

0

|

{

)

(

},

0

|

{

)

(

2 1 0































i i i i i i i i i

y

or

y

C

i

I

y

C

or

y

i

I

C

i

I











　

　

　

　

α

α

α

とし，さらに

_I

_u

₍

α

₎



_I

₀

₍

α

₎



_I

₁

₍

α

_),

　

_I

_l

₍

α

₎



_I

₀

₍

α

₎



_I

₂

₍

α

₎

と定めると，次式で二つの変数を選ぶ．

)}

(

|

)

(

argmin{y

)},

(

|

)

(

argmax{y

_{i i}

W

k

i

I

_d k

t

_{i i}

W

k

i

I

_l k

s





α



α

　





α



α

ここで，



_i

_W

_(α

₎

はベクトル



W

(

α

)



Qα



e

の第

_i

成分を表す．（すなわち





₁

j ij

Q

である） 通常，

y

(

)

y

(

k

)

t t k s s



W

α





W

α

であり，そうでなければ

b

(y

(

)

y

(

))

/

2

k t t k s s



W

α





W

α



とすれば，これ が最適解である． 矢島(東工大)：サポートベクターアルゴリズムの理論と実装 2.2.3. Smo-book.pdf [John C. Platt]







i i i i

y

K

b

f

(

x

)



(

x

,

x

)

Quadaratic Program:















i i i i j i j i j i j i i i

y

C

K

y

y

0

,

0

subject to

,

)

,

(

2

1

)

W(

max

,















　　

－

x

x

この最適解は次のKarush-Kuhn-Tucker(KKT)条件を満たす．