平成25年度 ミクロ計量経済学 講義ノート3: 多項選択モデル
被説明変数が、3つ以上の値をとるが、それぞれの値について、特に序数的な意味付けの ない場合のモデル化とその推定方法を紹介する。とくに、各個人が3つ以上の選択肢から一 つだけを選択している経済モデルの計量分析法について紹介する。
3.1 多項選択確率効用モデル
まず、分析の対象となるデータについて議論する。各個人がJ個の選択肢の中から、一つ だけを選ぶとする。データは、
({dij, xij}Jj=1), i = 1, . . . , n (1) というようになっている。各dij は2項変数であり、
dij =
1 iがjを選ぶ場合,
0 それ以外 (2)
となっている。なお、dik= 1であれば、dij = 0 (j ̸= k)である場合のみを考える。従って、
∑J
j=1dij = 1である。xijは説明変数である。個人の属性の変数、選択肢の属性の変数、ある いは個人ごとにことなる選択肢の属性を表す変数などである。Xi= ((xi1)′, . . . , (xiJ)′)′と定 義する。選択肢jを選ぶ確率Pr(dij|Xi)をモデル化し、そのモデルを推定することが目的で ある。
個人の選択のモデル化に次の確率効用モデルを使用する。jという選択肢からの効用を、 y∗ij = xi′jβj+ ϵij, (3) と定義する。ϵijは効用に影響を与える要素のうち観測できない部分である。なお、以下で は、βj = βの場合のみを考える。
• βj = βというのは、一般性を失わずに仮定できる。もし係数が異なるなら、(1(j = 1)xij, . . . , 1(j = J)xij)という新しい変数の組を用意することで、β = (β1′, . . . , βJ′)と いうjに依存する係数を使用したモデルと、もとのモデルは同値になる。
• 係数が同じモデルを条件付きモデル、変数が同じで係数が異なるモデルを多項モデル、 それらが混じったモデルを混合モデルと呼ぶようであるが、上でみたように、常に条 件付きモデルで書くことができるため、ここでは、そのような用語の区別はしない。 なお、このノートで考えるモデルは、厳密な定義では条件付きモデルと呼ばれるわけ であるが、多項選択モデルと呼ぶことにする。また、多項選択モデルと呼ことでさし たる誤解は生じないであろう。
個人iはyj∗iが最大となる選択肢を選ぶこととする。つまり、
dij =
1 すべてのk ̸= jにつて、y∗ji≥ y∗kiの場合,
0 あるkがあって、y∗ki> yj∗iの場合 (4)
となる。各個人iごとに式をまとめて、 y∗i
|{z}
J×1
= Xiβ + ϵi, (5)
と書く。
効用の観測できない部分であるϵiの分布を指定することで、Pr(dij|Xi)のモデル化が完了 する。例えば、ϵi∼ N (0, Ω)とすると、多項プロビットモデルになる。各ϵijが独立にType
I extreme分布に従うならば、多項ロジットモデルになる。
対数尤度関数は、θを母数として、 1
n
∑n i=1
∑J j=1
dijlog Pr{dij = 1|Xi; θ}. (6)
となる。
識別 確率効用モデルのすべての母数が識別できるわけではなく、推定には母数になんらか の制約が必要となる。この問題を考えるために、次の潜在変数からなる多項プロビットモデ ルを考える。
y∗i = Xiβ + ϵi, ϵi ∼ N (0, Ω). (7) 1. cをある定数としてy∗ji (j = 1, . . . , J)をy∗ji+ c (j = 1, . . . , J)に置き換えても観測さ
れる選択は変わらない。
2. またy∗i× cと置き換えても変化はない。
基本的に離散選択モデルの場合、効用の母数は識別されず、選択肢間での効用の差の大き さを標準化したものにある母数のみが識別される。ここでは、選択肢の中から一つ、例え ば、J番目のものを、比較の基準と置く。
次の選択肢ごとに定数項の異なるモデルを考える。
yj∗i = αj + βxij + ϵij (8) あるいは、y∗i
|{z}
J×1
= α
|{z}
J×1
+Xiβ + ϵi. (9)
次の行列、
∆J
|{z}
J×(J−1)
=
1 0 . . . 0 −1 0 1 . . . 0 −1 . . . . 0 0 . . . 1 −1
(10)
と、αJ = ∆JδとΩJ = ∆JΩ∆Jを定義すると、
∆Jy∗i = ∆Jα + ∆JXiβ + ∆Jϵi (11)
⇐⇒ ˜y∗i = αJ + ˜Xiβ + ˜ϵi (12)
となる。y˜∗iは、J番目の選択肢と比較したときの、それぞれの効用の差をまとめたベクト ルである。
y∗iを効用として考えたモデルと、y˜∗iを効用としたモデルは、同じ選択をもたらす。さら に、y˜∗iを正の数で定数倍しても同じ選択をもたらす。
こうすること、母数(α, β, Ω)の中で、最大限で(c × αJ, c × β, c2× ΩJ)(ただし、cはあ る一つの母数を定数にするようにきめる)までが識別できることがわかる。なお、cは、係 数の一つから取る場合と(その場合はその係数の絶対値は決まっており、符号のみがデータ から推定できる)、分散の一つから取る場合(その場合は、対応するϵ∗jiの分散が固定される) の2通りのどちらかを使う場合が多い。
上のような状況を表して、(αJ, β, ΩJ)は、(αJ· c, β · c, ΩJ · c2)と観測同値であるという。 ちなみに識別の定義は通常、真値と観測同値な母数が存在しないこと、である。以上の議論 に関しては、Keane (1992)を参照せよ。
尤度関数の計算 尤度関数は確率を評価すれば計算できる。確率は、
Pr(dij = 1|Xi, θ) = Pr(˜yj∗i ≥ ˜yk∗i, ∀k|Xi, θ)なおy˜∗ji= y∗ji− y∗Ji (13)
= Pr((˜xij− ˜xik
| {z }
˜ xijk
)′β ≥ ˜ϵik− ˜ϵij
| {z }
˜ ϵikj
, ∀k|Xi, θ) (14)
=
∫ . . .
∫ ∫ 1{˜xi
jk ≥ ˜ϵikj, ∀k}dF (˜ϵiij, . . . , ˜ϵiJj) (15) と表現できるが、J − 1重の積分であり、その計算には、何らかの工夫が必要となる。
いくつかの解決策が提示されている。
• 多項ロジットモデルを使う。
• J = 3の時には、Moffit and Butler (1982)を参照せよ。
• J が大きいとき、例えばJ = 5、ならシミュレーションによって、積分計算をする必 要がある。
3.2 多項ロジットモデル
多項ロジットモデルは、各選択確率を
Pr(dij = 1|Xi) = exp(βx
ij)
∑J
k=1exp(βxik)
. (16)
としてモデル化する。これは、確率的効用モデルのϵをType I extreme分布とすることで導 出できる。なお、識別のため、どれか一つの選択肢についてβxij = 0、つまり、exp(βxij) = 1 と標準化するのが通常である。このモデルの最尤推定は数値計算的に非常に簡単である。
IIA問題 しかし、多項ロジットモデルは「無関係な選択肢からの独立(Independence of Ir- relevant Alternatives, IIA)」という問題があることが知られている。これはオッズ比(Pr(dij = 1|Xi)/ Pr(dik= 1|Xi))が他の選択肢の存在の影響を受けないという問題である。
図1: 青バス赤バス
train bus
blue red
次の例を考える。市内の移動に3つの選択肢があるとする。
j =
1 =電車 2 =青バス 3 =赤バス
(J = 3) (17)
xi′jβ = µijとおくと、
Pr(dij = 1|Xi) = exp(µ
ij)
exp(µi1) + exp(µi2) + exp(µi3). (18) となる。仮に、µij = 1, ∀jとし、各選択肢を確率1/3で選択するとする。この時、電車と青 バスのオッズ比(Pr(di1 = 1)/ Pr(di2 = 1))は1である。
重要な問題は、この電車と青バスのオッズ比が赤バスの情報から影響を受けないことであ る。例えば、何らかの政策変化などがあり、µi3 → −∞となるとする。つまり、赤バスがも はや運行されないとする。しかし、その場合でも、電車と青バスのオッズ比は1で変化はな い。一方で、赤バスがなくなれば、青バスの需要が高まると予想するのが自然であろう。つ まり、ロジットモデルは代替効果を全く考慮に入れていなず、ロジットモデルではとらえる ことのできない、現実的で結果に影響を与えるような問題が存在する。
解決策 この問題を解決するためには他のモデルを使用するしかない。例えば、多項プロ ビットモデルではIIAの問題はなく、また誤差項の選択肢間の相関構造を考慮することも モデル上では容易い。しかし多項プロビットモデルの推定は、それほど容易ではなくシミュ レーションを使用する必要がある。一方で、計算の簡便なロジットモデルを拡張することで、 IIA問題を解決するアプローチもある。
IIA問題を回避できるロジットモデルの拡張としては、入れ子型ロジットモデルがある。
0 ≤ ρ ≤ 1というパラメーターを導入して、
Pr(電車|Xi) = exp(βx
i1)
exp(βxi1) + (exp(βxi2/ρ) + exp(βxi3/ρ))ρ, (19) Pr(青バス|バス, Xi) = exp(βx
i2/ρ)
exp(βxi2/ρ) + exp(βxi3/ρ) (20)
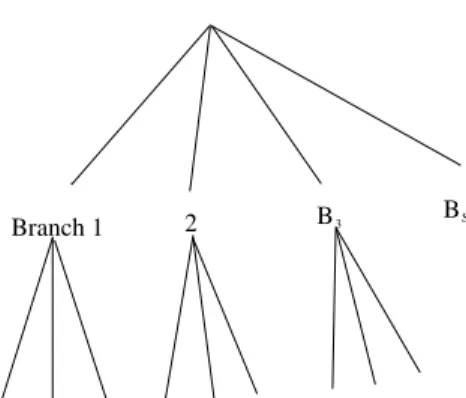
図2: 一般的な逐次的選択
Branch 1 2 B3 BS
と仮定するモデルである。
• ρ = 1なら、通常の多項ロジットモデルになる。
• ρ → 0なら、Pr(電車|Xi)) = exp(βxi1)
exp(βxi1)+1かつPr(バス|X
i)) = 1
exp(βxi1)+1かつPr(青バス|X i) = 1
exp(βxi1)+1limρ→0
exp(βxi2/ρ)
exp(βxi2/ρ)+exp(βxi3/ρ) となる。
一般的な場合のモデルは、
Pr(s組を選ぶ|Xi) =
(∑
j∈Bsexp(βX
ji/ρs)
)ρs
∑S s′=1
(∑
j∈Bs′exp(βXji/ρs′)
)ρs′ (21)
Pr(j|s組, Xi) = exp(βX
ji/ρs)
∑
j′∈Bsexp(βX
ji′/ρs)
(22) である。
なお、IIAの検定は、帰無仮説を
H0 : ρs = 1, ∀s ∈ {1, . . . , S} (23) とおいてできる。帰無仮説が正しいなら、IIAの問題は存在しない、あるいは実際にも成り 立っているので、その点を考慮したモデルを使う必要はない。検定法についてはHausman and McFadden (1984)を参照のこと。
入れ子型ロジットモデルの欠点は、入れ子構造をあらかじめ決めてしまう必要があること である。また、選択肢の分類にいくつかの候補があるとき、分類の仕方を変えると結果がか わる。他にも、多重に入れ子になっている場合には、入れ子にする順番を変更すると結果が かわる。そのため、入れ子構造を決める際には慎重に行う必要がある。
参考文献
[1] J. Hausman and D. McFadden. Specification tests for the multinomial logit model. Economet- rica, 52(5):1219–1240, 1984.
[2] M. P. Keane. A note on identification in the multinomial probit model. Journal of Business & Economic Statistics, 10(2):193–200, 1992.
[3] R. Moffit and J. S. Butler. A computationally efficient quadrature procedure for the one-factor multinomial probit model. Econometrica, 50(3):761–764, 1982.