J20 e IEEE TC 1978 10

On the Computational Complexity

)

^of

^{System Diagnosis}

HIDEO FUJIWARA, MEMBER, IEEE, AND KOZO KINOSHITA, MEMBER, IEEE

Abstract-In this paper we analyze the computational complexity ofsystemdiagnosis. We show that severalproblems for instanta- neous and sequential fault diagnosis ofsystens are polynomially complete and that for single-loop systems these problems are solvable in polynomial time.

Index Terms-Faultdiagnosis, polynomial time algorithm, poly- nomiallycomplete,self-diagnosablesystems, Turingmachines.

I. INTRODUCTION

THEAVAILABILITY ofcomputersis a matter ofprime concern, as well as their reliability, and consequently formal studies of self-diagnosabilityarerequired. A number ofpapers dealing with various aspects of self-diagnosable systemshave appeared. Preparata et al.[1]first introduced a graph-theoreticmodel of digital systems for the purpose of diagnosis of multiple faults, and presented methods of optimal connection assignments forone-stepandsequential fault-diagnosis procedures. In this model a system is made upofanumberof units whereeach unit is assumedto be testedbysomeother units. With this model,necessaryand sufficient conditions were given for such systems to be diagnosable forat most tfaulty units [1]-[6].

Moreover, the problem of identifying the faulty units based on the test outcomes of the system was also in- vestigated

[7]-[9].

However, in general, the

_problem

of finding ^a minimum set of faulty units is known to be polynomially complete

[7].

That is, this problem can be solved in polynomial time if and only if the traveling salesman,knapsack problem,etc., canbe solvedin polyno- mialtime. In thispaper we show that severalproblemsfor instantaneous and sequential fault diagnosis ofsystems are polynomially complete and that for single-loop systems these problems are solvable in polynomialtime.

II. PRELIMINARIES

Consider asystemofnoperating units capable of testing the correctness ofone another. The testing arrangements canberepresented byadirected graphG⁼

(V, E),

where the setofverticesV=_{{u1, u2,} ^..._,

_u1}

represents the units. For u ,

uj

E V, there is anedge fromvertexuito

_uj;

i.e.,

_{(ui, uj)}

E E, if andonlyif u,tests

_uj.

The testing unit

_ui

evaluates the tested unit

_uj

as either fault-free or faulty, the evaluation being

meaningful

only if

_ui

is fault-free. The test outcome is Manuscriptreceived March 11, 1977; revised November 14, 1977 and February 16, 1978.

Theauthorsarewith the Department of Electronic Engineering, Osaka University, Suita-shi, Osaka, Japan.

indicatedby theweight

_aij

onthe edge

_{(ui, uj)}

E E andobeys the following rule:

aij⁼

O,

^if

ui

^and

_uj

^{arefault-free} aij= ^{1, if}

ui

^{is fault-free and} uj^{is faulty}

aij

^{=O, 1, ifui is faulty.}

The test outcomes{a1,} ^=_ais termed thesyndrome ofthe system. Given a directedgraphG = (V, E)of a system S and a syndrome ^a =

_{aij}

of S, the fundamental problem is to identify the faulty units. It should be noted that eachfeasible set of faulty units ^F must satisfy the following two conditions:

1)

_aij

=1 for all

_{(ui, Uj)}

E E,such that

ui,

^Fand

_uj

E F;

2)

^{aij=0 for all}

(ui, uj)

^E

^E,

^{such that ui, uJE F.}

Wecallsuch subsetFofV tobeaconsistentfaultsetofS with respect to a.

Definition

1:

Asystem S, represented byadirectedgraph G⁼

(V, E),

is saidtobe one-stept-faultdiagnosableif, for anysyndromea,there existsat most oneconsistentfaultset F withrespect to a suchthat

_I

F <t, where X denotes the cardinality ofa set X.

It is easy to see that in a one-step t-fault diagnosable system all faulty units can be identified, provided the number of faulty units presentdoes not exceed t.

Let

_F,,,

bethesetofallconsistent faultsets withrespect to

a such that the number of faulty units present does not exceedt;i.e.,

F,

⁼

,{Fi Fi

^<

t, Fi

^{is a}consistent faultset with respect to a}.

Definition2: A system S,represented byadirectedgraph G, is said to be sequentially t-fault diagnosable if, for any syndrome a, either

_F,,,

= 4 or

_nFi

e

_{Ft,, Fi * 4..}

Inasequentially t-fault diagnosablesystem, ifthenumber of faulty units present does not exceed t,

_thennFi

e

_Ft,a

F,is notempty if there exists at least onefaulty unit.Thus we can regard all the units belongingto theintersectionasfaulty. Hence there exists a sequenceof applications oftestsand repairs of identified faulty units that allows allfaulty units originally present to be identified.

Let Pbe the classof languages accepted bydeterministic polynomial time-bounded one-tape Turing machines, and NP the class of languages accepted by nondeterministic polynomial time-bounded one-tape Turing machines

(see

Aho et al.

[13]).

Theproblem"IsP⁼ NP?" isalongstanding open problem in complexity theory. The notion of "P- complete" used here is that ofSahni

_[12].

0018-9340/78/1000-0881$00.75

©D

^{1978 IEEE}

Definition ^{3: A}problem_P1, ^{issaid tobe} P-reducibletoa

problem P2 (written ^{P1 oc}P2) if the existence of ^a deter- ministic polynomial time algorithm for P2 implies the existence ofadeterministicpolynomial timealgorithm for

P1.Definition 4: Two problems, P1 and P2,^areP-equivalent if P1 ^ocP2and P2 ocP1.

Definition 5: A problem

Pi

^{is saidtobe}P-complete if

_Pi

has^adeterministic polynomial time algorithm if and only if P⁼ NP. Let PC be the equivalence class of P-equivalent problems being P-complete.

III. COMPLEXITY OFSYSTEM DLIGNOSIS

One-step fault diagnosisistoidentify all faulty units in^a system instantaneously. In ^{a one-step} t-fault diagnosable system,there exists^a unique consistent fault ^set, provided that the number of faulty units doesnotexceedt.However, in general, there exists ^morethan ^oneconsistent fault set.

Hence, ^we regard the minimum consistent fault ^setasthe most likely consistent fault^set.Theproblem of finding such

a minimumfault^set isknownto beP-complete [7]. Sequential fault diagnosis isasequenceof applications of tests and repairs of identified faulty units that allows all faulty units originally present to be identified. Hence, in sequential fault-diagnosis procedures it is important to

compute

_nFi

e_Ft,a, F,.

Problem ¹ (Pl): Given ^a system S, represented by ^a directed graph G⁼ (V, E), ^a syndrome ^a, and a _positive

integer ^t,does there exist^a consistent faultsetFof S with respect toasuch that I^{F <t?}

Problem 2 (P2): Given ^{a system} S, represented by ^a directed graph G⁼ (V, E), ^a syndrome ^{a, a} unit u, and ^a positive integer t, does thereexist

_Fi

suchthat ^u

₀ Fi

^and

Fi^E_F,,,?

Problem 3 (P3): Given ^a system S, represented by ^a directed graph G⁼ (V, E), ^a syndrome ^{a, a} unit u,and a

positive integer t, does the unit ^ubelongto

_nFi

eFt,.

_Ft?

Problem 4 (P4): Given ^{a system} S, represented by ^a directedgraph G,^asyndrome^a,and^apositive integert,find

nFi

^{eFt, Fi.}

Problem5 (PS): Given ^a system S, represented by ^a directedgraph G,^asyndrome^a,and-^apositive integert,find atleast one unit in

_nFi(

Ft,, Fi ^ifnotempty.

Problem 6 (P6): Given ^a system S, represented by ^a directed graphG⁼ (V, E),^asyndrome^a,and^aunitu,does there exist

_Fi

such that ^u

_{0 Fi}

and

_Fi

E

_Flyl

?

Problem 7 (P7): Given ^a system S, represented by ^a directed graph G⁼ (V, E), and ^a syndrome ^a, find

nFi^eFlvl,a Fi.

In thissection,^weshowthat thepreviously stated prob- lems P1-P5 forsequential and one-stepfaultdiagnosis ^are P-complete and that problems P6 and P7 ^are solvable in polynomial time.

Lemmna)I PlocP2.

Proof: Given ^a system S represented by ^a directed graph G⁼ (V, E), ^a syndrome ^a=

_{{aij I} (ui, _uj)E},

^{and a}

positive integer t, construct a system S'

represented by

^a directed graph^G'=

(V', E')

such thatV' ⁼ V u

_{up,

Uq} and

E=

^{E u}

_{(UP,

^Uq),

_{(Uq, up)}.}

^Leta'bea

syndrome

^{of S' such}

that ^a'=a u

{a

=,

aq,,

0}.

It

caneasilybe shown thataset Fisaconsistent fault^setof Swithrespectto aifand

only

^{ifF is}aconsistent fault^setofS' withrespect to a'such thatup, Uq

₀

F.Hencewecan seethat a

polynomial

^time

algorithm

forP2

implies

^a

polynomial

time algorithm forPl. ^Q.E.D.

Maheshwari

and Hakimi

[7]

^haveshown that the

problem

of findingthe minimum consistent fault^{set is}

P-complete,

and thus

P1

^{EPC. It can}

easily

be shown that P⁼ NP impliesP2 E P. Fromthisand Lemma

1,

^wehaveP2 E PC. It can also be shown that Problems

_{P2, P3,}

and P4 ^are P-equivalent. Hence, we have thefollowing theorem. Theorem I

PI, P2, P3, andP4EPC.

Todiagnose^a

given

system

sequentially,

^{it isnot}

always

necessary to find all the units in

_{nFi t,ffF j,}

but it is necessary to

find

at least one unit in

_nFi

c

_Ft,oj.

This is Problem5, but evenforP5wecanshowittobe

_P-complete

in thefollowing theorem.

GivenasystemS,

represented by

^adirected

graph

G⁼

(V,

E),

^{asyndromea,anda}

^positive

^{integert, letusdefine theset}

X.

correspondingto aunitu

_innFi

e

_{Ft,6 Fi}

asfollows.

_X.

is the smallest set of vertices such that

1)

^uE

_X,,,

and

2)

^if

u; E X",

(u,, _uj)

^E Eand

_aij

⁼

O,

thenui ^E

_X..

LetS'bethe system represented bythedirected

graph

G' ⁼

(V', E')

such that

V'

=

_V-X.

andE' ⁼

_{{(ui, uj) (ui, uj)}

E E,

_ui,

ujE

V'}.

Let

a' ={aijIaijae ^{a, (u,, Uj) EE'}, t'}

^{= t-}

^IX.I

^and

Ft

^{, = {F}

I

^F

_I

^<

t', F'

^{is a}consistent fault setof S' with respect to

_a'}.

For the systems SandS', we have thefollowing lemma.

Lemma 2

1)

^{For any}

Fi

^c

Fta, Xu

^'

Fi.

2) _Ft,= {Fi

F

_Fi=--XU, Fi

^E

Ft,}.

3) _nFieFt,6Fe ⁼ AF,eF,',G F, UXI ^.

Proof: 1)

Suppose that thereexists^{a set F}such that

X.

^{F andFE}

_F,,,.

^Fromthis and the definition of

_X.

^we can see that there exists an edge

(ui, _uj)

^{EE such that}

ui,

uj

^E

Xu, ui

^{S F,}

uj

^{E F,and}

aij

⁼

^0.

^Thiscontradictsthat F is aconsistent faultset ofSwith respectto a.

2)

For any

Fi

^E F,,a,

_X.

'

_Fi,

and thus

_{Fi-X. Ft,,,.}

Hence

Ft,,

^{F!

^{F =}

Fi

^-

Xu, Fi

^EFt,

Conversely,weshow that for any F E

F,,,,

^thereexists^a set

_Fi

such that F! ⁼

Fi

^-

Xu

and

Fi

^E

_F,,a.

For any F! E

_F,,,,,,

F is a consistent faultset of S' with respect to a'. Hence,

_aij

^{= 1} for all

(ui, _UJ)

^{EE such that}

ui

₀

^{F' u}

_X.

and

_uj

^E F', and

ai

^{=0 for all}

(ui, uj)

^{E Esuch}

that

_{ui, uj 0}

F' u

_X..

From the definition of

_X.,

wehave that

_aij

^{= 1} for all

_{(ui, uj)}

E E such that

_ui

^,

Fu

u

_Xu

and

U E

_Xu.

Therefore, F;

^u

X,

is a consistent fault ^set ofS with respect to a. Clearly, F u

_X."=

⁴ and

_IF

u

_XuI

⁼

IFJl

⁺

^{I X.}

^{<t. Hence}

^Fi

^{= Fu}

^X.

^{is in}

^F,,

^and

Ft,,

^c{EFi|F=

^{Fi- Xu, Fi}

^Ei

Ft,,al

3) From 1)and 2) it is clear that

n _Fi= n (F-"-n -

Fi,^eFt,,,, ^{FicFt,a Fi Ft,,}

Hence

n

F

_n=

A

_F>UXU.

FieFt,a Fi,^e_Ft',,'

Q.E.D.

block B.

10 0 0 0 0 0 1 ] 1 1 1 1 1 0

i- i+ll--- 'W

_l i i+l s s+l ^uj'1

t_ L

(a)

1,0O O

I 0 0 0 0_@_ a-1 i i+l

a.

0 0 1 1 1 1 1 1 1 '0

W-. reo *0--^- -*J4

s- ^{s s+l} u.,

alternately fauy

alternately faulty

Theorem 2 P5EPC.

Proof: From Theorem 1, P4 E PC.

Clearly,

^{P5 oc P4.} Henceitsuffices to show P4 oc P5.

Givenasystem S,represented byadirectedgraphG=

(v,

E),

^{asyndromec,anda}positive integert, then we canfind

nFi

^EF,,, Fi, usingthe following algorithm.

ui-i ^{ui ui+l} uS

O : fault-free unit

*: faulty unit

(b) ^{Z! +} /2j

;-1US Us+l

alternately faul 1 _I0

u.j Lty (c) _rti/21

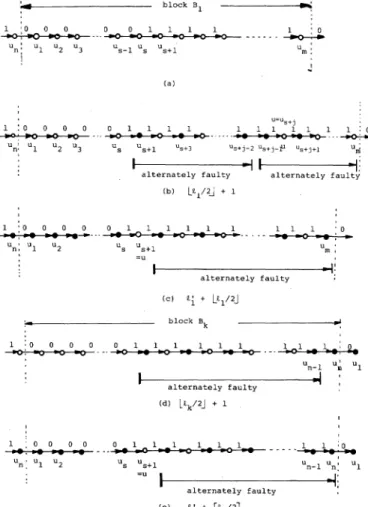
Fig. 1. Illustration forLemma 3.

Algorithm forP4

OUTPUT _{(the empty set);}

while t>0_do begin

use_thealgorithm for PStofind^atleast^oneunituin

nFi

^eFt,a^{Fiifnotempty;}

ifthealgorithm judges the intersection^tobeempty

then stop elsebei

- _{construct theset}

_X.

correspondingto u;

delete all units in X, from thesystem; t+t-

_IX-1;

OUTPUT 4-OUTPUT U X,

end end end

From Lemma 2, clearly this algorithm terminates and thenOUTPUT

_{=nFi Ft,a}

F,. Ifthe

_algorithm

forP5canbe done inpolynomial time,then theprevious algorithmfor^P4 is apolynomial time algorithm. Hence ^{P4 cc}P5. Q.E.D.

Theorem 3

P6 and P7 are_solvable in polynomial time.

Proof: Let xl,^x2, * ^x, bethebinary variables^corre- spondingtothe units ui,^u2, ,un, respectively, suchthat xi^{= 1 if unit} ul is fault-free, and ^{x,= 0}if unit ui is faulty. FromPreparata [2],^{we see}that^asetF isaconsistentfault

setofasystemS withrespect to ^asyndrome^aifandonly^if the assignment of0'stothevariablesinFand of l'stothe variablesnotinFgives the following Boolean expression the value 1:

nj xaiij ^{(xi V v} ajajj

aije a

Similarly, for a

consistent

fault set F, which does ^not contain a given unit Uk, the

previous expression

^{can be} reduced to the followingexpression:

Hi (Xi XjaijvXjaHj) -l (xjiikj

^v

Xjaij) ^{(xi V ik).}

aiija akiaE aic-a

i,j$#k

Therefore,thejust given Boolean

expression

^issatisfiable

[14]

if and onlyif

_{ui 0}

Fforsome F E

_F,a

Thisexpressionis in2-conjunctive normal form, and thusP6 isP-reducibleto the

2-satisfiability

problem which has a

polynomial

time algorithm

[14].

Hence P6 is solvablein

polynomial

^time.

We can see that u

₀

Ffor some FEF

_F.,

if and only if uXF

_eF.

^F. Therefore, using ^a polynomial time algo- rithm for

P6,

we candetermine whether u E

_nF

e

_Ff,

F for eachuE V,andthus we can construct

_n

FeF,^aFinpolyno- mialtime. Hence P7 issolvable in polynomial time.

Q.E.D. IV.

SINGLE-LOOP SYSTEMS

A single-loopsystemis asystem

consisting of

a

cycle

of units

_ul,

_{u2, **,}

_u.

in which unit

_ui

tests unit ui+

1,

1 ^<i <n^-1 and unit

un

^testsunit u1. ^Thenecessaryand sufficient conditionisgivenfor such

single-loop

systems^to besequentially t-fault diagnosable

[1], [2].

^{InSectionIIIwe}

have shown that, ⁱⁿ general, Problems P1-P5 are P- complete. ^{In this}

section,

^{we show that for}

single-loop

systems Problems P1-PS are all solvable in

_polynomial

time.

Given a

single-loop

systemS,

represented by

^adirected graphG⁼

(V, E)

anda

syndrome

a,letus

_partition

the

_loop

into blocks of units where each block

Bi

⁼

_{{ui, ui+1,}

^,

us, ^...

_,uj}

hastheweightpattemof the formO^...01 ...

_1,

as

illustratedinFig.

1(a).

Inthecasewhenthetest outcomes are alll's, this

partition

isone

partition having only

^oneblockV. Let

(ui, _Uj)

be anedgeinE;

_ui

iscalledthe tail and

_uj

the head ofthe edge

_{(ui, uj);} La]

^denotesthe greatest

integer

not

exceeding

a, while

_[al

denotes the smallest

integer

^not smaller than a.

Lemma 3

Let B1, B2, , Bk beall blocks ofsingle-loop system S with respect tosyndromea.Foraminimumconsistent fault set F with respect to a, we have

|Fl|=

_i=^Ek₁

[lJ/2]

where

_1i

is thenumber ofedgesofweight 1 whose tail is in block

_Bi.

Proof: If the syndrome^ais

_a,

where all testoutcomes arel's,thenwehave k= _1;i.e.,block B 1 contains all units in the system. In this case, clearly, the

cardinality

^{of the} minimum consistentfault set is

_[r1 /21.

If a is a syndrome where at least one test outcome 0 appears, then we can let

1i

bethenumberof

edges

of

_weight

0 whose heads are in blockB1,where

_Bi

=

_{tu,

_ui+1,

_{,.1 us,}

_,

uj}.

Let us be the last unitwhich is the head ofan

_edge

_of weight0

[see

Fig.

1(a)].

If

_us,

is

faulty,

then

_ui,

_uj+

_1,

,^{u are} allfaultyand we obtain the smallestset

_Fio

of

_faulty

unitsin block

_Bi,

asshown inFig.

l(b).

^{The numberofsuch}

faulty

units isII +Li,

/2J.

If us is

fault-free,

^thenwehave the smallest set

_Fi

1 offaultyunits in

_B1,

asshownin

_Fig.

1

(c).

^{The number} ofsuch faultyunits is

_r[1/21.

Since li >0,wehave li+

Lli/2jJ [li/21

^{for alli.}

Therefore,

FiI

^issmaller than

_Fio,

which

implies

that

_Fi

1 isthe smallest setoffaultyunits in

_Bi.

From

this,

^{wecan see}that the union of

_Fil

for all

Bi (1

^<i

k)

is the minimum consistentfault set,the

cardinality

of whichis

_E=

1

_[li/21.

Q.E.D. Given a single-loop system S

represented by

^adirected graph G⁼

(V, E)

and a

syndrome

a,^{we can} compute the value

_1i

for each block

Bi

ⁱⁿ

0(

^V

I)

^steps.

^Therefore,

^from

Lemma 3wehave an

_0(I

Vt

₎

algorithmfor

_computing

the

cardinality

oftheminimum consistent fault set F.

_Clearly,

IF

^tifand

^only

ifthere existsaconsistent faultsetF such that F

_I

<t. Hence by

computing |IF

^{we can solve}

Problem 1,and thus wehave the

following

theorem. Theorem4

Forsingle-loop systemsthereexistsadeterministic

algo-

rithmfor P1 of time complexity

0(

^V

I),

where

_VI

is the numberofunits.

For single-loop systems, Problems 2 and 3 are also solvablein time complexity 0t⁽ V ).

Theorem 5

Forsingle-loopsystems,thereexistsadeterministic algo- rithm for P2 and P3 oftime complexity

0(

V

_1).

Proof:Let G⁼

(V, E)

be thedirected graphrepresent- ingasingle-loopsystem Sandlet^abe asyndrome.LetFbea minimum consistent fault set with respect to ^a such that u

₀ F

foragivenunit u.Clearly,

_I

F ^<tifand onlyif there exists aconsistent fault set Fsuchthatu

₀

Fand F .< t. Therefore,thereexistsan

_0(I

V

_I )

algorithm forP2andP3 if wehavean

_0(I

Vt

₎

algorithm for

computing

the

cardinality

ofaminimum consistent fault set

F

with u

P. P

Hence,to complete the proof it suffices to show that thereexists an

0(I

^V

⁾

^{algorithm tocompute}

I

^{F withu}

^{0 P.}

__________________________ ^{block B} _I

1 0 0 0 0 0 1 1 1 1 1 :0

u: U1 _{U2 U3 Us1}^U _S+ U

(a)

U=Us+j

1 O O O 0 1 1 1 1 1 11 11 1 10

un Ul ^u2 3 ^U5 Us+l US+3 us+j-2us+jFP u5+j+l um

I

_-I]

alternately faulty alternately faulty (b) _LtI/21 ⁺ 1

1 .0 0 0 0 0 1 1 1 1 1 1 1 1 1 0

u _{1:u 2 us us+l ue}

=u

alternately faulty

(C) A; + _LQ1/2J

block Bk

10 0 0 0 0 1 1 1 1 1 1 11 lB

Un-l ^n- 01

alternately faulty (d) _Ltk/2j + 1

lOB _0e00_1D ~_{-t1 1 1} 1 l

Un' ^U1 u2 ua US+1 Un-1 ^U U1

=u I

alternately faulty (e) Ii ⁺ _Ft1/21 Fig.2. Illustrationfor Theorem 5.

Let V =

_{{ul, u2,} .,u5}

and let B 1,B2,

,Bkbe

, allblocks of V partitioned according to the syndrome a. If^a is a1 where all test outcomes are l's, then we have k= _1;

_i.e.,

block -B1 equals V. In this case,

clearly,

^{there exists a} minimumconsistentfault set

P

withu

₀ P,

and the cardinal- ity ofFis [n/2].

If ^a is a syndrome where at least one test outcome 0 appears, then without loss of

generality

^{we assumeu} E

B1,

B1 = _{{ul, U2,} , US, , Um}, anl= al2= ^...=_{as-I,s= 0}

and as,s

+1

⁼ *⁼

am,m,

⁼

1[see Fig. 2(a)].

^{Let Xbe theset}

ofunits

_{us +3,}

9_Us+5 * selected

alternately

^from

us+

until

_um.

Clearly,

_XI

⁼

_[ll

/21.

Case 1:u

₀

X.Clearly,thereexistsaminimum consistent fault setF with u ¢P, and thus It = =

[4/2].

Case 2: u E Xand u

_{* us+,.}

_Suppose that u⁼

_us+j

and unit u is

fault-free,

then wehave the smallest setof

_faulty

units{us+1, us+3 ^,Us+j-2;

_Us+j1,US

+j+l,Us+j+3, ^}in block

_Bl,

-asshownin

_Fig. 2(b).

Thenumberofsuch

_faulty

unitsis

[11/2]

+ 1. For otherblocks

_Bi,

the smallest number of

faulty

unitsis

_[ri /21. Therefore,

|IF L1l /2J

^{+ I +}_i=2^{E rl-1}k

Case 3: is=

us+1

and

_k2.2.

Suppose that unit is is

fault-free,

then we have the smallest set of

faulty

units in block B1 as shown inFig.

2(c).

The number of such

faulty

units is

_I'I

+

_[1

/2J. Inthiscase,unit

_u.

in block Bkis also recognizedto befaulty.Therefore,wehave the smallestsetof faulty unitsinblockBk,asshowninFig. 2(d).The number of such faulty units is

L[k/2j

^{+ 1. Hence, wehave}

k-i

l= _{[l/2J+ 1I}

⁺

_LIk/21+

¹⁺ _i=2

^E [ri/21.

Case 4: u= u+1, k = 1, and 11 ^>2. Suppose that u is

fault-free,

then we have the smallest set offaulty unitsas shown in Fig.

2(e).

The number of such faulty units is

11

⁺

r1 /21.

^Therefore,

If I =II

⁺

_rl,/2i.

Case 5: u =

_u,+,,

k= _{1, and 11}= 1. Clearly, u⁼u +1 ⁼u,,, and in this case there exists no consistent fault set

F

with u

₀

F.

In anyof thecasesmentioned above,wecancomputethe cardinality ofaminimumconsistent faultsetFwithu

₀

Fin computational time of

₀₍₁

V

_I).

Q.E.D. By applying an algorithm forP2 toeach unit

_ui

E V, we cansolve Problems4and 5.Therefore, fromTheorem 5we can seethat P4 and P5aresolvedby

0(

V|)algorithm for single-loop systems.

Theorem 6

Forsingle-loopsystems there exists adeterministicalgo- rithm for P4 and P5 of time

_{complexity 0(| VI).}

V. CONCLUSION

In this paper wehaveclarified the computational com- plexity of fault diagnosis in self-diagnosable systems. In general, several problems forone-stepandsequentially fault diagnosisareP-complete.However,for single-loopsystems such problems are all solvable in polynomial time.

ACKNOWLEDGMENT

The authors wish to thank Prof. H. Ozaki of Osaka University for hissupport and encouragement.

REFERENCES

[1] F. P. Preparata, G. Metze, and R. T. Chien, "On the connection assignment problemof diagnosablesystems," IEEETrans. Electron. Comput., vol.EC-16, pp. 848-854, Dec. 1967.

[2] ^F.P. Preparata, "Some results on sequentiallydiagnosablesystems," in Proc. HawaiiInt.Conf.System Sciences, pp. 623-626, 1968. [3] S. L. Hakimi and A. T. Amin, "Characterization of connection

assignment of diagnosable systems," IEEE Trans. Comput., vol. C-23, pp.86-88, Jan. 1974.

[4] F. J.Allan, T. Kameda, and S. Toida, "An approach to thediagnos- ability analysis ofasystem," IEEE Trans.Comput., vol. C-24, pp. 1040-1042, Oct. 1975.

[5] ^F.Barsi,^F. Grandoni,^andP.Maestrini,^"Atheory^ofdiagnosability

of digital systems," IEEE Trans. Comput., vol. C-25, pp. 585-593, June 1976.

[6] S. Toida, "System diagnosis and redundant tests," IEEE Trans. Comput., vol. C-25,pp. 1167-1170,Nov. 1976.

[7] ^{S. N. Maheshwari and S. L.} Hakimi, "On models fordiagnosable systems and probabilistic fault diagnosis," IEEE Trans. Comput., vol. C-25, pp. 228-236,Mar. 1976.

[8] T.Kameda, S. Toida, and F.J. Allan, "A diagnosingalgorithm for networks," Inform. Contr., vol. 29, pp. 141-148, 1975.

[9] A.M. Corluhan and S. L. Hakimi, "On an algorithmforidentifying faultsin at-diagnosable system," in Proc. Johns Hopkins Conf. Infor- mationSciencesand Systems, pp. 370-378, Apr. 1976.

[10] S. A. Cook, "The complexity of theorem proving procedures," ⁱⁿ ConfJ ^Rec.3rd ACM Symp. Theory ofComputing, pp. 151-158,1971. [11] R.M.Karp,"Reducibilityamong combinational problems,"inCom- plexity ofComputer Computations, R. E.Miller andJ. W.Thatcher, Ed.NewYork: Plenum, 1972,pp.85-104.

[12] S. Sahni, "Computationally related problems," SIAM J. Comput., vol. 5, pp.262-279, 1974.

[13] A.V. Aho, J. E.Hopcroft,andJ.D.Ullman,The Design andAnalysis of ComputerAlgorithms. Reading, MA: Addison-Wesley, 1974. [14] 0.H.Ibarra andS. K.Sahni, "Polynomiallycompletefault detection

problems," IEEE Trans. Comput., vol. C-24, pp. 242-249, Mar. 1975.

Hideo Fujiwara (S'70-M'74) was born in Nara, Japan, on February 9, 1946. He received the B.E., M.E.,^{and Ph.D.}degrees^inelectronicengi-

neering all from Osaka University,Osaka, Japan, in 1969, 1971,^and 1974,respectively.

He is currently a Research Assistant in the Department of Electronic Engineering, Osaka University. Hisresearch interests are switching theory and automatatheory, and hespecializesin thedevelopmentoftesting, testablelogicdesign, andsystemdiagnosis.

Dr. Fujiwara is a member of theInstitute of Electronics and Com- munication Engineers of Japan and the Information Processing Society of Japan.

Kozo Kinoshita (S'58-M'64) was born in Osaka, Japan, onJune 21, 1936. Hereceived the B.E., M.E., ^{and Ph.D.} degrees ⁱⁿ communication engineering all from Osaka University, Osaka, Japan,in 1959, 1961, and 1964, respectively.

Since1964 he has been with OsakaUniversity,

where he isnow anAssociate Professor of Elec- tronic Engineering. His fields of interest are switchingtheory, system and logical design, and fault diagnosis of information processing systems. Dr.Kinoshitais a member of the Institute of Electronicsand CommunicationEngineersof Japan and theInformation ProcessingSociety of Japan.