Plane Algebraic Curves Drawn by the Isogonal Conjugate for a Triangle : Applications of a Drawing Tool and Mathematica-香川大学学術情報リポジトリ

(1)

M｡z?l.ac.￡jlc.，瓦αga,gび,z＆/Z，58(2008)，1 −14

Plane Algebraic Curves Drawn

by the lsogonaI Conjugate

11)ra lriangle

Applications of a Drawing lTool and Mathematica

by (Received November 30, 2007) Abstrad

§1.1ntroduction

- １− ＫａｚｕｎｏｒｉＦＵＪＩＴＡ，ＫｅｉｓｕｋｅＭＡＴｓＵＭＯＴｏａｎｄＨｉｒｏｏＦＵＫＡｌｓＨＩ

ln this paper we present a comPuter tool tor drawing a locus of the isogonal conjugate to a point for a triangle whichnlovesalong a distinguishedcurve.The drawing tool Provides many plane algebraic curves with simPle cxpressions.

ln the sequel to [4]−[8]，[17]our study aims to develop a drawing tool on a display for experimenta1 research on various curves using computers.

ln elementary geometry we have five significant notions for a triangle; that is，the center of gravity，the center of an inscribed circle，the center of an escribed circle，the circumcenter and the orthocenter of a triangle. As a similar notion we have the isogonal conjugate to a point for a triangle.

W'hich curve is drawn as a locus of the isogonal conjugate to a point for a triangle which moves under a certain condition? ln this study we limit ourselves to the case where a triangle is fixed while the point moves along a distinguishedcurve. Then our

The last author was partially suppolted by Grant-in-Aid for Scientific Research （N0.19500761）， the Ministry of Education， Culture，Sports， Science and Technology， Japan.

(2)

K.FUJITA，K.MATsUMOTo and H. FUKAlsHI

main concem

is to find various unknown

curves with simple algebraic expressions as a

locus of the isogonal conjugate to a point for a triangle.

Forterminology of geometry throughout the paper，consult[2]−[3]and

[

151. §2.A

program

for drawing a locus

On a plane let us consider a given triangle △Å召C and a point ？ din1rent from the vertices of the triangle.

Reflect the lines connecting the vertices of △Å召C with jl)in the bisectors of the corresponding angles of the triangle. lttums out that three lines always intersect in a single point (or are parallelj.e.jntersects in the point of infinity oo)，which we denote j)'.The point 7)'is called the jgg回｢c凹/昭αzEto 7)for△Å召C ； the map ψ:7)ら j)'is called the js卯皿｢c明/昭a治現．

LetAG，z)．Ｂ(−1，0)，C(1， 0)be the vertices of a triangle，and j)(a，1')a point differet from the vertices. The point 7)″(χ,y)is determined as the intersection of two

straight lines 7)゛B alnd 7)″C given by

(*) １狸召７)'Ｃ：ｙｙ

-雨＋心−(1＋s)y

(1＋い(ト心)＋ハ，

づ(1−g)＋(ﾚs柚

(1−い(ﾚa)＋に

(･＋1)，

O-1）

M/hich curve is drawn as a locus of the isogonal conjugate 7）’toa point ？ for △Å召C whichnlovesalong a distinguishedcurve ｰ？

(3)

Plane Algebraic Curves Drawn by the lsogonal Conjugate for a Triangle

We

divide our operation of a drawing tool into the drawing part and the printing

part，

due to the circumstances of our computer machines.

PART ONE : ']Tb draw a locus of the isogonal col!jugate to a point for a given triangle. A program of our drawing tool for Case l of Theorem in §3 is written in visual Basic Ver. 6.0 by Microsoft Corporation and consists of the following fk)ur steps (see List l).

Step l. Set the coordinates axes and △Å召C in black.

Step 2. Set the initial position of a point 7)on curve 貿(in blue). Step 3. Plot the isogonal conjugate _jP'in red.

Step 4. When one moves the point 7)continuously along the curve貿by the mouse。 the point｣Ｐ’continuously draws a locus ，y with a solid line in red.

PART Two

: To process a bitmap file(bmp)bypひTEX

2 E

'

to exhibit it on another

display，and to print it.

OUTLINE

of the PROGRAM. Let

A(0,2)．Ｂ(−1，0)，C(1，0)andy:y＝3.Where

a

point ？(zりﾉ)on貿is

selected by the mouse, then the isogonal conjugate 7)″G,y)to

jl）is determined by the equations （＊）for Gμ）゜

The

program

for drawing a locus y

we

will have

the curve

ｙ

on a disPlay(Fig.1)

ぐ -15√百 -＼ＩＩノ／ (s,z)＝(0,2).

of the point 7)'is given in List l. ln this case

＋

レ

ぐ −3− う／Ｉ＝ 13 − 14 ζＪＩ４１

う

(4)

the dnpse．

Ｉ

＝

ニー1，the肪Perbola

Ｋ．ＦＵＪＩＴＡ，Ｋ．ＭＡＴｓＵＭＯＴｏａｎｄＨ．ＦＵＫＡｌｓＨＩ

§3.Algebraie

curves obtained as a locus of the isogonal conjugate

As a locus of the isogonal conjugate to a point for a given triangle we have various curves.ln this sectionwe exhibit some of them together with thecasesof plane algebraic curves with simple expressions whose graphs are not given in the standard texts of the subject[9]−[101，[121，[141，[161，[18]and[221.

Theorem. ￡α＆げz/zりbZ/｡w向μz/g訪,ujむ㎝ｎ７６２２ａｚ,Ｈ,。涌z ｢｡｢,2sαlaasげ治g

isogonat conjugate l）’toa point P jor a triangle△Å召C w/zjdzz?zθvEsα1θz7gが1どczjr祀ｰ。

Case l (Fig.1).

Å(0,2)，組−1,0)，C(1，0).

ｰ：ｙ＝３，涜

ｰ,9zπz4＆沁zg.

ｙ・１ぐ 15√jT4 -28

ｰ：ｊ十こ

1 ｙ

ｙ

・ぬ φ １

ダ

-う

う

＋

レ

ぐ

柏

3x十２ぐ︷ｊｌ

う

４１ ″ ｀ＪＩ

う

４ −

Case 2 (Fig.2).

Å(0,1)，組−1,0)，C(1,0)

゜t，z/zEEI/1ρ認．

う

４ − ３５ − ３

う

0,−2)，C(1,0)

玉４ − ３

Case 3 (Fig. 3).

Å(0,2)，組･

ｙ： χ２十y’1，z/1Edr/ε

(x−1)2(8−柚

(5)

Plane Algebraic Curves Drawn by the lsogona1 Conjugate for a Triangle Case 4 (Fig.4). Å(1，2)，

組-

１ｰ: y°χ2−1，，0)，C(1，0). the parabola

y:

x2−政y−y−4y−1＝0，the

hyperbola

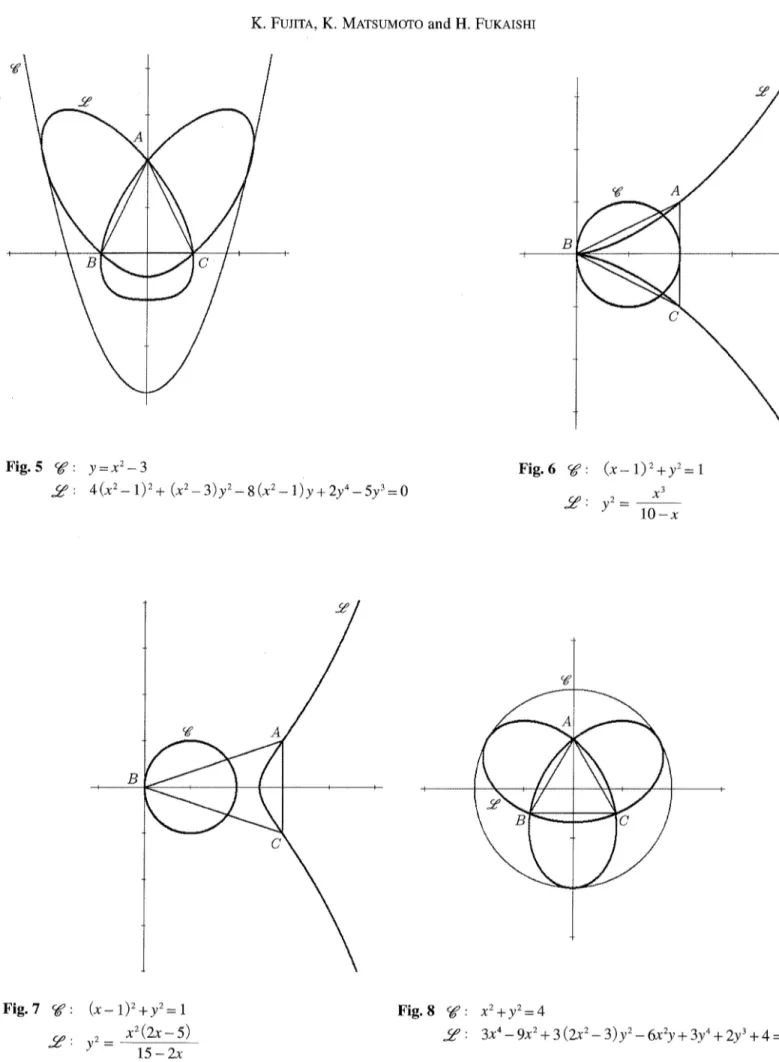
Case 5 (Fig.5).

Å(0,2)，j(−1，0)，C(1，0).

ｰ: y＝χ2−3，哨り7απzゐθ1α.

2ｸ: 4(？−1)2＋(x2−3)y2−8(x2−1)y十2y4

− 5y3 ＝

Case 6 (Fig.6).

Å(2，1)，組0,0)，

C(2，−1)

ｰ:（x−1）≒y2＝1，

ｙ

Case 7 (Fig.7

Å(3，

ｰ：

ｙ・ｅｊ

ゾ

ｊｌぐ - λ3 10−x z＆ｄｒ＆

，治

ｰCj∬θ一げ1)jθdgs.

j(0,0)，C(3，−1)

J−1)2十ゾニ1.the

circle

ゾ

-Case 8 (Fig.8).

Å(0，1)，j

貿

ｙ

Case 9 (Fig.9).

X2＋

Ｇ

ｙ

ｌｌ ./TX.

j(2x−5)

15−2λ7

じ

ぞ十ゾ

-3?−9ぞ

Ｙノ

凭４

５ − ４

う

酉一今一うラぐＣ酉 -２’ Ｉ２う０ 2− 6×2y 十3ﾀﾞ十2y3十４＝０

(1(゜o)，is given by the circle

−5− １ − ２

4，が1Edr&?，

＋3(2j−3)y

Å(0,2)，j(−1,0)，C(1,0)

ｰ: x＝k，the

straightling.

2政2−5λly十2砂2−3肪−21:＝0，がzEcθ㎡cjEdjθzz.

ln Fig. 9, the inverse image of the point of innnity，

(6)

K.FUJnA，K.MArsUMOTo and H. FUKAlsHI

Pmof. Let 7)(j，y)andj9'G,2y)

Case l.

Find the Groebner bases (see[11，[11])by

applying Mathematica

Ver 3.0by

W7olfram Research lnc･，to the following code

ｔｖ・ φ ＝２＝３

ｆ１：＝(ｕ+１+ｔＶ)ｍｂ-(ｔ＊(ｕ+１)-Ｖ)

ｆ２：＝(１-ｕ+ｔＶ)ｍｃ−(-ｔ＊(１-ｕ)+Ｖ)

ｆ３：ﾆy-mb*(x+1)

f4:=y-mc＊(x-1)

GroebnerBasis[{f1，f2,f3，f4}，{u,mb,mc,y,x}]

Then we obtain the term

−2十2χ2−

13y十ﾌy2

in the listof the generating Groebner bases.Therefore,we

have

as an equation of jf

ぐ

15√ﾛﾌ

28

う／＋ぐりｊｌ

う

１＝４１ ζＪＩ４１

う

(7)

Plane Algebraic Curves Drawn by the lsogonaI Conjugate for a Triangle

References

［１］フＷｸﾞW.Adams and R Loustaunau : / ､7zlrrり＆aごzjθz□∂Gy蚕,z2gr＆2jEs，Graduation Studies in Math.，Vbl.3，Amer.Math.Soc.，Providence，1994.

［2］H. S. M･ Coxeter : ﾉ削177＆lcljθnzθGEθ謂gzり’，2nd ed･， John xViley and Sons lnc･， New York，1980.〔コクセター（銀林浩・訳）：幾何学入門第２版，明治図書，東京，

1982.〕

［3］H.S.M.Coxeter and S. L.Greitzer : Ggθj?zgzりり?ａ心Ej，New Mathematical Library， Number 6， School Mathematics Study Group， Random House， lnc.，New York， 1967. 〔コークスター，グレイツァー（寺阪英孝・訳）：幾何学再入門，SMSG双書，

河出書房新社，束京，1970.〕

［4］K. Fujita and H. Fukaishi : Plane Algebraic CurvesDrawn by the Orthocenter of a Pedal Triangle￣Applications of a Drawing Tool and Mathematica， Ma?z. ac. ￡ゐc･，瓦昭αｗα び｢９函印私57（2007），51-72.

［5］K.Fqjita,A.Matsushima and H. Fukaishi : A Locus of the Orthocer!ter of a Triangle − lnstruction in Geometry by a Moving Locus on a Computer， Ma?7.ac.￡面c･，旭卯ｗα び㎡ｗ溺印77，55（2005），1-13.

［6］K.Fujita，A. Matsushima and H. Fukaishi : A Triangle with Three Distinguished Collinear Points lnstruction of Geometry by use of a Drawing Gamc on a DisPlay，Ｍｅｍ.凡z,1.￡血c.，瓦昭αwaび一ｗ｢りり7，55（2005），25-41.

［7］K.F1!jita,A. Matsushima and H. Fukaishi : A Triangle with Distinguished Concyclic Points￣lnstruction of Geometry by use of a Drawing Game on a Display，λ＆謂･JFiz‘］. ＆jz4c.，瓦αg,2wαび｢1ﾉε,･sj印77，56（2005），1-25.

［8］H.Fukaishi，K.R!jita and A. Matsushima : Alternative Geometric Proofs of Theorems for Concyclic Points for a Triangle，ﾙfa?2.瓦zc.￡jz4c.，jQgαwαび㎡wrsjりﾌﾉ，56 （2006），51-59.

［9］XV.Fulton : ﾒUg,治rz2jcC￡jrv6/W.A.Benjamin，New York， 1969.

［10］一松信・他：新数学事典，大阪書籍，大阪，1979.〔＝S.Hitotumatu et al.: Shin- S両1￡z包-j7z四，凸saka-shoseki，1979.〕［11］一松信：代数学入門第三課，近代科学社，東京，1994.〔＝S.Hitotumatu : Mzrりj￡4djθzzた,Åな＆ra，777ε771j ｢￡ε∬∂zz，Kindai-kagaku-sha/lbky0，1994.〕［12］飯高茂：平面曲線の幾何，共立出版，東京，2001.（＝S.litaka : GEθz?zg吋げ j）1αnECljry6，Kyoritsu-Shuppan，loky0,2001.〕［13］石谷茂：数学ひとり旅，現代数学社， Hitoritabi，Gendai-sngaku-sha， Kyoto， 1998.〕京都，1998.〔＝ S.lshitani : S卵a㎞

［14］河田敬義：代数曲線論入門，至文堂，東京，1975.〔＝￥Kawada

: 7zla凶d,9n9

−７−

(8)

K.FUJITA,K.MArsUMOTo and H. FUKAlsHI

Åな訪n2jむCz4rw 771εθり，Shibundo，Toky0，1975.〕

[15]小林幹雄：初等幾何学，共立出版，1958.〔＝M.Kobayashi: ￡凶2a畝り,G・・吻y， Kyoritsu一Shuppan/lokyo， 1958.〕

[16]E.Kunz : ｶlz7?)dzjczjθzl r∂ ？1αzlE/UgEゐΓαj,? Cgrvgs，Birkhauser，Boston，2005. (Translated from the original German by R. G.Belshoff.)

[17]A.Matsushima，K.R!jita and H. Fukaishi : A Locus of the Orthocenter of a Pedal Triangle￣lnstruction of Geometry by use of a Drawing Game on a Display， A＆謂.凡zc. Educ･，瓦αgαwα￡ﾉ7yliwMj印弑57(2007)，1-15.

［18］G.0rzech and M. 0rzech: 7）/αzl ｰÅなεゐΓαjcC￡4rw5，MarceIDekker， NewYork，1981. ［19］D.Pedoe : GEθ謂Ezり｡Dover Publ. lnc.，New York， 1970.

［20］坂井忠次：グラフと追跡，培風館，東京，1963.［＝C.Sakai: Ggφ ｢ｎ咄函，

Baifukan， lokyo， 1963.］

［21］Yvonne et Rend Sortais : ￡αG必剤ざ哨ε＆,7Mα,1μど，Hermann，1987，〔＝Tソルテー，Ｒ．ソルテー（戸田アレクシ哲・訳）：なぜ初等幾何は美しいか，東京出版，2002,〕

[22]R. J.Walker : Aな一ｍ必Cgn゛Es， Springer“Verlag，New York， 1950

Kazunori FUJITA

Department of Mathematics， Faculty of Education， Kagawa university 1-1 Saiwai-cho， Takamatsu-shl，Kagawa，760-8522，JAPAN

￡-sαjlaふ1ras: fujita＠ed.kagawa-u.ac.jp

Keisuke xlATsUMOTO

Student of Master Course， Graduate School of Education， Kagawa university 1-1 Saiwai-cho， Takamatsu-shi，Kagawa， 760-8522， JAPAN

Hiroo FUKAlsHI

Department of Mathematics， Faculty of Education， Kagawa university 1-I Saiwai-choドlakamatsu-shi，Kagawa，760-8522，JAPAN

(9)

−9−

Ｆｉａ．１ ‘ｉ：ｙ＝３

ｙ

Fig.3y

ぐ

Plane Algebraic Curves Drawn by the lsogona1 Conjugate for a Triangle

15､/百 28 マリ／ _＋ χ2＋y jﾀﾞ:y2 2＝1 (x−1)2(8 一一 3x十２ ( J一ぐ槌 ↓3 − 14 15 − 14 マノーう＝Ｉ Fig. 2 貿ｙ

Fig.4 y

y

λ 2 _＋ぐ＝１ダー_４

七づ

ｙ＝ｘ２−１ｙ一趾y−ダー4y−1’0

(10)

Fig.5貿

ｙ

ｙ４

=χ ２３

K.FUJITA，K.MATsUMOTo and H. FUKAlsHI

Fig. 6 （汐 (ぞ−1)2＋(ぞ→)ダー8(x2−1)y＋か4−y＝0

G−1)2十ダ＝１

ﾀﾞ：ｙ＝ χ3 10−X

(11)

Plane Algebraic Curves Drawn by the lsogona1 Conjugate for a Triangle Fig.9 ‘i: x＝灸 y: 2b;2−5xy＋2紗2−3勿−2友＝０一︱Ｉ一

(12)

ｉ

ｌ

K.FUJITA，K.MAjTsUMOTo and H. FUKAlsHI

List 1. A program

for drawing

a locus

一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一・／･ ●ｒ・ ● ● 一ｒｌ● Ｉ・・・

Spe(ﾆifying statements of the general variables

Dim sx， sy,ex，ey As Double

Dim ax， ay， bx， by, cx, cy As Double Dim pi As Double Dim tb, tc As Double Dim k As lnteger ＳｇＳ

Drawing the initialfigure

Private Sub Form_Activateo Dim r, X,Y As Double Forml｡Line(sx，0)-(ex，0) Forml.Line(0，sy)-(0，ey) sxn＝lnt(sx):syn ㎜ d ■

exn＝lnt(ex):eyn

＝lnt(sy) ＝lnt(ey) h＝0.05 FOr j ＝sxn To exn Forml.Line(i，−h)-( Next i ！・ − h） FOri＝syn To eyn Forml.Line(-h，i)-(h，i) Next i Forml.DrawWidth＝2 Forml.Line(ax，ay)-(bx，by),VbBlack Forml.Line(bx，by)-((:x，cy),vbBlack Forml.Line(cx，cy)-(ax，ay)，vbBlack Forml.DrawWidth＝1 tb＝A91(ax，aｼﾞ，bx，by，bx十1，by) t(二二A91(ax，ay， cx， cy，cx十1，cy) Forml.Line(sx，3)-(ex，3),vbGreen k＝1 End Sub ！・！！

-Setting the form， the coordinate axes and the initial values of the coordinates of each vertex of a trian9le

一一一 - 一一一

Private Sub Form_Loado Forml.Top＝500 Forml.Left＝500

(13)

X As Single, Y As Sin9le）一りＪＩ一 Forml.Wjdth SX＝−5,2 ex＝5.2 wx＝ex一SX

Plane Algebraic Curves Drawn by thelsogona1 Conjugate for a Triangle

-一 0.95 ゛ Screen.Width

wy＝wx ゛Forml.ScaleHeight / Forml .ScaleWidth sy ' -0.32り/vy ey＝0.68 ゛wy Forml.Scale(sx，ey)-(ex，sy) Forml.BackColor＝vbWhite Forml.DrawWidth＝1 pi＝4 ゛Atn(1) ａｘ一一 O: ay ＝2 bx＝−1:b･ CX＝1 End Sub １１ｙ＝０ cy° ０

Action corresponding to the left button of mouse Private Sub Form_MouseDown(Button As lnteger lfk＝2 Then k＝1 ExitSub End lf Disp x，3 k＝2 End Sub ｇＳ６

，ShiftAs lnteger, XAs Sin9le,Y As Sin9le）

Action corresponding to the movement

of mouse

Private Su lfk＝1 Disp x， End Sub １ｇ Ca ︲︲︲ｂＴ３ ICUI Form_MouseMove(Button As lnteger hen Exit Sub

ating the value of an an9le Private Function Agl(xa, ya, xb，yb，

＝＝ａｂＣ -ＸＣ， Sqr((xc − xb戸ヽ２十(yc − yb)ハ2) Sqr((xa−xc)ハ２十(ya − yc)ハ2) Sqr((xb − xa)ハ２十(yb − ya)ハ２) yc）一ｆ・−ｈ 1/︶！ t As lnteger，

lfa＜0.00000010rc＜0.0000001 Then Exit Function × lf − − 1 lf Ｅ (a∧2十ｃ△２−ｂ△２)／(２・ａ'ｃ) −XA2＜0.0000001 Then x＞O Then t＝0 lse

(14)

りｔ＝ｐｉ − − End l Else ｆ

K.FUnTA，K.MATsUMOTo and H, FUKAlsHI

t＝pi/2−Atn(X / Sqr(1−X△2)) End lf 」ニ lfj xa゛yb十xb゛yc十x（゛ya−xa゛yc−xb゛ya−xc゛yb ＜O Then t ＝-t A91＝t End Function ｇｉｌ Presentjng ｈｔｆｏ一

Private Sub Disp(px， Forml.DrawWidth e isogonal conjugate -３ Forml.PSet(px，py)，qBColor(9) sb＝A91(px，py，bx，by,cx，cy) mb＝Tan(tb − sb) sc＝A91(px，py，cx，cy，bx，by) mc＝Tan(tc − sc) qx＝(mbibx−m(ヅcx − by十cy) qy＝mb゛(qx − bx)十by Forml.PSet(qx，qy),vbRed End Sub

Private Sub Ext_Clicko

For x ＝ex To 20 ゛ex Step 0.1 Disp x，3 Nextx FOr x ＝2 Djs Next Ｘｐｘ０３゛sxTo sx Step 0.1 For x ＝sx To ex Step 0.001 Dispx，3 Next x End Sub ／(ｍｂ − ｍｃ)