整数/組合せ計画法の現状（その4）　巡回セールスマン問題

整数/組合せ計画法の現状(そのり

巡回セールスマン問題

1.問題 これまでの報告で重ねて指摘されたように，一般的な 整数計画問題に対して汎用性のある強力な解法は今のと ころ存在しないだけでなく，その本質的なむずかしさが 徐々に納得されつつある.そして，いきおい研究は特殊 な構造をもった問題へと向かっている.その中で巡回セ ールスマン問題については 1970年以降の研究に興味深い ものがある.本報告では 1970年以降の研究を中心に，そ れ以前の成果をも振り返りながら話を進めたいと思う. 巡回セールスマン問題とは，都市 t から都市 j へ行く のに必要なコストが Cij で与えられているとき，すべて の都市をちょうど一度訪れなければならないという条件 のもとで，旅行に必要なコストを最小にする訪問のJI原序 を求める問題である.つまり ，

n

( 都市の数)個の頂点、と コスト Cij を付加された n(n-I) 本の枝とから成るグラ フ(図1.1 )で，最小コストの巡回路(各頂点をちょうど 一度通る閉路)を求める問題である. したがって巡回路のどの性質に注目するかが解法上の 1 つの要点となる. 図1. 1 対象とするグラブ 1979 年 5 月号 整数計画法研究部会山本芳嗣 n(n-I) 次元のベクトノレ x=(X₁₂, X1S, …, :Cn，ト 1) に対 して，校集合 S(x) を， S( ぉ)

=

{

(

i

,

j)

I

Xij キ O} と定義すると，巡回セールスマン問題 PS は， ィ J t

s

., J t c ηZZ 4J4J πZ4 t レ u , a

,

、 -a d 』， 最

条件

E"36j=1(s=I

，

L

，

n)

、

l

j j=1 キ4

f

:

Xij=1

{j =1

， 2，・

"，

n)

i=l 1キj (1. 2) 校集合S(x)の作るグラフは連結 (1.3) Xij は0 あるいは 1 (i, j=I ,2, "'，河) (1.4) と書ける.この問題から条件(1.3) を取り除くと，よく 知られた割当問題となり，条件(1. 2) を， n

L

:

(Xij+Xji);:;;1

(i=

1, 2,… , n) j=l j キる で置きかえると， (Cij>O のもとで)最小コストの木(3 節参照)を求める問題となる.したがって，条件(1. 2)に 注目するか，条件(1.3) に注目するかで大きく 2 種の方 法を考えることができる.

2

.

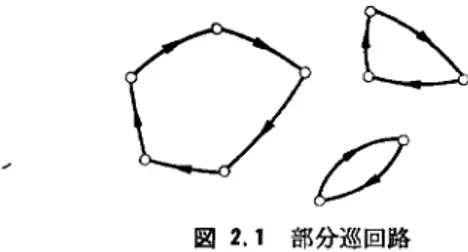
割当問題を用いた算法 割当問題の実行可能解zについて S(x)の作るグラフ は一般に図2.1のように部分巡回路(長さn未満の閉路) がいくつか集まった非連結なグラフとなる.したがって 割当問題に部分巡回路を含まない条件

L

:

Xu豆

ICI

ー 1

(長さn害満のすべて) (2. 1) (i,Jre

ri'

iJ

=

=

I V _I - ! \の閉路Cについて/ あるいは連結性の条件 /ゆキVc{1，2，…，却}\

L

:

L

:

Xi;;:;;1 なるすべての頂点集I (2.2) ieV jey _{\合Vについて /} を付け加えることによって巡回セールスマン問題を表わ すことができる. ここで ， ICI は閉路 C の長さを表わ す.これを一般的な解法で解けばよいことになるが，条

2

8

3

© 日本オペレーションズ・リサーチ学会. 無断複写・複製・転載を禁ず.

図 2.1 部分巡回路 件 (2.1) ， (2.2) はいずれもをの個数がぼう大なうえ，割 当問題のように容易に解ける問題ではない.したがって， 分校限定法で部分巡回路を排除するように分校を行ない ながら，繰り返し割当問題を解く算法が考えられる.今， (1

,

2)

,

(2

,

3)

,… ,

(k ー l ， k) ，(k

,

1) を割当問題を解いて得 られた部分巡回路とすると，全都市を訪れる巡回路では X12=O

,

X23=0

, …,

Xk-1.k=0

,

Xk.1=0 のいずれかが成り 立つから， P1 :

x

12= O P2 : X23= 0 Pk : Xk1=0 なる k 個の部分問題に分枝する方法が考えられる. この分校によって作られた部分問題の実行可能領域は 互いに排反ではないが， P1 :

x

12= O P2 : X₁₂= 1

,

X₂₃= 0 Pk : X12=X23=

…

=Xk-1.k= 1

,

Xk.1 = 0 とすれば排反にできる [3 ].また，巡回路であるために は 1 ， 2 ，… ， k の内の少なくとも l つの頂点から 1 ， 2，…， k 以外の頂点、へと路が延びていなければならな L 、から P1 : x1j=O (j=1

,

2

,…,

k

, j キ 1)

P

2: X2j = 0 (j=1

,

2

,…,

k

, j キ 2)

P

k : Xkj=O (j=1

,

2

,… ,

k

,

j キ k) と分校することもでき，この分校法は前の 2 つの方法と 比べてより多くの部分巡回路を排除できる [3]. さらに，

P

1: X1j = 0 (j=1

,

2

,…,

k

, j キ 1)

P2 : x1I=0 (1 キ 1 ， 2 ，… ， k) X2j = 0 (j= 1

,

2

,…,

k

,

j キ 2) Pk : X1I =X21=

…

=Xk-1.1=0 (1 キ 1 ， 2，

...,

k) Xkj=O (j=1

,

2

,…,

k

,

j キ k) とすれば，やはりこれら k 個の部分問題の実行可能領域 を排反にできる [10]. すべてのた j について Cij=Cji なる問題をとくに対称 問題といい，この問題についても以上の方法をそのまま 用いることができるが，対称性により i<j について変 数 X(j を用意すれば十分で，条件(1. 2) ， (2.2) はそれぞれ

L

:

X11+

L

:

Xjk=2 (j= 1

,

2

,… ,

n) (2.3) i<j

j<k-L

:

_Xlj 孟 2 ((.jle<V,yl (2.4) に置きかえることができる.ここで， (i

,

j) ε (V， V) は i E V

, j

E V あるいは iEV， jEV のいずれか一方が成り 立つことを示すものとする. Miliotis [23

,

24J は対称 問題を， O.

(1.

1)

, (1.

4)

,

(2.3) を解く.

1

.

条件 (2.4) の中で，その解によって満たされてい ない制約を捜す. 2. その制約を付け加えた問題を解き1.へもどる. という手"闘で解いているが，手順 0 と 2 で整数解を得る ために Gomory カットを用いた方法では， 0~100 の乱 数でコストを与えた90都市の問題 2 題を CDC7600 を用 いて， 4 秒足らずで解いている.しかも，報告されている 17題のいずれについても必要としたカットの本数は 30本 未満であることは注目に値する.また条件(1.4) (2.3) を 満たす解はbーマッチングとよばれ， Edmonds-Johnson [9J によって問題(1. 1) ，

(1.

4)

,

(2.3) を解く高々

o

(n4) の手聞の算法が提案されている. Bellmore-Malone [3J はこの算法を用いて UNIVAC 1108 で30都市の乱数コ ストの問題を 5 題，平均 32 1. 6 秒で解いたと報告してい る.

3

.

最小コストの木と巡路 話を簡単にするため，しばらく対称問題だけを扱うこ とにする.われわれが前節で扱ってきた問題では，セー ルスマンはすべての都市を巡った後，出発した都市にも どって来ることになっていたが，都市 l から都市 n へ向 かつて，すべての都市をちょうど一度通過してゆく路 (これを巡路という)を求める問題 Ps' 最小化

L

:

.

CtjXtj t<1 条件 L: Xij+

L

:

Xjk=2 4 く j く k n-1

L

:

X1j = 1 J=2 n-1

.

L

:

Xjn= 1 1=2 (j=2

,

3

, ...,

n ー 1) (3. 1) (3.2)

L

:

xiJ 孟(3 .3) (i

,

j)e(V

,

v)-を考えよう.連絡で閉絡を含まず，すべての頂点をつな ぎあわせている部分グラフ T をそのグラフの木(極大木) とよび，そのコスト C (T) を木に属する校のコストの総 和とする.また， C(T，(ρ， q)) を木 T に枝 (p， q) を付け 加えたときにできる閉路の校集合， D(T

, (s， t)) を木 T

D(T.(s. t)) 図 3.1 太線を木 T とすると，横に破線の引かれた 閉路が C(T， (p， q)). 一点鎖線の交わる校集 合が D(T， (5， t)) である. から校 (5， t) を取り除いたときにできる 2 つの部分木を 結ぶ校集合とすると(図 3. 1)， T が最小コストの木であ ることと， (i) T に属さない任意の校 (p， q) について， cpq=max {c/j

I

(i,

j

)

e C(T

,

(p

,

q))

},

(ii) T に属する任意の枝 (5， t) について， c.e=min{Cjjl (i

,j)

eD(T

,

(5

,

t))}

,

のそれぞれが同値であることが知られている.これらの 性質から最小コストの木を求めるためのつぎの 2 つの算 法を導くことができる. Kruskal の算法 [21J

O

.

T= ゆ， F=E( グラフの校集合)とする. 集合とする.

O

.

.

9

'

=

{PS '

},

u= + ∞とする.

1

.

.9'=併なら終了 (uを達成している巡路が最小コスト の巡路上そうでなければ2. へ.

2

.

タの中から問題 P を選びタ=ター {P} とする.

3

.

問題 P のコストの下での最小コストの木を作り， c(T) 孟 u なら1.へ. c(T) くu dl(T)=dn(T)=I

,

d/(T)=2 (i キ I ， n) なら u=c(T) として1.へ.そうなければ，ム (T)>I あるいは dπ (T)>I となっているか， ddT)>2 なる 頂点 i が存在するので，その中の 1 つの頂点を j とす る . Oj(T) のそれぞれの校のコストを+∞と修正した dj(T) 個の問題をタに付け加えて 2. へ. 今，コスト C=(C/j) のもとでの最小コストの木 T に 関する頂点 t の次数が ddT)>2 であるとする.このと き頂点 t に接続する枝のコストだけを一律に C'/j=CjJ+ π と上げると，新しいコスト C'=(C'jj) のもとでの最小 コストの木 T に関する頂点 t の次数 ddT') がめ (T) よ りも下がることが期待できる.しかも，このようなコス トの修正を行なっても巡路間のコストの大小関係は保た

1

.

cpq=min {Cjjl(i

,

j) e F} なる枝 (ρ， q) を選び， TU れる.実際 π=(πhtr2， ."，1I'n) によってコストを， (ρ， q) が閉路を含まなければ T=TU(ρ， q) ， F=F- C'jj=C/j+町 +πj

(

3

.

4

)

(p， q) として 2. へ.閉路を含めば F=Fー (p， q) として 1.へ. 2. ITI=n-1 となったら終了.そうでなければ1.へ. Prim-Dijkstra の算法[8 ，

3

0

J

O

.

任意に 1 つの頂点， たとえば頂点 1 ，を選んで U= {I

},

T= ゆとする.

1

.

U に属きない頂点 j について ん =Cj(jl.j=min

{

c

j

J

I

i

e

U}

を求め，頂点 j にラベル [i (j)， ßjJ を付ける. 2. ん =min{んJj<$U} なる頂点 k を選ぴ， U=UU {k

},

T = T

U

(i(k)

,

k) とする. 3. IUI=n となったら終了.そうでなければ 4. へ.

4

.

U に属きない頂点 j で ん >Ckj となる頂点 j のラベルを [k， CkjJ に変えて 2. へ. これらの算法の計算効率については[7]に詳しい議論が されている.このように簡単に最小コストの木が求まる ことと，巡路が 1 つの木であることを用いると，つぎの 分校限定法による算法を考えることができる. ここで ìldT) は頂点 t に接続する木 T の校集合， ddT) はその 本数(頂点 i の T に関する次数)を表わし，タは問題の 1979 年 5 月号 と修正した場合を考えると ， c(Htl ;;;'c(H2) なる 2 つの 巡路 Hb H2 について c' (Htl = .

I

:

_

_

(Cjj+ π汁 11:j) (i,j)eHl 旬 -1

I

:

Cij+ (π1+2

I

:

1

1

:

i+

1

1

:

n) <i

,

J)eHl i=2 n-l 2三I: cij+ (π1+2

I

:

11:/+πη) ぱ .JleH2 /=2

I

:

(Cil+的 +11: I)=c'(H2) (i

,

j leH2 が成立する.

C

h

r

i

s

t

o

f

i

d

e

s

[5

,

6

J は以上の性質を用い て，頂点罰金法と名付けた発見的算法を提案している. O. 十分大きな正の数 M を用いて， 11:1=πn=M， 的 =0 (i キ I ， n) として (3 .4)によって C'=(C'jj) を作る(この修正によ りコスト U のもとでの最小コストの木に関する頂点 1

,

n の次数は必ず 1 となる).

1

.

C' での最小コストの木 T を求める. 2. ddT) =2(i=2

, 3 ， … ， n- I) であれば T は最小コス

トの巡路となるので終了.そうでなければ何らかの方 法で罰金 π=(π2 ，1t'a，… ，11:n-1) を決めて C'/j:=C'ij+ 11:i+ πj として1.へ.

2

8

5

© 日本オペレーションズ・リサーチ学会. 無断複写・複製・転載を禁ず.

この算法によってかなり効率良く最適解が得られたと 報告されている(前金をつぎの (3.5)(3.6) によって決め た場合には， 1O~60都市の乱数コストの問題が 33題解か れており 60 都市問題 3 題の平均反復回数と平均時間 は CDC 6600で， 111 回， 13.6秒である)

[6

]が，残念な がら常に最適解を作り出すとは限らないことが示されて いる [16]. 罰金 π の決め方としてつぎのようなものが提 察されている. ( i) r>O を用いて， πi=r(ddT) ー 2) ddT)>2 なる頂点 t について 向 =-r ddT) =1 (i キ l ， n) 11

(

i

i

)

反復ごとに r:=a'r(O く a< l) として (i) を用いる.

(

i

i

i

)

ゐ (T)>2 の場合ゐ (T) の校 (s， t) それぞれについ て， Ciωjω=min{Cij

I

(i,

j)

E

D( T

,

(s

,

t))

,

J

,

J キ s} e ト (3.5) を求め π.=min {Ci(t )jω -C. tI (s

,

t

)

E

0.( T)} } とする. d.(T)=1 の場合は頂点 s に接続する T に属さな い校 (s， が)それぞれについて，

Ci(tl )j(tη=min{Cij

I

(i， j) ε C(T， (s

,

t'))

,

ì 脚注

J

,

J キ s} を求め e ト (3.6)

1

l

:

.=max

{Ci (tlげはり -Cst， 1 (s

,

t') <$T} とする.

4

.

最小コストの“ 1-木"と巡回路 前節では巡路が 1 つの木で、あることを用いて問題 Ps' を解く算法について話してきたが，つぎに同様な考え方 を問題 PS にも応用してみよう.そのためには，巡回路 に対して木に相当するものを見っけなければならない.

Held-Karp [16

,

1 7]はそのような性質をもつものとし て“ト木"を定義している.グラフから 1 つの頂点，た とえば，頂点、 1 ，とそれに接続する枝集合，ム，を取り 去ったグラフ G

1

を作り ， G

1

の木と 01 の任意の 2 本の枝 とをあわせたグラフをト木と定義する(図 4. 1).この定 義から明らかなように巡回路は 1 木である.そのうえ， 最小コストのト木は G1の最小コストの木と 01 の最もコ ストの小さい 2 本の枝をあわせて作ることができる.ま た，罰金 π を用いて (3.4) によってコストを修正しても d_s(T)>2 の場合の町の決め方にならえば， Ci (tl )j(t円 =max{cijl(i，j) EC(T

,

(s， t')) ， i， j キ s} とすべきである.

2

8

6

図 4.1 1-木 やはり巡回路のコスト相互の大小関係も変わらない.し たがって前節の頂点罰金法を問題 P

S

に対しても適用で きるが，ここではこの算法を違った角度からながめてみ ることにする.前節でも触れたように頂点罰金法では必 ずしも最適解が得られるとは限らないので，最適解を得 るには分校限定法を用いざるを得ないが，その際，部分 問題の最適解の良い(なるべく大きな)下界を求めるこ とは限定操作のうえで重要である.すべての 1-木に 1 ， 2 ， … ， k， … ， K と番号を付け，コスト C のもとでの k 番目 の 1-木 Tkのコストを Ck> 問題 P

S

の最適解H* のコス トを C* と書くと，コスト Ci/=Cij+ 町 +πj のもとでの n n それぞれのコストは Ck+

L

;

1l:iddT_k) ， げ +2 L; πt とな る.したがって H* が 1 つの 1-木であることから， n n

c*+2

L

;

1l:i 主主 min{Ck+

L

;

πiddT_k) Ik=I

,

2

,

…

,

K} なる関係が得られる. つまり， 的k=ddTk) ー 2 ， Vk= (V1k> v2k>

"',

Vnk)t とすると， n も C* ミ;;;min{ck+ L; 町 ddTk)

I

k=I

,

2

,

…

,

K}-2

L;1l:

i

=min

{Ck+ πtVkl k=I

,

2

,

…

,

K} が任意の π について成立する.ここで， w( π)

=min

{ck+ πtVkl k=I

,

2

,

…

,

K} (4.

1

)

とすると最良の下界を求めるためには， 最大化叩 (π(4.2) を解けば良いことになる. (4. 1)からわかるようにこの 問題は区分的線形凹関数の最大化問題である.図 4.2 の 1 本の直線(実際は n 次元超平面)が 1 ;本のト木に対応し ている.とくに巡回路では Vk=O であるから，1r軸に平 行な直線が巡回路に対応していることがわかる. 図 4.2 (a) のようにうまく π を決めるとコスト Cij+町+町での 最小コストのト木が巡回路になる(したがって問題 PS の最適解)こともあるが，一般には図 4.2 (b) のようにど のように π を決めても巡回路が最小コストのト木として 現われない場合がある.この場合には分校を行なう必要 があるが，それは巡回路に対応する水平な直線を下から おおい隠している何本かの直線を取り去ることに対応し ている.

ω(π) 図 4.2(a) w(π) 新しい変数却を用いれば，問題 (4.2) は線形計画問題 最大化 ω 条件叩孟 Ck+ 炉内 (k=I ， 2 ， … ， K) に書き直すことができる.この双対問題 b 品 目 s b h

c

K Z M レ u ， a1 ・ 、 E E E J ' ,, 最 条件 Yk;?'O

(k=

1, 2,… , K) K K L:

Yk=l

, L:

(-Vk)Yk=O

k

=

l

k

=

l

を改訂単体法を用いて解けば，初めにすべてのト木を 知っている必要がないうえ，価格ベクトルを (0，11:10 11:2 ， …，11:η) とすると新しく基底に入れるべき列ベクトル (1 ， -V1k ， … ， -v叫 )t を求めるには， " n n

Ck 一 {O-L:1I:

i

Vik}={Ck+

L: πidj{ Tk)} 一 {0+2 L:町} を最小にする 1-木を求めれば良いことになるが，結局こ れは Cij+ 町 +1I:j のもとでの最小コストの 1-木を求める ことになる.残念ながらこの算法の収束は遅いことが知 られている [16J. Held-Karp は問題 (4.2) を π叶 1=πν+ε(πν， d ν) ・ dν

(

4

.

3

)

と反復法で解くことを提案している.彼らが [16J で示し た方法は，目的関数 w(π) の炉での上昇方向 d" を求め 区分的線形関数 w(π) の区切り目まで dν 方向に進むよ う ε(πν， dν) を求めて， (4.3) で炉+1を決め，……という ものである .T をト木とし ， T の校 (s， t) と T に属さな い校 (i， j) について ， TU(i, j) ー (s， t) が再びト木となる とき 2 本の枝が交換可能であるとよぶことにすると， ε(πν ， dν)=min Cst+ πsν+π♂キ Cij+ 1I:i"+ πf あるいは ds"+dt" キ di.+dj• となる ， T に関して交換可能な校 ω(π) π 図 4.2(b) 叩 (π) Cst+ π♂ +πt.+ ε (ds.+dt.) =Cij+ πr 十 πj.+ ε (di"+dj.) となる e. と選べぽ良いことが示される. また彼らはつぎのような反復法を提案している [17J. 今，iiJ く maxw(π) を目標値として設定し，叩 (π) ミ~W な る π を見つける問題を考えると，この問題は凸多面体 P面 ={π Jw(π) ミ~iiJ} ={πJ ck+ πtVk ;?，iiJ (k=

1

,

2

,…, K)} の 1 点を見つける問題となる.

Motzkin-Schoenberg

[

2

5

J

.

Agmon[ 1

J は一般的な凸多面体

A={xJ αitx_三五九

(i=I

,

2

, …, m)} の点を求める反復法として，

O

.

初期点、がを与え， ν=0 とする. 1. x. が満たしていない制約の内で超平面 Hi={xJait x=btl までの距離が最大のものを選び Hん〉とする.

2

.

a.=(biω-ai(.)t

x

.

)

/

I

I

a

t

c

.

)

11' として ， 0< ，1 主立を 用いてお叶 l=Xν +Àa.aiω とし ν.-ν+1 として1.へ. を提案しており，こうして作り出される点列 {x.} が，

(

i)

xν キ%&1 +1ν=0 ， 1 ，.・.)

(ii) A の任意の点 U について IIx.-yll ;?， IIxV+1- yll (ν=0， 1 ，…) なる性質をもっ(このとき点列 {x"} は A に関して， Féjer 単調であるという)ことを示して彼らの算法の収 束を保証している Pw の 1 点を求める問題についても， k(π) をコスト Cij

+

1I:

i

+町のもとでの最小コストの 1 一木 の番号とし， 0<ε く À.~玉 2 か =λν ( iiJ ー即(伊 ))/IIvk(炉)112 として， π叶_{1=πν +t.Vk( πν)}

₍

₄

_.

₄

₎

によって点列{伊}を作ると， {伊}は P面に関して Féjer 単調であることが示せて(図4.4). {π.} は有限回 の対 (s， t)E T と (i，j)

*

'

T が存在 で P面に入るか， P面の境界に収束するかのいずれかが して， 成立する.

Held-Karp

[17J は (4.4) で t.=i( 一定)とし 1979 年 5 月号 © 日本オペレーションズ・リサーチ学会. 無断複写・複製・転載を禁ず.

2

8

7

1T レ 図 4.4 P面と点列 {πJ て条件，サイズの異なった 19題の対称問題を解いている が，分校を行なう前に得られた下界は最適解の値に非常 に近く，両者の差がないものが 7 題あったことが報告さ れている.その後この算法の改良が提案されており [15 ， 32J ，たとえば [15J には IBM 360/75 を用いて 70都市の 乱数コストの問題を 15題平均78秒で解いたと報告されて いる.これまで，話を対称問題に限ってきたが，非対称 な問題についても条件(1.3)を， 8(31) はト木である に置きかえることができる.その際

O(λ， μ) =min{ck+1tYk+ 戸 Zkl k=I ， 2 ， ・ .， K}

(

4

.

5

)

を最大にする 1， μ を求めれば最良の下界が得られる [2 ].ここで，頂点 t から出る (i に入る )1-木 T の枝の 本数を di+(T) (ddT)) とすると Yk=(d₁+(T_k) ー 1 ，… ， dn+(Tk) ー l)t zk=(d₁-(T

_k

) ー 1 ，… ， dn-(T_k) ー I) t である.この算法によって UNIVAC 1108 を用いて， 60都市の乱数コストの問題が約35秒で解かれている. 本節で述べた算法は Geoffrion [IIJ のラグランジュ 緩和法(第 3 回報告の双対法参照)の一種であり，ラグラ ンジュ変数え， μ を介して目的関数(1. 1)に条件(1. 2) を 組み込んだものが (4.5) で，ラグランジュ変数 π を介入 して(1. 1) に条件 (2.3) を組み込んだものが (4.1) である. そして，いずれについても目的関数に組み込まれずに残 された条件 r8(x) はト木である」は第 3 節で述べたよ うに元問題と比べて非常に扱いが容易であることがこれ らの算法の効率に寄与している.

5

.

その他の話題 巡路(巡回路)は各頂点の次数が 2 あるいは 1 と定めら れた木(ト木)であるから，次数が制限された最小コスト の木(ト木)を効率良く求めることができれば前節の算法 を加速できる見込みがある.

Glover-Klingman[

12J は つぎの 2 つの事実を示している. Y(m)={TIT は木， ddT)=m} とし， T を Y(m) の中の最小コストの木とする. (i) I(i,j)

eò

,

- T

Cpq

_一

cu=min イ C(j 一 Ck!

I

(k

,

l)

e

C(T

, (i, j)) ト

I

-ﾒl とすると ， T'=TU (P， q) ー (s， t) は Y(m+ 1) の最 小コストの木である. (ii) l(k

,

l)eòdT)

Cpq 一cst=min

1

Cij-Ck!1(i

,

j

)

e

D(T

,

(k

, l)) ト

I

-ﾒl とすると ， T'=Tu (P， q) ー (s， t) はもグ (mー 1) の最 小コストの木である.

(

i

)

(ii) を用いれば，次数に制限のない最小コストの 木から出発して，指定された次数をもっ最小コストの木 を作り出すことができる . Y(m) の最小コストの木を求 める問題はグラフの校集合上に定義された 2 つのマトロ イド(グラフ的マトロイドと分割マトロイド)の最小コ ストの共通基底を求める問題に定式化でき，その問題の ための算法もいくつか提案されている [13 ，

19

,

2

2

]

.

Murty[26

,

27]は巡回路と割当問題の基底解の関係に 注目し， n 互 31(j=1 (j

=1

,

2

,"',

n)

π

I

;

Xi.i=1 (i=I

,

2

, …,

n) j= n n E 五 Ctj 3lij=ß の作る制約行列で，変数:V1h.1:22

,… ,

Xnn

,

Xiljh 3Ji2jZ

,…,

XtnJ

_n

に対応する列が実行可能基底を作るとき，

(i

"j

Il,

(i

2

,

j2)

, "',

(in， jη) はそのコストが P 以下の巡回路である ことを示している.彼は，あらかじめ指定された列(こ こでは変数 X

u

， Xzz，… ， X

nn

に対応する列)を含む実行可 能基底を求める問題を基本問題と名付け，最小被覆問題 (第 5 回報告参照)を繰り返し解いてゆく，本質的には列 挙法的な算法を提案しているが，計算結果は報告されて いない.巡回路に対応する 0， 1 ベクトル 31

=

(3112

,

3113

,

…，品川ー 1) の集合を X

H

， その凸包を coXH と書くこ とにし， 一対の巡回路 Hl' H2 に対応するベクトルが coXH上で隣接しているとき ， H1 と H. が隣接している ということにする.

(

_JH は巡回路.Hキ H" Hキ H2•) ~..=i

HI

__ト 日 I HlnH.çH~HIUH.. とし ， He 身グ12 に対して，

H=(H

1nH.)

U

(H

1U H

2

-H)

が巡回路であるとき ， H と H の組を補巡回路対とよぶ.

Rao[3 1]は I 12I 豆 1 なら H1 と H2は隣接しており， H1 と H2が隣接しているなら æ'12 は補巡回路対を含ま ない(だからといって 1 æ'121 孟 l とは限らなし、)ことを 示しているが，いずれの条件も必要十分ではない.実は 一対の巡回路が隣接しているかどうかを判定する問題は NP 一完全(第 6 回報告参照)であることが示されている

[

2

9

J

.

ところが H1から始まり H2で終わる互いに隣 接した巡回路の列の中で最短のものの長さをd(H

_h

H2) とし ， COXH の直径を，

P(COXH)

=maxd(Hし Hj) と定義する p(COXH) 話 2 とであることが示されている

[

2

8

]

.

6

.

おわりに 本稿では数多い発見的算法についてはほとんど取り上 げることができなかったが，これまでに述べた算法を用 いて最適解を求める場合にも，発見的算法によって初め に良い実行可能解を知っていることは限定操作のうえで 非常に重要であることを付け加えておく.興味のある読 者は総合報告[4 J ，文献表[14， 20J を参照していただき たい.最後に原稿に対し貴重な御助言をくださった整数 計画法研究部会の方々に感謝いたします. 参芳文献

[

1

J Agmon

,

S.

, “

The R

elaxation Method f

o

r

Linear

Inequalitiesヘ Canadian

J

.

Math. 6

(1

9

5

4

)

3

8

2

-

3

9

6

.

[

2

J Bazaraa

,

M. S.

,

Goode

,

J

.

J.

,

'‘

The T

ravelｭ

ing Salesman: A Duality

Approach ヘ Math.

P

r

o

g

.

1

3

(1

9

7

7

)

2

2

1

-

2

3

7

.

[3 J Bellmore

,

M.

,

Malone

,

J

.

C.

, “

Pathology

o

f

Traveling Salesman Subtour-Elimination

Algorithms ヘ o

p

e

r

a

t

i

o

n

s

Research 1

9

(1

9

7

1)

2

7

8

-

3

0

7

.

[4 J Bellmore

,

M. Nemhauser

,

G. L.

, “

The Traｭ

v

e

l

i

n

g

Salesman Problem: A

Surveyヘ Ope­

r

a

t

i

o

n

s

Research 1

6

(

1

9

6

8

)

5

3

8

-

5

5

8

.

[

5

J Christofides

,

N.

,“

The S

h

o

r

t

e

s

t

Hamiltonian

Chain o

f

a

Graphヘ SIAM

J

.

Appl. Math. 1

9

(1

9

7

0

)

6

8

9

-

6

9

6

.

[6J

一一一 Graph

Theory: An Algorithmic Appｭ

roach

,

(Academic Press

,

New York

,

1

9

7

5

)

.

[7 J Cheriton

,

D.

,

Tarjan

,

R .E.

, “

Finding Minｭ

imum Spanning

Treesヘ SJAM

J

.

C01叫p.

5

(

1

9

7

6

)

7

2

4

-

7

4

2

.

[8 J

Di

jkstra

,

E

.

W.

, “

A Note on Two Problems

i

n

Connexion with

Graphsヘ N

u

m

e

r

i

s

c

h

e

M

a-1979 年 5 月号

t

h

e

m

a

t

i

k

1 (

1

9

5

9

)

2

6

9

-

2

7

1

.

[9 J Edmonds

,

J.

,

Johnson

,

E.

, “

Matching: A

Well-Solved Class o

f

Integer Linear Proｭ

grams" i

n

Combinatorial S

t

r

u

c

t

u

r

e

s

and

Their Applications (Gordon and Breach

,

New

York

,

1

9

7

0

)

.

[

I

O

J

Garfinkel

,

R. S.

, “

On P

a

r

t

i

t

i

o

n

i

n

g

t

h

e

Feaｭ

s

i

b

l

e

Set i

n

Branch-and-Bound Algorithm

f

o

r

t

h

e

Asymmetric Traveling-Salesman Proｭ

blemヘ Operations

Research 2

1

(1

9

7

3

)

3

4

0

-

3

4

3

.

[

I

I

J

Geoffrion

,

A. M.

, “

Lagrangean R

elaxation

f

o

r

Integer Programming"

,

Math. P

r

o

g

.

Study

2

(1

9

7

4

)

8

2

-

1

1

4

.

[

1

2

J

Glover

,

F.

,

Klingman

,

D.

, “

Finding Miniｭ

mum Spanning Trees with a Fixed Number

o

f

Links a

t

a Node" i

n

Combinatorial Progｭ

ramming: Methods and Applications (

D

.

Rei

del

,

Holland

,

1

9

7

5

)

.

[

1

3

J

Greene

,

C.

,

Magnanti

,

T.

, “

Some A

bstract

Pivot Algorithm"

,

SJAM J

.

Apρ1.

Math. 2

9

(1

9

7

5

)

5

3

0

-

5

3

9

.

[

1

4

J

Golden

,

D. L

.

Magnanti

,

T. L.

, “

Determin-i

s

t

i

c

Network Optimization: A Bibliography"

,

Networks 7 (

1

9

7

7

)

1

4

9

-

1

8

3

.

[

1

5

J

Hansen

,

K. H.

,

Krarup

,

J.

, “

Improvements

。f

the Held-Karp Algorithm f

o

r

t

h

e

Symmeｭ

t

r

i

c

Traveling-Salesman

Problemぺ Math.

P

r

o

g

.

7 (

1

9

7

4

)

8

7

-

9

6

.

[

1

6

J

Held

,

M.

,

Karp

,

R

.

M.

, “

The T

raveling

Salesman Problem and Minimum Spanning

Trees ぺ Operations

Research 1

8

(

1

9

7

0

)

1

1

3

8

1

1

6

2

.

[

17

]

一一“ The

Traveling Salesman Problem and

Minimum Spanning Trees Part

IIヘ Math.

P

r

o

g

.

1

(1

9

7

1)

6

-

2

5

.

[

1

8

J

Held

,

M.

,

Wolfe

,

P.

,

Crowder

,

H. P.

,“

Val-i

d

a

t

i

o

n

o

f

Subgradient

Optimizationヘ Math.

P

r

o

g

.

6

(1

9

7

4

)

6

2

-

8

8

.

[

1

9

J

Ir

i

,

M.

,

Tomizawa

,

N.

, “

An Algorithm f

o

r

Finding an Optimal

‘

Independen

t'

Assignｭ

mentヘ J.

Operations Rescarch S

o

c

i

e

t

y

of

Jaρ­

an 1

9

(

1

9

7

6

)

3

2

-

5

7

.

[

2

0

J

Kastning

,

C

.

(ed.)

,

I

n

t

e

g

e

r

Programming

and Related Areas:A C

l

a

s

s

j

f

i

e

d

Bibliography

,

Lecture Notes i

n

Economics and Mathemaｭ

t

i

c

a

l

Systems 1

2

8

(Springer

,

1

9

7

6

)

.

2

8

9

[

2

1

J

Kruskal

,

J

.

B.,“

On t

h

e

S

h

o

r

t

e

s

t

Subtree o

f

a

Graph and t

h

e

Traveling Salesman Prob

lem"

,

Proceed仇gs

of t

h

e

American Mathemaｭ

t

i

c

a

l

S

o

c

i

e

t

y

2

(1

9

5

6

)

4

8

-

5

0

.

[

2

2

J

Lawler

,

E.

L., ,‘

Matroid I

n

t

e

r

s

e

c

t

i

o

n

Algoｭ

rithmヘ Math.

P

r

o

g

.

9

(1

9

7

5

)

3

1

-

5

6

.

[

2

3

J

Miliotis

,

P.

, “

Integer Programming Apｭ

proaches t

o

t

h

e

Traveling Salesman

Problemぺ

Math. P

r

o

g

.

1

0

(

1

9

7

6

)

3

6

7

-

3

7

8

.

[

2

4

J

一一一

“

Using C

utting Planes t

o

Solve t

h

e

Symmetric Traveling Salesman

Problemぺ

Math. P

r

o

g

.

1

5

(

1

9

7

8

)

1

7

7

-

1

8

8

.

[

2

5

J

Motzkin

,

T. S.

,

Schoenberg

,

1

.

J.

, “

The

Relaxation Method f

o

r

Linear

Inequalitiesヘ

Canadian J

.

Math. 6 (

1

9

5

4

)

3

9

3

-

4

0

4

.

[

2

6

J

Murty

,

K

.

G.

, “

On t

h

e

Tours o

f

a Travelｭ

ing

Salesmanぺ SIAM

J

.

C

o

n

t

r

o

l

7 (

1

9

6

9

)

1

2

2

-

1

3

1

.

[27J ー←ー“ A

Fundamental Problem i

n

Linear

I

n

e

q

u

a

l

i

t

i

e

s

with A

p

p

l

i

c

a

t

i

o

n

s

t

o

t

h

e

Travelｭ

ing Salesman

Problemヘ Math.

P

r

o

g

.

2

(1

9

7

2

)

数理パズルを楽しもう (19)

に o から 4 までの 5 種類の色を塗ります.する と，どの 2 色を交互にたどっても， 6 個の頂点、を 1 度 ずつ通って元にもどりま す.正八角形の 8 辺と 20 本の対角線についても 0 から 6 までの 7 種類の 色を使って，どの 2 色も 8 個の頂点を 1 度ずつ通 2 るように塗り分けてくだ さい. 。 5 4 3 (4 月号 (231 ベージ)の解答〕 三角形の 1 辺 BC に平 行に，点Mから線分MN ，点 G から線分 GH をそれぞれ 閃のように引く.すると， AB は AMの 4 倍であるから，

MN=B

C/4

となる.また， CN は CG の 3 倍であるから，

GH=MN/3 = B

C/12

となる.ところで，ム FBC とム FGH は相似形であ り，点、 F から対辺までの高さの比は 12: 1 である.一方，

2

9

0

2

9

6

-

3

0

8

.

[

2

8

J

Padberg

,

M. W.

,

Rao

,

M. R.

,“

The T

ravelｭ

ing Salesman Problem and a C

l

a

s

s

o

f

Polyｭ

hedra o

f

Diameter

Twoぺ Math.

Prog.7

(1

9

7

4

)

3

2

-

4

5

.

[

2

9

J

Papadimitriou

,

C

.

H.

, “

The Adjacency Reｭ

l

a

t

i

o

n

on t

h

e

Traveling Salesman Polytope i

s

NP-Completeヘ Math.

P

r

o

g

.

1

4

(

1

9

7

8

)

3

1

2

-

3

2

4

.

[

3

0

J

Prim

,

R

.

C.

, “

Shortest C

onnection Matrix

Network and Some

Generalizationぺ Bell

Sysｭ

tem T

e

c

h

.

J

.

3

6

(1

9

5

7)

1

3

8

9

-

1

4

0

1

.

[

3

1

J

Rao

,

M. R.

, “

Adjacency o

f

t

h

e

Traveling

Salesman Tours and 0

-

1

Verticesぺ SIAM

J

.

Appl. Math. 3

0

(1

9

7

6

)

1

9

1

-

1

9

8

.

[

3

2

J

Smith

,

T.

H.,

Thompson

,

G. L.

, “

A L

i

f

o

I

m

p

l

i

c

i

t

Enumeration Search Algorithm f

o

r

t

h

e

Symmetric Traveling Salesman Problem

Using Held and Karp's I-Tree Relaxation"

,

Annals of D

i

s

c

r

e

t

e

Mathematics 1

(1

9

7

7

)

4

7

9

-

4

9

3

.

(やまもと・よしつぐ 慶応義塾大学) A C B 点、 A から辺 BC までの高さは，点 G から辺 BC までの高 きの 4 倍であるから，点、 F から辺 BC までの高さの

4x 13/12=13/3

(倍) となる.よって，ム FBC の面積はム ABC の面積の 3/13倍となる.まったく同理由で，ム DCA とム EAB の面積もそれぞれム ABC の面積の 3/13倍となるから， これらの 3 つの三角形の面積の和は9/13倍である.よっ て，残りの部分として与えられる 6DEF の面積は， 6ABC の面積の 4/13倍となる.なお，この方法は一般 の n 等分についても適用できる(1

J

.

(

1) Graham

,

L

.

A.

,

I

n

g

e

n

i

o

u

s

Mathematical

Proble押zs

and Methods

,

Dover Pub.

,

New