卒業論文
マルコフチェーンを用いたラグビー戦略最適化
早稲田大学
基幹理工学部応用数理学科
学籍番号 1W110238-2
重森 圭太
1 はじめに
この研究では、世界の強豪チームであるNZ(ニュージーランド)とSA(南アフリカ)の試合から戦術選 択確率やボールの保持率といった必要なデータを取り、そのデータを22状態のマルコフチェーンを用いた理 論に当てはめ、ラグビーの戦略がトライ確率にどう影響するかを明らかにしていく。現代の世界基準のラグ ビーの戦略では、キックを使い陣地を取るのが主流となっている。特に、自陣22mより手前では、ボール を保持している場合キックを蹴ることがセオリーとなっている(文献[4]参照)。過去の類似の研究として、文 献[1]では、架空のラグビーチームを使い自分で確率を設定して、少ない状態でトライ確率を求めラグビーの 戦術の評価をしている。文献[6]では、サッカーの試合を吸収マルコフ連鎖によってモデル化し、実際の試合 のデータをもとにサッカーのフォーメーションを評価している。また、状態をボール保持と得点という2つの パターンで表している。上記の論文の欠点として、文献[1]では、架空のチームを自分で設定し少ない状態を 使っているので現実と乖離している恐れがある。文献[6]では、状態数が少ないことが挙げられる。それに対 して、本研究ではグランドを22状態という細かな状態に分けて、実際の試合で収集したデータをもとに導き だした確率を使用しラグビーの戦術面での評価をし戦略最適化を目指す。
2 マルコフチェーンを用いた戦略分析方法
2.1 分析方法
ラグビーグランドを進行方向ごとにそれぞれ11等分する(図1参照)。これは、トライゾーンを除いたグラ ンドの10等分がラグビーの戦術決定においておおよそ指標となる分け方だからである。ボールの位置をマル コフチェーンの状態として考える。NZがボールを保持している状態と、SAがボールを保持している状態の マルコフチェーンを考え戦略を分析していく。
マルコフチェーンとは、未来の状態は現在の状態にのみ依存するという理論の確率手法である(文献[5]参照)。 この理論を用いた文献[1]では、架空のチームを少ない状態で分析した。利点として、全ての確率を自分で設 定することが出来るので、多種多様なチームを比較することが出来る。しかし、欠点として自分で確率を設定 し、少ない状態を用いているので現実のラグビーとは乖離している可能性がある。本研究では、その欠点を解 消するために、実際の試合からの確率を用い22状態という多くの状態を用いて分析していく。
Xt:時刻tのボールの位置(状態)とする(離散)。
Xt=
0 SAのトライ状態 ...
21 N Zのトライ状態
(1)
図1 11等分したラグビーグランド(文献[1]より引用)
次に、考える戦術について述べる。戦術はボールを保持しているチームが選択することができる。戦術は Attack,High Punt,No Touch Kich(Kick Passを含む),Long Kick(Touch Kick)の4つとする。この4つの 戦術はラグビーの一般的な戦略であり、戦略の解説は表1を参照する。
表1 ラグビー戦術解説
戦術 解説
Attack パスやランを使ってデフェンスを突破する戦略
High Punt ボールを高く蹴り上げ、相手と競り合うことによりボールを前に運ぶ戦略
No Touch Kick ボールを外に直接出せない状況(自陣22mより前)でのキックにより陣地を回復する戦略
Long Kick 自陣22mより後ろの状態で直接キックによってボールを外に出し陣地を回復する戦術
4つの戦術がそれぞれ、全ての戦術のうちどれだけ選択されるかを表したものを戦術選択確率とする。ま た、Xt= dにおける両チームの戦術選択確率の変数を表2のように定める。なので、
λAd+ λHd+ λN d+ λLd= 1 (2)
µAd+ µHd+ µN d+ µLd= 1 (3)
である。
さらに、4つの戦術において、それぞれ戦術を選択したチームが、ボールをどれだけ保持できるかのボール保 持率を考える。また、Xt= dにおける両チームのボール保持率の変数、各戦術の進める地域数を表2のよう に定める。
表2 NZ,SAの戦術選択確率とボール保持率のXt= dにおける変数
戦術 進める地域 NZの戦術選択確率 SAの戦術選択確率 NZボール保持率 SAボール保持率
Attack 1 λAd µAd pAd kAd
High Punt 1 λHd µHd pHd kHd
No Touch Kick 2 λN d µN d pN d kN d
Long Kick 3 λLd µLd pLd kLd
4つの戦術の中でも、AttackはKickの3戦術とは違い、デフェンスを突破し前進する、デフェンスを突破 できず留まる、相手のデフェンスに押し戻される3パターンが考えられる。その3パターンをGain(状態が 1つ前に進む)、Stay(同じ状態に留まる)、Back(1つ後ろの状態に戻される)とする。Attackの戦術を選 択したとき、Gain,Stay,Backになるそれぞれ3つの確率を考える。
Gain,Stay,Backした時に、それぞれどれだけボールを保持できたかをGain,Stay,Backのボール保持率とす
る。表3,4では、Xt= dでの両チームのGain,Stay,Backの確率とボール保持率の変数を定める。
nGd+ nSd+ nBd= 1 (4)
sGd+ sSd+ sBd= 1 (5)
である(表3,4参照)。
表3 NZのGain,Stay,Backの確率とボール保持率 のXt= dにおける変数
NZ 確率 ボール保持率 Gain nGd hGd
Stay nSd hSd
Back nBd hBd
表4 SAのGain,Stay,Backの確率とボール保持率 のXt= dにおける変数
SA 確率 ボール保持率 Gain sGd qGd
Stay sSd qSd
Back sBd qBd
表2で定めた各戦術の進める地域数、戦術選択確率、ボール保持率、表3,4で定めた確率とボール保持率を 用いて起こりうる全遷移を考える。Xt= d(NZボール)への全遷移は図2となる。
図2 Xt= dへの遷移
図2の矢印で表した、各状態からXt= dへ遷移する条件を表5で説明する。
表5 状態dへ遷移する条件
状態dへの遷移 条件
d-6→d NZがLong Kickを選択しボールを保持
d-4→d NZがNo Touch Kickを選択しボールを保持
d-3→d SAがAttackを選択し、Backになりボールを不保持
d-2→d NZがAttackを選択し、Gainになりボールを保持orNZがHigh Puntを選択しボール保持
d-1→d SAがAttackを選択し、Stayになりボールを不保持
d→d NZがAttackを選択し、Stayになりボールを保持
d+1→d SAがAttackを選択し、Gainになりボールを不保持orSAがHigh Puntを選択しボール不保持
d+2→d NZがAttackを選択し、Backになりボールを保持
d+3→d SAがNo Touch Kickを選択しボールを不保持
d+5→d SAがLong Kickを選択しボールを不保持
図2の遷移確率を表2,3,4のXt= dにおける変数を用いて、式に表すと式(6)の通りになる。 Pd,d−6 = λLd−6pLd−6
Pd,d−4 = λN d−4pN d−4
Pd,d−3 = µAd−3sBd−3(1 − qBd−3)
Pd,d−2 = λHd−2pHd−2+ λAd−2nGd−2hGd−2
Pd,d−1 = µAd−1sSd−1(1 − qSd−1) Pd,d= λAdnSdhSd
Pd,d+1= µHd+1(1 − kHd+1) + µAd+1sGd+1(1 − qGd+1) Pd,d+2= λAd+2nBd+2hBd+2
Pd,d+3= µN d+3(1 − kN d+3) Pd,d+5= µLd+5(1 − kLd+5)
(6)
これらの確率、式を次の章で用いて推移確率行列を求めていく。
2.2 データ収集方法
この節ではデータの収集方法について述べる。2014年Rugby ChampionshipのNZ対SAの2試合の全プ レーの戦術を、Attack,High Punt,No Touch Kick,Long Kickの4つの戦術に分類した。4つの戦術それぞれ が、全戦術からどれほど選択されたかを表す戦術選択確率と、4つの戦術を選択した時ボールをどれだけ保持 できたかを表すボール保持率を収集する。その結果を表6にまとめる。
表6 NZ,SAの戦術選択確率とボール保持率の実際の数値
戦術 進める地域 NZの戦術選択確率 SAの戦術選択確率 NZボール保持率 SAボール保持率
Attack 1 18/23 68/89 64/81 54/89
High Punt 1 8/207 6/89 1/8 0
No Touch Kick 2 3/23 23/178 7/27 3/23
Long Kick 3 10/207 7/178 0 0
表6が示すように両チームのLong Kickのボール保持率は0であることがわかる。
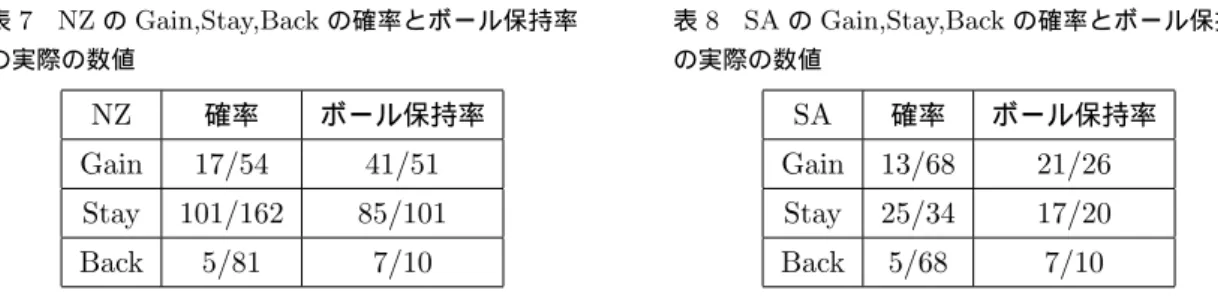
次に、ボールを保持しているチームがAttackの戦術を選択した時、Gain(状態が1つ前に進む)、Stay(同じ 状態に留まる)、Back(1つ後ろの状態に戻される)になる確率と、Gain,Stay,Backになった時どれだけボー ルを保持できたかのボール保持率を試合から収集する。その結果を表7,8にまとめる。
表7 NZのGain,Stay,Backの確率とボール保持率 の実際の数値
NZ 確率 ボール保持率 Gain 17/54 41/51 Stay 101/162 85/101
Back 5/81 7/10
表8 SAのGain,Stay,Backの確率とボール保持率 の実際の数値
SA 確率 ボール保持率 Gain 13/68 21/26 Stay 25/34 17/20 Back 5/68 7/10
表7,8が示すように、NZとSAのGainの確率に少し差がある以外は似た数値になっていることがわかる。
2.3 マルコフチェーンを用いたトライ確率の計算
トライの状態0,21以外の遷移を表した推移確率行列Qと、全状態からトライ状態0,21への遷移を表した 推移確率行列Tを求めていく。
X(t)は時刻tでのマルコフチェーンの状態である。 状態iにいる確率は、
Pi(t) = P [X(t) = i] (7)
時刻tにおける状態をベクトルで表すと
πt=( P1(t) . . . P20(t) ) (8)
この時、トライの状態からは移動しないので、トライの状態である0,21を除く状態iから状態jへ移る確 率を
Pij= P [X(t) = j|X(t − 1) = i] (9)
と書ける。そして、20行20列の推移確率行列Qは以下のようになる。
Q =
P1,1 . . . P1,20
... . .. ... P20,1 . . . P20,20
(10)
全ての状態からのトライの状態への20行2列の推移確率行列Tは、
T =
P1,0 P1,21
... ... P20,0 P20,21
(11)
時刻tのトライとなる確率をZとすると、
Z = πtT = π0QtT (12)
よってNZとSAの確率は以下の式によって求められる(文献[1]より引用)。(I-Q)が逆行列を持つとき、
Z =
∞
∑
t=0
πtQT =
∞
∑
t=0
π0QtT = π0(
∞
∑
n=0
Qt)T = π0(I − Q)−1T (13)
Iは単位行列である。
3 結果
3.1 Attack のみでのトライ確率
では、実際にNZとSAのトライ確率を求めていく。Attackのみのトライ確率を求めることでKickがラ グビーの戦術においてどれほど重要か認識できる。なので、ここではKickを考慮したモデルの前に、戦術が Attackのみの場合のNZとSAのトライ確率を計算していく。
実際の試合から求めた確率(表7,表8参照)と式(6)を用いて、20行20列の推移確率行列Qの各成分を求 める。今回はAttackのみなので、式(6)に、λAd = 1,µAd= 1,Gain,Stay,Backの確率とボール保持率は表 3,4の実際の数値を代入する。Kickは考慮しないのでその他の確率は0である。ルールにより自分で自陣の トライゾーンの持ち込んだ場合は、トライゾーンの1つ前の状態の相手ボールとなる。つまり、状態1から状 態2、状態20から状態19へ遷移する。
求めた各成分を表にしたものが表9である(有効数字3桁)。
表9 行列Qの各成分
0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0.0368 0.625 0.11 0.0515 0.0221 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0.0432 0.0988 0.525 0.0617 0.253 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0.154 0.0368 0.625 0.11 0.0515 0.0221 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0.0185 0.0432 0.0988 0.525 0.0617 0.253 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0.154 0.0368 0.625 0.11 0.0515 0.0221 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0.0185 0.0432 0.0988 0.525 0.0617 0.253 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0.154 0.0368 0.625 0.11 0.0515 0.0221 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0.0185 0.0432 0.0988 0.525 0.0617 0.253 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0.154 0.0368 0.625 0.11 0.0515 0.0221 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0.0185 0.0432 0.0988 0.525 0.0617 0.253 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0.154 0.0368 0.625 0.11 0.0515 0.0221 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0.0185 0.0432 0.0988 0.525 0.0617 0.253 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0.154 0.0368 0.625 0.11 0.0515 0.0221 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0.0185 0.0432 0.0988 0.525 0.0617 0.253 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0.154 0.0368 0.625 0.11 0.0515 0.0221 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0.0185 0.0432 0.0988 0.525 0.0617 0.253 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.154 0.0368 0.625 0.11 0.0515
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0185 0.0432 0.0988 0.525 0.0617
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0
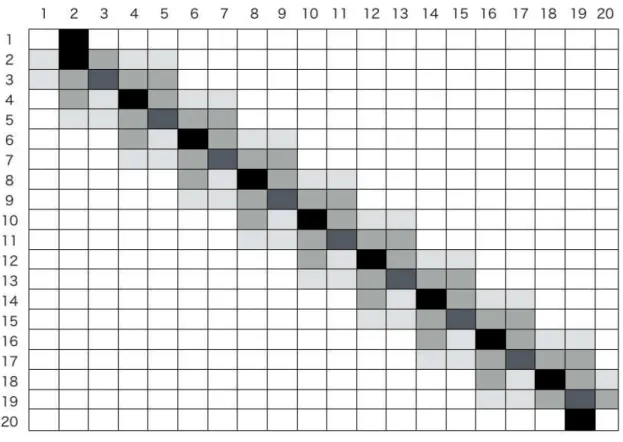
この行列Qの数値の大小を濃淡に対応させることによって表すと図3となる。図3から、行列の対角線上の 数値が大きくなっているこる。つまり、Attackのみでは他の状態に遷移しにくいことがわかる。
図3 行列Qの数値を濃淡で表した図
次に、20行2列の推移確率行列Tを求める。Attackのみを考えるのでトライの状態に移ることができる状 態は、NZのトライの状態をdとすると、d-2,d-3の2つの状態のみである(図2参照)。(SAの場合d+2,d+3 となる。)行列Qと同じ数値を式(6)に代入すると行列Tは式(14)となる。
T =
0 0
21/136 0 1/54 0
0 0
0 0
0 0
0 0
0 0
0 0
0 0
0 0
0 0
0 0
0 0
0 0
0 0
0 0
0 3/136 0 41/162
0 0
(14)
Kick Offはコイントスによって決まるので確率は1/2ずつである。よってπ0は、
π0=( 0 0 . . . 1/2 1/2 . . . 0 0 ) (15)
このQ,T,π0用いて下記の式に代入しNZ,SAのAttackのみでの確率を求めると、SAのトライ確率ZSA,NZ のトライ確率ZN Zは、
Z =
∞
∑
n=0
πnQT =
∞
∑
n=0
π0QnT = π0(
∞
∑
n=0
Qn)T = π0(I − Q)−1T (16)
= (ZSA, ZN Z) (17)
= (0.1763798983, 0.82362010169) (18)
Attackのみでのトライ確率は、NZが約82%、SAが約18%という結果になった。この結果の要因として2 つ考えられる。1つ目の要因は、NZのAttackにおけるGainの確率高さがこの結果になったと考えること ができる。2つ目は、20状態という多くの状態を用いたことにより僅かな差が徐々に広がったのではないか と考えることができる。実際に、4状態での確率を比較した場合では、計算過程は同じなので省略するが、NZ のトライ確率ZN Zは約59%、SAのトライ確率ZSAは約41%という結果になった。
しかしながら、実際に私がデータを収集した試合の結果は1勝1敗のイーブンであり、どちらも5点差以内で
3.2 Kick を考慮したモデル
前節の結果によりKickが実際の試合においてトライに大きな影響を与えていることがわかった。したがっ て、この節ではKickを考慮したモデルによりKickの選択確率がトライにどのような影響を及ぼすのかを考 えていく。特に、自陣22m内でのKickについて検証していく。まず、NZの自陣22m内のみでKickを選 択できる状態とすることにより、自陣22m内ではKickを選択するというセオリーが正しいのかを検証する。 NZとSAのAttackのサイン選択確率λAd, µAdを以下のように定める。NZの自陣22m内の状態は3,5であ る(図1参照)。状態3,5のAttackの選択確率λAdをxとおき、その他の状態のAttackの選択確率λAd, µAd は1とする。表10,11にまとめる。
表10 NZの各状態のAttack選択確率λAd
NZ Attack選択確率λAd
λA3 x
λA5 x
λA7 1
λA9 1
... ...
λA19 1
表11 SAの各状態のAttack選択確率µAd SA Attack選択確率µAd
µA2 1
µA4 1
µA6 1
µA8 1
... ...
µA18 1
ここで、Kickの選択確率λLd+ Attackの選択確率λAd= 1である。Attackの選択確率λAdの変数xは、 0 ≤ x ≤ 1とする。
KickはLong Kickを選択し、Kickのボール保持率は0とする。
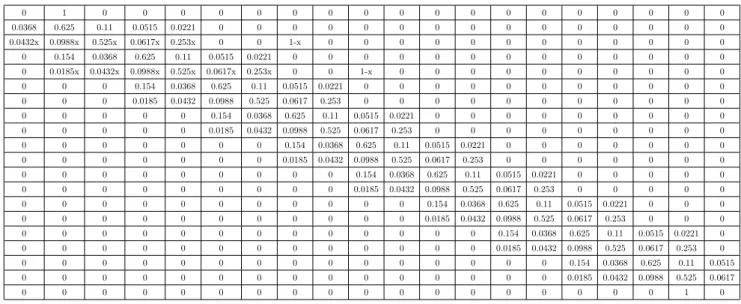
実際の試合から求めた確率(表7,表8参照)と式(6)を用いて、20行20列の推移確率行列Qの各成分を求 める。状態3,5以外は、前節のAttackのみの各成分と同じである。状態3,5は、式(6)にλAd = x, λLd = 1 − x,Gain,Stay,Backの確率とボール保持率は表7,8の実際の数値を代入する。求めた行列Qの各成分を表 にしたものが表12である(有効数字3桁)。
表12 行列Qの各成分
0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0.0368 0.625 0.11 0.0515 0.0221 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0.0432x 0.0988x 0.525x 0.0617x 0.253x 0 0 1-x 0 0 0 0 0 0 0 0 0 0 0 0
0 0.154 0.0368 0.625 0.11 0.0515 0.0221 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0.0185x 0.0432x 0.0988x 0.525x 0.0617x 0.253x 0 0 1-x 0 0 0 0 0 0 0 0 0 0
0 0 0 0.154 0.0368 0.625 0.11 0.0515 0.0221 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0.0185 0.0432 0.0988 0.525 0.0617 0.253 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0.154 0.0368 0.625 0.11 0.0515 0.0221 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0.0185 0.0432 0.0988 0.525 0.0617 0.253 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0.154 0.0368 0.625 0.11 0.0515 0.0221 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0.0185 0.0432 0.0988 0.525 0.0617 0.253 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0.154 0.0368 0.625 0.11 0.0515 0.0221 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0.0185 0.0432 0.0988 0.525 0.0617 0.253 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0.154 0.0368 0.625 0.11 0.0515 0.0221 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0.0185 0.0432 0.0988 0.525 0.0617 0.253 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0.154 0.0368 0.625 0.11 0.0515 0.0221 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0.0185 0.0432 0.0988 0.525 0.0617 0.253 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.154 0.0368 0.625 0.11 0.0515
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0185 0.0432 0.0988 0.525 0.0617
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0
次に、20行2列の推移確率行列Tを求める。トライの状態へ移ることのできる状態は、Long Kickのボール 保持率が0なので、Attackのみを考えればよい。したがって、前節の行列Tと同じ状態d-2,d-3を考えれば よい。(SAの場合d+2,d+3となる。)行列Qと同じ数値を式(6)に代入すると行列Tは式(19)となる。
T =
0 0
21/136 0 x/54 0
0 0
0 0
0 0
0 0
0 0
0 0
0 0
0 0
0 0
0 0
0 0
0 0
0 0
0 0
0 3/136 0 41/162
0 0
(19)
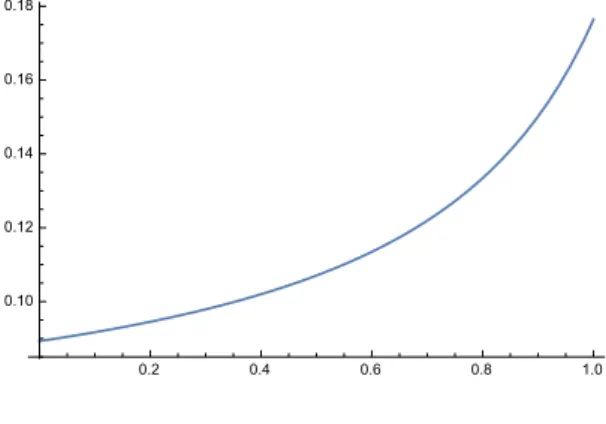
このQ,T,π0を式(13)に代入しMathematicaで計算する。結果を横軸をAttack選択確率x,縦軸トライ確 率Zととりグラフにすると図4,5となる。
図4 Attack選 択 確 率xとNZの ト ラ イ 確 率ZN Z
の相関関係
図5 Attack選 択 確 率xとSAの ト ラ イ 確 率ZSA
の相関関係
図4,5が示すように、NZの状態3,5のAttack選択確率xを増やすとNZのトライ確率ZN Zは減少し、SA のトライ確率ZSAは増加している。2つのグラフを重ね合わせたものが図6である。
図6 Attack選択確率xと両チームのトライ確率ZN Zの相関関係
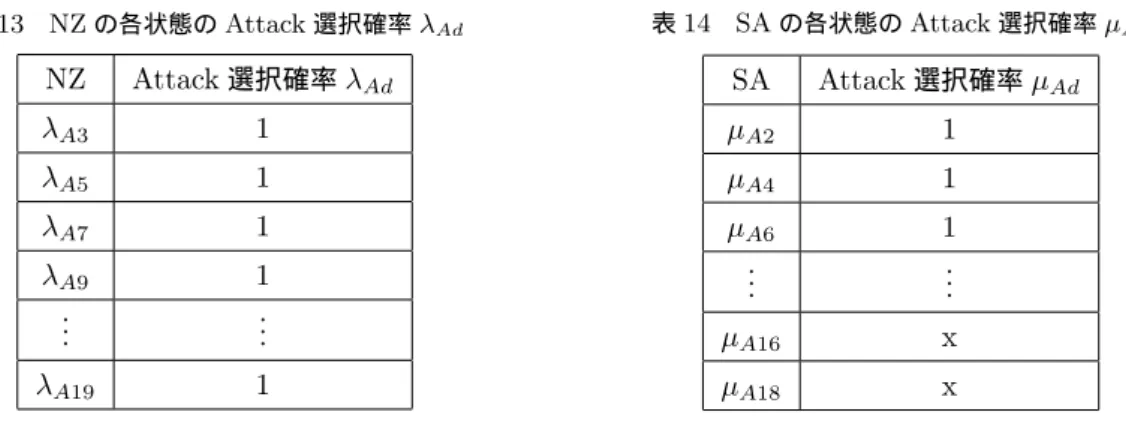
次に、先ほどと逆の状況である、SAのみ22m内でKickを使える状況で結果を出していく。 表13,表14は両チームの各状態でのAttackの選択確率λAd, µAdをまとめた表である。
表13 NZの各状態のAttack選択確率λAd NZ Attack選択確率λAd
λA3 1
λA5 1
λA7 1
λA9 1
... ...
λA19 1
表14 SAの各状態のAttack選択確率µAd
SA Attack選択確率µAd
µA2 1
µA4 1
µA6 1
... ...
µA16 x
µA18 x
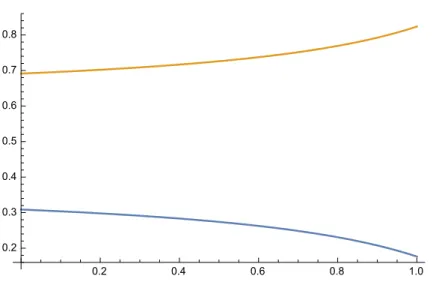
同じ計算過程によって導きだした結果を横軸をAttack選択確率x,縦軸トライ確率Zととりグラフにした ものが図7,8である。
図7 Attack選 択 確 率xとNZの ト ラ イ 確 率ZN Z
の相関関係
図8 Attack選 択 確 率xとSAの ト ラ イ 確 率ZSA
の相関関係
図7,8が示すように、SAの状態16,18のAttack選択確率xを増やすとNZのトライ確率ZN Zは増加し、 SAのトライ確率ZSAは減少している。図7,8の2つのグラフを重ね合わせたものが図9である。
図9 Attack選択確率xと両チームのトライ確率Zの相関関係
図9では、SAのみ22m内でKickを使える状況にしたので、図6とは反対にAttack選択確率xを増やす とNZのトライ確率ZN Zは増加し、SAのトライ確率ZSAは減少している。
4 結論
図6が示すように、NZのトライ確率ZN Zは状態3,5のAttackの選択確率xを1に近づけるほど減少し、 SAのトライ確率ZSAは増加していることがわかる。そして、図9が示すようにNZのトライ確率ZN Zは状 態16,18のAttackの選択確率xを1に近づけるほど増加し、SAのトライ確率ZSAは減少していることがわ かる。つまり、自陣22m内では全てKickを選択することが最もラグビーの戦略においてトライの確率を増や し、相手のトライの確率を減らすことのできる戦略なのである。この結果は、ラグビーのセオリーである22m 内では戦術はキックを選択することが正しいということがわかる。22m内で全てAttackを選択するより全 てKickを選択する方が自チームのトライ確率を約10%高めることができ、相手チームのトライ確率を約10
%下げることがわかる。今回の論文では、自陣22m内の戦略に焦点を絞って研究したが、それ以外の地域で の戦略についても研究する価値があると考えられる。また、データの数を更に増やし、状態ごとの確率などを 求めるとさらに正確な結果を導くことが可能である。
5 謝辞
本論文を書くにあたり、丁寧に指導して頂いた豊泉洋教授と基礎となる理論を作って頂いた片山大輔氏に感 謝致します。また、普段から自分のことを手助けして頂いた豊泉研究室の先輩方、同期の皆様にも感謝致し ます。
参考文献
[1] 片山大輔,ラグビーにおけるサイン選択の最適化,2014 [2] 穴太克則,マルコフ連鎖に基づく打者評価モデル,1988
[3] 廣津信義、吉井秀邦、青葉幸洋、吉村雅文,時間内で得点を競う球技の試合における確率計算の方法,2010 [4] http://rugbynomikata.info/entry10.html
[5] R.B.シナジ、訳.今野紀雄/林俊一、マルコフ連鎖から格子確率モデルへ 現代確率論の基礎と応用、2001 [6] 吸収マルコフ連鎖によるサッカーのフォーメーション評価、篠原裕佑、藤本衡、
![図 1 11等分したラグビーグランド ( 文献 [1] より引用 )](https://thumb-ap.123doks.com/thumbv2/123deta/5705168.18084/3.892.130.736.100.448/図111等分したラグビーグランド文献1より引用.webp)