スキルモデルに応じたゴルフプレー戦略の Q 学習による獲得
菅原 翔悟 ,
†川村 秀憲 ,
†鈴木 恵二
†スポーツとしてのゴルフにおいてスコアを向上させる手段として,スキルを向上させる方法に加え, どのクラブでどこに打つかといった戦略もまた重要なものである.本稿では,この戦略に注目し,同 じスキルレベルでも戦略の最適化によりスコアを向上させることを目的に,シミュレーションモデル の構築,Q 学習の適用により得られた結果の評価を行う.
Q-learning based on Skill Model for Acquiring Strategy of Golf
1. 序 論
ゴル フを 簡略 化し て考 える と,ボ ール をク ラブ で 打って,カップの中に入れ,最終的に打った回数が少 ない人が勝者となる競技である.打数(スコア)を減 少させるためには,飛距離を伸ばす,正確性を上げる, が重要と考えられ,使用するクラブ・ボールの改良や, 効率的なスイングの研究などが行われてきた.また近 年では,具体的にどのようなスキルがスコアに影響を 与えているか,というような研究も行われている.6)
PGA TOUR2)とは,アメリカ合衆国における男子
プロのゴルフツアーを運営する団体である.運営する 大会において,参加選手ごとのスコアや,何打目にコー ス上のどこにボールを打ったかなど,詳細なデータを 全て記録している.また,この膨大なデータを研究機 関に提供しており,そのデータをもとにした研究も行 われている.これらの研究6)7)8)10)では,フェアウェ イキープ率・サンドセーブ率などの具体的な数値を選 手ごとに比較して,それぞれの要素がどの程度勝利に 関係するかの調査や,飛距離と正確性ではどちらを優 先すべきかをシミュレーションで実験するなど,ゴル ファー個人のスキルに着目した研究が行われている.
一方,スコアの向上に重要な別の要素として,現在 のボール位置に対してどのクラブで次にどこを狙う かという,行動の選択を改善する方法がある.今現在 ボールのある地点で,スコアを減少させることのでき
† 北海道大学大学院 情報科学研究科
複合情報学専攻複雑系工学講座 調和系工学研究室
〒060-0818 札幌市北区北 14 条西 9 丁目
†† sugawara@complex.ist.hokudai.ac.jp
る行動が存在するとしたとき,その行動を発見するこ とができれば,スキルが変化せずともスコアを改善す ることができるという予測をたてる.
このとき,ある地点でどのような行動をとるかを決 定する指針を,戦略と呼ぶこととする.ある技術,あ る戦略からスコアの期待値(期待スコア)が求められ るとすると,スキルを変えず戦略だけを変化させた ときに,期待スコアが最小となる戦略を最適戦略と考 える.
本稿では戦略の最適化によるスコア向上を目指し, シミュレーションモデルの構築と戦略を求める方法と してQ学習を適用し,スキルに応じた戦略獲得を目 的とする.
2. モデリング
本章ではゴルフコース,ゴルファーのショットのシ ミュレーションモデルを説明し,1ホールの期待スコ アを最小化する最適化問題を考える.
2.1 コ ー ス
競 技 は 1 8 ホ ー ル( 1 ラ ウ ン ド )を 単 位 と し て プ レーをし,全域をコースと呼ぶ。プレーに影響を与え るであろうコースの環境には,地面の起伏や風・天気 などの天候,芝の長さ,木の高さや枝葉の密度などが 挙げられるが、今回それらは考慮しない.地面の起伏 や木の高さも考えないため,ボールやコースの状態は 高さのない2次元座標内で考える.
ゴルフコースを芝の長さなど地面の状態から,以下 のような区域に分類する。
( 1 ) ティー イ ン グ グ ラ ウ ン ド(Teeing ground) ティーの位置をティーインググラウンドの中の 1
ある1点にあらかじめ決めておく. ( 2 ) フェアウェイ(Fairway)
( 3 ) ラフ(Rough) ( 4 ) バンカー(Bunker)
( 5 ) ウォー タ ー ハ ザ ー ド・ラ テ ラ ル ウォー タ ー ハ ザード(WH) 池に入った場合は全てラテラル ウォーターハザードとみなす.簡単のため,最後 にボールが池を横切った地点にボールをドロッ プする.また,池に入った場合1打の罰が与え られる.
( 6 ) 林(Woods)
林は木の高さの情報は持たず,地面の状態は ラフとする.ボールが林の領域を通過すること により,林領域特有の確率によってボールの落 下地点が決まるものとする.
( 7 ) グリーン(Green)
図1 コースの状態例
これらの区域の状態をコースの状態と呼び,コース 状態の集合Stateを以下のように定義する。
State= {teeing ground, F airway, Rough, Bunker, W H, W oods, Green, Cup}(1)
2.2 ショ ット
ショットはパッティング,ティーショット,アプロー チショットやバンカーショットなどに分類できる.以下 では,パッティングとその他のショットに分けて説明 する.
2.2.1 パッティング
パッティングはグリーン上でのみ行われるものとす る.パッティングにおいて重要と考えられるグリーン 上の起伏や芝の状態などを考慮しないため,「Strokes Gained-Putting: Baseline probabilities chart」2)(以 下Putting Baselineと表記)を用いて,カップまで の残り距離に応じたパット数・またはパット数の期待 値を求める.パット数とは,カップにボールが入るま でにかかるパッティングショットの打数である.
2.2.2 その他のショット
ある地点から目標地点となる方向と距離を定めて
図2 フィートごとの1∼3パットで入る確率
図3 フィートごとの期待パット数
ボールを打ったとき,そのボールの落下地点は目標地 点そのものではなくゴルファーの技術や風など,様々 な要素からの影響を受けて変化する.それらの影響が 確率的に与えられ,ボールの落下地点がある確率分布 で表わされると仮定し,今回は正規分布とした. ( 1 ) クラブ集合 Club
Club= {Driver, 3-wood, 5-wood, 2-iron, 3-iron, 4-iron, 5-iron, 6-iron, 7-iron, 8-iron, 9-iron, P W, SW }
(2) ( 2 ) クラブごとの平均飛距離 r(club) 上記クラ ブごとに平均飛距離があらかじめ定まっている ものとする.ここで飛距離はボールの着地地点 までの距離であり,ボールの地面上での転がり を無視する.またショットの開始地点から着地 地点までのボールの軌道は直線的とする.
( 3 ) 水平打ち出し方向 θ 以後,水平打ち出し方
向を省略して方向とのみ表記することがある.
0 ≤ θ < 2π (3)
( 4 ) クラブごとの飛距離・方向の分散 σr2, σθ2 ( 5 ) ボールの位置 x
ボールは2次元座標上に存在するとする. 以上のことから,ボールの現在地をx=(x,y),使用 するクラブをclubとしたとき,飛距離r(club)と方
向θ がそれぞれ正規分布に従うとすると, r′∼ N (r(club), σ2r) (4)
θ′∼ N (θ, σθ2) (5)
よって,ボールを打った後の落下地点x’=(x’,y’)は, 以下のように表わされる.
( x′ y′
)
= (
x y
) +
( r′cosθ′ r′sinθ′
)
(6)
2.3 ス キ ル
スキルが高いほど目標地点の付近にボールが落下し やすく,スキルが低い場合は目標から大きく外れる可 能性が高いとし,上記でパッティング以外のショット は正規分布に従って落下位置が定まるとしたため,ス キルの高低を正規分布の分散の大小で表すことができ る.また,クラブごとの飛距離もスキルの要素の1つ とする.
よってスキルskillをクラブごとの平均飛距離と,飛 距離の分散,方向の分散の3つから定義し,ゴルファー ごとにあらかじめ定まっているとする.
skill= {r, σr2, σ2θ} (7)
2.4 シミュレーションモデル
現在のボール位置,ゴルファーのスキル,とってい る戦略を条件とし,それから定まる次のボール位置 がある確率密度関数で求められるとする.まず,ゴル ファーの行動a,ボールの置かれている地点s,そし て戦略stを定義する.
( 1 ) ゴルファーの行動a
使用するクラブc∈ Club,打ち出し方向θ か ら定義する.
a= {c, θ} (8)
行動集合をAとし,a∈ Aである.
( 2 ) ボールの置かれている地点s
状態集合をSとし,s∈ Sである. ( 3 ) 戦略st
戦略とはボールの位置状態があるsのときに, 行動集合Aからどのようなaを選ぶか,とい うことを表すルールである.つまり状態集合か ら行動集合への写像を表す.
st: S → A (9)
戦略は1ホール単位で考える.
xnをn打目を打ち終わった時点でのボールの位置 とし,x0は打ち始めの地点,x1は1打目を打った後の ボールの地点を示す.あるボールの位置がxn,戦略が st,技術がskillという条件のもとで、次のボールの位置 がxn+1となる条件付き確率はp(xn+1|xn, st, skill) となり,これを以下の確率密度関数で置き換える.
p(xn+1 | xn, st, skill)
= f (xn+1; xn, xn−1, st, skill) (10) 関数fは最終的なボールの落下地点の分布であり, 以下の3つの分布から表わされる.
• コース上に障害物がない状況での,skillとボール がある地点のコース状態から決定されるボールの 落下地点の分布g(xn+1; xn, st, skill)
• 林を通過するときのボールの落下地点の分布 h(xn+1; x′n+1, xn)
• 池に落下したときのボールの落下地点の分布 j(xn+1; x′n+1, xn, xn−1)
x′n+1をxnから分布gによって決まる位置,x′′n+1 をx′n+1から分布hによって決まる位置とし,そして 最終的な次のボール位置xn+1はx′′n+1から分布jに よって決定されるとする.関数fは,以上のことから 次のように求められる.
f(xn+1; xn, xn−1, st, skill) =
∫ ∫
g(x′n+1; xn, st, skill) · h(x′′n+1; x′n+1, xn)
·j(xn+1; x′′n+1, xn, xn−1 ) dx′n+1dx′′n+1
(11) ( 1 ) g(xn+1; xn, st, skill)
g(xn+1; xn, st, skill) = ˜g(r, θ) (12) とおく.rとθ は正規分布に従うので,ある定 数Ar,Aθと,飛距離と方向の平均µr,µθ,飛 距離と方向の分散σ2r,σθ2を用いて,
gr(r) = {
Arexp−(r−µ2σ2r)2
r · · · 0 ≤ r 0 · · · r < 0
(13)
gθ(θ) =
Aθexp−(θ−µ2σ2θ)2
θ
· · · µθ− π ≤ θ < µθ+ π 0 · · · else
(14) 定数Ar,Aθは正規化された関数を,設定した 範囲で積分すると,値が1となるように定義し た数である.
r と θ が 互 い に 独 立 で あ る と す る と ,gr(r), gθ(θ)から,˜g(r, θ)は,
˜
g (r, θ) = gr(r)gθ(θ)
=
ArAθexp [
−1 2
{ (r−µr
σr
)2
+(θ−µσθθ)
2}]
· · · 0 ≤ r, µθ− π ≤ θ < µθ+ π 0 · · · else
(15)
また,積分すると,
∫ ∫
˜
g(r, θ)drdθ = 1 (16) σrとσθの分散の大きさはフェアウェイ・ティー インググラウンドを基準にし,その他のコース 状態(ラフ,バンカー,林の中)ではその値の 2倍とする.
( 2 ) h(xn+1; x′n+1, xn)
xnをボールの始点,x′n+1を分布gによっ て決まるボールの終点(落下地点),xn+1を 分布hによって新たに決まるボールの終点とす る.またxnからxn+1までの経路をC,xnか らx′n+1までの経路をC′とする.
ある地点xが林かどうか判定する関数w(x)と, ボールが始点からxまで到達したとき,通過 した林の長さを求める関数L(x)を以下に定義 する.
w(x) =
{ 1 · · · (W oods)
0 · · · (no W oods) · · · x ∈ C′ (17)
L(x) =
∫
C
w(x′)dx′· · · x ∈ C (18)
次に,ボールが木にぶつからない場合とぶつか る場合の,2つの場合に分けてボールの落下地 点を定義する.
木にぶつからない条件 木にボールがぶつか らないとき,xn+1とx′n+1が一致する.
δ(xn+1− x′n+1) (19) 木にぶつかる条件 林を通過する始めの方は
高い確率でボールが落ち,奥の方にボール が到達する確率は低い.よって林の中のあ る位置にボールが存在する確率は,林を通 過する距離が増えるほど低くなる.本研究 で は 指 数 関 数 的 に 確 率 が 減 少 す る も の と する.
q(x) = w(x) · λe−λL(x)· · · x ∈ C (20) λは林の木の密度を表す定数である. 最後に木にぶつかる確率Phitと,ぶつからな い確率Pthroughを求めると,
Phit=
∫
C′
w(x) · λe−λ∥x−xn∥dx (21) Pthrough= 1 − Phit (22) よって,
h (xn+1; x′n+1, xn)
= Phit× q(xn+1)
+ Pthrough× δ(xn+1− x′n+1) (23) ( 3 ) j(xn+1; x′n+1, xn, xn−1)
まず,xnをボールの始点,x′n+1を分布gと 分布hによって決まるボールの終点(落下地 点),xn+1を新たに決まるボールの終点とす る.それを,t∈ [0, 1]を使って以下のように表 わす.
x′n+1= xn+ t(x′n+1− xn) (24) また,ある地点tがWHかどうか判定する関 数W H(t)を定義する.
W H(t) =
{ 1 · · · (W H)
0 · · · (not W H) (25) xn+1の1つ前にボールがあった地点は,n打 目 に 打った ボ ー ル が 池 に 入 ら な かった 場 合 は xn,n-1打目に打ったボールが池に入った場合 はxn−1である.それぞれについて,
n打目のボールが池に入らなかった場合 ボー ルが池に入らなかったとき,xn+1とx′n+1 が一致する.
δ(xn+1− x′n+1) (26) n-1打目のボールが池に入った場合 ε >0の
十分小さな任意の実数εを考えたとき, {
W H(t) = 0 · · · (t∗− ε ≤ t ≤ t∗) W H(t) = 1 · · · (t∗< t≤ t∗+ ε) (27) となる最大のt∗をt0と定義する.よって,
δ[xn+1− {xn−1+ t0(x′n− x′n−1)}] (28) つまり,
j (xn+1; x′n+1, xn, xn−1)
= δ(xn+1− x′n+1)
+ δ[xn+1− {xn−1+ t0(x′n− x′n−1)}] (29) 2.5 期待スコアの最小化
前述のモデルによって,ゴルフを「期待スコアを最 小化する最適化問題」として考える.あるskillのゴ ルファーが戦略stをとったときの,1つのホールで の期待スコアを,
E[N (st, skill)] =
∞
∑
n=0
Pn× n (30)
で表わす.nは打数,Pnはn打目でボールがカッ
プに入る確率である.あるホールでのティーの位置を xstart,カップの位置をxcupとする.
Pn=
∫
p(xcup|xn−1, st, skill) · p(xn−1)dxn−1
(31) p(xn−1) =
∫
p(xn−1|xn−2, st, skill)
· p(xn−2)dxn−2 (32) p(x0)は,δ 関数を用いて
p(x0) = δ(x0− xstart) (33) となる.δ 関数とは,
δ(i) = {
∞ (i = 0)
0 (i ̸= 0) (34)
となる関数である.この関数はi̸= 0となる確率が 0であることを表す.
p(xn+1|xn, st, skill)は,前述のシミュレーション モデルで定義した関数である.
よって目的関数は, min
st E[N (st, skill)] (35)
3. Q 学 習
前章で期待スコアを最小化する最適化問題を定義し たが,解析的に解くのは困難である.ゴルフの環境が マルコフ性を満たしていると仮定し,マルコフ決定過 程におけるQ学習を用いて数値的に解く.
本章では,具体的なスキルなどのパラメータを設定 し,Q学習の詳細について説明する.また,学習途中 の戦略に従ったときのスコアのなどから,学習の進度 を分析した.
3.1 パラメータの設定
モデルとQ学習の2つについての詳細を説明する.
3.1.1 モデルの詳細
今回はPGA TOURに参加している男子プロを戦
略指示の対象者として想定する.
r,σr2,σ2θ それぞれの値は,Fried10) らの研究や, 公開されているPGA TOURに参加している選手の 平均データ2)4)を参考に決定した.
σr,σθはボールのある地点のコース状態がフェア ウェイかティーインググラウンドのときで,ラフやバ ンカーではその値の2倍とする.また,今回実験では, アメリカのジョージア州オーガスタにある,「オーガス タ・ナショナル・ゴルフクラブ」1) の全18ホール を使用する.
図4 クラブ別のr,σr,σθ,単位はヤード
3.1.2 Q学習の詳細 ( 1 ) 行動空間
方向は0∼359度までで,整数値をとるこ ととする.
SWで出せる飛距離より短い飛距離のクラブ がないので,仮のクラブを用意する.仮のクラ ブはSWの飛距離の90%から10%まで10 刻みで9本用意し,それらの分散はSWと同じ ものとする.よって使用できるクラブは合計で 22本となる.このクラブ集合をClub′とし, Club⊂ Club′である.
( 2 ) 状態空間
状態空間をグリッドで分割して離散化すると 計算量を減少させることができるが,グリッド が大きくなると戦略が粗くなってしまう.それ をふまえて今回は約2ヤード四方のグリッドで 離散化する.ボールのある地点sは,s ∈ Z2 である.
( 3 ) 行動選択
行動選択はε グリィーディーを用いる. ( 4 ) 報酬
報酬は1回ボールを打つごとに−1与えられ, ボールが池に入ったときと,ボールがコース画 像からはみでてしまった場合(OB)は,さらに
−1が与えられる.OBの場合,ボールを打つ前 の位置にボールをドロップする.グリーン上に ボールがのった場合はホールまでの残り距離に 応じた期待パット数が報酬として与えられる. ( 5 ) Qテーブルの初期化
グリーンにボールがのった時点でエピソード を終了する.そのためグリーンを含む地点のQ 値は全て0とし,Q値の更新も行わない.そ の他の地点についてはパー4のコースなら全て
−4,パー3のコースなら−3というように設定 する.
( 6 ) 学習アルゴリズム
以 上 の こ と を ふ ま え て 学 習 を 行 う.ティー ショットからグリーンにボールがのるまでを1 エピソードとし,それを繰り返し行ってQテー ブルを更新していく.
学習率αは0.1,割引率γ は0.9,エピソード 数は1千万回とする.
3.2 学 習 結 果
ここではグリーン上にボールがのったときは,カッ プまでの残り距離に応じて確率的にカップインまでの パット数を決定する.また,カップまでの残り距離が カップの半径より小さい場合は,そのままカップに入っ たものとし,パッティングを行わない.
各ホールで,10万エピソードごとに学習途中の戦 略を出力し,その戦略に従って1万回ティーショット からカップインするまでシミュレーションを行う.ま た,スコアが12以上となった場合はそのホールをリ タイヤするという条件を加える.結果を見るためのス コア以外の代表的な指標を以下に示す.
• フェアウェイキープ率 パー3以外のコースで, ティーショットを打った後の地点がフェアウェイ となった割合である.PGA TOURの平均は70
%程度の値である.
• パーオン率 ホールごとのパーから2を引いた打 数(パー4のホールなら2打で,パー5なら3打) でグリーンにのせることをパーオンと呼ぶ.パー オンした割合をパーオン率と呼ぶ.PGA TOUR の平均は約65%である.
• サンドセーブ率 バンカーにボールが入ったとき, バンカーショットを含めて2打以内でカップに入 れる割合である.PGA TOURの平均は約50
%である.
3.2.1 スコアの平均値と標準偏差
ほとんどのホールで,平均スコア・標準偏差ともに ある値に向かって収束している様子が見られる.ゴル フのスコアは負の数や0となることがなく,改善でき るスコアには限界値がある.そのため平均スコアを下 げるためには分散を下げる必要がある.パー3のホー ルでは,行動がランダムに選択されることに影響を受 け,学習の途中でスコアが多くなる場合がある.
3.2.2 パーオン率
ある値に向けて収束する様子が見られる.平均スコ アと同じで,パー3のホールではたまにパーオンしな い戦略を学習する.
図5 上:3番ホール,パー4 下:12番ホール,パー3 横軸の値× 10 万回のエピソードでの戦略をとった場合の,平 均スコアと標準偏差をプロットしたグラフ
図6 上:2番ホール,パー5,下:6番ホール,パー3 横軸の値× 10 万回のエピソードでの戦略をとった場合の,パー オン率をプロットしたグラフ
学習により,9割以上の確率でパーオンする戦略を 見つけられるということがわかった.
4. 実 験
前章ではQ学習の詳細について説明したが,学習が 正しく行われているか,実際に行われている大会の結 果と比較することにより確かめた.また,ゴルファー の技術を変化させた場合にどのような戦略の違いが生 まれるか実験を行った.
図7 PGA ave.:前章と同じ値 unskillfull:大きい場合 skillfull:小さい場合
skillはr,σ2r,σ2θの3つの値から成るが,今回は前 章の設定の分散(PGA ave.)をもとに,より分散が大 きい場合(unskillfull)と分散が小さい場合(skillfull) を考える.rはそれぞれの場合で同じ値とし,前章の 値を用いる.つまりスキルの違う3種類のゴルファー
(PGA ave.,unskillfull,skillfull)で比較を行う. Q学習はそれぞれのスキルで1千万エピソード行 い,一定回数ごとに途中の戦略を出力し,その中で最 も平均スコアが低くなる戦略を用いる.
4.1 Q学習の結果と実際の大会の結果の比較 2011年にオーガスタ・ナショナルで行われた大会
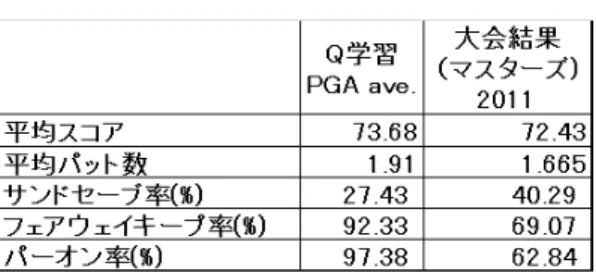
(マスターズと呼ばれる)に参加した全てのゴルファー の結果を平均したものと,本計算モデルにおいて,プロ の平均値をもとにしたスキルを持つゴルファー(PGA ave.)で学習を行った場合を比較した.それぞれのホー ルのスコア,18ホールの合計スコアを比較すると,実 際の大会とほとんど変わらないことがわかり,学習が 成功していることが確認できる.
4.2 期待スコアを減少させる戦略を学習しているか フェアウェイキープ率を見ると,ほとんどのホール で8割以上の値となっている.つまり林やラフなど, スコアが悪くなるような場所にボールを打たない戦略
図8 Q 学習の結果と実際の大会結果の比較
図9 Q 学習の結果と実際の大会結果の,各ホールの平均スコア
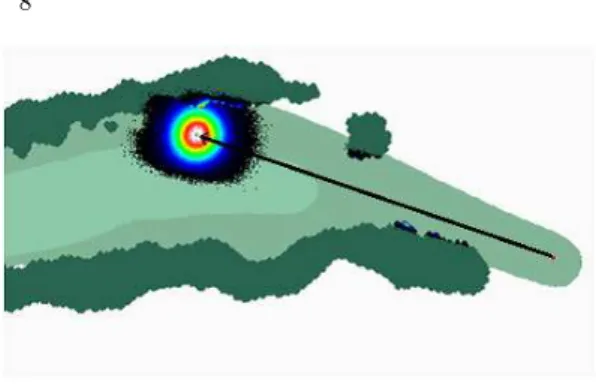
を学習していることがわかる.また,最も値が低い10 番ホールでとられている行動を見ると,フェアウェイ を狙うと林に打ち込んでしまうため,木に当たる確率 の低い所を狙った結果ラフとなっているということが わかり,このホールでも正しく学習が行われているこ とが確認できた.
図10 各ホールでのフェアウェイキープ率(PGA ave.)
4.3 スキルの違いによって戦略がどのように変化 するか
スキルが高い場合(skillfull)と低い場合(unskill- full)で,選択したクラブの飛距離の平均値を各打順 ごとに求めて比較した.スキルが高いと飛距離の長い クラブを使用してもミスショットとなる確率が低いた め,より飛距離の長いクラブを選択しやすく,逆にス キルが低いと,ショットの誤差が少ない飛距離の短い
図11 10 番ホールのティーショット:学習した行動
クラブを選択するという結果となった.学習した結果 が,現実世界で言われる「初心者は飛距離の短いクラ ブで刻め」と同じ結果となったのは興味深い.
図12 各打順で使用したクラブの飛距離の平均値
5. 結 論
実験によりQ学習によってスコアを改善する戦略 を求めることができるということがわかった.最終的 な目標としてプレー中リアルタイムに行動を指示する ことを考えており,Q学習では計算量の問題で実現 できない.だがリアルタイムに計算できるヒューリス ティックな手法を考えるとき,Q学習によって得られ た結果はそのような手法の評価を行うために必要なも のである.
今後は,得られた知見を活かしたヒューリスティッ クな行動選択法を考えていく.また,ゴルフの環境が 持つ様々な要素のうち,必要最低限のものでモデルを 構成したので,戦略に関係すると思われる他の要素に ついてもモデリングする必要がある.例えばショット におけるボールの落下分布を正規分布と仮定したが, 実際は人それぞれの技術や癖で違う分布になるはずで ある.そのような分布の推定法についても考えていき たい.
参 考 文 献 1) http://www.masters.com/
マスターズ・トーナメント公式サイト 2) http://pgatour.com/
PGA TOUR公式サイト
3) http://www.tbs.co.jp/masters/ TBS Mastersホームページ
4) http://www.mytrackman.com/TrackMan.On line.DrivingRange/Index.aspx
TRACK MANホームページ
5) Christopher Archibald, Alon Altman, Yoav Shoham : Success, strategy and skill: an exper- imental study, AAMAS ’10 Proceedings of the 9th International Conference on Autonomous Agents and Multiagent Systems, volume 1 - Volume 1 (2010)
6) Mark Broadie, Soonmin Ko : A SIMULA- TION MODEL TO ANALYZE THE IMPACT OF DISTANCE AND DIRECTION ON GOLF SCORES, Winter Simulation Conference, Pro- ceedings of the 2009 Issue, pp.3109-3120 7) Robert A. CONNOLLY, Richard J. RENDLE-
MAN JR. : Skill, Luck, and Streaky Play on the PGA Tour, Journal of the American Statistical Association, March 2008, vol.103, pp.74-88 8) Matulya Bansal, Mark Broadie : A SIMULA-
TION MODEL TO ANALYZE THE IMPACT OF HOLE SIZE ON PUTTING IN GOLF, Winter Simulation Conference, Proceedings of the 2008 Issue, pp.2826-2834
9) Andrew Gelman, Deborah Nolan : A Proba- bility Model for Golf Putting, Teaching States- tics vol.24, issue.3, pp.93-95, Autumn 2002 10) Fried, Harold O., Lambrinos, James, Tyner,
James : Evaluating the performance of profes- sional golfers on the PGA, LPGA and SPGA tours, European Journal of Operational Re- search. vol.154, 2 April, pp.548-561
11) Moran, Kieran : Identification of the biome- chanical performance determining factors of the 5 iron golf swing when hitting for maximum distance, Master of Science thesis, Dublin City University
12) David L. Gilden, Stephanie Gray Wilson : Streaks in skilled performance, PSYCHO- NOMIC BULLETIN & REVIEW vol.2, num.2, pp.260-265
13) Richard S. Sutton and Andrew G. Barto : Re- inforcement Learning,森北出版株式会社