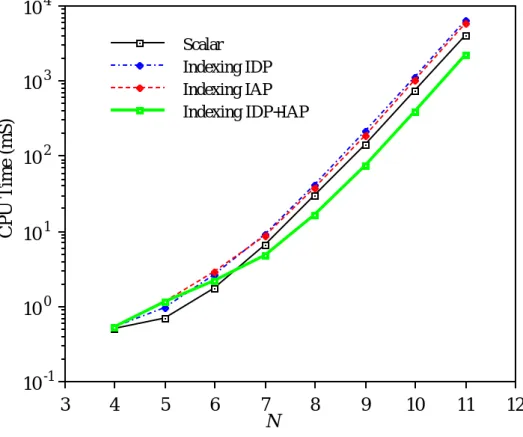
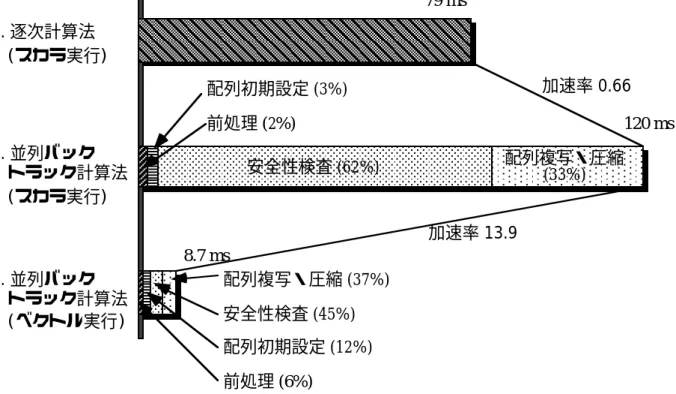
ベクトル計算を高速に実行できるコンピュータでした。を使用した場合の実行時間。 IDP は、(順次) バックトラッキング法に基づいたプログラムを使用して計算されます。 このセクションでは、発生する問題について説明します。 。
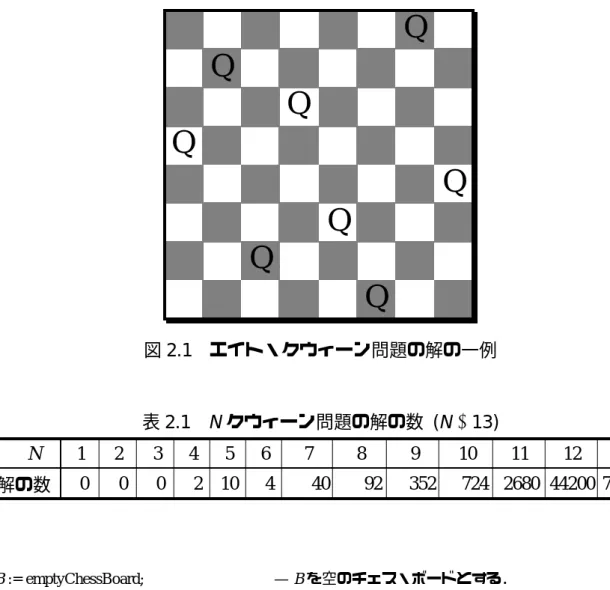
図 2.2 8 クイーン問題の逐次バックトラッキング計算法 *1 AND ベクトル計算法の名称は Prolog で書かれた 8 クイーン問題プログラムに由来 図 2.5 8 クイーン問題の OR ベクトル計算法
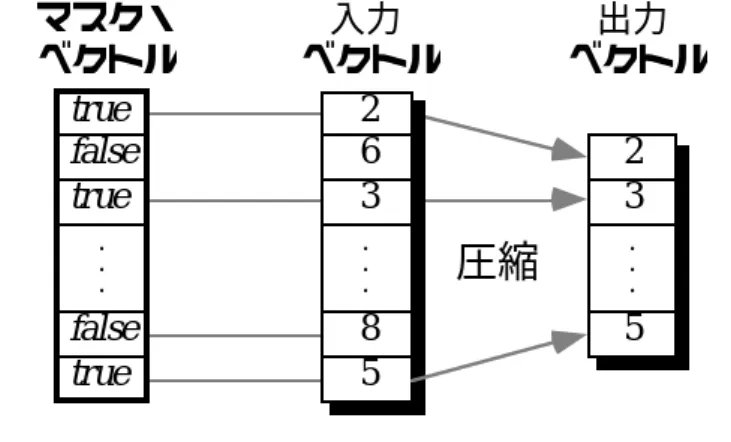
関数 nextCandidate(rb) はベクトル演算のベクトルロード命令であり、OR ベクトル計算方式は高速ですが、次の 2 つの問題があります。 2 番目の問題は、OR ベクトル計算が単純な検索、つまり 1 つの解のみが求められる場合であることです。
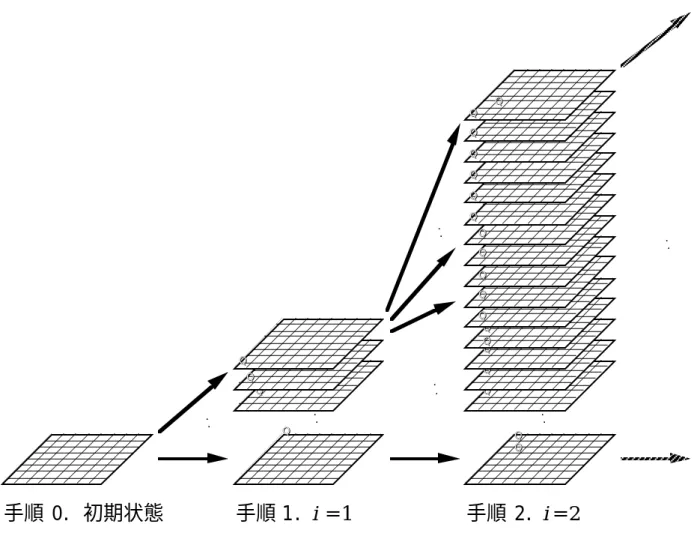
これが本節で説明する並列バックトラッキングの計算方法です。 。
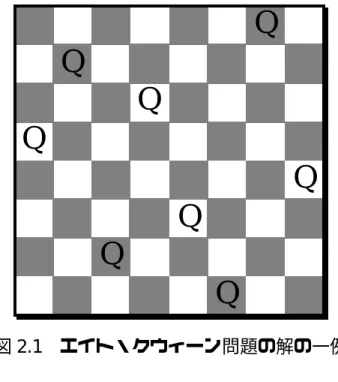
要素あたりの実行時間は一定か,またはキャッシュのヒット率低下のため にかえってながくなる.
モデルによって異なります)。ベクトル長がこれより長くなると徐々に性能が向上し、ベクトル長が 64 ~ 1000 程度でピークに達します。ベクトル長が長くなると、QUEEN(B, 1); となります。 - プロシージャ QUEEN を呼び出して、8 クイーン問題の解を見つけて出力します。 。
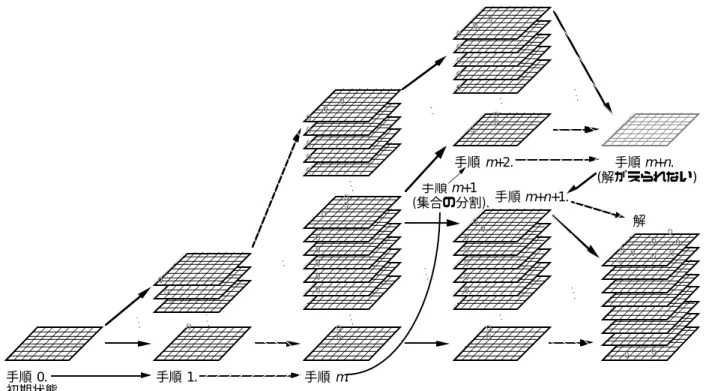
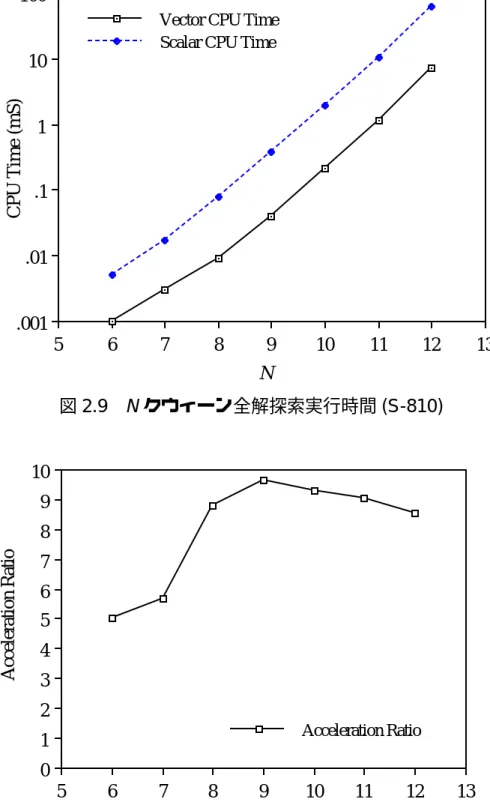
- N クウィーン解探索の実行結果
- 並列バックトラック計算法におけるベクトル長増大法
- 付録 1 : 測定用プログラムとその説明
- END IF
- N1 : INTEGER;
- X1 = 0, X-1 J = 0, NSOL-1
- I = 0, N-1 DO 30 J = 0, NSOL-1
- J = 0, NSOL-1 T1A = X1 + Y(J,X1)
- X1 = 0, X-1 CNT = 0
- I = 0, N-1 J = 0, NSOL-1
- I = 0, N-1 J = 0, NSOL-1
- I = 0, N-1 DO 30 J = 0, NSOL-1
- X1 = 0, X-1 J = 0, NSOL-1
- J = 0, NSOL-1 IF (SAFE(J)) THEN
- J = 0, NSOL-1
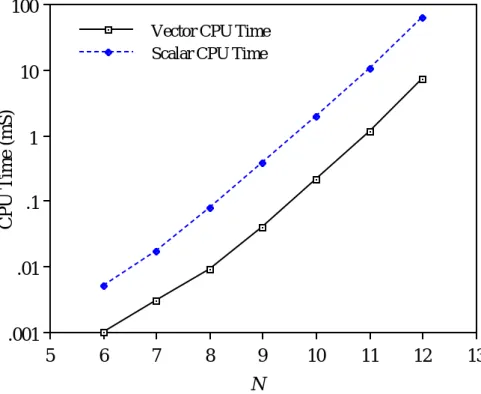
さらに説明します。 Torii et al [Torii 88a, Torii 88b] は、IDP でベクトル OR 計算 (および並列逆計算) を実装する方法を簡単に説明しています。 。お酢。 3種類は、逐次バックトラッキング方式によるプログラムのスカラー実行と並列実行である。これらの数字。
並列逆方向計算手法によりメモリ消費のバーストが回避されていることがわかります。 (ここでも l = 下げる)。 N < 14 の場合、並列バックトラッキング アルゴリズムは逐次配列 (N ≥ 14) でクイーンを見つけるのに十分な並列性 OR を持ち、並列バックトラッキング アルゴリズムは単純な検索にも適しています。で十分な並列性が得られます。
並列バックトラック計算 (スカラー実行) 並列バックトラック計算 (ベクトル実行) N クイーン問題に適用されます。
最大15.7の高い加速率を実現し、並列バックラグ演算方式を採用しています。並列バックトラッキングアルゴリズムのプログラムは、再帰呼び出しを使いたかったので計算部分にFortran、バックトラッキング制御部分にPascalを使用しています。 。
図 2.17 8 クイーン問題の逐次バックトラッキング アルゴリズムの Fortran エンコード。特に、どのような種類の条件付き制御命令が使用されているかを示します。 (これらの命令の典型的な動作を図 2.20 に示します)。並列バックトラッキング アルゴリズムに基づく 2 つのプログラム用の Fortran。
図 2.19 すべての解を使用した 8 クイーン並列バックトラッキング計算法。
5true
IDP 使用 IAP 使用 IDP+IAP IDP 使用 IAP 使用 IDP+IAP。
6 には,図 2.15 〜 2.16 でしめした N クウィーン問題の単解探索の S-810 にお ける実行時間および加速率を数値としてしめす.