ii

基礎オペレーションズリサーチ（下）

逆瀬川浩孝

2013

年秋学期

目次

5 階層的意思決定法 143 5.1 問題の設定 . . . 143 5.2 評価基準の総合化 . . . 144 5.3 一対比較 . . . 148 5.4 総合評価値の計算 . . . 153 5.5 計算方式の理屈 . . . 155 5.6 整合性の検討. . . 156 5.7 評価基準の階層化 . . . 159 5.8 感度分析 . . . 161 5.9 階層的意思決定法の実施例 . . . 164 6 日程計画・日程管理 165 6.1 はじめに . . . 165 6.2 簡単な例題 新製品開発. . . 165 6.3 P ERT による日程計画の実行手順 . . . 169 6.4 アローダイアグラム . . . 169 6.5 P ERT 計算 . . . 175 6.6 P ERT 手法の問題点 . . . 184 6.7 資源制約の下での最適化問題 . . . 186 6.8 日程管理 . . . 188 7 在庫管理 191 7.1 在庫管理の問題状況 . . . 191 7.2 在庫の役割 . . . 192 7.3 累積グラフによる在庫管理 . . . 194 7.4 在庫管理費用を考慮した在庫管理 . . . 199

7.5 経済的発注量(Economic Order Quantity, EOQ) . . . 200

7.6 定期発注方式と定量発注方式 . . . 207

7.8 レベニューマネジメント . . . 216 7.9 多品目の在庫管理–ＡＢＣ分析. . . 217 8 シミュレーション 221 8.1 はじめに . . . 221 8.2 シミュレーションの種類 . . . 222 8.3 確率的シミュレーション . . . 227 8.4 離散事象シミュレーションの例、在庫管理 . . . 227 8.5 ランダム事象の生成と擬似乱数 . . . 233 8.6 ばらつきのまとめ方 . . . 236 9 待ち行列モデル 244 9.1 はじめに . . . 244 9.2 累積グラフを使った分析 . . . 246 9.3 定常条件 . . . 252 9.4 バスの待ち時間 . . . 254 9.5 携帯電話の呼損率 . . . 258 9.6 待ち行列モデルのシミュレーションによる分析 . . . 262 10 金融工学 270 10.1 リスク管理 . . . 270 10.2 平均分散モデル . . . 271 10.3 効用、効用関数 . . . 272 10.4 デリバティブ（派生証券） . . . 282 10.5 コールオプションの価格 . . . 284 10.6 天候デリバティブ . . . 290

5

階層的意思決定法

5.1

問題の設定

Ａさんは念願かなって免許が取れたので、車を購入することにしました。いろいろ検討した結 果、候補はトヨタの「プリウス」、ニッサンの「キューブ」、ベンツの「A180」の三つの車種に絞 られたのですが、そこから先は、価格や維持費で言えばニッサン、環境を考えれば（環境に優し い）トヨタ、装備や満足度からはベンツ、となってなかなか決まりません。さてどうしたもので しょう？ あなたならどうしますか？ この問題のように、いくつかの選択肢があり、その選択基準が複数存在する場合は、こちらを 立てればあちらが立たず、あちらを立てればこちらが立たず、というジレンマに陥ります。予算 が伴わなければどうしようもない、というような絶対制約条件があれば考慮の余地はありません が、そうでない場合、なかなか思案がまとまりません。 たとえば、評価基準が二つあったとして、その基準が数量で計れるものとしましょう。そうす ると、それぞれの選択肢ごとに、各評価基準の値を計算して、それを二つの評価基準を直交軸と する座標形にプロットしてみると、散布図ができます（採用試験の基礎教養と専門知識の点数を 想像してください）。それぞれの評価値が大きいほど良いという基準であれば、プロットした点 が右上にあればあるほど評価が高い、ということになります。 パレート最適点 たとえば上の左図では、選択肢Ａがどの評価基準を取ってみても他の選択肢より値が大きいの ですから、選択肢Aを選ぶことに反対する人はいないはずです。しかし、プロットしたものが 右図のようだと話は変わってきます。どの選択肢をとっても、それぞれに特徴があり、どれが 「もっとも良い」ということはありません。両方の基準でトップではないけれど、両方の基準と も劣っていることはないというような点、つまり、その点より右上に点がない、という点をパ レート最適点といいます。パレートParetoはイタリアの経済学者の名前です。 多くの意思決定では、このように判断が一意に定まらないのが普通でしょう。そこで、そのよ うな状況を想定し、なんとか、最終決着を付けるための合理的な方法を考えてみましょう。

練習5.1 あれこれ迷うとき、あなたならばどうしますか。携帯電話の買い換えを検討している という場面を想定して、三つ程度の評価基準と、三つ程度の候補機種を選び、あなたの方法を適 用して候補を一つに絞りなさい。その決定法は他の人にも納得してもらえそうですか。 評価基準： 候補機種： 選考方法：

5.2

評価基準の総合化

車を買い換える問題の検討を続けることにします。普通に考えると、たとえば、価格、燃費、 装備、機能、満足度、環境のように、考えられる選択の基準をリストアップして、それらのうち のどれを１番重視するか、ということをあらゆる角度から徹底的に検討して、もっとも重要だと 思われる一つの判断基準（それを、評価基準と言います）に絞り、その基準で１番優れているも のを選ぶ、という手しかないように思われます（結局は一番安いのが良いと思うよ！ なんたっ て走りでしょう！）。 5.2.1 数量化 しかし、その基準が他の基準に比べて絶対視出来るものでないかぎりは、その基準でトップで なくとも、残りの基準でそこそこの評価が得られる車種を選ぶという選択もありえます。つま り、際だった特徴はないけれど、可もなければ不可もなし、という車種がどの基準でも２番目に なったとすると、そっちを選ぶ方が良いかもしれません。それも一つの決定方法でしょう。 そこで、それぞれの基準がどれくらい重要であるか、それぞれの基準のもとで各候補はどれく らいに評価されるのか、ということを数量化して、各候補を点数によって格付けするという方法 を考えることにしましょう。あまり基準が多いと説明するのが大変なので、取りあえず価格、装 備、環境の三つに絞ることにします。総合点の計算は以下の手順で実行します。 手順１． それぞれの評価基準がどれくらい重要かをウェイト付けします。たとえば価格、装 備、環境の順で重要だと考えるならば、価格を0.6、装備を0.3、環境を0.1、というよう に。ウェイトは合計が1になるようにしてください。 手順２． それぞれの評価基準のもとで、三つの車種ごとの評価を点数化します。たとえば価格 基準で考えたときは、トヨタ0.5、ニッサン0.4、ベンツ0.1のように。この場合も、合計 点数が1になるようにしてください。 手順３． 手順1で決めた各評価基準のウェイトを手順2で決めたそれぞれの評価基準ごとの点 数に掛けて、各候補ごとに、価格基準の点数、装備基準の点数、環境基準の点数を合計し

たものをそれぞれの候補の総合得点とし、その総合得点が一番大きいものを最終候補者と します。 計算は電卓でもできますが、Excelを使う場合は内積を計算する関数sumproduct()が使えま す。たとえば上の問題の場合、B4 : D4に三つの評価基準のウェイトが入力され、B5 : B7に１番 目の評価基準のもとでの三つの代替案の点数が、C5 : C7に２番目の評価基準のもとでの点数が、 D5 : D7に３番目の評価基準のもとでの点数が、それぞれ入力されているとした場合、セルE5に 「=sumproduct($B$4:$D$4,B5:D5)」と入力すると、１番目の代替案の総合点が計算されます。 セルE6, E7にはセルE5をコピーすれば同様に、２番目、３番目の代替案の総合点が計算され ます。 一般的な問題設定で説明を整理しておきましょう。評価基準がM 個、可能な実行案・選択肢 （代替案ともいう、今の例では、トヨタを買う、ニッサンを買う、ベンツを買う、ということ）が N個あったとしましょう。評価基準のウェイトをw₁, w₂, ..., w_M、k番目の評価基準のもとで代 替案の点数をq_k1, q_k2, ..., q_kN とします。このとき代替案iの総合ウェイトV_iは Vi= w1q1i+ w2q2i+ ... + wMqMi, i = 1, 2, ..., N (1) と計算されます。このようにして計算された総合ウェイトV₁, V₂, ..., V_N のうちでもっとも大き い点を得た代替案を最終的な意思決定としよう、というのがこの方法です。 5.2.2 階層図 上の考え方は、（お菓子の）パイを切り分ける場面を想定すると理解しやすいでしょう。たと えば、価格、装備、環境のウェイトが0.6, 0.3, 0.1ならば、その比率に応じてパイを三つに分割 します。次に価格基準の下でトヨタ、ニッサン、ベンツのウェイトが0.5, 0.4, 0.1ならば、価格 に切り分けられた60%のパイを5 : 4 : 1に分割してそれぞれトヨタ、ニッサン、ベンツに分配 するのです。つまり、全体の比率に直すと0.6 × 0.5 = 0.3がトヨタ、0.6 × 0.4 = 0.24がニッサ ン、0.6 × 0.1 = 0.06がベンツの取り分になるというわけです。同じことを装備、環境について 行い、最後に、トヨタ、ニッサン、ベンツの合計取り分を計算すると、トヨタ、ニッサン、ベン ツのパイの取り分、つまり総合ウェイトが計算できる、というわけです。 ウェイト付けによる総合評価値の計算（イメージ図）

基準の数や代替案の数がこの程度ならばパイの分配でも良いのですが、数が多くなった場合の ことを考えて、別の図表現を考えます。全体を価格、装備、環境に分配し、その分配されたもの を各々の基準で代替案に再分配するという流れは、階層構造を意識して、下のような図に表すと 分かりやすいでしょう。最初の箱が決めるべき問題、２段目にはその問題を解くために用いられ る評価基準の候補、最後の段はその問題の解決案（代替案）が並んでいます。 階層図 正確には、各基準から三つの代替案が枝分かれしているはずですが、どの基準からも共通の枝 が分岐しているので、省略して上のように描くことにします。このようにして描かれた図は階層 図と呼ばれます。 5.2.3 階層的意思決定法（ＡＨＰ法） いくつかの評価基準があって単純には評価が定まらないとき、上のような方法は一つの合理的 な評価を与える賢いやり方のように思われます。このように、意思決定の基準を階層図に表し、 ウェイトを分配し、総合ウェイトに大きさによって候補を絞っていく意思決定の方法を階層的意 思決定法と言います。アメリカ生まれの手法で、Analytic Hierarchy Processを和訳した用語で すが、英語の頭文字を取ってAHP法と呼ばれることの方が多いようです。 言われてみれば至極ごもっとも、「法」というほどの大げさなものではないかもしれませんが、 そこに気がついた人（トマスサーティThomas Saaty）が偉い。単純な方法ですが、いくつか問 題が残ります。以下の節では二つの問題を取り上げることにします。 一つはウェイトや点数の決め方の問題、 もう一つは評価基準の絞り込みの問題 です。

練習5.2（練習5.1の続き）携帯電話を買い換えることを想定し、上の方法に従って最終案を一 つに絞り込んで下さい。(1)三つの候補機種（代替案）をリストアップしなさい。 (A) 、(B) 、(C) (2)三つの評価基準をリストアップし、その重要度を（合計が１になるように）決めなさい （イ） 、（ロ） 、（ハ） （イ）：（ロ）：（ハ）＝w₁: w₂: w₃＝ ： ： (3)各基準ごとに、（合計が１になるように）代替案の重み付けをしなさい （イ）基準 (A) : (B) : (C) = q₁₁: q₁₂: q₁₃＝ ： ： （ロ）基準 (A) : (B) : (C) = q₂₁: q₂₂: q₂₃＝ ： ： （ハ）基準 (A) : (B) : (C) = q₃₁: q₃₂: q₃₃＝ ： ： (4)各代替案の総合点数を計算しなさい。練習5.1の結論と一致しましたか。 代替案 (A) = 代替案 (B) = 代替案 (C) =

5.3

一対比較

評価基準にウェイトを付けたり、ある評価基準のもとで各候補の点数（ウェイト）を付ける場 合、上の例のように比較対象が三つくらいならば直接点数付けができるかもしれませんが、数が 増えた場合は判断に迷うことが多くなることが予想されます。特に、全く質の異なる評価基準に ウェイトを付けなければいけないとしたら、たとえ三つでも、いつまでも決まらないかもしれま せん。 しかし、もしそのうちの二つだけを取り出して、「どちらを重視しますか」と言われれば、そ れほど迷わずに決めることが出来るのではないかと思われます。そこで、他の基準は無視して、 二つだけを取り出して比較する（それを一対比較と言います）ことを、あらゆる二つの組み合わ せについて実施し、それらの結果を総合して、各評価基準のウェイト付けをしよう、という考え 方が考案されました。この一対比較の方法が導入されたことにより、どんな人にとっても容易に 全体のウェイト付けが可能になり、多数の評価基準がある場合にでも合理的な意思決定が可能に なったのです。 5.3.1 一対比較の方法 一対比較の方法と、その結果をウェイト計算に結び付ける方法を、ここでは車の選択の問題 で、三つ選ばれた評価基準、すなわち「価格」、「装備」、「環境」のウェイト付けを例にとって説 明します。例えば、次のような図を提示して質問します。 「環境」基準のことは忘れて、「価格」基準と「装備」基準の相対重要度を図で表現してくださ い。「価格」基準が「装備」基準に比べて相対的に重要だと思うならば中央のティックマークより 左側に、「装備」基準が「価格」基準に比べて相対的に重要だと思うならば中央のティックマーク より右側に、○を付けてください。重要さの度合いが大きくなるにつれて、中央のティックマー クより離れたところに○を付けるようにしてください。 同じことを、「価格」基準と「環境」基準、「装備」基準と「環境」基準に対しても実行してく ださい。

一対比較はこれでおしまいです。どうでしょうか、これならば、「価格」基準と「環境」基準の ように、評価の物差しが異なる価値基準に対しても、何とか順序づけができそうですね。 次いで、一対比較の結果を数量化します。二つの基準が同等の場合は中央のティックマークに ○が付くはずですが、その場合は双方に1点を与えます。○の付いた位置が中央のティックマー クから離れるほど い点を与えますが、例えばティックマーク一つを2点と考え重要な基準の方 に3点、5点、7点、9点を与え、重要でなかった方にはその逆数の点を与えることにします。○ をティックマークの間に描いた場合は偶数の点を与えます。例えば、次のようになった場合は、 価格に5点、環境に5分の1点を与えます。 これらの結果を次のようにして一つの表にまとめておきましょう。三つの基準を1, 2, 3と し、i基準をk基準を比較したときの i基準の点をa_ik、k基準の点をa_ki とします。また、 aii = 1(i = 1, 2, 3)とすれば、A = (aik)という3 × 3の行列が定まります。この行列を評価基 準の一対比較行列と言います。 一対比較行列 価格(1) 装備(2) 環境(3) 価格(1) 1 5 装備(2) 1/5 1 環境(3) 1 練習5.3 練習5.2で挙げた三つの基準について、上で説明した方な図を作って一対比較を実施 し、その結果を、一対比較行列にまとめなさい。 一対比較 （イ） （ロ） （ハ） （イ） 1 （ロ） 1 （ハ） 1 5.3.2 ウェイトの計算 さて、この一対比較表の情報を使って、三つの評価基準の「総合的な」評価値を計算するには どうすれば良いでしょうか。次のような一対比較行列が得られたとして、その計算法を説明しま しょう。

価格(1) 装備(2) 環境(3) 価格(1) 1 3 9 装備(2) 1/3 1 5 環境(3) 1/9 1/5 1 一つの方法は数字を行ごとに見ることで得られます。価格の行に大きな数字が並んでいるとい うことは、価格基準が重視されていることを意味しますから、行ごとの平均点の大きさに応じて 評価値を決めれば良さそうです。ただし、この場合は、後でその理屈を説明するように、単純な 平均ではなく、幾何平均、つまり、三つの数字の積の３乗根を使います。 3 √ 3 × 9 : 3 r 1 3 × 5 : 3 r 1 9 × 1 5 = 3 : 1.186 : 0.281 = 0.672 : 0.265 : 0.063 一般に、評価基準の数がMの場合は、各評価基準からみたM 個の数字の幾何平均を計算し、そ れらを和が１になるように比例配分してウェイトを決めます。 幾何平均を計算するためにはM乗根が必要です。EXCELがあれば「ˆ(1/M)」によって計算 できますが、パソコンがないと暗算ではむつかしいでしょう。そこで、（演習用に）別の簡易計 算法を考えます。数字を列ごとにまとめてみると、数字の小さいものほど重視されていることが 分かります。そこで、その合計の逆数に比例してウェイトを決めるという方法も見込みがありそ うです。上の例で言うと、 1 1 +1 3 +19 : 1 3 + 1 +1 5 : _{9 + 5 + 1}1 = ₁₃9 : ₂₁5 : ₁₅1 = 0.694 : 0.239 : 0.067 のようにウェイトを決めるのです。これならば、パソコンが無くても計算できるでしょう。 特に、もし評価基準が二つしかない場合、第１基準を第２基準に比べてa倍重視するとした場 合は、一対比較行列は A = µ 1 a 1/a 1 ¶ となるので、そのウェイト比は幾何平均の場合、 √ a : √1 a = a : 1 あるいは、合計の逆数の場合、 1 1 +1 a : _{a + 1}1 = a : 1 というように、どちらの計算法でも指定したウェイト比が得られることに注目してください。 基準が三つ以上の場合は、二つの方法で、結果が微妙に違いますが、もともとが大ざっぱな方 法ですから、あまり気にすることはありません。練習問題の計算は２番目の方法を使ってくだ さい。

練習5.4 練習5.3で作った一対比較行列からウェイトを求めるための表を完成させなさい。表 の最初の３行３列は一対比較行列を書き写してください。４行目に各列の要素の合計、5行目に その逆数を計算し、５行目の数字を合計が１になるように調整したものを「ウェイト」の行に記 入して下さい。また、この方式で求めたウェイトと、練習5.2で決めたウェイトとを比較してご らん。 一対比較 （イ） （ロ） （ハ） （イ） 1 （ロ） 1 （ハ） 1 各列の合計 列合計の逆数 ウェイト（合計が1になるように）

5.3.3 参考 一対比較の妥当性 一対比較によるウェイト付けが「正しい」かどうかをチェックすることはなかなかむつかしい 問題ですが、数量的に順序付けられる基準を持ったものを一対比較して、その結果から計算され たウェイトと、数量を使った絶対的なウェイトを比較することで、ある程度尤もらしさを裏付け ることが出来ます。例えば、次の問題を試してみてください。 練習5.5 次の図形の面積の大きさを一対比較法によって比較し、そこから図形の総合ウェイト を計算しなさい。ここでは「重視する」という言葉を「大きい」に置き換えて比較します。例え ば、AはCと比べて6倍大きいと思ったら、b_AC= 6, b_CA = 1/6とするのです。 一対比較 (A) (B) (C) (D) (A)北海道 1 (B)本州 1 (C) 四国 1 (D) 九州・沖縄 1 列合計の逆数 ウェイト 正確な比率は、...、調べてください。かなり良い線を行っていると思います。

5.4

総合評価値の計算

評価基準のウェイトが決まったら、次のステップは各基準毎に代替案のウェイト付けをするこ とです。この場合も、代替案を全部並べてウェイトを付けるよりは、二つずつ取り出して一対比 較する方が正確に判断することが出来るでしょう。例えば、価格基準の下での代替案を評価する 場合は、他の条件を無視して、価格だけを考慮したときに、トヨタとニッサンはどちらをどれく らい重視するか、トヨタとベンツの比較はどうか、ニッサンとベンツの比較はどうか、というこ とを判断し、上のような一対比較行列にまとめ、説明したような手順で各代替案のウェイトを計 算します。 装備基準、環境基準に対しても同じ手順を当てはめ、各基準の下での各代替案のウェイトを計 算します。それぞれのウェイトが計算できればあとは練習5.2と同じような手順で各代替案の総 合ウェイトが求まるでしょう。そのウェイトがもっとも大きくなったものが、推奨案、というわ けです。 このようにして、人間の判断の曖昧さをうまい具合に数量化して数量比較可能なレベルに落と し込んだ、というのがこの階層的意思決定法の画期的な点です。これならば、好き嫌いのような 感性が絡んでくるような曖昧な基準による意思決定にも応用が出来そうです。

練習5.6 携帯電話の例（練習5.2）で各基準の下での各代替案のウェイトを求め、練習5.4の結 果を使って各代替案の総合ウェイトを計算しなさい。 (1)各基準の下で代替案のウェイト付けをしなさい。（各基準ごとに合計が1になるようにする） 「（イ）基準」の下で、代替案(A), (B), (C)の一対比較、ウェイト計算 基準： (A) (B) (C) (A) 1 (B) 1 (C) 1 列合計の逆数 ウェイト q₁₁= q₁₂= q₁₃= 「（ロ）基準」の下で、代替案(A), (B), (C)の一対比較、ウェイト計算 基準： (A) (B) (C) (A) 1 (B) 1 (C) 1 列合計の逆数 ウェイト q₂₁= q₂₂= q₂₃= 「（ハ）基準」の下で、代替案(A), (B), (C)の一対比較、ウェイト計算 基準： (A) (B) (C) (A) 1 (B) 1 (C) 1 列合計の逆数 ウェイト q₃₁= q₃₂= q₃₃= (2)各代替案の総合ウェイトを計算しなさい。 代替案(A) 代替案(B) 代替案(C)

5.5

計算方式の理屈

一対比較行列から、ウェイトを計算する手順の理屈を考えてみましょう。一対比較行列を A = (aik)とします。もし、三つの評価基準の絶対的ウェイトを持っている人がいたとしたら、 その人の一対比較行列はどういう特徴があるでしょうか。その人の絶対的ウェイトを{w_i}とす ると、おそらく基準iの基準kに対する重要度は、絶対的ウェイトに基づいてw_i: w_kである、 つまり「i基準のk基準に対する相対重要度はw_i/w_kである」と答えるに違いありません。した がって、その人の理想的な一対比較行列は次のように表すことができるでしょう。 D =    w1/w1 w1/w2 w1/w3 w2/w1 w2/w2 w2/w3 w3/w1 w3/w2 w3/w3    (2) この理想的な一対比較行列を基にウェイトを計算すると、列合計の逆数の分母はどの列も共通で w1+ w2+ w3= 1となりますから、各評価基準のウェイト（比）はw1 : w2: w3となり、正確 なウェイトが計算されていることが分かります。行ごとに幾何平均を取る場合も同じような結果 が得られることを確かめてください。 実際の一対比較では絶対基準があるわけではなく、また、重要度の数字もティックマークの倍 数という、きわめていい加減な「数量化」に基づいているので、このような絶対基準による評価 のように都合良くはいきません。しかし、理性的な人間ならば上のような考え方をある程度前提 として評価すると考えられるので、ここで導入した簡易的な方法の有効性が期待できます。実 際、日本地図の実験で見たように、全体のバランスは気にせずに、二つ同士の一対比較を積み上 げていっても全体のウェイト比が適切な値に落ち着いたように、いろいろな実証的な実験から、 人間の量的判断は意外と合理的、ということが分かっています。 練習5.7 各行の積の三乗根を計算し、それの合計が１になるように調整すると、w₁: w₂: w₃に なることを証明しなさい。 5.5.1 参考 固有値 ウェイトの計算法として列和の逆数を採用しましたが、後ほど出てくる整合性の検討のよう に、数学的な理論展開をする場合には、別の計算法を導入しておく必要があります。それは行列 の固有値を利用するものです。 上の理想的一対比較行列Dから出発します。Dに右からウェイトベクトルを掛けるとウェイ トベクトルを３倍したものに等しくなることに注意してください。 D ×   w_w1₂ w3   =   w_w1₂/w_/w1_{1 w}w₂1_/w/w₂2 _ww₂1_/w/w3₃ w3/w1 w3/w2 w3/w3     w_w1₂ w3   = 3   w_w1₂ w3  

これは真のウェイトベクトルが理想的な一対比較行列Dの固有値3に対する右固有ベクトルで あることを示しています。また、行列Dの性質から、その最大固有値は3であることが分かっ ています。 一般に、 比較対象がM 個ある場合、上の行列Dに対応する行列の最大固有値はM である ということが分かっています。したがって、もし実際に得られた一対比較行列Aが理想的な一 対比較行列Dに近いならば、実際には未知のDの代わりに、Aの最大固有値を求め、その固有 値に対する右固有ベクトルを求めることにより、Dの固有ベクトル、すなわち求めたいウェイト ベクトルの近似値が計算できることが期待できます。 固有ベクトルを計算するのは面倒な手続きを必要としますが、都合の良いことに、幾何平均 （あるいは、列和の逆数）を用いたウェイトは、真の固有ベクトルとそれほど大差がないという ことが実験的に確かめられていますので、実用的にはこれからも固有値の替わりに簡易計算法を 使って計算しても構いません。つまり、真の一対比較行列の固有ベクトルを求める、という最終 目標を達成するために、（真の一対比較行列が分からないので）実際に得られた一対比較行列の 固有ベクトルで近似するのですが、それも面倒なので、列和の逆数を基準化したベクトルでさら に近似した、というのが上で説明したウェイトの計算法です。 注意 行列の固有値、固有ベクトルって何ですか。どうやって計算しますか。線形代数の教科書 を復習しておきなさい。

5.6

整合性の検討

一対比較が理想的に行われれば、たとえば価格を装備より重視し、装備を環境より重視すると したならば、価格を環境を比べたとき、前者を（非常に）重視するはずですが、人間のやること なので、必ずしもそのように首尾一貫しているとはかぎりません。価格を環境よりやや重視す る、という評価ならばまだしも、価格より環境を重視する、という全く矛盾した評価を下す可能 性もないわけではありません（価格より環境を重視、環境より装備を重視、装備より価格を重視、 従って、価格より価格を重視！？）。 矛盾のある一対比較は不注意によることが多いので、そのような一対比較からはあまり意味の ある結論は期待出来ません。そこで一対比較行列が矛盾していないかどうかを判定して、判定 がクロならば一対比較をやり直す、という手順が必要になります。それを整合性の検討といい ます。 5.6.1 整合度指標 一対比較の質問に対する回答をまとめた一対比較行列をA = {a_ik}、そこから計算されたウェ イトを{v_i}とします。もしそのウェイトが「本当の」ウェイトに近いものであるならば、その 人の一対比較は aik≈ _vvi k となっているはずです。

そこで、{v_i}を使って作った理想的な一対比較行列をD = {d_ik}として（d_ik= v_i/v_kです） aik/dikが1に近いかどうかを調べてみることにします、といっても各項バラバラに調べるのは 面倒なので、それらの平均値 β = 1 9 3 X i,k=1 aik dik = 1 9 3 X i,k=1 aikv_vk i を計算し、 C.I. =_{3 − 1}3 (β − 1) = 3β − 3₂ (3) が0に近ければ一対比較は正しく行われたと判断します。この指標C.I.を整合度と言います。 βを計算する式は要素毎の割算という面倒な計算になっていますが、d_ik= d−1_ki という関係に着 目すると、行列AとDの積の対角要素の合計を9で割ったものであることが分かります。 β = 1₉ 3 X i,k=1 aik dik = β = 1 9 3 X i,k=1 aikdki= 1₉ 3 X i=1 Ã ₃ X k=1 aikdki ! 一般に評価基準がM 個の場合の整合度は、上のように作られた一対比較行列Aと、理想的な 一対比較行列Dを使ってA × Dを計算し、A × Dの対角要素の平均、つまり対角要素の合計を M で割ったものをbとし（上の3βに対応する）、 C.I. = _{M − 1}b − M によって計算されます。 これは幾何平均や合計の逆数を使った方法と同様に整合度を求める簡便法です。整合度C.I. の正確な定義は、一対比較行列Aの最大固有値をλ_maxとしたとき C.I. =λmax_{M − 1}− M (4) によって定義されます。前節の説明で分かるように、理想的な一対比較が行われていればb = M になりますから整合度は0になります。しかし、その判断が曖昧さを増すにしたがって、行列A の最大固有値は大きくなって行くので、整合度がある一定の値以下の場合に、一対比較に整合性 があると評価されます。整合度があまり大きい値になった場合は要注意ですが、その境界は曖 昧で、 その基準は経験的に0.1以下、あるいは大きくても0.15以下 とされています。整合度チェックに合格しないということは一対比較に矛盾があるかもしれな い、ということの警告を意味しますから、もう１度一対比較をやり直す必要があります。 練習5.8 練習5.3で作った一対比較行列の整合度C.I.を計算しなさい。 b= C.I. =

5.6.2 参考 整合比 整合性をチェックするもう一つの指標は整合比(C.R.)と呼ばれるものです。これは整合性を 全く無視して勝手に（支離滅裂に）一対比較をした結果から式(4)のような計算を行なったとき 得られる整合度の値の平均値（これをランダム整合度R.I.といいます、表参照）と実際に得られ た整合度（C.I.）を用いて C.R. = C.I._R.I. によって定義されます。このC.R.も小さければ小さいほど整合性が優れているといえます。経 験的には0.2より大きければ整合性に問題ありと判断して、一対比較をやりなおすのが望ましい とされています。 表 ランダム整合度表 M 3 4 5 6 7 8 9 10 R.I. 0.58 0.90 1.12 1.24 1.32 1.41 1.45 1.49 練習5.9 自分の作った一対比較行列について、ランダム整合度R.I.を使って、整合比C.R.を 計算しなさい。 C.R. = 練習5.10 意図的に矛盾する一対比較行列表を作り、整合度C.I.、整合比C.R.を計算しなさい。 たとえば、自分の作った一対比較行列の中で、一つの要素を9から 1₉まで動かして、整合度がど れくらい大きくなるのか、0.15以内に収まるのはどの程度までの誤差か、チェックしなさい。

5.7

評価基準の階層化

ウェイトの計算と並んでもう一つの問題は、評価基準としてどのような要因をピックアップす ればよいか、ということです。これまでの説明では車購入時の評価基準を価格、装備、環境の三 つに絞って意思決定をしましたが、実際にはもっといろいろな評価基準があり、ちょっと考えた だけでも以下のようなものがあります。 価格、燃費、維持費、ローンの条件、税金、下取り価格、ブランド（メーカ）、車のタイプ、 スタイル（外見）、色、車内容積、排気量、操作性、マニュアルかオートマチックか、加速 性、シート材質、オプションの選択肢、カーナビ、オーディオの充実度、装備（エアバッ ク、車体強度など）、乗り心地、居住性、ゆったり感、環境に対する配慮、リサイクル性、 キーレスか、拡張性、トランクの広さ、販売店の感じ、アフターケア、などなど せっかくいろいろな評価基準を総合化する方法を見つけたわけですから、評価基準も最初から三 つに絞らず、もっといろいろな要因を取り上げて納得の行くものにして行く努力が必要です。し かし、これらすべてについて代替案の一対比較をするのは事実上不可能でしょう。 評価基準を選ぶ場合には、評価基準の多さとは別に次のような問題もあります。もし、評価基 準として、「経済性（なるべく安いもの）」基準と「機能」基準を選び、それらに2 : 1のウェイト を与えたとしましょう。もし、同じ人が別の時に「価格」「維持費」「装備」の三つを評価基準と して一対比較をしたと考えてください。「経済性」を重視するならば「価格」と「機能」を比較し た場合も「価格」を重視し、「維持費」と「機能」を比較した場合も「維持費」を重視することに なり、両方とも2 : 1に近いウェイト比を付けるでしょう。「価格」は購入前、「維持費」は購入 後の「経済性」の主要因なので、二つの基準のウェイトを合わせたものが「経済性」基準のウェ イトになる、と考えると、「経済性（価格と維持費）」と「機能」のウェイト比は4 : 1になってし まい、最初の評価結果とは異なり、「経済性」基準を不当に重視する結果になってしまいます。 このような問題を回避するために、評価基準をリストアップしたら、同じような性質の基準を 一つのカテゴリーにまとめるようにします。一対比較の手間を考えて、カテゴリーの数は高々５ ないし６程度に絞ってください。一つのカテゴリーの中でも、同じような性質の基準がある場合 はサブカテゴリー化するようにし、一対比較する対象は常に高々５ないし６程度になるように抑 えます。 このように、基準となる性質を大分類から中分類、小分類に階層化したものは階層図に表現す ることができます。上の例で言うと、まず「経済性」「機能」の二つの基準でウェイトを付け、 「経済性」に付与されたウェイトを「価格」「維持費」の二つの基準に分割する、と考えるのです。 それを次のような図で表すことにします。

評価項目の階層化 たくさんある評価基準を適当にグルーピングし、重要なものからそうでないものまで並べ替 え、最終の決定に至るまでの意思決定のプロセスを階層構造化することによって一見収拾のつか ない評価基準の集合をまとめ上げる工夫を考えたのが、この手法がよく使われるようになった原 因の一つです。タイトルの階層的意思決定法はこのような階層化の考え方を全面に押し出した ネーミングといっても良いでしょう。 練習5.11 携帯電話を買い換えることを想定し、評価基準となるものをなるべく多くリストアッ プしなさい。それらを階層化し、階層図にまとめなさい。友達とブレーンストーミングをやって みてはいかが。

5.8

感度分析

一対比較による評価基準のウェイト比はそのときの気分や、キャンペーンなど外部からの情報 でも揺らぐものです。ウェイト比が違うとそれに基づいて計算されたウェイトも違い、総合点も 違ってきますから、結論が変わってくる可能性があります。あまり結論がコロコロ変わるようだ と、方法自体も信頼がおけないものにみえてきますから、ウェイトの違いがどの程度結論に反映 されるのかを押さえておく必要があります。 5.8.1 評価基準の評価の変動 価格、装備、環境のウェイトをw₁, w₂, w₃、価格基準の下でトヨタ、ニッサン、ベンツの点数を t1, n1, b1、装備基準の下でトヨタ、ニッサン、ベンツの点数をt₂, n₂, b₂、環境基準の下でトヨタ、 ニッサン、ベンツの点数をt₃, n₃, b₃とすると、たとえば、トヨタの総合点はw₁t₁+ w₂t₂+ w₃t₃ のように計算できます。ここで、たとえば、 環境基準をもっと重視して選ぼう というように判断基準が変わったとしたら総合点はどのような影響を受けるでしょうか。 ウェイトの合計は１でなければいけませんから、環境のウェイトを増やせば、他のウェイトを 減らさなければいけませんが、問題を単純にするために、価格と装備のウェイト比（w₁: w₂）は 変えないようにして環境のウェイトを増やすようにします。例えば、トヨタの総合点はつぎのよ うに書き換えることが出来ることに注意してください。 w1t1+ w2t2+ w3t3= (w1+ w2) µ w1 w1+ w2t1+ w2 w1+ w2t2 ¶ + w3t3 (5) ここでw₃を動かしてみようということなのですが、w₃を動かしてもw₁: w₂は変えないように するということから、w₁/(w₁+ w₂), w₂/(w₁+ w₂)は変わりません。また、t₁, t₂は価格、装備 の基準の下での得点ですから、環境のウェイトを変えても変わりません。結局、 w1 w1+ w2t1+ w2 w1+ w2t2(= y) はw₃が変わっても影響されない量です。したがって、トヨタの総合点はw₃の１次関数として 表すことが出来ます。 w1t1+ w2t2+ w3t3= (1 − w3)y + w3t3 (6) ニッサン、ベンツの総合点についても同様な変形をすれば、w₃の変化によるトヨタ、ニッサン、 ベンツの総合点の変化を調べることができます。 下の図はそのようにして描いた図の例です。横軸はw₃、縦軸は総合点です。３本の線は三つ の車種の総合点を表しています。この図からは、現在の環境のウェイトが0.1と低く見積もって いるためにトヨタの総合点は最下位ですが、もし、環境のウェイトをもう少し上げて50%くら い重要視しよう、というように意識が変わってくると、トヨタの評価がトップになるということ が分かります。逆に、環境という評価基準が多少重要視されるようになったとしても、30%以上 重要視することはないだろうと判断した場合は、一対比較が多少ぶれてウェイトが変わったとし ても、最終結果に影響を及ぼさない、ということが主張できます。このように、状況が少し変化

したら決定がどのように変化するか（しないか）を検討するプロセスを感度分析(sensitivity analysis)といいます。 図1 環境基準の感度分析 5.8.2 モデル分析の意味 感度分析は階層的意思決定法に限らず、モデル分析を適用する場合に、必ず必要となる後処理 過程です。モデルはある問題を分析する際に、当面必要な要因だけをピックアップして作り上げ たものですから、そのモデルに含まれない要因も数多く存在します。また、モデルを構築する際 に使われたパラメータの値も、過去のデータ、あるいは経験に基づいて一時的に決めらること が多く、必ずしも正当性を主張できるものとばかりはいえません。そこで、パラメータの値が ちょっと変わったらどうなるのか、モデルの構造が少し変わったらどうなるのか、モデル分析の 仮定がくずれたらどうなるのか、というようなことをきちんと分析しておかないと、そのモデル の有用性が適切に主張できないことになります。 5.8.3 階層的意思決定法の信頼性、有用性 階層的意思決定法は、その時々の気分で左右されるかもしれない一対比較から出発した曖昧な 評価法で、信頼性に欠けるように思われますが、考えてみれば、何か物事を決めるときに、費用 が少ないとかもうけが大きいというように、判断基準が数量的な評価関数で説明出来る場面はま れで、どっちと決めかねることは多いように思われます。 経験やカン、感性のような曖昧な基準に頼ることなく合理的な意思決定が必要ということか ら、オペレーションズリサーチの考え方が広く世に受け入れられてきたのですが、やはりそれ抜 きにしては考えられない、ということが（考えてみれば当たり前のことですが）だんだんと分 かってきました。しかし、それでも意思決定は合理的な説明が出来なければいけない、というこ とは譲ることが出来ません。そこで考えたのが、曖昧さを数量化できないか、ということでした。 感性的な基準でも、比較対象が二つならば優劣を判断することは可能だろう、というのが出発 点です。すべてのペアに対して一対比較をすれば、全体としてのウェイトが計算できる、という 道筋を示したのが数学の力です。さらに、判断基準がたくさんあっても階層化して考えれば適正

なウェイト付けが可能、としたのが階層的意思決定法の考え方でした。 優劣を付けるだけならば他にも方法があるかもしれませんが、それに感度分析の考え方を導入 したことにより、階層的意思決定法は実用的な価値を持つことになったのです。評価基準は曖昧 ですから、最終的に計算された総合ウェイトはそれほど信用できるものとは考えられませんし、 そう解釈すべきものでもありません。判断がずれたら総合ウェイトがどれだけずれるか、という ことに関心を持たなければいけませんが、逆に、もし判断が多少ずれたとしても総合ウェイトの 大小関係は変わらないということが分かれば、評価が多少曖昧でもそれほど神経質になる必要は ない、ということになるでしょう。 最適な代替案を選ぶというよりは、ある代替案はどのように評価しても総合ウェイトが他より 大きくなることはないということが分かれば、それを候補から外すことが出来ます。ある基準に ついてその評価が総合ウェイトの変動に影響を与えているとすれば、その評価についてより詳し く検討しよう、というような力のいれどころを特定することが出来るようになります。 このようにして、階層的意思決定法は、評価の曖昧な意思決定の問題点を洗い出すことができ る、有効な手法ということができます。 練習5.12 携帯電話の例で、もっともウェイトの高かった評価基準について、感度分析を実行し なさい。

5.9

階層的意思決定法の実施例

最後に掲載した参考図書には階層的意思決定法（AHP）を実際の問題に適用した例がいくつも 説明されています。その一例を挙げれば ・コンピュータの機種選定 ・セールスマンの成績評価 ・新エネルギーシステムの評価 ・公共交通システムの評価 ・街路樹の選定 ・アンケート調査による要求品質の推定 ・ワープロソフトの評価 などです。今まで、何となく「感じ」で決めていたようなことでも、その判断基準を階層図にま とめウェイトを数量的にはっきりさせることで意思決定のやり方に新たな視点を提供した、とい う点でこのAHP法は画期的な方法といってよいでしょう。 もちろん、どんな方法でも万能ということはなく、これでおしまいというわけには行きませ ん。AHP法の場合も、この分析によって得られた総合評価で高い点を得たからといって、それ を直ちに意思決定に結びつけるのは早計というものです。評価基準のリストアップ、その階層 化、ウェイトの計算など、いずれもものの見方は一つとは限りません。むしろ、この方法は問題 の整理や新たな問題点の発見など、問題に関わる人たちの間のコミュニケーションの場と捕らえ たほうがよいでしょう。 練習5.13 スキー旅行の行く先、パソコンの機種の選定、就職業種の選択、研究室の選択、プロ バイダの選択、など評価基準が多そうな問題を選んで、いろいろな階層図を描き、友人と議論し てみて、階層図がどう変わって行くか体験してみてください。

参考図書

[1]刀根薫「ゲーム感覚意思決定法」日科技連出版社(1986) [2]八巻 直一、高井英造「問題解決のためのAHP入門」日本評論社(2005) [3]刀根薫、真鍋龍太郎編「ＡＨＰ事例集」日科技連出版社（1990） [4]木下栄蔵、大屋 隆生「戦略的意思決定手法ＡＨＰ」朝倉書店（2007）

6

日程計画・日程管理

6.1

はじめに

土木・建設工事、新製品開発、ロケットの打ち上げ、イベント企画、など、大規模なプロジェ クトの計画を立て、その進捗状況を管理することは大変な労力が必要です。プロジェクトが大型 になり、作業工程が複雑になれば、納期までに仕上がる計画が立てられるのかどうかすらも分か らない、ということも起こる危険性があります。さらに、企画立案されたプロジェクトが実行に 移された場合、事前の計画通り行くということはまれで、初期の計画を変更しなければならない ということも頻繁に起こります。このように、複雑なプロジェクトの実施計画を合理的に立案 し、進捗状況に応じて計画の変更が容易に行なえる手法がP ERT/CP M（Program Evaluation

and Review Technique / Critical Path Method）です。

P ERT は1950年代の後半にアメリカの海軍が新兵器（ポラリスミサイル）を開発する際に、 考案されたもので、この手法を使うことによって ・プロジェクトを完了するのに最低どれくらいかかるか ・どの作業が完了時刻に影響を与えているか ・どの作業が余裕があるか、それはどれくらいか ・完了予定期日より早い締め切りが設定されたとき、どう対処するか ・資金や人員の制約があったとき、最適な計画はどのようなものか ・作業の進捗状況・遅れをどのように管理するか ・途中で計画が変更になったとき、どのように対処するか などの問題に有効な解決手段を提供します。以下で例題を使って、これらのいくつかがどのよう に解かれていくのかを見てみましょう。

6.2

簡単な例題

新製品開発

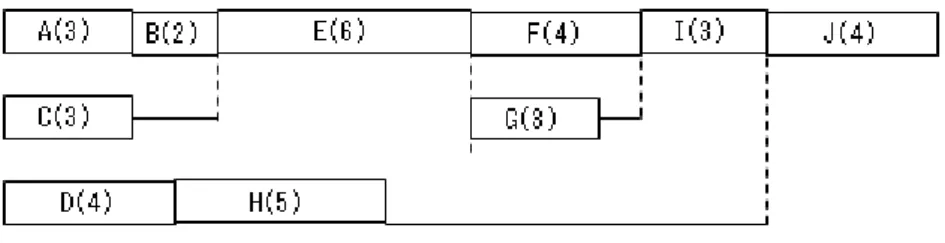
ある企業で新製品の開発を企画したとしましょう。完成に至るまでの過程には、顧客アンケー トを取って市場の動きを把握し、他社競合商品を研究するところから始まって、基本設計、試作 品の検討、資材の調達など、多くの作業が必要になります。一つ一つの作業単位をノードとし て、ワークフローをネットワークに表現できたとしても、ネットワークが複雑に入り組んでスパ ゲッティ状態のものになってしまい、全体の見通しを立てることは困難です。このような問題に おいて、たとえば、新製品を市場に出せるのはもっとも早くていつになるのか、あるいは進行を 予定より３ヶ月早めて新製品を市場に送り込みたい、とするならばどの作業をスピードアップし なければならないか、という極めて現実的な要求に対して、どのようにアプローチしたらよいで しょうか。 実際の状況はもっと複雑ですが、P ERT の手法を理解するために簡単化した問題を考えます。 まず、作業を特定し、そのワークフローを書く必要がありますが、いきなり図を書かないで、作 業のリストとそれぞれの先行作業、後続作業が何であるかを表にまとめることから始めます。一 つの「作業」をどう決めるか、ということはのちのちの分析をするうえで大きな影響を及ぼしま

すから十分に検討しなければなりませんが、それは問題ごとに異なりますので、ここでは具体的 な方策については立ち入らないことにします。 ここで例として用いる簡単な問題は、下の表のように、AからJ までの10個の作業からなる プロジェクトです。各作業ごとに先行作業が何かということと、その作業の完了までに必要な時 間（見積り作業時間といいます）を書いておきます。 表2.1 新製品開発プロジェクト作業一覧 作業記号 作業内容 見積り作業時間 先行作業 A 顧客アンケート調査 3 − B アンケート結果の分析 2 A C 実験結果の整理 3 − D 競合製品の調査 4 − E 基本構想の立案 6 B, C, D F 実装構想の具体化 4 E G 回路構想の具体化 3 E H 競合製品の原価分析 5 D I 原価見積り 3 F, G J 構想の手直しと最終決定 4 H, I 例えば作業Eを実施するのに作業Aも終わっていなければいけませんが、それは作業Bを終え ているための必要条件ですので、この先行作業リストには含めません。「直接の」先行作業、と いう意味だと思ってください。先行作業表が与えられれば、後続作業が何かは決定できることに 注意してください。例えば、作業Eの後続作業は作業Fと作業Gです。作業J には後続作業 がありません。 これらの作業の流れを把握し、プロジェクトの全体像を見るためには作業の流れ図がよく用い られます。作業をノードにして、直接の先行作業と後続作業を向きの付いたアークで結ぶネット ワーク図で、たとえば下の図のようなものがそうです。 図2.1 作業のフローダイアグラム 作業の流れ、先行・後続関係を見るためにはこのフローダイアグラムも十分に実用的ですが、 作業の時間的な進行具合が不明確という点で不十分です。時間的な進行を管理するための図とし ては、スケジューリングで用いられるガントチャートがあります。次の図はその一例です。時間 軸を左から右に流れるよう取り、作業を作業時間に比例した長さの１本の棒で表し、先行作業、 後続作業の関係を考えながら、それらの棒をつなげて行くことにより、プロジェクト全体を把握 しようという考え方です。

図2.2 ガントチャートもどき この図から、プロジェクトは予定通りすすめば22単位時間で終了し、たとえば、作業A, B, E などがちょっとでも遅れるとプロジェクト全体の完成が遅れるという意味で、納期の管理をきち んとしなければいけない作業群だ、ということなどが分かります。作業の数が少ないときはこれ でも十分に明快な表現になりますが、平行して多数の作業が進行する場合は先行する作業群をす べて把握することは難しくなりそうだということが容易に予想されます。そこでP ERT 技法が 登場します。

練習6.1 次の表2.2はあるプロジェクトの見積り作業時間と先行作業をまとめたものです。各 作業の後続作業を表に記入しなさい。また、この表の右側にプロジェクトの「フローダイアグラ ム（フローチャート）」を描いてごらんなさい。 表2.2 プロジェクト作業一覧 記号 見積もり作業時間 先行作業 後続作業 A 3 − B 4 − C 5 − D 5 A E 2 A F 3 B G 6 B, C H 6 E, F I 2 D J 3 I, H K 4 G, H, I 練習6.2 表2.2のプロジェクトの「ガントチャート」を描きなさい。

6.3 P ERT

による日程計画の実行手順

新しい手法といっても、特別な装置や知識を要求されるようなものではありません。作業たち を左から右に流れるようなネットワーク上に配置して、図式表現するという考え方は同じです が、ちょっとした発想の転換によって、それがとても便利な道具に変身するのです。「図式表現」 と書きましたが、上で見たように作業群が多くなった場合、ネットワーク図は、「スパゲッティ のような」混乱したものになって使い物になりません。 P ERT の良いところは、概念的にはネットワーク図を想定しますが、実際の図を描かなくて も、作業の段取りに必要な情報が表2.1のような一覧表が与えられただけで「計算」できてしま うことにあります。プロジェクトが完成するまでにどれくらいかかるのか、どの作業がボトル ネックになっているのか、余裕のある作業はどれか、その余裕はどれくらいあるのか、などなど。 P ERT は以下の手順によって実行されます。 1. 作業リストの作成（所要時間、先行・後続作業の確定、費用・資源の見積り） 2. P ERT ネットワーク（アローダイアグラム）の作成 3. 完了時間、余裕時間、クリティカルパスの計算 4. 資源（時間、人員、資材、．．．）制約の下での最適化問題を解く P ERTを適用するのに手順２は必要ない、ということを書きましたが、現場とのコミュニケー ションを考えると、EXCELの表のような出力だけでは頼りないので、視覚化しておくことも 実際には欠かせないステップです。ここでも、アローダイアグラムを基本に説明して行きます。

6.4

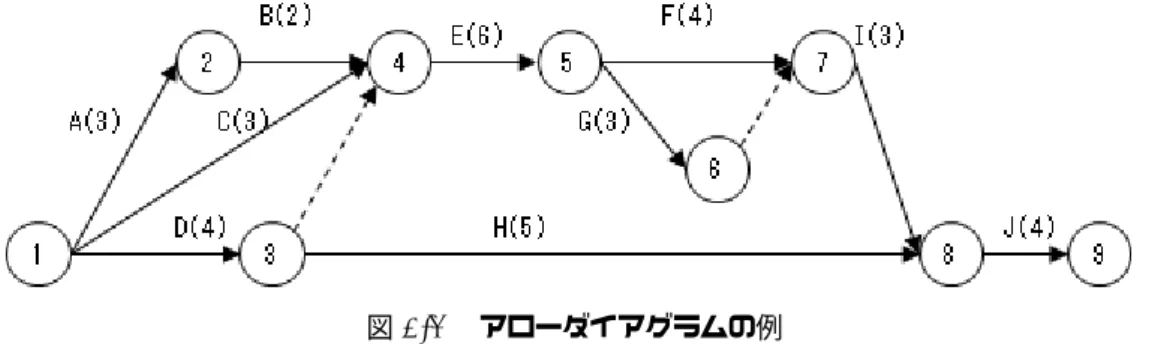
アローダイアグラム

P ERTを特徴づけるのがアローダイアグラムと呼ばれる有向グラフ、すなわち、有限個のノー ドとノード間を結ぶ向きの付いた向きのついた枝（アーク、矢印とも言います）からなるネット ワークです。フローダイアグラムでは作業を一つのノードに対応させましたが、ここでは作業を 一つの矢印に対応させ、作業の開始、終了という「状態」をノードで表現することにします（こ れが「発想の転換」です）。 次の図はアローダイアグラムの一例で、矢印に添えたアルファベットが作業の記号です。たと えば、ノード番号４は「作業B, C, Dを終えて作業Eを開始できるという状態」を表現してい ます。また、それによって、作業Eの先行作業は作業B, C, Dであることもわかります。点線 の矢印はすぐ後で説明しますが、矢印を順に追って行くと、このアローダイアグラムは図2.1の フローダイアグラムを書き換えたものだということがお分かりでしょう。

図2.3 アローダイアグラムの例 さて、アローダイアグラムの描き方を説明しましょう。 規則１ 同じノード対を二本以上の枝（矢印）で結んではいけない。枝は作業を表す。 矢印の始点ノードは作業の開始ノード、終点ノードは作業の完了ノードということがありま す。始点ノード、終点（終端）ノードの番号をそれぞれi, kとしたとき、その矢印で表される作 業を、作業(i, k)と言います。作業をノード対と同一視するために、この規則が必要になります。 ガントチャートの対比で説明すれば、ノードiは作業(i, k)を開始できる準備が整った状態を表 し、ノードkは作業(i, k)が完了して次の作業を始める準備が整った状態を表す、ということが できます。 規則２ 作業Aが作業Bの先行作業ならば、Aを表す矢印からスタートして矢印をたどってB を表す矢印に推移できなければいけない。 この例では、ノード２は作業Aが終了し、次の作業が開始できる状態を表し、それはまた、作 業Aの後続作業Bを開始する準備が整った状態なので、このようにつなげて良いことになりま す。先行作業、後続作業が複数ある場合も同様。例えば、次の図は作業C, D, Eはすべて作業 A, Bを先行作業としている場合です。状態３は作業C, D, Eを開始できる準備が完全に整った 状態、ということが出来ます。 普通に考えれば作業をノードに置くフローダイアグラムの方が先に思い浮かび、作業を矢印 で表現するというのは最初ちょっと違和感があります。しかし、ガントチャートの棒グラフを

矢印に変えたものと考えれば、全く異質な考え方というわけでもないということが分かります。 実際、 のように矢印の長さを時間に比例させれば、作業Bは作業Aより早く終わる、という状況を読 み取ることが出来、作業のつながりと時間の進行を同時に表現することが可能で、表現の幅が広 がっていることが分かるでしょう。 以上の約束だけで作業全体をネットワーク化しようとすると、すぐに障害が発生します。たと えば、作業Cの先行作業は作業Aのみ、作業Dの先行作業は作業A, B、という状況を考えて みてください。そのまま素直にネットワークを描くと次のようになるでしょう。 作業Cの先行作業はAだけ、作業Dの先行作業はAの他にBも必要ということから、この図 のように、どうしてもAという作業を表す矢印が二本必要になり、「一つの作業は１本の矢印で 表す」という規則に抵触します。しかし、無理にどちらか１本の矢印を消そうとすると、作業 Cの開始ノードは作業Aの完了ノードと同じ、作業Dの開始ノードは作業Aと作業Bの完了 ノードと同じ、という条件を同時に満たすことは不可能です。 そこでP ERT ではダミー作業というウラワザを使います。ダミー作業は作業時間０の作業 で、アローダイアグラムでは点線の矢印で表します。 上の図で作業Dはノード４に入ってくる矢印の作業すなわち作業Bと作業(3, 4)が終わらない と開始できません。作業(3, 4)は作業Aが終わらないと開始できませんが、作業Aが終わると、 作業(3, 4)も直ちに終了するという約束です。したがって、ノード4は作業A, Bが完了した状 態、となり、作業A, Bを先行作業とする作業Dはこのノードを始点とすることが出来るので す。一方、作業Cはダミー作業とは関係なく、作業Aが完了すれば直ちに開始することができ ます。 規則３ 作業時間が0の作業（これをダミー作業という）を任意に付け加えることが出来る。

作業B, C は、同じ先行作業Aを持ち、同じ後続作業Dを持つ、という場合も、ダミー作業 を使う必要があります。作業BとCの開始ノードは作業Aの完了ノード、作業BとCの完了 ノードは作業Dの開始ノードですから、作業Bも作業Cも、作業Aを完了したという状態と、 作業Dが開始出来るという状態を結ぶのが自然です。しかし、これは「二つのノードを２本以 上の矢印で結んではいけない」という規則に反します。 そこでダミー作業を導入して次のように表現します。 矢印(2, 3)に作業Cを、矢印(2, 4)に作業Bを割り当てても構いませんが、所要時間を考慮 すると、上の図の方が混乱が無いでしょう。また、ダミー作業は流れを変えない限り、いくつ描 いても、どこに描いても自由です。例えば、上の図で、新たにノード3′を作り、矢印(2, 4)を消 して、作業Cを表す矢印(2, 3′)と、ダミー作業を表す矢印(3′, 4)に置き換えても結果は変わり ません。特に基準があるわけではありませんが、不要なダミー作業はあまり描かないようにする のが、賢明です。 いくつかの、例題を解いてみてください。断りがなければ、プロジェクトの一部分だけを取 り出したものを考えて、与えられた条件だけが成り立っていることが分かるものであれば十分 です。

練習6.3 作業Dの先行作業は作業Cと作業B、作業Fの先行作業は作業Cだけ、という場合 のアローダイアグラム（その部分だけ）を描きなさい。 練習6.4 作業F が終わると作業Gと作業H を開始することができる、作業Gと作業H が終 わると作業Jが開始できる、という場合のアローダイアグラムを描きなさい。 練習6.5 作業Dは作業Aが完了すれば開始できる、作業Eは作業Aと作業Bが完了すれば 開始できる、作業F は作業A, B, Cが完了すれば開始できる、という場合のアローダイアグラ ムを描きなさい。ダミー作業はなるべく最小限に留めてください。 最後にプロジェクト全体をまとめるために、プロジェクトの開始ノードと完了ノードを定義し ます。 規則４ ノード番号１はプロジェクトの開始ノードと言い、先行作業のない作業を表す矢印はす べて、そのプロジェクトの開始ノードを始点とする。 規則５ プロジェクトの完了ノードという特別なノードを作り、後続作業のない作業の終端ノー ドはこの完了ノードと一致させる。 170ページ、図2.3のノード1がプロジェクト開始ノード、ノード9がプロジェクト完了ノード です。 プロジェクト開始ノード、プロジェクト完了ノードを一つに絞るというのは、すぐに説明しま すが、後のP ERT 計算で重要な意味を持ってきます。たとえば、こういう風に考えてみてくだ さい。プロジェクトの開始直前には出陣式？お清め？という部分作業があり、全ての作業に先行 する、と考えれば、先行作業の無い作業は全て、その出陣式が終わったという状態からスタート

しなければいけません。出陣式が終わったという状態がプロジェクト開始ノードです。 一方、プロジェクトが完了したら、竣工式？打ち上げ？という部分作業があり、全ての作業は それまでに終了していなければいけない、と考えると、後続作業のない作業はすべて、この竣工 式が開始できる状態を終点ノードとすべきだということになります。竣工式が開始できる状態が プロジェクトの完了ノードです。 アローダイアグラムの説明は以上でおしまいです。プロジェクトの開始ノードから完了ノード まですべての作業を先行・後続の関係を保ちながら埋め込んだダイアグラムを描くことは経験が 必要ですが、規模が小さければそれほど困難なことではありません。また、同じプロジェクトで も、ダミー作業の使い方の違いから描く人によって異なることはあり得ますので、どれが正解と いうことはありません。 練習6.6 作業A, B, C, D, Eからなるプロジェクトで、作業A, B には先行作業が無く、作業 C, Dの先行作業は作業A、作業Eの先行作業は作業B, Dという場合の、P ERTネットワーク を描きなさい。 練習6.7 168ページの練習問題6.1で与えられたプロジェクトのP ERT ネットワークを描きな さい。