1.3.2
球座標での変数分離法(3.3.2 Spherical Coordinates)
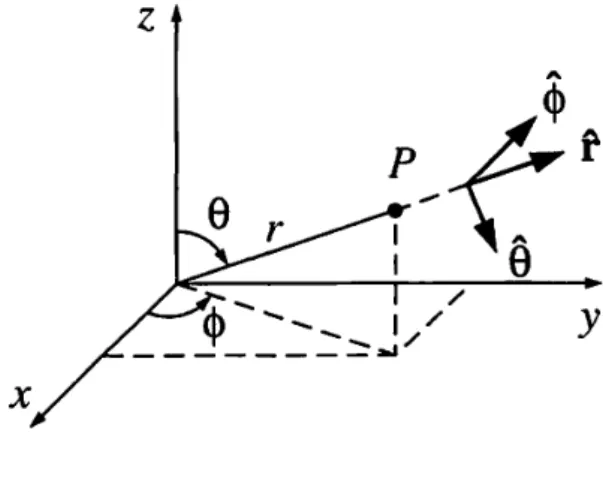
図 1.15: 球座標.
境界が球面で与えられる場合は,球座標による変数分離が有効である.デカルト座標から球座標への変換は x = r cos φ sin θ, y = r sin φ sin θ, z = r cos θ (1.93) で与えられる.球座標での Laplace 方程式は ∇2V = 1 r2 ∂ ∂r ! r2∂V ∂r " + 1 r2sin θ ∂ ∂θ ! sin θ∂V ∂θ " + 1 r2sin2θ ∂2V ∂φ2 = 0 (1.94) で与えられる.(1.94) の導出の詳細はこの節の最後に補足1として与える.ここでは簡単のため,ポテンシャ ルは z 軸周りで対称,すなわち V が方位角 φ に依存しない場合を考えることにしよう.このとき Laplace 方 程式は 1 r2 ∂ ∂r ! r2∂V ∂r " + 1 r2sin θ ∂ ∂θ ! sin θ∂V ∂θ " = 0 (1.95) となる.ここで解を変数分離形 V (r, θ) = R(r)Θ(θ) (1.96) に仮定する.(1.96) 式を (1.95) 式に代入して V で割ると 1 R d dr ! r2dR dr " + 1 Θ sin θ d dθ ! sin θdΘ dθ " = 0 (1.97) 書き換えると 1 R d dr ! r2dR dr " =− 1 Θ sin θ d dθ ! sin θdΘ dθ " (1.98) となる.左辺は r のみに依存し右辺は θ のみに依存するので,両辺は定数でなければならない.この定数を, 後の便宜のために,l(l + 1) と書くことにすると 1 R d dr ! r2dR ∂r " = l(l + 1), 1 Θ sin θ d dθ ! sin θdΘ dθ " =−l(l + 1) (1.99) となる. 動径関数 R に対する微分方程式は 1 R d dr ! r2dR dr " = l(l + 1) (1.100)
となる.一般解は R = Arl+ B rl+1 (1.101) で与えられる.ただし A, B は任意の定数である.二階の微分方程式なので,一般解は二つの未定定数 A, B を含んでいる.(1.101) 式が微分方程式 (1.100) の解であることは,以下のように容易に確かめられる. r2dR dr = r 2[lArr−1− (l + 1) B rl+2] = lAr l+1 − (l + 1)Brl (1.102) d dr ! r2dR dr " = d dr # lArl+1 − (l + 1)Brl $ = l(l + 1)Arl+ l(l + 1) B rl+1 = l(l + 1)R (1.103) 次に角度方程式 1 Θ sin θ d dθ ! sin θdΘ dθ " =−l(l + 1) (1.104) を考える.この微分方程式は,l が負でない整数のときにのみ,物理的に意味のある解,つまり 0 ≤ θ ≤ 2π の範囲で有限で連続な一価関数の解を持つことが知られている.この解は Legendre 多項式とよばれる. Θ(θ) = Pl(cos θ) (1.105) Legendre 多項式についての詳細と,角度関数が方位角 φ に依存する場合(球面調和関数)については補足 2 を参照のこと.ここでは Legendre 多項式のいくつかの重要な性質のみを記す.Legendre 多項式の一般的な 表式は Rodorigues の公式によって与えられる. Pl(x) = 1 2ll! ! d dx "l (x2− 1)l (1.106) 最初の数個の Legendre 多項式の具体的な表式を以下に示す. P0(x) = 1 P1(x) = x P2(x) = (3x2− 1)/2 P3(x) = (5x3− 3x)/2 P4(x) = (35x4− 30x2+ 3)/8 P5(x) = (63x5− 70x3+ 15x)/8 (1.107) 上式を見てもわかるように,Pl(x) は x の l 次の多項式である.また,l が偶数のときは偶数次の項のみを含 み,l が奇数のときは奇数次の項のみを含む.(1.106) 式の因子 (1/2ll!) は P l(1) = 1 となるように選ばれてい る.Legendre 多項式 Pl(x) は−1 ≤ x ≤ 1 で完全直交系を作ることが知られている. % 1 −1 Pl(x)Pl!(x)dx = % π 0
Pl(cos θ)Pl!(cos θ) sin θdθ = 2
2l + 1δll! (1.108) この性質は境界条件を満たす解を構成するために重要な役割を果たす. 以上によって,軸対称な場合の Laplace 方程式の変数分離解が V (r, θ) = ! Arl+ B rl+1 " Pl(cos θ) (1.109) と求まった.デカルト座標の時と同様に,(1.109) は無限個の解の組を与える.一般的な解はそれらの線形結 合で与えられる. V (r, θ) = ∞ & l=0 ! Alrl+ Bl rl+1 " Pl(cos θ) (1.110) 係数 Alは与えられた境界条件を満たすように定める.その際には Legendre 多項式の直交関係 (1.108) を利 用する.
例題(Example 3.6):境界面でポテンシャルが与えられている場合 (1) 半径 R の球面上でポテンシャルの角度依存性 V0(θ) が定まっているとき,球の内部でのポテンシャル を求めよ.球の内部には電荷は存在しないものとする. 解答:原点 r = 0 でポテンシャルが有限であるためには (1.110) で全ての l で Bl= 0 でなければならない. よって V (r, θ) = ∞ ! l=0 AlrlPl(cos θ) (1.111) 球面上での境界条件を満足するためには V (R, θ) = ∞ ! l=0 AlRlPl(cos θ) = V0(θ) (1.112) 上述のように Legendre 多項式は完全系を作ることがわかっているので,係数 Alを適当に選ぶことにより任 意の V0(θ) に対して境界条件を満たす解を作ることができる.係数 Alを (1.112) 式の両辺に Pl!(cos θ) sin θ をかけて θ で積分する. ∞ ! l=0 AlRl " π 0
dθ sin θPl!(cos θ)Pl(cos θ) = " π 0 dθ sin θPl!(cos θ)V0(θ) (1.113) ここで Legendre 多項式の直交関係 (1.108) を使うと Al!Rl ! 2Rl 2l + 1 = " π 0 V0(θ)Pl(cos θ) sin θdθ (1.114) よって Al= 2l + 1 2Rl " π 0 V0(θ)Pl(cos θ) sin θdθ (1.115) を得る.これを (1.111) 式に代入すれば解が得られる. 具体的な例として, V0(θ) = k sin2(θ/2) (1.116) である場合を考える.sin2(θ/2) = (1 − cos θ)/2 および P0(x) = 1, P1(x) = x より (1.116) 式は V0(θ) = k 2(1− cos θ) = k 2[P0(cos θ)− P1(cos θ)] (1.117) と書ける.これを Alの表式 (1.115) に代入して Legendre 多項式の直交関係 (1.108) を使うと A0= k 2, A1=− k 2R, Al= 0 (l"= 0, 1) (1.118) を得る.これを (1.111) 式に代入すればポテンシャルは V (r, θ) = k 2 # P0(cos θ)− 1 RP1(cos θ) $ = k 2 % 1−R1 cos θ & (1.119) となる. 例題(Example 3.7):境界面でポテンシャルが与えられている場合 (2) 半径 R の球面上でポテンシャルの角度依存性 V0(θ) が定まっているとき,球の外部でのポテンシャル を求めよ.球の外部には電荷は存在しないものとする. 解答:この場合,無限遠方ではポテンシャルは 0(r → ∞ で V = 0) でなければならない.この条件を満た すためには,全ての l に対して Al= 0 でなければならない.よって V (r, θ) = ∞ ! l=0 Bl rl+1Pl(cos θ) (1.120)
球面上での境界条件を満足するためには V (R, θ) = ∞ ! l=0 Bl Rl+1Pl(cos θ) = V0(θ) (1.121) (1.121) 式の両辺に Pl!(cos θ) sin θ をかけて θ で積分すると, Bl= 2l + 1 2 R l+1" π 0 V0(θ)Pl(cos θ) sin θdθ (1.122) を得る.これを (1.120) 式に代入すれば解が得られる. 例題(Example 3.8):一様電場中に導体球が置かれている場合 一様な電場 E = E0ˆz の中に帯電していない半径 R の導体球が置かれている.(図 1.16)導体中の正電荷 は電場による力を受け z の正の方向に移動する.逆に,負電荷は電場からの力によって z の負の方向に移 動する.このようにして誘起された電荷は導体球周辺の電場を変形させる.このとき,導体球外部におけ る電場を求めよ. 図 1.16: 一様電場中に置かれた導体球. 解答:導体球面上は等電位であるから,V (R, θ) = V0とする.また,導体球から遠く離れた場所では電場は 一様で E = E0ˆz であるから V → −E0z + C (1.123) となる.ここで C は xy 面内での無限遠方をポテンシャルの基準点にとると V (z = 0) → 0 より C = 0 とな る3.以上より,この問題の境界条件は (i) V = V0 when r = R (ii) V → −E0r cos θ for r# R
(iii) 導体球は帯電していない.(導体球に誘起された電荷の総和は 0.) (1.124) で与えられる.この問題では条件 (iii) が必要となることに注意されたい.これは,導体球が孤立している(接 地されていない)ので導体球面上でのポテンシャルが指定されていないからである.境界条件 (i)-(iii) を満た すように一般解 (1.110) の係数 Al, Blを求めなければならない. 3Griffiths のテキストでは導体球面上をポテンシャルの基準として V 0= 0 として,対称性により(電場の xy 成分が 0 であるから) xy 面内では等電位であり,したがって C = V0= 0 と結論している.ここでは直感的な議論に頼らずにとりあえず V0を未定の定数と おいて,後で境界条件より定めることにする.
まず先に境界条件 (ii) を考える.r が大きければ Blの項は無視できるので ∞
! l=0
AlrlPl(cos θ) =−E0r cos θ (1.125)
となる.ここで P1(x) = x より (1.125) 式は ∞ !
l=0
AlrlPl(cos θ) =−E0rP1(cos θ) (1.126) と書ける.両辺に Pl!(cos θ) sin θ をかけて θ で積分すると,直交性により l = l"の項だけが残るので,これ より A1=−E0, Al= 0 (l"= 1) (1.127) を得る. 次に境界条件 (i) を考える. V (R, θ) = ∞ ! l=0 " AlRl+ Bl Rl+1 # Pl(cos θ) = V0 (1.128) 前と同様に,Legendre 多項式の直交性により B0 R = V0, AlR l+ Bl Rl+1 = 0 (l"= 0) (1.129) を得る.ただし,(1.127) より A0= 0 であることを用いた.上式と (1.127) より B0= RV0, B1=−A1R3= E0R3, Bl= 0 (l"= 0, 1) (1.130) を得る.(1.127),(1.130) 式を (1.110) 式に代入すると V (r, θ) = RV0 r − E0 " r−R 3 r2 # cos θ (1.131) を得る. 最後に条件 (iii) より未定定数 V0を決める.導体球面上に誘起された電荷の密度分布は σ(θ) =−#0 ∂V ∂r $ $ $ $r=R= #0 RV0 r2 + #0E0 " 1 + 2R 3 r3 # cos θ $ $ $ $r=R= #0 V0 R + 3#0E0cos θ (1.132) となる.これを球面上で積分すると% da = 2πR2%π 0 sin θdθ より (1.132) 式第2項からの寄与は消えて,誘起 電荷の総和は Q = & daσ = 4πR#0V0 (1.133) となる.条件 Q = 0 より,V0= 0 を得る. 結局,ポテンシャルは V (r, θ) =−E0 " r−R 3 r2 # cos θ (1.134) となる.また,表面誘起電荷密度は σ(θ) == 3#0E0cos θ (1.135) で与えられる.これは上半球 (0 ≤ θ ≤ π/2) で正,下半球 (π/2 ≤ θ ≤ π) で負となる.ポテンシャル (1.134) 式は二つの寄与からなる.V = Vex+ Vsphereと書いて
Vex=−E0r cos θ, Vsphere= E0 R3
r2 cos θ (1.136)
もし仮に導体球が帯電していて,表面電荷の電荷の総和が Q であったとすると,(1.131) 式は V (r, θ) = Q 4π#0r− E0 ! r−R 3 r2 " cos θ (1.137) となる.右辺第一項は原点に点電荷 Q が置かれたときのポテンシャルを表している.
補足1:球座標表示における Laplacian の導出
球座標 (1.93) による Laplacian の表式 ∇2V = 1 r2 ∂ ∂r ! r2∂V ∂r " + 1 r2sin θ ∂ ∂θ ! sin θ∂V ∂θ " + 1 r2sin2θ ∂2V ∂φ2 (1.138) を導出しよう. このために,まず極座標表示による gradient の表式 ∇V = ∂V∂rˆr +1 r ∂V ∂θθ +ˆ 1 r sin θ ∂V ∂φφˆ (1.139) を導こう.ここで ˆr, ˆθ, ˆφ はそれぞれ r, θ, φ 方向の単位ベクトルであり,以下で与えられる. ˆr = ∂r ∂r # #∂r ∂r ## = cos φ sin θˆx + sin φ sin θˆy + cos θˆz (1.140) ˆ θ = ∂r ∂θ # #∂r ∂θ #
# = cos φ cos θˆx + sin φ cos θˆy− sin θˆz (1.141) ˆ φ = ∂r ∂φ # # #∂r ∂φ # # #
=− sin φˆx + cos φˆy (1.142)
である.(1.139) を示すために,まず ∂V /∂r をデカルト座標を用いて表すと ∂V ∂r = ∂V ∂x ∂x ∂r + ∂V ∂y ∂y ∂r + ∂V ∂z ∂z ∂r =∇V · ∂r ∂r (1.143) ここで (1.140) 式を用いると ∂V ∂r =∇V · ˆr # # # #∂r∂r # # # # = ∇V · ˆr (1.144) を得る.ここで,|∂r/∂r| = 1 を用いた.同様に ∂V ∂θ = ∂V ∂x ∂x ∂θ + ∂V ∂y ∂y ∂θ + ∂V ∂z ∂z ∂θ =∇V · ∂r ∂θ (1.145) ここで (1.141) 式及び |∂r/∂θ| = r より ∂V ∂θ =∇V · ˆθ # # # #∂r∂θ # # # # = r∇V ·θˆ (1.146) ∂V ∂φ = ∂V ∂x ∂x ∂φ+ ∂V ∂y ∂y ∂φ+ ∂V ∂z ∂z ∂φ =∇V · ∂r ∂φ (1.147) ここで (1.142) 式及び |∂r/∂φ| = r sin θ より ∂V ∂φ =∇V · ˆφ # # # #∂φ∂r # # # # = r sin θ∇V ·φˆ (1.148) ここで,ˆr, ˆθ, ˆφ が互いに直交する基底ベクトルであることから ∇V = (∇V · ˆr)ˆr + (∇V · ˆφ) ˆφ + (∇V · ˆθ)ˆθ (1.149)
と書けるはずである.この式と (1.144),(1.146),(1.148) 式を比較すれば (1.139) が得られる.また,これより ∇ 演算子は ∇ = ˆr∂r∂ + ˆθ1 r ∂ ∂θ+ ˆφ 1 r sin θ ∂ ∂φ (1.150) と書けることがわかる. 次に,Laplace 演算子は ∇2V = ∇ · ∇V (1.151) に (1.150) 式を用いると ∇2V = ! ˆr∂ ∂r + ˆθ 1 r ∂ ∂θ + ˆφ 1 r sin θ ∂ ∂φ " · ! ∂V ∂rˆr + 1 r ∂V ∂θθ +ˆ 1 r sin θ ∂V ∂φφˆ " = ∂ 2V ∂r2 + 1 r2 ∂2V ∂θ2 + 1 r2sin2θ ∂2V ∂φ2 + ∂V ∂r !1 rθˆ· ∂ˆr ∂θ+ 1 r sin θφˆ· ∂ˆr ∂φ " +1 r ∂V ∂θ # 1 rθˆ· ∂ ˆθ ∂θ + 1 r sin θφˆ · ∂ ˆθ ∂φ $ + 1 r sin θ ∂V ∂φ # 1 rθˆ· ∂ ˆφ ∂θ + 1 r sin θφˆ· ∂ ˆφ ∂φ $ (1.152) となる.ここで,球座標表示での ∇ を2回作用させる際には単位ベクトル (ˆr, ˆθ, ˆφ) の微分も考慮しなければ ならないことに注意せよ.また,単位ベクトルの r 微分は 0 であることを用いている.単位ベクトルの表式 (1.140)-(1.142) を用いると, ˆ θ·∂ˆr∂θ = 1, φˆ ·∂φ∂ˆr = sin θ (1.153) ˆ θ·∂ ˆθ ∂θ = 0, φˆ · ∂ ˆθ ∂φ = cos θ (1.154) ˆ θ·∂ ˆφ ∂θ = 0, φˆ· ∂ ˆφ ∂φ = 0 (1.155) を示せる.これらを (1.152) に用いると =∂ 2V ∂r2 + 1 r2 ∂2V ∂θ2 + 1 r2sin2θ ∂2V ∂φ2 + 2 r ∂V ∂r + cos θ r2sin θ ∂V ∂θ = 1 r2 ∂ ∂r ! r2∂V ∂r " + 1 r2sin θ ∂ ∂θ ! sin θ∂V ∂θ " + 1 r2sin2θ ∂2V ∂φ2 (1.156) を得る.よって (1.138) 式を導けた.
補足2:Ledengre 多項式と球面調和関数
ここでは一般にポテンシャル V が方位角にも依存する場合を考える.変数分離形 V (r, θ, φ) = Y (θ, φ)R(r) (1.157) を仮定すると,角度関数 Y (θ, φ) は以下の角度方程式に従う. % 1 sin θ ∂ ∂θ ! sin θ ∂ ∂θ " + 1 sin2θ ∂2V ∂φ2 & Y (θ, φ) =−l(l + 1)Y (θ, φ) (1.158) の解を求めよう.角度関数に対してさらに変数分離形 Y (θ, φ) = Θ(θ)Φ(φ) (1.159) を仮定すると −Φ1 d 2Φ dφ2 = 1 Θsin θ d dθ ! sin θdΘ dθ " + l(l + 1) sin2θ (1.160)を得る.左辺は φ のみの関数,右辺は θ のみの関数であるから,両辺は定数でなければならない.この定数 を便宜的に(後に便利なように)m2をおこう.こうして,Φ と Θ に対する二つの方程式を得る. d2Φ dφ2 =−m 2Φ(φ) (1.161) 1 sin θ d dθ ! sin θdΘ dθ " + # l(l + 1)− m 2 sin2θ $ Θ = 0 (1.162) まず,Φ に対する解は容易に Φ(φ) = e±imφ (1.163) であることがわかる.ここで Φ が φ の一価関数であるためには
Φ(φ + 2pi) = Φ(φ)⇒ eim(φ+2π)= eim(φ) (1.164)
したがって m は整数でなければならない. m = 0,±1, ±2, · · · (1.165) 次に,Θ に対する解を求めるために変数を θ から z = cos θ に変換し Θ(θ) = P (cos θ) = P (z) (1.166) と記す.dz = − sin θdθ より P に対する微分方程式は d dz # (1− z2)dP dz $ + # l(l + 1)− m 2 1− z2 $ P = 0 (1.167) となる.この方程式は一般化された Legendre 方程式とよばれる.求める解が物理的に意味のある波動関数を 表すためには,解は −1 ≤ z ≤ 1 の範囲で有限で連続な一価関数でなければならない. まず最初に,簡単な場合として m = 0,つまり角度関数が方位角依存性を持たない場合を考えよう.この ときの P (z) に対する方程式 d dz # (1− z2)dP dz $ + l(l + 1)P = 0 (1.168) は Legendre 方程式とよばれる.ここで,解を次のベキ級数の形に仮定しよう. P (z) = zα ∞ % j=0 ajzj (1.169) これを Legendre 方程式 (1.168) に代入すると ∞ % j=0 & (α + j)(α + j− 1)ajzα+j−2− [(α + j)(α + j + 1) − l(l + 1)] ajzα+j'= 0 (1.170) を得る.これが |z| ≤ 1 のすべての z に対して成り立つためには z のべきの係数はそれぞれ全て 0 でなけれ ばならない.(べき級数の一意性) まず,zα−2, zα−1の係数が 0 の条件より α(α− 1)a0= 0 (1.171) (α + 1)αa1= 0 (1.172) を得る.上の二式は,以下のように書くこともできる. a0$= 0 であればα = 0 又はα = 1 (1.173) a1$= 0 であればα = 0 又はα = −1 (1.174)
また,一般の次数のべきについては aj+2= !(α + j)(α + j + 1) − l(l + 1) (α + j + 1)(α + j + 2) " aj (1.175) となる.少し考えれば,(1.173) と (1.174) は全く同等であり,a0か a1のどちらか一方が 0 でないように選 べばそれで十分であることがわかる.そこで,a0"= 0, a1= 0 であるとする.これより α については α = 0 又はα = 1 (1.176) を得る.このとき (1.175) 式より,べき級数解は α = 0 なら偶数べきだけを含み,α = 1 なら奇数べきだけ を含むことがわかる. α = 0, α = 1 のどちらの場合でも,べき級数は次の性質をもつことが証明できる. (i)l の値に関係なく,z2< 1 の場合にはべき級数は収束する. (ii) 有限級数でない場合には,z =±1 で級数は発散する. たとえば,l = 0, α = 1 とするとべき級数は P (z) = z + 1 3z 3+1 5z 5+ · · · (1.177) となる.(ただし a0= 1 とした.)この級数は関数 Q0(z) = 1 2ln 1 + z 1− z (1.178) のべき級数展開に等しく,明らかに z = ±1 で発散する.一般に l の値に対しても,級数が無限に続くときに は z = ±1 で対数的な発散があることを示すことができる.以上より,|z| ≤ 1 の領域で有限な解を得るため にはべき級数が有限個で終わることが要求される.そのためには,(1.175) 式の分子がある j = jmaxで 0 に なる必要がある.つまり, (α + jmax)(α + jmax+ 1) = l(l + 1) (1.179) であれば良い.このとき j ≥ jmaxに対しては aj = 0 となる.α と jmaxは 0 か正の整数であるから,l が 0 か正の整数であるときのみ (1.179) 式は満たされる.また,α = 0 なら jmax= l,α = 1 なら jmax= l− 1 と なるが,いずれの場合も P (z) の最高次数の項は zlをもつ項となる. 以上のように求まった多項式は Legendre 多項式 Pl(z) とよばれる.最初の数個の Legendre 多項式の具体 的な表式を以下に示す. P0(z) = 1 P1(z) = z P2(z) = (3z2− 1)/2 P3(z) = (5z3− 3z)/2 P4(z) = (35z4− 30z2+ 3)/8 P5(z) = (63z5− 70z3+ 15z)/8 (1.180) 上式を見てもわかるように,Pl(z) は z の l 次の多項式である.また,l が偶数のときは偶数次の項のみを含 み,l が奇数のときは奇数次の項のみを含む.また,Pl(1) = 1 となるように規格化されている.Legendre 多 項式の一般的な表式として以下の Rodorigues の公式が知られている. Pl(z) = 1 2ll! # d dz $l (z2 − 1)l (1.181) (1.181) 式の因子 (1/2ll!) は P l(1) = 1 となるための規格化因子である. Legendre 多項式 Pl(z) は−1 ≤ z ≤ 1 で完全直交系を作る.直交関係は % 1 −1 Pl(z)Pl!(z)dx = % π 0
Pl(cos θ)Pl!(cos θ) sin θdθ = 2
で与えられる. 角度関数が方位角依存性を持つ場合は,一般の m != 0 に対して一般化された Legendre 方程式 (1.167) の 解を求める必要がある.詳細は省略するが,Legendre 方程式 (m = 0) の場合と同様に,区間 −1 ≤ n ≤ 1 で 解が有限であるためにはパラメータ l, m は以下の条件を満たさなければならないことが示される. (1)l は 0 または正の整数であること. (2)m は−l, −l + 1, · · · , 0, · · · , l − 1, l の値のみを取り得ること. このような性質を持つ解を Legendre 陪多項式 Pm l (z) という.m > 0 の場合,この関数は Plm(z) = (−1)m(1− z2)m/2 dm dzmPl(z) = (−1)m 2ll! (1− z 2)m/2 dl+m dzl+m(z 2 − 1)l (1.183) によって定義される.微分方程式 (1.167) は m2だけに依存し,整数 m の符号にはよらないので Pm l (z) = Pl−m(z) である. 与えられた m に対して Legendre 陪多項式は直交系を作る.直交関係は以下で与えられる. ! 1 −1 Plm(z)Plm! (z)dz = 2 2l + 1 (l + m)! (l− m)!δll! (1.184) 以上をまとめると,規格化された角度関数は Ylm(θ, φ) = (−1)(m+|m|)/2 "
(2l + 1)(l− |m|)!4π(l + |m|)!Pl|m|(cos θ)eimφ (1.185) となる.ここで l = 0, 1, 2,· · · , m =−l, −l + 1, · · · , l − 1, l (1.186) である.この関数 Ymlを球面調和関数という.球面調和関数は以下の正規直交条件を満たす. ! π 0 sin θdθ ! 2π 0 dφYl∗!m!(θ, φ)Ylm(θ, φ) = δll!δmm! (1.187) 以下に l = 0, 1, 2 の球面調和関数の具体的表式を示す. l = 0 : Y00= 1 √ 4π l = 1 : Y1±1=∓ # 3 8πsin θe ±iφ, Y 10= # 3 4πcos θ l = 2 : Y2±2= # 15 32π sin 2θe±2iφ, Y 2±1= # 15
8πsin θ cos θe ±iφ Y20= # 5 16π(3 cos 2θ − 1) (1.188)